A Hyper-Pseudoelastic Model of Cyclic Stress-Softening Effect for Rubber Composites
Abstract
:1. Introduction
2. Basic Laws of Stress-Softening Effect
- (1)
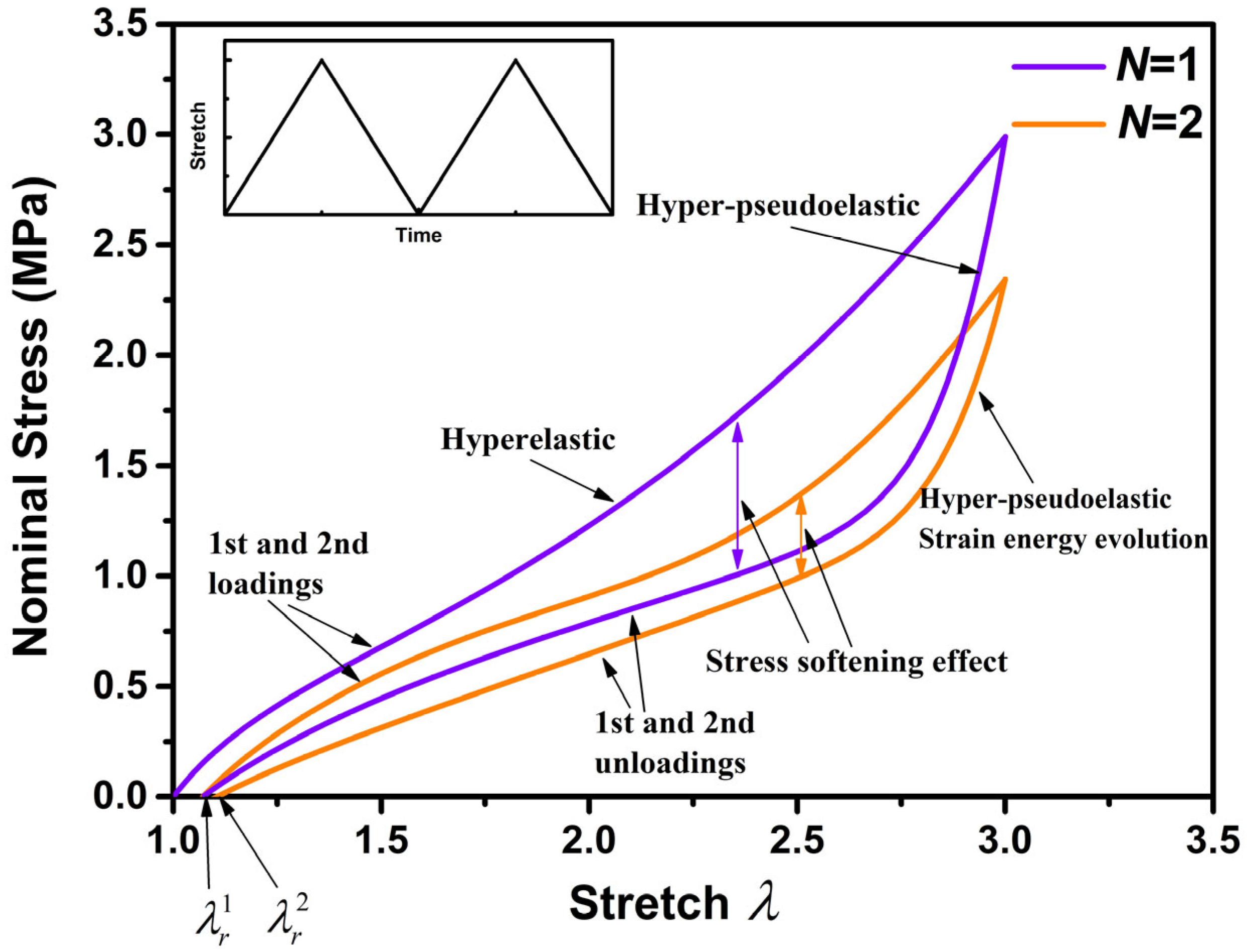
- The area enclosed by the loading–unloading curve gradually decreases with the increase of the cyclic loading–unloading order.
- (2)
- In the presence of residual deformation, a negative load must be applied to completely restore the rubber composites to a non-deformed state; that is, the unloading nominal stress is less than 0 when the principal stretch equals 1. In addition, the residual deformation increases with the increase of the loading–unloading order, and the residual deformation of the rubber composites mainly occurs during the first loading–unloading process.
- (3)
- The nominal stress difference corresponding to the previous loading–unloading curve is greater than that corresponding to the subsequent loading–unloading curve under the same stretch, which actually confirms the basic law (1).
- (4)
- The previous loading curves are always above the subsequent loading curves, and the unloading curves also have the same feature. And there is an intersection point between the previous unloading curve and the subsequent loading curve.
- (5)
- When the maximum stretch amplitude remains unchanged, the stress-softening effect corresponding to the first loading–unloading process is the most obvious. After several loading–unloading, the stress response tends to be stable. A similar phenomenon was also observed by Dorfmann et al. [18], Simo [33], and Sasso et al. [38].
- (6)
- Compared with 20 phr filled rubber composite, 60 phr filled rubber composite has a more obvious stress-softening effect, which indicates that the stress-softening effect is more significant with the increase of filler content in rubber composites.
3. Hyper-Pseudoelastic Model of Cyclic Stress-Softening Effect
3.1. No Residual Deformation Effect
3.2. Residual Deformation Effect
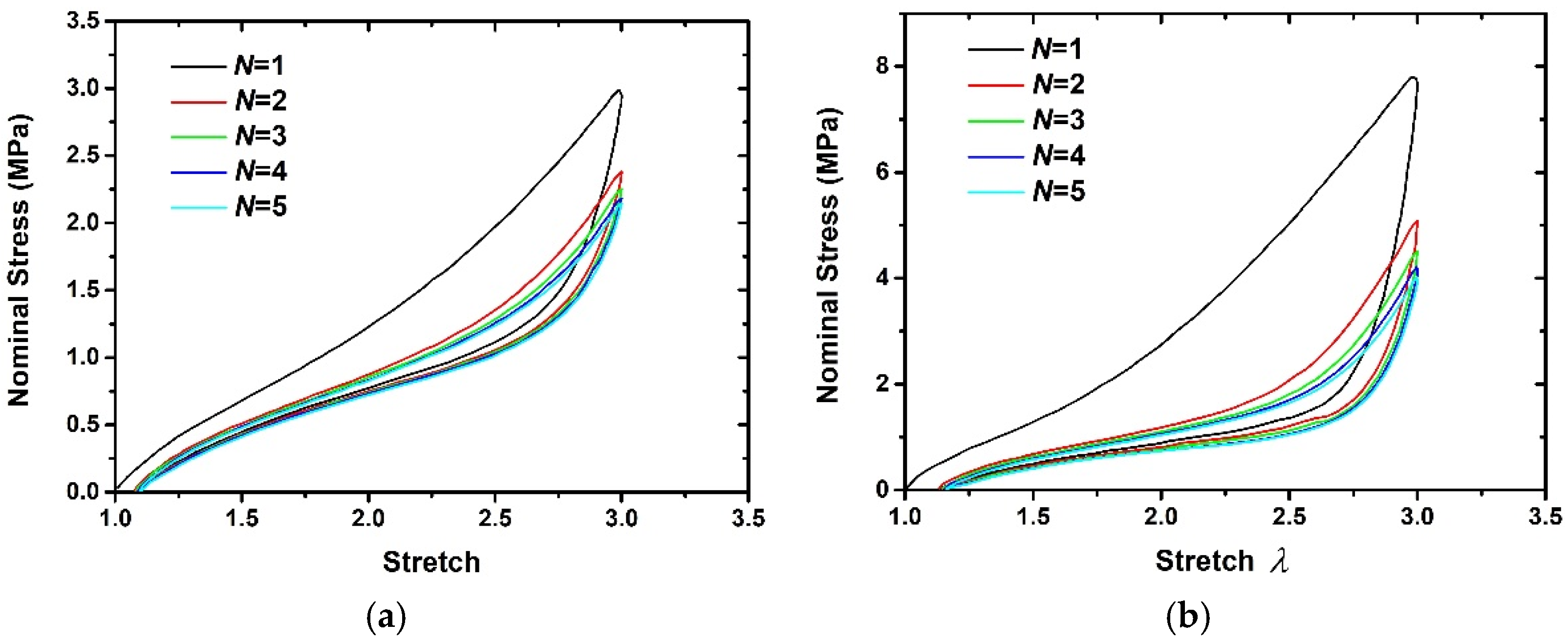
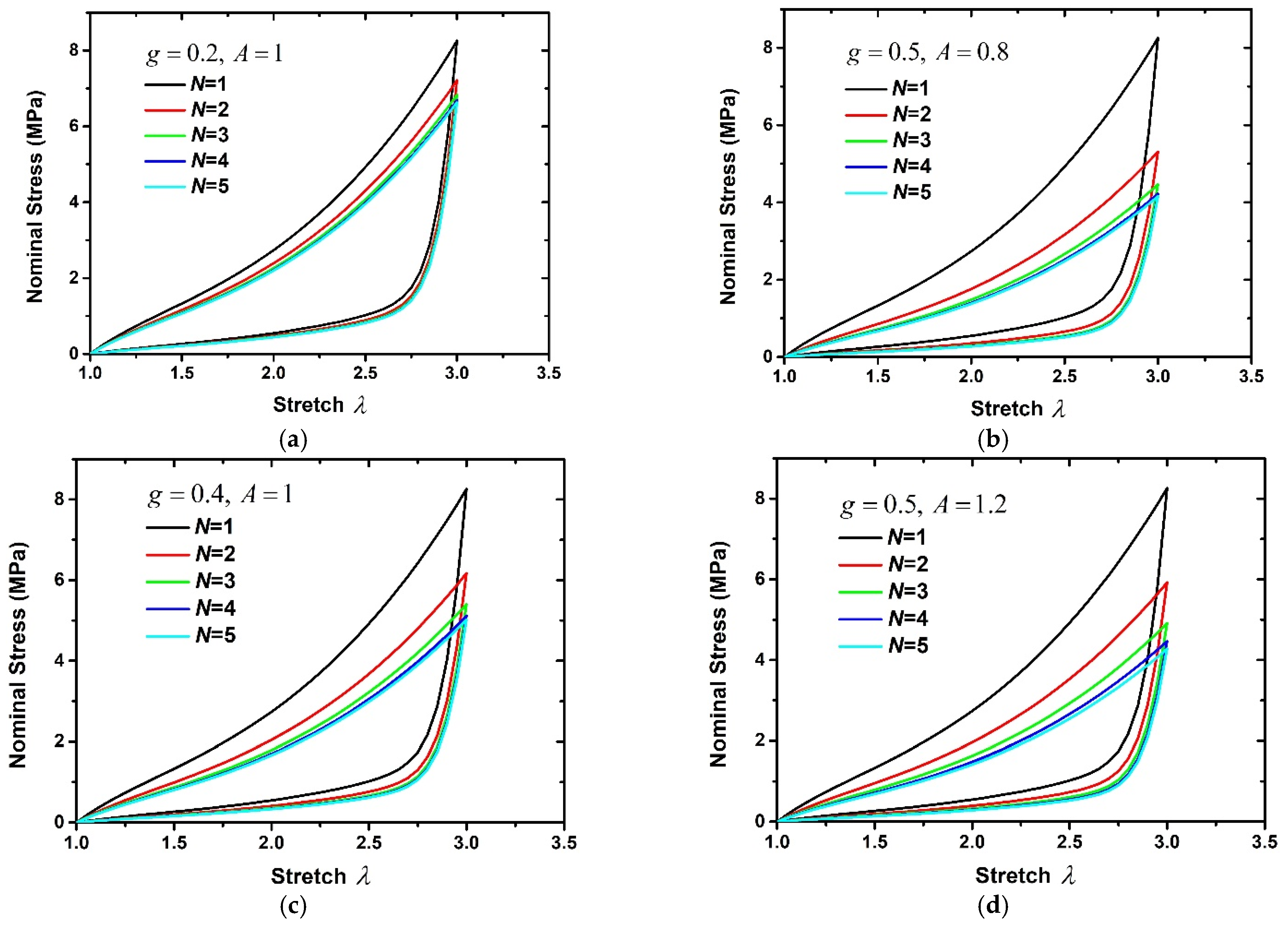
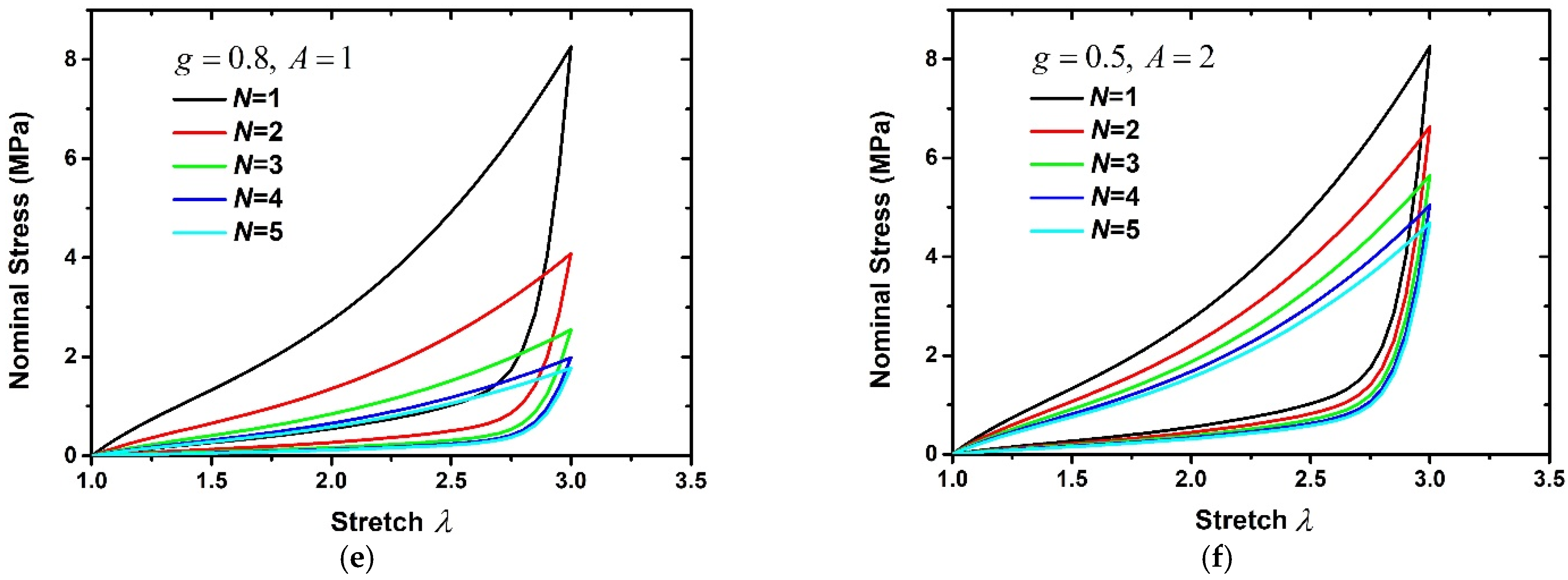
4. Results and Discussion
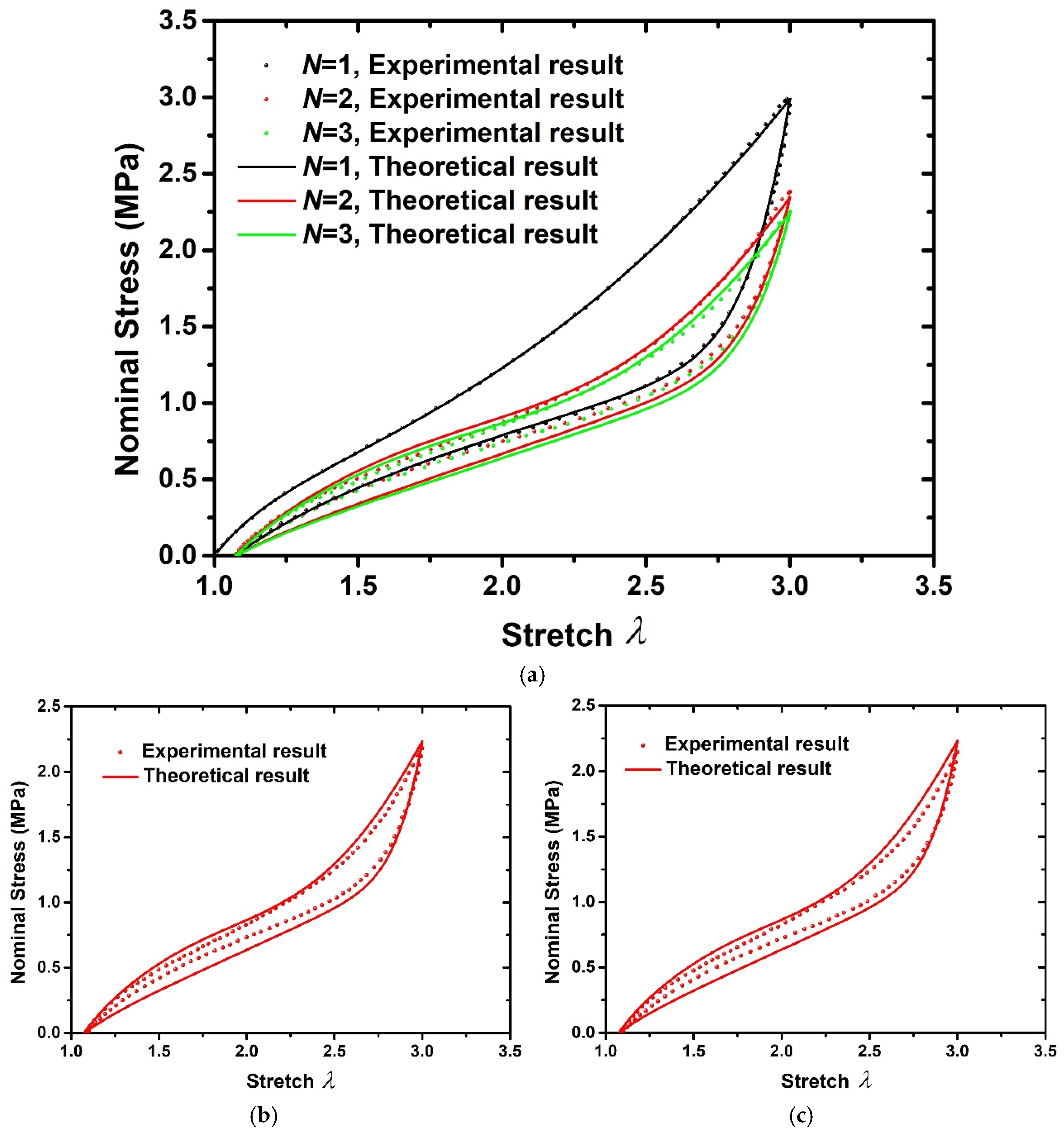
4.1. No Residual Deformation Effect
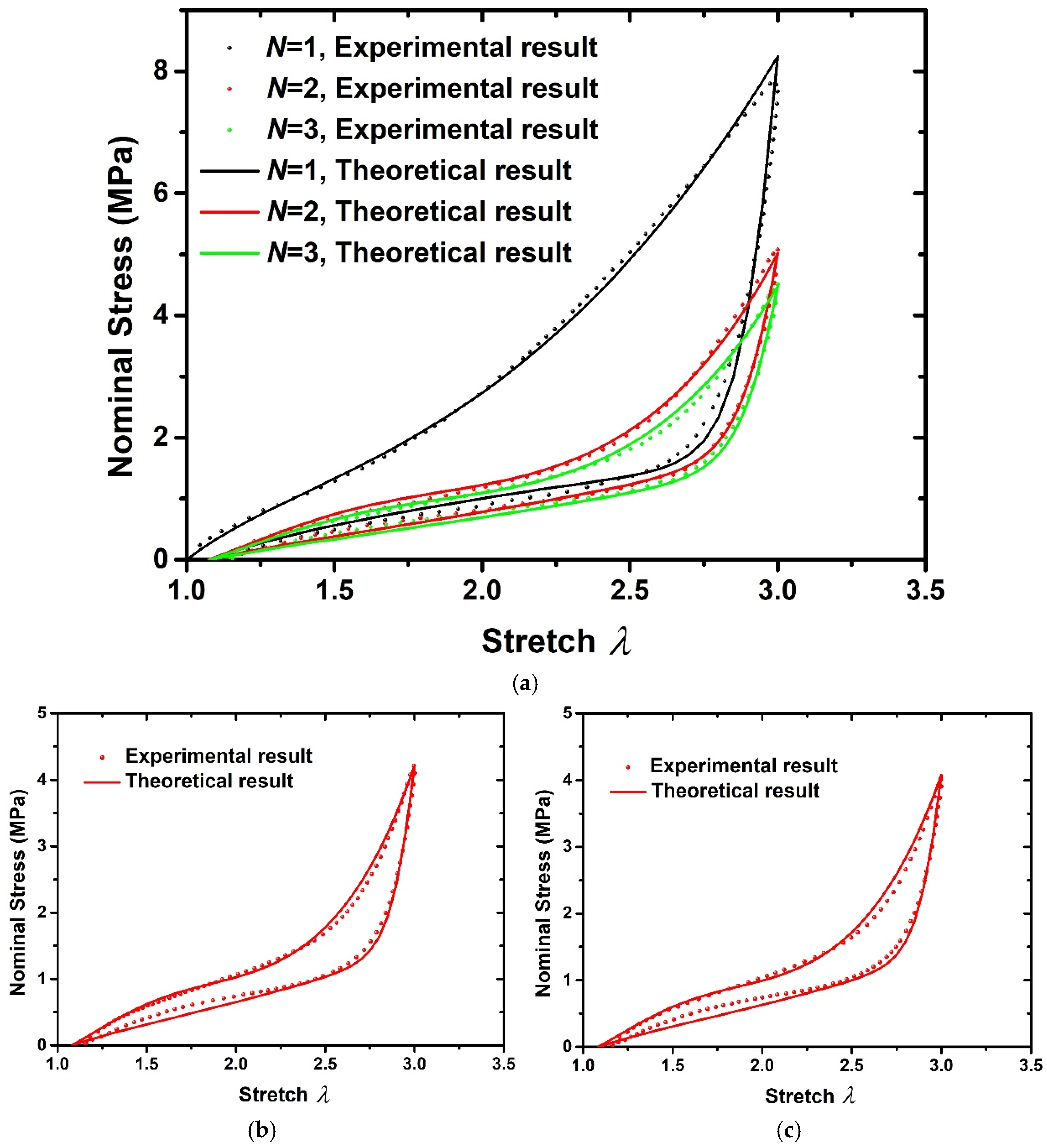
4.2. Residual Deformation Effect
5. Conclusions
- (1)
- A detailed analysis of the cyclic loading–unloading experimental results of rubber composites has been carried out. The basic laws of stress-softening effect are summarized to guide the derivation of the hyper-pseudoelastic model. It can be found that the stress-softening effect and residual deformation of rubber composites corresponding to different loading–unloading orders are different, especially the nominal stress–stretch curves of initial loading–unloading and subsequent loading–unloading are significantly different.
- (2)
- The hyper-pseudoelastic model in the cyclic loading–unloading process is proposed, in which a strain energy evolution function similar to (1-D) in continuum damage mechanics is introduced to characterize the cyclic stress-softening effect. The specific expressions of the strain energy evolution function with or without residual deformation effect are given, and the constraints that the strain energy evolution function needs to satisfy are also obtained based on the basic laws of the stress-softening effect. The hyper-pseudoelastic model establishes the theoretical relationship between strain energy and cyclic loading–unloading order directly, which provides great convenience in deriving the stress response corresponding to arbitrary loading–unloading order.
- (3)
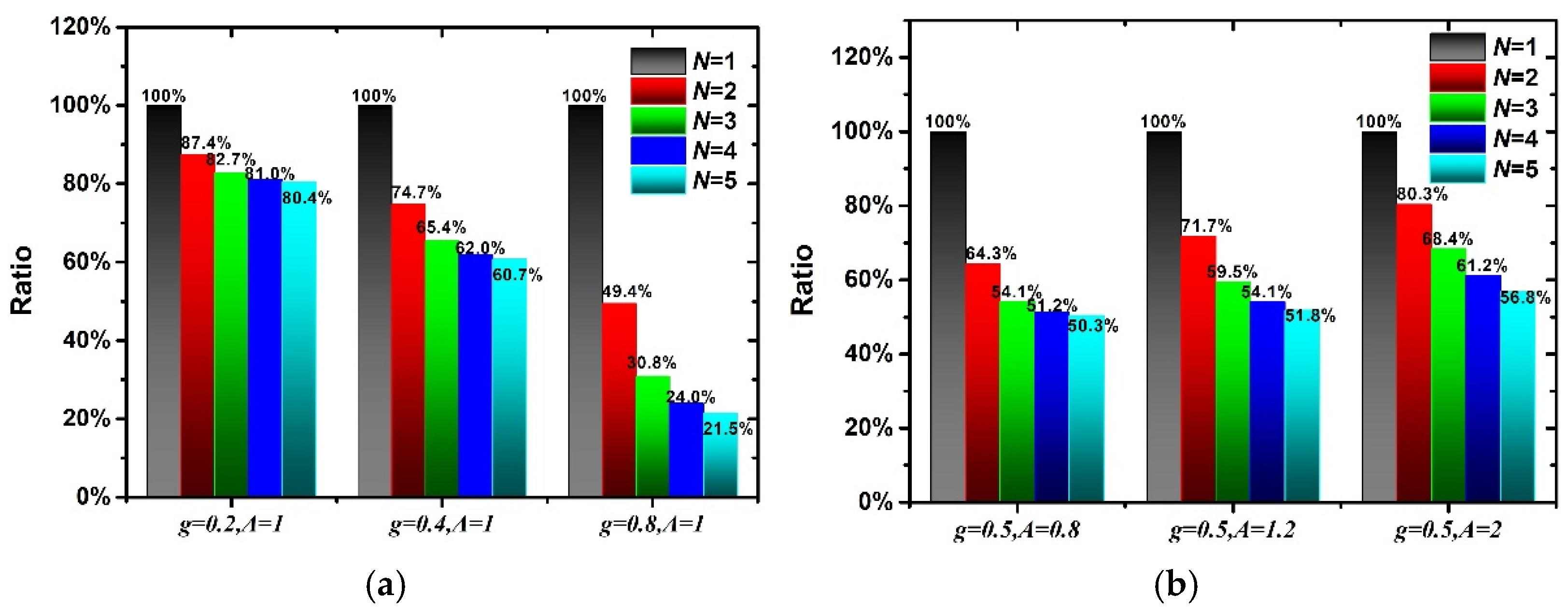
- The influences of the material parameters on the cyclic loading–unloading curve are discussed. The research results show that g mainly controls the degree of stress softening of rubber composites, while A mainly plays a role in fine-tuning the stress–stretch curve. Additionally, the dissipation energy is larger when g is smaller, or A is larger corresponding to the same loading–unloading order.
- (4)
- Based on the nominal stress–stretch experimental results of cyclic loading–unloading processes, the calibration method of material parameters and specific expression of strain energy evolution function with residual deformation effect are obtained. Further, the hyper-pseudoelastic model is verified by comparing the theoretical results with experimental results. The proposed model can predict the cyclic stress-softening effect of rubber composites with different filler contents effectively.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mullins, L.; Tobin, N.R. Theoretical model for the elastic behavior of filler-reinforced vulcanized rubbers. Rubber Chem. Technol. 1957, 30, 555–571. [Google Scholar] [CrossRef]
- Danilova, S.N.; Yarusova, S.B.; Kulchin, Y.N.; Zhevtun, I.G.; Buravlev, I.Y.; Okhlopkova, A.A.; Gordienko, P.S.; Subbotin, E.P. UHMWPE/CaSiO3 nanocomposite: Mechanical and tribological properties. Polymers 2021, 13, 570. [Google Scholar] [CrossRef] [PubMed]
- Danilova, S.N.; Yarusova, S.B.; Lazareva, N.N.; Buravlev, I.Y.; Shichalin, O.O.; Papynov, E.K.; Zhevtun, I.G.; Gordienko, P.S.; Okhlopkova, A.A. A study of the wear mechanism of composites modified with silicate filler. Ceramics 2022, 5, 731–747. [Google Scholar] [CrossRef]
- Dong, Y.; Ke, Y.; Zheng, Z.; Yang, H.; Yao, X. Effect of stress relaxation on sealing performance of the fabric rubber seal. Compos. Sci. Technol. 2017, 151, 291–301. [Google Scholar] [CrossRef]
- Dong, Y.; Yang, H.; Yan, H.; Yao, X. Design and characteristics of fabric rubber sealing based on microchannel model. Compos. Struct. 2019, 229, 111463. [Google Scholar] [CrossRef]
- Dorfmann, A.; Ogden, R.W. A constitutive model for the Mullins effect with permanent set in particle-reinforced rubber. Int. J. Solids Struct. 2004, 41, 1855–1878. [Google Scholar] [CrossRef]
- Dargazany, R.; Itskov, M. A network evolution model for the anisotropic Mullins effect in carbon black filled rubbers. Int. J. Solids Struct. 2009, 46, 2967–2977. [Google Scholar] [CrossRef] [Green Version]
- Rault, J.; Marchal, J.; Judeinstein, P.; Albouy, P. Stress-induced crystallization and reinforcement in filled natural rubbers: 2H NMR study. Macromolecules 2006, 39, 8356–8368. [Google Scholar] [CrossRef]
- Horgan, C.; Ogden, R.W.; Saccomandi, G. A theory of stress softening of elastomers based on finite chain extensibility. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2004, 460, 1737–1754. [Google Scholar] [CrossRef]
- Mullins, L. Effect of stretching on the properties of rubber. Rubber Chem. Technol. 1948, 21, 281–300. [Google Scholar] [CrossRef]
- Mullins, L. Softening of rubber by deformation. Rubber Chem. Technol. 1969, 42, 339–362. [Google Scholar] [CrossRef]
- Marckmann, G.; Verron, E.; Gornet, L.; Chagnon, G.; Charrier, P.; Fort, P. A theory of network alteration for the Mullins effect. J. Mech. Phys. Solids 2002, 50, 2011–2028. [Google Scholar] [CrossRef] [Green Version]
- Xiang, Y.; Zhong, D.; Rudykh, S.; Zhou, H.; Qu, S.; Yang, W. A review of physically based and thermodynamically based constitutive models for soft materials. J. Appl. Mech. 2020, 87, 110801. [Google Scholar] [CrossRef]
- Zhao, X. A theory for large deformation and damage of interpenetrating polymer networks. J. Mech. Phys. Solids 2012, 60, 319–332. [Google Scholar] [CrossRef]
- Bergström, J.; Boyce, M. Constitutive modeling of the large strain time-dependent behavior of elastomers. J. Mech. Phys. Solids 1998, 46, 931–954. [Google Scholar] [CrossRef]
- Vandenbroucke, A.; Laurent, H.; Aït Hocine, N.; Rio, G. A Hyperelasto-Visco-Hysteresis model for an elastomeric behaviour: Experimental and numerical investigations. Comp. Mater. Sci. 2010, 48, 495–503. [Google Scholar] [CrossRef]
- Beatty, M.F. The Mullins effect in a pure shear. J. Elast. 2000, 59, 369–392. [Google Scholar] [CrossRef]
- Dorfmann, A.; Pancheri, F. A constitutive model for the Mullins effect with changes in material symmetry. Int. J. Non-Linear Mech. 2012, 47, 874–887. [Google Scholar] [CrossRef]
- Wang, Z.; Tang, J.; Bai, R.; Zhang, W.; Lian, T.; Lu, T.; Wang, T. A phenomenological model for shakedown of tough hydrogels under cyclic loads. J. Appl. Mech. 2018, 85, 091005. [Google Scholar] [CrossRef]
- Bai, R.; Yang, Q.; Tang, J.; Morelle, X.P.; Vlassak, J.; Suo, Z. Fatigue fracture of tough hydrogels. Extrem. Mech. Lett. 2017, 15, 91–96. [Google Scholar] [CrossRef]
- Govindjee, S.; Simo, J. A micro-mechanically based continuum damage model for carbon black-filled rubbers incorporating Mullins effect. J. Mech. Phys. Solids 1991, 39, 87–112. [Google Scholar] [CrossRef]
- Göktepe, S.; Miehe, C. A micro-macro approach to rubber-like materials. Part III: The micro-sphere model of anisotropic Mullins-type damage. J. Mech. Phys. Solids 2005, 53, 2259–2283. [Google Scholar] [CrossRef]
- Cantourneta, S.; Desmorat, R.; Besson, J. Mullins effect and cyclic stress softening of filled elastomers by internal sliding and friction thermodynamics model. Int. J. Solids Struct. 2009, 46, 2255–2264. [Google Scholar] [CrossRef]
- Raghunath, R.; Juhre, D.; Klüppel, M. A physically motivated model for filled elastomers including strain rate and amplitude dependency in finite viscoelasticity. Int. J. Plast. 2016, 78, 223–241. [Google Scholar] [CrossRef]
- Zhong, D.; Xiang, Y.; Yin, T.; Yu, H.; Qu, S.; Yang, W. A physically-based damage model for soft elastomeric materials with anisotropic Mullins effect. Int. J. Solids Struct. 2019, 176–177, 121–134. [Google Scholar] [CrossRef]
- Zhu, P.; Zhong, Z. Constitutive modelling for the Mullins effect with permanent set and induced anisotropy in particle-filled rubbers. Appl. Math. Model. 2021, 97, 19–35. [Google Scholar] [CrossRef]
- Qian, D.; Meng, F. Modelling Mullins effect induced by chain delamination and reattachment. Polymer 2021, 222, 123608. [Google Scholar] [CrossRef]
- Beatty, M.F.; Krishnaswamy, S. A theory of stress-softening in incompressible isotropic materials. J. Mech. Phys. Solids 2000, 48, 1931–1965. [Google Scholar] [CrossRef]
- Miehe, C.; Göktepe, S.; Lulei, F. A micro-macro approach to rubber-like materials-Part I: The non-affine micro-sphere model of rubber elasticity. J. Mech. Phys. Solids 2004, 52, 2617–2660. [Google Scholar] [CrossRef]
- Ayoub, G.; Zaïri, F.; Naït-Abdelaziz, M.; Gloaguen, J.M.; Kridli, G. A visco-hyperelastic damage model for cyclic stress-softening, hysteresis and permanent set in rubber using the network alteration theory. Int. J. Plast. 2014, 54, 19–33. [Google Scholar] [CrossRef]
- Mullins, L.; Tobin, N.R. Stress softening in rubber vulcanizates. Part I. Use of a strain amplification factor to describe the elastic behavior of filler-reinforced vulcanized rubber. J. Appl. Polym. Sci. 1965, 9, 2993–3009. [Google Scholar] [CrossRef]
- Lu, T.; Wang, J.; Yang, R.; Wang, T. A constitutive model for soft materials incorporating viscoelasticity and Mullins effect. J. Appl. Mech. 2017, 84, 021010. [Google Scholar] [CrossRef]
- Simo, J.C. On a fully three-dimensional finite-strain viscoelastic damage model: Formulation and computational aspects. Comput. Methods Appl. Mech. Eng. 1987, 60, 153–173. [Google Scholar] [CrossRef]
- Dassault Systemes SIMULIA Corp. Abaqus Analysis User’s Manual Version 6.14; Dassault Systemes SIMULIA Corp: Providence, RI, USA, 2014. [Google Scholar]
- Dorfmann, A.; Ogden, R.W. A pseudo-elastic model for loading, partial unloading and reloading of particle-reinforced rubber. Int. J. Solids Struct. 2003, 40, 2699–2714. [Google Scholar] [CrossRef]
- Fazekas, B.; Goda, T.J. Closed-form and numerical stress solution-based parameter identification for incompressible hyper-viscoelastic solids subjected to various loading modes. Int. J. Mech. Sci. 2019, 151, 650–660. [Google Scholar] [CrossRef]
- Fazekas, B.; Goda, T.J. New numerical stress solutions to calibrate hyper-visco-pseudo-elastic material models effectively. Mater. Des. 2020, 194, 108861. [Google Scholar] [CrossRef]
- Sasso, M.; Chiappini, G.; Rossi, M.; Cortese, L.; Mancini, E. Visco-Hyper-Pseudo-Elastic characterization of a Fluoro-Silicone rubber. Exp. Mech. 2014, 54, 315–328. [Google Scholar] [CrossRef]
- Ogden, R.W.; Roxburgh, D.G. A pseudo-elastic model for the Mullins effect in filled rubber. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1999, 455, 2861–2877. [Google Scholar] [CrossRef]
- Ogden, R.W.; Roxburgh, D.G. An energy-based model of the Mullins effect. In Proceedings of the First European Conference on Constitutive Models for Rubber, Vienna, Austria, 9–10 September 1999; pp. 23–28. [Google Scholar]
- Ogden, R.W. Large deformation isotropic elasticity-on the correlation of theory and experiment for incompressible rubberlike solids. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1972, 326, 565–584. [Google Scholar] [CrossRef]
- Ogden, R.W. Large deformation isotropic elasticity: On the correlation of theory and experiment for compressible rubberlike solids. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1972, 328, 567–583. [Google Scholar] [CrossRef]
- Zhang, Y. Solving large-scale linear programs by interior-point methods under the Matlab Environment. Optim. Methods Softw. 1998, 10, 1–31. [Google Scholar] [CrossRef]

| 20 phr | Hyperelastic material parameters | |||||
| 0.05 | 4.221 | −0.815 | −0.156 | −0.286 | −4.63 | |
| Pseudoelastic material parameters | ||||||
| 0.491 | 0.596 | 0.963 | 0.753 | 0.438 | 1.952 | |
| 60 phr | Hyperelastic material parameters | |||||
| −1.528 | −1.011 | 0.223 | 4.205 | −1.134 × 10−3 | −4.399 | |
| Pseudoelastic material parameters | ||||||
| 0.354 | 0.496 | 1.25 | 0.965 | 0.3 | 0.16 | |
| 20 phr | ||||||
| 0.466 | 0.343 | −0.011 | 0.028 | −0.085 | −0.136 | |
| 0.468 | −0.526 | −7.003 | 2.46 | −0.375 | ||
| 60 phr | ||||||
| 0.34 | 1.33 | −0.08 | 0.104 | −0.173 | 0.375 | |
| 0 | 0.479 | −3.688 | 5.479 | 8.99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, Y.; Fu, Y.; He, C.; Fang, D. A Hyper-Pseudoelastic Model of Cyclic Stress-Softening Effect for Rubber Composites. Polymers 2023, 15, 3033. https://doi.org/10.3390/polym15143033
Dong Y, Fu Y, He C, Fang D. A Hyper-Pseudoelastic Model of Cyclic Stress-Softening Effect for Rubber Composites. Polymers. 2023; 15(14):3033. https://doi.org/10.3390/polym15143033
Chicago/Turabian StyleDong, Yifeng, Yutong Fu, Chunwang He, and Daining Fang. 2023. "A Hyper-Pseudoelastic Model of Cyclic Stress-Softening Effect for Rubber Composites" Polymers 15, no. 14: 3033. https://doi.org/10.3390/polym15143033






