Effects of Slit Edge Notches on Mechanical Properties of 3D-Printed PA12 Nylon Kirigami Specimens
Abstract
:1. Introduction
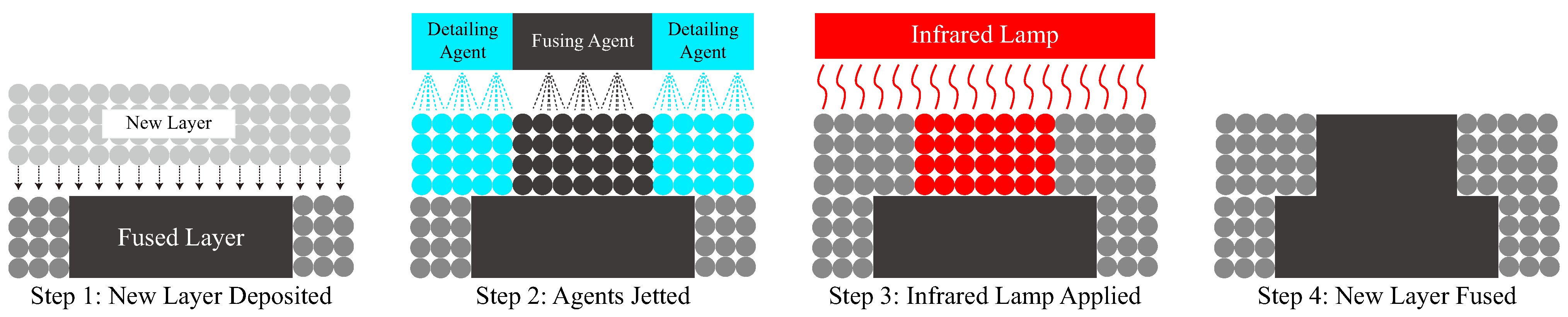
2. Design and Fabrication of Kirigami Samples
3. Experimental Setup
3.1. Experimental Setup for the Tensile Test of Kirigami-Inspired Samples
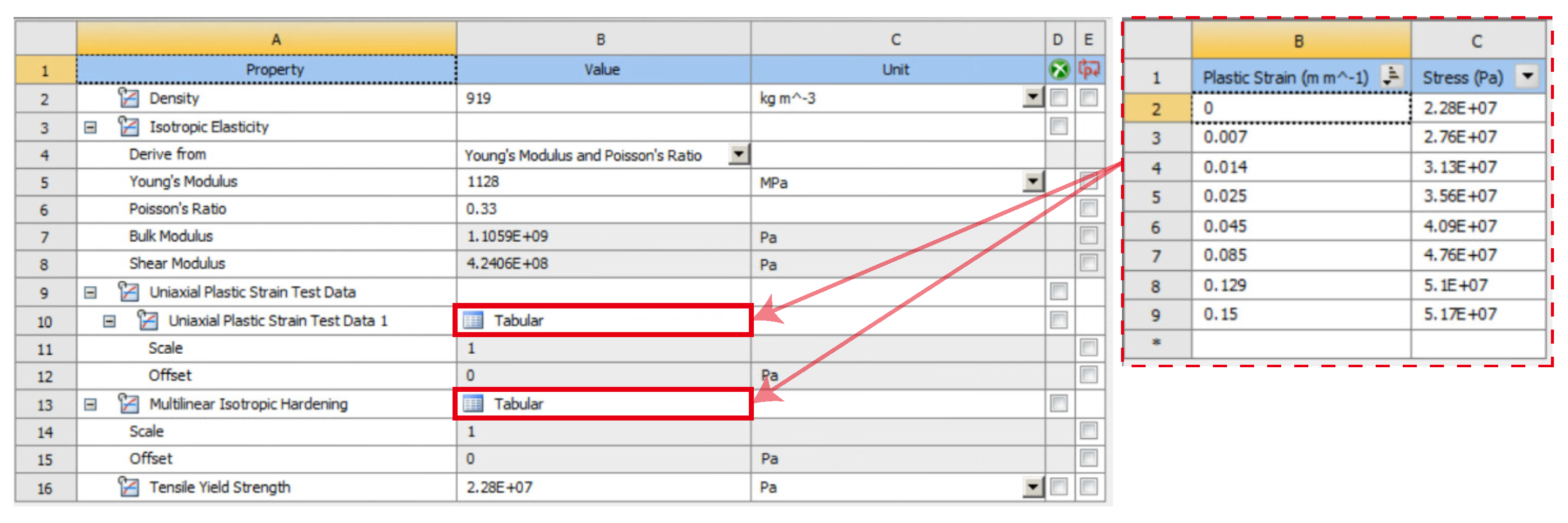
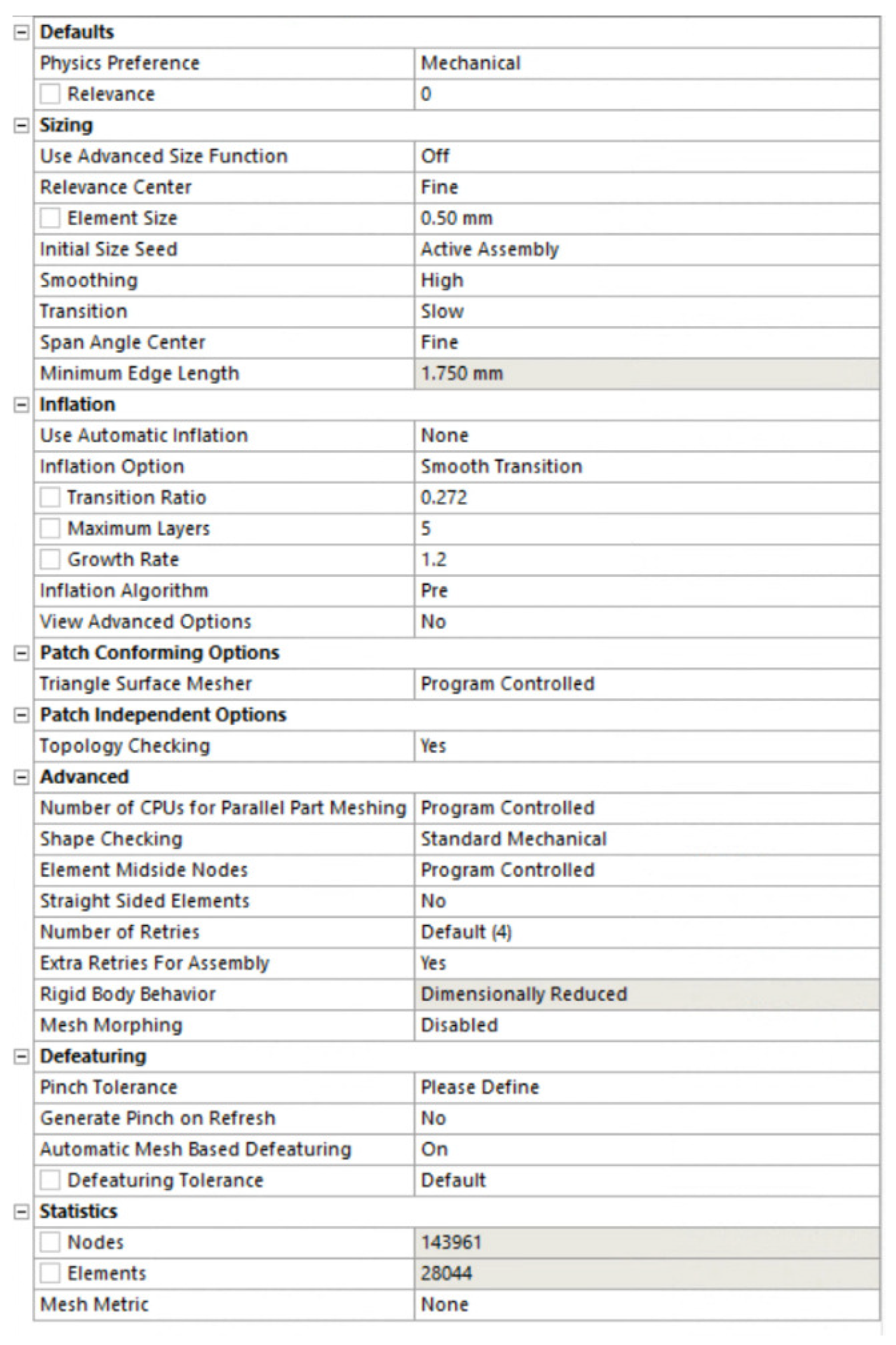
3.2. Experimental Setup for Finite Element Analysis (FEA)
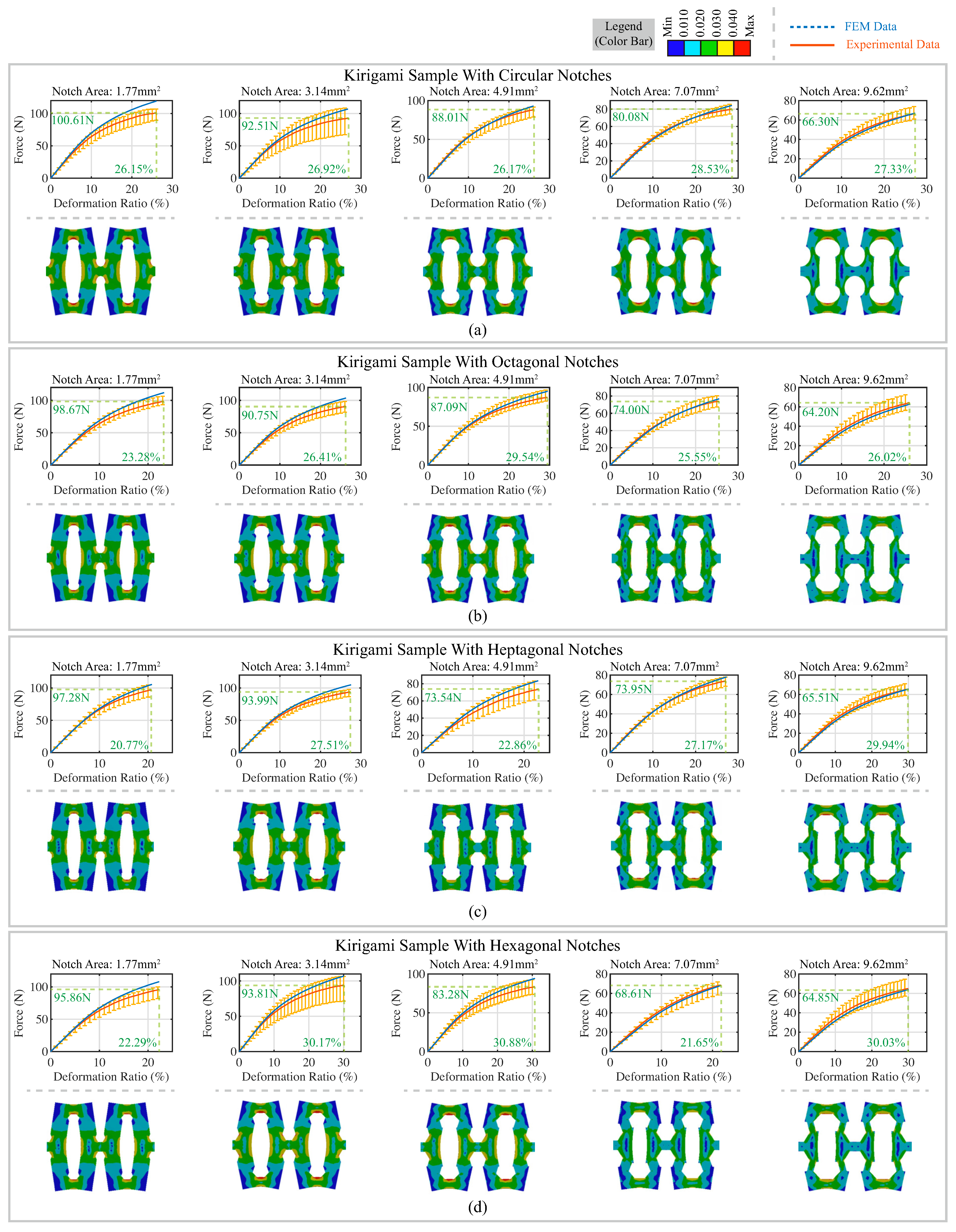
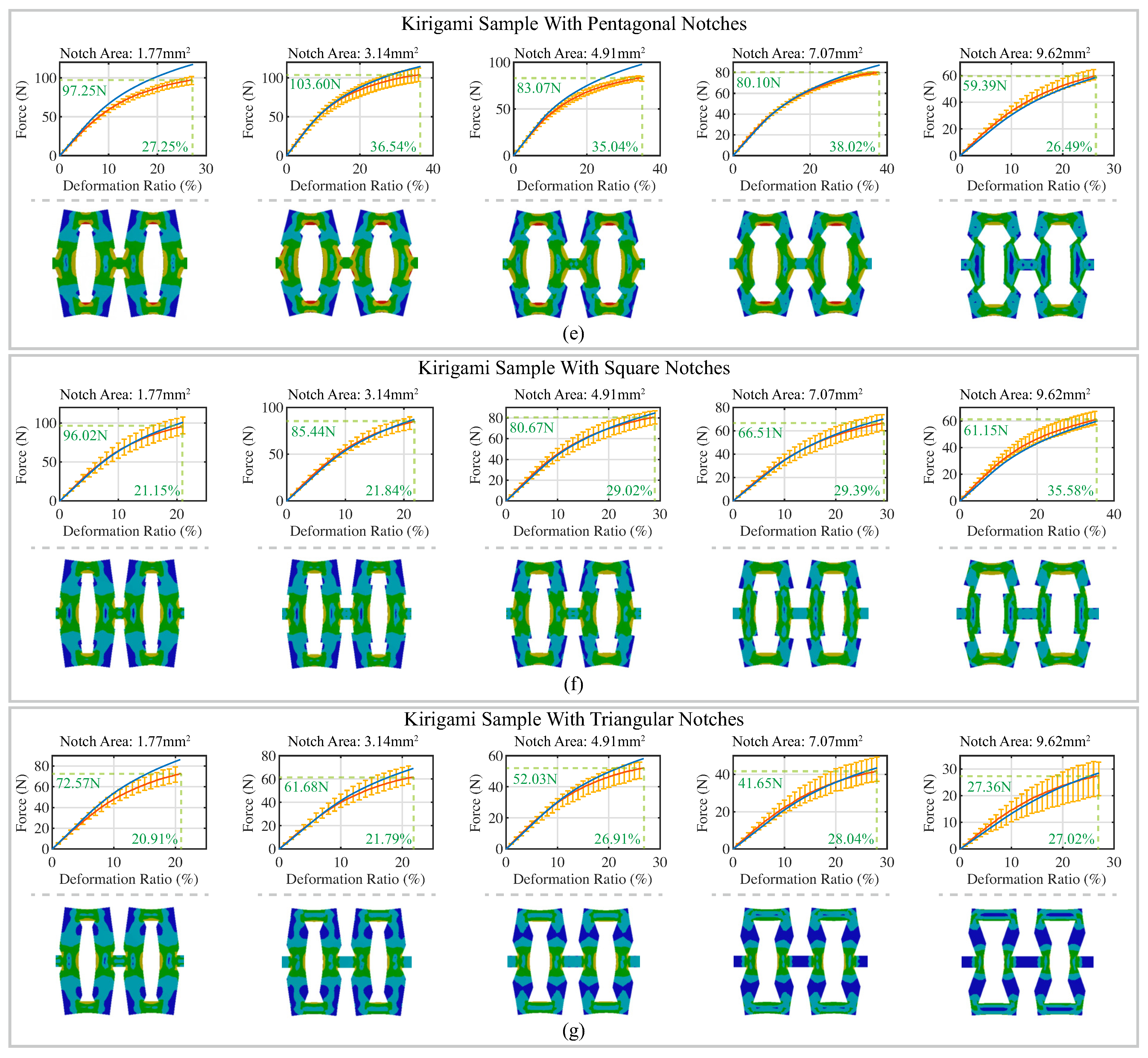
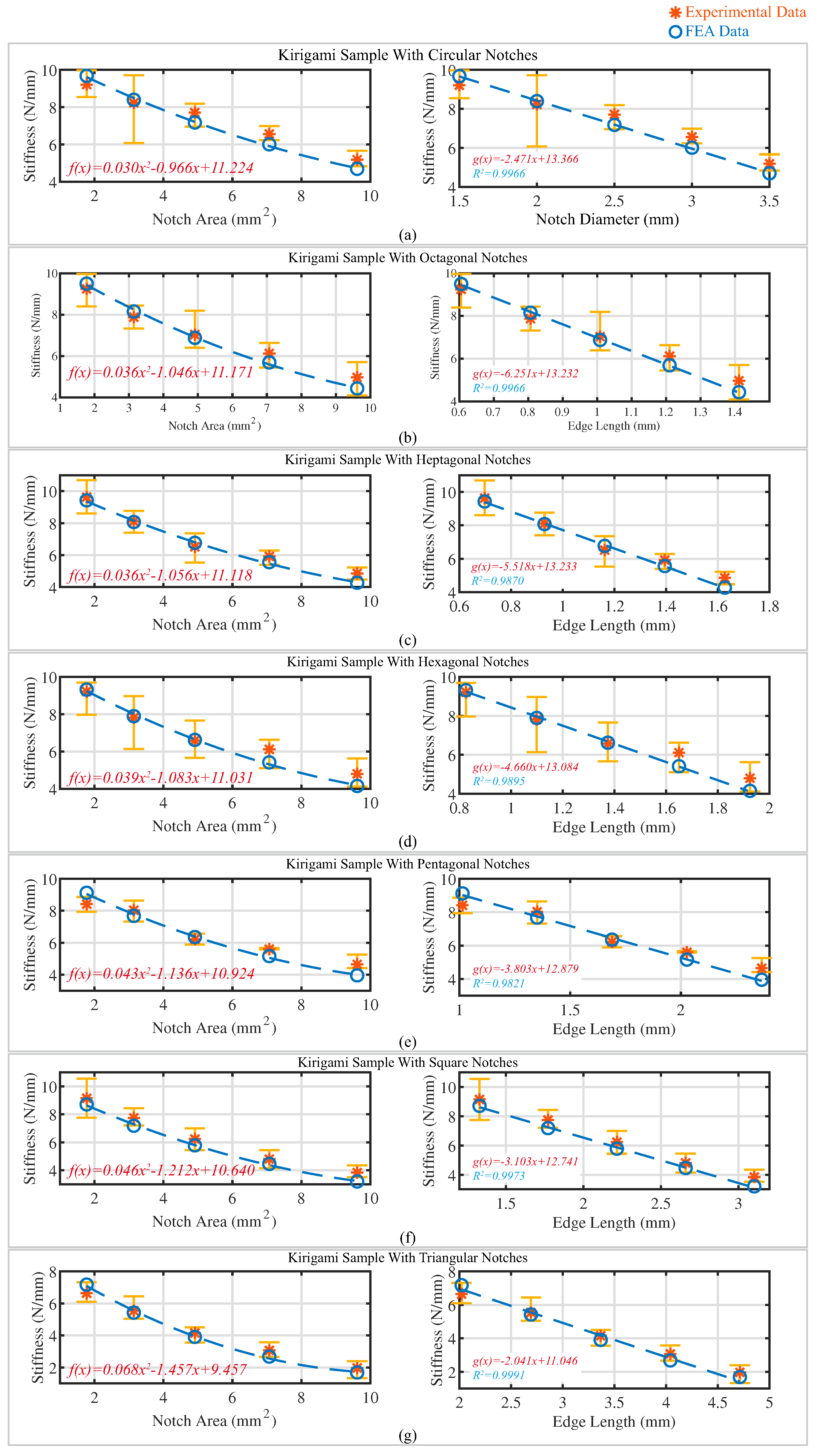
4. Experimental Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FEA | finite element analysis |
| MJF | multi-jet fusion |
| FFF | fused filament fabrication |
| PBF | powder bed fusion |
| SLS | selective laser sintering |
| TPU | Thermoplastic Polyurethane |
| PA | polyamide |
| CAD | computer-aided design |
| DAQ | data acquisition |
| ISO | International Organization for Standardization |
| ASTM | American Society for Testing and Materials |
Appendix A. Additional Finite Element Analysis Data
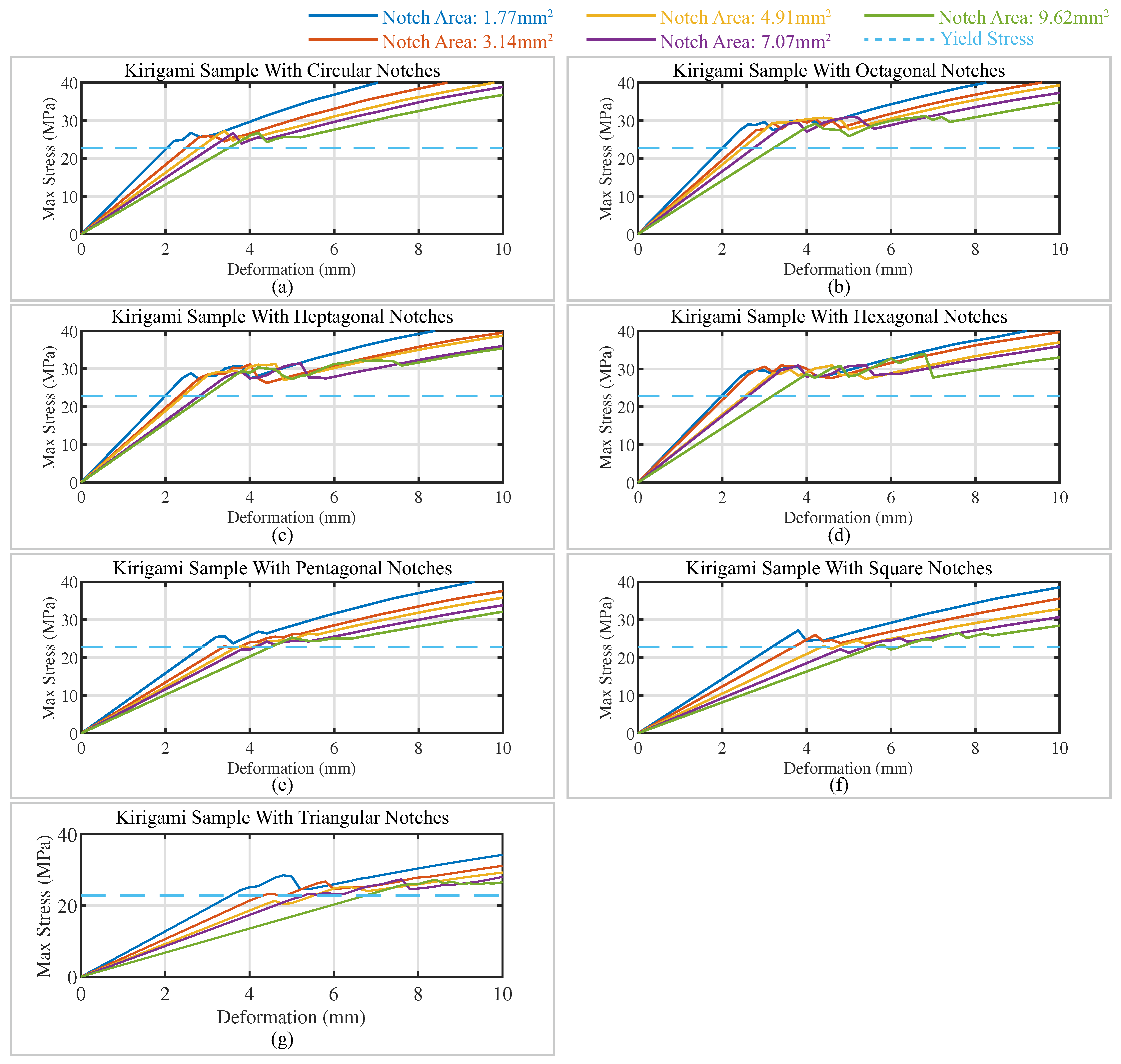
| Notch Area (mm2) | 1.77 | 3.14 | 4.91 | 7.07 | 9.62 | ||
|---|---|---|---|---|---|---|---|
| Yield Deformation (mm) | |||||||
| Notch Shape | |||||||
| Circle | 2.04 | 2.49 | 2.81 | 3.07 | 3.50 | ||
| Octagon | 2.01 | 2.33 | 2.49 | 2.75 | 3.22 | ||
| Heptagon | 1.99 | 2.32 | 2.41 | 2.80 | 2.94 | ||
| Hexagon | 1.98 | 2.09 | 2.54 | 2.60 | 3.18 | ||
| Pentagon | 2.87 | 3.38 | 3.74 | 4.14 | 4.50 | ||
| Square | 3.18 | 3.69 | 4.36 | 5.38 | 5.60 | ||
| Triangle | 3.56 | 4.33 | 5.52 | 5.29 | 6.75 | ||
| Notch Shape | Strain Energy U (mJ) (1.77 mm2) | Strain Energy U (mJ) (3.14 mm2) | Strain Energy U (mJ)(4.91 mm2) | Strain Energy U (mJ) (7.07 mm2) | Strain Energy U (mJ) (9.62 mm2) |
|---|---|---|---|---|---|
| Circle | 18.95 | 18.31 | 20.82 | 20.29 | 20.29 |
| Octagon | 18.60 | 17.80 | 19.97 | 19.23 | 19.16 |
| Heptagon | 18.45 | 17.62 | 19.65 | 18.80 | 18.46 |
| Hexagon | 18.24 | 17.23 | 19.23 | 18.30 | 17.95 |
| Pentagon | 17.82 | 16.72 | 18.43 | 17.43 | 17.11 |
| Square | 16.99 | 15.64 | 16.75 | 15.04 | 13.82 |
| Triangle | 14.00 | 11.80 | 11.33 | 9.06 | 7.30 |
Appendix B. Additional Information in Finite Element Analysis Setup
Appendix C. Finite Element Analysis Results of Slit Height-Reduced Kirigami Samples
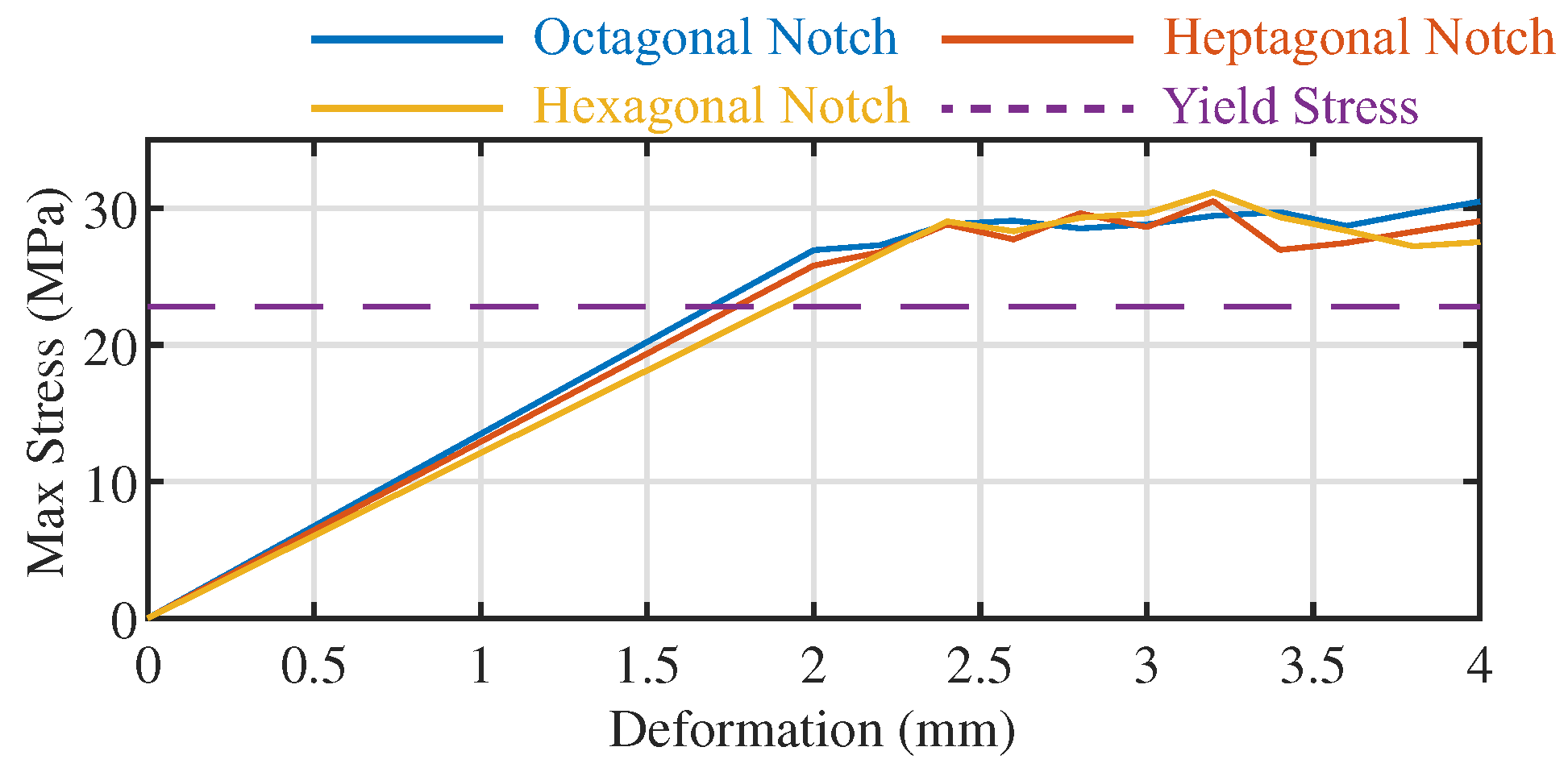
| Notch Shape | Yield Deformation (mm) | FEA Estimated Stiffness (N/mm) |
|---|---|---|
| Octagonal | 1.69 | 12.24 |
| Heptagonal | 1.77 | 12.17 |
| Hexagonal | 1.89 | 12.04 |
References
- Isobe, M.; Okumura, K. Initial rigid response and softening transition of highly stretchable kirigami sheet materials. Sci. Rep. 2016, 6, 24758. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hart, G.W. Modular kirigami. In Bridges Donostia: Mathematics, Music, Art, Architecture, Culture; Tarquin Publications: London, UK, 2007; pp. 1–8. [Google Scholar]
- Vella, D. Buffering by buckling as a route for elastic deformation. Nat. Rev. Phys. 2019, 1, 425–436. [Google Scholar] [CrossRef]
- Firouzeh, A.; Higashisaka, T.; Nagato, K.; Cho, K.; Paik, J. Stretchable kirigami components for composite meso-scale robots. IEEE Robot. Autom. Lett. 2020, 5, 1883–1890. [Google Scholar] [CrossRef]
- Suzuki, H.; Wood, R.J. Origami-inspired miniature manipulator for teleoperated microsurgery. Nat. Mach. Intell. 2020, 2, 437–446. [Google Scholar] [CrossRef]
- Rafsanjani, A.; Zhang, Y.; Liu, B.; Rubinstein, S.M.; Bertoldi, K. Kirigami skins make a simple soft actuator crawl. Sci. Robot. 2018, 3, eaar7555. [Google Scholar] [CrossRef]
- Sedal, A.; Memar, A.H.; Liu, T.; Mengüç, Y.; Corson, N. Design of deployable soft robots through plastic deformation of kirigami structures. IEEE Robot. Autom. Lett. 2020, 5, 2272–2279. [Google Scholar] [CrossRef]
- Cheng, Y.C.; Lu, H.C.; Lee, X.; Zeng, H.; Priimagi, A. Kirigami-based light-induced shape-morphing and locomotion. Adv. Mater. 2020, 32, 1906233. [Google Scholar] [CrossRef] [Green Version]
- Yang, D.; Wang, H.; Luo, S.; Wang, C.; Zhang, S.; Guo, S. Paper-cut flexible multifunctional electronics using MoS2 nanosheet. Nanomaterials 2019, 9, 922. [Google Scholar] [CrossRef] [Green Version]
- Yang, C.; Zhang, H.; Liu, Y.; Yu, Z.; Wei, X.; Hu, Y. Kirigami-Inspired Deformable 3D Structures Conformable to Curved Biological Surface. Adv. Sci. 2018, 5, 1801070. [Google Scholar] [CrossRef] [Green Version]
- Gao, B.; Elbaz, A.; He, Z.; Xie, Z.; Xu, H.; Liu, S.; Su, E.; Liu, H.; Gu, Z. Bioinspired kirigami fish-based highly stretched wearable biosensor for human biochemical–physiological hybrid monitoring. Adv. Mater. Technol. 2018, 3, 1700308. [Google Scholar] [CrossRef]
- Zhao, R.; Lin, S.; Yuk, H.; Zhao, X. Kirigami enhances film adhesion. Soft Matter 2018, 14, 2515–2525. [Google Scholar] [CrossRef] [PubMed]
- Shu, J.; Wang, J.; Lau, S.C.Y.; Su, Y.; Heung, K.H.L.; Shi, X.; Li, Z.; Tong, R.K.y. Soft Robots’ Dynamic Posture Perception Using Kirigami-Inspired Flexible Sensors with Porous Structures and Long Short-Term Memory (LSTM) Neural Networks. Sensors 2022, 22, 7705. [Google Scholar] [CrossRef] [PubMed]
- Shu, J.; Wang, J.; Su, Y.; Liu, H.; Li, Z.; Tong, R.K.Y. An End-to-end Posture Perception Method for Soft Bending Actuators Based on Kirigami-inspired Piezoresistive Sensors. In Proceedings of the 2022 IEEE-EMBS International Conference on Wearable and Implantable Body Sensor Networks (BSN), Ioannina, Greece, 27–30 September 2022; pp. 1–5. [Google Scholar]
- Yu, H.C.; Hao, X.P.; Zhang, C.W.; Zheng, S.Y.; Du, M.; Liang, S.; Wu, Z.L.; Zheng, Q. Engineering tough metallosupramolecular hydrogel films with kirigami structures for compliant soft electronics. Small 2021, 17, 2103836. [Google Scholar] [CrossRef] [PubMed]
- Cai, J.; Akbarzadeh, A. Hierarchical kirigami-inspired graphene and carbon nanotube metamaterials: Tunability of thermo-mechanic properties. Mater. Des. 2021, 206, 109811. [Google Scholar] [CrossRef]
- Ma, J.; Dai, H.; Chai, S.; Chen, Y. Energy absorption of sandwich structures with a kirigami-inspired pyramid foldcore under quasi-static compression and shear. Mater. Des. 2021, 206, 109808. [Google Scholar] [CrossRef]
- Ming, S.; Song, Z.; Li, T.; Du, K.; Zhou, C.; Wang, B. The energy absorption of thin-walled tubes designed by origami approach applied to the ends. Mater. Des. 2020, 192, 108725. [Google Scholar] [CrossRef]
- Niknam, H.; Sarvestani, H.Y.; Jakubinek, M.; Ashrafi, B.; Akbarzadeh, A. 3D printed accordion-like materials: A design route to achieve ultrastretchability. Addit. Manuf. 2020, 34, 101215. [Google Scholar] [CrossRef]
- Bobbert, F.; Janbaz, S.; van Manen, T.; Li, Y.; Zadpoor, A. Russian doll deployable meta-implants: Fusion of kirigami, origami, and multi-stability. Mater. Des. 2020, 191, 108624. [Google Scholar] [CrossRef]
- Lamoureux, A.; Lee, K.; Shlian, M.; Forrest, S.R.; Shtein, M. Dynamic kirigami structures for integrated solar tracking. Nat. Commun. 2015, 6, 8092. [Google Scholar] [CrossRef] [Green Version]
- Zhou, X.; Parida, K.; Halevi, O.; Liu, Y.; Xiong, J.; Magdassi, S.; Lee, P.S. All 3D-printed stretchable piezoelectric nanogenerator with non-protruding kirigami structure. Nano Energy 2020, 72, 104676. [Google Scholar] [CrossRef]
- Noroozi, R.; Arif, Z.U.; Taghvaei, H.; Khalid, M.Y.; Sahbafar, H.; Hadi, A.; Sadeghianmaryan, A.; Chen, X. 3D and 4D Bioprinting Technologies: A Game Changer for the Biomedical Sector? Ann. Biomed. Eng. 2023, 51, 1683–1712. [Google Scholar] [CrossRef] [PubMed]
- Khalid, M.Y.; Arif, Z.U.; Ahmed, W.; Umer, R.; Zolfagharian, A.; Bodaghi, M. 4D printing: Technological developments in robotics applications. Sens. Actuators A Phys. 2022, 343, 113670. [Google Scholar] [CrossRef]
- Hedayati, R.; Roudbarian, N.; Tahmasiyan, S.; Bodaghi, M. Gradient origami metamaterials for programming out-of-plane curvatures. Adv. Eng. Mater. 2023, 2201838. [Google Scholar] [CrossRef]
- Han, D.; Zhao, L.; Chen, S.; Wang, G.; Chan, K. Critical transitions in the shape morphing of kirigami metallic glass. J. Mater. Sci. Technol. 2021, 61, 204–212. [Google Scholar] [CrossRef]
- Nakajima, J.; Fayazbakhsh, K.; Teshima, Y. Experimental study on tensile properties of 3D printed flexible kirigami specimens. Addit. Manuf. 2020, 32, 101100. [Google Scholar] [CrossRef]
- Chen, S.; Chan, K.; Han, D.; Zhao, L.; Wu, F. Programmable super elastic kirigami metallic glasses. Mater. Des. 2019, 169, 107687. [Google Scholar] [CrossRef]
- Chen, K.; Yuan, M.; Zheng, H.; Chen, S. On the determination and optimization of apparent “elastic limit” of kirigami metallic glasses. Phys. B Condens. Matter 2021, 609, 412901. [Google Scholar] [CrossRef]
- Sun, R.; Zhang, B.; Yang, L.; Zhang, W.; Farrow, I.; Scarpa, F.; Rossiter, J. Kirigami stretchable strain sensors with enhanced piezoelectricity induced by topological electrodes. Appl. Phys. Lett. 2018, 112, 251904. [Google Scholar] [CrossRef] [Green Version]
- Fujita, T.; Nakagawa, D.; Komiya, K.; Ohira, S.; Hanasaki, I. Resilient Mechanical Metamaterial Based on Cellulose Nanopaper with Kirigami Structure. Nanomaterials 2022, 12, 2431. [Google Scholar] [CrossRef]
- Qi, Z.; Campbell, D.K.; Park, H.S. Atomistic simulations of tension-induced large deformation and stretchability in graphene kirigami. Phys. Rev. B 2014, 90, 245437. [Google Scholar] [CrossRef] [Green Version]
- An, N.; Domel, A.G.; Zhou, J.; Rafsanjani, A.; Bertoldi, K. Programmable hierarchical kirigami. Adv. Funct. Mater. 2020, 30, 1906711. [Google Scholar] [CrossRef]
- Tao, J.; Khosravi, H.; Deshpande, V.; Li, S. Engineering by Cuts: How Kirigami Principle Enables Unique Mechanical Properties and Functionalities. Adv. Sci. 2022, 10, 2204733. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, C. Buckling of ultrastretchable kirigami metastructures for mechanical programmability and energy harvesting. Int. J. Solids Struct. 2021, 213, 93–102. [Google Scholar] [CrossRef]
- Isobe, M.; Okumura, K. Discontinuity in the In-plane to Out-of-plane Transition of Kirigami. J. Phys. Soc. Jpn. 2019, 88, 025001. [Google Scholar] [CrossRef]
- Zehnder, A.T. Griffith theory of fracture. In Encyclopedia of Tribology; Wang, Q.J., Chung, Y.-W., Eds.; Springer: Boston, MA, USA, 2013; pp. 1570–1573. [Google Scholar]
- Avanzini, A.; Battini, D.; Pandini, S. Static and fatigue behavior in presence of notches for polyamide 12 (PA12) additively manufactured via Multi Jet Fusion™ process. Int. J. Fatigue 2022, 161, 106912. [Google Scholar] [CrossRef]
- Razavi, S.M.J.; Avanzini, A.; Cornacchia, G.; Giorleo, L.; Berto, F. Effect of heat treatment on fatigue behavior of as-built notched Co-Cr-Mo parts produced by Selective Laser Melting. Int. J. Fatigue 2021, 142, 105926. [Google Scholar] [CrossRef]
- Razavi, S.M.J.; Ferro, P.; Berto, F.; Torgersen, J. Fatigue strength of blunt V-notched specimens produced by selective laser melting of Ti-6Al-4V. Theor. Appl. Fract. Mech. 2018, 97, 376–384. [Google Scholar] [CrossRef] [Green Version]
- Baratta, F.; Neal, D. Stress-concentration factors in U-shaped and semi-elliptical edge notches. J. Strain Anal. 1970, 5, 121–127. [Google Scholar] [CrossRef]
- Pei, H.; Jing, J.; Chen, Y.; Guo, J.; Chen, N. 3D printing of PVDF-based piezoelectric nanogenerator from programmable metamaterial design: Promising strategy for flexible electronic skin. Nano Energy 2023, 109, 108303. [Google Scholar] [CrossRef]
- Arif, Z.U.; Khalid, M.Y.; Noroozi, R.; Hossain, M.; Shi, H.H.; Tariq, A.; Ramakrishna, S.; Umer, R. Additive manufacturing of sustainable biomaterials for biomedical applications. Asian J. Pharm. Sci. 2023, 18, 100812. [Google Scholar] [CrossRef]
- Khalid, M.Y.; Arif, Z.U.; Ahmed, W. 4D printing: Technological and manufacturing renaissance. Macromol. Mater. Eng. 2022, 307, 2200003. [Google Scholar] [CrossRef]
- Marchildon, K. Polyamides–Still strong after seventy years. Macromol. React. Eng. 2011, 5, 22–54. [Google Scholar] [CrossRef]
- Touris, A.; Turcios, A.; Mintz, E.; Pulugurtha, S.R.; Thor, P.; Jolly, M.; Jalgaonkar, U. Effect of molecular weight and hydration on the tensile properties of polyamide 12. Results Mater. 2020, 8, 100149. [Google Scholar] [CrossRef]
- Hamzehei, R.; Bodaghi, M.; Iglesias Martinez, J.A.; Ji, Q.; Ulliac, G.; Kadic, M.; Wang, C.; Zolfagharian, A.; Wu, N. Parrot Beak-Inspired metamaterials with friction and interlocking mechanisms 3D/4D printed in micro and macro scales for supreme energy absorption/dissipation. Adv. Eng. Mater. 2023, 25, 2201842. [Google Scholar] [CrossRef]
- Arif, Z.U.; Khalid, M.Y.; Noroozi, R.; Sadeghianmaryan, A.; Jalalvand, M.; Hossain, M. Recent advances in 3D-printed polylactide and polycaprolactone-based biomaterials for tissue engineering applications. Int. J. Biol. Macromol. 2022, 218, 930–968. [Google Scholar] [CrossRef]
- Tan, L.J.; Zhu, W.; Zhou, K. Recent progress on polymer materials for additive manufacturing. Adv. Funct. Mater. 2020, 30, 2003062. [Google Scholar] [CrossRef]
- ISO/ASTM 52900:2015; Additive Manufacturing-General Principles–Terminology. International Organization for Standardization: Geneva, Switzerland, 2015.
- Fu, X.; Zhang, X.; Huang, Z. Axial crushing of Nylon and Al/Nylon hybrid tubes by FDM 3D printing. Compos. Struct. 2021, 256, 113055. [Google Scholar] [CrossRef]
- Guessasma, S.; Belhabib, S.; Nouri, H. Effect of printing temperature on microstructure, thermal behavior and tensile properties of 3D printed nylon using fused deposition modeling. J. Appl. Polym. Sci. 2021, 138, 50162. [Google Scholar] [CrossRef]
- Zhang, X.; Fan, W.; Liu, T. Fused deposition modeling 3D printing of polyamide-based composites and its applications. Compos. Commun. 2020, 21, 100413. [Google Scholar] [CrossRef]
- Calignano, F.; Lorusso, M.; Roppolo, I.; Minetola, P. Investigation of the mechanical properties of a carbon fibre-reinforced nylon filament for 3D printing. Machines 2020, 8, 52. [Google Scholar] [CrossRef]
- Cai, C.; Tey, W.S.; Chen, J.; Zhu, W.; Liu, X.; Liu, T.; Zhao, L.; Zhou, K. Comparative study on 3D printing of polyamide 12 by selective laser sintering and multi jet fusion. J. Mater. Process. Technol. 2021, 288, 116882. [Google Scholar] [CrossRef]
- Morales-Planas, S.; Minguella-Canela, J.; Lluma-Fuentes, J.; Travieso-Rodriguez, J.A.; García-Granada, A.A. Multi Jet Fusion PA12 manufacturing parameters for watertightness, strength and tolerances. Materials 2018, 11, 1472. [Google Scholar]
- Adach, M.; Sokołowski, P.; Piwowarczyk, T.; Nowak, K. Study on geometry, dimensional accuracy and structure of parts produced by multi jet fusion. Materials 2021, 14, 4510. [Google Scholar] [CrossRef]
- ul Haq, M.R.; Nazir, A.; Jeng, J.Y. Design for additive manufacturing of variable dimension wave springs analyzed using experimental and finite element methods. Addit. Manuf. 2021, 44, 102032. [Google Scholar]
- Habib, F.; Iovenitti, P.; Masood, S.; Nikzad, M. Fabrication of polymeric lattice structures for optimum energy absorption using Multi Jet Fusion technology. Mater. Des. 2018, 155, 86–98. [Google Scholar] [CrossRef]
- Gardan, J. Additive manufacturing technologies: State of the art and trends. Int. J. Prod. Res. 2016, 54, 3118–3132. [Google Scholar] [CrossRef]
- Riedelbauch, J.; Rietzel, D.; Witt, G. Analysis of material aging and the influence on the mechanical properties of polyamide 12 in the Multi Jet Fusion process. Addit. Manuf. 2019, 27, 259–266. [Google Scholar] [CrossRef]
- Lee, K.P.M.; Pandelidi, C.; Kajtaz, M. Build orientation effects on mechanical properties and porosity of polyamide-11 fabricated via multi jet fusion. Addit. Manuf. 2020, 36, 101533. [Google Scholar] [CrossRef]
- ISO/ASTM 52921:2013; Standard Terminology for Additive Manufacturing–Coordinate Systems and Test Methodologies. International Organization for Standardization: Geneva, Switzerland, 2013.
- ASTM D638-14; Standard Test Method for Tensile Properties of Plastics. American Society for Testing and Materials: West Conshohocken, PA, USA, 2015.
- Zolfagharian, A.; Bodaghi, M.; Hamzehei, R.; Parr, L.; Fard, M.; Rolfe, B.F. 3D-printed programmable mechanical metamaterials for vibration isolation and buckling control. Sustainability 2022, 14, 6831. [Google Scholar] [CrossRef]
- Arshad, A.B.; Nazir, A.; Jeng, J.Y. The effect of fillets and crossbars on mechanical properties of lattice structures fabricated using additive manufacturing. Int. J. Adv. Manuf. Technol. 2020, 111, 931–943. [Google Scholar] [CrossRef]
- Sillani, F.; Kleijnen, R.G.; Vetterli, M.; Schmid, M.; Wegener, K. Selective laser sintering and multi jet fusion: Process-induced modification of the raw materials and analyses of parts performance. Addit. Manuf. 2019, 27, 32–41. [Google Scholar] [CrossRef]
- Lei, Q.E.; Shu, J.; Wang, J.; Cheung, H.Y.; Cheung, J.P.Y.; Wong, W.F.; Lau, S.C.Y.; Yip, J.; Tong, R.K.y. Design and Characterize of Kirigami-inspired Springs and the Application in Vertebrae Exoskeleton for Adolescent Idiopathic Scoliosis Brace Treatment. Front. Mech. Eng. 2023, 9, 21. [Google Scholar] [CrossRef]




| Parameter | Description | Value (mm) |
|---|---|---|
| W | Width of Kirigami Pattern | 16 |
| Slit Width | 12.5 | |
| Overall Width of Sample | 30 | |
| L | Length of Kirigami Pattern | 80 |
| Overall Length of Sample | 100 | |
| Length of Clamping Region | 9.5 | |
| Length of Single Unit | 7 | |
| d | Distance Between Two Slits /Slits and Sample Edge | 1.75 |
| h | Kirigami Slit Height | 1 |
| t | Thickness of Sample | 3 |
| Mechanical Properties | Value | ||
|---|---|---|---|
| Density | 1.01 g/cm [66] | ||
| Young’s modulus | 1128 MPa [67] | ||
| Poisson’s ratio | 0.3 [66] | ||
| Yield strength | 22.8 MPa [59] | ||
| Ultimate strength | 46 MPa [66] | ||
| True Stress (MPa) | True Plastic Strain (mm/mm) | True Stress (MPa) | True Plastic Strain (mm/mm) |
| 22.8 | 0 | 40.9 | 0.045 |
| 27.6 | 0.007 | 47.6 | 0.085 |
| 31.3 | 0.014 | 51.0 | 0.129 |
| 35.6 | 0.025 | 51.7 | 0.150 |
| Settings | Element Size | Relevance Center | Smoothing | Transition | Span Angle Center |
|---|---|---|---|---|---|
| 0.5 mm | Fine | High | Slow | Fine |
| Notch Shape | Notch Area (mm2) | FEA Estimated Stiffness (N/mm) | Experimental Stiffness (N/mm) | Error (N/mm) | Error Percentage (%) |
|---|---|---|---|---|---|
| Circle | 1.77 | 9.68 | 9.21 | −0.47 | −4.83 |
| 3.14 | 8.39 | 8.23 | −0.17 | −1.97 | |
| 4.91 | 7.18 | 7.71 | 0.53 | 7.40 | |
| 7.07 | 6.01 | 6.56 | 0.55 | 9.21 | |
| 9.62 | 4.69 | 5.19 | 0.49 | 10.49 | |
| Octagon | 1.77 | 9.50 | 9.25 | −0.25 | −2.65 |
| 3.14 | 8.15 | 7.87 | −0.28 | −3.43 | |
| 4.91 | 6.88 | 7.03 | 0.15 | 2.18 | |
| 7.07 | 5.69 | 6.12 | 0.43 | 7.63 | |
| 9.62 | 4.43 | 4.97 | 0.53 | 12.06 | |
| Heptagon | 1.77 | 9.63 | 10.00 | 0.37 | 3.87 |
| 3.14 | 8.07 | 8.11 | 0.04 | 0.52 | |
| 4.91 | 6.77 | 6.52 | −0.25 | −3.69 | |
| 7.07 | 5.56 | 5.92 | 0.36 | 6.47 | |
| 9.62 | 4.27 | 4.85 | 0.58 | 13.68 | |
| Hexagon | 1.77 | 9.31 | 9.21 | −0.11 | −1.14 |
| 3.14 | 7.89 | 7.81 | −0.08 | −1.03 | |
| 4.91 | 6.62 | 6.58 | −0.04 | −0.63 | |
| 7.07 | 5.41 | 6.11 | 0.70 | 12.91 | |
| 9.62 | 4.15 | 4.80 | 0.65 | 15.60 | |
| Pentagon | 1.77 | 9.12 | 8.41 | −0.71 | −7.81 |
| 3.14 | 7.68 | 8.03 | 0.35 | 4.61 | |
| 4.91 | 6.36 | 6.22 | −0.14 | −2.18 | |
| 7.07 | 5.16 | 5.60 | 0.44 | 8.48 | |
| 9.62 | 3.96 | 4.65 | 0.69 | 17.41 | |
| Square | 1.77 | 8.71 | 9.15 | 0.44 | 5.03 |
| 3.14 | 7.18 | 7.74 | 0.56 | 7.81 | |
| 4.91 | 5.78 | 6.23 | 0.45 | 7.80 | |
| 7.07 | 4.46 | 4.80 | 0.35 | 7.77 | |
| 9.62 | 3.20 | 3.84 | 0.64 | 20.01 | |
| Triangle | 1.77 | 7.18 | 6.64 | −0.54 | −7.46 |
| 3.14 | 5.42 | 5.54 | 0.12 | 2.23 | |
| 4.91 | 3.91 | 4.15 | 0.25 | 6.30 | |
| 7.07 | 2.68 | 3.07 | 0.39 | 14.56 | |
| 9.62 | 1.68 | 1.96 | 0.28 | 16.49 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shu, J.; Wang, J.; Li, Z.; Tong, K.-y. Effects of Slit Edge Notches on Mechanical Properties of 3D-Printed PA12 Nylon Kirigami Specimens. Polymers 2023, 15, 3082. https://doi.org/10.3390/polym15143082
Shu J, Wang J, Li Z, Tong K-y. Effects of Slit Edge Notches on Mechanical Properties of 3D-Printed PA12 Nylon Kirigami Specimens. Polymers. 2023; 15(14):3082. https://doi.org/10.3390/polym15143082
Chicago/Turabian StyleShu, Jing, Junming Wang, Zheng Li, and Kai-yu (Raymond) Tong. 2023. "Effects of Slit Edge Notches on Mechanical Properties of 3D-Printed PA12 Nylon Kirigami Specimens" Polymers 15, no. 14: 3082. https://doi.org/10.3390/polym15143082






