Self-Vibration of Liquid Crystal Elastomer Strings under Steady Illumination
Abstract
:1. Introduction
2. Theoretical Model and Formulation
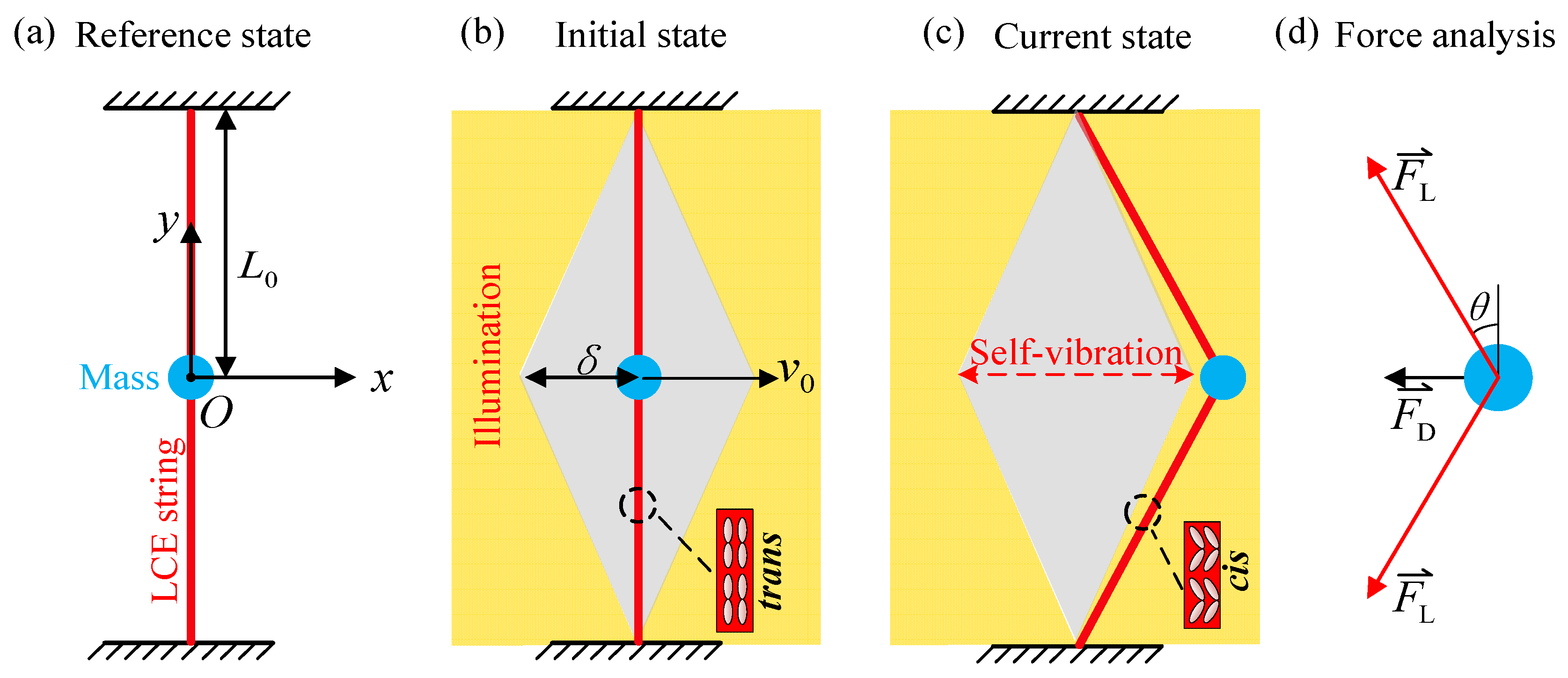
2.1. Dynamics of Self-Vibration of LCE Strings
2.2. Dynamic LCE Model
2.3. Nondimensionalization
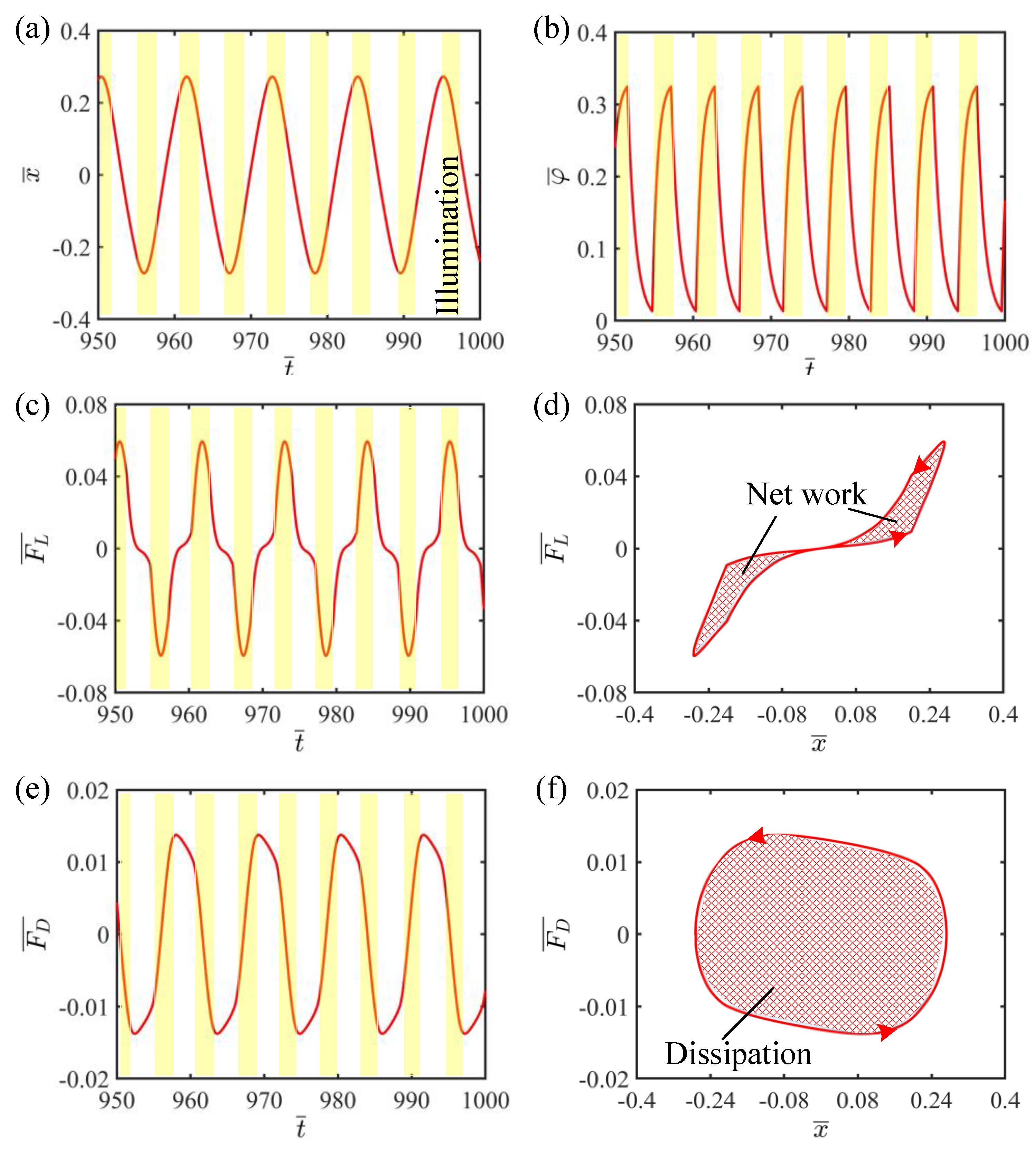
3. Two Motion Regimes and Mechanism of Self-Vibration
3.1. Two Motion Regimes
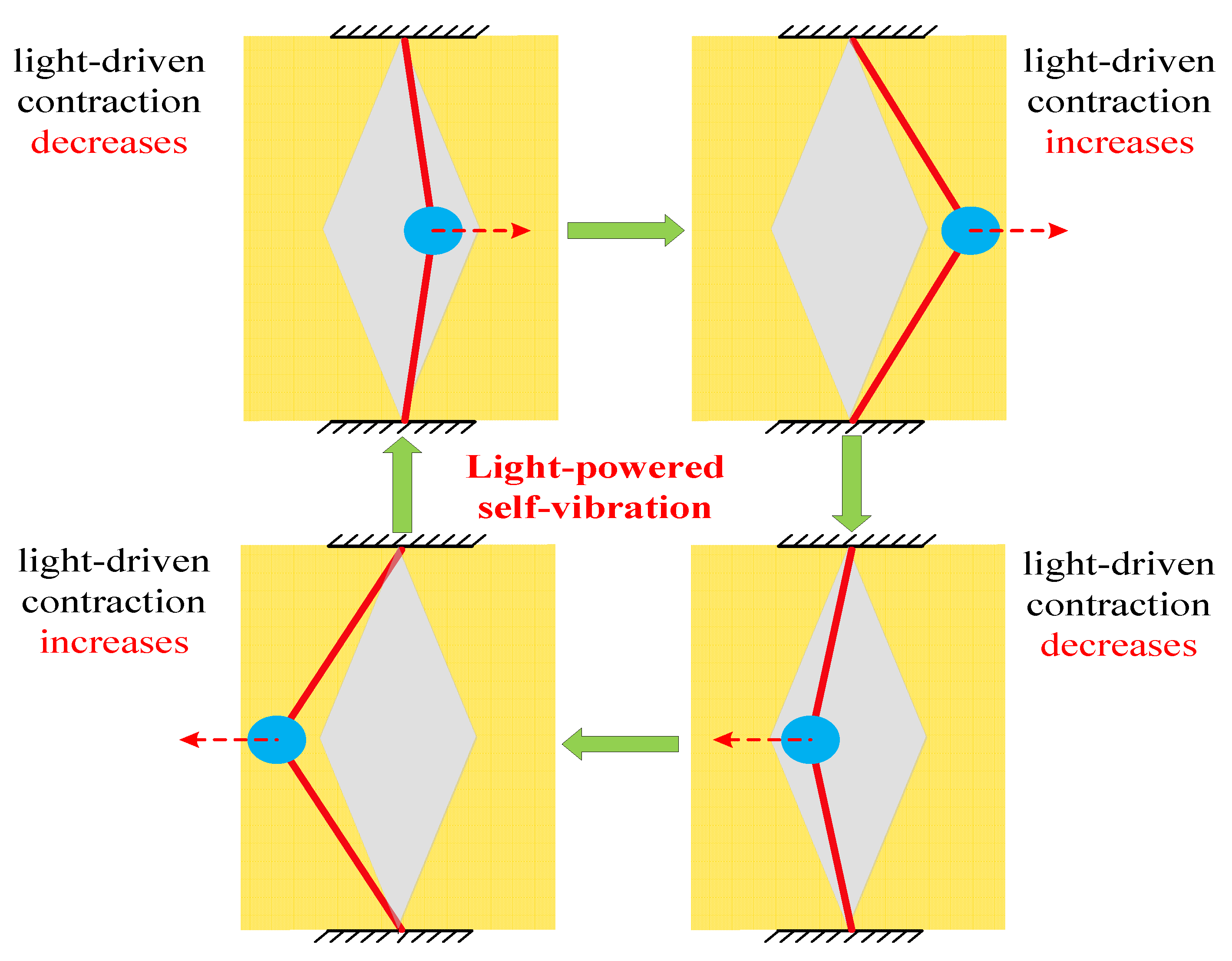
3.2. Mechanism of Self-Vibration
4. Parametric Study
4.1. Effect of the Light Intensity
4.2. Effect of the Contraction Coefficient of LCE
4.3. Effect of the Elastic Coefficient of LCE
4.4. Effect of the Initial Velocity
4.5. Effect of the Damping Coefficient
4.6. Effect of the Width of Shade
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, X.; Tan, C.F.; Chan, K.H.; Lu, X.; Zhu, L.; Kim, S.; Ho, G.W. In-built thermo-mechanical cooperative feedback mecha-nism for self-propelled multimodal locomotion and electricity generation. Nat. Commun. 2018, 9, 3438. [Google Scholar] [CrossRef]
- Ge, F.; Yang, R.; Tong, X.; Camerel, F.; Zhao, Y. A multifunctional dyedoped liquid crystal polymer actuator: Light-guided transportation, turning in locomotion, and autonomous motion. Angew. Chem. Int. Ed. 2018, 57, 11758–11763. [Google Scholar] [CrossRef] [PubMed]
- Zeng, H.; Lahikainen, M.; Liu, L.; Ahmed, Z.; Wani, O.M.; Wang, M.; Yang, H.; Priimagi, A. Light-fuelled freestyle self-oscillators. Nat. Commun. 2019, 10, 1–9. [Google Scholar] [CrossRef]
- Li, M.-H.; Keller, P.; Li, B.; Wang, X.; Brunet, M. Light-Driven Side-On Nematic Elastomer Actuators. Adv. Mater. 2003, 15, 569–572. [Google Scholar] [CrossRef]
- Nocentini, S.; Parmeggiani, C.; Martella, D.; Wiersma, D.S. Optically Driven Soft Micro Robotics. Adv. Opt. Mater. 2018, 6, 1800207. [Google Scholar] [CrossRef]
- Preston, D.J.; Jiang, H.J.; Sanchez, V.; Rothemund, P.; Rawson, J.; Nemitz, M.P.; Lee, W.; Suo, Z.; Walsh, C.J.; Whitesides, G.M. A soft ring oscillator. Sci. Robot. 2019, 4, 5496. [Google Scholar] [CrossRef]
- Ding, W. Self-Excited Vibration; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Zhao, J.; Xu, P.; Yu, Y.; Li, K. Controllable vibration of liquid crystal elastomer beams under periodic illumination. Int. J. Mech. Sci. 2020, 170, 105366. [Google Scholar] [CrossRef]
- Fang, P.; Dai, L.; Hou, Y.; Du, M.; Luyou, W. The Study of Identification Method for Dynamic Behavior of High-Dimensional Nonlinear System. Shock. Vib. 2019, 2019, 1–9. [Google Scholar] [CrossRef]
- Cross, M.; Greenside, H. Pattern Formation and Dynamics in Nonequilibrium Systems; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar] [CrossRef]
- Pivnenko, M.; Fedoryako, A.; Kutulya, L.; Seminozhenko, V. Resonance Phenomena in a Ferroelectric Liquid Crystal Near the Phase Transition SmA–SmC*. Mol. Cryst. Liq. Cryst. 1999, 328, 111–118. [Google Scholar] [CrossRef]
- Li, K.; Zhang, B.; Cheng, Q.; Dai, Y.; Yu, Y. Light-Fueled Synchronization of Two Coupled Liquid Crystal Elastomer Self-Oscillators. Polymers 2023, 15, 2886. [Google Scholar] [CrossRef]
- Thomson, W.T. Theory of Vibration with Applications, 5th ed.; Prentice-Hall: Hoboken, NJ, USA, 2005. [Google Scholar]
- Xu, P.; Wu, H.; Dai, Y.; Li, K. Self-sustained chaotic floating of a liquid crystal elastomer balloon under steady illumination. Heliyon 2023, 9, e14447. [Google Scholar] [CrossRef] [PubMed]
- Kumar, K.; Knie, C.; Bléger, D.; Peletier, M.A.; Friedrich, H.; Hecht, S.; Broer, D.; Debije, M.G.; Schening, A. A chaotic self-oscillating sunlight-driven polymer actuator. Nat. Communicat. 2016, 7, 11975. [Google Scholar] [CrossRef] [PubMed]
- Grosso, M.; Keunings, R.; Crescitelli, S.; Maffettone, P.L. Prediction of Chaotic Dynamics in Sheared Liquid Crystalline Polymers. Phys. Rev. Lett. 2001, 86, 3184–3187. [Google Scholar] [CrossRef] [PubMed]
- Kageyama, Y.; Ikegami, T.; Satonaga, S.; Obara, K.; Sato, H.; Takeda, S. Light-driven flipping of azobenzene assemblies-sparse crystal structures and responsive behavior to polarized light. Chem. Eur. J. 2020, 26, 10759–10768. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Qi, M.; Zhu, Y.; Huang, D.; Zhang, X.; Lin, L.; Yan, X. Mechanical response of the isolated cantilever with a floating potential in steady electrostatic field. Int. J. Mech. Sci. 2019, 161, 105066. [Google Scholar] [CrossRef]
- Lu, X.; Zhang, H.; Fei, G.; Yu, B.; Tong, X.; Xia, H.; Zhao, Y. Liquid-Crystalline Dynamic Networks Doped with Gold Nanorods Showing Enhanced Photocontrol of Actuation. Adv. Mater. 2018, 30, e1706597. [Google Scholar] [CrossRef] [PubMed]
- Tang, R.; Liu, Z.; Xu, D.; Liu, J.; Yu, L.; Yu, H. Optical pendulum generator based on photomechanical liquid-crystalline actuators. ACS Appl. Mater. Interfaces 2015, 7, 8393–8397. [Google Scholar] [CrossRef]
- Zhao, D.; Liu, Y. A prototype for light-electric harvester based on light sensitive liquid crystal elastomer cantilever. Energy 2020, 198, 117351. [Google Scholar] [CrossRef]
- Yang, L.; Chang, L.; Hu, Y.; Huang, M.; Ji, Q.; Lu, P.; Liu, J.; Chen, W.; Wu, Y. An Autonomous Soft Actuator with Light-Driven Self-Sustained Wavelike Oscillation for Phototactic Self-Locomotion and Power Generation. Adv. Funct. Mater. 2020, 30, 1908842. [Google Scholar] [CrossRef]
- Chun, S.; Pang, C.; Cho, S.B. A Micropillar-Assisted Versatile Strategy for Highly Sensitive and Efficient Triboelectric Energy Generation under In-Plane Stimuli. Adv. Mater. 2019, 32, e1905539. [Google Scholar] [CrossRef]
- White, T.J.; Broer, D.J. Programmable and adaptive mechanics with liquid crystal polymer networks and elastomers. Nat. Mater. 2015, 14, 1087–1098. [Google Scholar] [CrossRef] [PubMed]
- Charroyer, L.; Chiello, O.; Sinou, J.-J. Self-excited vibrations of a non-smooth contact dynamical system with planar friction based on the shooting method. Int. J. Mech. Sci. 2018, 144, 90–101. [Google Scholar] [CrossRef]
- Zhang, Z.; Duan, N.; Lin, C.; Hua, H. Coupled dynamic analysis of a heavily-loaded propulsion shafting system with continuous bearing-shaft friction. Int. J. Mech Sci. 2020, 172, 105431. [Google Scholar] [CrossRef]
- Zheng, R.; Ma, L.; Feng, W.; Pan, J.; Wang, Z.; Chen, Z.; Zhang, Y.; Li, C.; Chen, P.; Bisoyi, H.K.; et al. Autonomous Self-Sustained Liquid Crystal Actuators Enabling Active Photonic Applications. Adv. Funct. Mater. 2023, 2301142, (online version). [Google Scholar] [CrossRef]
- Ma, L.L.; Liu, C.; Wu, S.; Chen, P.; Chen, Q.; Qian, J.; Ge, S.; Wu, Y.; Hu, W.; Lu, Y. Programmable self-propelling actuators enabled by a dynamic helical medium. Sci. Adv. 2021, 7, 32. [Google Scholar] [CrossRef]
- Guo, Y.; Liu, N.; Cao, Q.; Cheng, X.; Zhang, P.; Guan, Q.; Zheng, W.; He, G.; Chen, J. Photothermal Diol for NIR-Responsive Liquid Crystal Elastomers. ACS Appl. Polym. Mater. 2022, 4, 6202–6210. [Google Scholar] [CrossRef]
- Cui, Y.; Yin, Y.; Wang, C.; Sim, K.; Li, Y.; Yu, C.; Song, J. Transient thermo-mechanical analysis for bimorph soft robot based on thermally responsive liquid crystal elastomers. Appl. Math. Mech. 2019, 40, 943–952. [Google Scholar] [CrossRef]
- Na, Y.H.; Aburaya, Y.; Orihara, H.; Hiraoka, K. Measurement of electrically induced shear strain in a chiral smectic liq-uid-crystal elastomer. Phys. Rev. E 2011, 83, 061709. [Google Scholar] [CrossRef]
- Haberl, J.M.; Sánchez-Ferrer, A.; Mihut, A.M.; Dietsch, H.; Hirt, A.M.; Mezzenga, R. Liquid-Crystalline Elastomer-Nanoparticle Hybrids with Reversible Switch of Magnetic Memory. Adv. Mater. 2013, 25, 1787–1791. [Google Scholar] [CrossRef]
- Noorjahan; Pathak, S.; Jain, K.; Pant, R. Improved magneto-viscoelasticity of cross-linked PVA hydrogels using magnetic nanoparticles. Colloids Surfaces A Physicochem. Eng. Asp. 2018, 539, 273–279. [Google Scholar] [CrossRef]
- Yoshida, R. Self-Oscillating Gels Driven by the Belousov-Zhabotinsky Reaction as Novel Smart Materials. Adv. Mater. 2010, 22, 3463–3483. [Google Scholar] [CrossRef] [PubMed]
- Hua, M.; Kim, C.; Du, Y.; Wu, D.; Bai, R.; He, X. Swaying gel: Chemo-mechanical self-oscillation based on dynamic buckling. Matter 2021, 4, 1029–1041. [Google Scholar] [CrossRef]
- Boissonade, J.; Kepper, P.D. Multiple types of spatio-temporal oscillations induced by differential diffusion in the Landolt reaction. Phys. Chem. Chem. Phys. 2011, 13, 4132–4137. [Google Scholar] [CrossRef] [PubMed]
- Koibuchi, H. Bending of Thin Liquid Crystal Elastomer under Irradiation of Visible Light: Finsler Geometry Modeling. Polymers 2018, 10, 757. [Google Scholar] [CrossRef]
- Camacho-Lopez, M.; Finkelmann, H.; Palffy-Muhoray, P.; Shelley, M. Fast liquid-crystal elastomer swims into the dark. Nat. Mater. 2004, 3, 307–310. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, J.; Yang, S. Multi-functional liquid crystal elastomer composites. Appl. Phys. Rev. 2022, 9, 011301. [Google Scholar] [CrossRef]
- Bubnov, A.; Domenici, V.; Hamplová, V.; Kašpar, M.; Zalar, B. First liquid single crystal elastomer containing lactic acid derivative as chiral co-monomer: Synthesis and properties. Polymer 2011, 52, 4490–4497. [Google Scholar] [CrossRef]
- Milavec, J.; Domenici, V.; Zupancic, B.; Rešetic, A.; Bubnov, A.; Zalar, B. Deuteron nmr resolved mesogen vs. crosslinker mo-lecular order and reorientational exchange in liquid single crystal elastomers. Phys. Chem. Chem. Phys. 2016, 18, 4071–4077. [Google Scholar] [CrossRef] [PubMed]
- Rešetic, A.; Milavec, J.; Domenici, V.; Zupancic, B.; Bubnov, A.; Zalar, B. Stress-strain and thermomechanical characterization of nematic to smectic a transition in a strongly-crosslinked bimesogenic liquid crystal elastomer. Polymer 2018, 158, 96–102. [Google Scholar] [CrossRef]
- Hu, Y.; Ji, Q.; Huang, M.; Chang, L.; Zhang, C.; Wu, G.; Zi, B.; Bao, N.; Chen, W.; Wu, Y. Light-Driven Self-Oscillating Actuators with Phototactic Locomotion Based on Black Phosphorus Heterostructure. Angew. Chem. Int. Ed. 2021, 60, 20511–20517. [Google Scholar] [CrossRef]
- Wu, J.; Yao, S.; Zhang, H.; Man, W.; Bai, Z.; Zhang, F.; Wang, X.; Fang, D.; Zhang, Y. Liquid crystal elastomer metamaterials with giant biaxial thermal shrinkage for enhancing skin regeneration. Adv. Mat. 2021, 33, 2170356. [Google Scholar] [CrossRef]
- Shen, Q.; Trabia, S.; Stalbaum, T.; Palmre, V.; Kim, K.; Oh, I.-K. A multiple-shape memory polymer-metal composite actuator capable of programmable control, creating complex 3D motion of bending, twisting, and oscillation. Sci. Rep. 2016, 6, 24462. [Google Scholar] [CrossRef] [PubMed]
- Manna, R.K.; Shklyaev, O.E.; Balazs, A.C. Chemical pumps and flflexible sheets spontaneously form self-regulating oscillators in solution. Proc. Nat. Acad. Sci. USA 2021, 118, e2022987118. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Myung, N.V.; Yin, Y. Light-powered soft steam engines for self-adaptive oscillation and biomimetic swimming. Sci. Robot. 2021, 6, eabi4523. [Google Scholar] [CrossRef]
- Serak, S.; Tabiryan, N.; Vergara, R.; White, T.J.; Vaia, R.A.; Bunning, T.J. Liquid crystalline polymer cantilever oscillators fueled by light. Soft Matter 2010, 6, 779–783. [Google Scholar] [CrossRef]
- Ahn, C.; Li, K.; Cai, S. Light or Thermally Powered Autonomous Rolling of an Elastomer Rod. ACS Appl. Mater. Interfaces 2018, 10, 25689–25696. [Google Scholar] [CrossRef] [PubMed]
- Bazir, A.; Baumann, A.; Ziebert, F.; Kulić, I.M. Dynamics of fifiberboids. Soft Matter 2020, 16, 5210–5223. [Google Scholar] [CrossRef]
- Gelebart, A.H.; Mulder, D.; Varga, M.; Konya, A.; Vantomme, G.; Meijer, E.; Selinger, R. Making waves in a photoactive polymer film. Nature 2017, 546, 632–636. [Google Scholar] [CrossRef]
- Zhou, L.; Dai, Y.; Fang, J.; Li, K. Light-powered self-oscillation in liquid crystal elastomer auxetic metamaterials with large volume change. Int. J. Mech. Sci. 2023, 254, 108423. [Google Scholar] [CrossRef]
- Cheng, Q.; Cheng, W.; Dai, Y.; Li, K. Self-oscillating floating of a spherical liquid crystal elastomer balloon under steady illumination. Int. J. Mech. Sci. 2023, 241, 107985. [Google Scholar] [CrossRef]
- Kuenstler, A.S.; Chen, Y.; Bui, P.; Kim, H.; DeSimone, A.; Jin, L.; Hayward, R.C. Blueprinting Photothermal Shape-Morphing of Liquid Crystal Elastomers. Adv. Mater. 2020, 32, e2000609. [Google Scholar] [CrossRef]
- Ge, D.; Dai, Y.; Li, K. Self-Sustained Euler Buckling of an Optically Responsive Rod with Different Boundary Constraints. Polymers 2023, 15, 316. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.; Berg, J.v.D.; Crosby, A.J. Autonomous snapping and jumping polymer gels. Nat. Mater. 2021, 20, 1695–1701. [Google Scholar] [CrossRef]
- He, Q.; Wang, Z.; Wang, Y.; Wang, Z.; Li, C.; Annapooranan, R.; Zeng, J.; Chen, R.; Cai, S. Electrospun liquid crystal elastomer microfifiber actuator. Sci. Robot. 2021, 6, eabi9704. [Google Scholar] [CrossRef] [PubMed]
- Yu, Y.; Du, C.; Li, K.; Cai, S. Controllable and versatile self-motivated motion of a fiber on a hot surface. Extreme Mech. Lett. 2022, 57, 101918. [Google Scholar] [CrossRef]
- Ge, D.L.; Dai, Y.T.; Li, K. Light-powered self-spinning of a button spinner. Int. J. Mechan. Sci. 2023, 238, 107824. [Google Scholar] [CrossRef]
- Liu, J.; Zhao, J.; Wu, H.; Dai, Y.; Li, K. Self-Oscillating Curling of a Liquid Crystal Elastomer Beam under Steady Light. Polymers 2023, 15, 344. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Y.; Lu, H.; Lee, X.; Zeng, H.; Priimagi, A. Kirigami-based light-induced shapemorphing and locomotion. Adv. Mater. 2019, 32, 1906233. [Google Scholar] [CrossRef]
- Chakrabarti; Choi, G.P.; Mahadevan, L. Self-excited motions of volatile drops on swellable sheets. Phys. Rev. Lett. 2020, 124, 258002. [Google Scholar] [CrossRef]
- Hauser, A.W.; Sundaram, S.; Hayward, R.C. Photothermocapillary Oscillators. Phys. Rev. Lett. 2018, 121, 158001. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Sundaram, S.; Kang, J.-H.; Tanjeem, N.; Emrick, T.; Hayward, R.C. Coupled oscillation and spinning of photothermal particles in Marangoni optical traps. Proc. Natl. Acad. Sci. USA 2021, 118, e2024581118. [Google Scholar] [CrossRef] [PubMed]
- Warner, M.; Terentjev, E.M. Liquid Crystal Elastomers; Oxford University Press: Oxford, UK, 2007. [Google Scholar]
- Bai, R.; Bhattacharya, K. Photomechanical coupling in photoactive nematic elastomers. J. Mech. Phys. Solids 2020, 144, 104115. [Google Scholar] [CrossRef]
- Parrany, M. Nonlinear light-induced vibration behavior of liquid crystal elastomer beam. Int. J. Mech. Sci. 2018, 136, 179–187. [Google Scholar] [CrossRef]
- Gelebart, A.H.; Vantomme, G.; Meijer, E.; Broer, D. Mastering the photothermal effect in liquid crystal networks: A general approach for self-sustained mechanical oscillators. Adv. Mater. 2017, 29, 1606712. [Google Scholar] [CrossRef]
- Ghislaine, V.; Gelebart, A.; Broer, D.; Meijer, E. A four-blade light-driven plastic mill based on hydrazone liquid-crystal net-works. Tetrahedron 2017, 73, 4963–4967. [Google Scholar]
- Finkelmann, H.; Nishikawa, E.; Pereira, G.G.; Warner, M. A New Opto-Mechanical Effect in Solids. Phys. Rev. Lett. 2001, 87, 015501. [Google Scholar] [CrossRef]
- Dunn, M.L. Photomechanics of mono- and polydomain liquid crystal elastomer films. J. Appl. Phys. 2007, 102, 013506. [Google Scholar] [CrossRef]
- Nägele, T.; Hoche, R.; Zinth, W.; Wachtveitl, J. Femtosecond photoisomerization of cis-azobenzene. Chem. Phys. Lett. 1997, 272, 489–495. [Google Scholar] [CrossRef]
- Jampani, V.S.R.; Volpe, R.H.; de Sousa, K.R.; Machado, J.F.; Yakacki, C.M.; Lagerwall, J.P.F. Liquid crystal elastomer shell actuators with negative order parameter. Sci. Adv. 2019, 5, eaaw2476. [Google Scholar] [CrossRef]
- Lee, V.; Bhattacharya, K. Actuation of cylindrical nematic elastomer balloons. J. Appl. Phys. 2021, 129, 114701. [Google Scholar] [CrossRef]
- Torras, N.; Zinoviev, K.E.; Marshall, J.E.; Terentjev, E.M.; Esteve, J. Bending kinetics of a photo-actuating nematic elastomer cantilever. Appl. Phys. Lett. 2011, 99, 254102. [Google Scholar] [CrossRef]







| Parameter | Definition | Value | Unit |
|---|---|---|---|
| light intensity | 0~100 | kW/m2 | |
| contraction coefficient | 0~0.5 | / | |
| elastic coefficient | 1~50 | N/m | |
| thermally driven relaxation time | 0.01~0.5 | s | |
| light absorption constant | 0.00022 | m2/s·W | |
| mass | 0~2 | kg | |
| damping coefficient | 0~0.5 | kg/s | |
| initial velocity | 0~0.4 | m/s | |
| width of shade | 0~0.1 | m | |
| original length of LCE | 0.01~0.2 | m |
| Parameter | ||||||
| Value | 0~1 | 0~0.5 | 0~10 | 0~1 | 0~0.2 | 0~0.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, H.; Dai, Y.; Li, K. Self-Vibration of Liquid Crystal Elastomer Strings under Steady Illumination. Polymers 2023, 15, 3483. https://doi.org/10.3390/polym15163483
Wu H, Dai Y, Li K. Self-Vibration of Liquid Crystal Elastomer Strings under Steady Illumination. Polymers. 2023; 15(16):3483. https://doi.org/10.3390/polym15163483
Chicago/Turabian StyleWu, Haiyang, Yuntong Dai, and Kai Li. 2023. "Self-Vibration of Liquid Crystal Elastomer Strings under Steady Illumination" Polymers 15, no. 16: 3483. https://doi.org/10.3390/polym15163483





