Hybrid Lattice Particle Modelling Approach for Polymeric Materials Subject to High Strain Rate Loads
Abstract
:1. Introduction
- (1)
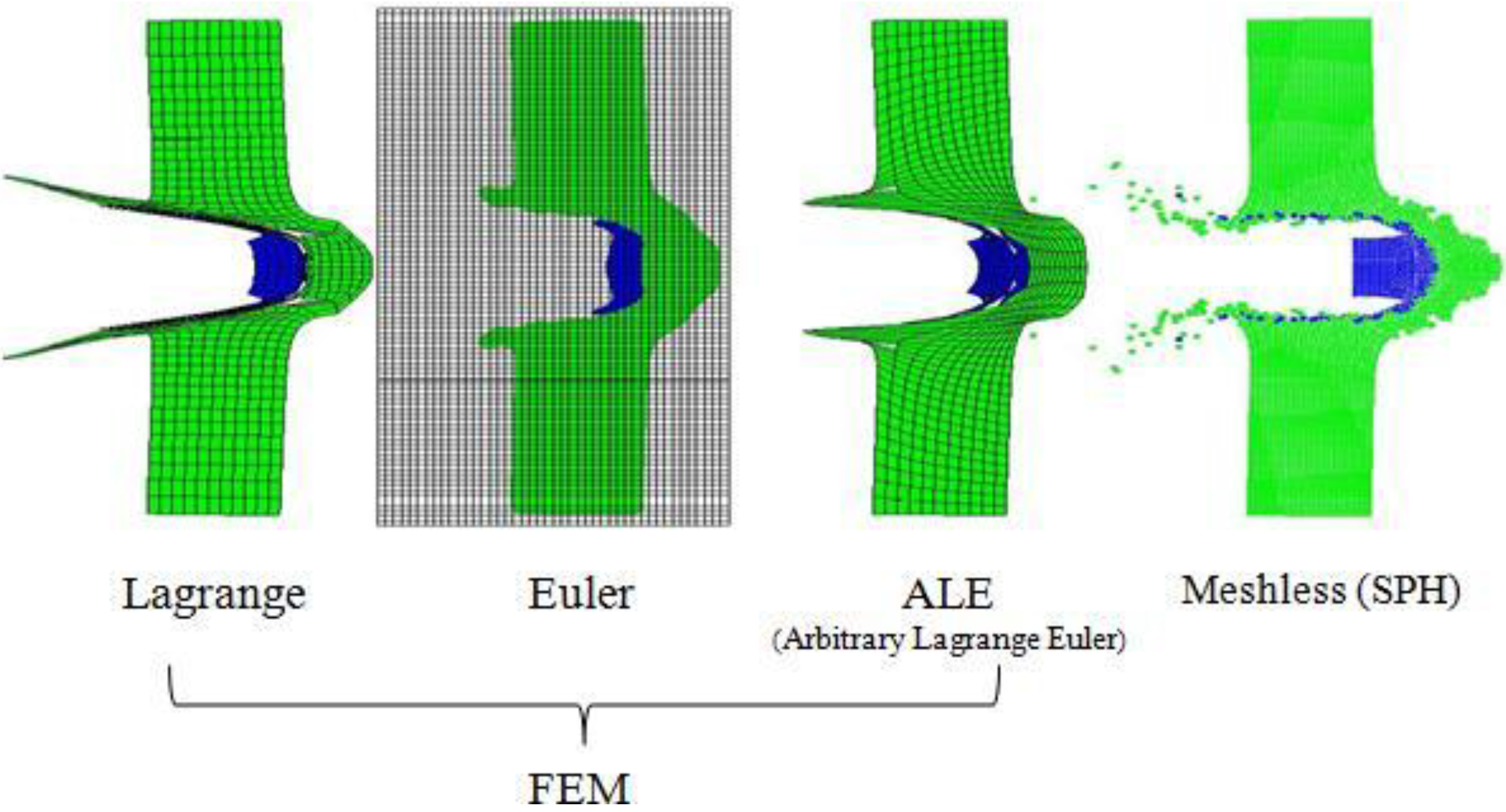
- In PFC and its inherited subclass of developed methods, each particle's size is physically accounted for, e.g., circular discs or spheres used for 2D or 3D, respectively. In summary, three disadvantages of PFC are obvious: (i) particle packing causes porosity of material. It is obviously not suitable for compact/condense materials; (ii) material's Poisson's ratio cannot be related to the pattern of the packed particles; and (iii) expensive computation is spent in keeping track of the instantaneous contact positions and the evolving geometry of all elements.
- (2)
- In SPH, a kernel density function, or weight function, is employed to define each particle's reaction domain, and continuum constitutive equations are then applied to particles within the domain. In recent years, several new techniques have been established to modify the kernel function to improve the computation accuracy. These new techniques are element-free Galerkin method (EFGM) [21], reproducing kernel particle method (RKPM) [22] and partition of unity method (PUM) [23,24]. As was mentioned by Belytschko [25], in most cases, these approaches are identical. On the whole, SPH is currently still at an immature status in technique and needs considerable improvement so as to overcome the two major limits of (i) that the SPH was developed with in mind more fluid modelling than solid modelling. However, for solids, pre-fracture particle-particle interactions are different from the failed, while they are conserved in fluids. For instance, a blend of two separate parts of fluid follows the same constitutive equations, whereas a mixture of two separate solid parts does not follows the same interactive formulas as one integrated body applies. Consequently, post-fracture interaction of solids cannot be readily traced since the kernel density function cannot distinguish if the particles are pre-fractured or to be failed; and (ii) high complexity in computation. SPH is a time-consuming technique while the inherited meshless derivatives are even more expensive [25].
| Lattice Model (LM) | Particle Model (PM) | Hybrid Lattice Particle Model (HLPM) | |
|---|---|---|---|
| Particle interaction | spring (axial/angular), beam, etc. | Leonard-Jones potential (axial only) | spring (axial/angular) mimicking the Leonard-Jones potential |
| Interaction neighborhood | not limited to nearest neighbor | nearest neighbor only | not limited to nearest neighbor |
| Mesh system | small deformation | large deformation | large deformation |
| Poisson’s ratio | flexible | fixed | flexible |
| Time process | static | dynamic based on Newton’s second law | dynamic based on Newton’s second law |
| Force-displacement relation | Displacement (strain) interpreted from force (stress) | Force interpreted from displacement (distance between particles) | Force interpreted from displacement (distance between particles) |

- (1)
- Easy for the determination of input parameters. Five conservative/equivalent rules (mass, potential energy, Young’s modulus, tensile/compressive strength and Poisson's ratio) are required to determine the material's properties for the input datasheet.
- (2)
- Easy for implementation and high computation efficiency. Since the physical size of each particle is ignored rather than its equivalent mass, the algorithm of coding a HLPM computation is fairly easy; meanwhile, since no computation is spent in keeping track of the instantaneous contact positions and the evolving geometry of all elements, the HLPM computing cost is greatly reduced.
- (3)
- Easy for tracing the post-fracture interactions. In HLPM, a pre-defined neighborhood in a lattice structure represents the integrated and non-fractured body of material. During a simulation process, any fractured member will change this originally defined neighborhood, and the particles within the fractured region will be re-defined with a different interaction rule from the non-fractured. For instance, among the no-fractured particles are considered both repulsive and attractive effects based on their tensile or compressive movement, whereas among the fractured particles are only considered repulsive interactions once the distance between the particle pair is smaller than their original equilibrium spacing. Consequently, interactions among fragments can be readily and accurately predicted.
- (4)
- A multi-scale model. In the case of lattice spacing decreasing to a few Angstroms, we will recover a molecular dynamics (MD) model with, say, a Leonard-Jones potential. This implies that HLPM is an upscaled MD and can be flexibly applied to various length scale problems, if a proper equivalent macroscopic potential is provided.
2. Review Hybrid Lattice Particle Modelling Development
2.1. Mechanical HLPM
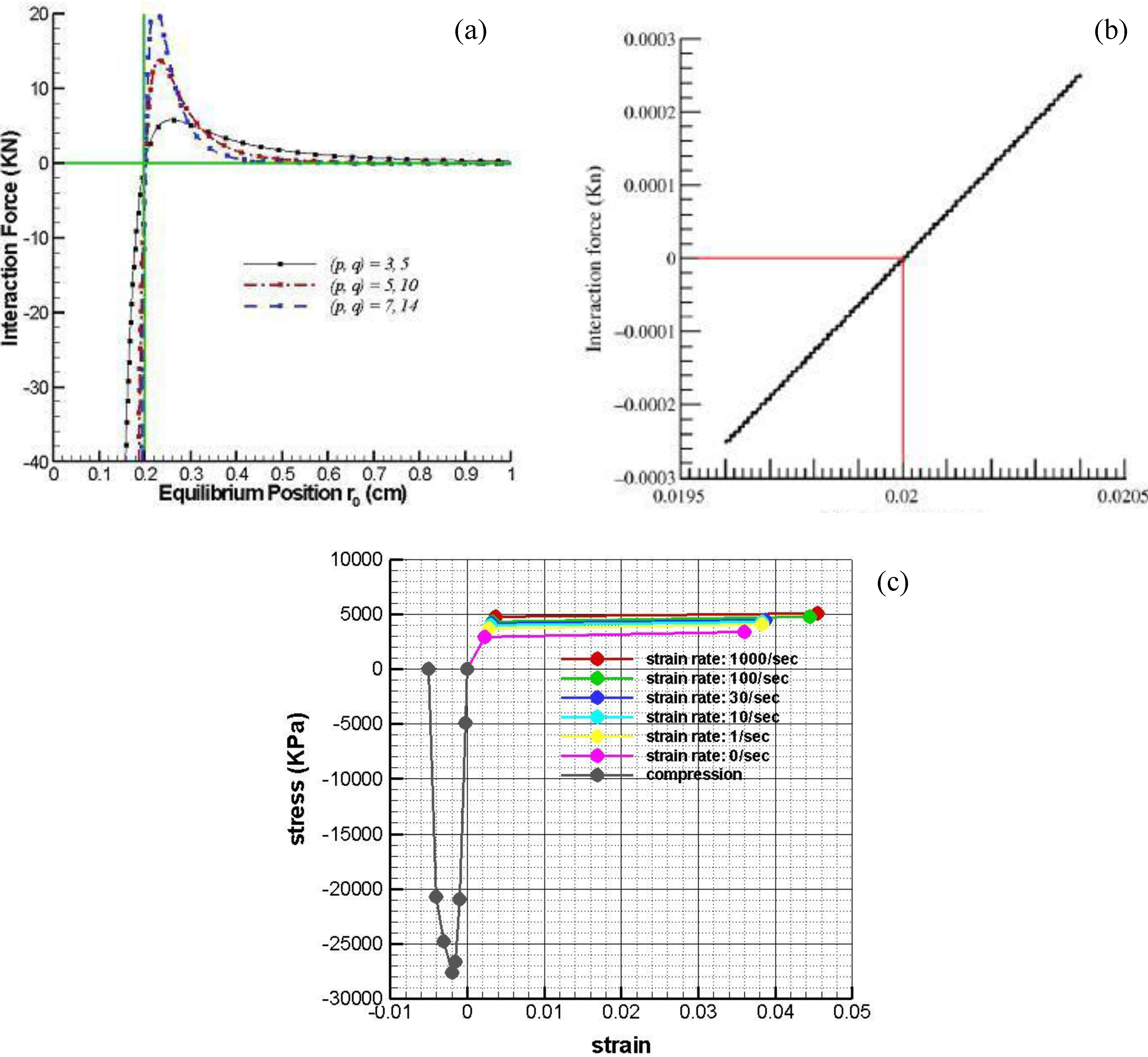
2.1.1. Lennard-Jones type interaction
2.1.2. Linear type interaction

2.1.3. Polynomial type interaction
2.2. Thermal HLPM

3. Review of HLPM for Polymeric Materials Subject to High Strain Rate Loads
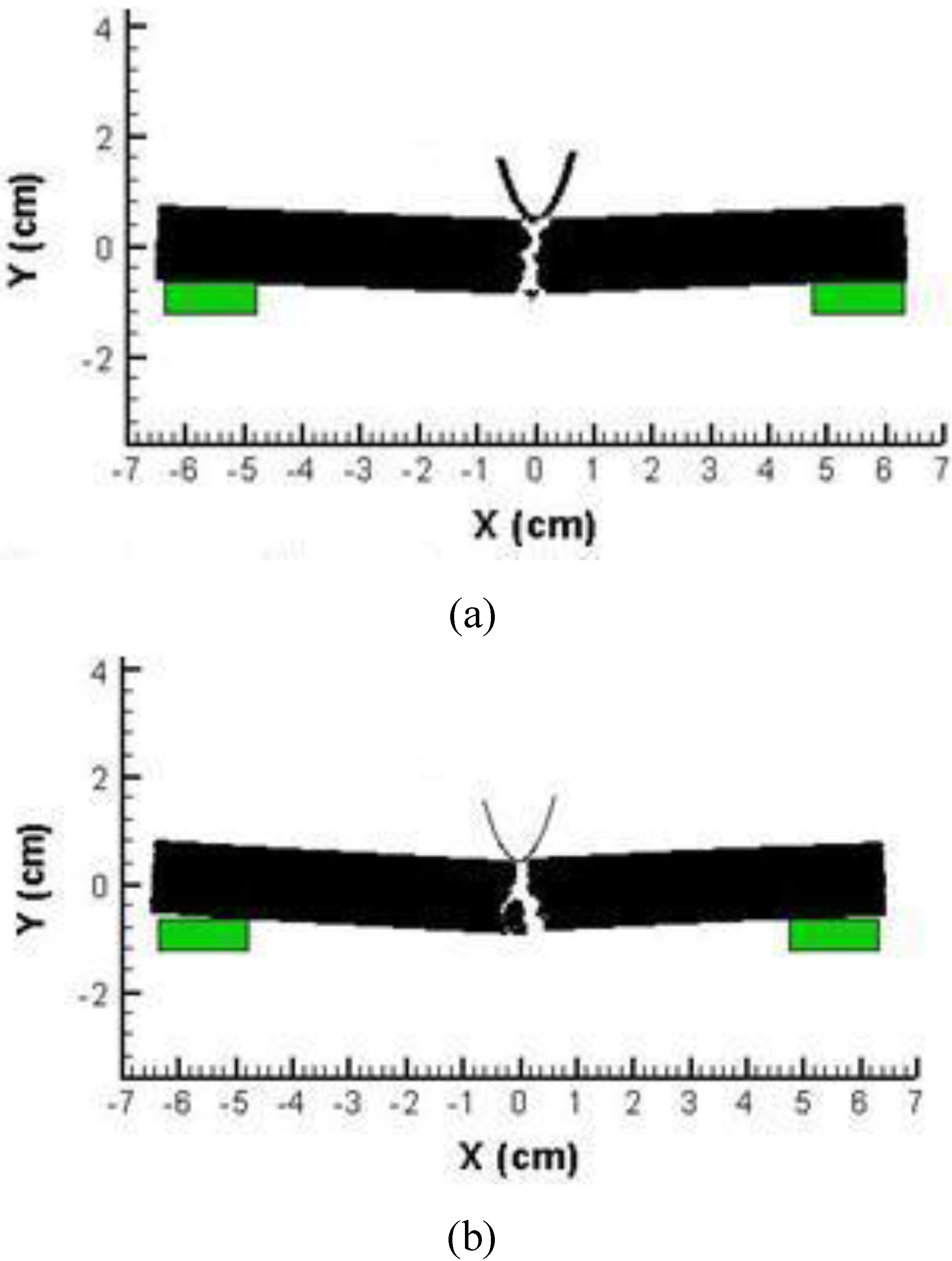
3.1. Prediction of crack pattern in epoxy plate
3.2. Indentation of polymeric materials
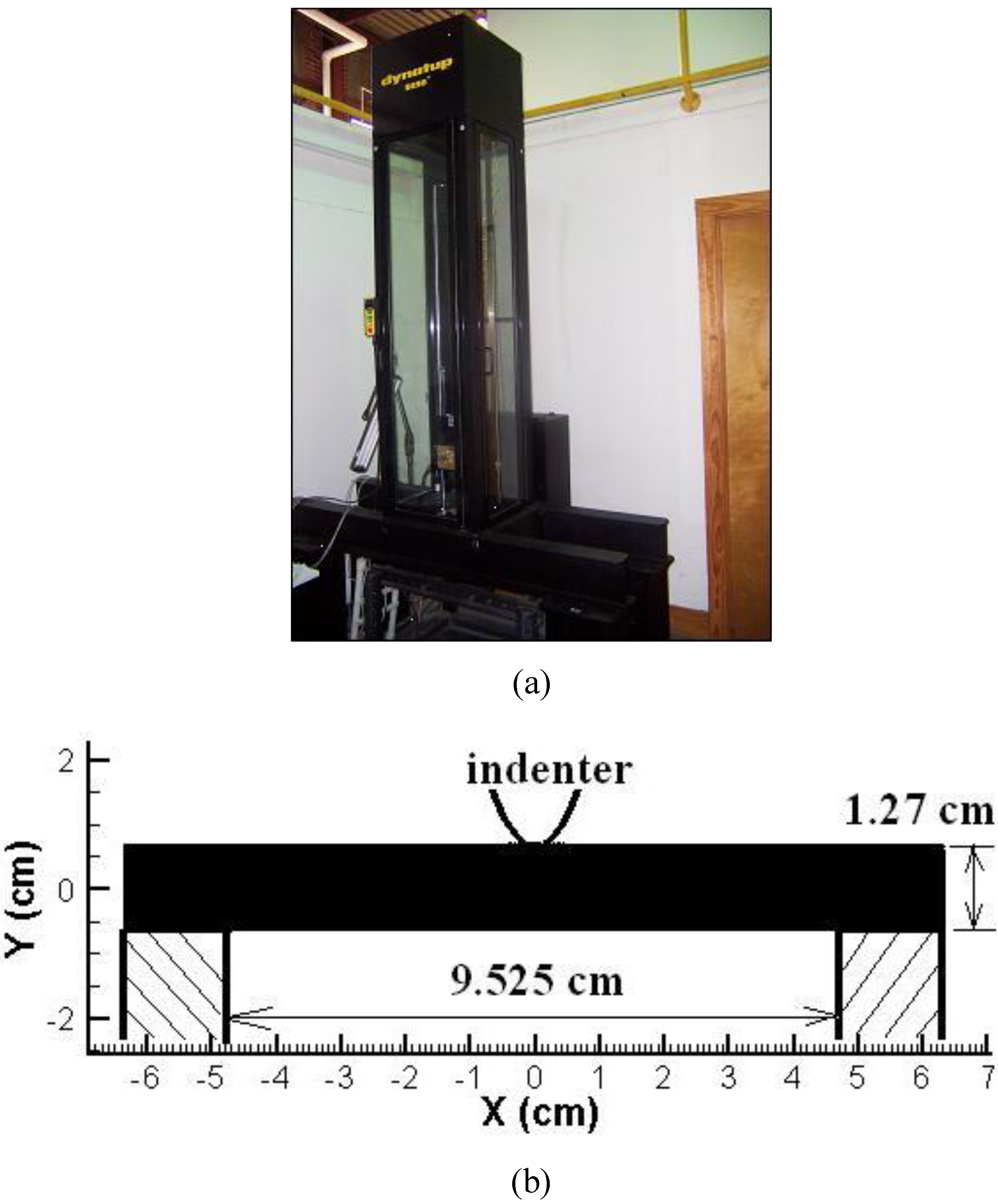
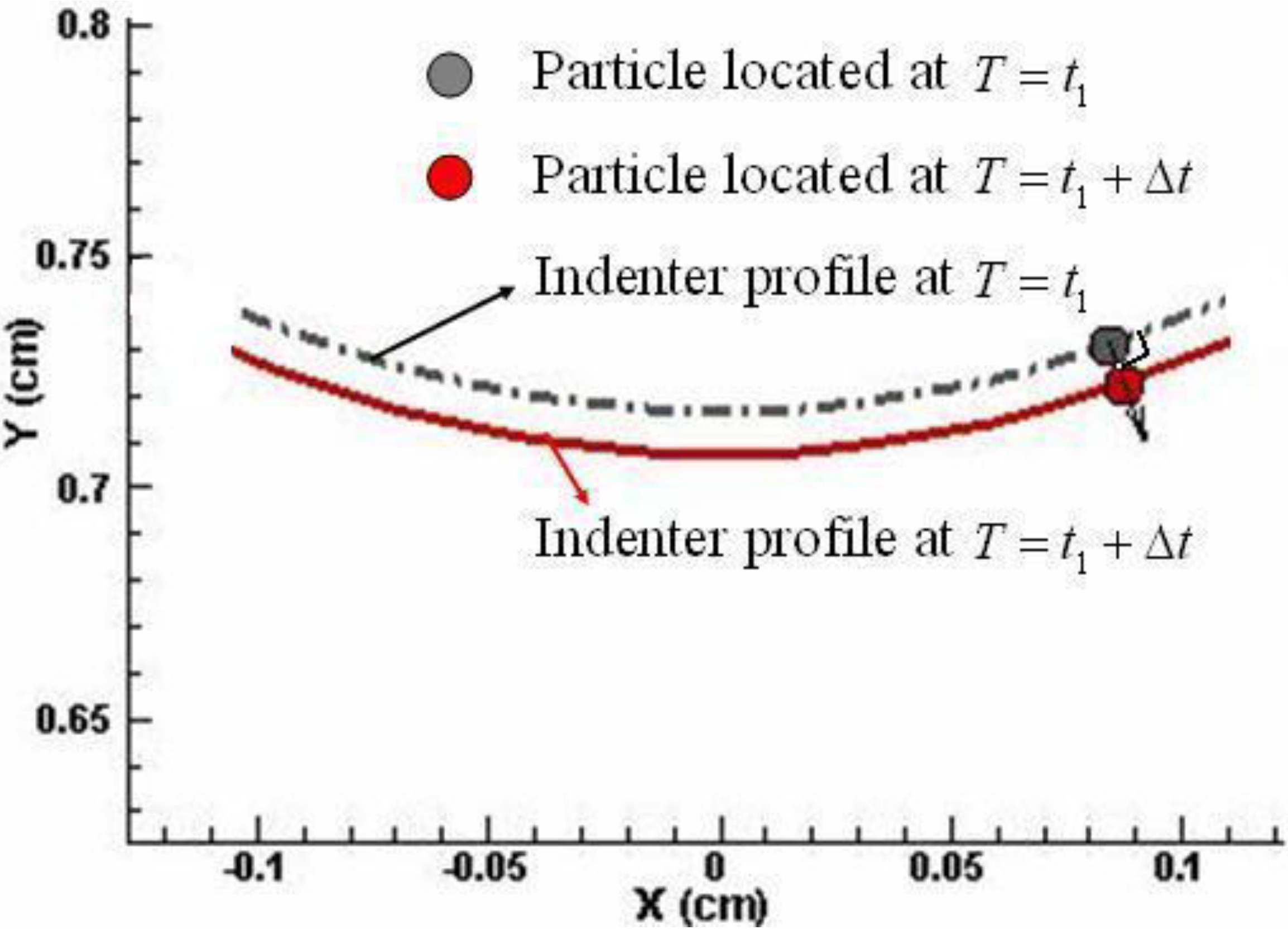
3.2.1. Indentation of nylon-6,6
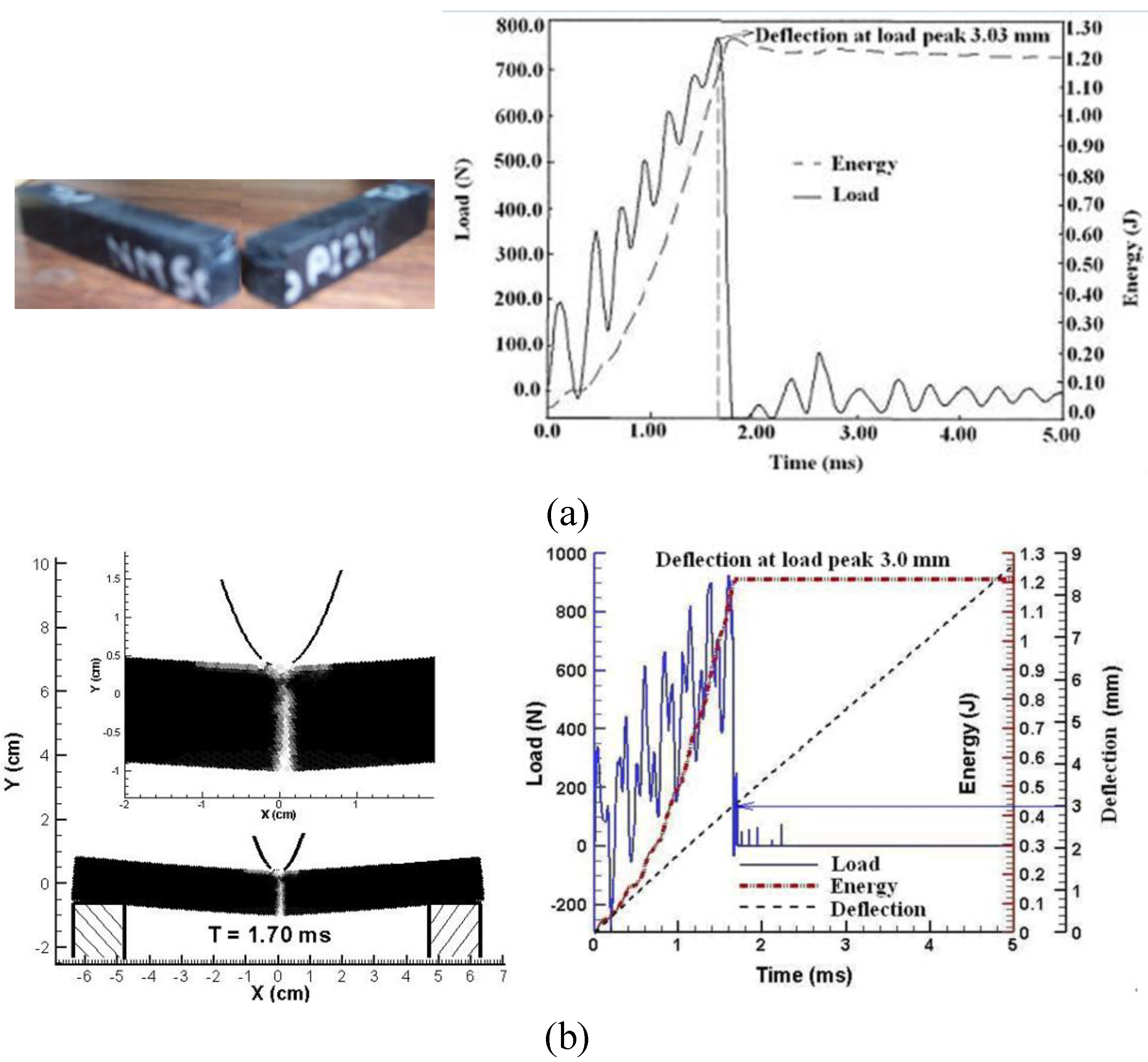
3.2.2. Indentation of vinyl ester

3.2.3. Punctuation of vinyl ester
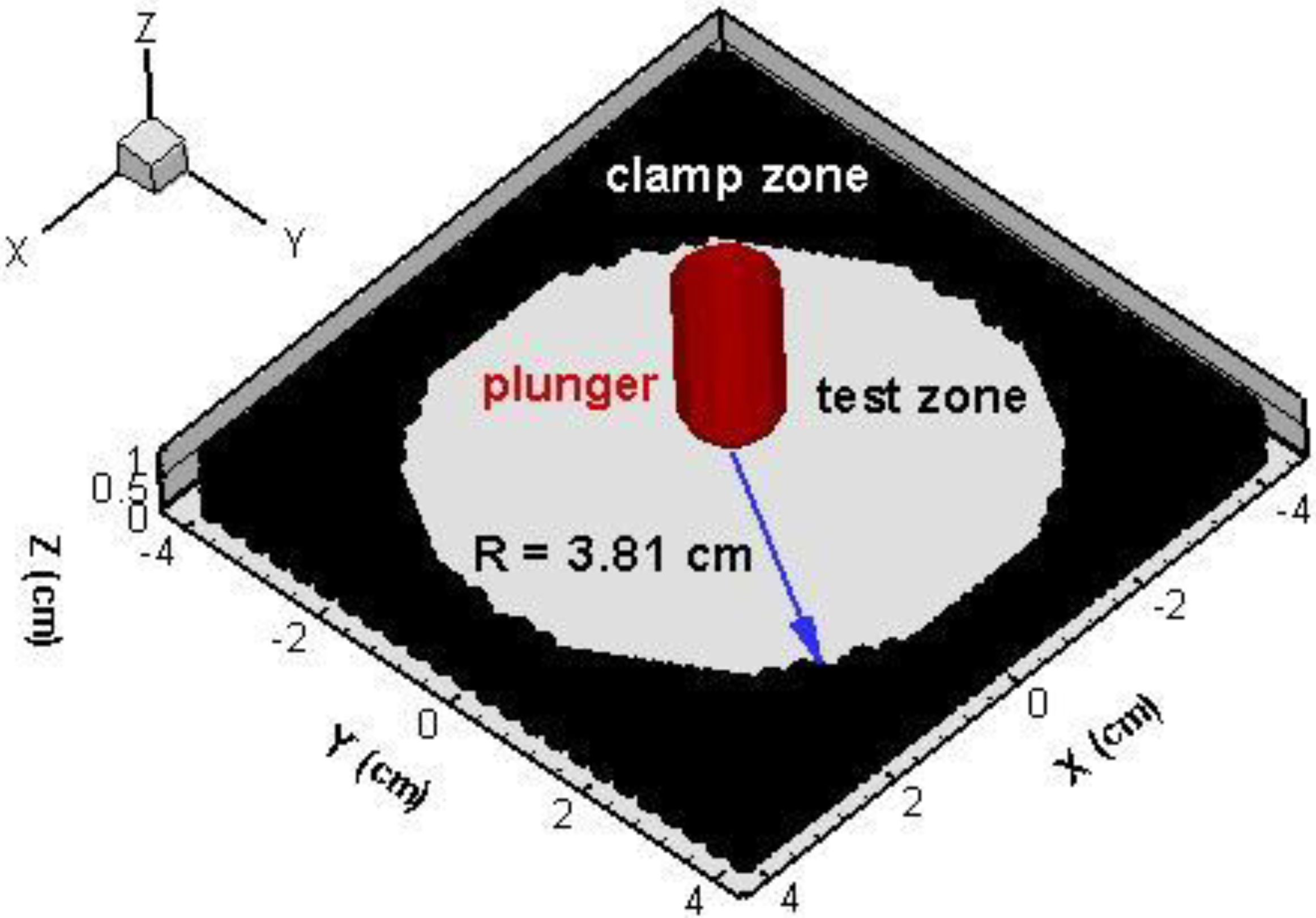
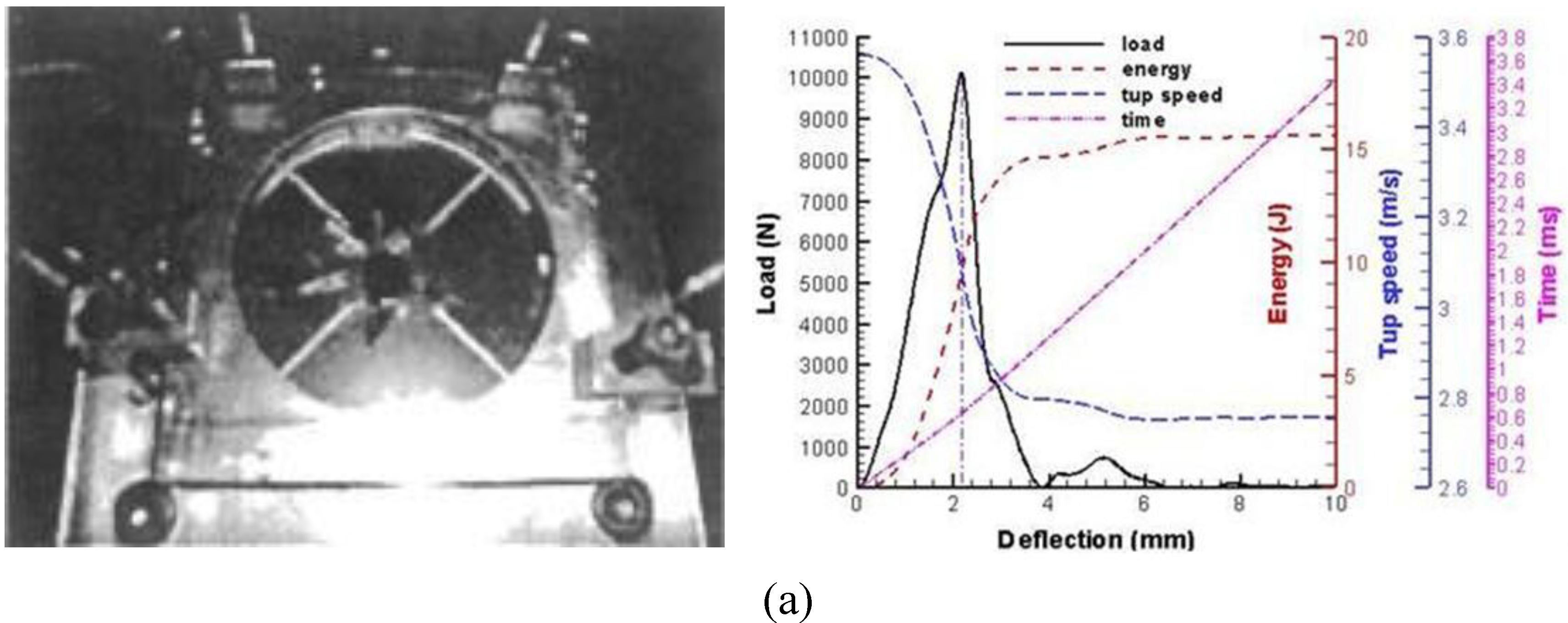
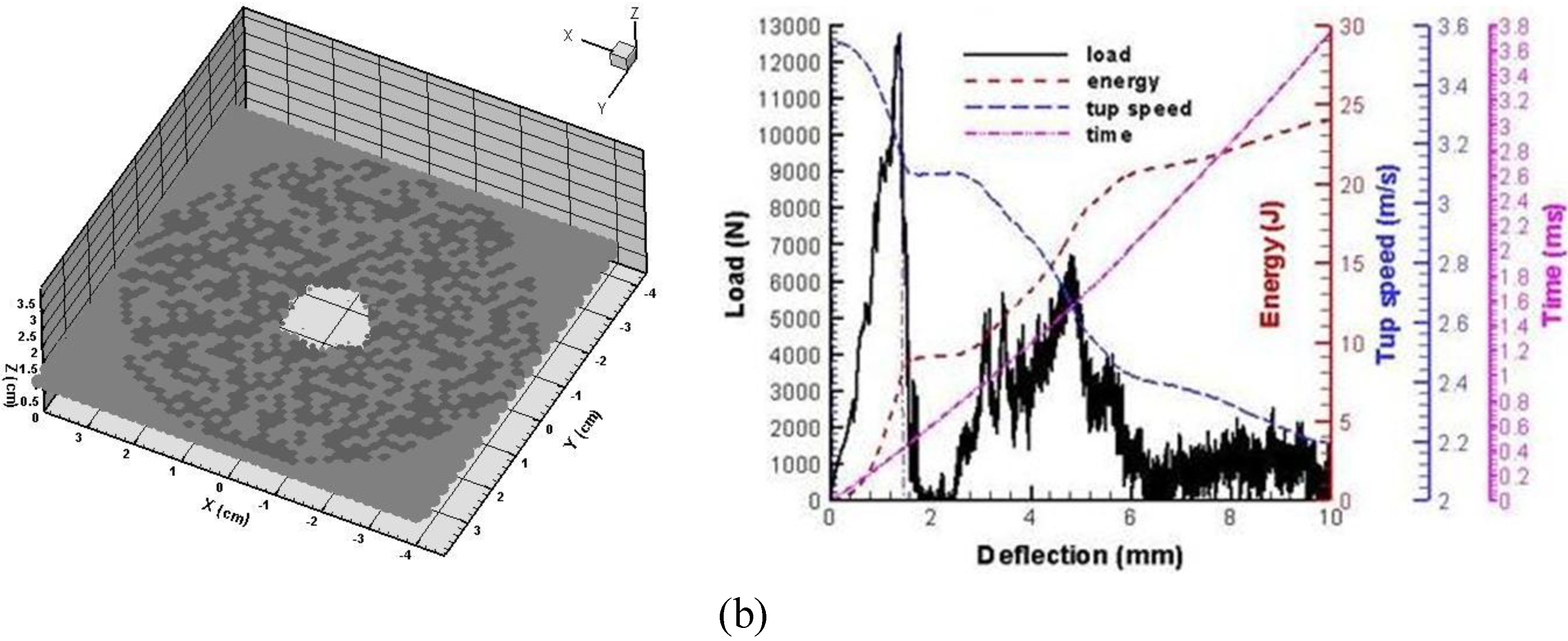
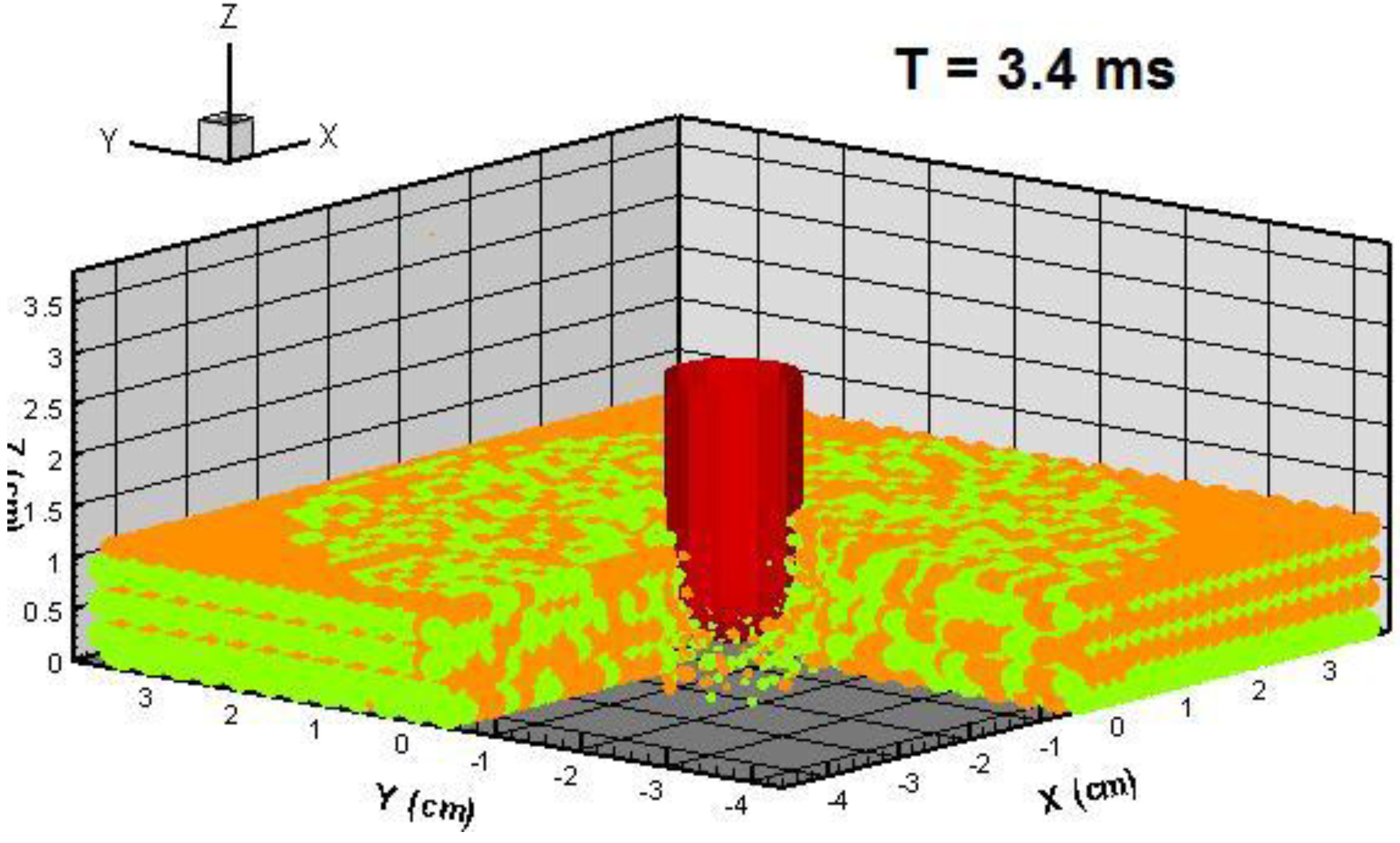
4. HLPM Prediction of Wave Propagation and Wave Induced Fracture
4.1. HLPM prediction of wave propagation in 1D and 2D elastic-brittle material
4.1.1. Dynamic boundary condition

4.1.2. Kinematic boundary condition
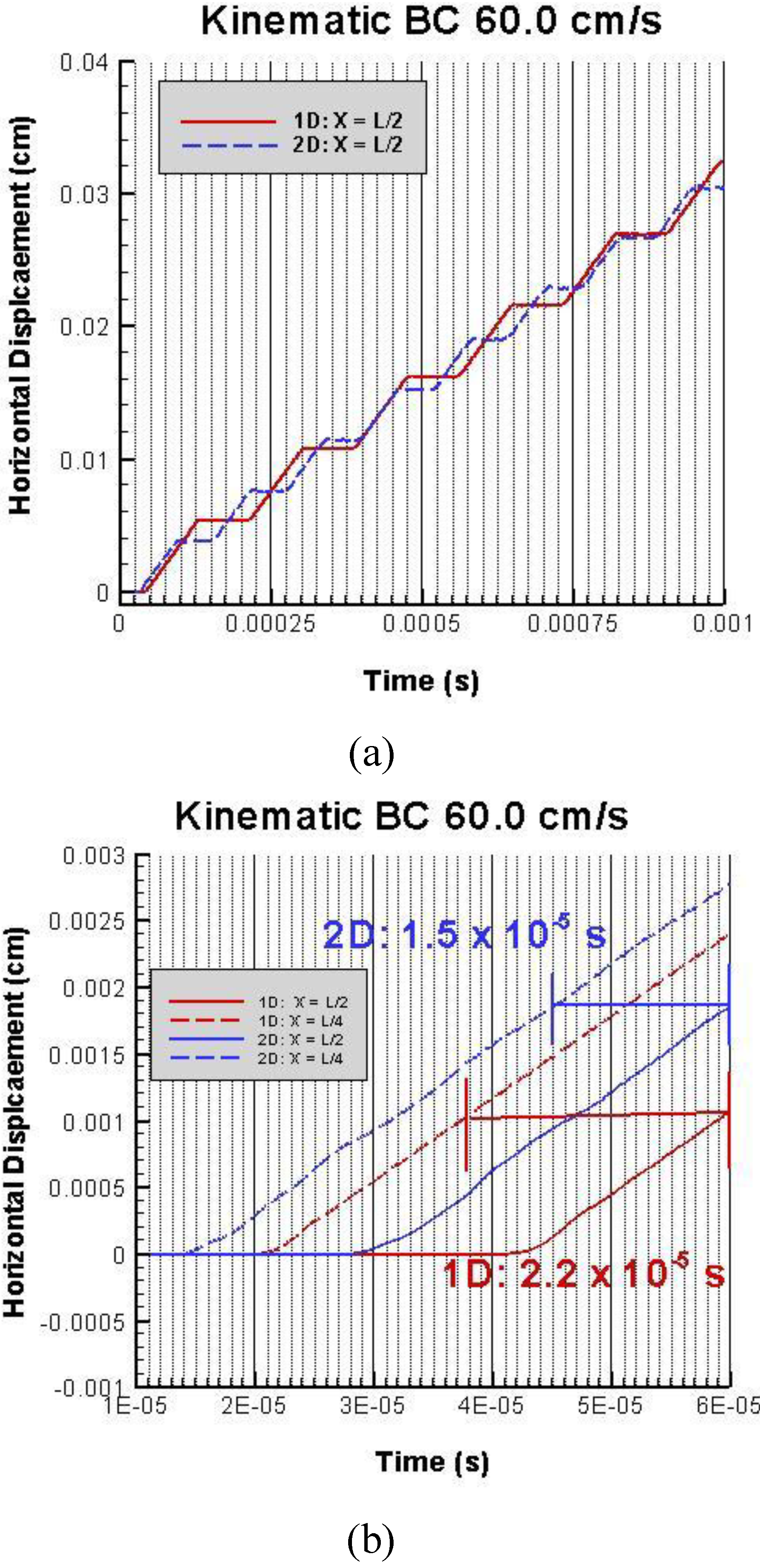
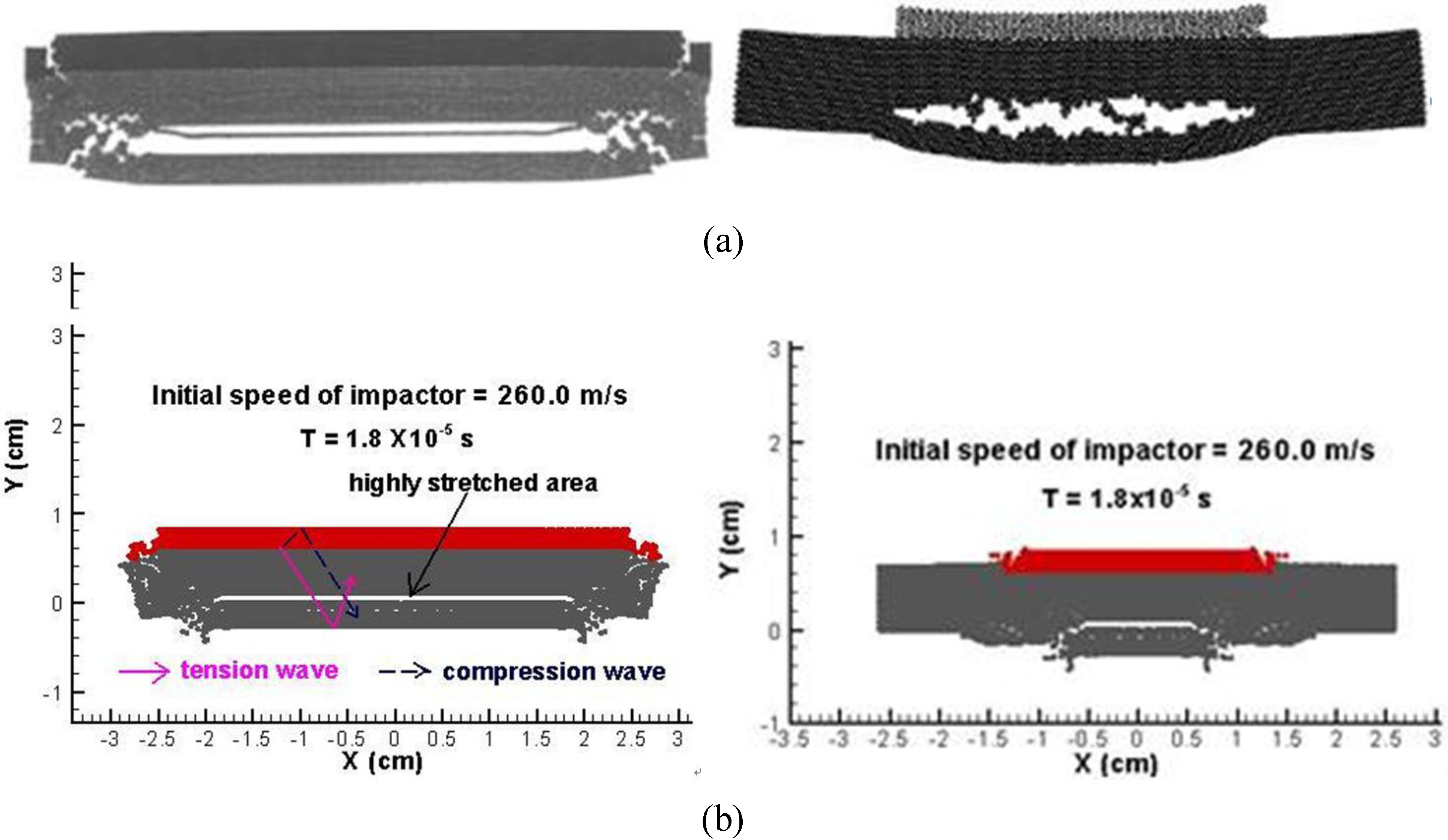
4.2. HLPM study of wave induced fracture—spall crack formation
5. Concluding Remarks
- (1)
- No need for remeshing. Re-meshing is known as an overwhelming challenge for FEM whereas HLPM does not suffer from it at all. In HLPM, fracture is created when a bond (spring) is broken by translational force. This provides HLPM a unique power to be able to quite easily overcome the “discontinuity of material” problem.
- (2)
- No stress intensity required. In HLPM, a bond (spring) is broken and fracture is thus resulted wherever the critical failure strain is reached.
- (3)
- HLPM can accurately predict the dynamic fragmentation of polymeric materials under high strain rate loading conditions, and can correctly capture wave propagation of solids.
- (1)
- Genuine 3D interaction force formulas that will be developed following Keating's approach [31].
- (2)
- More adequate impact mode will be developed so as to accurately describe the shear friction between the projectile and the penetrated target.
- (3)
- Rigorous validation work will continuously validate and calibrate the HLPM model, and test its suitability to different physical problems.
- (4)
- HLPM will be employed in various important applications, such as impact, blasting, thermally-induced breakage problems.
Acknowledgement
References
- Ferry, J.D. Viscoelastic Properties of Polymers, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 1980; Chapter 11. [Google Scholar]
- Mishra, S.; Sonawane, S.; Chitodkar, V. Comparative Study on Improvement in Mechanical and Flame Retarding Properties of Epoxy-CaCO3 Nano and Commercial Composites. Polym. Plast. Technol. Eng. 2005, 44, 463–473. [Google Scholar] [CrossRef]
- Wang, Z.; Massam, J.; Pinnavaia, T.J. Epoxy-Clay Nano Composites. In Polymer-Clay Nano Composites; Wiley: Hoboken, NJ, USA, 2000; pp. 127–148. [Google Scholar]
- Zhu, J.; Imam, A.; Crane, R.; Lozano, K.; Khabashesku, V.N.; Barrera, E.V. Processing a Glass Fiber Reinforced Vinyl Ester Composite with Nanotube Enhancement of Interlaminar Shear Strength. Compos. Sci. Technol. 2007, 67, 1509–1517. [Google Scholar] [CrossRef]
- Xia, Z.; Ellyin, F. Time-Dependent Behaviour and Viscoelastic Constitutive Modelling of an Epoxy Polymer. Polym. Polym. Compos. 1998, 6(No. 2). [Google Scholar]
- ASTM Standard D-4065-01; Standard Practice for Plastics: Dynamic Mechanical Properties: Determination and Report of Procedures; ASTM International: West Conshohocken, PA, USA, 2000.
- Hutton, D.V. Fundamentals of Finite Element Analysis; McGraw-Hill: New York, NY, USA, 2004. [Google Scholar]
- Quan, X.; Birnbaum, N.K.; Cowler, M.S.; Gerber, B.I.; Clegg, R.A.; Hayhurst, C.J. Numerical Simulation of Structural Deformation under Shock and Impact Loads Using a Coupled Multi-Solver Approach. In Proceedings of the 5th Asia-Pacific Conference on Shock and Impact Loads on Structures, Hunan, China, November 12–14, 2003.
- Belytschko, T.; Loehnert, S.; Song, J.H. Multiscale Aggregating Discontinuities: A Method for Circumventing Loss of Material Stability. Int. J. Numer. Meth. Engng. 2008, 73, 869–894. [Google Scholar] [CrossRef]
- Monaghan, J. Smoothed Particle Hydrodynamics. Rep. Prog. Phys. 2005, 68, 1703–1759. [Google Scholar] [CrossRef]
- Cundall, P.A. Computer Simulations of Dense Sphere Assemblies. In Micromechanics of Granular Materials; Satake, M., Jenkins, J.T., Eds.; Elsevier: Amsterdam, The Netherlands, 1988; pp. 113–123. [Google Scholar]
- Meguro, M.; Tagel-Din, H. Applied Element Method for Structural Analysis: Theory and Application for Linear Materials. Structural Eng./Earthquake Eng., JSCE 2000, 17, 1–14. [Google Scholar]
- Wang, G.; Ostoja-Starzewski, M.; Radziszewski, P.; Ourriban, M. Particle Modelling of Dynamic Fragmentation-II: Fracture in Single- and Multi-Phase Materials. Comp. Mat. Sci. 2006, 35, 116–133. [Google Scholar] [CrossRef]
- Wang, G.; Ostoja-Starzewski, M. Particle Modelling of Dynamic Fragmentation-I: Theoretical Considerations. Comput. Mater. Sci. 2005, 33, 429–442. [Google Scholar] [CrossRef]
- Wang, G.; Al-Ostaz, A.; Cheng, A.H.D.; Radziszewski, P. Particle Modelling and Its Current Success in the Simulations of Dynamic Fragmentation of Solids. In Strength of Materials; Nova Science Publishers: New York, NY, USA, 2009; pp. 157–182. [Google Scholar]
- Wang, G.; Al-Ostaz, A.; Cheng, A.H.D.; Mantena, P.R. Hybrid Lattice Particle Modelling: Theoretical Considerations for a 2-D Elastic Spring Network for Dynamic Fracture Simulations. Comput. Mater. Sci. 2009, 44, 1126–1134. [Google Scholar] [CrossRef]
- Oñate, E.; Idelsohn, S.R.; Pin, F.D.; Aubry, R. The Particle Finite Element Method. An Overview. Int. J. Comput. Method 2004, 1, 267–307. [Google Scholar] [CrossRef]
- Chen, Z.; Brannon, R. An Evaluation of the Material Point Method; Sand Report; Sandia National Laboratories: Livermore, CA, USA, 2002.
- Cusatis, G.; Zdenek, Z.P.; Cedolin, L. Confinement-Shear Lattice Model for Concrete Damage in Tension and Compression: I. Theory. ASCE J. Engrg. Mech. 2003, 129, 1439–1448. [Google Scholar] [CrossRef]
- Cusatis, G.; Zdenek, Z.P.; Cedolin, L. Confinement-Shear Lattice Model for Concrete Damage in Tension and Compression: II. Computation and Validation. ASCE J. Engrg. Mech. 2003, 129, 1449–1458. [Google Scholar] [CrossRef]
- Belytschko, T.; Organ, D.; Gerlach, C. Element-Free Galerkin Methods for Dynamic Fracture in Concrete. Comp. Methods Appl. Mech. Engrg. 2000, 187, 385–399. [Google Scholar] [CrossRef]
- Liu, W.K.; Jun, S.; Zhang, Y.F. Reproducing Kernel Particle Methods. Int. J. Numer. Methods Fluids 2005, 20, 1081–1106. [Google Scholar] [CrossRef]
- Melenk, J.M.; Babuska, I. The Partition of Unity Finite Element Method: Basic Theory and Applications. Comp. Methods Appl. Mech. Engrg. 1996, 139, 289–314. [Google Scholar] [CrossRef]
- Babuska, I.; Melenk, J.M. The Partition of Unity Method. Int. J. Numer. Methods Engrg. 1997, 40, 727–758. [Google Scholar] [CrossRef]
- Belytschko, T.; Krongauz, Y.; Organ, D. Meshlessmethod: An Overview and Recent Development. Comp. Methods Appl. Mech. Engrg. 1996, 139, 3–47. [Google Scholar] [CrossRef]
- Ostoja-Starzewski, M. Lattice Models in Micromechanics. Appl. Mech. Rev. 2002, 55, 35–60. [Google Scholar] [CrossRef]
- Fred, I. Numerical Simulation of Differential Equations; Academic Press: New York, NY, USA, 1979. [Google Scholar]
- Zukas, J. Introduction to Hydrocodes; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Ashby, M.F.; Jones, D.R.H. Engineering Materials 1: An Introduction to Their Properties and Applications; Pergamon Press: New York, NY, USA, 1980. [Google Scholar]
- Wang, G.; Al-Ostaz, A.; Cheng, A.H.D.; Mantena, P.R. Particle Modelling of a Polymeric Material (Nylon-6, 6) due to the Impact of a Rigid Indenter. Comp. Mat. Sci. 2008, 44, 449–463. [Google Scholar] [CrossRef]
- Keating, P.N. Relationship between the Macroscopic and Microscopic Theory of Crystal Elasticity. I. Primitive Crystals. Phys. Rev. 1966, 152, 774–779. [Google Scholar] [CrossRef]
- Wang, G.; Radziszewski, P.; Ouellet, J. Particle Modelling Simulation of Thermal Effects on Ore Breakage. Comp. Mat. Sci. 2008, 43, 892–901. [Google Scholar] [CrossRef]
- Walkiwicz, J.W.; Kazonich, G.; McGill, S.L. Microwave heating characteristics of selected minerals and compounds. Miner. Metallurg. Process. 1988, 5, 39–42. [Google Scholar]
- Hockney, R.W.; Eastwood, J.W. Computer Simulation Using Particles; Institute of Physics Publishing: Philadelphia, PA, USA, 1988. [Google Scholar]
- Al-Ostaz, A.; Jasiuk, I. Crack Initiation and Propagation in Materials with Randomly Distributed Holes. Eng. Fract. Mech. 1997, 58, 395–420. [Google Scholar] [CrossRef]
- Ostoja-Starzewski, M.; Wang, G. Particle Modelling of Random Crack Patterns in Epoxy Plates. Probab. Eng. Mech. 2006, 21, 267–275. [Google Scholar] [CrossRef]
- Wang, G. Particle Modelling of Polymeric Material Indentation Study. Eng. Fract. Mech. 2009, 76, 1386–1395. [Google Scholar]
- Wang, G.; Al-Ostaz, A.; Cheng, A.H.D.; Mantena, P.R. Hybrid Lattice Particle Modelling of Wave Propagation Induced Fracture of Solids. Comp. Methods Appl. Mech. Eng. 2009, 199, 197–205. [Google Scholar] [CrossRef]
- Meyers, M.A. Dynamic Behavior of Materials; Wiley-interscience: Malden, MA, USA, 1994. [Google Scholar]
- Krivtsov, A.M. Relation between Spall Strength and Mesoparticle Velocity Dispersion. Int. J. Impact Eng. 1999, 23, 477–487. [Google Scholar] [CrossRef]
- Krivtsov, A.M. Computer Simulation of Spall Crack Formation. In Proceedings of the 4th European Conference on Structural Dynamics, Eurodyn'99, Prague, Czech Republic, June 7–10, 1999; pp. 475–477.
© 2010 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Wang, G.; Cheng, A.H.-D.; Ostoja-Starzewski, M.; Al-Ostaz, A.; Radziszewski, P. Hybrid Lattice Particle Modelling Approach for Polymeric Materials Subject to High Strain Rate Loads. Polymers 2010, 2, 3-30. https://doi.org/10.3390/polym2010003
Wang G, Cheng AH-D, Ostoja-Starzewski M, Al-Ostaz A, Radziszewski P. Hybrid Lattice Particle Modelling Approach for Polymeric Materials Subject to High Strain Rate Loads. Polymers. 2010; 2(1):3-30. https://doi.org/10.3390/polym2010003
Chicago/Turabian StyleWang, Ge, Alexander H.-D. Cheng, Martin Ostoja-Starzewski, Ahmed Al-Ostaz, and Peter Radziszewski. 2010. "Hybrid Lattice Particle Modelling Approach for Polymeric Materials Subject to High Strain Rate Loads" Polymers 2, no. 1: 3-30. https://doi.org/10.3390/polym2010003