Systems Biology: The Role of Engineering in the Reverse Engineering of Biological Signaling
Abstract
:1. Introduction
2. Homeostasis and Control Engineering
- If the state remains steady, there is an automatic arrangement whereby any tendency toward change is effectively met by increased action of the factor or factors which resist the change. (Cited in [10].)
2.1. Perfect Adaptation and the Internal Model Principle
2.2. Fundamental Constraints on Sensitivity Minimization
- Factors which may be antagonistic in one region, where they effect a balance, may be cooperative in another region. (Cited in [10].)
3. Extracting Information in the Presence of Noise
3.1. Statistical Inference and Bayes's Rule
3.2. Noise Suppression through Temporal Filtering
4. Information-Theoretic Analyses of Signaling Pathways
4.1. Quantifying the Amount of Information in a Signal
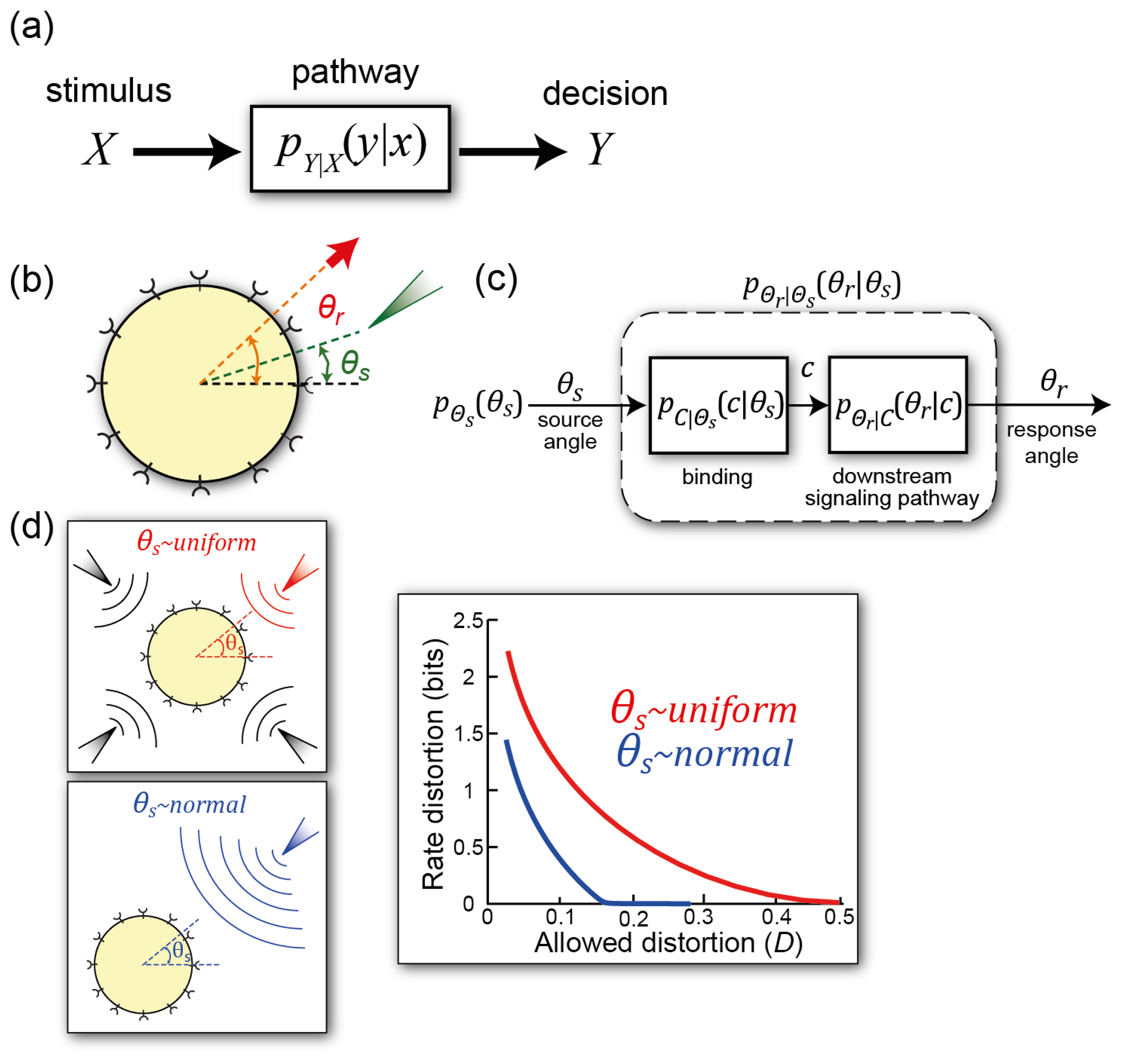
4.2. Information Transmission in Binary Decision Processes
4.3. Information Processing During Eukaryotic Chemotaxis
5. Conclusions
Acknowledgments
A. Appendix
A.1. Derivation of the Transfer Function
A.2. Simulations
References
- Hartwell, L.H.; Hopfield, J.J.; Leibler, S.; Murray, A.W. From molecular to modular cell biology. Nature 1999, 402, 47–52. [Google Scholar]
- Csete, M.E.; Doyle, J.C. Reverse engineering of biological complexity. Science 2002, 295, 1664–1669. [Google Scholar]
- Bennett, S. A History of Control Engineering, 1800–1930; Peregrinus: Stevenage, UK, 1979. [Google Scholar]
- Iglesias, P.; Ingalls, B. Control Theory and Systems Biology; MIT Press: Cambridge, MA, USA, 2010. [Google Scholar]
- Rato, C.; Amirova, S.R.; Bates, D.G.; Stansfield, I.; Wallace, H.M. Translational recoding as a feedback controller: Systems approaches reveal polyamine-specific effects on the antizyme ribosomal frameshift. Nucleic Acids Res. 2011, 39, 4587–4597. [Google Scholar]
- Milias-Argeitis, A.; Summers, S.; Stewart-Ornstein, J.; Zuleta, I.; Pincus, D.; El-Samad, H.; Khammash, M.; Lygeros, J. In silico feedback for in vivo regulation of a gene expression circuit. Nat. Biotechnol. 2011, 29, 1114–1116. [Google Scholar]
- Cosentino, C.; Salerno, L.; Passanti, A.; Merola, A.; Bates, D.G.; Amato, F. Structural bistability of the GAL regulatory network and characterization of its domains of attraction. J. Comput. Biol. 2012, 19, 148–162. [Google Scholar]
- Sheppard, P.W.; Rathinam, M.; Khammash, M. SPSens: A software package for stochastic parameter sensitivity analysis of biochemical reaction networks. Bioinformatics 2013, 29, 140–142. [Google Scholar]
- Neuert, G.; Munsky, B.; Tan, R.Z.; Teytelman, L.; Khammash, M.; van Oudenaarden, A. Systematic identification of signal-activated stochastic gene regulation. Science 2013, 339, 584–587. [Google Scholar]
- Cooper, S.J. From claude bernard to walter cannon. Emergence of the concept of homeostasis. Appetite 2008, 51, 419–427. [Google Scholar]
- Cannon, W. The Wisdom of the Body; W.W. Norton: New York, NY, USA, 1932. [Google Scholar]
- Ma, W.; Trusina, A.; El-Samad, H.; Lim, W.A.; Tang, C. Defining network topologies that can achieve biochemical adaptation. Cell 2009, 138, 760–773. [Google Scholar]
- Åström, K.; Murray, R. Feedback Systems: An Introduction for Scientists and Engineers; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Francis, B.; Wonham, W. Internal model principle of control-theory. Automatica 1975, 12, 457–465. [Google Scholar]
- Sontag, E. Adaptation and regulation with signal detection implies internal model. Syst. Control Lett. 2003, 50, 119–126. [Google Scholar]
- Alon, U.; Surette, M.G.; Barkai, N.; Leibler, S. Robustness in bacterial chemotaxis. Nature 1999, 397, 168–171. [Google Scholar]
- Barkai, N.; Leibler, S. Robustness in simple biochemical networks. Nature 1997, 387, 913–917. [Google Scholar]
- Yi, T.M.; Huang, Y.; Simon, M.I.; Doyle, J. Robust perfect adaptation in bacterial chemotaxis through integral feedback control. Proc. Natl. Acad. Sci. USA 2000, 97, 4649–4653. [Google Scholar]
- Hohmann, S. Osmotic stress signaling and osmoadaptation in yeasts. Microbiol. Mol. Biol. Rev. 2002, 66, 300–372. [Google Scholar]
- Mettetal, J.T.; Muzzey, D.; Gomez-Uribe, C.; van Oudenaarden, A. The frequency dependence of osmo-adaptation in Saccharomyces cerevisiae. Science 2008, 319, 482–484. [Google Scholar]
- Muzzey, D.; Gomez-Uribe, C.A.; Mettetal, J.T.; van Oudenaarden, A. A systems-level analysis of perfect adaptation in yeast osmoregulation. Cell 2009, 138, 160–171. [Google Scholar]
- Mangan, S.; Alon, U. Structure and function of the feed-forward loop network motif. Proc. Natl. Acad. Sci. USA 2003, 100, 11980–11985. [Google Scholar]
- Koshland, D.E. A response regulator model in a simple sensory system. Science 1977, 196, 1055–1063. [Google Scholar]
- Levchenko, A.; Iglesias, P.A. Models of eukaryotic gradient sensing: Application to chemotaxis of amoebae and neutrophils. Biophys. J. 2002, 82, 50–63. [Google Scholar]
- Iglesias, P.A.; Devreotes, P.N. Navigating through models of chemotaxis. Curr. Opin. Cell Biol. 2008, 20, 35–40. [Google Scholar]
- Takeda, K.; Shao, D.; Adler, M.; Charest, P.G.; Loomis, W.F.; Levine, H.; Groisman, A.; Rappel, W.J.; Firtel, R.A. Incoherent feedforward control governs adaptation of activated ras in a eukaryotic chemotaxis pathway. Sci. Signal 2012, 5, ra2. [Google Scholar] [CrossRef]
- Krishnan, J.; Iglesias, P.A. Analysis of the signal transduction properties of a module of spatial sensing in eukaryotic chemotaxis. Bull. Math. Biol. 2003, 65, 95–128. [Google Scholar]
- Shoval, O.; Goentoro, L.; Hart, Y.; Mayo, A.; Sontag, E.; Alon, U. Fold-change detection and scalar symmetry of sensory input fields. Proc. Natl. Acad. Sci. USA 2010, 107, 15995–16000. [Google Scholar]
- Bode, H. Network Analysis and Feedback Amplifier Design; D. Van Nostrand: New York, NY, USA, 1945. [Google Scholar]
- Serón, M.; Braslavsky, J.; Goodwin, G. Fundamental Limitations in Filtering and Control; Springer: London, UK, 1997. [Google Scholar]
- Iglesias, P. Tradeoffs in linear time-varying sysems: An analogue of Bode's sensitivity integral. Automatica 2001, 37, 1541–1550. [Google Scholar]
- Zang, G.; Iglesias, P. Nonlinear extension of Bode's integral based on an information-theoretic interpretation. Syst. Contr. Lett. 2003, 50, 11–19. [Google Scholar]
- Chandra, F.A.; Buzi, G.; Doyle, J.C. Glycolytic oscillations and limits on robust efficiency. Science 2011, 333, 187–192. [Google Scholar]
- Rao, C.V.; Wolf, D.M.; Arkin, A.P. Control, exploitation and tolerance of intracellular noise. Nature 2002, 420, 231–237. [Google Scholar]
- Munsky, B.; Neuert, G.; van Oudenaarden, A. Using gene expression noise to understand gene regulation. Science 2012, 336, 183–187. [Google Scholar]
- Berg, H.C.; Purcell, E.M. Physics of chemoreception. Biophys. J. 1977, 20, 193–219. [Google Scholar]
- Perkins, T.J.; Swain, P.S. Strategies for cellular decision-making. Mol. Syst. Biol. 2009, 5, 326. [Google Scholar] [CrossRef]
- Libby, E.; Perkins, T.J.; Swain, P.S. Noisy information processing through transcriptional regulation. Proc. Natl. Acad. Sci. USA 2007, 104, 7151–7156. [Google Scholar]
- Sartori, P.; Tu, Y. Noise filtering strategies in adaptive biochemical signaling networks: Application to E. coli chemotaxis. J. Stat. Phys. 2011, 142, 1206–1217. [Google Scholar]
- Chou, C.S.; Bardwell, L.; Nie, Q.; Yi, T.M. Noise filtering tradeoffs in spatial gradient sensing and cell polarization response. BMC Syst. Biol. 2011, 5, 196. [Google Scholar] [CrossRef]
- Strong, S.; Freedman, B.; Bialek, W.; Koberle, R. Adaptation and optimal chemotactic strategy in E. coli. Phys. Rev. E 1998, 57, 4604–4617. [Google Scholar]
- Samoilov, M.; Arkin, A.; Ross, J. Signal Processing by Simple Chemical Systems. J. Phys. Chem. A 2002, 106, 10205–10221. [Google Scholar]
- Andrews, B.W.; Yi, T.M.; Iglesias, P.A. Optimal noise filtering in the chemotactic response of Escherichia coli. PLoS Comput. Biol. 2006, 2, e154. [Google Scholar]
- Lan, G.; Sartori, P.; Neumann, S.; Sourjik, V.; Tu, Y. The energy-speed-accuracy tradeoff in sensory adaptation. Nat. Phys. 2012, 8, 422–428. [Google Scholar]
- Bialek, W. Physical limits to sensation and perception. Annu. Rev. Biophys. Biophys. Chem. 1987, 16, 455–478. [Google Scholar]
- Kalman, R. A new approach to linear filtering and prediction problems. Trans. ASME—J. Basic Eng. Series D 1960, 82, 35–45. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27. [Google Scholar]
- Cover, T.; Thomas, J. Elements of Information Theory, 2nd. ed.; Wiley: Hoboken, NJ, USA, 2006. [Google Scholar]
- Waltermann, C.; Klipp, E. Information theory based approaches to cellular signaling. Biochim. Biophys. Acta 2011, 1810, 924–932. [Google Scholar]
- Brennan, M.D.; Cheong, R.; Levchenko, A. Systems biology. How information theory handles cell signaling and uncertainty. Science 2012, 338, 334–335. [Google Scholar]
- Rhee, A.; Cheong, R.; Levchenko, A. The application of information theory to biochemical signaling systems. Phys. Biol. 2012, 9, 045011. [Google Scholar] [CrossRef]
- Tkačik, G.; Callan, C.G.; Bialek, W. Information flow and optimization in transcriptional regulation. Proc. Natl. Acad. Sci. USA 2008, 105, 12265–12270. [Google Scholar]
- Hormoz, S. Cross talk and interference enhance information capacity of a signaling pathway. Biophys. J. 2013, 104, 1170–1180. [Google Scholar]
- Janetopoulos, C.; Ma, L.; Devreotes, P.N.; Iglesias, P.A. Chemoattractant-induced phosphatidylinositol 3,4,5-trisphosphate accumulation is spatially amplified and adapts, independent of the actin cytoskeleton. Proc. Natl. Acad. Sci. USA 2004, 101, 8951–8956. [Google Scholar]
- Andrews, B.W.; Iglesias, P.A. An information-theoretic characterization of the optimal gradient sensing response of cells. PLoS Comput. Biol. 2007, 3, e153. [Google Scholar]
- Cheong, R.; Rhee, A.; Wang, C.J.; Nemenman, I.; Levchenko, A. Information transduction capacity of noisy biochemical signaling networks. Science 2011, 334, 354–358. [Google Scholar]
- Lestas, I.; Vinnicombe, G.; Paulsson, J. Fundamental limits on the suppression of molecular fluctuations. Nature 2010, 467, 174–178. [Google Scholar]
- Hamming, R. Error detecting and error correcting codes. Bell Syst. Tech. J. 1950, 29, 147–160. [Google Scholar]
- Porter, J.R.; Andrews, B.W.; Iglesias, P.A. A framework for designing and analyzing binary decision-making strategies in cellular systems. Integr. Biol. (Camb) 2012, 4, 310–317. [Google Scholar]
- Fuller, D.; Chen, W.; Adler, M.; Groisman, A.; Levine, H.; Rappel, W.J.; Loomis, W.F. External and internal constraints on eukaryotic chemotaxis. Proc. Natl. Acad. Sci. USA 2010, 107, 9656–9659. [Google Scholar]
- Hu, B.; Chen, W.; Levine, H.; Rappel, W.J. Quantifying information transmission in eukaryotic gradient sensing and chemotactic response. J. Stat. Phys. 2011, 142, 1167–1186. [Google Scholar]
- Mortimer, D.; Dayan, P.; Burrage, K.; Goodhill, G.J. Bayes-optimal chemotaxis. Neural Comput. 2011, 23, 336–373. [Google Scholar]
- Yuan, J.; Chan, S.; Mortimer, D.; Nguyen, H.; Goodhill, G.J. Optimality and saturation in axonal chemotaxis. Neural Comput. 2013, 25, 833–853. [Google Scholar]
- Thomas, P.; Matuschek, H.; Grima, R. Intrinsic noise analyzer: A software package for the exploration of stochastic biochemical kinetics using the system size expansion. PLoS One 2012, 7, e38518. [Google Scholar]
- Munsky, B.; Khammash, M. The finite state projection algorithm for the solution of the chemical master equation. J. Chem. Phys. 2006, 124, 044104:1–044104:13. [Google Scholar]
- Lillacci, G.; Khammash, M. Parameter estimation and model selection in computational biology. PLoS Comput. Biol. 2010, 6, e10000696. [Google Scholar]
- Porter, J.R.; Burg, J.S.; Espenshade, P.J.; Iglesias, PA. Identifying a static nonlinear structure in a biological system using noisy, sparse data. J. Theor. Biol. 2012, 300, 232–241. [Google Scholar]
- Neuert, G.; Munsky, B.; Tan, R.Z.; Teytelman, L.; Khammash, M.; van Oudenaarden, A. Systematic identification of signal-activated stochastic gene regulation. Science 2013, 339, 584–587. [Google Scholar]
- Del Vecchio, D.; Ninfa, A.J.; Sontag, E.D. Modular cell biology: Retroactivity and insulation. Mol. Syst. Biol. 2008, 4, 161–10.1038/msb4100204. [Google Scholar]
- Randall, A.; Guye, P.; Gupta, S.; Duportet, X.; Weiss, R. Design and connection of robust genetic circuits. Meth. Enzymol. 2011, 497, 159–186. [Google Scholar]
- Wu, K.; Rao, C.V. Computational methods in synthetic biology: Towards computer-aided part design. Curr. Opin. Chem. Biol. 2012, 16, 318–322. [Google Scholar]
- Kording, K. Decision theory: What “should” the nervous system do? Science 2007, 318, 606–610. [Google Scholar]
- Doyle, J.C.; Csete, M. Architecture, constraints, and behavior. Proc. Natl. Acad. Sci. USA 2011, 108 Suppl 3, 15624–15630. [Google Scholar]
- Gillespie, D.T. Stochastic simulation of chemical kinetics. Annu. Rev. Phys. Chem. 2007, 58, 35–55. [Google Scholar]

© 2013 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Iglesias, P.A. Systems Biology: The Role of Engineering in the Reverse Engineering of Biological Signaling. Cells 2013, 2, 393-413. https://doi.org/10.3390/cells2020393
Iglesias PA. Systems Biology: The Role of Engineering in the Reverse Engineering of Biological Signaling. Cells. 2013; 2(2):393-413. https://doi.org/10.3390/cells2020393
Chicago/Turabian StyleIglesias, Pablo A. 2013. "Systems Biology: The Role of Engineering in the Reverse Engineering of Biological Signaling" Cells 2, no. 2: 393-413. https://doi.org/10.3390/cells2020393