Broad-Band Transmission Characteristics of Polarizations in Foggy Environments
Abstract
:1. Introduction
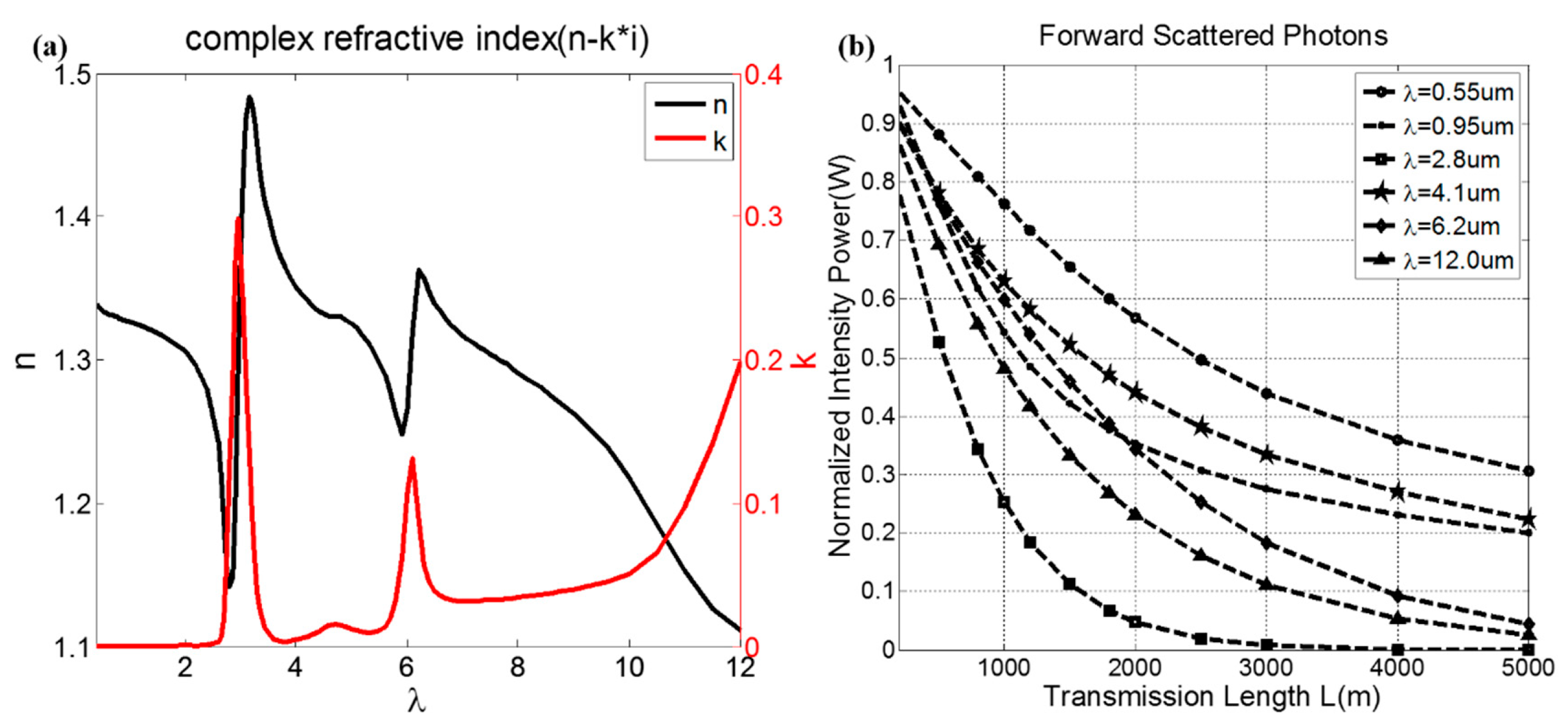
2. Experiments
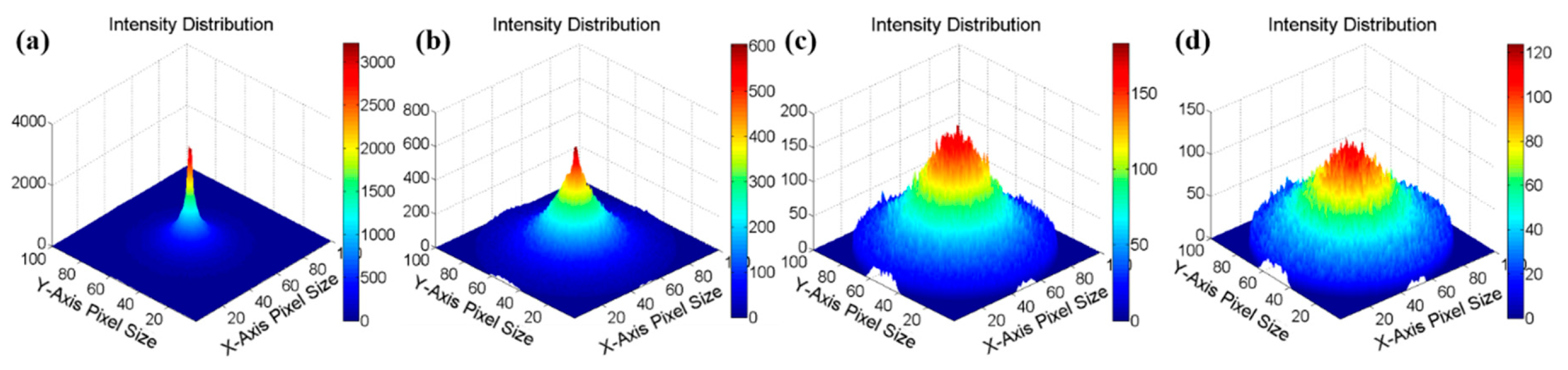
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Stewart, D.A.; Essenwanger, O.M. A survey of fog and related optical propagation characteristics. Rev. Geophys. 1982, 20, 481–495. [Google Scholar] [CrossRef]
- Ramella-Roman, J.C.; Prahl, S.A.; Jacques, S.L. Three Monte Carlo programs of polarized light transport into scattering media: Part I. Opt. Express 2005, 13, 4420–4438. [Google Scholar] [CrossRef] [PubMed]
- Ramella-Roman, J.C.; Prahl, S.A.; Jacques, S.L. Three Monte Carlo programs of polarized light transport into scattering media: Part II. Opt. Express 2005, 13, 10392–10405. [Google Scholar] [CrossRef] [PubMed]
- Yao, G.; Wang, L.V. Propagation of polarized light in turbid media: Simulated animation sequences. Opt. Express 2000, 7, 198–203. [Google Scholar] [CrossRef] [PubMed]
- Xu, M.; Alfano, R.R. Circular polarization memory of light. Phys. Rev. E 2005, 72, 065601. [Google Scholar] [CrossRef] [PubMed]
- Sun, P.; Ma, Y.; Liu, W.; Xu, C.; Sun, X. Experimentally determined characteristics of the degree of polarization of backscattered light from polystyrene sphere suspensions. J. Opt. 2013, 15, 55708. [Google Scholar] [CrossRef]
- Schechner, Y.Y.; Narasimhan, S.G.; Nayar, S.K. Polarization-based vision through haze. Appl. Opt. 2003, 42, 511–525. [Google Scholar] [CrossRef] [PubMed]
- Dereniak, E.L. Detection range enhancement using circularly polarized light in scattering environments for infrared wavelengths. Appl. Opt. 2015, 54, 2266. [Google Scholar]
- van der Laan, J.D.; Wright, J.B.; Scrymgeour, D.A.; Kemme, S.A.; Dereniak, E.L. Evolution of circular and linear polarization in scattering environments. Opt. Express 2015, 23, 31874. [Google Scholar] [CrossRef] [PubMed]
- van der Laan, J.D.; Wright, J.B.; Kemme, S.A.; Scrymgeour, D.A. Superior signal persistence of circularly polarized light in polydisperse, real-world fog environments. Appl. Opt. 2018, 57, 5464–5473. [Google Scholar] [CrossRef]
- Hu, H.; Zhao, L.; Li, X.; Wang, H.; Yang, J.; Li, K.; Liu, T. Polarimetric image recovery in turbid media employing circularly polarized light. Opt. Express 2018, 26, 25047–25059. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Hu, H.; Zhao, L.; Wang, H.; Han, Q.; Cheng, Z.; Liu, T. Pseudo-polarimetric Method for Dense Haze Removal. IEEE Photonics J. 2019, 11, 1–11. [Google Scholar] [CrossRef]
- Liu, F.; Han, P.; Wei, Y.; Yang, K.; Huang, S.; Li, X.; Zhang, G.; Bai, L.; Shao, X. Deeply seeing through highly turbid water by active polarization imaging. Opt. Lett. 2018, 43, 4903–4906. [Google Scholar] [CrossRef]
- Shen, F.; Zhang, B.; Guo, K.; Yin, Z.; Guo, Z. The Depolarization Performances of the Polarized Light in Different Scattering Media Systems. IEEE Photonics J. 2018, 10, 1–12. [Google Scholar] [CrossRef]
- Xu, Q.; Guo, Z.; Tao, Q.; Jiao, W.; Qu, S.; Gao, J. A novel method of retrieving the polarization qubits after being transmitted in turbid media. J. Opt. 2015, 17, 35606. [Google Scholar] [CrossRef]
- Xu, Q.; Guo, Z.; Tao, Q.; Jiao, W.; Wang, X.; Qu, S.; Gao, J. Transmitting characteristics of polarization information under seawater. Appl. Opt. 2015, 54, 6584–6588. [Google Scholar] [CrossRef] [PubMed]
- Tao, Q.; Sun, Y.; Shen, F.; Xu, Q.; Gao, J.; Guo, Z. Active imaging with the aids of polarization retrieve in turbid media system. Opt. Commun. 2016, 359, 405–410. [Google Scholar] [CrossRef]
- Xu, Q.; Guo, Z.; Tao, Q.; Jiao, W.; Qu, S.; Gao, J. Multi-spectral characteristics of polarization retrieve in various atmospheric conditions. Opt. Commun. 2015, 339, 167–170. [Google Scholar] [CrossRef]
- Tao, Q.; Guo, Z.; Xu, Q.; Jiao, W.; Wang, X.; Qu, S.; Gao, J. Retrieving the polarization information for satellite-to-ground light communication. J. Opt. 2015, 17, 085701. [Google Scholar] [CrossRef]
- Shen, F.; Wang, K.; Tao, Q.; Xu, X.; Wu, R.; Guo, K.; Zhou, H.; Yin, Z.; Guo, Z. Polarization imaging performances based on different retrieving Mueller matrixes. Opt.-Int. J. Light Electron Opt. 2018, 153, 50–57. [Google Scholar] [CrossRef]
- Koschmieder, H. Theorie der horizontalen Sichtweite. Beitrage zur Physik der freien Atmosphare. Meteorol. Z. 1924, 12, 3353. [Google Scholar]
- Brinkworth, B.J. Radiative transport properties of fogs. Q. J. R. Meteorol. Soc. 1964, 90, 204–207. [Google Scholar] [CrossRef]
- Al Naboulsi, M.C.; Sizun, H.; de Fornel, F. Fog attenuation prediction for optical and infrared waves. Opt. Eng. 2004, 43, 319–330. [Google Scholar] [CrossRef]
- Kaplan, B.; Ledanois, G.; Drévillon, B. Mueller matrix of dense polystyrene latex sphere suspensions: Measurements and Monte Carlo simulation. Appl. Opt. 2001, 40, 2769–2777. [Google Scholar] [CrossRef] [PubMed]
- Koračin, D.; Dorman, C.E.; Lewis, J.M.; Hudson, J.G.; Wilcox, E.M.; Torregrosa, A. Marine fog: A review. Atmos. Res. 2014, 143, 142–175. [Google Scholar] [CrossRef]
- Orgill, M.M. An Examination of the Evolution of Radiation and Advection Fogs; Science and Technology Corp.: Las Cruces, NM, USA, 1993. [Google Scholar]
- Doicu, A.; Wriedt, T.; Eremin, Y.A. Light Scattering by Systems of Particles: Null-Field Method with Discrete Sources: Theory and Programs; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Swami, M.K.; Manhas, S.; Patel, H.; Gupta, P.K. Mueller matrix measurements on absorbing turbid medium. Appl. Opt. 2010, 49, 3458–3464. [Google Scholar] [CrossRef] [PubMed]
- Tanzid, M.; Hogan, N.J.; Sobhani, A.; Robatjazi, H.; Pediredla, A.K.; Samaniego, A.; Veeraraghavan, A.; Halas, N.J. Absorption-induced image resolution enhancement in scattering media. ACS Photonics 2016, 3, 1787–1793. [Google Scholar] [CrossRef]
- Kunkel, B.A. Microphysical Properties of Fog at Otis AFB. Air Force Geophysics Laboratories; Air Force Systems Command, United States Air Force: Baltimore, MD, USA, 1982. [Google Scholar]
- Garland, J.A. Some fog droplet size distributions obtained by an impaction method. Q. J. R. Meteorol. Soc. 1971, 97, 483–494. [Google Scholar] [CrossRef]
- Yorikawa, H.; Muramatsu, S. Logarithmic normal distribution of particle size from a luminescence line-shape analysis in porous silicon. Appl. Phys. Lett. 1997, 71, 644–646. [Google Scholar] [CrossRef]
- Macdonald, C.M.; Jacques, S.L.; Meglinski, I.V. Circular polarization memory in polydisperse scattering media. Phys. Rev. E 2015, 91, 33204. [Google Scholar] [CrossRef] [PubMed] [Green Version]






© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, T.; Shen, F.; Wang, K.; Guo, K.; Liu, X.; Wang, F.; Peng, Z.; Cui, Y.; Sun, R.; Ding, Z.; et al. Broad-Band Transmission Characteristics of Polarizations in Foggy Environments. Atmosphere 2019, 10, 342. https://doi.org/10.3390/atmos10060342
Hu T, Shen F, Wang K, Guo K, Liu X, Wang F, Peng Z, Cui Y, Sun R, Ding Z, et al. Broad-Band Transmission Characteristics of Polarizations in Foggy Environments. Atmosphere. 2019; 10(6):342. https://doi.org/10.3390/atmos10060342
Chicago/Turabian StyleHu, Tianwei, Fei Shen, Kaipeng Wang, Kai Guo, Xiao Liu, Feng Wang, Zhiyong Peng, Yuemeng Cui, Rui Sun, Zhizhong Ding, and et al. 2019. "Broad-Band Transmission Characteristics of Polarizations in Foggy Environments" Atmosphere 10, no. 6: 342. https://doi.org/10.3390/atmos10060342
APA StyleHu, T., Shen, F., Wang, K., Guo, K., Liu, X., Wang, F., Peng, Z., Cui, Y., Sun, R., Ding, Z., Gao, J., & Guo, Z. (2019). Broad-Band Transmission Characteristics of Polarizations in Foggy Environments. Atmosphere, 10(6), 342. https://doi.org/10.3390/atmos10060342





