The Linkage of the Precipitation in the Selenga River Basin to Midsummer Atmospheric Blocking
Abstract
:1. Introduction
2. Data, Method and Description of the Selenga River Basin
2.1. Blocking Index Algorithm
2.2. Data
2.3. Method
2.4. The Selenga Basin Description
3. Result
3.1. The Linkage between Blocking and Precipitation
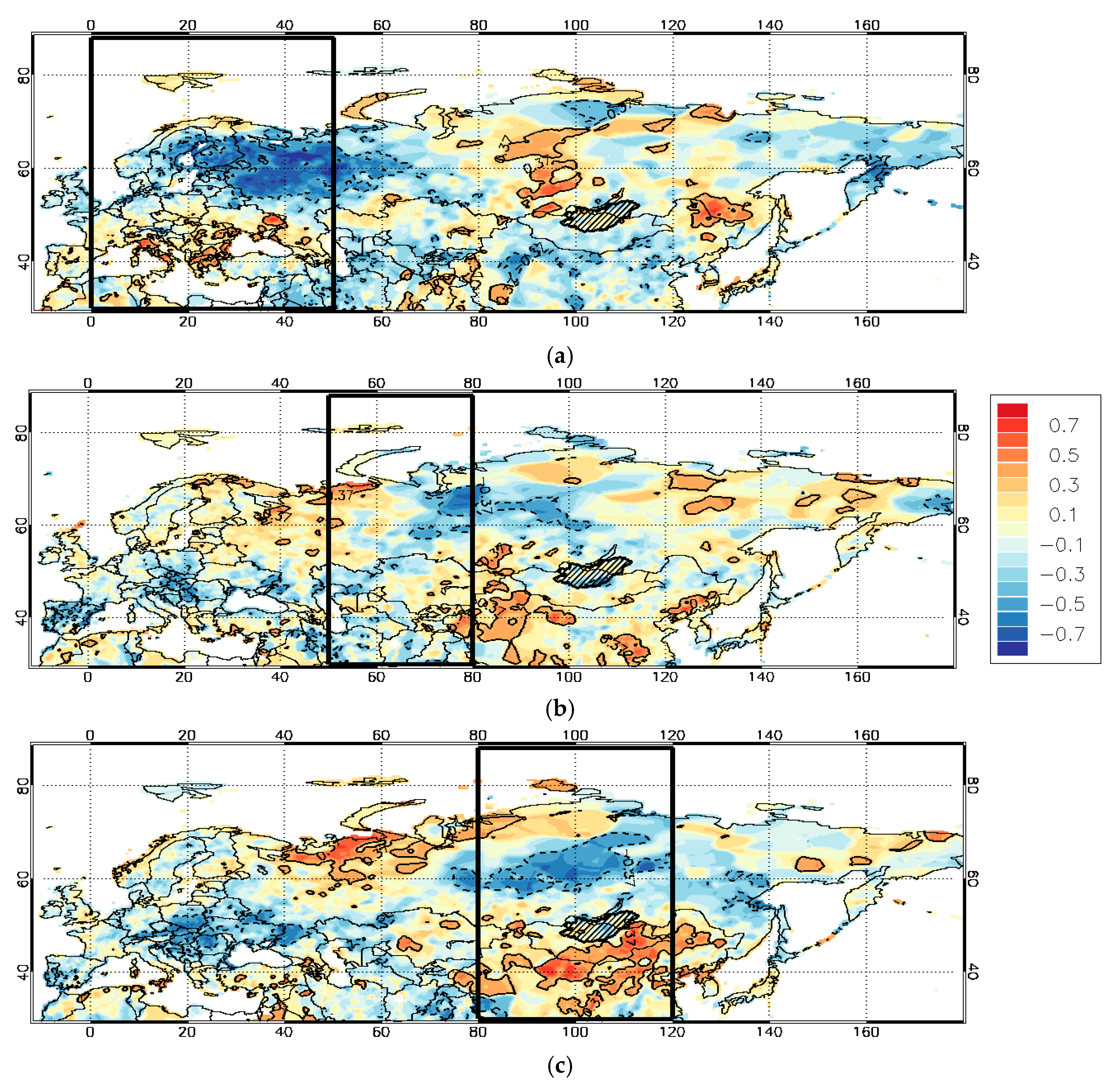
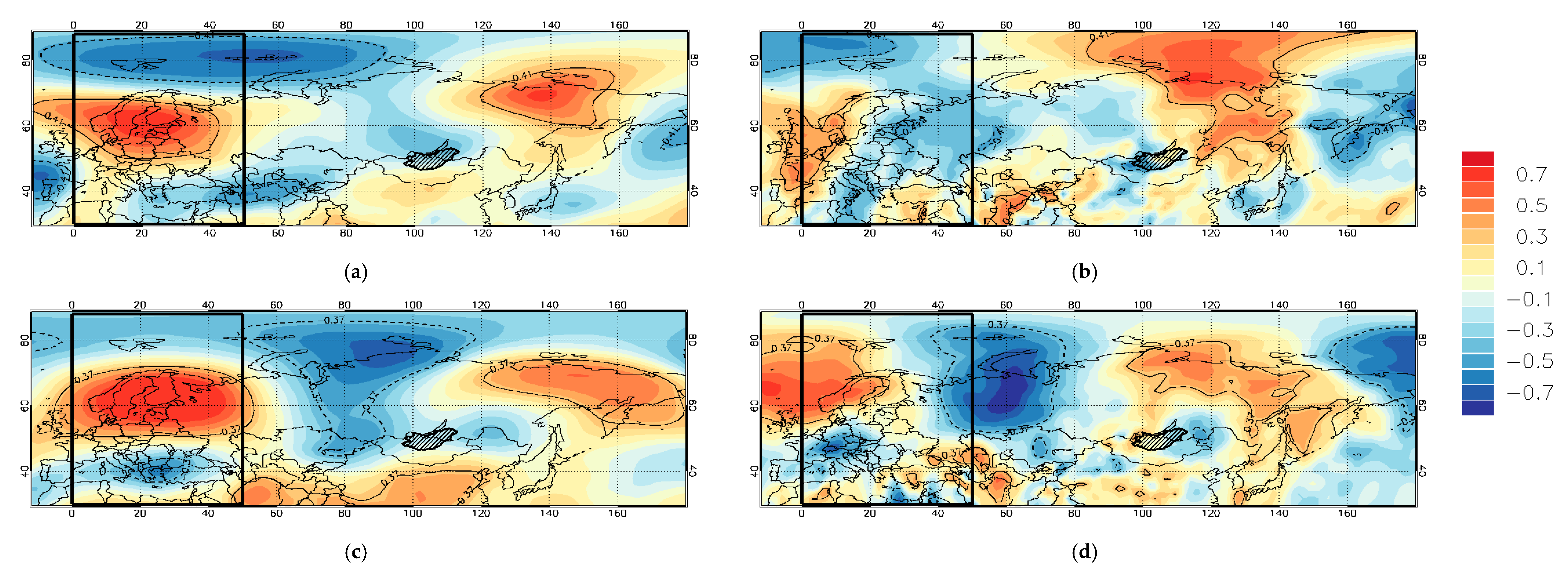
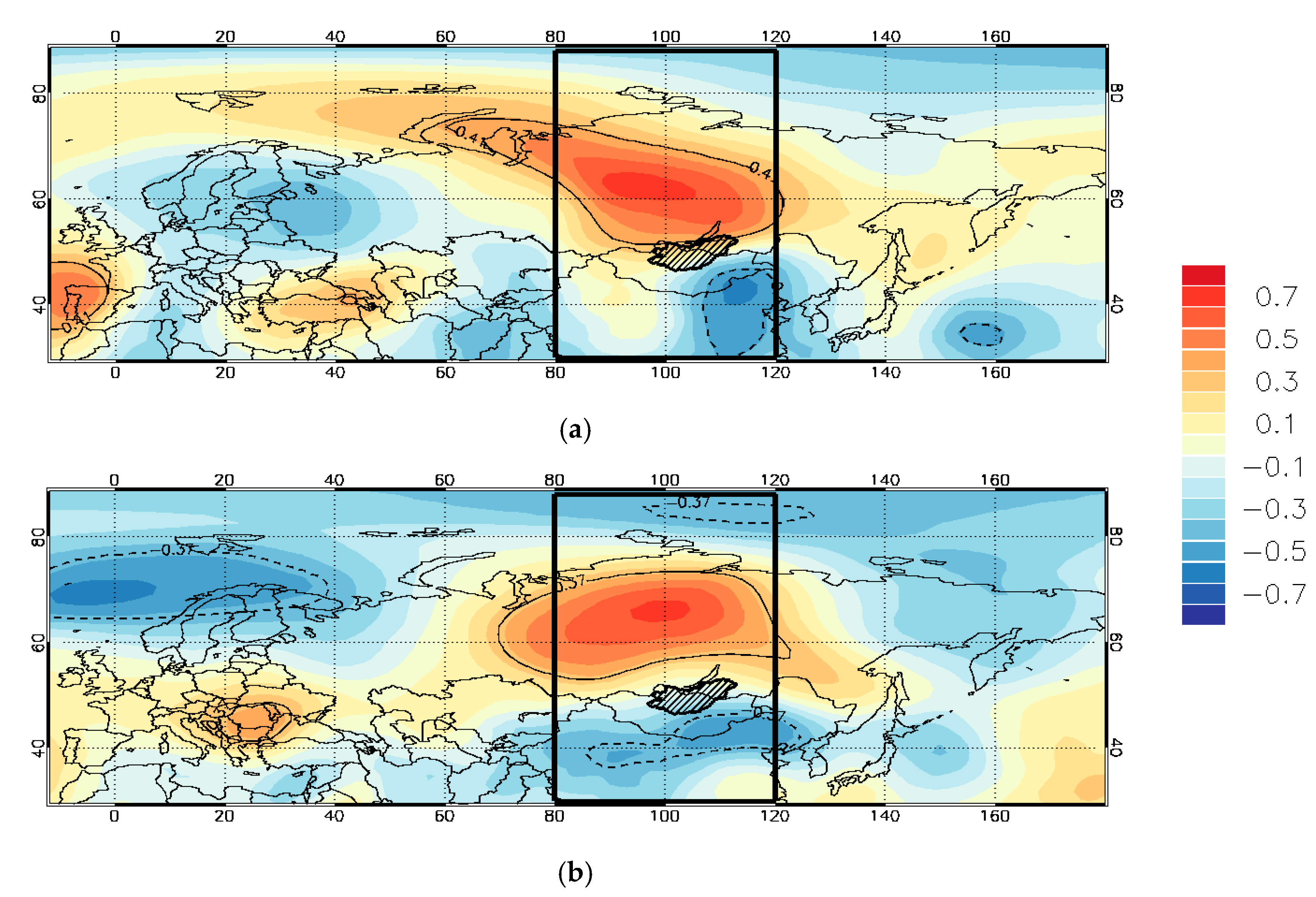
3.2. The Linkage between Blocking, Precipitation, and Atmospheric Circulation over Eurasia
3.2.1. The Change of European Blocking and Precipitation in the Russian Part of the Selenga River Basin
3.2.2. The Change of Eastern Siberia/Mongolia Blocking and TMPS
4. Summary
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bychkov, I.V.; Nikitin, V.M. Water-level regulation of Lake Baikal: Problems and possible solutions. Geogr. Nat. Resour. 2015, 36, 215–224. [Google Scholar] [CrossRef]
- Bolgov, M.V.; Buber, A.L.; Korobkina, E.A.; Lyubushin, A.A.; Filippova, I.A. Lake Baikal: Extreme level as a rare hydrological event. Water Resour. 2017, 44, 522–536. [Google Scholar] [CrossRef]
- Ko, S.; Lee, K.W. Risks and Opportunities of the Energy Sector in East Siberia and the Russian Far East: For Better Risk Management and Sustainable Energy Development; LIT: Collegeville, MN, USA, 2012. [Google Scholar]
- Berezhnykh, T.V.; Marchenko, O.Y.; Abasov, N.V.; Mordvinov, V.I. Changes in the summertime atmospheric circulation over East Asia and formation of long-lasting low-water periods within the Selenga river basin. Geogr. Nat. Resour. 2012, 33, 223–229. [Google Scholar] [CrossRef]
- Kasimov, N.; Karthe, D.; Chalov, S. Environmental change in the Selenga River—Lake Baikal Basin. Reg. Environ. Chang. 2017, 17, 1945–1949. [Google Scholar] [CrossRef]
- Chalov, S.R.; Jarsjö, J.; Kasimov, N.S.; Romanchenko, A.O.; Pietroń, J.; Thorslund, J.; Promakhova, E.V. Spatio-temporal variation of sediment transport in the Selenga River Basin, Mongolia, and Russia. Environ. Earth Sci. 2014, 73, 663–680. [Google Scholar] [CrossRef]
- Moreido, V.M.; Kalugin, A.S. Assessing possible changes in Selenga R. water regime in the XXI century based on a runoff formation model. Water Resour. 2017, 44, 390–398. [Google Scholar] [CrossRef]
- Frolova, N.L.; Belyakova, P.A.; Grigoriev, V.Y.; Sazonov, A.A.; Zotov, L.V.; Jarsjö, J. Runoff fluctuations in the Selenga River Basin. Reg. Environ. Chang. 2017, 17, 1965–1976. [Google Scholar] [CrossRef]
- Vaskovskii, M.G. (Ed.) Surface Water Resources of the USSR the Lake Baikal Watershed Basin; Gidrometeoizdat: Leningrad, Russia, 1973. (In Russian) [Google Scholar]
- Marchenko, O.Yu.; Mordvinov, V.I.; Antokhin, P.N. Conditions of formation and long-term variability of summer precipitation in the Selenga Basin. Atmos. Ocean. Opt. 2012, 25, 1084–1090, (In Russia, English abstract). [Google Scholar]
- Iwasaki, H.; Nii, T. The Break in the Mongolian Rainy Season and Its Relation to the Stationary Rossby Wave along the Asian Jet. J. Clim. 2006, 19, 3394–3405. [Google Scholar] [CrossRef]
- Iwao, K.; Takahashi, M. A Precipitation Seesaw Mode between Northeast Asia and Siberia in Summer Caused by Rossby Waves over the Eurasian Continent. J. Clim. 2008, 21, 2401–2419. [Google Scholar] [CrossRef]
- Kornienko, V.I. Features of the hydrological cycle of Transbaikalia and mountainous territories adjacent to the north and north-east. Trudy GGO 1968, 227, 129–142. (In Russian) [Google Scholar]
- Park, Y.-J.; Ahn, J.-B. Characteristics of atmospheric circulation over East Asia associated with summer blocking. J. Geophys. Res. Atmos. 2014, 119, 726–738. [Google Scholar] [CrossRef]
- Rex, D.F. Blocking Action in the Middle Troposphere and its Effect upon Regional Climate. Tellus 1950, 2, 196–211. [Google Scholar]
- Pelly, J.L.; Hoskins, B.J. A New Perspective on Blocking. J. Atmos. Sci. 2003, 60, 743–755. [Google Scholar] [CrossRef]
- Palmén, E.; Newton, C.W. Atmospheric Circulation Systems: Their Structure and Physical Interpretation; Academic Press: Cambridge, MA, USA, 1969. [Google Scholar]
- Nakamura, N.; Huang, C.S.Y. Atmospheric blocking as a traffic jam in the jet stream. Science 2018, 361, 42–47. [Google Scholar] [CrossRef]
- Mokhov, I.I.; Timazhev, A.V.; Lupo, A.R. Changes in atmospheric blocking characteristics within Euro-Atlantic region and Northern Hemisphere as a whole in the 21st century from model simulations using RCP anthropogenic scenarios. Glob. Planet. Chang. 2014, 122, 265–270. [Google Scholar] [CrossRef]
- Tyrlis, E.; Hoskins, B.J. Aspects of a Northern Hemisphere Atmospheric Blocking Climatology. J. Atmos. Sci. 2008, 65, 1638–1652. [Google Scholar] [CrossRef]
- Barriopedro, D.; García-Herrera, R.; Lupo, A.R.; Hernández, E. A Climatology of Northern Hemisphere Blocking. J. Clim. 2006, 19, 1042–1063. [Google Scholar] [CrossRef] [Green Version]
- Tibaldi, S.; Molteni, F. On the operational predictability of blocking. Tellus A 1990, 42, 343–365. [Google Scholar] [CrossRef] [Green Version]
- Lenggenhager, S.; Croci-Maspoli, M.; Brönnimann, S.; Martius, O. On the dynamical coupling between atmospheric blocks and heavy precipitation events: A discussion of the southern Alpine flood in October 2000. Q. J. R. Meteorol. Soc. 2019, 145, 530–545. [Google Scholar] [CrossRef]
- Rimbu, N.; Stefan, S.; Busuioc, A.; Georgescu, F. Links between blocking circulation and precipitation extremes over Romania in summer. Int. J. Climatol. 2015, 36, 369–376. [Google Scholar] [CrossRef]
- Yamada, T.J.; Takeuchi, D.; Farukh, M.A.; Kitano, Y. Climatological Characteristics of Heavy Rainfall in Northern Pakistan and Atmospheric Blocking over Western Russia. J. Clim. 2016, 29, 7743–7754. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Ji, L.; Lin, W.; Ni, Y. The maintenance of the blocking over the Ural Mountains during the second Meiyu period in the summer of 1998. Adv. Atmos. Sci. 2001, 18, 87–105. [Google Scholar]
- Chen, G.T.-J.; Wang, C.-C.; Wang, A.-H. A Case Study of Subtropical Frontogenesis during a Blocking Event. Mon. Weather Rev. 2007, 135, 2588–2609. [Google Scholar] [CrossRef] [Green Version]
- Antokhina, O.Y.; Antokhin, P.N.; Martynova, Y.V.; Mordvinov, V.I. The impact of atmospheric blocking on spatial distributions of summertime precipitation over Eurasia. IOP Conf. Ser. Earth Environ. Sci. 2016, 48, 012035. [Google Scholar] [CrossRef]
- Nakamura, H.; Nakamura, M.; Anderson, J.L. The Role of High- and Low-Frequency Dynamics in Blocking Formation. Mon. Weather Rev. 1997, 125, 2074–2093. [Google Scholar] [CrossRef] [Green Version]
- Masato, G.; Hoskins, B.J.; Woollings, T.J. Wave-breaking characteristics of midlatitude blocking. Q. J. R. Meteorol. Soc. 2011, 138, 1285–1296. [Google Scholar] [CrossRef]
- Schubert, S.D.; Wang, H.; Koster, R.D.; Suarez, M.J.; Groisman, P.Y. Northern Eurasian Heat Waves and Droughts. J. Clim. 2014, 27, 3169–3207. [Google Scholar] [CrossRef]
- Li, J.; Ruan, C. Corrigendum: The North Atlantic-Eurasian teleconnection in summer and its effects on Eurasian climates (2018 Environ. Res. Lett. 13 024007). Environ. Res. Lett. 2018, 13, 129501. [Google Scholar] [CrossRef]
- Antokhina, O.Y.; Antokhin, P.N.; Devyatova, E.V.; Martynova, Y.V. Atmospheric Blockings in Western Siberia. Part 2. Long-term Variations in Blocking Frequency and Their Relation with Climatic Variability over Asia. Russ. Meteorol. Hydrol. 2018, 43, 143–151. [Google Scholar] [CrossRef]
- Coumou, D.; Capua, G.D.; Vavrus, S.; Wang, L.; Wang, S. The influence of Arctic amplification on mid-latitude summer circulation. Nat. Commun. 2018, 9. [Google Scholar] [CrossRef] [PubMed]
- Lejenäs, H.; Økland, H. Characteristics of northern hemisphere blocking as determined from a long time series of observational data. Tellus A 1983, 35A, 350–362. [Google Scholar] [CrossRef]
- Schneider, U.; Becker, A.; Finger, P.; Meyer-Christoffer, A.; Ziese, M.; Rudolf, B. GPCC’s new land surface precipitation climatology based on quality-controlled in situ data and its role in quantifying the global water cycle. Theor. Appl. Climatol. 2013, 115, 15–40. [Google Scholar] [CrossRef]
- Schneider, U.; Becker, A.; Finger, P.; Meyer-Christoffer, A.; Ziese, M. GPCC Full Data Monthly Product Version 2018 at 0.25°: Monthly Land-Surface Precipitation from Rain-Gauges Built on GTS-Based and Historical Data; WMO: Geneva, Switzerland, 2018. [Google Scholar]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- North, G.R.; Bell, T.L.; Cahalan, R.F.; Moeng, F.J. Sampling Errors in the Estimation of Empirical Orthogonal Functions. Mon. Weather Rev. 1982, 110, 699–706. [Google Scholar] [CrossRef]
- Wirth, V.; Riemer, M.; Chang, E.K.M.; Martius, O. Rossby Wave Packets on the Midlatitude Waveguide—A Review. Mon. Weather Rev. 2018, 146, 1965–2001. [Google Scholar] [CrossRef]
- Sinyukovich, V. The water balance of the Selenga river basin. Geogr. Nat. Resour. 2008, 29, 54–56. [Google Scholar] [CrossRef]
- Antokhina, O.Y.; Antokhin, P.N.; Devyatova, E.V.; Mordvinov, V.I. Dynamic Processes in the Atmosphere Determining Summertime Precipitation Anomalies in The Eastern Siberia And Mongolia Fundame. Appl. Climatol. 2018, 5, 10–27, (In Russian with English summary). [Google Scholar]
- Chen, H.; Teng, F.; Zhang, W.; Liao, H. Impacts of Anomalous Midlatitude Cyclone Activity over East Asia during Summer on the Decadal Mode of East Asian Summer Monsoon and Its Possible Mechanism. J. Clim. 2017, 30, 739–753. [Google Scholar] [CrossRef]
- Sato, N.; Takahashi, M. Dynamical Processes Related to the Appearance of Quasi-Stationary Waves on the Subtropical Jet in the Midsummer Northern Hemisphere. J. Clim. 2006, 19, 1531–1544. [Google Scholar] [CrossRef]













| Total Precipitation in the Selenga Basin | Blocking Region | |||
|---|---|---|---|---|
| European Blocks | Urals–Western Siberia Blocks | Eastern Siberia–Mongolia Blocks | Russian Far East–Okhotsk Sea Blocks | |
| Mongolian part precipitation | −0.31 | 0.20 | 0.61 | 0.31 |
| Russian part precipitation | 0.55 | 0.43 | 0.11 | 0.31 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Antokhina, O.Y.; Antokhin, P.N.; Martynova, Y.V.; Mordvinov, V.I. The Linkage of the Precipitation in the Selenga River Basin to Midsummer Atmospheric Blocking. Atmosphere 2019, 10, 343. https://doi.org/10.3390/atmos10060343
Antokhina OY, Antokhin PN, Martynova YV, Mordvinov VI. The Linkage of the Precipitation in the Selenga River Basin to Midsummer Atmospheric Blocking. Atmosphere. 2019; 10(6):343. https://doi.org/10.3390/atmos10060343
Chicago/Turabian StyleAntokhina, Olga Yu., Pavel N. Antokhin, Yuliya V. Martynova, and Vladimir I. Mordvinov. 2019. "The Linkage of the Precipitation in the Selenga River Basin to Midsummer Atmospheric Blocking" Atmosphere 10, no. 6: 343. https://doi.org/10.3390/atmos10060343
APA StyleAntokhina, O. Y., Antokhin, P. N., Martynova, Y. V., & Mordvinov, V. I. (2019). The Linkage of the Precipitation in the Selenga River Basin to Midsummer Atmospheric Blocking. Atmosphere, 10(6), 343. https://doi.org/10.3390/atmos10060343






