Abstract
We present a comprehensive catalog of geomagnetic storms (GSs) with a Dst index nT detected during solar cycles (SCs) 23 and 24 (1996–2019). About 550 events were identified in the Kyoto database and used as a starting point for this study. The solar origin of the GSs, in terms of coronal mass ejections (CMEs), solar flares (SFs), and in situ-observed energetic particles, was identified where possible using temporal constraints and wide Earth-directed ejecta. In addition, any accompanied interplanetary (IP) sources, such as ICMEs and IP shock waves detected at 1 AU, are also considered. The resulting occurrence rates and correlation plots are presented and discussed in the space weather framework.
1. Introduction
The term geomagnetic storm (GS) is used to describe, in general, a significant disruption in Earth’s magnetosphere, driven by structures in the solar wind [1]. The concept was proposed for the first time by Alexander von Humboldt as magnetic storms, in order to describe and link between the rapid magnetic declination variations and the appearance of the Northern Lights phenomena [2]. This ground-based disturbance intensifies and prolongs when a prevalent southward-directed magnetic field () is present [3].
The fundamental cause of these storms lies in the magnetic interaction between a planetary magnetosphere and the interplanetary magnetic field (IMF) [4]. A GS is a phenomenon of energy transfer between (ejecta in) the solar wind and the terrestrial magnetosphere based on the mechanism of magnetic reconnection [1]. The latter process is sufficiently effective when the IMF of the plasma structure is southward-directed [5]. During the reconnection, solar wind plasma is injected and transported to the night-side magnetosphere. However, the protons drift to the west, whereas the electrons to the east, thus forming a ‘ring current’ around the Earth. It is this current that eventually causes a sharp decrease in the magnetic field measured by ground-based stations [6].
The strongest GSs occur when coronal mass ejections (CMEs) are expelled in the Earth direction, arrive at 1 AU as soon as about 12–13 h (based on the fastest ejecta ever recorded) and up to 5–6 days later (based on typical slow solar wind speed). These are termed interplanetary (IP) CMEs or ICMEs, creating conditions for magnetic field-line reconnection [5,7,8,9,10,11]. The reliable identification of (I)CME geoeffectiveness is a topic of ongoing research [12].
There are other recognized sources of the geomagnetic disturbances predominantly driven by fast solar wind streams and occasionally repeating with the solar rotation (termed recurrent GSs). Such structures are the high-speed streams (HSSs), crossings of the heliospheric current sheet, and corotating interaction regions (CIRs) [12]. The resulting GSs are often of weaker intensity, but longer in duration.
The effects by ICMEs/IP shocks and HSSs/CIRs are also responsible for different effects on the terrestrial radiation belts [13], whereas fast variations of the magnetic field vector are currently linked to geomagnetically induced currents (GICs) in ground-based conduction systems [14,15], which subsequently may cause transformer damages. On the other hand, the Starlink satellite failure in February 2022 happened during the course of a weak GS [16] with the exact reasons still being debatable, e.g., see [17] and the references therein. Novel techniques, such as machine learning algorithms for the classification of GSs, are also being tested [18].
In general, the GS progresses through three phases. It commences with a sudden compression of the magnetosphere due to an increase in the dynamic pressure of the solar wind. This phase, known as sudden storm commencement (SSC), is characterized by an abrupt positive variation of the disturbance storm time (Dst) index. The subsequent phase is referred to as the main phase. Here, the Dst index takes negative values during the injection of energized plasma in the equatorial ring current, ultimately reaching its minimum value. This is followed by the recovery phase, wherein particle transport into the ring current decelerates, enabling various loss processes to diminish ring current particle fluxes to their quiet-time level. This process is reflected by the Dst values, which start to rise until they return to pre-sudden commencement levels, signifying the restoration of the geomagnetic field to pre-storm levels [3,4,19].
Various indices are used to measure the GS intensity (see, e.g., https://www.ngdc.noaa.gov/stp/geomag/indices.html, accessed on 26 November 2023), and the commonly used ones are listed below:
- Dst is a geomagnetic index that measures the magnitude of the GSs. It is calculated based on the average value of the horizontal component of the Earth’s magnetic field. The intensity is expressed in negative values and measured in nano-Teslas [20,21,22]. This index is directly related to the total kinetic energy of the ring current particles and the overall energetics of the GS. The Sym-H index is the 1 min resolution of Dst index.
- The Kp (planetary) index quantifies the disturbance of the horizontal component of Earth’s magnetic field due to geomagnetic activity. It ranges from 0 to 9, with higher values indicating more-severe disturbances [23,24].
- The Ap (planetary) index is another measure of geomagnetic activity, representing the planetary averaged amplitude of the magnetic field. It provides a daily average value [25].
- The Auroral Electrojet (AE) index measures the level of geomagnetic activity in the auroral zone. It is also used as an indication of the strength of the GS [26].
- The AA index is a global index of magnetic activity from the K indices of two nearly antipodal magnetic observatories in England and Australia. Its variation, the AA index, is the three-hourly equivalent amplitude antipodal index.
- Other indices or variations of the above (https://isgi.unistra.fr/indices_asy.php, accessed on 26 November 2023).
There is no unique definition of the strength of the GSs concerning the Dst index, as the thresholds differ between different authors (the amplitude of the Dst index will preferably be used in the text): moderate ( |Dst| nT), intense ( |Dst| nT), and super-storms (|Dst| nT) were introduced by [3]; intense |Dst| nT and super-intense |Dst| nT were proposed by [27]; many teams use the term ‘major’ for |Dst| nT; whereas the strongest GSs on record (following the Carrington–Hodgson event on 1–2 September 1859) are named ‘extreme’ [28]. A combination between two indices was proposed by [3,24], where the GSs are categorized into weak (30 < |Dst| < 50 nT, with 0 ≤ Kp ≤ 5), moderate ( |Dst| nT, with 5 < Kp < 7), and intense (|Dst| nT, with 7 ≤ Kp ≤ 9).
Alternatively, NASA employs the NOAA Space Weather Scale (https://www.swpc.noaa.gov/noaa-scales-explanation, accessed on 26 November 2023) to categorize the intensity of GSs. Known as the G-scale, it spans from G1, denoting minor storms, to G5, representing extreme events. A G1 storm, classified as minor, may result in slight fluctuations in power grids and minor disruptions to satellite operations. A G2 storm, categorized as moderate, can trigger voltage alarms in power systems, potential transformer damage, and increased drag on low Earth orbit satellites. G3 storms, characterized as strong, have the potential to induce voltage control issues, transformer damage, and satellite surface charging. Severe G4 storms can lead to widespread voltage control problems, transformer damage, and satellite surface charging. In the most-extreme cases, G5 storms can lead to a complete collapse of power systems, prolonged surface charging of satellites, and even damage to pipeline systems. The engineering aspects of this scale impressively demonstrate the importance of the GSs (and their precursors) to space weather research [29]. The term space weather is considered here in a broader framework of all direct and indirect influences of the solar activity phenomena on the terrestrial atmospheric layers, technology, and human safety [30]. A focused study on the space weather effects (including the strength and structure of GSs) on satellite operations was recently compiled [17].
A rich volume of research has been devoted to the GS phenomenon, e.g., see [27,31,32] for literature reviews, since a representative description goes beyond the scope of this report. For example, very early on, it was established that the Dst index varies with the conditions in the IP space [33], and the topic continued to be further explored with the availability of new satellite data, e.g., [7,34]. Recent studies over two solar cycles (SCs) confirm the stronger trends between the Dst and the IP parameters compared to solar eruptive phenomena. Namely, a recent study [35] explored the Pearson correlations between 111 GSs with |Dst| nT and a variety of physical parameters in SC23 and 24, confirming strong relationships with total B-field, the product between solar wind speed and the -component and the ICME speed. Moderate correlations are reported with the solar wind speed and pressure and weak/no clear correlation with plasma density, solar flare (SF) class, CME speed and angular width (AW), and the fluxes and fluences of energetic particles. Over the same time period, another study [32] extended the list of GSs with |Dst| nT to 179 in SC23 and 85 in SC24 or a reduction of 47% of the GS activity being present. They reported correlations between several GS indices (SymH, Kp, and AE) with solar wind speed, IMF , and their product and confirmed the high correlations in SC23, but not in SC24.
In order to explore the statistical relationship, a list of GSs needs to be compiled with carefully identified parent solar and/or accompanied IP activity. Lists of historical GSs can be found in [36,37]. Examples of major GSs (|Dst| nT) generated by CIRs were presented by [38], another study in SC24 was completed by [39], but no list was provided, whereas 12 cases in 1996–2016 were reported by [40]. Due to the lack of a comprehensive listing covering the period of interest for our study, we will not consider the effects of CIRs separately.
Previous catalogs of GSs considered SC23 or earlier time periods and have been reported in the past with a different focus: to search for solar and IP origin of major (|Dst| nT) GSs [41]; to study the 50 most intense in the Dst index GSs [42]; to explore extreme GSs [36]. An important aspect of any follow-up studies is the ability to compare the results. This is impeded to a degree when no catalog is provided, as in the case of the recently completed statistical analysis with the IP parameters covering SC23 and 24 by [32].
The aim of this study was to provide an open-access catalog of GSs with a Dst index nT, together with their solar and IP sources in SC23 and 24 (1996–2019). We upgraded a previous study focused on SC24 [43] and propose a source identity based on an association study between the GS peaks and the timing and physical properties of the IP structures and CMEs. The here presented GSs can be additionally affected by HSSs/CIRs, which was not accounted for with the performed analyses. In contrast, a set of criteria was applied on the entire list of GSs, resulting in certain/uncertain associations. Our catalog aims to serve as a basis of a living document with additions and corrections being periodically implemented, e.g., filtering out a possible contamination by CIRs, especially for the weaker GSs. The online version of the list will be supported at https://catalogs.astro.bas.bg/ (accessed on 26 November 2023).
2. Methodology
2.1. Data
In order to characterize the strength of the GS storm, we used the Dst index provided by the World Data Center for Geomagnetism, Kyoto: https://wdc.kugi.kyoto-u.ac.jp/dstdir/index.html (accessed on 26 November 2023). The final values of the Dst index are currently available through the end of 2016, whereas for the period 2017–2019 of our list, we used the provisional ones; however, only minor changes in the Dst index were expected. Based on the visual inspection of the monthly Dst-curves and to the best of our abilities, we identified 546 GSs where the Dst value dropped below the adopted threshold for this study of nT, as reported to the nearest hour. No identification of the onset and end times of each GS was attempted by us; instead, we focused on the amplitude of the Dst index. For the purposes of this statistical analysis, pre-event disturbances were also not considered. However, we noticed that the identity of 49 GSs seemed to be compromised due to a previous event or an extended turbulent period according to our assessment. These GSs are denoted as ‘uncertain’ in our list.
Apart from the Dst index, we collected the readily provided characteristics of ICMEs, IP shock waves, CMEs, and in situ-observed energetic particles, using data from various spacecraft positioned at the Lagrangian point L1 or at geostationary orbit for the SFs.
The speeds of the ICMEs observed close to Earth have been already identified and reported in several sources. A catalog of ICME timing and characteristics based on Wind satellite data is provided at: https://wind.nasa.gov/ICME_catalog/ICME_catalog_viewer.php (accessed on 26 November 2023). An alternative ICME catalog using data from the ACE satellite can be found here: https://izw1.caltech.edu/ACE/ASC/DATA/level3/icmetable2.htm (accessed on 26 November 2023). We preferred the latter, as the catalog gives also the solar origin (i.e., the parent CMEs) for some of the ICMEs.
The timing and speeds of IP shocks using Wind observations are given in great detail by https://lweb.cfa.harvard.edu/shocks/ (accessed on 26 November 2023), where we used the median reported value for the shock speed. Alternative sources for IP shocks, both from the Wind and ACE spacecraft, can be found at http://www.ipshocks.fi/database (accessed on 26 November 2023); however, due to some temporary access interruptions, we could not use this database for our study.
The properties of the CMEs were collected from the well-known CDAW SOHO/LASCO database https://cdaw.gsfc.nasa.gov/CME_list/ (accessed on 26 November 2023). The following parameters were adopted: timing (first occurrence above the occulting disk); linear speed, i.e., the on-sky projected speed, obtained by fitting a straight line to the height–time measurements of the fastest segment of the leading edge of the CME; AW, i.e., the sky-plane width of CMEs, which is typically measured in the field of view between 1.5 and 6 solar radii; and the measurement position angle (MPA), as measured from the north and advancing in the counterclockwise direction. Both AW and MPA are reported in degrees.
In order to quantify the geomagnetic effects due to phenomena (e.g., electromagnetic emissions or particles) originating at the same solar eruption, SFs and solar energetic particles are also considered. These are the ones physically related to the already identified CME eruption. The SF information was taken from a GOES-based list with the timing, soft X-ray (SXR) class, and helio-locations: https://www.ngdc.noaa.gov/stp/space-weather/solar-data/solar-features/solar-flares/x-rays/goes/xrs/ (accessed on 26 November 2023). For the case of the in situ-observed particles, e.g., protons (SEPs) and electrons (SEEs), we compared their associated CMEs and SFs (identified previously) with the GS-associated CMEs and SFs in our list. The matching cases were selected, and only the peak particle fluxes were used here, as provided by the respective catalogs: Wind/EPACT SEP catalog http://www.stil.bas.bg/SEPcatalog/ (accessed on 26 November 2023) (19–28 MeV) and ACE/EPAM SEE catalog https://www.nriag.sci.eg/ace_electron_catalog/ (accessed on 26 November 2023) (103–175 keV), reported in [44] and [45], respectively.
2.2. Association Procedure
When associating the IP counterpart of a GS, we only employed timing constraints. The travel time of the disturbance first detected at L1 to the magnetosphere was estimated to be within one hour, depending on the speed. Since we did not quantitatively evaluate the onset time of the GSs, but used their peak times instead, we needed to allow for a wider time window between the hour of the minimum Dst and its driver at L1. Namely, we searched for an identified ICME and IP shock wave within a 1-day period prior to the GS peak time. Based on this guideline, we could identify 228 ICMEs (or about a 42% of occurrence rate) and 179 IP shock waves (close to 33%, respectively). In the majority of the cases, the IP phenomenon identified by us was a unique candidate.
The following criteria for the search of the solar driver of GSs were used: Starting from the hour of minimum value of the Dst measurement (depicting the GS peak), we isolated 3- and 5-day periods ahead of each GS. These periods cover the characteristic travel time of ejecta from the Sun to Earth. Longer periods are possible, though less probable to cause detectable geomagnetic response. Firstly, in a shorter time period, we looked for Earth-directed ejecta, namely a halo CME (with an AW of 360°), with the fastest candidate being selected. In the case of no candidates, we searched for a halo CME with a speed above 600 kms in the wider time window. The imposed threshold for the speed was subjective to a degree; however, we kept the requirement as the ejecta should be faster than the typical speeds of the slow solar wind. Furthermore, we set an additional requirement for the AW to be above 90°. This set of criteria (or quality flagging) was applied to the entire GS event list. For the major GSs (|Dst| nT), ∼100 cases, we adopted the associations from our previous work [35].
A main source of uncertainty on the solar origin identification followed from the non-fulfillment of the adopted association criteria. As a rule, all proposed associations within a 3-day period were considered as certain, whereas those within a 3- to 5-day period were denoted as uncertain. Any other cases that diverged to a small degree from the above-described criteria were also considered uncertain associations (e.g., the candidate was a non-halo CME with the specified 3-day period, slow CME, or other deviations from the rules, but reported as a GS origin by other online catalogs, as described above). From the entire GS list, we could identify in total 330 CMEs or the occurrence rate of 60%, split into 157 (≲29%) certain and 173 (≳31%) uncertain solar origin associations. The large amount of uncertain CME associations was due to the majority of weak GSs in our list.
Furthermore, we investigated the certain vs. uncertain CME association among the 49 uncertain GSs and obtained 4 vs. 17 cases, respectively (whereas the remaining 28 uncertain GSs had no CME association). Due to the low fraction of uncertain GS-related CMEs, the entire GS distribution will be considered as certain only.
The SF association with GSs was performed via the SF inter-connection to CMEs. The later procedure is relatively easy to complete and was based on the timing (within 1 h) and helio-location (the SF position to be within 90° of the reported MPA of the CME). Thus, concerning the SF as a solar origin, we obtained 227 GSs with an SF or 42%. Based on the certain/uncertain label of the CME, we obtained 118 (22%) certain SFs and 109 (20%) uncertain ones.
From the entire list, only 90 SEPs (16%) and 110 SEEs (20%) could be associated with GSs, based on the reported CMEs and SFs linked to these particles. Since the CMEs played the role of an intermediary here as well, the certain and uncertain labels of the particles were due to certain and uncertain types of CMEs.
For visualization purposes, we used the entire GS sample, or over SC23 and 24. For completeness, we calculated occurrence rates separately for SC23 and SC24. All three considered time periods are summarized in Table A1 in Appendix A.
The IP driver proposed by us and solar origin are not immune to misidentifications and should be regarded as a first approximation only. IP structures such as HSSs and/or CIRs can be the true cause of many of the weaker GSs. For example, a catalog of high-speed streams and GSs is available at http://www.geodin.ro/varsiti/ (accessed on 26 November 2023), but only during SC24. As already explained above, due to the lack of a consistent list of solar wind streams and their link to GSs over the last two SCs, we will not consider this aspect in our analyses.
Another important and very helpful online tool for inspecting plasma structures in the heliosphere is provided by http://helioweather.net/archive/ (accessed on 26 November 2023). Again, the coverage was only during SC24, and the information from these simulations could only be applied over a smaller fraction of our list. For the consistency of the association procedure over both SCs, we had to drop this source.
3. Results
3.1. Catalog of GSs
The total number of GSs in SC23+24 after our visual identification amounted to 546; see Table A2 in Appendix B; of these, 361 (or 66%) occurred in SC23 and 185 (34%) in SC24, plotted in the left side of Figure 1 using a stacked histogram. The dark-colored bars denote the number of certain events and the fraction of light-gray-colored bars the uncertain GSs. The SC24 was also weaker in terms of GSs with a 51% drop.
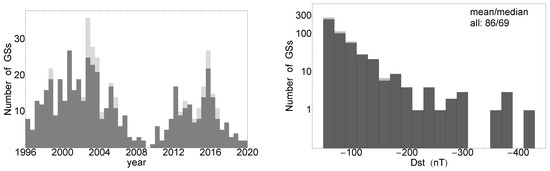
Figure 1.
Yearly distribution of the GSs on the left (bin width of 0.5 years) and Dst index distribution on the right (bin width 20 nT). Certain events are shown in dark and uncertain in light gray color.
The distribution of GSs according to their Dst index is shown in Figure 1 (right) for the entire time period, SC23+24. The strongest GS in our list had a Dst index of nT, whereas the majority of the GSs had |Dst| nT. For better visualization, we used the log10-linear format. The power law distribution of the phenomena can be recognized, at least for the weak GSs: when the |Dst| is between 50 and 200 nT, the magnitude of the slope is ≲0.03, whereas above 200 nT we notice a flat distribution consisting of a few GSs. At the lower end of the Dst distribution cluster are the uncertain GSs: these GSs had, on average, lower mean and median |Dst| values (in the range of 57–74 nT) regardless of the time period of interest. The certain GSs, on the other hand, had the same values as for the entire sample (from 66 to 92 nT in absolute values), whereas, for the entire sample (denoted by ‘all’ in the plot), the values were 86/69. All mean and median values are summarized in Table 1 for each of the time periods of interest.

Table 1.
Mean/median values for the entire sample (given in bold font) and separately for the certain and uncertain categories for each of the considered phenomena denoted by ‘type’. Units: absolute value of Dst in nT; speeds in kms; SEP flux in differential proton flux units (DPFU) or protons/(cm sr s MeV); SEE flux in differential electron flux units (DEFU) or electrons/(cm sr s keV). The exact sample size is given in parentheses.
3.2. IP Origin
For SC23+24, we identified 42% (228/546) ICME events and 33% (179/546) IP shock waves with similar fractions for the ICMEs in each of the two SCs; see Table A1. For completeness, Table 1 gives the mean and median values for the speeds of the GS-associated ICMEs and IP shock waves for the certain, uncertain, and both categories. However, the number of uncertain (according to the GS identity) ICME and IP shocks was minimal. This is why, for the plots and correlations with the IP phenomena, we will not differentiate into two categories. The mean/median values of the entire sample (given in bold font in Table 1) were nearly identical to those of certain categories.
The scatter plots between the speeds and the Dst index are shown in Figure 2 and Figure 3 (left) in the same linear scale for comparison. On the right are shown the histograms for the speeds of the GS-associated phenomena, ICME or IP shock, respectively. A clustering at small values i.e., for the speed at around 500 kms and for the |Dst| nT) was evident. The extent of IP shock wave speeds was slightly larger than the range in speeds covered by the ICMEs (after the exclusion of the outlier). The mean/median values of the speeds can be inspected from Table 1. The median values of the ICME and IP shock speeds were similar, 460–480 kms, whereas the sample of the IP shock speeds had a larger mean value by about 40 kms compared to the ICME sample (Table 1).
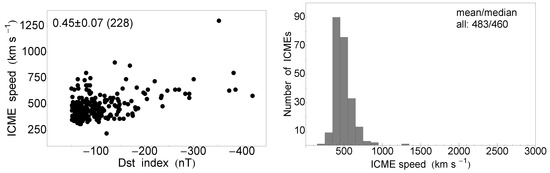
Figure 2.
Scatter plots between the Dst index (nT) and the ICME speed (on the left) and its distribution (on the right, bin width of 100 kms) for the entire event sample.
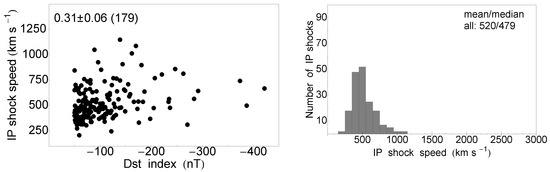
Figure 3.
Scatter plots between the Dst index (nT) and the IP shock speed (on the left) and its distribution (on the right, bin width of 100 kms) for the entire event sample.
In both cases, there was a rough positive trend in the correlation between the speeds of IP phenomena and the GS strength, as shown in each plot, however not very strong due to the large spread. For quantitative comparison, we used Pearson correlation coefficients, whereas for the uncertainty, we used the bootstrapping method, as described in [44,45]. A slightly better correlation was obtained between the |Dst| and ICME speeds (), compared to the IP shock speeds (). The sample size is given in parentheses in the plots. In terms of the SC trends, the values for the speeds in SC23 tend to be slightly larger than those in SC24, especially for the IP shocks.
3.3. Solar Origin
The solar origin of GSs is given via the GS-associated CMEs, SFs, SEPs and SEEs with occurrence rates in SC23+24 as follows, 60%, 42%, 16% and 20%, respectively, with only slight variations (of the order of several percents) between the SCs; see Table A1 for the details. The focal point here is the association of the CMEs, and here, we will recognize certain and uncertain cases. Specifically, Figure 4 shows the scatter plot between the CME linear speed and Dst index (on the left) and the histogram of the CME speed (on the right). Empty circles and light gray color denote uncertain events, whereas filled circles and dark color denote certain events. The uncertain CME associations were concentrated for slower ejecta with mean/median values of 915/791 kms; see also Table 1. The mean/median values for the speeds of the certain-type CMEs were around 1000 kms and were the same as the mean values of the entire CME sample (though the median value for the latter was lower, 874 kms).
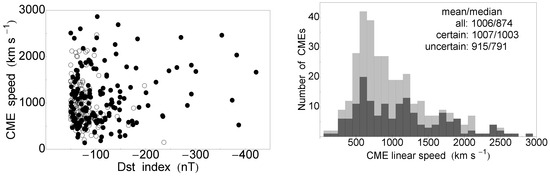
Figure 4.
Scatter plots between the Dst index (nT) and the CME linear speed (on the left) and the CMEs’ speed distribution (on the right, bin width of 100 kms). Empty circles and light gray color denote uncertain events, whereas filled circles and dark color the certain events.
Overall, no clear correlations could be identified between the GSs and CME speed properties; see Figure 4 (left) for neither of the categories: certain: ; uncertain: ; all: . The abrupt starting line is due to the threshold selection of nT. Similarly, the relationship with the CME AW is shown in Figure 5 (left), and no correlation with the Dst index was obtained: certain: ; uncertain: ; all: . There was an over-representation of halo CMEs, and the majority of non-halo cases (<300 degrees) were uncertain.
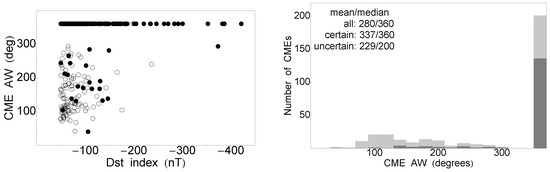
Figure 5.
Scatter plots between the Dst index (nT) and the CME AW (on the left) and the CME AW distribution (on the right, bin width of 20 degrees). Plotting style as in Figure 4.
The remaining phenomena (SF class and energetic particle flux) covered a range of several orders of magnitudes. This is why the scatter plots are given in log10–log10 form; see Figure 6, Figure 7 and Figure 8 (left). There was no correlation between the SF class or particle intensities with the Dst index, and the uncertainty was very large, due to the relatively small sample size. The Pearson correlations were calculated between the log10 values, and the results for the SFs are: certain: , uncertain: , all: . Similarly, for the SEPs, we obtained the following: certain: , uncertain: , all: , whereas for the SEEs we had: certain: , uncertain: , all: . The sample size is given in Table 1.
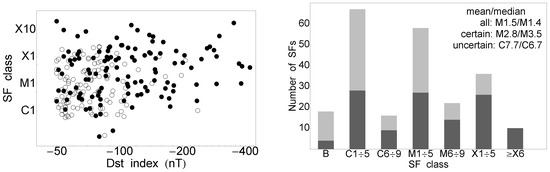
Figure 6.
Scatter plots between the Dst index (nT) and the SF class (on the left) and the SF class distribution (on the right). Plotting style as in Figure 4.
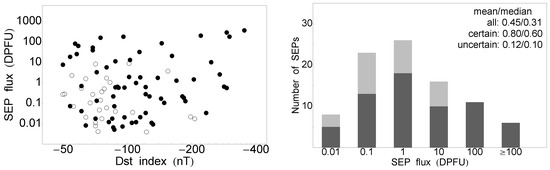
Figure 7.
Scatter plots between the Dst index (nT) and the SEP flux (on the left) and the SEP flux distribution (on the right). Plotting style as in Figure 4.
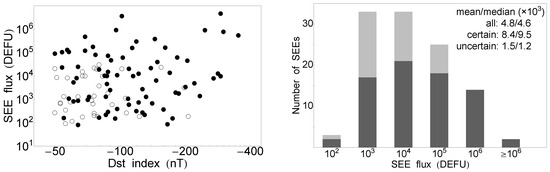
Figure 8.
Scatter plots between the Dst index (nT) and the SEE flux (on the left) and the SEE flux distribution (on the right). Plotting style as in Figure 4.
All histograms (on the right) are given in binned format, as denoted by the x-label. Overall, the certain sample tended to have the largest mean/median values, followed by the entire sample, and the smallest values were for the uncertain GS-associated SFs, SEPs, and SEEs. The exact mean/median values in SC23+24 are given in the plots.
In the histogram for the SFs, the bins for a given class, e.g., X, were significantly smaller than those of the C- and M-class, the latter two groups being also the most-abundant ones. Also, the number of events denoted by 6 ÷ 9 was always less than the sample denoted by 1 ÷ 5, independent of the SF class. The mean/median values of the SF class for the certain and all GS-associated SFs were in the lower M-class range, whereas for the uncertain ones, they decreased to the C-class values. Furthermore, we calculated the mean/median value for the helio-locations of the entire sample of GS-associated SFs (no plots are shown) and obtained S01/S06 for the helio-latitude and W04/W05 for the helio-longitude.
Concerning the particle distributions in Figure 7 and Figure 8, the peak of the distribution was shifted towards the middle, where there were also mean/median values for the certain and also for the entire sample. For completeness, the mean/median values were calculated in the three time periods (Table 1); however, they reflect the weight of the largest bins of the distributions.
4. Discussion
When comparing our results with previously published results of GSs over the same time periods by [32], we noted there were fewer reported events, namely 179 in SC23 and 85 in SC24 (no catalog supplied). Even after eliminating our uncertain GS identification (leading to 331 in SC23 and 166 in SC24), the differences were considerable. The cause of such discrepancies could be due to the different selection criteria applied in either case. According to the results by [32], there was a 47% drop in the geomagnetic activity in SC24 compared to the previous one, which is similar to the one obtained by us of 51% (for the entire GS sample and, similarly, for the certain GSs only). This is one of the studies that explored the relationship between GSs and IP parameters over the same two SCs. The obtained trends by [32] (see their Figures 7 and 8) between the GS indices with the product between solar wind speed and is reminiscent of the overall trends between the Dst index with ICME and IP shock speeds obtained in our work (Figure 2 and Figure 3).
Another statistical work over SC23 and 24 [35] that presented the occurrence rates between the GSs and the different solar origin phenomena, however, focused on major GSs with Dst nT. Apart from the occurrence rate for the IP shocks (33%, 179/546), which was not considered there, we could still compare the results on GS-associated phenomena. Below, we compare, from one side, the upper limits of the occurrence rates as obtained in our study (with a sample size of 546) and, on the other, the corresponding values in our previous work [35] (with a sample size of 111), namely:
- GSs–ICMEs: 42% (228/546) vs. 85% (94/111);
- GSs–CMEs: 60% (330/546) vs. 72% (80/111);
- GSs–SFs: 42% (227/546) vs. 55% (61/111);
- GSs–SEPs: 16% (90/546) vs. 34% (38/111);
- GSs–SEEs: 20% (110/546) vs. 30% (33/111).
The values obtained in this study (based on a larger sample with numerous weaker GSs) were all smaller. This can be explained by the fact that larger eruptions manifest overall as stronger solar and IP phenomena. Furthermore, we investigated their correlation trends as depicted in the scatter plots and quantified them in terms of the Pearson correlation coefficients. We focused on the results only over SC23+24, and the results in this study were again predominantly lower (but, mostly, not statistically significant) compared to those reported previously by [35], namely:
- Dst–ICME speed: (228) vs. 0.62 (94);
- Dst–CME speed: (330) vs. 0.30 (80);
- Dst–CME AW: (330) vs. 0.26 (80);
- Dst–SF class: (227) vs. 0.19 (61);
- Dst–SEP flux: (90) vs. 0.35 (38);
- Dst–SEE flux: (110) vs. 0.27 (33).
When considering the mean/median values, both studies revealed only marginal differences for the CME speed, but overall, smaller values for the solar parameters. The latter was particularly pronounced in the case of SEE flux, which was two orders of magnitude lower, whereas the SF class and SEP flux were lower by one order of magnitude.
The applicability of statistical results reached an upper limit especially when the sample contained a large amount of scatter and a physical relationship can be easily lost. Moreover, the parameters used for the correlations are often subject to limitations or errors. A greater effort needs to be devoted to the association procedure itself in order to develop procedures for improving its accuracy. A reliable identification of GS precursors would be of use for the development of novel schemes and the improvement of existing forecasting schemes.
Our motivation for the inclusion of GS-related SFs was grounded in the improved understanding of the overall complexity and magnetic environment of the underlying active region that gives rise to the pair SF–CME. The structure and orientation of ICMEs based on the magnetic footprints of their CME counterparts and subsequent IP propagation/rotation/deflection are still subjects of ongoing research [46]. The electromagnetic emission is also the first signal to be observed after a solar activity event, and its GS precursor potential deserves further examination.
Chronologically, the second space weather phenomena to arrive are the fluxes of electrons, followed by the protons. They possess a latent space weather risk due to their radiation hazards for equipment and humans. Since the charged particles follow a magnetic path, they may well be deflected in the IP space due to magnetic irregularities (in plasma structures), and their forecasting potential is still uncertain. The simultaneous impact of SEP and SEE fluxes from follow-up events to an ongoing GS also awaits a large-scale investigation, although a few single-case studies have been attempted [35]. For example in our earlier analyses [47], low-energy protons tended to be over-represented at minor-to-moderate GSs with |Dst| nT, compared to major GSs with |Dst| nT, despite the larger scatter of the distribution. In summary, with this extended study, we confirmed previous studies on the correlations between GSs and the IP/solar origin of GSs [32,35].
5. Conclusions
This work offers a consistent list of 546 GSs with Dst index nT in SC23 and 24. ICMEs and IP shock waves preceding the GSs were identified as their most-probable IP origin, whereas the solar origin was based on (fast, halo) CMEs, 3 to 5 days prior to the GSs. Despite the large fraction of uncertain CME (and their secondary) associations, our results were consistent with previous research on the correlations with IP phenomena and with the relationships between solar phenomena and larger GSs.
The focus in this study was set on selected IP and solar phenomena. The GS strength can be correlated with other available physical quantities related to ICMEs, such as plasma density, components of the measured speed, magnetic and electric fields, or a combination thereof, e.g., see [12,32,35,48] and the references therein. The weak correlation between the Dst index and ICME/IP shock speeds could well be due to the limitation to just one of the physical parameters measured in situ. A comprehensive investigation over a large GS sample and using the complete set of physical parameters of ICMEs is still lacking.
A few notable conclusions on the geoeffective IP and solar phenomena, based on the analysis performed here, are listed below:
- Half of the GSs were linked to the arrival of an ICME with IP shocks also present;
- Positive trends in the correlation between the Dst and the speeds of ICMEs and IP shocks were obtained, confirming previous results [32,35];
- There were similar numbers of CMEs (halo and high speed, 330) and ICMEs (228);
- CME to ICME deceleration during its propagation in the solar wind was from 1000/874 to 483/460 kms in mean/median values;
- No correlation was found between the Dst and the parameters of the solar events (CME speed, CME AW, SF class, or SEP/SEE flux);
- The GS-related solar events originated close to the solar disk center.
The compiled catalog with the values and timings of the GSs and their associated phenomena will be released as open access via the platform https://catalogs.astro.bas.bg/ (assessed on 26 November 2023) and revised when necessary in the future.
Author Contributions
The authors contributed equally to this work. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Bulgarian–Egyptian inter-academy project by the Bulgarian Academy of Sciences IC-EG/08/2022-2024 and the Egyptian Academy of Scientific Research and Technology (ASRT)/NRIAG (ASRT/BAS/2022-2023/10116).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The complete version of the GS catalog will be released at https://catalogs.astro.bas.bg/.
Acknowledgments
The authors thank the ground-based and space data providers for their free access policy: Kyoto World Data Center—Kyoto, National Aeronautics and Space Administration, and the European Space Agency.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of the data; in the writing of the manuscript; nor in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| ACE/EPAM | Satellite and instrument for particle detection |
| AU | Astronomical unit |
| AW | Angular width |
| CDAW | Coordinated Data Analyses Workshop |
| CIR | Co-rotating interaction region |
| CME | Coronal mass ejection |
| DEFU | Differential electron flux units |
| DPFU | Differential proton flux units |
| GIC | Geomagnetically induced current |
| GS | Geomagnetic storm |
| HSS | High-speed solar wind stream |
| ICME | Interplanetary CME |
| IMF | Interplanetary magnetic field |
| IP | Interplanetary |
| MPA | Measurement position angle |
| NASA | National Aeronautics and Space Administration |
| NOAA | National Oceanic and Atmospheric Administration |
| SC | Solar cycle |
| SEE | Solar energetic electron |
| SEP | Solar energetic proton |
| SF | Solar flare |
| SOHO/LASCO | Satellite and instrument for CME detection |
| SSC | Sudden storm commencement |
| SXR | Soft X-ray |
| Wind/EPACT | Satellite and instrument for particle detection |
Appendix A. Summary of Occurrence Rates

Table A1.
Occurrence rates in % of the GS-associated IP and solar phenomena. In parenthesis are shown the fraction of the event type (from Table 1) to the same number of GSs in each of the time periods.
Table A1.
Occurrence rates in % of the GS-associated IP and solar phenomena. In parenthesis are shown the fraction of the event type (from Table 1) to the same number of GSs in each of the time periods.
| Type | SC23 | SC24 | SC23+24 |
|---|---|---|---|
| ICMEs | 44% (159/361) | 37% (69/185) | 42% (228/546) |
| IP shocks | 35% (127/361) | 14% (52/185) | 33% (179/546) |
| CMEs | 61% (220/361) | 59% (110/185) | 60% (330/546) |
| - certain | 32% (114/361) | 23% (43/185) | 29% (157/546) |
| SFs | 43% (157/361) | 39% (70/185) | 42% (227/546) |
| - certain | 24% (86/361) | 17% (32/185) | 22% (118/546) |
| SEPs | 16% (57/361) | 19% (33/185) | 16% (90/546) |
| - certain | 12% (43/361) | 11% (20/185) | 12% (63/546) |
| SEEs | 19% (69/361) | 22% (41/185) | 20% (110/546) |
| - certain | 14% (51/361) | 12% (23/185) | 14% (74/546) |
Appendix B. Catalog of GSs with Proposed IP and Solar Origin (1996–2019)

Table A2.
A catalog of GSs with identified IP and solar origin. The timings of the latter will be given in the online version. The Dst index is in nT; speed in kms; AW in degrees; rounded SEP flux in DPFU; SEE flux in DEFU. The SF class and location are according to the GOES reports. Abbreviations: u—uncertain; dg—data gap; no—no event found.
Table A2.
A catalog of GSs with identified IP and solar origin. The timings of the latter will be given in the online version. The Dst index is in nT; speed in kms; AW in degrees; rounded SEP flux in DPFU; SEE flux in DEFU. The SF class and location are according to the GOES reports. Abbreviations: u—uncertain; dg—data gap; no—no event found.
| GS | ICME | IP Shock | CME | SF | SEP | SEE | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| yyyy | mm | dd | h | Dst | Speed | Speed | Speed | AW | Class | Location | Flux | Flux |
| 1996 | 1 | 13 | 11 | −90 | no | no | 499 u | 18 | no | no | no | no |
| 1996 | 3 | 11 | 4 | −60 | no | no | u | u | no | no | no | no |
| 1996 | 3 | 20 | 24 | −54 | no | no | 418 u | 59 | no | no | no | no |
| 1996 | 3 | 21 | 23 | −66 | no | no | u | u | no | no | no | no |
| 1996 | 3 | 24 | 3 | −53 | no | no | u | u | no | no | no | no |
| 1996 | 3 | 25 | 2 | −60 | no | no | u | u | no | no | no | no |
| 1996 | 4 | 15 | 1 | −56 | no | no | u | u | no | no | no | no |
| 1996 | 4 | 17 | 9 | −52 | no | no | u | u | no | no | no | no |
| 1996 | 9 | 12 | 9 | −54 | no | no | u | u | no | no | no | no |
| 1996 | 9 | 23 | 8 | −51 | no | no | 410 | 27 | no | no | no | no |
| 1996 | 9 | 27 | 1 | −50 | no | no | u | u | no | no | no | no |
| 1996 | 10 | 19 | 17 | −52 | no | no | u | u | no | no | no | no |
| 1996 | 10 | 23 | 5 | −105 | no | no | 470 u | 170 | B6.0 | no | no | no |
| 1997 | 1 | 10 | 10 | −78 | 450 | 434 | 136 | 360 | no | no | no | no |
| 1997 | 2 | 10 | 11 | −68 | 450 | 618 | 490 | 360 | no | no | no | no |
| 1997 | 2 | 11 | 10 | −60 | no | no | u | u | no | no | no | no |
| 1997 | 2 | 17 | 9 | −54 | no | no | u | u | no | no | no | no |
| 1997 | 2 | 27 | 24 | −86 | no | 543 | 905 u | 209 | B7.2 | no | no | no |
| 1997 | 3 | 28 | 24 | −63 | no | no | u | u | no | no | no | no |
| 1997 | 4 | 11 | 5 | −82 | 460 | 337 | 878 | 360 | C6.8 | S30E19 | 0.0118 | no |
| 1997 | 4 | 17 | 6 | −77 | no | 389 | dg | dg | no | no | no | no |
| 1997 | 4 | 22 | 1 | −107 | 360 | no | u | u | no | no | no | no |
| 1997 | 5 | 2 | 1 | −64 | no | 361 | 255 u | 360 | no | no | no | no |
| 1997 | 5 | 15 | 13 | −115 | 450 | 443 | 464 u | 360 | C1.3 | no | 0.0202 | no |
| 1997 | 5 | 27 | 5 | −73 | 340 | 303 | 296 u | 165 | M1.3 | N05W12 | 0.004 | no |
| 1997 | 6 | 9 | 4 | −84 | 380 | no | u | u | no | no | no | no |
| 1997 | 9 | 3 | 23 | −98 | 410 | 368 | 371 | 360 | M1.4 | N30E17 | no | no |
| 1997 | 9 | 18 | 6 | −56 | no | no | u | u | no | no | no | no |
| 1997 | 10 | 1 | 16 | −98 | 450 | no | 359 | 360 | no | no | no | no |
| 1997 | 10 | 10 | 20 | −65 | 430 | 471 | 506 | 103 | no | no | no | no |
| 1997 | 10 | 11 | 4 | −130 | 400 | no | 1271 | 167 | no | no | 0.0108 | 213 |
| 1997 | 10 | 25 | 3 | −64 | no | no | 523 | 360 | C3.3 | N16E07 | no | 79 |
| 1997 | 10 | 27 | 23 | −60 | 500 | no | 503 | 360 | no | no | no | no |
| 1997 | 11 | 7 | 5 | −110 | 400 | no | 785 | 360 | X2.1 | S14W33 | 0.9518 | 19,795 |
| 1997 | 11 | 10 | 3 | −54 | no | no | 1556 | 360 | X9.4 | S18W63 | 18.13 | 102,017 |
| 1997 | 11 | 23 | 7 | −108 | 510 | 377 | 611 u | 360 | C1.6 | no | no | no |
| 1997 | 12 | 11 | 11 | −60 | 350 | 375 | 397 u | 223 | no | no | no | no |
| 1997 | 12 | 30 | 20 | −77 | 370 | 386 | 197 u | 360 | no | no | no | no |
| 1998 | 1 | 7 | 5 | −77 | 400 | 406 | 438 | 360 | B6.4 | N24W42 | no | no |
| 1998 | 1 | 30 | 12 | −55 | 380 | no | 693 | 360 | C1.1 | N21E25 | no | no |
| 1998 | 2 | 18 | 1 | −100 | 400 | no | u | u | no | no | no | no |
| 1998 | 2 | 18 | 20 | −51 | 440 | 451 | u | u | no | no | no | no |
| 1998 | 2 | 20 | 1 | −50 | no | no | u | u | no | no | no | no |
| 1998 | 3 | 10 | 21 | −116 | no | no | 659 u | 79 | no | no | no | no |
| 1998 | 3 | 21 | 16 | −85 | no | no | 636 | 174 | no | no | no | no |
| 1998 | 3 | 25 | 17 | −56 | 400 | no | u | u | no | no | no | no |
| 1998 | 3 | 29 | 20 | −54 | no | no | 761 | 104 | C5.3 | no | no | no |
| 1998 | 4 | 24 | 8 | −69 | no | 402 | 1863 | 243 | M1.4 | u | 37.6 | 461,152 |
| 1998 | 4 | 26 | 18 | −63 | no | no | 1691 | 360 | X1.2 | S17E102 | no | no |
| 1998 | 5 | 2 | 18 | −85 | 520 | 631 | 1374 | 360 | M6.8 | S18E20 | 0.0173 | 9955 |
| 1998 | 5 | 4 | 6 | −205 | 550 | 474 | 938 | 360 | X1.1 | S15W15 | 1.423 | 43,760 |
| 1998 | 6 | 6 | 22 | −50 | no | no | 818 | 147 | no | no | no | no |
| 1998 | 6 | 14 | 11 | −55 | 340 | 273 | 1223 u | 177 | M1.4 | no | no | no |
| 1998 | 6 | 26 | 5 | −101 | 470 | no | 278 u | 119 | no | no | no | u |
| 1998 | 7 | 16 | 17 | −58 | no | no | dg | dg | no | no | no | no |
| 1998 | 8 | 6 | 12 | −138 | 360 | 475 | dg | dg | no | no | no | no |
| 1998 | 8 | 7 | 6 | −108 | 450 | no | dg | dg | no | no | no | no |
| 1998 | 8 | 20 | 21 | −67 | 320 | 321 | dg | dg | no | no | no | no |
| 1998 | 8 | 27 | 10 | −155 | 650 | 708 | dg | dg | X1.0 | no | 3.609 | 22,947 |
| 1998 | 9 | 1 | 17 | −55 | no | no | dg | dg | no | no | no | no |
| 1998 | 9 | 18 | 14 | −51 | no | no | dg | dg | no | no | no | no |
| 1998 | 9 | 25 | 10 | −207 | 640 | 768 | dg | dg | M7.1 | N18E09 | 0.0167 | 182 |
| 1998 | 10 | 1 | 2 | −58 | no | no | dg | dg | no | no | no | no |
| 1998 | 10 | 2 | 22 | −56 | no | 660 | dg | dg | no | no | no | no |
| 1998 | 10 | 7 | 23 | −70 | no | no | dg | dg | no | no | no | no |
| 1998 | 10 | 19 | 16 | −112 | 390 | no | 262 | 360 | no | no | no | no |
| 1998 | 10 | 20 u | 22 | −71 | no | no | u | u | no | no | no | no |
| 1998 | 10 | 22 u | 19 | −53 | 520 | no | u | u | no | no | no | no |
| 1998 | 11 | 6 | 9 | −61 | no | no | 661 u | 169 | C4.4 | S25E44 | no | no |
| 1998 | 11 | 7 u | 17 | −81 | 450 | no | 523 | 360 | C1.6 | N11W01 | no | no |
| 1998 | 11 | 8 | 7 | −149 | 450 | 645 | 1118 | 360 | M8.4 | N22W18 | no | u |
| 1998 | 11 | 9 | 18 | −142 | no | no | u | u | no | no | no | no |
| 1998 | 11 | 13 | 22 | −131 | 390 | 406 | 325 | 190 | no | no | no | no |
| 1998 | 12 | 11 | 16 | −69 | no | no | 806 u | 73 | no | no | no | no |
| 1998 | 12 | 25 | 12 | −57 | no | no | 752 u | 22 | no | no | no | no |
| 1998 | 12 | 29 | 12 | −58 | 400 | 464 | u | u | no | no | no | no |
| 1999 | 1 | 14 | 1 | −112 | 420 | 413 | u | u | no | no | no | no |
| 1999 | 1 | 23 | 23 | −52 | 570 | 701 | dg | dg | no | no | no | no |
| 1999 | 2 | 18 | 10 | −123 | 540 | 700 | dg | dg | M3.2 | S23W14 | 0.0038 | 180 |
| 1999 | 3 | 1 | 1 | −94 | no | no | u | u | no | no | no | no |
| 1999 | 3 | 4 | 24 | −52 | no | no | u | u | no | no | no | no |
| 1999 | 3 | 7 | 11 | −57 | no | no | u | u | no | no | no | no |
| 1999 | 3 | 10 | 9 | −81 | 410 | 501 | u | u | no | no | no | no |
| 1999 | 3 | 29 | 15 | −56 | no | no | u | u | no | no | no | no |
| 1999 | 4 | 17 | 8 | −91 | 410 | 456 | 291 u | 261 | no | no | no | no |
| 1999 | 7 | 31 | 2 | −53 | 480 | no | 462 | 360 | M2.3 | S15E03 | no | no |
| 1999 | 8 | 23 | 1 | −66 | 460 | no | 736 | 265 | C2.6 | N23E27 | no | no |
| 1999 | 9 | 13 | 5 | −74 | no | 531 | 1467 u | 125 | B7.0 | no | no | no |
| 1999 | 9 | 16 | 9 | −67 | no | 544 | 898 u | 182 | C4.9 | N21E02 | no | no |
| 1999 | 9 | 22 | 24 | −173 | 530 | 466 | 604 | 360 | C2.8 | no | no | no |
| 1999 | 9 | 27 | 19 | −64 | no | no | 1150 u | 77 | no | no | no | no |
| 1999 | 9 | 30 | 4 | −61 | no | no | u | u | no | no | no | no |
| 1999 | 10 | 10 | 19 | −67 | no | no | u | u | no | no | no | no |
| 1999 | 10 | 22 | 7 | −237 | 480 | 476 | 144 u | 240 | C1.0 | no | no | no |
| 1999 | 10 | 28 | 18 | −66 | no | no | 1127 u | 114 | C1.5 | u | no | no |
| 1999 | 11 | 7 | 16 | −67 | no | no | u | u | no | no | no | no |
| 1999 | 11 | 8 | 15 | −73 | no | no | u | u | no | no | no | no |
| 1999 | 11 | 11 | 7 | −55 | no | no | 631 u | 87 | C5.0 | u | no | no |
| 1999 | 11 | 13 | 9 | −69 | 450 | no | dg | dg | no | no | no | no |
| 1999 | 11 | 13 | 23 | −106 | 440 | 466 | dg | dg | no | no | no | no |
| 1999 | 11 | 16 | 17 | −79 | no | no | 1104 u | 41 | C4.6 | S12E44 | no | no |
| 1999 | 11 | 24 | 10 | −50 | no | no | dg | dg | no | no | no | no |
| 1999 | 12 | 13 | 10 | −85 | 440 | 553 | dg | dg | no | no | no | no |
| 1999 | 12 | 31 | 24 | −50 | no | no | u | u | no | no | no | no |
| 2000 | 1 | 11 | 22 | −81 | no | no | 1813 u | 67 | C5.8 | N23W42 | no | no |
| 2000 | 1 | 23 | 1 | −97 | 380 | no | 739 | 360 | M3.9 | S19E11 | 0.0201 | 381 |
| 2000 | 2 | 12 | 12 | −133 | 540 | 638 | 1003 | 360 | C7.3 | N31E04 | no | no |
| 2000 | 3 | 31 | 12 | −60 | 420 | no | 1177 | 360 | u | u | u | u |
| 2000 | 4 | 5 | 2 | −63 | no | no | 532 u | 113 | no | no | no | no |
| 2000 | 4 | 7 | 1 | −292 | 560 | 642 | 1188 | 360 | C9.7 | N16W66 | 0.5441 | 9431 |
| 2000 | 4 | 16 | 12 | −79 | no | no | 409 u | 360 | M3.1 | S14W01 | no | no |
| 2000 | 4 | 24 | 15 | −61 | 500 | no | u | u | no | no | no | no |
| 2000 | 5 | 17 | 6 | −92 | 550 | no | 666 u | 182 | C3.7 | S22E65 | no | no |
| 2000 | 5 | 24 | 9 | −147 | 530 | 656 | 629 | 138 | no | no | no | no |
| 2000 | 5 | 29 | 21 | −54 | no | no | u | u | no | no | no | no |
| 2000 | 6 | 8 | 20 | −90 | 610 | no | 1119 | 360 | X2.3 | N20E18 | 0.6162 | 2432 |
| 2000 | 6 | 26 | 18 | −76 | 520 | no | 847 u | 198 | M3.0 | N26W72 | 0.017 | 21,306 |
| 2000 | 7 | 16 | 1 | −301 | 740 | no | 1674 | 360 | X5.7 | N22W07 | 174.3 | 750,613 |
| 2000 | 7 | 20 | 10 | −93 | 530 | 638 | 788 u | 116 | C5.3 | N13E30 | no | no |
| 2000 | 7 | 22 | 18 | −63 | no | 497 | dg | dg | no | no | no | no |
| 2000 | 7 | 23 | 23 | −68 | 360 | no | dg | dg | no | no | no | no |
| 2000 | 7 | 29 | 12 | −71 | 440 | no | 1287 u | 271 | M8.0 | N06W08 | no | no |
| 2000 | 8 | 11 | 7 | −106 | 430 | 380 | 597 | 40 | no | no | no | no |
| 2000 | 8 | 12 | 10 | −235 | 580 | 563 | 702 | 360 | C2.3 | N11W11 | no | no |
| 2000 | 8 | 29 | 7 | −60 | no | no | 518 u | 178 | M1.4 | S15E67 | no | no |
| 2000 | 9 | 12 | 20 | −73 | no | no | 761 u | 176 | no | no | u | u |
| 2000 | 9 | 17 | 24 | −201 | 600 | no | 1215 | 360 | M5.9 | N14E07 | no | 3300 |
| 2000 | 9 | 19 | 15 | −77 | no | no | 1056 u | 100 | no | no | no | no |
| 2000 | 9 | 26 | 3 | −55 | no | no | u | u | no | no | no | no |
| 2000 | 9 | 30 | 15 | −76 | no | 454 | 587 u | 360 | M1.8 | N09W18 | no | 250 |
| 2000 | 10 | 3 | 13 | −79 | no | 462 | 820 u | 136 | C5.2 | N17W52 | no | 181 |
| 2000 | 10 | 4 | 21 | −143 | 400 | no | 703 u | 170 | M1.0 | S22E36 | no | no |
| 2000 | 10 | 5 | 8 | −175 | no | 538 | 525 | 360 | C1.4 | S09E07 | no | 149 |
| 2000 | 10 | 5 | 14 | −182 | 450 | no | 569 | 360 | C8.4 | no | no | u |
| 2000 | 10 | 13 | 6 | −71 | no | 526 | 798 u | 175 | C6.7 | N01W14 | 0.0075 | no |
| 2000 | 10 | 14 | 15 | −107 | 400 | no | 506 u | 360 | u | u | no | 257 |
| 2000 | 10 | 23 | 8 | −53 | no | no | u | u | no | no | no | no |
| 2000 | 10 | 29 | 4 | −127 | 380 | 390 | 770 | 360 | C4.0 | N06W60 | 0.2115 | 2665 |
| 2000 | 11 | 4 | 10 | −50 | no | 429 | 801 | 360 | C2.2 | S17E39 | no | no |
| 2000 | 11 | 6 | 22 | −159 | 510 | 611 | 291 | 360 | C3.2 | N02W02 | no | 357 |
| 2000 | 11 | 10 | 13 | −96 | no | 925 | 1738 | 170 | M7.4 | N10W77 | 173.2 | 888,533 |
| 2000 | 11 | 27 | 2 | −80 | 540 | 524 | 1245 u | 360 | X2.3 | N22W07 | 1.643 | 29,353 |
| 2000 | 11 | 29 | 14 | −119 | 540 | 604 | 671 | 360 | X1.9 | N20W23 | no | 28,8203 |
| 2000 | 12 | 23 | 5 | −62 | 320 | 314 | 510 | 360 | C7.0 | N15S01 | no | no |
| 2001 | 1 | 24 | 19 | −61 | 400 | 615 | 1507 | 360 | M7.7 | S07S46 | 0.0399 | 793 |
| 2001 | 2 | 13 | 22 | −50 | no | 651 | 956 u | 360 | no? | N37W03 | no | no |
| 2001 | 3 | 5 | 3 | −73 | 440 | no | 631 u | 237 | C1.2 | S09W27 | no | no |
| 2001 | 3 | 20 | 14 | −149 | 360 | 441 | 271 | 281 | no | no | no | no |
| 2001 | 3 | 23 | 17 | −75 | no | 382 | 389 u | 360 | no | N20W0 | no | no |
| 2001 | 3 | 28 | 16 | −87 | 610 | 552 | 906 u | 360 | M1.7 | N15E22 | no | u |
| 2001 | 3 | 31 | 9 | −387 | 640 | 498 | 519 | 360 | M4.3 | S10E30 | no | no |
| 2001 | 3 | 31 | 22 | −284 | 600 | 565 | 942 | 360 | X1.7 | N20E19 | 0.6266 | 12,355 |
| 2001 | 4 | 5 | 8 | −50 | 650 | 845 | 2505 | 244 | X20 | no | 7.389 | 87782 |
| 2001 | 4 | 9 | 7 | −63 | 740 | 696 | 1270 | 360 | X5.6 | S21E31 | no | u |
| 2001 | 4 | 11 | 24 | −271 | 640 | 310 | 2411 | 360 | X2.3 | S23W09 | 2.499 | 7716 |
| 2001 | 4 | 13 | 16 | −77 | 730 | no | 1103 | 360 | M2.3 | S22W27 | no | 77,982 |
| 2001 | 4 | 18 | 7 | −114 | 430 | 602 | 1199 | 167 | X14.4 | S20W85 | 31.3 | 153,434 |
| 2001 | 4 | 22 | 16 | −102 | 350 | 381 | 2465 u | 360 | C2.2 | S15W90 | 8.5 | 19,759 |
| 2001 | 5 | 10 | 4 | −76 | 430 | no | 1223 u | 205 | C3.9 | N25W35 | 0.3542 | 1356 |
| 2001 | 6 | 18 | 9 | −61 | no | 336 | 1701 | 360 | no | no | 0.6736 | 5220 |
| 2001 | 8 | 17 | 22 | −105 | 500 | 519 | 618 | 360 | C2.3 | N24W19 | 0.0107 | no |
| 2001 | 9 | 13 | 8 | −57 | 410 | 449 | 791 u | 360 | C3.2 | N13E35 | no | u |
| 2001 | 9 | 23 | 19 | −73 | 440 | no | 436 u | 360 | no | no | no | no |
| 2001 | 9 | 26 | 2 | −102 | no | 851 | 2402 | 360 | X2.6 | S16E23 | 1.88 | 3,551,563 |
| 2001 | 9 | 30 | 21 | −66 | 560 | 483 | 509 u | 182 | C3.8 | S20W27 | no | no |
| 2001 | 10 | 1 | 9 | −148 | 490 | no | 846 | 360 | M3.3 | S18W36 | no | no |
| 2001 | 10 | 2 | 13 | −104 | 490 | no | 773 u | 109 | M1.2 | no | no | no |
| 2001 | 10 | 3 | 15 | −166 | 500 | no | 509 u | 216 | M1.8 | N13E03 | no | no |
| 2001 | 10 | 9 | 16 | −64 | no | 382 | 1537 | 360 | no | no | no | no |
| 2001 | 10 | 12 | 13 | −71 | 560 | 579 | 973 | 360 | M1.4 | S28E08 | no | no |
| 2001 | 10 | 19 | 22 | −57 | no | no | u | u | no | no | no | no |
| 2001 | 10 | 21 | 22 | −187 | 460 | 636 | 901 | 360 | X1.6 | N15W29 | 0.1236 | 1739 |
| 2001 | 10 | 28 | 12 | −157 | 360 | 589 | 1092 | 360 | X1.3 | S16W21 | no | no |
| 2001 | 11 | 1 | 11 | −106 | 330 | 395 | 592 u | 200 | C3.4 | no | no | no |
| 2001 | 11 | 6 | 7 | −292 | 600 | no | 1810 | 360 | X1.0 | N06W18 | 277.3 | 4,512,846 |
| 2001 | 11 | 24 | 17 | −221 | 720 | 804 | 1443 | 360 | M3.8 | S25W67 | 196.7 | 4715 |
| 2001 | 12 | 21 | 23 | −67 | no | 552 | 1025 u | 103 | no | no | no | 170 |
| 2001 | 12 | 24 | 11 | −55 | no | 306 | 769 u | 108 | C2.4 | no | no | no |
| 2001 | 12 | 30 | 6 | −58 | 400 | 669 | 1446 | 212 | M7.1 | N08W54 | 24.47 | 103,570 |
| 2002 | 1 | 11 | 7 | −72 | no | no | 1794 | 360 | no | no | no | no |
| 2002 | 2 | 2 | 10 | −86 | no | no | 1136 | 360 | no | no | 0.2095 | 1267 |
| 2002 | 2 | 5 | 21 | −82 | no | no | u | u | no | no | no | no |
| 2002 | 3 | 1 | 2 | −71 | 390 | no | u | u | no | no | no | no |
| 2002 | 3 | 24 | 10 | −100 | 450 | 517 | 603 | 360 | no | no | no | no |
| 2002 | 4 | 18 | 8 | −127 | 480 | 517 | 720 | 360 | M1.2 | S15W01 | no | 267 |
| 2002 | 4 | 19 u | 19 | −126 | no | 768 | u | u | no | no | no | no |
| 2002 | 4 | 20 | 9 | −149 | 500 | no | 1240 | 360 | M2.6 | S14W34 | 0.1024 | 38,361 |
| 2002 | 4 | 23 | 16 | −57 | no | 644 | 2393 | 360 | X1.5 | S14W84 | 79.07 | 127,221 |
| 2002 | 5 | 11 | 20 | −110 | 430 | 483 | 614 | 360 | C4.2 | S12W07 | no | no |
| 2002 | 5 | 14 | 21 | −63 | no | no | 1154 u | 120 | C1.2 | S18W43 | no | no |
| 2002 | 5 | 19 | 7 | −58 | no | 545 | 600 | 360 | C4.5 | S23E15 | no | no |
| 2002 | 5 | 23 | 18 | −109 | 590 | 737 | 1246 | 186 | C9.7 | N17E36 | no | 1032 |
| 2002 | 5 | 27 | 9 | −64 | no | no | 1557 u | 360 | C5.0 | S30W34 | 1.517 | no |
| 2002 | 8 | 1 | 14 | −51 | no | no | u | u | no | no | no | no |
| 2002 | 8 | 2 | 6 | −102 | 460 | 496 | 562 | 236 | no | no | no | no |
| 2002 | 8 | 02 u | 23 | −69 | no | no | u | u | no | no | no | no |
| 2002 | 8 | 4 | 6 | −58 | no | no | u | u | no | no | no | no |
| 2002 | 8 | 19 | 8 | −53 | no | 672 | u | u | no | no | no | no |
| 2002 | 8 | 20 | 1 | −71 | no | 535 | u | u | no | no | no | no |
| 2002 | 8 | 21 | 7 | −106 | 460 | no | 1585 u | 360 | M5.2 | S14E20 | 0.0349 | 1082 |
| 2002 | 9 | 4 | 6 | −109 | no | 340 | u | u | no | no | no | no |
| 2002 | 9 | 8 | 1 | −181 | 470 | 897 | 1748 | 360 | C5.2 | N09E28 | 0.2118 | 1886 |
| 2002 | 9 | 10 | 1 | −69 | no | no | 909 u | 360 | no | no | no | no |
| 2002 | 9 | 11 | 23 | −90 | no | no | u | u | no | no | no | no |
| 2002 | 10 | 1 | 21 | −176 | 390 | 331 | 881 u | 104 | no | no | no | no |
| 2002 | 10 | 2 u | 5 | −158 | no | no | u | u | no | no | no | no |
| 2002 | 10 | 4 | 9 | −146 | 430 | no | u | u | no | no | no | no |
| 2002 | 10 | 5 | 16 | −102 | no | no | 903 u | 190 | B9.2 | S18E20 | no | no |
| 2002 | 10 | 7 | 8 | −115 | no | no | 743 u | 230 | no | no | no | no |
| 2002 | 10 | 8 u | 5 | −108 | no | no | u | u | no | no | no | no |
| 2002 | 10 | 14 | 14 | −100 | no | no | u | u | no | no | no | no |
| 2002 | 10 | 15 u | 19 | −70 | no | no | 1009 u | 264 | M2.2 | S08E66 | no | u |
| 2002 | 10 | 16 | 21 | −63 | no | no | 1694 u | 360 | no | no | no | no |
| 2002 | 10 | 24 | 21 | −98 | no | no | 640 u | 360 | no | no | no | no |
| 2002 | 10 | 25 u | 2 | −91 | no | no | u | u | no | no | no | no |
| 2002 | 10 | 26 u | 20 | −62 | no | no | 1052 u | 119 | C6.6 | S04W62 | no | no |
| 2002 | 10 | 27 u | 16 | −65 | no | no | 689 u | 286 | no | no | no | no |
| 2002 | 10 | 28 u | 5 | −63 | no | no | 629 u | 360 | no | no | no | no |
| 2002 | 10 | 30 u | 19 | −52 | no | no | 2115 u | 360 | no | no | no | no |
| 2002 | 11 | 3 | 4 | −74 | no | no | u | u | no | no | no | no |
| 2002 | 11 | 18 | 23 | −52 | 380 | no | 1185 | 360 | no | no | no | no |
| 2002 | 11 | 20 | 21 | −87 | no | 392 | 1008 u | 119 | C2.4 | no | no | no |
| 2002 | 11 | 21 | 11 | −128 | no | no | 938 u | 123 | no | no | no | no |
| 2002 | 11 | 27 | 7 | −64 | no | no | 1077 | 360 | no | no | no | 851 |
| 2002 | 12 | 19 | 21 | −72 | no | no | u | u | no | no | no | no |
| 2002 | 12 | 20 u | 6 | −64 | no | no | u | u | no | no | no | no |
| 2002 | 12 | 21 u | 4 | −75 | 440 | no | u | u | no | no | no | no |
| 2002 | 12 | 23 | 12 | −67 | no | no | 1092 u | 360 | M2.7 | N15W09 | 0.1002 | 9777 |
| 2002 | 12 | 27 | 5 17 | −68 | no | no | u | u | no | no | no | no |
| 2003 | 1 | 30 | 1 | −66 | no | no | 1053 u | 267 | C2.4 | S17W23 | no | no |
| 2003 | 2 | 2 | 18 | −72 | 510 | no | 620 | 138 | no | no | no | no |
| 2003 | 2 | 4 | 10 | −74 | no | no | u | u | no | no | no | no |
| 2003 | 2 | 4 u | 24 | −54 | no | no | u | u | no | no | no | no |
| 2003 | 2 | 27 | 22 | −66 | no | no | u | u | no | no | no | no |
| 2003 | 3 | 4 | 1 | −67 | no | no | u | u | no | no | no | no |
| 2003 | 3 | 16 | 22 | −60 | no | no | 1021 u | 91 | C1.3 | S12E09 | dg | no |
| 2003 | 3 | 20 | 20 | −64 | 650 | no | 1601 | 209 | X1.5 | S15W46 | 0.008 | 23,895 |
| 2003 | 3 | 27 | 18 | −56 | no | no | 1505 u | 82 | C1.9 | S17E77 | no | no |
| 2003 | 3 | 29 u | 7 | −63 | no | no | u | u | no | no | no | no |
| 2003 | 3 | 29 u | 21 | −70 | no | no | u | u | no | no | no | no |
| 2003 | 3 | 31 u | 16 | −78 | no | no | 664 u | 111 | no | no | no | no |
| 2003 | 4 | 2 | 23 | −53 | no | no | u | u | no | no | no | no |
| 2003 | 4 | 4 | 24 | −62 | no | no | 885 u | 87 | no | no | no | no |
| 2003 | 4 | 25 | 23 | −53 | no | no | 899 u | 148 | B7.2 | no | no | no |
| 2003 | 4 | 30 | 3 | −67 | no | no | 991 u | 95 | no | no | no | no |
| 2003 | 5 | 10 | 9 | −84 | 680 | no | u | u | no | no | no | no |
| 2003 | 5 | 22 | 3 | −73 | no | no | 866 u | 101 | B8.3 | u | no | no |
| 2003 | 5 | 30 | 1 | −144 | 600 | 907 | 1366 | 360 | X3.6 | S07W20 | 0.1636 | no |
| 2003 | 5 | 31 | 6 | −63 | 680 | no | 1237 | 360 | X1.2 | S06W37 | no | 7886 |
| 2003 | 6 | 2 | 9 | −91 | no | no | 1835 | 360 | M9.3 | S07W65 | 0.5543 | 45,772 |
| 2003 | 6 | 8 | 23 | −50 | no | no | 1458 u | 239 | no | no | no | no |
| 2003 | 6 | 16 u | 17 | −59 | no | no | u | u | no | no | no | no |
| 2003 | 6 | 16 | 23 | −68 | 510 | no | u | u | no | no | no | no |
| 2003 | 6 | 17 | 9 | −81 | no | no | 1215 u | 179 | no | no | no | no |
| 2003 | 6 | 18 | 10 | −141 | 480 | 479 | 2053 | 360 | X1.3 | S07E80 | no | 656 |
| 2003 | 6 | 21 | 10 | −50 | no | no | 1813 u | 360 | M6.8 | S08E58 | 0.2634 | 20,103 |
| 2003 | 6 | 24 | 14 | −55 | no | no | u | u | no | no | no | no |
| 2003 | 7 | 11 | 11 | −55 | no | no | u | u | no | no | no | no |
| 2003 | 7 | 12 | 6 | −105 | no | no | u | u | no | no | no | no |
| 2003 | 7 | 16 | 14 | −90 | no | no | u | u | no | no | no | no |
| 2003 | 7 | 19 | 1 | −50 | no | no | u | u | no | no | no | no |
| 2003 | 7 | 27 | 8 | −57 | no | no | u | u | no | no | no | no |
| 2003 | 8 | 6 | 7 | −60 | 440 | no | 699 u | 360 | no | no | no | no |
| 2003 | 8 | 7 | 22 | −61 | no | no | u | u | no | no | no | no |
| 2003 | 8 | 18 | 16 | −148 | 450 | no | 378 | 360 | no | no | no | no |
| 2003 | 8 | 21 | 24 | −68 | no | no | u | u | no | no | no | no |
| 2003 | 9 | 17 | 24 | −65 | no | no | u | u | no | no | no | no |
| 2003 | 9 | 24 | 8 | −59 | no | no | 646 | 360 | no | no | no | no |
| 2003 | 10 | 14 | 23 | −85 | no | no | u | u | no | no | no | no |
| 2003 | 10 | 17 | 7 | −53 | no | no | u | u | no | no | no | no |
| 2003 | 10 | 20 u | 22 | −57 | no | no | 627 u | 360 | no | no | no | no |
| 2003 | 10 | 22 u | 7 | −61 | 520 | no | u | u | no | no | no | no |
| 2003 | 10 | 27 | 5 | −52 | 470 | no | 1406 u | 236 | M1.7 | S04E13 | u | u |
| 2003 | 10 | 30 | 1 | −353 | 1300 | no | 2459 | 360 | X17.2 | S16E68 | 353.2 | 530,064 |
| 2003 | 10 | 30 | 23 | −383 | 800 | no | 2029 | 360 | M1.0 | S15W02 | no | no |
| 2003 | 11 | 4 | 11 | −69 | no | 759 | 2598 | 360 | X8.3 | S14W56 | 50.99 | 116,852 |
| 2003 | 11 | 11 | 14 | −62 | no | no | 2008 u | 360 | no | no | no | no |
| 2003 | 11 | 20 | 21 | −422 | 580 | 666 | 1660 | 360 | M3.9 | N00E18 | u | u |
| 2003 | 11 | 22 | 23 | −87 | no | no | 669 | 360 | M9.6 | N01W08 | 0.0694 | 9787 |
| 2003 | 12 | 6 | 5 | −55 | no | no | 1393 u | 150 | C7.2 | S19W91 | 2.225 | 1281 |
| 2003 | 12 | 8 u | 22 | −54 | no | no | 676 u | 95 | C2.2 | S17W38 | no | no |
| 2003 | 12 | 10 u | 20 | −51 | no | no | u | u | no | no | no | no |
| 2004 | 1 | 7 | 14 | −50 | no | no | 1469 u | 166 | C2.5 | no | no | no |
| 2004 | 1 | 15 | 17 | −50 | no | no | u | u | no | no | no | no |
| 2004 | 1 | 22 | 14 | −130 | 560 | no | 965 | 360 | no | no | no | no |
| 2004 | 1 | 25 u | 4 | −81 | 490 | no | 762 u | 360 | C1.2 | S19E29 | no | no |
| 2004 | 1 | 27 u | 2 | −62 | no | no | u | u | no | no | no | no |
| 2004 | 2 | 11 | 18 | −93 | no | no | u | u | no | no | no | no |
| 2004 | 3 | 9 | 24 | −72 | no | no | u | u | no | no | no | no |
| 2004 | 3 | 11 | 24 | −63 | no | no | u | u | no | no | no | no |
| 2004 | 4 | 4 | 1 | −117 | 440 | no | 652 u | 113 | no | no | no | no |
| 2004 | 4 | 5 | 20 | −62 | no | no | u | u | no | no | no | no |
| 2004 | 7 | 17 | 3 | −76 | no | no | 747 u | 360 | M5.4 | N12W52 | no | 198 |
| 2004 | 7 | 23 | 3 | −99 | 560 | 454 | 710 | 360 | M8.6 | N10E35 | no | no |
| 2004 | 7 | 25 | 17 | −136 | 560 | 561 | 899 | 132 | C5.3 | N04E10 | no | u |
| 2004 | 7 | 27 | 14 | −170 | 870 | 1086 | 1333 | 360 | M1.1 | N08E33 | 1.245 | 13,269 |
| 2004 | 8 | 9 | 22 | −51 | no | no | 1004 | 360 | no | no | no | no |
| 2004 | 8 | 30 | 23 | −129 | 390 | 483 | u | u | no | no | no | no |
| 2004 | 11 | 8 | 7 | −374 | 630 | 742 | 1055 | 293 | M5.4 | N08E18 | no | no |
| 2004 | 11 | 10 | 11 | −263 | 640 | 813 | 1759 | 360 | X2.0 | N09W17 | u | no |
| 2004 | 11 | 25 | 8 | −53 | no | no | 649 u | 102 | no | no | no | no |
| 2004 | 11 | 28 | 7 | −50 | no | no | u | u | no | no | no | no |
| 2004 | 12 | 13 | 3 | −56 | 400 | no | 611 | 360 | C2.5 | N01W07 | no | no |
| 2005 | 1 | 8 | 3 | −93 | 460 | 560 | 735 | 360 | B1.8 | S15E15 | no | no |
| 2005 | 1 | 12 | 11 | −50 | no | no | 870 u | 164 | M2.4 | S09E69 | no | no |
| 2005 | 1 | 17 | 4 | −65 | 520 | 539 | 455 | 360 | C4.2 | S06E15 | no | no |
| 2005 | 1 | 18 | 9 | −103 | no | no | 2861 | 360 | X2.6 | N14W08 | 12.71 | 59,664 |
| 2005 | 1 | 19 u | 11 | −80 | 800 | no | 2094 u | 360 | X2.2 | N13W19 | u | u |
| 2005 | 1 | 22 | 6 | −97 | no | no | 2020 u | 360 | X1.3 | N15W51 | no | no |
| 2005 | 2 | 7 | 22 | −57 | no | no | 711 u | 139 | no | no | no | no |
| 2005 | 2 | 18 | 3 | −80 | 410 | no | 1135 | 360 | C4.9 | S03W23 | no | 162 |
| 2005 | 3 | 7 | 1 | −54 | no | no | u | u | no | no | no | no |
| 2005 | 4 | 5 | 5 | −70 | no | 472 | u | u | no | no | no | no |
| 2005 | 4 | 12 | 6 | −62 | no | no | u | u | no | no | no | no |
| 2005 | 5 | 8 | 3 | −82 | no | 438 | u | u | no | no | no | no |
| 2005 | 5 | 8 | 19 | −110 | no | 476 | 1180 | 360 | C7.8 | N04W67 | no | no |
| 2005 | 5 | 15 | 9 | −247 | 630 | 858 | 1689 | 360 | M8.0 | N12E11 | 9.876 | 879,497 |
| 2005 | 5 | 20 | 9 | −83 | 430 | no | 405 u | 140 | C1.2 | N15W27 | no | u |
| 2005 | 5 | 30 | 14 | −113 | 460 | u | 586 | 360 | no | no | no | no |
| 2005 | 6 | 13 | 1 | −106 | 480 | no | u | u | no | no | no | no |
| 2005 | 6 | 23 | 11 | −85 | no | no | 614 u | 103 | B1.2 | S13W51 | no | no |
| 2005 | 7 | 9 | 21 | −55 | no | no | 772 u | 360 | C1.3 | S08E34 | no | no |
| 2005 | 7 | 10 | 21 | −92 | 430 | 533 | 683 u | 360 | M4.9 | N09E03 | no | 579 |
| 2005 | 7 | 18 | 7 | −67 | 420 | 378 | 2115 u | 360 | X1.2 | N11W90 | no | 14,743 |
| 2005 | 8 | 24 | 12 | −184 | 660 | 536 | 2378 | 360 | M5.6 | S13W65 | 0.1792 | 59,728 |
| 2005 | 8 | 31 | 20 | −122 | no | no | 1600 | 360 | no | no | 0.0328 | 714 |
| 2005 | 9 | 4 | 10 | −71 | pd | no | 1384 u | 360 | no | no | no | no |
| 2005 | 9 | 10 u | 23 | −73 | no | 544 | 1291 u | 126 | M1.4 | S12E88 | no | no |
| 2005 | 9 | 11 | 11 | −139 | 900 | 1147 | 2257 | 360 | X6.2 | S10E58 | no | no |
| 2005 | 9 | 12 u | 22 | −89 | 750 | 1048 | 1893 | 360 | X2.1 | S13E47 | no | no |
| 2005 | 9 | 13 u | 13 | −86 | 630 | no | 1922 | 360 | M3.0 | S16E39 | no | no |
| 2005 | 9 | 15 | 17 | −80 | 680 | 661 | 1866 | 360 | X1.5 | S09E10 | 5.515 | 18,409 |
| 2005 | 10 | 8 | 8 | −50 | no | no | u | u | no | no | no | no |
| 2005 | 10 | 31 | 21 | −74 | 360 | no | u | u | no | no | no | no |
| 2005 | 12 | 11 | 19 | −55 | 480 | no | 673 u | 360 | B5.5 | N15E14 | no | no |
| 2006 | 1 | 26 | 4 | −51 | no | no | u | u | no | no | no | no |
| 2006 | 3 | 7 | 2 | −52 | no | no | u | u | no | no | no | no |
| 2006 | 4 | 5 | 16 | −79 | no | no | u | u | no | no | no | no |
| 2006 | 4 | 9 | 8 | −82 | no | no | u | u | no | no | no | no |
| 2006 | 4 | 14 | 10 | −98 | 520 | no | u | u | no | no | no | no |
| 2006 | 5 | 6 | 22 | −53 | no | no | 487 u | 360 | C1.0 | S17W02 | no | no |
| 2006 | 8 | 20 | 2 | −79 | 400 | 460 | 888 | 360 | C3.6 | S14W13 | no | no |
| 2006 | 9 | 24 | 10 | −55 | no | 402 | u | u | no | no | no | no |
| 2006 | 10 | 1 | 6 | −51 | no | 356 | u | u | no | no | no | no |
| 2006 | 10 | 13 | 23 | −55 | no | no | u | u | no | no | no | no |
| 2006 | 10 | 29 | 9 | −50 | no | no | u | u | no | no | no | no |
| 2006 | 11 | 10 | 2 | −63 | no | 360 | 1994 u | 360 | C8.8 | no | no | no |
| 2006 | 11 | 30 | 14 | −74 | 420 | no | u | u | no | no | no | no |
| 2006 | 12 | 6 | 13 | −55 | no | no | u | u | no | no | no | no |
| 2006 | 12 | 15 | 8 | −162 | 740 | 1012 | 1774 | 360 | X3.4 | S06W23 | 20.17 | 158,754 |
| 2007 | 3 | 24 | 9 | −72 | no | no | u | u | no | no | no | no |
| 2007 | 4 | 1 | 9 | −63 | no | no | u | u | no | no | no | no |
| 2007 | 5 | 23 | 14 | −58 | no | no | 958 u | 106 | no | no | no | u |
| 2007 | 10 | 25 | 22 | −53 | no | 433 | u | u | no | no | no | no |
| 2007 | 11 | 20 | 21 | −59 | 460 | 442 | u | u | no | no | no | no |
| 2008 | 2 | 28 | 8 | −52 | no | no | u | u | no | no | no | no |
| 2008 | 3 | 9 | 6 | −86 | no | no | u | u | no | no | no | no |
| 2008 | 3 | 27 | 22 | −56 | no | no | 1103 u | 112 | M1.7 | S13E78 | no | no |
| 2008 | 9 | 4 | 5 | −51 | no | no | u | u | no | no | no | no |
| 2008 | 10 | 11 | 12 | −54 | no | no | u | u | no | no | no | no |
| 2009 | 7 | 22 | 7 | −83 | 330 | 337 | u | u | no | no | no | no |
| 2010 | 2 | 15 | 24 | −59 | no | 336 | 509 u | 360 | M8.3 | N26E11 | no | 744 |
| 2010 | 4 | 6 | 15 | −81 | 640 | no | 668 | 360 | B7.4 | S25W00 | no | no |
| 2010 | 4 | 12 | 2 | −67 | 410 | 465 | u | u | no | no | no | no |
| 2010 | 5 | 2 | 19 | −71 | no | no | u | u | no | no | no | no |
| 2010 | 5 | 29 | 13 | −80 | 360 | no | 427 | 360 | B1.1 | N13W31 | no | no |
| 2010 | 6 | 4 | 2 | −53 | no | no | u | u | no | no | no | no |
| 2010 | 8 | 4 | 2 20 | −74 | 530 | 537 | 850 | 360 | C3.2 | N20E36 | no | no |
| 2010 | 10 | 11 | 20 | −75 | no | no | u | u | no | no | no | no |
| 2011 | 2 | 4 | 22 | −63 | 430 | no | 437 | 360 | no | no | no | no |
| 2011 | 3 | 1 | 15 | −88 | no | no | u | u | no | no | no | no |
| 2011 | 3 | 11 | 6 | −83 | no | no | 2125 u | 360 | M3.7 | N31W53 | 1.012 | 9316 |
| 2011 | 4 | 6 | 19 | −60 | no | no | 2081 u | 109 | no | no | no | no |
| 2011 | 5 | 28 | 12 | −80 | 510 | no | 657 u | 122 | no | no | no | no |
| 2011 | 7 | 5 | 1 | −59 | nd | no | 511 u | 196 | no | no | no | no |
| 2011 | 8 | 6 | 4 | −115 | no | 577 | 1315 | 360 | M9.3 | N19W36 | 1.79 | 9625 |
| 2011 | 9 | 10 | 5 | −75 | 470 | no | 575 u | 360 | X2.1 | N14W18 | 0.1368 | 622 |
| 2011 | 9 | 17 | 16 | −72 | 430 | 506 | 746 u | 199 | no | no | no | no |
| 2011 | 9 | 26 | 24 | −118 | 580 | 556 | 1915 | 360 | M7.1 | N10E56 | no | no |
| 2011 | 9 | 28 | 7 | −68 | no | no | 972 u | 360 | M3.0 | N12E42 | no | no |
| 2011 | 10 | 25 | 2 | −147 | 460 | no | 1005 | 360 | M1.3 | N25W77 | no | 6239 |
| 2011 | 11 | 1 | 16 | −66 | 380 | 334 | 570 | 360 | no | no | no | no |
| 2012 | 1 | 23 | 6 | −71 | 450 | 443 | 1120 | 360 | M3.2 | N32E22 | 0.0173 | 939 |
| 2012 | 1 | 25 | 11 | −75 | no | 736 | 2175 | 360 | M8.7 | N28W21 | 153.2 | 170,580 |
| 2012 | 2 | 15 | 17 | −67 | 370 | no | 533 u | 360 | no | no | no | no |
| 2012 | 2 | 19 | 5 | −63 | no | no | 538 u | 360 | no | no | no | no |
| 2012 | 2 | 27 | 20 | −57 | 440 | no | 1039 u | 97 | B5.9 | no | no | no |
| 2012 | 3 | 2 | 2 | −54 | nd | no | 466 u | 360 | no | no | no | no |
| 2012 | 3 | 4 | 2 | −50 | no | no | 710 u | 206 | M3.3 | N16E83 | no | no |
| 2012 | 3 | 7 | 10 | −88 | no | 480 | 1306 u | 360 | M2.0 | N19E61 | 0.0384 | 1801 |
| 2012 | 3 | 9 | 9 | −145 | 550 | no | 2684 | 360 | X5.4 | N17E27 | 82.93 | 370,966 |
| 2012 | 3 | 12 | 17 | −64 | no | no | 1296 | 360 | M8.4 | N17W24 | no | no |
| 2012 | 3 | 15 | 21 | −88 | 680 | no | 1884 | 360 | M7.9 | N17W66 | 10.91 | 70,886 |
| 2012 | 3 | 28 | 5 | −68 | no | no | 1390 u | 360 | no | no | no | no |
| 2012 | 4 | 5 | 8 | −64 | no | no | u | u | no | no | no | no |
| 2012 | 4 | 13 | 5 | −60 | no | no | 921 u | 360 | C3.9 | N20W65 | no | 111 |
| 2012 | 4 | 24 | 5 | −120 | 370 | 425 | u | u | no | no | no | no |
| 2012 | 6 | 12 | 2 | −67 | no | no | u | u | no | no | no | no |
| 2012 | 6 | 17 | 14 | −86 | 440 | 483 | 987 | 360 | M1.9 | S17E06 | 0.0064 | 212 |
| 2012 | 7 | 9 | 13 | −78 | 410 | no | 1828 u | 360 | X1.1 | S13W59 | 0.4885 | 19,052 |
| 2012 | 7 | 15 | 17 | −139 | 490 | 746 | 885 | 360 | X1.4 | S15W01 | 1.683 | 21,061 |
| 2012 | 9 | 3 | 11 | −69 | 310 | 429 | 1442 u | 360 | C8.4 | S19E42 | 0.2617 | 9584 |
| 2012 | 9 | 5 | 6 | −64 | 500 | 482 | 538 | 360 | C2.9 | N03W05 | no | no |
| 2012 | 10 | 1 | 5 | −122 | 370 | 447 | 947 | 360 | C3.7 | N06W34 | 0.2716 | 12,151 |
| 2012 | 10 | 8 u | 13 | −99 | no | 465 | u | u | no | no | no | no |
| 2012 | 10 | 9 | 9 | −109 | 390 | no | 612 | 284 | no | no | no | no |
| 2012 | 10 | 13 | 8 | −90 | 490 | 465 | 692 u | 122 | C2.0 | S26E86 | no | no |
| 2012 | 11 | 1 | 21 | −65 | 340 | 390 | 317 | 360 | no | no | no | no |
| 2012 | 11 | 14 | 8 | −108 | 380 | no | u | u | no | no | no | no |
| 2013 | 1 | 17 | 24 | −52 | 390 | 335 | 798 u | 162 | no | no | no | no |
| 2013 | 1 | 26 | 23 | −51 | no | 354 | u | u | no | no | no | no |
| 2013 | 3 | 1 | 11 | −55 | no | no | 622 u | 138 | B8.3 | S19W05 | no | no |
| 2013 | 3 | 17 | 21 | −132 | 520 | 765 | 1063 | 360 | X1.1 | N11E11 | 0.009 | 1247 |
| 2013 | 3 | 29 | 17 | −59 | no | 206 | 663 u | 177 | B6.8 | no | no | no |
| 2013 | 5 | 1 | 19 | −72 | 430 | 447 | u | u | no | no | no | no |
| 2013 | 5 | 18 | 5 | −61 | no | 452 | 1366 u | 360 | X1.2 | N12E64 | 0.5234 | u |
| 2013 | 5 | 19 u | 15 | −51 | no | 497 | 1345 | 360 | M3.2 | N12E57 | no | no |
| 2013 | 5 | 25 | 7 | −59 | no | 624 | 1466 | 360 | 50 | N14W87 | 61.84 | no |
| 2013 | 5 | 25 u | 20 | −56 | no | 475 | u | u | no | no | no | no |
| 2013 | 6 | 1 | 9 | −124 | no | no | u | u | no | no | no | no |
| 2013 | 6 | 7 | 3 | −78 | 430 | no | 709 u | 123 | no | no | no | no |
| 2013 | 6 | 29 | 7 | −102 | 390 | no | u | u | no | no | no | no |
| 2013 | 7 | 6 | 19 | −87 | 350 | no | 807 u | 267 | M1.5 | S11E82 | no | no |
| 2013 | 7 | 10 | 22 | −56 | no | no | u | u | no | no | no | no |
| 2013 | 7 | 14 | 23 | −81 | 430 | no | 449 u | 360 | B7.6 | N19E14 | no | no |
| 2013 | 8 | 5 | 3 | −50 | no | no | u | u | no | no | no | no |
| 2013 | 8 | 27 | 22 | −59 | no | no | u | u | no | no | no | no |
| 2013 | 10 | 2 | 8 | −72 | 470 | 654 | 1179 | 360 | C1.2 | N10W43 | 3.208 | no |
| 2013 | 10 | 9 | 2 | −69 | 480 | no | 567 | 360 | C1.1 | S16W13 | no | no |
| 2013 | 10 | 30 | 24 | −54 | no | 337 | 695 | 360 | X1.0 | N04W66 | 0.0701 | 22,413 |
| 2013 | 11 | 7 | 13 | −50 | no | no | 1040 u | 360 | no | no | no | 259.94 |
| 2013 | 11 | 9 | 9 | −80 | 420 | 428 | 1033 u | 360 | M1.8 | S11W97 | 0.0578 | 3644 |
| 2013 | 11 | 11 | 8 | −68 | nd | no | 497 u | 360 | no | no | no | no |
| 2013 | 12 | 8 | 9 | −66 | no | 329 | u | u | no | no | no | no |
| 2014 | 2 | 19 | 9 | −119 | 520 | 621 | 634 | 360 | M1.1 | S11E01 | no | 305 |
| 2014 | 2 | 20 | 13 | −95 | 490 | no | 779 | 360 | no | no | 0.0071 | 147 |
| 2014 | 2 | 22 u | 2 | −64 | n | no | 612 u | 360 | no | no | 0.0199 | 1263 |
| 2014 | 2 | 23 | 20 | −55 | no | no | 1252 | 360 | no | no | no | 156 |
| 2014 | 2 | 27 | 24 | −97 | no | 436 | 2147 | 360 | X4.9 | S12E82 | 0.566 | 10,469 |
| 2014 | 3 | 1 | 9 | −52 | no | no | u | u | no | no | no | no |
| 2014 | 4 | 12 | 10 | −87 | 350 | no | 514 u | 360 | no | no | no | no |
| 2014 | 4 | 30 | 10 | −67 | 310 | no | u | u | no | no | no | no |
| 2014 | 8 | 27 | 19 | −79 | no | no | 551 u | 360 | M5.9 | S07E75 | no | no |
| 2014 | 9 | 12 | 24 | −88 | 600 | no | 1267 | 360 | X1.6 | N14E02 | 0.5808 | 14,581 |
| 2014 | 10 | 9 | 8 | −51 | no | no | u | u | no | no | no | no |
| 2014 | 10 | 28 | 2 | −57 | no | no | u | u | no | no | no | no |
| 2014 | 11 | 10 | 18 | −65 | 480 | no | 795 u | 293 | X1.6 | N15E33 | no | no |
| 2014 | 11 | 16 | 8 | −59 | no | no | 710 u | 115 | no | no | no | no |
| 2014 | 12 | 12 | 17 | −53 | no | no | 1086 u | 228 | C5.9 | S18W89 | no | no |
| 2014 | 12 | 22 | 6 | −71 | 380 | no | 587 u | 360 | M8.7 | S20E09 | 0.0107 | no |
| 2014 | 12 | 23 u | 23 | −57 | no | no | 1195 u | 360 | M6.9 | S11E15 | no | 7979 |
| 2014 | 12 | 24 u | 23 | −53 | no | no | 830 u | 257 | X1.8 | S21W24 | no | no |
| 2014 | 12 | 26 u | 2 | −57 | no | no | 669 u | 360 | M1.0 | S14W25 | no | no |
| 2015 | 1 | 4 | 22 | −78 | pd | no | 902 u | 126 | no | no | no | no |
| 2015 | 1 | 7 | 12 | −107 | 450 | no | u | u | no | no | no | no |
| 2015 | 2 | 2 | 7 | −55 | no | no | u | u | no | no | no | no |
| 2015 | 2 | 18 | 1 | −69 | no | no | u | u | no | no | no | no |
| 2015 | 2 | 24 | 8 | −58 | no | no | 1120 | 360 | no | no | no | 1046 |
| 2015 | 3 | 1 | 9 | −56 | no | no | u | u | no | no | no | no |
| 2015 | 3 | 2 | 9 | −64 | no | no | 999 u | 360 | no | no | no | no |
| 2015 | 3 | 17 | 23 | −234 | 560 | 536 | 719 | 360 | C9.1 | S22W25 | 0.0325 | 1345 |
| 2015 | 4 | 10 | 5 | −60 | no | 382 | u | u | no | no | no | no |
| 2015 | 4 | 11 | 10 | −85 | 380 | no | u | u | no | no | no | no |
| 2015 | 4 | 15 u | 21 | −62 | no | no | u | u | no | no | no | no |
| 2015 | 4 | 16 u | 8 | −81 | no | 371 | u | u | no | no | no | no |
| 2015 | 4 | 16 | 24 | −88 | no | prev | 1198 | 360 | no | no | no | 284 |
| 2015 | 6 | 8 | 9 | −67 | no | 368 | u | u | no | no | no | no |
| 2015 | 6 | 23 | 5 | −198 | 610 | 368 | 1366 u | 360 | M2.0 | N12E16 | 0.021 | 3019 |
| 2015 | 6 | 25 | 17 | −81 | 550 | 748 | 1209 u | 360 | M6.5 | N12W08 | no | no |
| 2015 | 6 | 26 u | 18 | −51 | 490 | no | 1627 u | 360 | M7.9 | N09W42 | 0.2726 | 8319 |
| 2015 | 7 | 5 | 6 | −74 | no | no | 1435 u | 360 | no | no | 0.045 | 859 |
| 2015 | 7 | 13 | 16 | −68 | 490 | no | u | u | no | no | no | no |
| 2015 | 7 | 23 | 9 | −72 | no | no | 782 u | 194 | C2.1 | S25W62 | u | u |
| 2015 | 8 | 16 | 8 | −98 | 500 | 477 | 647 u | 204 | B7.0 | no | no | no |
| 2015 | 8 | 19 | 7 | −64 | no | no | 622 u | X1.0 | u | no | no | no |
| 2015 | 8 | 23 | 9 | −57 | no | no | 547 u | 360 | M1.2 | S15E13 | no | no |
| 2015 | 8 | 26 u | 22 | −79 | no | no | u | u | no | no | no | no |
| 2015 | 8 | 27 u | 6 | −92 | no | no | u | u | no | no | no | no |
| 2015 | 8 | 27 | 21 | −103 | 370 | no | u | u | no | no | no | no |
| 2015 | 8 | 28 u | 10 | −102 | no | no | u | u | no | no | no | no |
| 2015 | 9 | 4 | 7 | −50 | no | no | u | u | no | no | no | no |
| 2015 | 9 | 7 | 21 | −75 | no | no | u | u | no | no | no | no |
| 2015 | 9 | 9 | 13 | −105 | 460 | no | u | u | no | no | no | no |
| 2015 | 9 | 11 | 15 | −87 | no | no | 556 u | 146 | no | no | no | no |
| 2015 | 9 | 20 | 16 | −81 | 510 | 716 | 823 | 131 | C2.6 | S21W10 | no | no |
| 2015 | 10 | 4 | 10 | −63 | no | no | 602 u | 128 | no | no | no | no |
| 2015 | 10 | 6 | 20 | −52 | no | no | 914 u | 106 | C1.6 | S18W66 | no | no |
| 2015 | 10 | 7 | 10 | −101 | no | no | 714 u | 102 | no | no | no | no |
| 2015 | 10 | 7 | 23 | −124 | no | no | 900 u | 145 | no | no | no | no |
| 2015 | 10 | 18 | 10 | −56 | no | no | 770 | 79 | B6.4 | S06E76 | no | 90 |
| 2015 | 11 | 3 u | 13 | −51 | no | no | 751 u | 114 | C1.3 | N07E30 | no | no |
| 2015 | 11 | 4 | 13 | −56 | 640 | no | 867 | 360 | no | no | no | no |
| 2015 | 11 | 7 | 7 | −87 | 500 | no | 578 | 360 | M3.7 | N09W04 | 0.005 | 4425 |
| 2015 | 11 | 9 u | 17 | −55 | no | no | u | u | no | no | no | no |
| 2015 | 11 | 10 | 14 | −56 | no | no | 1041 u | 273 | M3.9 | S11E41 | 0.0675 | 338 |
| 2015 | 12 | 14 | 20 | −55 | no | no | 628 u | 84 | C1.4 | S15E52 | no | no |
| 2015 | 12 | 20 | 23 | −166 | 400 | 536 | 579 | 360 | C6.6 | S13W04 | no | 84 |
| 2016 | 1 | 1 | 1 | −110 | 440 | no | 1212 | 360 | M1.8 | S23W11 | 0.0115 | 572 |
| 2016 | 1 | 20 | 17 | −101 | 370 | no | 1730 | 360 | no | no | no | no |
| 2016 | 2 | 1 | 9 | −53 | no | no | 684 u | 71 | C3.3 | N09W50 | no | 689 |
| 2016 | 2 | 3 | 3 | −57 | no | no | 901 u | 118 | C2.0 | S20W63 | no | no |
| 2016 | 2 | 16 | 20 | −65 | no | no | 719 u | 360 | C8.9 | N09W08 | no | no |
| 2016 | 2 | 18 | 1 | −62 | no | no | u | u | no | no | no | no |
| 2016 | 3 | 6 | 22 | −99 | pd | no | 644 u | 158 | no | no | no | no |
| 2016 | 3 | 15 | 8 | −50 | no | 398 | 641 u | 79 | no | no | no | no |
| 2016 | 3 | 16 u | 24 | −56 | no | no | u | u | no | no | no | no |
| 2016 | 4 | 2 | 24 | −59 | no | no | u | u | no | no | no | no |
| 2016 | 4 | 7 | 22 | −61 | no | no | u | u | no | no | no | no |
| 2016 | 4 | 13 | 2 | −56 | no | no | u | u | no | no | no | no |
| 2016 | 4 | 14 | 21 | −61 | 420 | no | 543 u | 136 | no | no | no | no |
| 2016 | 4 | 16 | 22 | −58 | nd | no | u | u | no | no | no | no |
| 2016 | 5 | 8 | 8 | −95 | no | no | u | u | no | no | no | no |
| 2016 | 8 | 3 | 16 | −52 | pd | no | u | u | no | no | no | no |
| 2016 | 8 | 23 | 22 | −73 | no | no | u | u | no | no | no | no |
| 2016 | 9 | 1 | 10 | −57 | no | no | u | u | no | no | no | no |
| 2016 | 9 | 2 u | 3 | −59 | no | no | u | u | no | no | no | no |
| 2016 | 9 | 28 u | 18 | −51 | no | no | u | u | no | no | no | no |
| 2016 | 9 | 29 u | 10 | −65 | no | no | u | u | no | no | no | no |
| 2016 | 10 | 4 | 10 | −50 | no | no | 818 u | 76 | no | no | no | no |
| 2016 | 10 | 13 | 18 | −110 | 390 | 415 | 179 | 360 | no | no | no | no |
| 2016 | 10 | 25 | 18 | −65 | no | no | u | u | no | no | no | no |
| 2016 | 10 | 29 | 4 | −70 | no | no | u | u | no | no | no | no |
| 2016 | 11 | 10 | 18 | −60 | 360 | 344 | u | u | no | no | no | no |
| 2017 | 3 | 1 | 22 | −61 | no | no | u | u | no | no | no | no |
| 2017 | 3 | 27 | 15 | −70 | no | no | u | u | no | no | no | no |
| 2017 | 3 | 31 | 7 | −51 | no | no | u | u | no | no | no | no |
| 2017 | 4 | 22 | 17 | −51 | no | no | 926 | 360 | C5.5 | N14E77 | no | no |
| 2017 | 5 | 28 | 8 | −125 | 360 | 373 | u | u | no | no | no | no |
| 2017 | 7 | 16 | 16 | −72 | 520 | no | 1200 | 360 | M2.4 | S06W29 | 0.1284 | 1248 |
| 2017 | 8 | 31 | 12 | −51 | no | 418 | u | u | no | no | no | no |
| 2017 | 9 | 8 | 2 | −122 | 220 | 245 | 1571 | 360 | X9.3 | S08W33 | 0.604 | u |
| 2017 | 9 | 8 | 18 | −109 | no | no | u | u | no | no | no | no |
| 2017 | 9 | 28 | 7 | −56 | no | no | u | u | no | no | no | no |
| 2017 | 10 | 14 | 6 | −53 | no | no | 741 u | 109 | no | no | no | 639 |
| 2017 | 11 | 8 | 2 | −73 | no | no | u | u | no | no | no | no |
| 2018 | 3 | 18 | 22 | −50 | no | no | u | u | no | no | no | no |
| 2018 | 4 | 20 | 10 | −66 | no | 313 | u | u | no | no | no | no |
| 2018 | 5 | 6 | 3 | −57 | no | 376 | u | u | no | no | no | no |
| 2018 | 8 | 26 | 7 | −175 | 410 | no | u | u | no | no | no | no |
| 2018 | 9 | 11 | 11 | −60 | no | no | u | u | no | no | no | no |
| 2018 | 10 | 7 | 22 | −53 | no | no | u | u | no | no | no | no |
| 2018 | 11 | 5 | 6 | −53 | no | no | u | u | no | no | no | no |
| 2019 | 5 | 11 | 22 | −51 | 350 | 411 | 745 u | M9.6 | u | no | no | no |
| 2019 | 5 | 14 | 8 | −65 | 470 | no | u | u | no | no | no | no |
| 2019 | 8 | 5 | 21 | −53 | no | no | u | u | no | no | no | no |
| 2019 | 9 | 1 | 7 | −52 | no | no | u | u | no | no | no | no |
References
- Dungey, J.W. Interplanetary Magnetic Field and the Auroral Zones. Phys. Rev. Lett. 1961, 6, 47–48. [Google Scholar] [CrossRef]
- Lakhina, G.; Tsurutani, B.; Gonzalez, W.; Alex, S. Humboldt, Alexander Von And Magnetic Storms. In Encyclopedia of Geomagnetism and Paleomagnetism; Gubbins, D., Herrero-Bervera, E., Eds.; Springer: Dordrecht, The Netherlands, 2007. [Google Scholar] [CrossRef]
- Gonzalez, W.D.; Joselyn, J.A.; Kamide, Y.; Kroehl, H.W.; Rostoker, G.; Tsurutani, B.T.; Vasyliunas, V.M. What is a geomagnetic storm? J. Geophys. Res. 1994, 99, 5771–5792. [Google Scholar] [CrossRef]
- Lazzús, J.A.; Salfate, I.; Vega-Jorquera, P. Intense Geomagnetic Storms in The Maximum Phase of Solar Cycle 24 Observed From a Low-Latitude Ground Station. Geofis. Int. 2022, 61, 267–286. [Google Scholar] [CrossRef]
- Tsurutani, B.T.; Gonzalez, W.D.; Tang, F.; Akasofu, S.I.; Smith, E.J. Origin of interplanetary southward magnetic fields responsible for major magnetic storms near solar maximum (1978–1979). J. Geophys. Res. 1988, 93, 8519–8531. [Google Scholar] [CrossRef]
- Akasofu, S.I.; Chapman, S. The Development of the Main Phase of Magnetic Storms. J. Geophys. Res. 1963, 68, 125–129. [Google Scholar] [CrossRef]
- Gosling, J.T.; McComas, D.J.; Phillips, J.L.; Bame, S.J. Geomagnetic activity associated with earth passage of interplanetary shock disturbances and coronal mass ejections. J. Geophys. Res. 1991, 96, 7831–7839. [Google Scholar] [CrossRef]
- Gopalswamy, N.; Yashiro, S.; Michalek, G.; Xie, H.; Lepping, R.P.; Howard, R.A. Solar source of the largest geomagnetic storm of cycle 23. Geophys. Rev. Lett. 2005, 32, L12S09. [Google Scholar] [CrossRef]
- Chen, P.F. Coronal Mass Ejections: Models and Their Observational Basis. Living Rev. Sol. Phys. 2011, 8, 1. [Google Scholar] [CrossRef]
- Joshi, N.C.; Bankoti, N.S.; Pande, S.; Pande, B.; Pandey, K. Relationship between interplanetary field/plasma parameters with geomagnetic indices and their behavior during intense geomagnetic storms. New Astron. 2011, 16, 366–385. [Google Scholar] [CrossRef]
- Webb, D.F.; Howard, T.A. Coronal Mass Ejections: Observations. Living Rev. Sol. Phys. 2012, 9, 3. [Google Scholar] [CrossRef]
- Telloni, D.; Antonucci, E.; Bemporad, A.; Bianchi, T.; Bruno, R.; Fineschi, S.; Magli, E.; Nicolini, G.; Susino, R. Detection of Coronal Mass Ejections at L1 and Forecast of Their Geoeffectiveness. Astrophys. J. 2019, 885, 120. [Google Scholar] [CrossRef]
- Marchezi, J.P.; Dai, L.; Alves, L.R.; Da Silva, L.A.; Sibeck, D.G.; Lago, A.D.; Souza, V.M.; Jauer, P.R.; Veira, L.E.A.; Cardoso, F.R.; et al. Electron Flux Variability and Ultra-Low Frequency Wave Activity in the Outer Radiation Belt under the Influence of Interplanetary Coronal Mass Ejections and High-Speed Solar Wind Streams: A Statistical Analysis From the Van Allen Probes Era. J. Geophys. Res. (Space Phys.) 2022, 127, e29887. [Google Scholar] [CrossRef]
- Schillings, A.; Palin, L.; Opgenoorth, H.J.; Hamrin, M.; Rosenqvist, L.; Gjerloev, J.W.; Juusola, L.; Barnes, R. Distribution and Occurrence Frequency of dB/dt Spikes During Magnetic Storms 1980–2020. Space Weather 2022, 20, e2021SW002953. [Google Scholar] [CrossRef]
- Milan, S.E.; Imber, S.M.; Fleetham, A.L.; Gjerloev, J. Solar Cycle and Solar Wind Dependence of the Occurrence of Large dB/dt Events at High Latitudes. J. Geophys. Res. (Space Phys.) 2023, 128, e2022JA030953. [Google Scholar] [CrossRef]
- Hapgood, M.; Liu, H.; Lugaz, N. SpaceX—Sailing Close to the Space Weather? Space Weather 2022, 20, e2022SW003074. [Google Scholar] [CrossRef]
- Miteva, R.; Samwel, S.W.; Tkatchova, S. Space Weather Effects on Satellites. Astronomy 2023, 2, 165–179. [Google Scholar] [CrossRef]
- McCuen, B.A.; Moldwin, M.B.; Steinmetz, E.S.; Engebretson, M.J. Automated High-Frequency Geomagnetic Disturbance Classifier: A Machine Learning Approach to Identifying Noise while Retaining High-Frequency Components of the Geomagnetic Field. J. Geophys. Res. (Space Phys.) 2023, 128, e2022JA030842. [Google Scholar] [CrossRef]
- Loewe, C.A.; Prölss, G.W. Classification and mean behavior of magnetic storms. J. Geophys. Res. 1997, 102, 14209–14214. [Google Scholar] [CrossRef]
- Mayaud, P.N. Derivation, Meaning, and Use of Geomagnetic Indices. Geophys. Monogr. Ser. 1980, 22, 607. [Google Scholar] [CrossRef]
- Banerjee, A.; Bej, A.; Chatterjee, T.N. On the existence of a long range correlation in the Geomagnetic Disturbance storm time (Dst) index. Astrophys. Space Sci. 2012, 337, 23–32. [Google Scholar] [CrossRef]
- Borovsky, J.E.; Shprits, Y.Y. Is the Dst Index Sufficient to Define All Geospace Storms? J. Geophys. Res. (Space Phys.) 2017, 122, 11543–11547. [Google Scholar] [CrossRef]
- Bartels, J.; Veldkamp, J. International data on magnetic disturbances, fourth quarter, 1953. J. Geophys. Res. 1954, 59, 297–302. [Google Scholar] [CrossRef]
- Matzka, J.; Stolle, C.; Yamazaki, Y.; Bronkalla, O.; Morschhauser, A. The Geomagnetic Kp Index and Derived Indices of Geomagnetic Activity. Space Weather 2021, 19, e2020SW002641. [Google Scholar] [CrossRef]
- McPherron, R.L. Determination of linear filters for predicting Ap during Jan. 1997. Geophys. Rev. Lett. 1998, 25, 3035–3038. [Google Scholar] [CrossRef]
- Kamide, Y.; Rostoker, G. What Is the Physical Meaning of the AE Index? EOS Trans. 2004, 85, 188–192. [Google Scholar] [CrossRef]
- Lakhina, G.S.; Tsurutani, B.T. Geomagnetic storms: Historical perspective to modern view. Geosci. Lett. 2016, 3, 5. [Google Scholar] [CrossRef]
- Tsurutani, B.T.; Gonzalez, W.D.; Lakhina, G.S.; Alex, S. The extreme magnetic storm of 1–2 September 1859. J. Geophys. Res. (Space Physics) 2003, 108, 1268. [Google Scholar] [CrossRef]
- Lockwood, M.; Owens, M.J.; Barnard, L.A.; Scott, C.J.; Watt, C.E.; Bentley, S. Space climate and space weather over the past 400 years: 2. Proxy indicators of geomagnetic storm and substorm occurrence. J. Space Weather Space Clim. 2018, 8, A12. [Google Scholar] [CrossRef]
- Temmer, M. Space weather: The solar perspective. Living Rev. Sol. Phys. 2021, 18, 4. [Google Scholar] [CrossRef]
- Akasofu, S.I. A Historical Review of the Geomagnetic Storm-Producing Plasma Flows from the Sun. Space Sci. Rev. 2011, 164, 85–132. [Google Scholar] [CrossRef]
- Manu, V.; Balan, N.; Zhang, Q.H.; Xing, Z.Y. Association of the Main Phase of the Geomagnetic Storms in Solar Cycles 23 and 24 with Corresponding Solar Wind-IMF Parameters. J. Geophys. Res. (Space Phys.) 2022, 127, e2022JA030747. [Google Scholar] [CrossRef]
- Burton, R.K.; McPherron, R.L.; Russell, C.T. An empirical relationship between interplanetary conditions and Dst. J. Geophys. Res. 1975, 80, 4204. [Google Scholar] [CrossRef]
- Gopalswamy, N. Solar connections of geoeffective magnetic structures. J. Atmos. Sol.-Terr. Phys. 2008, 70, 2078–2100. [Google Scholar] [CrossRef]
- Samwel, S.; Miteva, R. Correlations between space weather parameters during intense geomagnetic storms: Analytical study. Adv. Space Res. 2023, 72, 3440–3453. [Google Scholar] [CrossRef]
- Vennerstrom, S.; Lefevre, L.; Dumbović, M.; Crosby, N.; Malandraki, O.; Patsou, I.; Clette, F.; Veronig, A.; Vršnak, B.; Leer, K.; et al. Extreme Geomagnetic Storms—1868–2010. Sol. Phys. 2016, 291, 1447–1481. [Google Scholar] [CrossRef]
- Balan, N.; Zhang, Q.H.; Xing, Z.; Skoug, R.; Shiokawa, K.; Lühr, H.; Tulasi Ram, S.; Otsuka, Y.; Zhao, L. Capability of Geomagnetic Storm Parameters to Identify Severe Space Weather. Astrophys. J. 2019, 887, 51. [Google Scholar] [CrossRef]
- Richardson, I.G.; Webb, D.F.; Zhang, J.; Berdichevsky, D.B.; Biesecker, D.A.; Kasper, J.C.; Kataoka, R.; Steinberg, J.T.; Thompson, B.J.; Wu, C.C.; et al. Major geomagnetic storms (Dst ≤ −100 nT) generated by corotating interaction regions. J. Geophys. Res. (Space Phys.) 2006, 111, A07S09. [Google Scholar] [CrossRef]
- Dumitrache, C.; Popescu, N.A. The solar cycle 24 geomagnetic storms triggered by ICMEs and CIRs. Rom. Astron. J. 2018, 28, 177–186. [Google Scholar]
- Choraghe, K.; Shaikh, Z.; Raghav, A.; Ghag, K.; Dhamane, O. Intense (SYM − H ⩽ −100 nT) geomagnetic storms induced by planar magnetic structures in co-rotating interaction regions. Adv. Space Res. 2023, 72, 3220–3228. [Google Scholar] [CrossRef]
- Zhang, J.; Richardson, I.G.; Webb, D.F.; Gopalswamy, N.; Huttunen, E.; Kasper, J.C.; Nitta, N.V.; Poomvises, W.; Thompson, B.J.; Wu, C.C.; et al. Solar and interplanetary sources of major geomagnetic storms (Dst ≤ −100 nT) during 1996–2005. J. Geophys. Res. (Space Phys.) 2007, 112, A10102. [Google Scholar] [CrossRef]
- Miteva, R. On extreme space weather events: Solar eruptions, energetic protons and geomagnetic storms. Adv. Space Res. 2020, 66, 1977–1991. [Google Scholar] [CrossRef]
- Miteva, R.; Samwel, S.W.; Nedal, M. Geomagnetic Storms and their Solar Origin in Solar Cycle 24 (2009–2019). In Proceedings of the XIII Bulgarian-Serbian Astronomical Conference, BSAC 2022, Velingrad, Bulgaria, 3–7 October 2022; Semkov, E., Dimitrijevic, M.S., Dechev, M., Simic, Z., Eds.; Astronomical Society “Rudjer Boskovic”: Belgrade, Serbia, 2023; pp. 125–135, ISBN ISBN 978-868903525-4. [Google Scholar]
- Miteva, R.; Samwel, S.W.; Costa-Duarte, M.V. The Wind/EPACT Proton Event Catalog (1996–2016). Sol. Phys. 2018, 293, 27. [Google Scholar] [CrossRef]
- Samwel, S.W.; Miteva, R. Catalogue of in situ observed solar energetic electrons from ACE/EPAM instrument. Mon. Not. R. Astron. Soc. 2021, 505, 5212–5227. [Google Scholar] [CrossRef]
- Kilpua, E.; Lugaz, N.; Mays, M.L.; Temmer, M. Forecasting the Structure and Orientation of Earthbound Coronal Mass Ejections. Space Weather 2019, 17, 498–526. [Google Scholar] [CrossRef]
- Miteva, R.; Samwel, S.W.; Zabunov, S. Multi-Energy Proton Events and Geomagnetic Storms in Solar Cycles 23 and 24. In Proceedings of the SES-2020 Conference, Sofia, Bulgaria, 4–6 November 2020; pp. 64–68. [Google Scholar]
- Mansilla, G.A. Solar wind and IMF parameters associated with geomagnetic storms with Dst < −50 nT. Phys. Scr. 2008, 78, 045902. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).