Improving Air Pollution Modelling in Complex Terrain with a Coupled WRF–LOTOS–EUROS Approach: A Case Study in Aburrá Valley, Colombia
Abstract
:1. Introduction
2. Materials and Methods
2.1. LOTOS–EUROS Model
2.2. Meteorological Model Weather Research Forecast
2.3. Experimental Setup
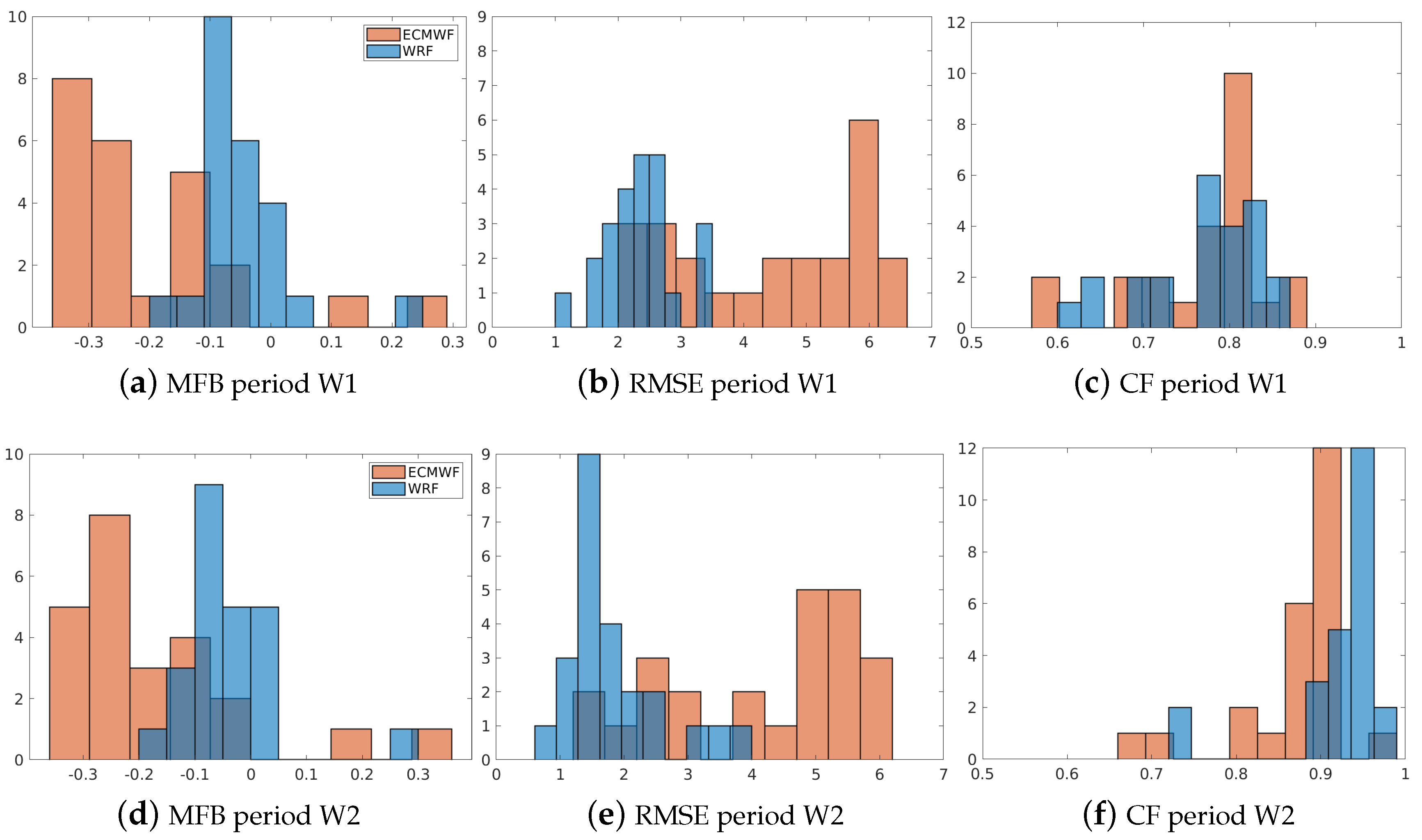
2.4. Statistical Performance Metrics
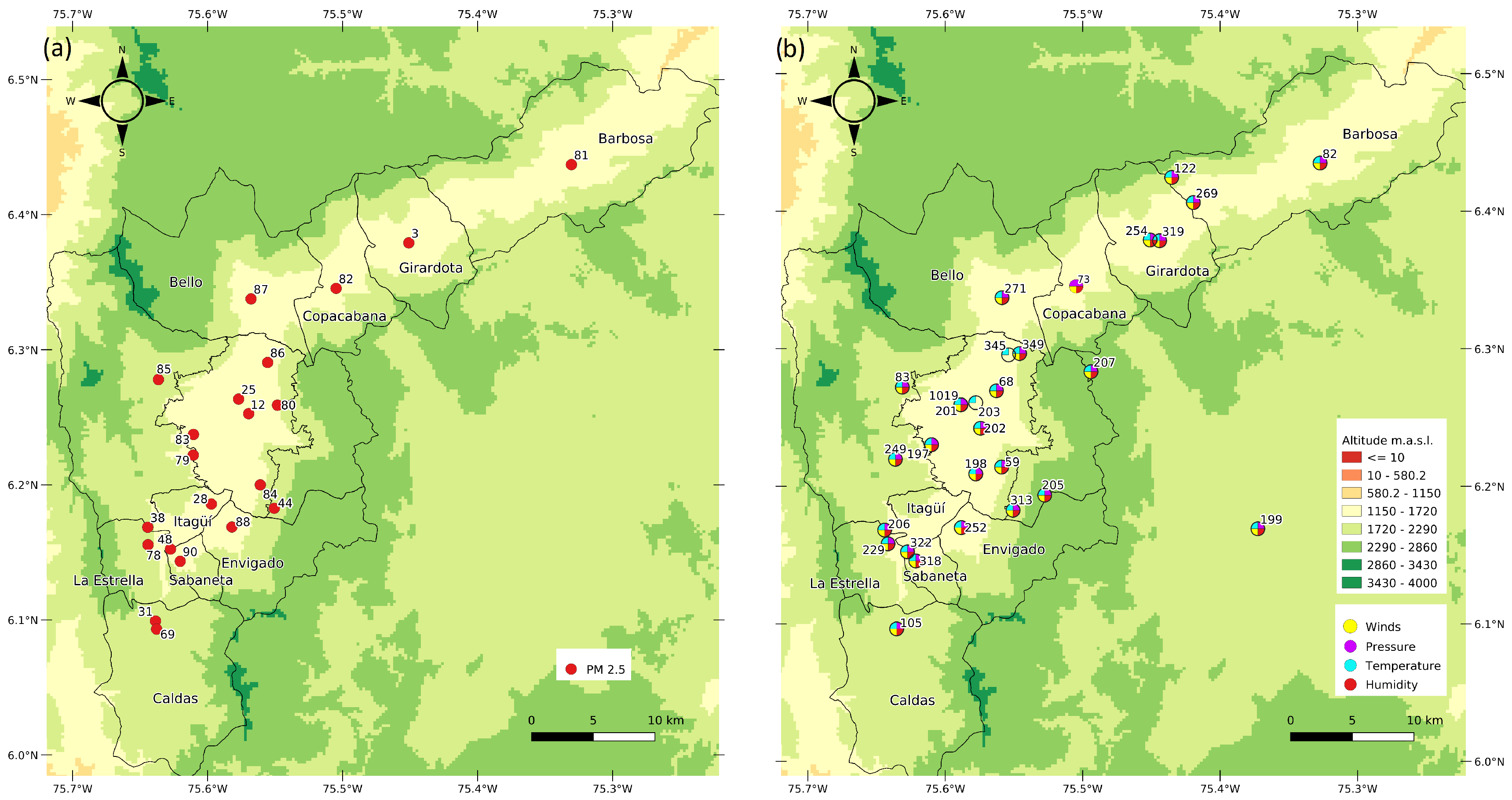
2.5. Ground-Based Sensor Network for Validation
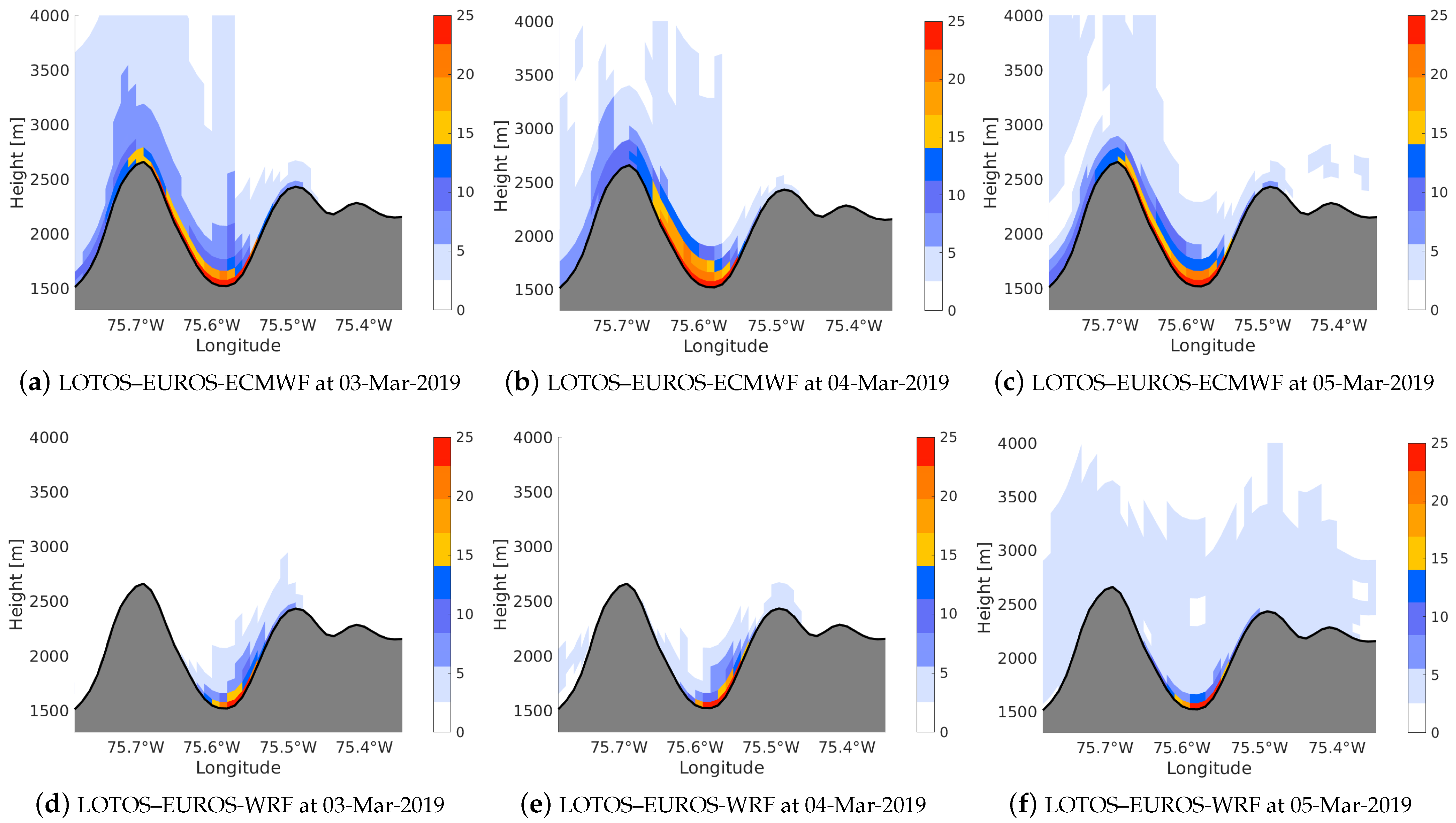
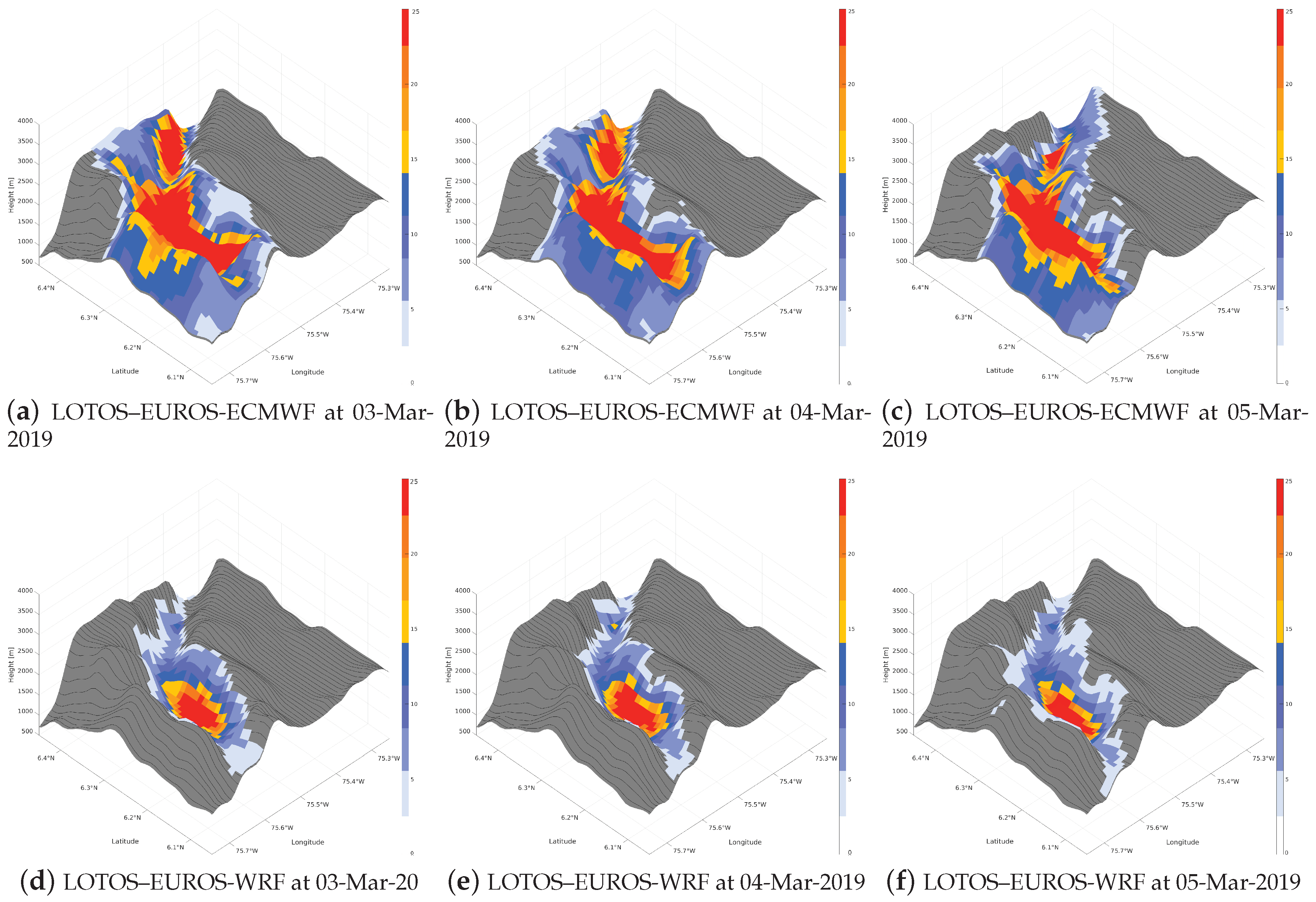
3. Results and Discussion
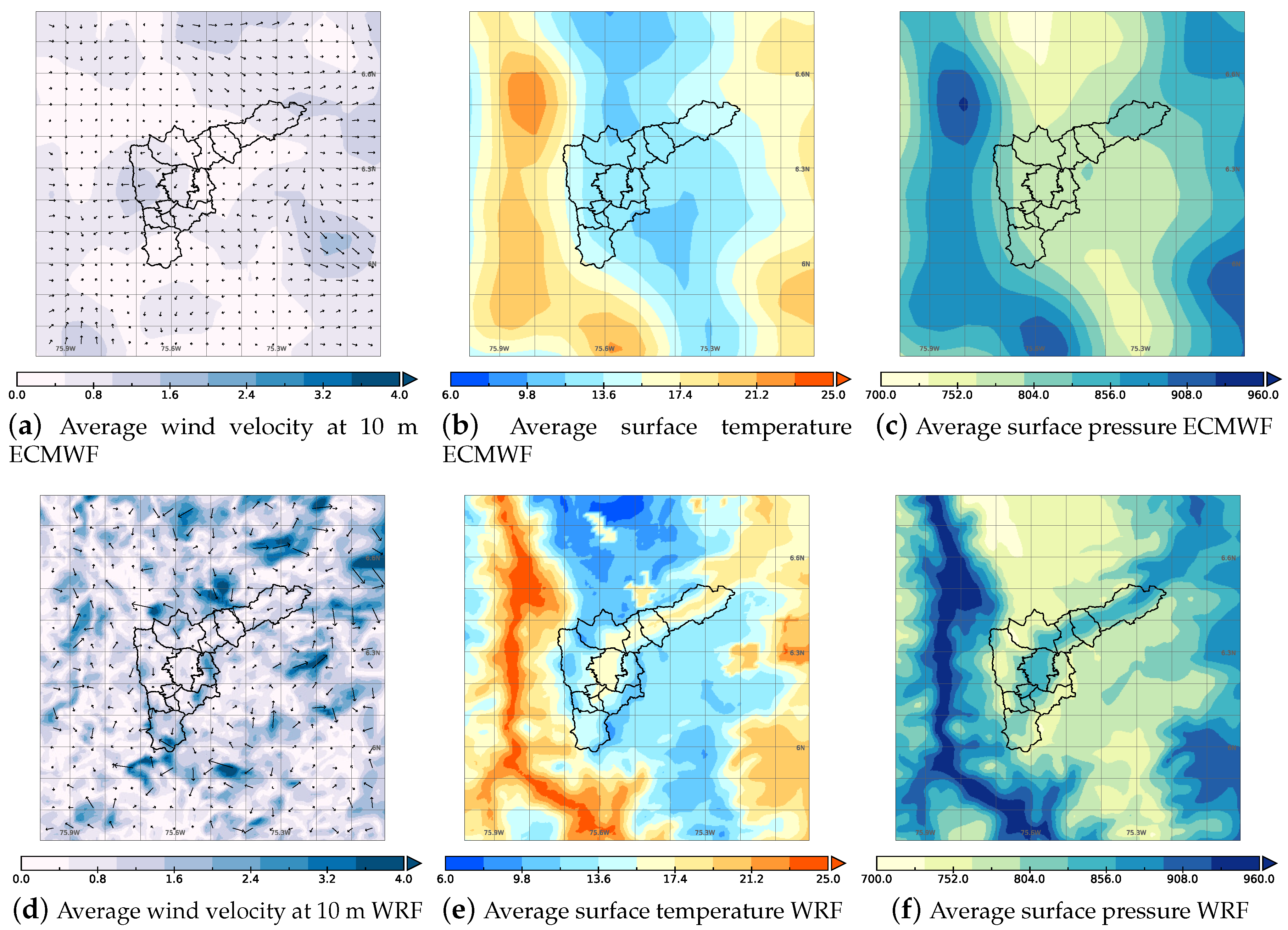
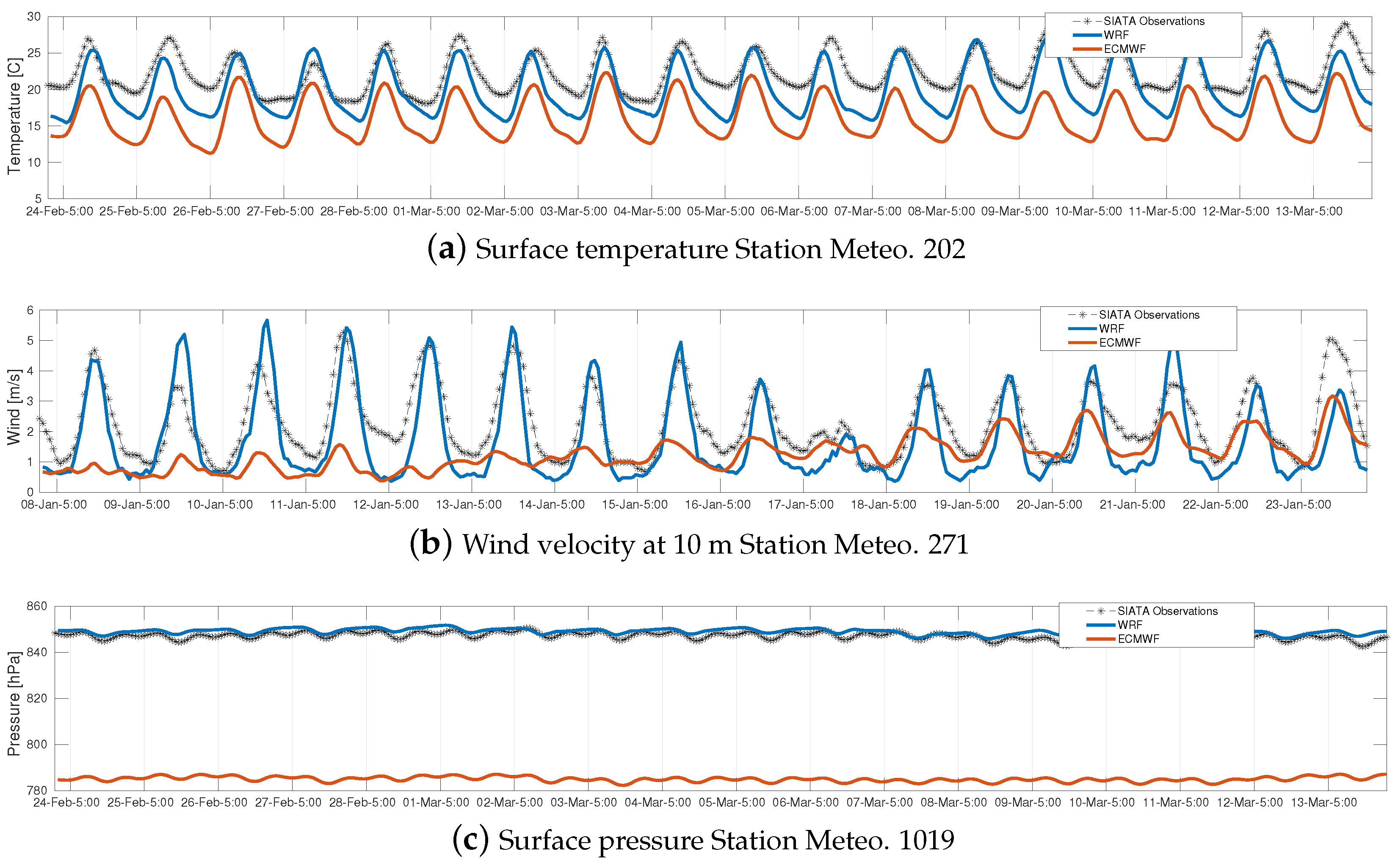
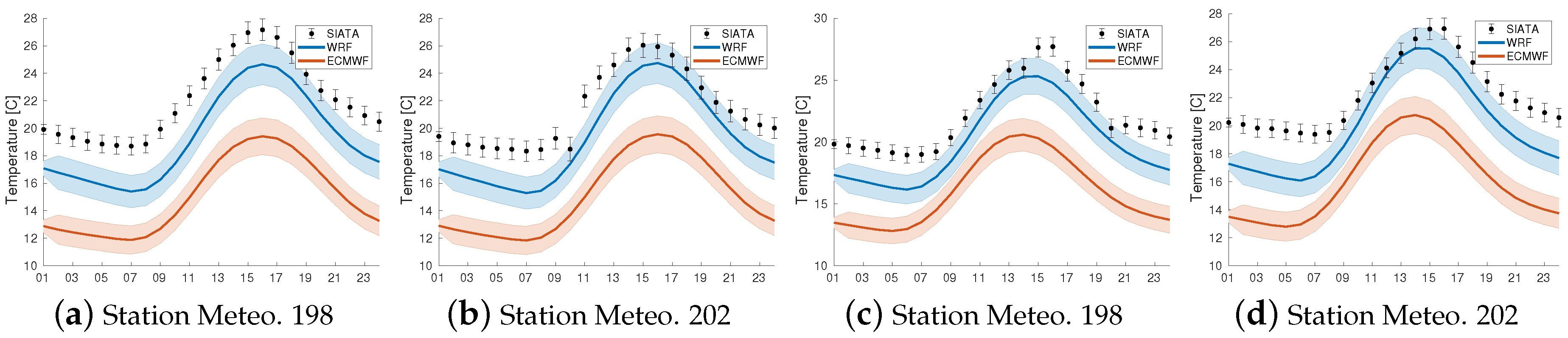
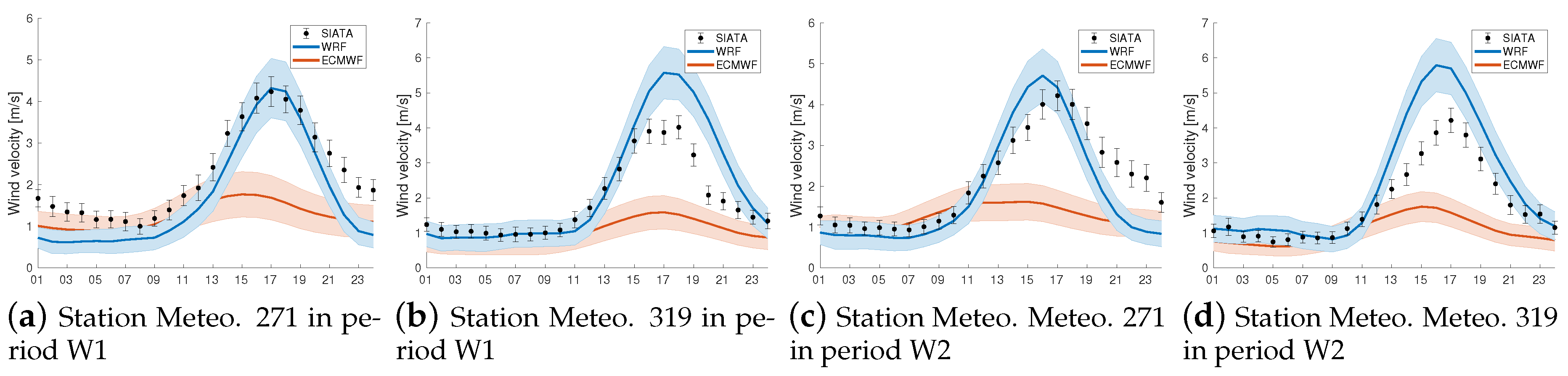
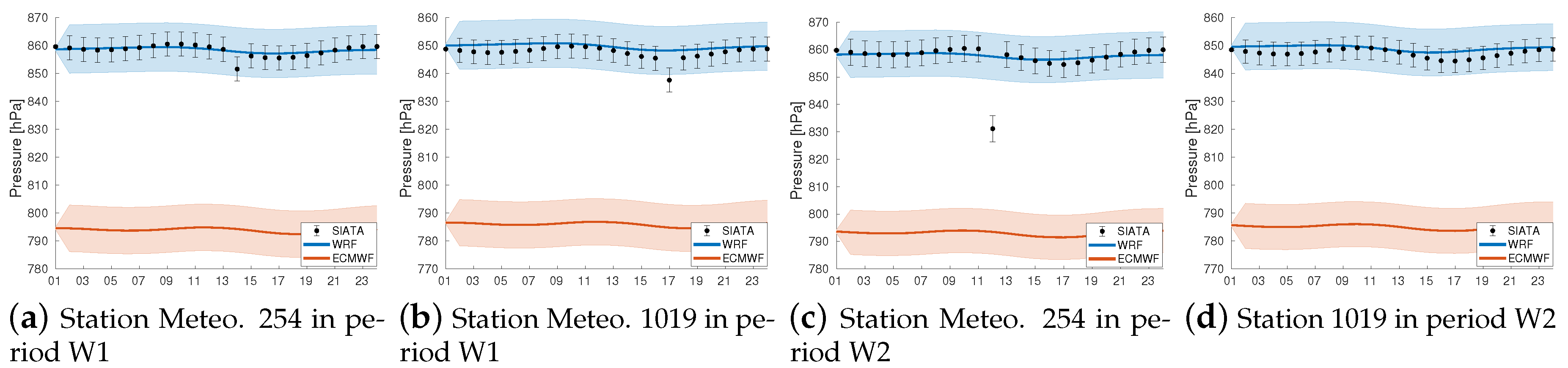
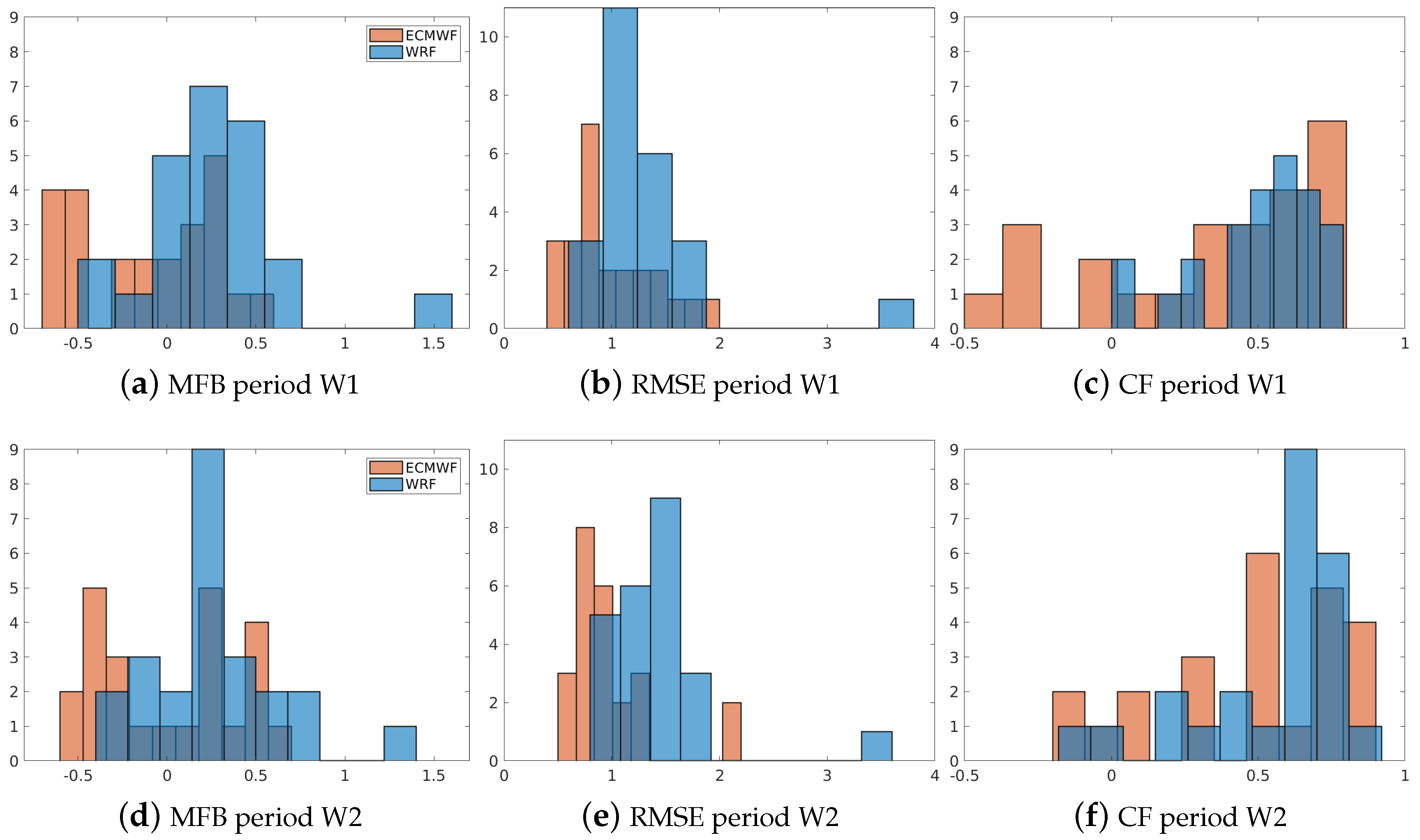
3.1. Comparison of ECMWF and WRF Meteorology
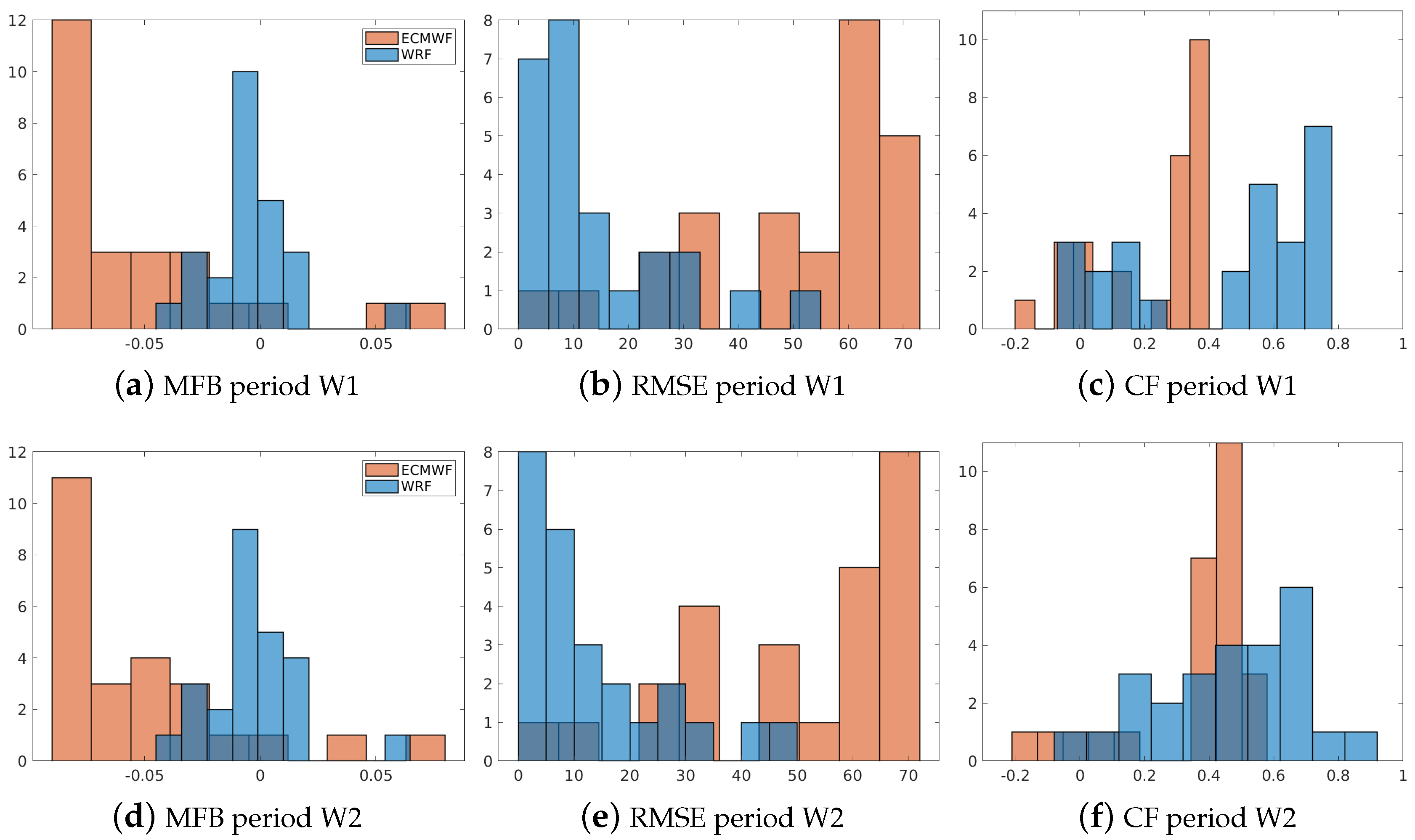
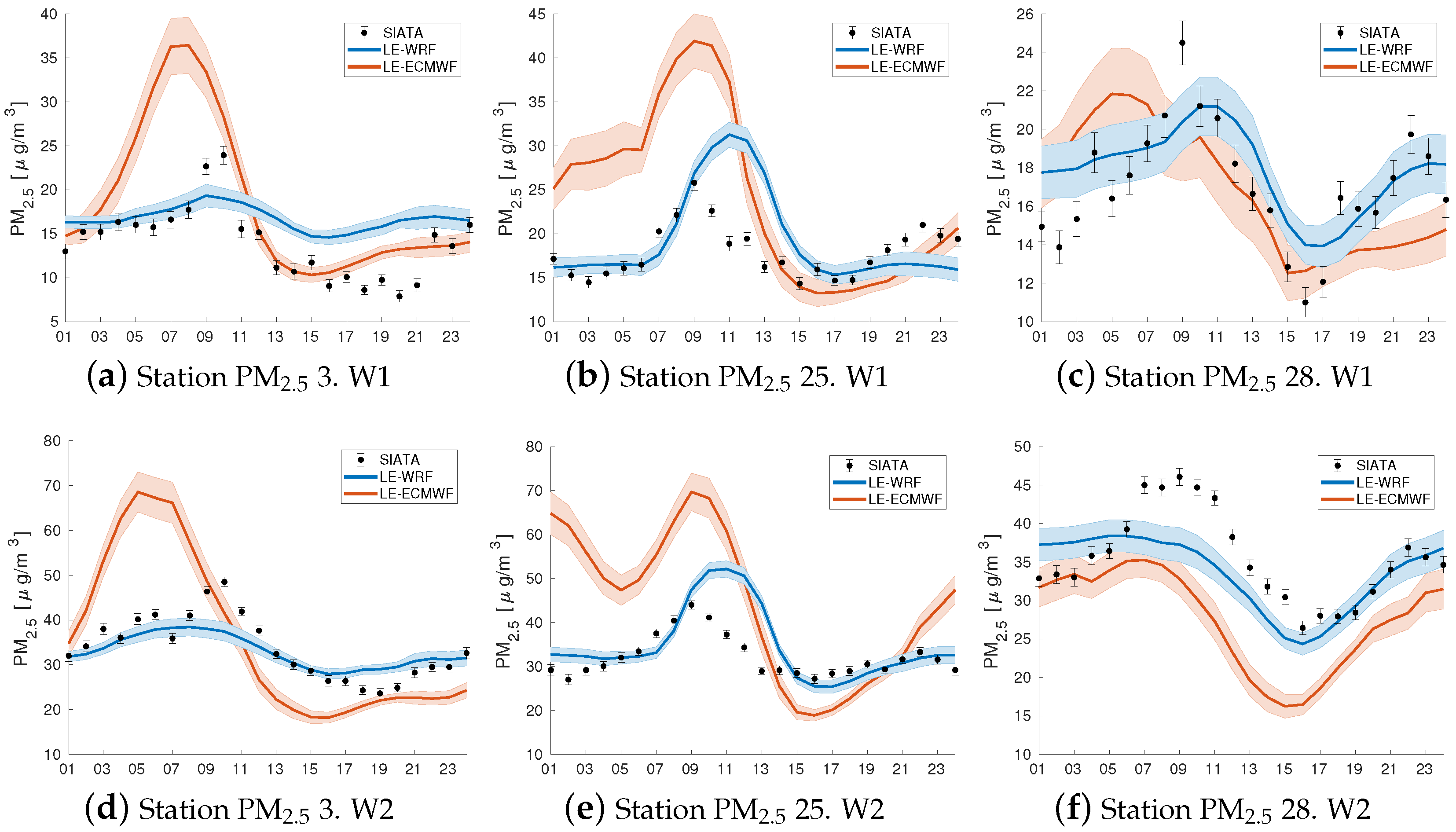
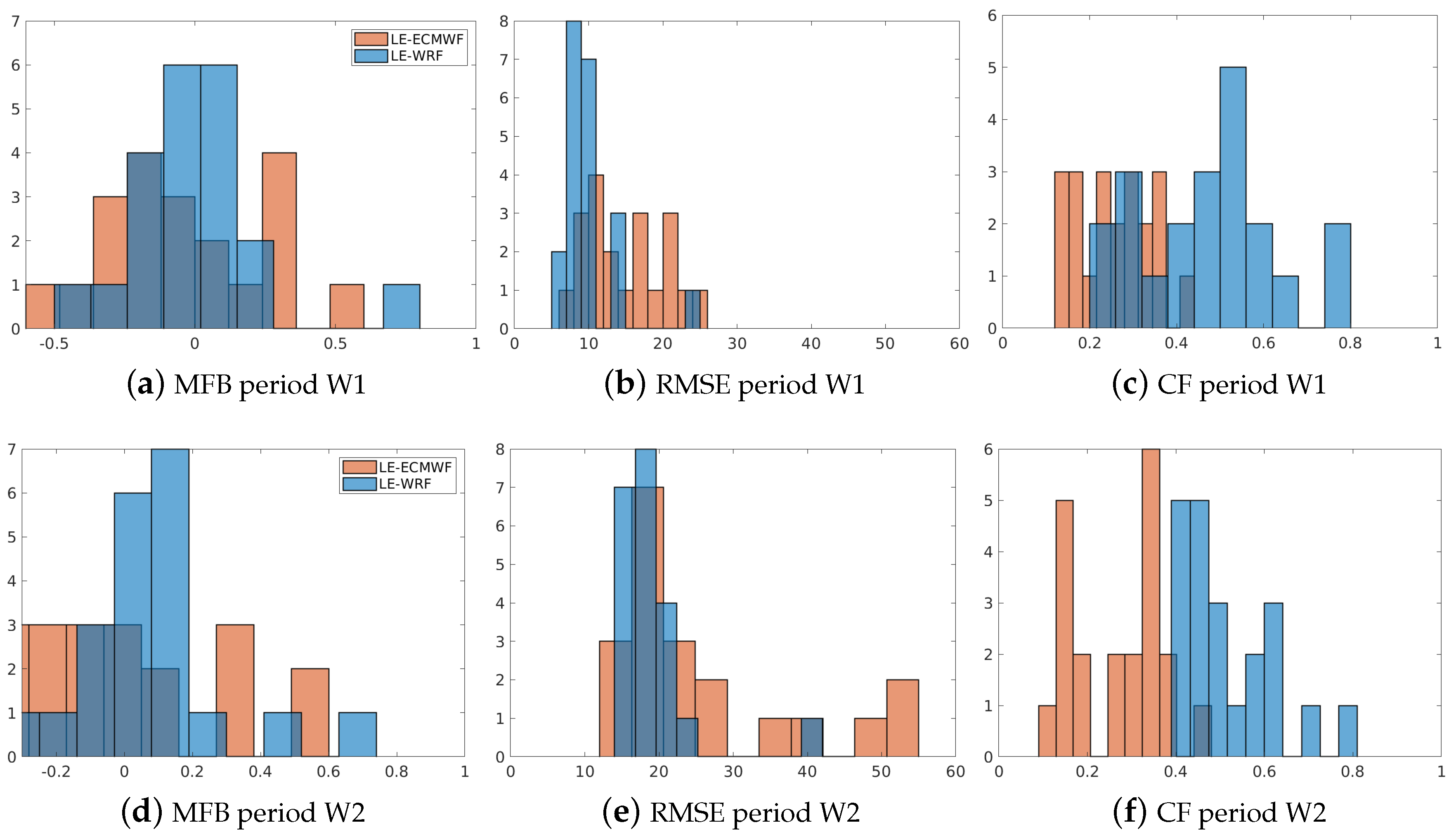
3.2. Comparison of Pollutants Dispersion Patterns of LOTOS–EUROS Model with Both Meteorology
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Montoya, O.L.; Niño-Ruiz, E.D.; Pinel, N. On the mathematical modelling and data assimilation for air pollution assessment in the Tropical Andes. Environ. Sci. Pollut. Res. 2020, 27, 35993–36012. [Google Scholar] [CrossRef] [PubMed]
- Mejía, L.H. Caracterización de la Capa límite Atmosférica en el valle de aburrá a partir de la Información de Sensores Remotos y Radiosondeos. Master’s Thesis, Universidad Nacional de Colombia-Sede Medellín, Medellín, Colombia, 2015. Línea de Investigación: Ciencias de la tierra y del espacio-Meteorología. [Google Scholar]
- Jiménez, J.F. Altura de la Capa de Mezcla en un área Urbana Montañosa y Tropical. Caso de Estudio: Valle de Aburrá (Colombia). Ph.D. Thesis, Universidad de Antioquia, Medellín, Colombia, 2016. [Google Scholar]
- Bedoya, J.; Martãnez, E. Calidad del Aire en el Valle de Aburrã Antioquia-Colombia. Dyna 2009, 76, 7–15. [Google Scholar]
- Rendón, A.M.; Salazar, J.F.; Palacio, C.A.; Wirth, V. Temperature Inversion Breakup with Impacts on Air Quality in Urban Valleys Influenced by Topographic Shading. J. Appl. Meteorol. Climatol. 2015, 54, 302–321. [Google Scholar] [CrossRef]
- Manders, A.; Kranenburg, R.; Segers, A.; Hendriks, C.; Jacobs, H.; Schaap, M. Use of WRF meteorology in the LOTOS-EUROS chemistry transport model. In Proceedings of the 11th International Conference on Air Quality—Science and Application, Barcelona, Spain, 12–16 March 2018. [Google Scholar]
- Escudero, M.; Segers, A.; Kranenburg, R.; Querol, X.; Alastuey, A.; Borge, R.; De La Paz, D.; Gangoiti, G.; Schaap, M. Analysis of summer O3 in the Madrid air basin with the LOTOS-EUROS chemical transport model. Atmos. Chem. Phys. 2019, 19, 14211–14232. [Google Scholar] [CrossRef]
- Arasa, R.; Soler, M.R.; Olid, M. Numerical experiments to determine MM5/WRF-CMAQ sensitivity to various PBL and land-surface schemes in north-eastern Spain: Application to a case study in summer 2009. Int. J. Environ. Pollut. 2012, 48, 105–116. [Google Scholar] [CrossRef]
- Tuccella, P.; Curci, G.; Visconti, G.; Bessagnet, B.; Menut, L.; Park, R.J. Modeling of gas and aerosol with WRF/Chem over Europe: Evaluation and sensitivity study. J. Geophys. Res. Atmos. 2012, 117, 1–15. [Google Scholar] [CrossRef]
- Hu, X.M.; Klein, P.M.; Xue, M. Evaluation of the updated YSU planetary boundary layer scheme within WRF for wind resource and air quality assessments. J. Geophys. Res. Atmos. 2013, 118, 10490–10505. [Google Scholar] [CrossRef]
- Žabkar, R.; Koračin, D.; Rakovec, J. A WRF/Chem sensitivity study using ensemble modelling for a high ozone episode in Slovenia and the Northern Adriatic area. Atmos. Environ. 2013, 77, 990–1004. [Google Scholar] [CrossRef]
- Srinivas, C.V.; Hari Prasad, K.B.; Naidu, C.V.; Baskaran, R.; Venkatraman, B. Sensitivity Analysis of Atmospheric Dispersion Simulations by FLEXPART to the WRF-Simulated Meteorological Predictions in a Coastal Environment. Pure Appl. Geophys. 2016, 173, 675–700. [Google Scholar] [CrossRef]
- Kumar, A.; Jiménez, R.; Belalcázar, L.C.; Rojas, N.Y. Application of WRF-Chem Model to Simulate PM10 Concentration over Bogota. Aerosol Air Qual. Res. 2016, 16, 1206–1221. [Google Scholar] [CrossRef]
- Henao, J.J.; Mejía, J.F.; Rendón, A.M.; Salazar, J.F. Sub-kilometer dispersion simulation of a CO tracer for an inter-Andean urban valley. Atmos. Pollut. Res. 2020, 11, 928–945. [Google Scholar] [CrossRef]
- Georgiou, G.K.; Christoudias, T.; Proestos, Y.; Kushta, J.; Pikridas, M.; Sciare, J.; Savvides, C.; Lelieveld, J. Evaluation of WRF-Chem model (v3. 9.1. 1) real-time air quality forecasts over the Eastern Mediterranean. Geosci. Model Dev. 2022, 15, 4129–4146. [Google Scholar] [CrossRef]
- Lopez-Restrepo, S.; Yarce, A.; Pinel, N.; Quintero, O.L.; Segers, A.; Heemink, A.W. Urban air quality modeling using low-cost sensor network and data assimilation in the aburrá valley, colombia. Atmosphere 2021, 12, 91. [Google Scholar] [CrossRef]
- Lopez-Restrepo, S.; Nino-Ruiz, E.D.; Guzman-Reyes, L.G.; Yarce, A.; Quintero, O.L.; Pinel, N.; Segers, A.; Heemink, A.W. An efficient ensemble Kalman Filter implementation via shrinkage covariance matrix estimation: Exploiting prior knowledge. Comput. Geosci. 2021, 25, 985–1003. [Google Scholar] [CrossRef]
- Posada-Marín, J.A.; Rendón, A.M.; Salazar, J.F.; Mejía, J.F.; Villegas, J.C. WRF downscaling improves ERA-Interim representation of precipitation around a tropical Andean valley during El Niño: Implications for GCM-scale simulation of precipitation over complex terrain. Clim. Dyn. 2018, 52, 3609–3629. [Google Scholar] [CrossRef]
- Reboredo, B.; Arasa, R.; Codina, B. Evaluating Sensitivity to Different Options and Parameterizations of a Coupled Air Quality Modelling System over Bogotá, Colombia. Part I: WRF Model Configuration. Open J. Air Pollut. 2015, 4, 47–64. [Google Scholar] [CrossRef]
- Brunner, D.; Savage, N.; Jorba, O.; Eder, B.; Giordano, L.; Badia, A.; Balzarini, A.; Baró, R.; Bianconi, R.; Chemel, C.; et al. Comparative analysis of meteorological performance of coupled chemistry-meteorology models in the context of AQMEII phase 2. Atmos. Environ. 2015, 115, 470–498. [Google Scholar] [CrossRef]
- Herrera-Mejía, L.; Hoyos, C.D. Characterization of the atmospheric boundary layer in a narrow tropical valley using remote-sensing and radiosonde observations and the WRF model: The Aburrá Valley case-study. Q. J. R. Meteorol. Soc. 2019, 145, 2641–2665. [Google Scholar] [CrossRef]
- Mues, a.; Kuenen, J.; Hendriks, C.; Manders, a.; Segers, a.; Scholz, Y.; Hueglin, C.; Builtjes, P.; Schaap, M. Sensitivity of air pollution simulations with LOTOS-EUROS to the temporal distribution of anthropogenic emissions. Atmos. Chem. Phys. 2014, 14, 939–955. [Google Scholar] [CrossRef]
- Manders, A.M.M.; Builtjes, P.J.H.; Curier, L.; Denier Van Der Gon, H.A.C.; Hendriks, C.; Jonkers, S.; Kranenburg, R.; Kuenen, J.J.P.; Segers, A.J.; Timmermans, R.M.A.; et al. Curriculum vitae of the LOTOS–EUROS (v2.0) chemistry transport model. Geosci. Model Dev. 2017, 10, 4145–4173. [Google Scholar] [CrossRef]
- Sauter, F.; der Swaluw, E.V.; Manders-groot, A.; Kruit, R.W.; Segers, A.; Eskes, H. TNO Report TNO-060-UT-2012-01451; Technical Report; TNO: Utrecht, The Netherlands, 2012. [Google Scholar]
- Van Loon, M.; Builtjes, P.J.H.; Segers, a.J. Data assimilation of ozone in the atmospheric transport chemistry model LOTOS. Environ. Model. Softw. 2000, 15, 603–609. [Google Scholar] [CrossRef]
- Cáceres, R. Impacto de la Asimilación Radar en el Pronóstico de Precipitación a Muy Corto Plazo Usando el Modelo WRF. Ph.D. Thesis, Universidad de Barcelona, Barcelona, Spain, 2018. [Google Scholar]
- Skamarock, W.; Klemp, J.; Dudhia, J.; Gill, D.; Zhiquan, L.; Berner, J.; Wang, W.; Powers, J.; Duda, M.G.; Barker, D.M.; et al. A Description of the Advanced Research WRF Model Version 4; NCAR Technical Note NCAR/TN-475+STR; NCAR: Boulder, CO, USA, 2019; p. 145. [Google Scholar] [CrossRef]
- Jiménez-Sánchez, G.; Markowski, P.M.; Jewtoukoff, V.; Young, G.S.; Stensrud, D.J. The Orinoco Low-Level Jet: An Investigation of Its Characteristics and Evolution Using the WRF Model. J. Geophys. Res. Atmos. 2019, 124, 10696–10711. [Google Scholar] [CrossRef]
- Arregocés, H.A.; Rojano, R.; Restrepo, G. Sensitivity analysis of planetary boundary layer schemes using the WRF model in Northern Colombia during 2016 dry season. Dyn. Atmos. Ocean. 2021, 96, 101261. [Google Scholar] [CrossRef]
- Danielson, J.; Gesch, D. Global Multi-Resolution Terrain Elevation Data 2010 (GMTED2010); U.S. Geological Survey Open-File Report 2011–1073; U.S. Geological Survey: Reston, VA, USA, 2011; 26p. [CrossRef]
- Petrescu, A.M.R.; Abad-Viñas, R.; Janssens-Maenhout, G.; Blujdea, V.N.B.; Grassi, G. Global estimates of carbon stock changes in living forest biomass: EDGARv4.3—Time series from 1990 to 2010. Biogeosciences 2012, 9, 3437–3447. [Google Scholar] [CrossRef]
- Boylan, J.W.; Russell, A.G. PM and light extinction model performance metrics, goals, and criteria for three-dimensional air quality models. Atmos. Environ. 2006, 40, 4946–4959, Special issue on Model Evaluation: Evaluation of Urban and Regional Eulerian Air Quality Models. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE): Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Yu, S.; Eder, B.; Dennis, R.; Chu, S.H.; Schwartz, S.E. New unbiased symmetric metrics for evaluation of air quality models. Atmos. Sci. Lett. 2006, 7, 26–34. [Google Scholar] [CrossRef]
- Hoyos, C.D.; Herrera-Mejía, L.; Roldán-Henao, N.; Isaza, A. Effects of fireworks on particulate matter concentration in a narrow valley: The case of the Medellín metropolitan area. Environ. Monit. Assess. 2019, 192, 6. [Google Scholar] [CrossRef]
- Lopez-Restrepo, S.; Yarce, A.; Pinel, N.; Quintero, O.L.; Segers, A.; Heemink, A.W. Forecasting PM10 and PM2.5 in the Aburrá Valley (Medellín, Colombia) via EnKF based data assimilation. Atmos. Environ. 2020, 232, 117507. [Google Scholar] [CrossRef]
- Fernández-González, S.; Martín, M.L.; García-Ortega, E.; Merino, A.; Lorenzana, J.; Sánchez, J.L.; Valero, F.; Rodrigo, J.S. Sensitivity analysis of the WRF model: Wind-resource assessment for complex terrain. J. Appl. Meteorol. Climatol. 2018, 57, 733–753. [Google Scholar] [CrossRef]
- Wu, C.; Luo, K.; Wang, Q.; Fan, J. Simulated potential wind power sensitivity to the planetary boundary layer parameterizations combined with various topography datasets in the weather research and forecasting model. Energy 2022, 239, 122047. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhi, J.; Gill, D.O.; Barker, D.M.; Duda, M.G.; Huang, X.Y.; Wang, W.; Powers, J.G. A Description of the Advanced Research WRF Version 3; Technical Report; NCAR: Boulder, CO, USA, 2008; p. 113. [Google Scholar] [CrossRef]
| WRF | |||
| Domain | Latitude | Longitude | Resolution grid |
| D1 | −8.86401, 19.0911 | −86.6947, −59.2753 | 30 |
| D2 | −4.94672, 14.7199 | −84.929, −65.0916 | 10 |
| D3 | 3.7342, 9.0649 | −78.1088, −73.6774 | 3.3 |
| D4 | 5.3792, 7.2945 | −76.4586, −74.9814 | 1.1 |
| LOTOS–EUROS | |||
| Domain | Latitude | Longitude | Resolution grid |
| D1 | −8.5, 18 | −84, −60 | 27 |
| D2 | 2, 11 | −80.5, −70 | 9 |
| D3 | 5.2, 8.9 | −77.2, −73.9 | 3 |
| D4 | 5.7, 6.8 | −76, −75 | 1 |
| Process | Scheme |
|---|---|
| Microphysics | Single moment 6-class |
| Land surface | Thermal diffusion scheme |
| PBL | MYJ |
| Surface | Monin–Obukhov (Janjic Eta) |
| Radiation | CAM scheme |
| Meteorology | ECMWF; D1: 14 km km, D2, D3, D4: 7 km km |
| Initial and boundary | LOTOS–EUROS (D3). Temp.res: 1 h. |
| conditions | Spat.Res: 3 km × 3 km |
| Biogenic emissions | MEGAN Spat.res: 10 km × 10 km |
| Fire emissions | MACC/CAMS GFAS Spat.res: 10 km × 10 km |
| Landuse | GLC2000. Spat.res: 1 km × 1 km |
| lOrography | GMTED2010. Spat.res: 2 km × 2 km |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hinestroza-Ramirez, J.E.; Lopez-Restrepo, S.; Yarce Botero, A.; Segers, A.; Rendon-Perez, A.M.; Isaza-Cadavid, S.; Heemink, A.; Quintero, O.L. Improving Air Pollution Modelling in Complex Terrain with a Coupled WRF–LOTOS–EUROS Approach: A Case Study in Aburrá Valley, Colombia. Atmosphere 2023, 14, 738. https://doi.org/10.3390/atmos14040738
Hinestroza-Ramirez JE, Lopez-Restrepo S, Yarce Botero A, Segers A, Rendon-Perez AM, Isaza-Cadavid S, Heemink A, Quintero OL. Improving Air Pollution Modelling in Complex Terrain with a Coupled WRF–LOTOS–EUROS Approach: A Case Study in Aburrá Valley, Colombia. Atmosphere. 2023; 14(4):738. https://doi.org/10.3390/atmos14040738
Chicago/Turabian StyleHinestroza-Ramirez, Jhon E., Santiago Lopez-Restrepo, Andrés Yarce Botero, Arjo Segers, Angela M. Rendon-Perez, Santiago Isaza-Cadavid, Arnold Heemink, and Olga Lucia Quintero. 2023. "Improving Air Pollution Modelling in Complex Terrain with a Coupled WRF–LOTOS–EUROS Approach: A Case Study in Aburrá Valley, Colombia" Atmosphere 14, no. 4: 738. https://doi.org/10.3390/atmos14040738






