Thermospheric Mass Density Modelling during Geomagnetic Quiet and Weakly Disturbed Time
Abstract
:1. Introduction
2. TMD Data Sets
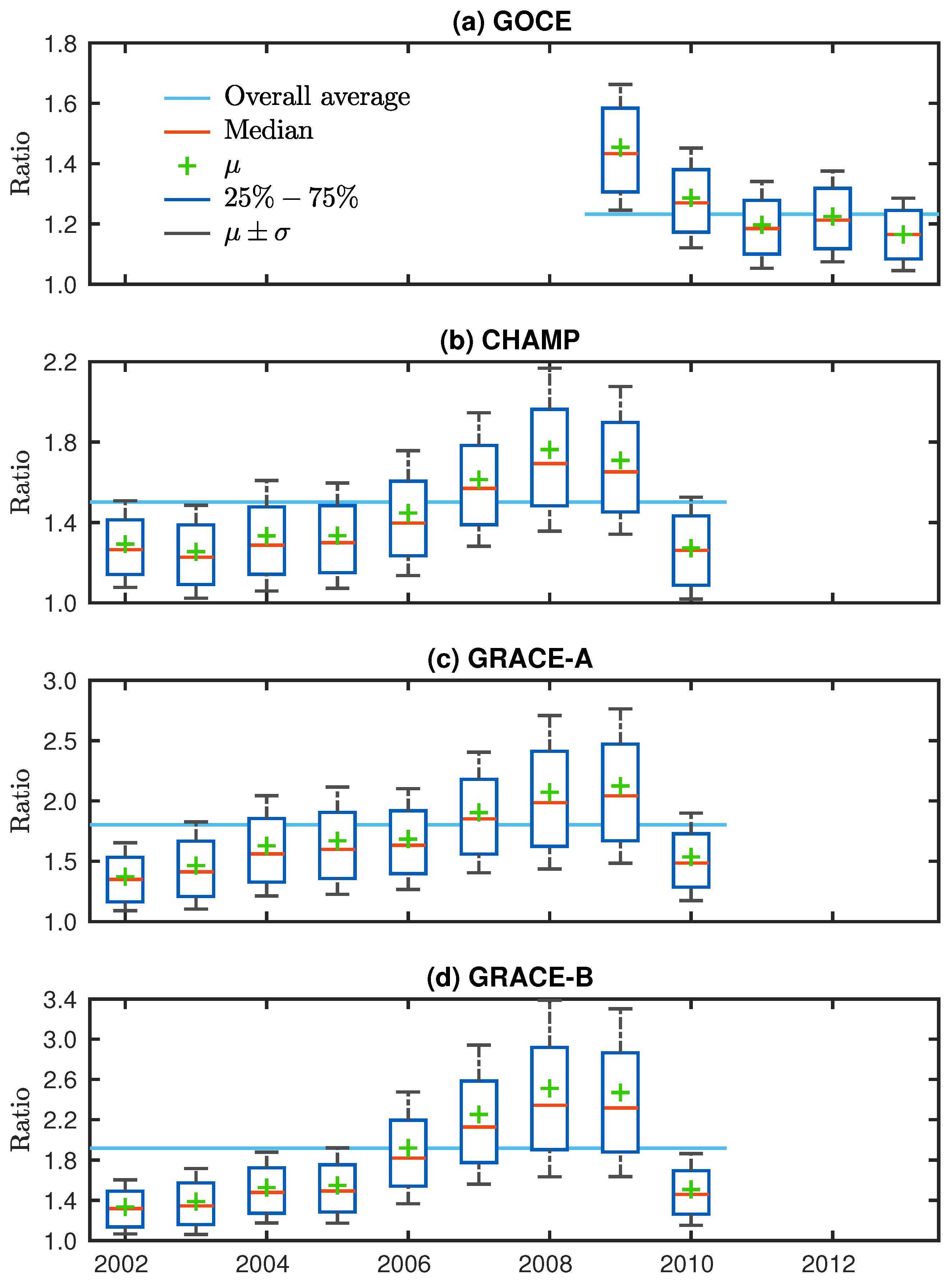
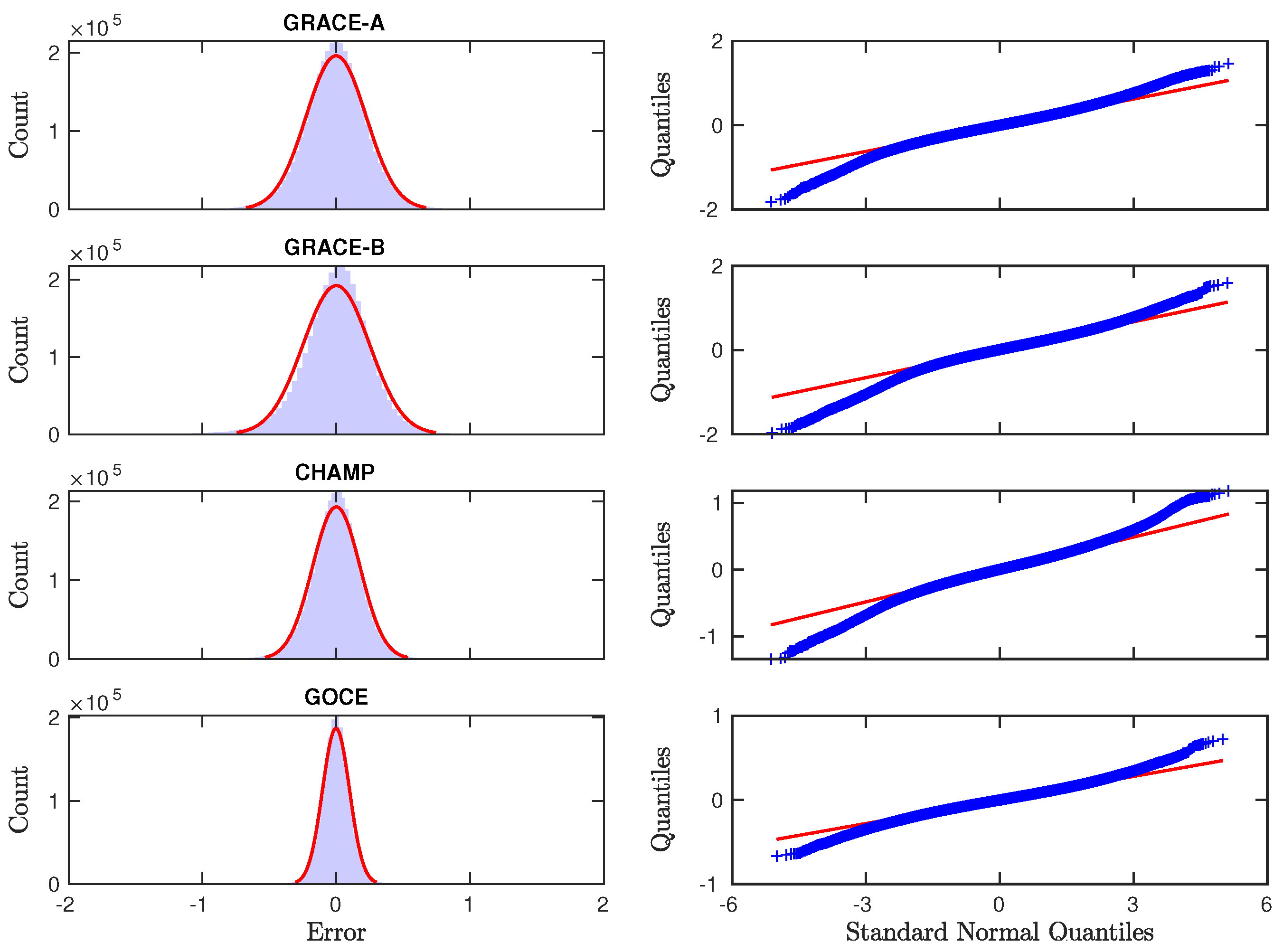
2.1. Data Reprocessing
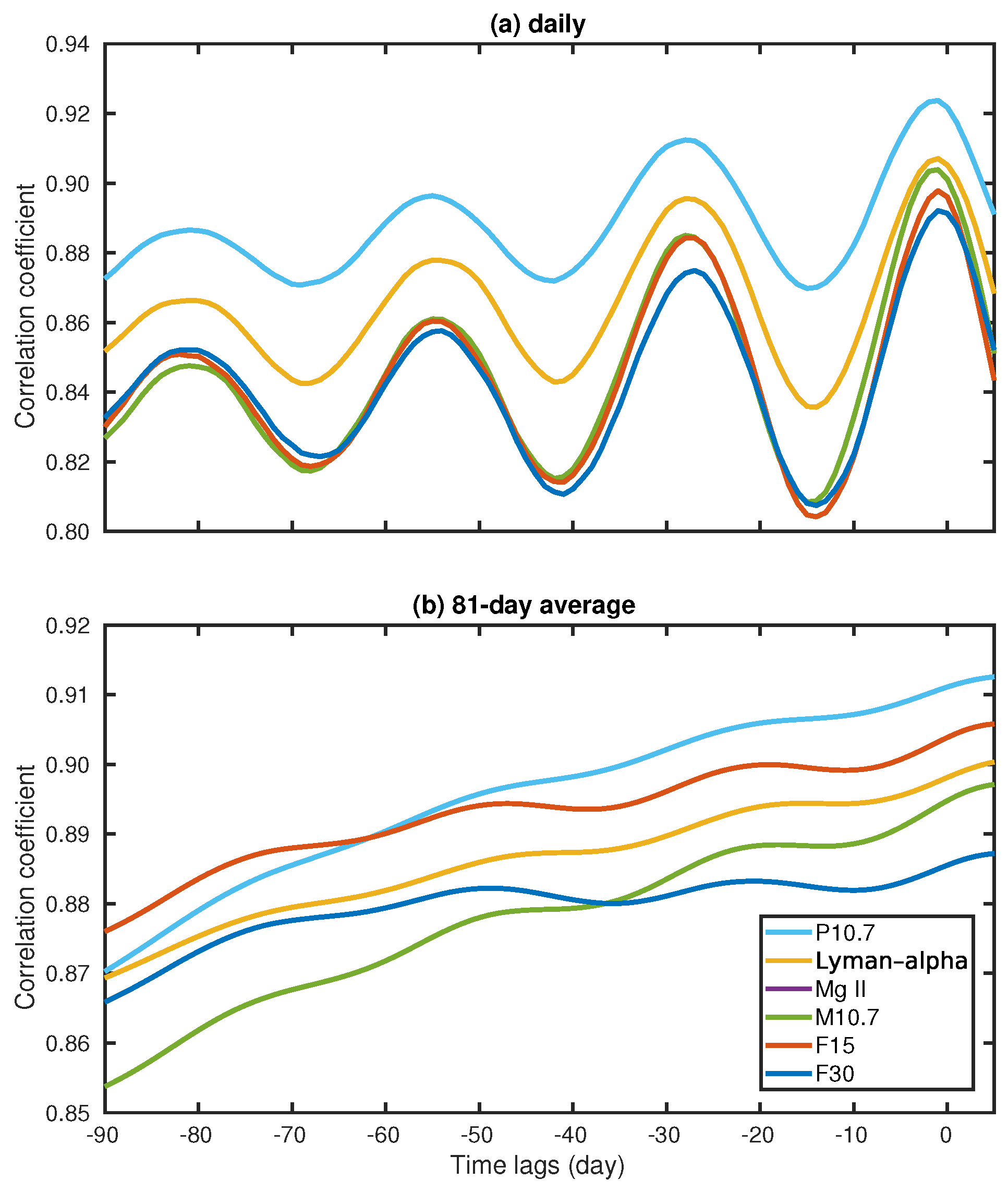
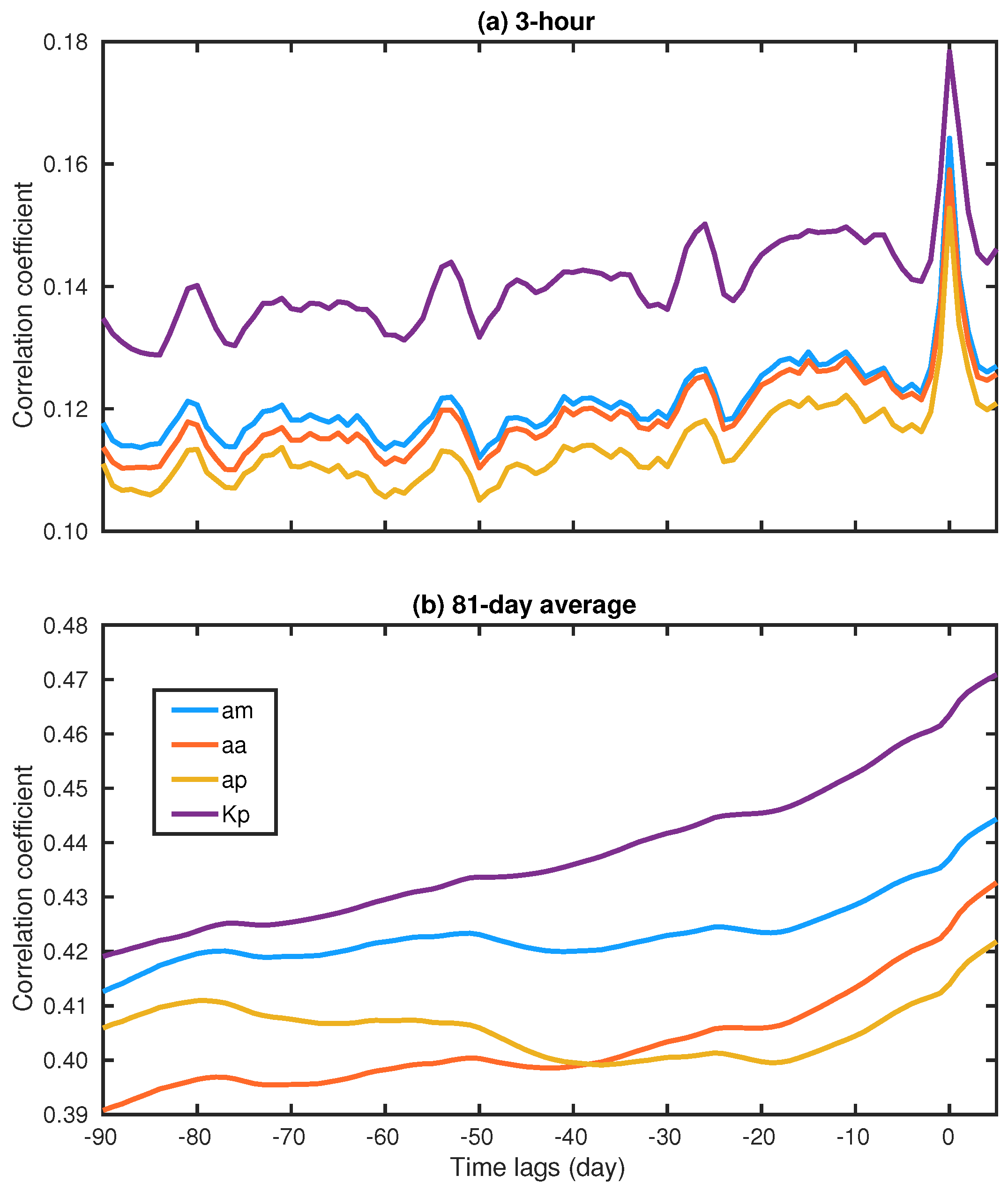
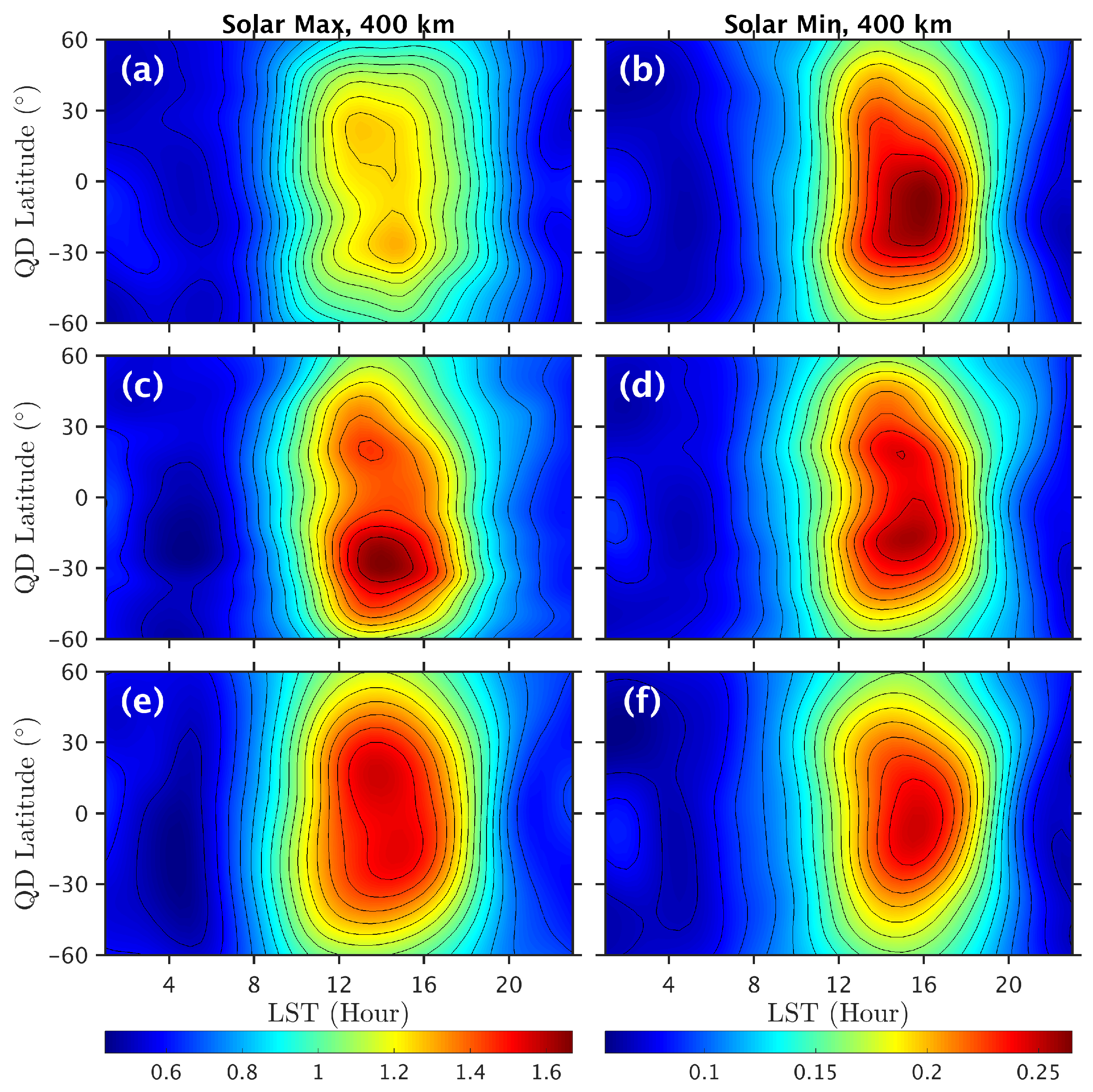
2.2. Response of TMD to Space Weather Indices
3. Modelling Methods
3.1. Fourier Analysis
3.2. Spherical Harmonics Analysis
3.3. Artificial Neural Networks
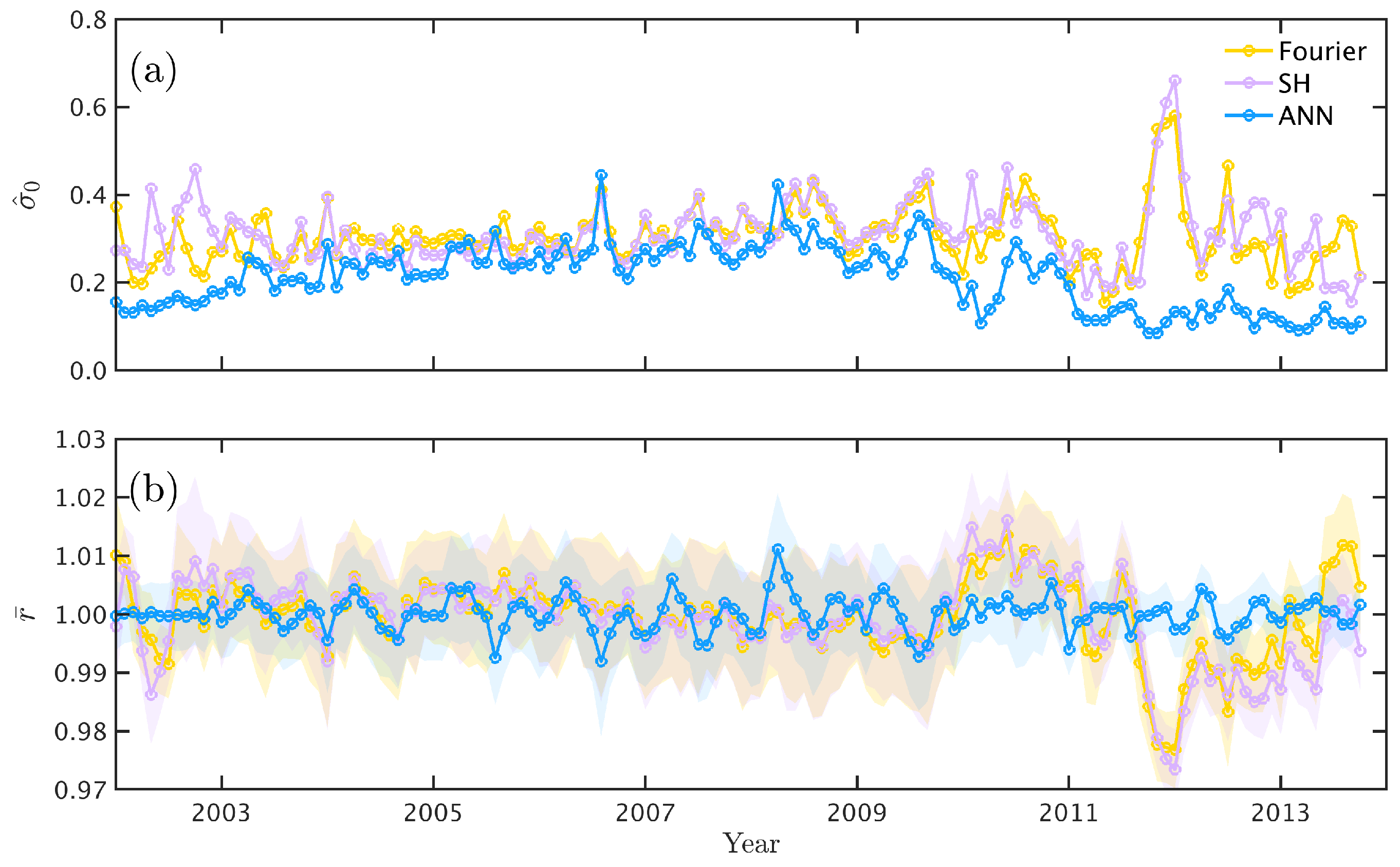
4. Results and Discussion
4.1. Fourier-Based Model
4.2. SH-Based Models
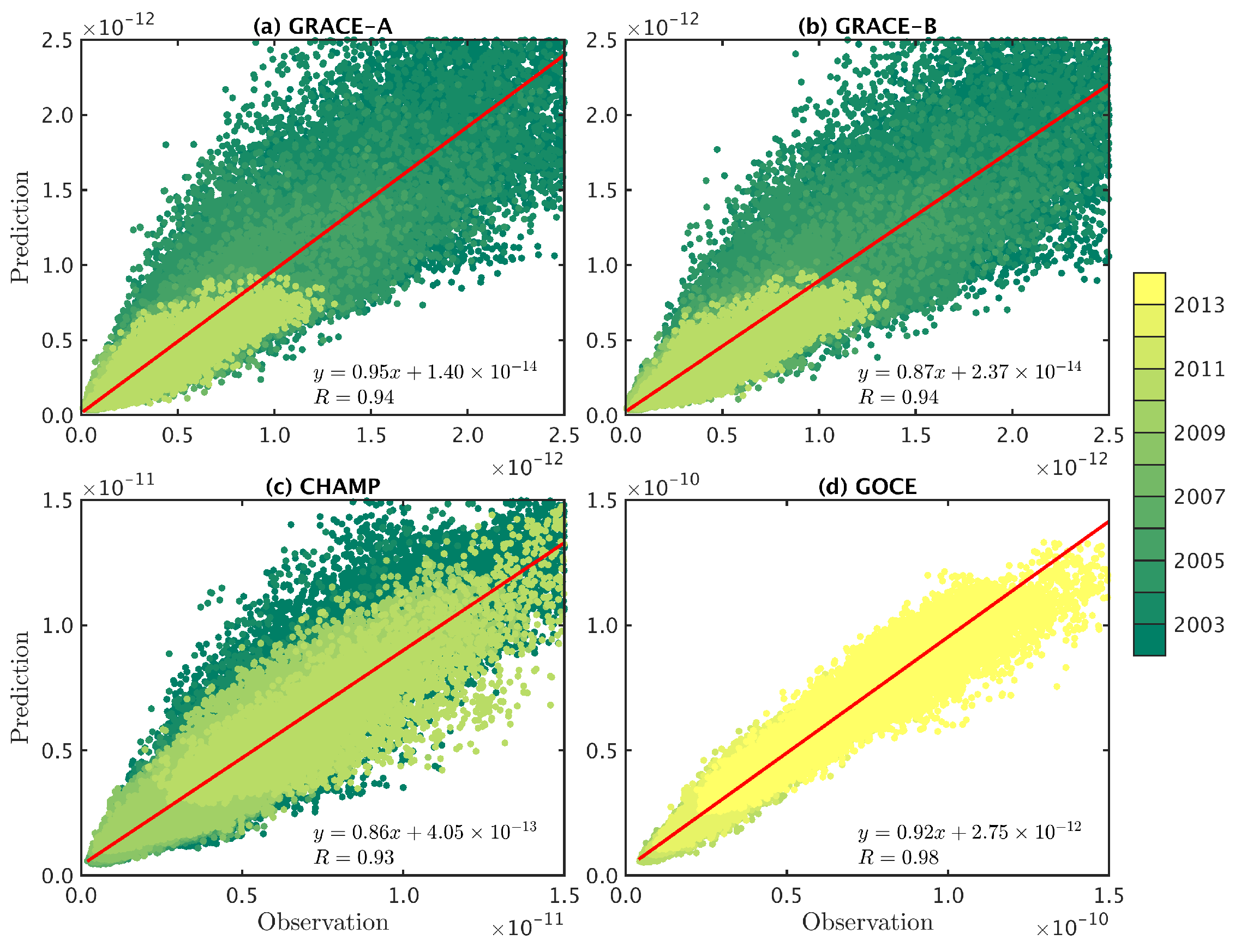
4.3. ANN-Based Models
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LEO | Low Earth Orbit |
| TMD | Thermospheric mass density |
| SH | Spherical harmonics |
| ANN | Artificial neural network |
Appendix A. The Terms f in the Fourier Model
Appendix B. The Function G in SH-Based Model
References
- Doornbos, E. Thermospheric Density and Wind Determination from Satellite Dynamics; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar] [CrossRef]
- Ruan, H.; Lei, J.; Dou, X.; Liu, S.; Aa, E. An exospheric temperature model based On CHAMP observations and TIEGCM simulations. Space Weather 2018, 16, 147–156. [Google Scholar] [CrossRef]
- Richmond, A.D.; Ridley, E.C.; Roble, R.G. A thermosphere/ionosphere general circulation model with coupled electrodynamics. Geophys. Res. Lett. 1992, 19, 601–604. [Google Scholar] [CrossRef]
- Foster, B. TIEGCM Documentation, Release 2.0; Report; National Center for Atmospheric Research/High Altitude: Boulder, CO, USA, 2016. [Google Scholar]
- Bruinsma, S.; Arnold, D.; Jaggi, A.; Sanchez-Ortiz, N. Semi-empirical thermosphere model evaluation at low altitude with GOCE densities. J. Space Weather. Space Clim. 2017, 7, A4. [Google Scholar] [CrossRef]
- Bowman, B.R.; Tobiska, W.K.; Marcos, F.A.; Huang, C.Y.; Lin, C.S.; Burke, W.J. A new empirical thermospheric density model JB2008 using new solar and geomagnetic indices. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Honolulu, HI, USA, 18–21 August 2008; p. 6438. [Google Scholar] [CrossRef]
- Qian, L.; Solomon, S.C. Thermospheric Density: An Overview of Temporal and Spatial Variations. Space Sci. Rev. 2012, 168, 147–173. [Google Scholar] [CrossRef]
- Emmert, J.T. Thermospheric mass density: A review. Adv. Space Res. 2015, 56, 773–824. [Google Scholar] [CrossRef]
- He, C.; Yang, Y.; Carter, B.; Kerr, E.; Wu, S.; Deleflie, F.; Cai, H.; Zhang, K.; Sagnières, L.; Norman, R. Review and comparison of empirical thermospheric mass density models. Prog. Aerosp. Sci. 2018, 103, 31–51. [Google Scholar] [CrossRef]
- Sutton, E.K. Effects of Solar Disturbances on the Thermosphere Densities and Winds from CHAMP and GRACE Satellite Accelerometer Data. Ph.D. Thesis, Department of Aerospace Engineering Sciences, University of Colorado at Boulder, Boulder, CO, USA, 2008. [Google Scholar]
- Doornbos, E.; Van Den IJssel, J.; Luhr, H.; Forster, M.; Koppenwallner, G. Neutral Density and Crosswind Determination from Arbitrarily Oriented Multiaxis Accelerometers on Satellites. J. Spacecr. Rocket. 2010, 47, 580–589. [Google Scholar] [CrossRef]
- Mehta, P.M.; Walker, A.C.; Sutton, E.K.; Godinez, H.C. New density estimates derived using accelerometers on board the CHAMP and GRACE satellites. Space Weather 2017, 15, 558–576. [Google Scholar] [CrossRef]
- Liu, H.; Hirano, T.; Watanabe, S. Empirical model of the thermospheric mass density based on CHAMP satellite observations. J. Geophys. Res. Space Phys. 2013, 118, 843–848. [Google Scholar] [CrossRef]
- Xiong, C.; Lühr, H.; Schmidt, M.; Bloßfeld, M.; Rudenko, S. An empirical model of the thermospheric mass density derived from CHAMP satellite. Ann. Geophys. 2018, 36, 1141–1152. [Google Scholar] [CrossRef]
- Yamazaki, Y.; Kosch, M.J.; Sutton, E.K. A model of high-latitude thermospheric density. J. Geophys. Res. Space Phys. 2015, 120, 7903–7917. [Google Scholar] [CrossRef]
- Calabia, A.; Jin, S.G. New modes and mechanisms of thermospheric mass density variations from GRACE accelerometers. J. Geophys. Res. Space Phys. 2016, 121, 11191–11211. [Google Scholar] [CrossRef]
- Perez, D.; Wohlberg, B.; Lovell, T.A.; Shoemaker, M.; Bevilacqua, R. Orbit-centered atmospheric density prediction using artificial neural networks. Acta Astronaut. 2014, 98, 9–23. [Google Scholar] [CrossRef]
- Chen, H.; Liu, H.; Hanada, T. Storm-time atmospheric density modeling using neural networks and its application in orbit propagation. Adv. Space Res. 2014, 53, 558–567. [Google Scholar] [CrossRef]
- Pardini, C.; Moe, K.; Anselmo, L. Thermospheric density model biases at the 23rd sunspot maximum. Planet. Space Sci. 2012, 67, 130–146. [Google Scholar] [CrossRef]
- Laundal, K.M.; Gjerloev, J. What is the appropriate coordinate system for magnetometer data when analyzing ionospheric currents? J. Geophys. Res. Space Phys. 2014, 119, 8637–8647. [Google Scholar] [CrossRef]
- Lei, J.; Matsuo, T.; Dou, X.; Sutton, E.; Luan, X. Annual and semiannual variations of thermospheric density: EOF analysis of CHAMP and GRACE data. J. Geophys. Res. Space Phys. 2012, 117, A01310. [Google Scholar] [CrossRef]
- Weimer, D.R.; Sutton, E.K.; Mlynczak, M.G.; Hunt, L.A. Intercalibration of neutral density measurements for mapping the thermosphere. J. Geophys. Res. Space Phys. 2016, 121, 5975–5990. [Google Scholar] [CrossRef]
- Bruinsma, S.; Forbes, J.M.; Nerem, R.S.; Zhang, X. Thermosphere density response to the 20–21 November 2003 solar and geomagnetic storm from CHAMP and GRACE accelerometer data. J. Geophys. Res. 2006, 111, A06303. [Google Scholar] [CrossRef]
- Xu, J.Y.; Wang, W.B.; Gao, H. The longitudinal variation of the daily mean thermospheric mass density. J. Geophys. Res. Space Phys. 2013, 118, 515–523. [Google Scholar] [CrossRef]
- Leonard, J.M.; Forbes, J.M.; Born, G.H. Impact of tidal density variability on orbital and reentry predictions. Space Weather 2012, 10, S12003. [Google Scholar] [CrossRef]
- Shi, C.; Li, W.W.; Li, M.; Zhao, Q.L.; Sang, J.Z. Calibrating the scale of the NRLMSISE00 model during solar maximum using the two line elements dataset. Adv. Space Res. 2015, 56, 1–9. [Google Scholar] [CrossRef]
- Doornbos, E.; Klinkrad, H.; Visser, P. Use of two-line element data for thermosphere neutral density model calibration. Adv. Space Res. 2008, 41, 1115–1122. [Google Scholar] [CrossRef]
- Laundal, K.M.; Richmond, A.D. Magnetic Coordinate Systems. Space Sci. Rev. 2017, 206, 27–59. [Google Scholar] [CrossRef]
- He, C. Precise Thermospheric Mass Density Modelling for Orbit Prediction of Low Earth Orbiters. Ph.D. Thesis, RMIT University, Melbourne, Australia, 2019. [Google Scholar]
- Marquardt, D.W. An algorithm for least-squares estimation of nonlinear parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Drob, D.P.; Emmert, J.T.; Crowley, G.; Picone, J.M.; Shepherd, G.G.; Skinner, W.; Hays, P.; Niciejewski, R.J.; Larsen, M.; She, C.Y.; et al. An empirical model of the Earth’s horizontal wind fields: HWM07. J. Geophys. Res. Space Phys. 2008, 113, A12304. [Google Scholar] [CrossRef]
- Drob, D.P.; Emmert, J.T.; Meriwether, J.W.; Makela, J.J.; Doornbos, E.; Conde, M.; Hernandez, G.; Noto, J.; Zawdie, K.A.; McDonald, S.E.; et al. An update to the Horizontal Wind Model (HWM): The quiet time thermosphere. Earth Space Sci. 2015, 2, 301–319. [Google Scholar] [CrossRef]
- He, C.; Wu, S.; Wang, X.; Hu, A.; Wang, Q.; Zhang, K. A new voxel-based model for the determination of atmospheric weighted mean temperature in GPS atmospheric sounding. Atmos. Meas. Tech. 2017, 10, 2045–2060. [Google Scholar] [CrossRef]
- Picone, J.M.; Hedin, A.E.; Drob, D.P.; Aikin, A.C. NRLMSISE-00 empirical model of the atmosphere: Statistical comparisons and scientific issues. J. Geophys. Res. Space Phys. 2002, 107, 1468. [Google Scholar] [CrossRef]
- Chen, J.; Li, W.; Li, S.; Chen, H.; Zhao, X.; Peng, J.; Chen, Y.; Deng, H. Two-Stage Solar Flare Forecasting Based on Convolutional Neural Networks. Space: Sci. Technol. 2022, 2022, 9761567. [Google Scholar] [CrossRef]
- Li, W.; Liu, L.; Chen, Y.; Xiao, Z.; Le, H.; Zhang, R. Improving the Extraction Ability of Thermospheric Mass Density Variations From Observational Data by Deep Learning. Space Weather 2023, 21, e2022SW003376. [Google Scholar] [CrossRef]
- Li, W.; Zhao, D.; He, C.; Shen, Y.; Hu, A.; Zhang, K. Application of a Multi-Layer Artificial Neural Network in a 3-D Global Electron Density Model Using the Long-Term Observations of COSMIC, Fengyun-3C, and Digisonde. Space Weather 2021, 19, e2020SW002605. [Google Scholar] [CrossRef]
- Emmert, J.T.; Picone, J.M. Climatology of globally averaged thermospheric mass density. J. Geophys. Res. Space Phys. 2010, 115, A09326. [Google Scholar] [CrossRef]
| Model | Inputs | No. Inputs | No. Coefficients | No. Neurons |
|---|---|---|---|---|
| Fourier | , , h, , , , | 7 | 170 | |
| SH-1 | , , h, , , , | 7 | 102 | |
| SH-2 | , , h, , , , | 7 | 300 | |
| ANN-1 | ,, h, , , , , , , , | 11 | 66 | 5 |
| 131 | 10 | |||
| 261 | 20 | |||
| 651 | 50 | |||
| 1301 | 100 | |||
| ANN-2 | , , h, , (), , (), , (), , () | 33 | 176 | 5 |
| 351 | 10 | |||
| 701 | 20 | |||
| 1751 | 50 | |||
| 3501 | 100 | |||
| ANN-3 | , , h, , , , , , , , | 11 | 291 | 10-10-5 |
| 506 | 15-15-5 | |||
| 591 | 15-15-10 | |||
| 881 | 20-20-10 | |||
| 991 | 20-20-15 |
| Coordinate–Time | GRACE-A | GRACE-B | CHAMP | GOCE | Overall |
|---|---|---|---|---|---|
| GEO-LST | 0.3338 | 0.3712 | 0.2890 | 0.1354 | 0.3099 |
| GEO-MLT | 0.3410 | 0.3765 | 0.2842 | 0.1465 | 0.3133 |
| GSM-LT | 0.3030 | 0.3390 | 0.2353 | 0.1140 | 0.2742 |
| GSM-LST | 0.3011 | 0.3353 | 0.2260 | 0.1193 | 0.2704 |
| QD-LST | 0.3331 | 0.3705 | 0.2891 | 0.1363 | 0.3095 |
| Coordinates | Time | ||
|---|---|---|---|
| LT | LST | MLT | |
| GEO | 0.3147 | 0.3146 | 0.3173 |
| GSM | 0.3102 | 0.3103 | 0.3110 |
| SM | 0.3185 | 0.3184 | 0.3173 |
| DIP | 0.3242 | 0.3241 | 0.3274 |
| CD | 0.3162 | 0.3162 | 0.3162 |
| ED | 0.3169 | 0.3168 | 0.3165 |
| QD | 0.3174 | 0.3173 | 0.3165 |
| MA | 0.3174 | 0.3173 | 0.3165 |
| Coordinate–Time | GRACE-A | GRACE-B | CHAMP | GOCE | Overall |
|---|---|---|---|---|---|
| GEO-LT | 0.2716 | 0.3085 | 0.2261 | 0.1592 | 0.2557 |
| GEO-LST | 0.2711 | 0.3079 | 0.2248 | 0.1630 | 0.2554 |
| GEO-MLT | 0.2745 | 0.3114 | 0.2264 | 0.1639 | 0.2580 |
| GSM-LT | 0.2677 | 0.3032 | 0.2211 | 0.1580 | 0.2514 |
| GSM-LST | 0.2678 | 0.3033 | 0.2211 | 0.1583 | 0.2515 |
| QD-LST | 0.2762 | 0.3130 | 0.2287 | 0.1614 | 0.2594 |
| Coordinate–Time | Neurons in Hidden Layer | R | ||
|---|---|---|---|---|
| GEO-LST | 5 | 0.2718 | 1.0392 | 0.9881 |
| 10 | 0.2419 | 1.0307 | 0.9882 | |
| 20 | 0.2255 | 1.0267 | 0.9927 | |
| 50 | 0.2085 | 1.0226 | 0.9948 | |
| 100 | 0.2019 | 1.0211 | 0.9954 | |
| GSM-LT | 5 | 0.2501 | 1.0332 | 0.9922 |
| 10 | 0.2442 | 1.0315 | 0.9878 | |
| 20 | 0.2234 | 1.0283 | 0.9943 | |
| 50 | 0.2117 | 1.0233 | 0.9949 | |
| 100 | 0.2053 | 1.0218 | 0.9952 | |
| QD-LST | 5 | 0.2656 | 1.0374 | 0.9882 |
| 10 | 0.2393 | 1.0302 | 0.9902 | |
| 20 | 0.2252 | 1.0264 | 0.9936 | |
| 50 | 0.2111 | 1.0256 | 0.9946 | |
| 100 | 0.2028 | 1.0226 | 0.9952 |
| Coordinate–Time | Neurons in Hidden Layers | R | ||
|---|---|---|---|---|
| GEO-LST | 5 | 0.2426 | 1.0309 | 0.9918 |
| 10 | 0.2202 | 1.0251 | 0.9931 | |
| 20 | 0.2117 | 1.0229 | 0.9948 | |
| 50 | 0.2027 | 1.0213 | 0.9952 | |
| 100 | 0.1920 | 1.0199 | 0.9955 | |
| GSM-LT | 5 | 0.2391 | 1.0302 | 0.9906 |
| 10 | 0.2216 | 1.0259 | 0.9931 | |
| 20 | 0.2125 | 1.0234 | 0.9946 | |
| 50 | 0.2013 | 1.0208 | 0.9951 | |
| 100 | 0.1904 | 1.0189 | 0.9950 | |
| QD-LST | 5 | 0.2447 | 1.0316 | 0.9911 |
| 10 | 0.2392 | 1.0307 | 0.9898 | |
| 20 | 0.2143 | 1.0241 | 0.9948 | |
| 50 | 0.2006 | 1.0207 | 0.9951 | |
| 100 | 0.1959 | 1.0199 | 0.9950 |
| Coordinate–Time | Neurons in Hidden Layers | R | ||
|---|---|---|---|---|
| GEO-LST | 10-10-5 | 0.2159 | 1.0242 | 0.9949 |
| 15-15-5 | 0.2077 | 1.0224 | 0.9951 | |
| 15-15-10 | 0.2047 | 1.0218 | 0.9953 | |
| 20-20-10 | 0.2032 | 1.0217 | 0.9956 | |
| 20-20-15 | 0.2032 | 1.0208 | 0.9954 | |
| GEO-MLT | 10-10-5 | 0.2216 | 1.0255 | 0.9950 |
| 15-15-5 | 0.2114 | 1.0238 | 0.9953 | |
| 15-15-10 | 0.2106 | 1.0230 | 0.9953 | |
| 20-20-10 | 0.2049 | 1.0239 | 0.9955 | |
| 20-20-15 | 0.2032 | 1.0212 | 0.9957 | |
| GSM-LST | 10-10-5 | 0.2199 | 1.0253 | 0.9942 |
| 15-15-5 | 0.2100 | 1.0229 | 0.9952 | |
| 15-15-10 | 0.2087 | 1.0227 | 0.9951 | |
| 20-20-10 | 0.2038 | 1.0216 | 0.9953 | |
| 20-20-15 | 0.2032 | 1.0202 | 0.9954 | |
| QD-LST | 10-10-5 | 0.2166 | 1.0235 | 0.9943 |
| 15-15-5 | 0.2084 | 1.0221 | 0.9951 | |
| 15-15-10 | 0.2076 | 1.0240 | 0.9952 | |
| 20-20-10 | 0.2041 | 1.0221 | 0.9954 | |
| 20-20-15 | 0.2032 | 1.0219 | 0.9953 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, C.; Li, W.; Hu, A.; Zheng, D.; Cai, H.; Xiong, Z. Thermospheric Mass Density Modelling during Geomagnetic Quiet and Weakly Disturbed Time. Atmosphere 2024, 15, 72. https://doi.org/10.3390/atmos15010072
He C, Li W, Hu A, Zheng D, Cai H, Xiong Z. Thermospheric Mass Density Modelling during Geomagnetic Quiet and Weakly Disturbed Time. Atmosphere. 2024; 15(1):72. https://doi.org/10.3390/atmos15010072
Chicago/Turabian StyleHe, Changyong, Wang Li, Andong Hu, Dunyong Zheng, Han Cai, and Zhaohui Xiong. 2024. "Thermospheric Mass Density Modelling during Geomagnetic Quiet and Weakly Disturbed Time" Atmosphere 15, no. 1: 72. https://doi.org/10.3390/atmos15010072





