A Hydraulic Friction Model for One-Dimensional Unsteady Channel Flows with Experimental Demonstration
Abstract
:1. Introduction
2. Materials and Methods
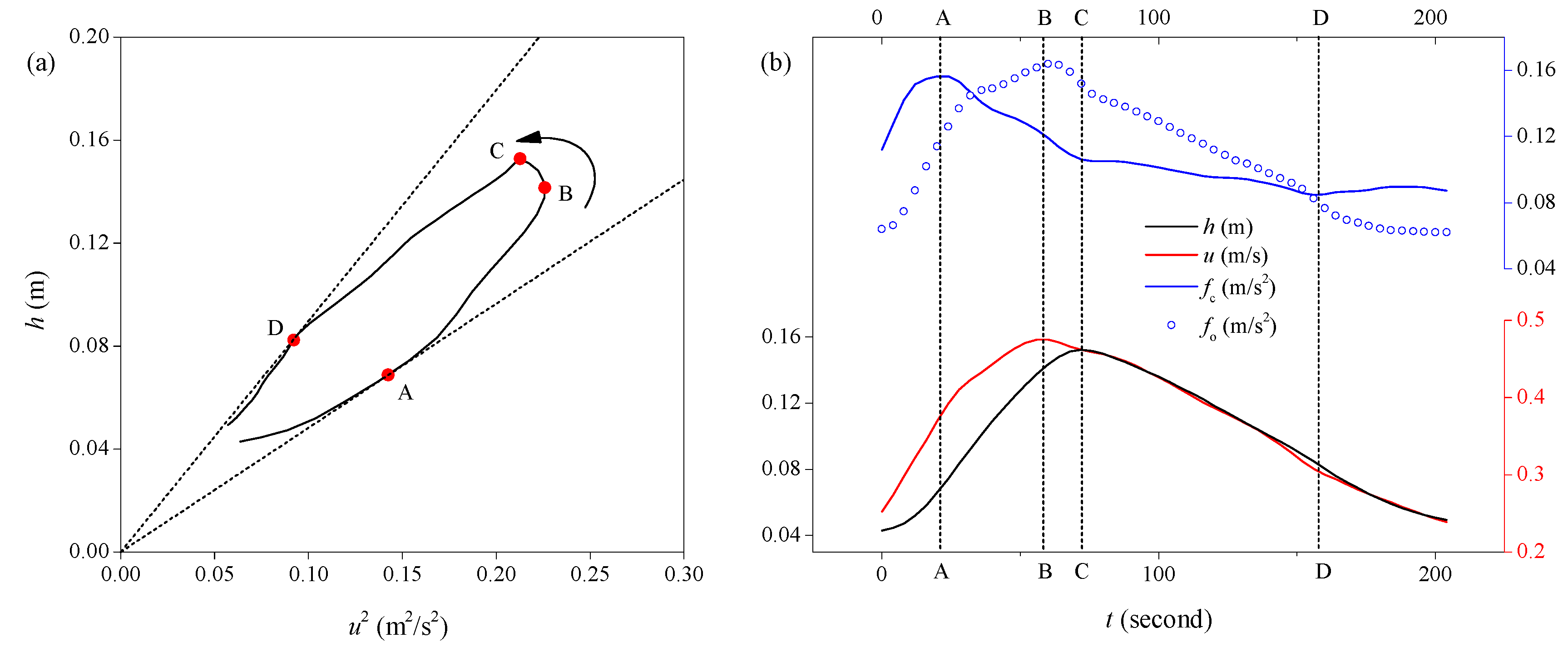
2.1. Analysis of Unsteady Friction
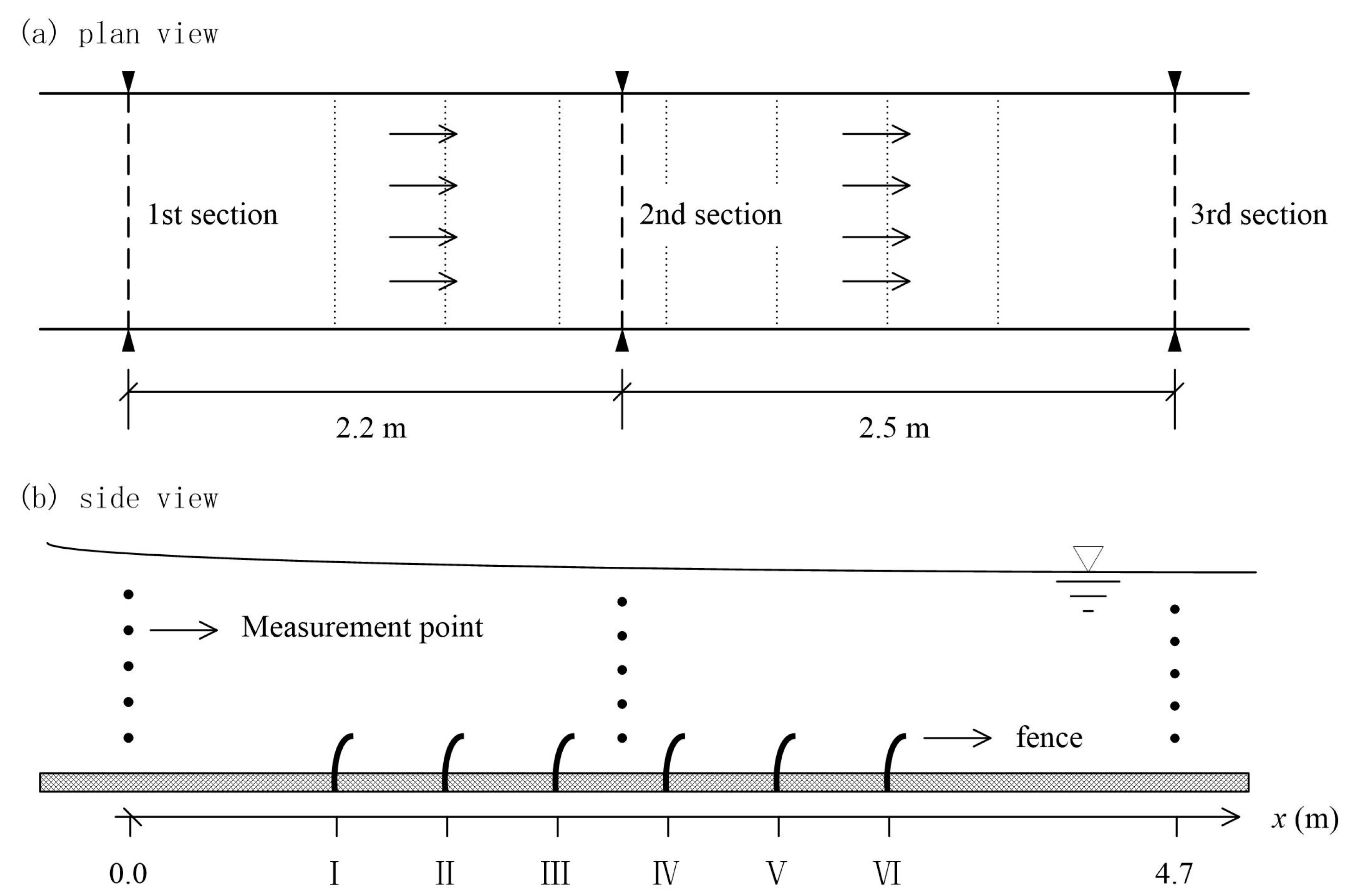
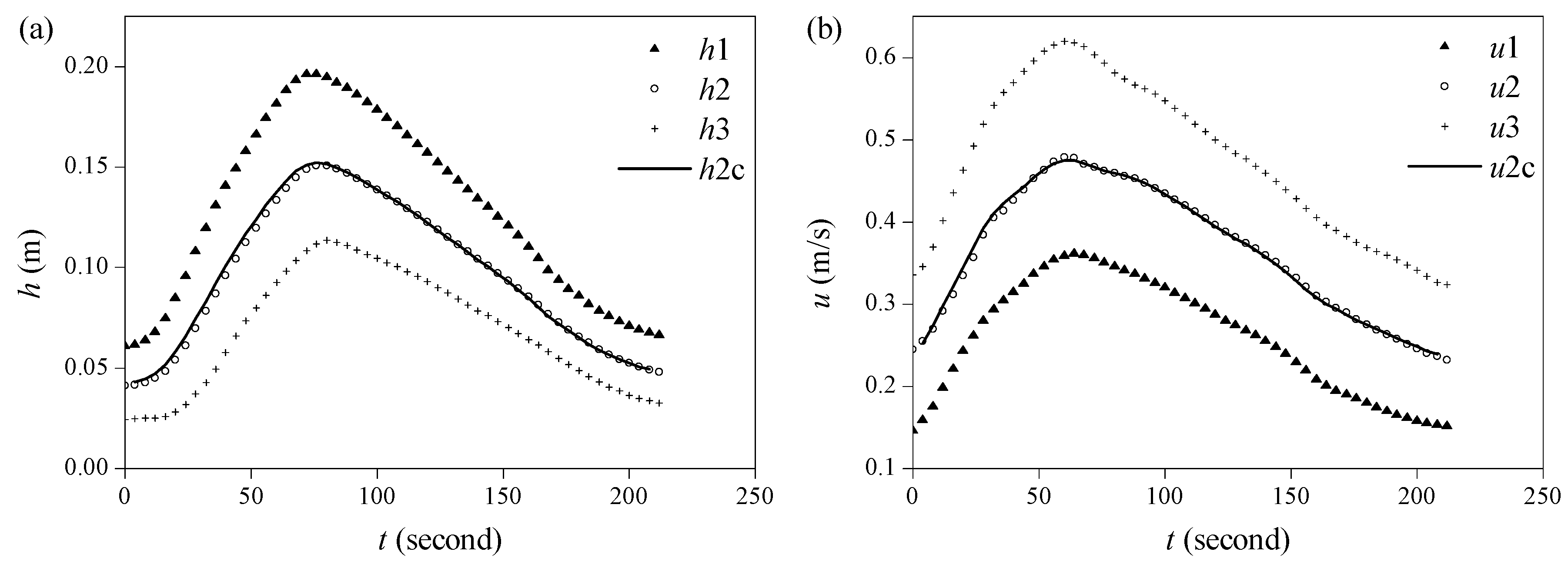
2.2. Experimental Procedure
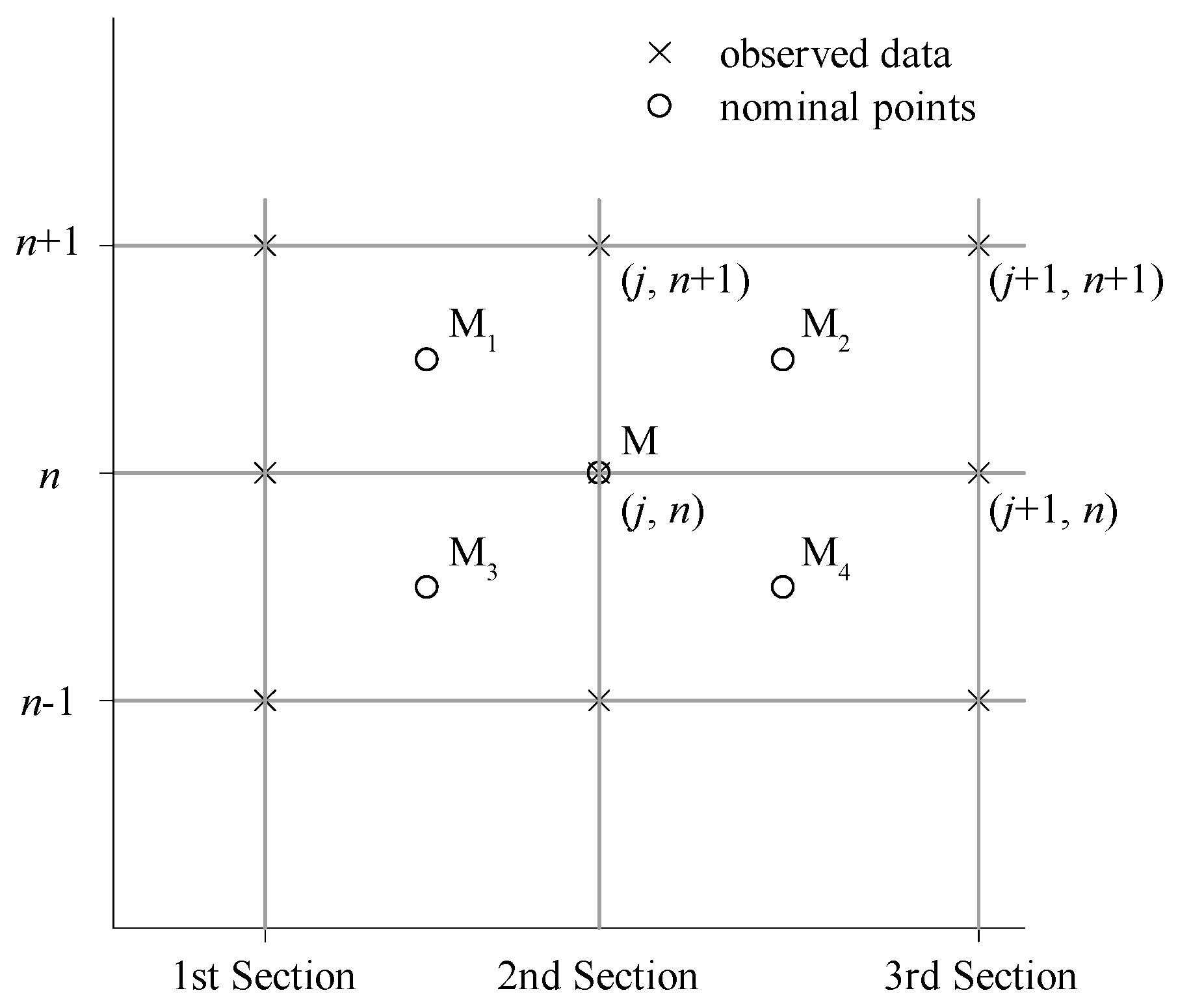
3. Analysis of Model Structure
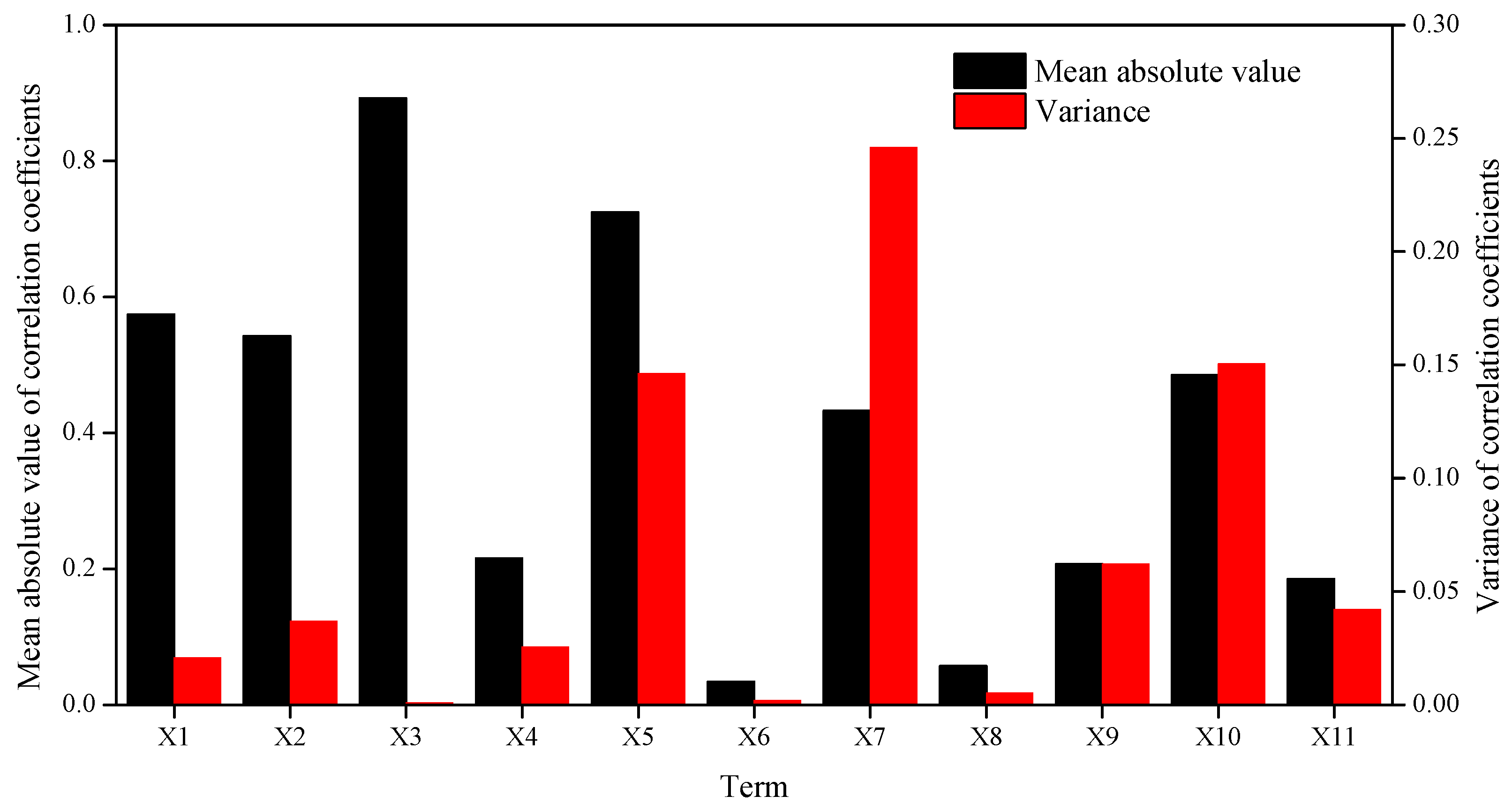
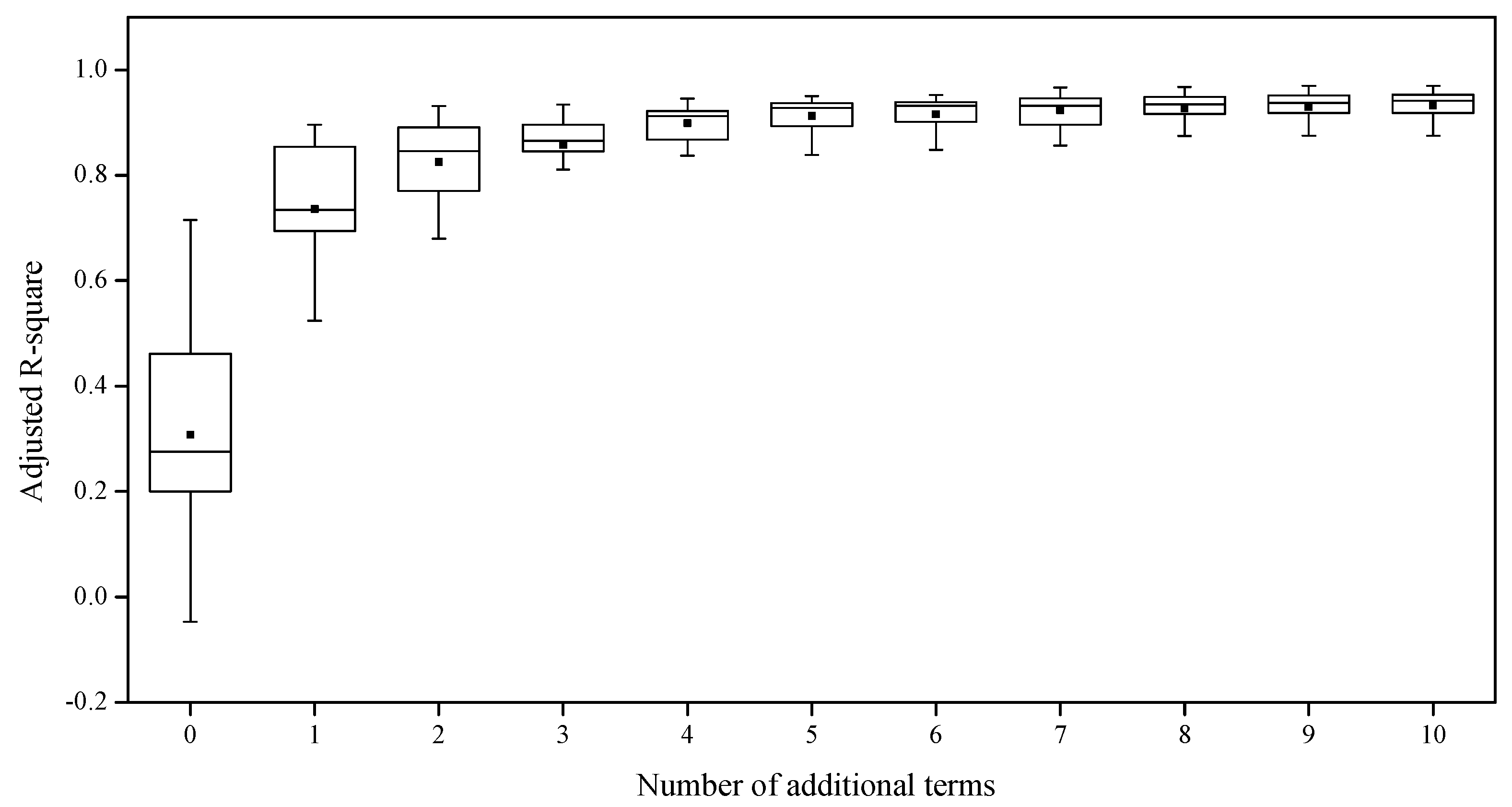
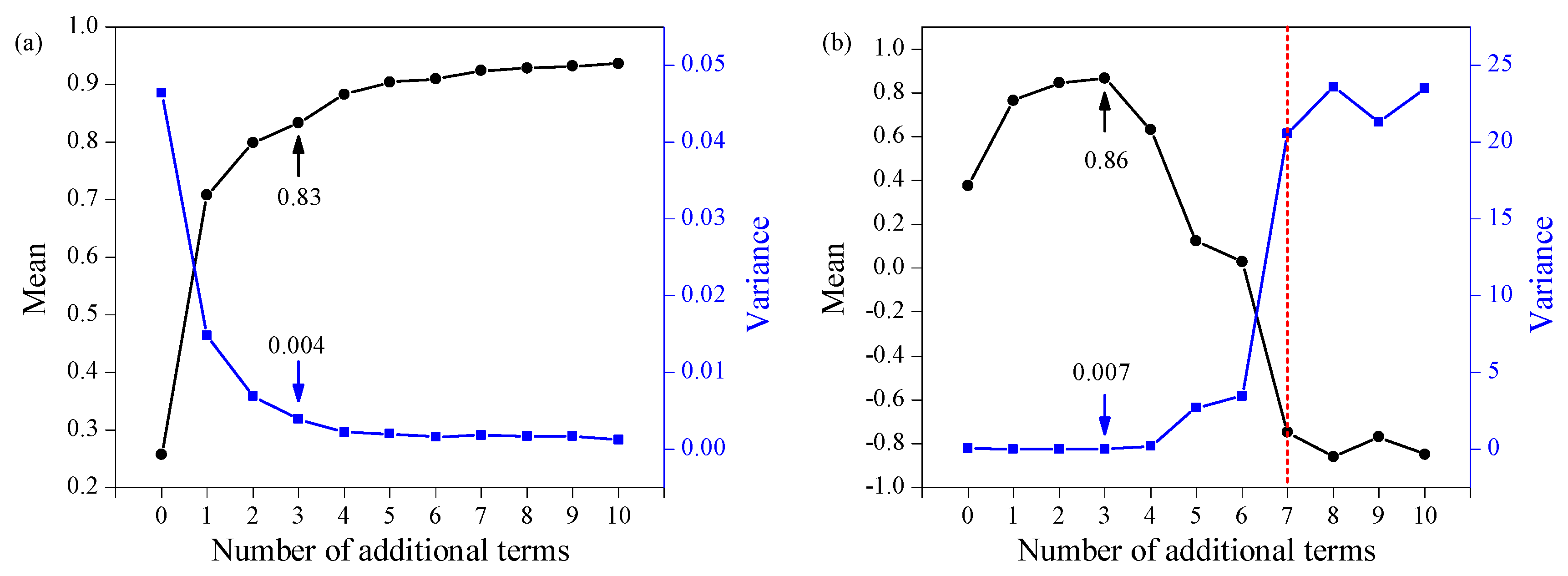
3.1. Single-Factor Analysis
3.2. Multifactorial Analysis
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wang, D.W.; Chen, J.G.; Fu, X.D. Review of flow resistance of mountain rivers. J. Hydraul. Eng. 2012, 43, 12–19. [Google Scholar]
- Graf, W.H.; Song, T. Bed-shear stress in non-uniform and unsteady open-channel flows. J. Hydraul. Res. 1995, 33, 699–704. [Google Scholar] [CrossRef]
- Ghimire, B.; Deng, Z.-Q. Event flow hydrograph-based method for shear velocity estimation. J. Hydraul. Res. 2011, 49, 272–275. [Google Scholar] [CrossRef]
- Mrokowska, M.M.; Rowiński, P.M.; Kalinowska, M.B. Evaluation of friction velocity in unsteady flow experiments. J. Hydraul. Res. 2015, 53, 659–669. [Google Scholar] [CrossRef]
- Mrokowska, M.M.; Rowiński, P.M.; Kalinowska, M.B. A methodological approach of estimating resistance to flow under unsteady flow conditions. Hydrol. Earth Syst. Sci. 2015, 19, 4041–4053. [Google Scholar] [CrossRef]
- Fread, D.L. Channel Routing. In Hydrological Forecasting; Springer: Cham, Switzerland, 1985. [Google Scholar]
- Haizhou, T.; Graf, W.H. Friction in unsteady open-channel flow over gravel beds. J. Hydraul. Res. 1993, 31, 99–110. [Google Scholar] [CrossRef]
- Aleixo, R.; Soares-Frazão, S.; Zech, Y. Velocity-field measurements in a dam-break flow using a PTV Voronoï imaging technique. Exp. Fluids 2011, 50, 1633–1649. [Google Scholar] [CrossRef]
- Bombar, G. The Hysteresis and Shear Velocity in Unsteady Flows. J. Appl. Fluid Mech. 2016, 9, 839–853. [Google Scholar] [CrossRef]
- Renaat, S.D.; Verhoeven, R.; Krein, A. Simulation of sediment transport during flood events: Laboratory work and field experiments. Int. Assoc. Sci. Hydrol. Bull. 2001, 46, 599–610. [Google Scholar]
- Guney, M.S.; Bombar, G.; Aksoy, A.O. Experimental Study of the Coarse Surface Development Effect on the Bimodal Bed-Load Transport under Unsteady Flow Conditions. J. Hydraul. Eng. 2013, 139, 12–21. [Google Scholar] [CrossRef]
- Henderson, F.M. Flood waves in prismatic channels. J. Hydraul. Div. 1963, 89, 39–67. [Google Scholar]
- Dey, S.; Lambert, M.F. Reynolds Stress and Bed Shear in Nonuniform Unsteady Open-Channel Flow. J. Hydraul. Eng. 2005, 131, 610–614. [Google Scholar] [CrossRef]
- Cheng, N.S. Resistance Coefficients for Artificial and Natural Coarse-Bed Channels: Alternative Approach for Large-Scale Roughness. J. Hydraul. Eng. 2015, 141. [Google Scholar] [CrossRef]
- Roushangar, K.; Mouaze, D.; Shiri, J. Evaluation of genetic programming-based models for simulating friction factor in alluvial channels. J. Hydrol. 2014, 517, 1154–1161. [Google Scholar] [CrossRef]
- Strupczewski, W.G.; Szymkiewicz, R. Analysis of paradoxes arising from the Chezy formula with constant roughness: II. Flow area-discharge curve. Hydrol. Sci. J. 1996, 41, 659–673. [Google Scholar] [CrossRef]
- Strupczewski, W.G.; Szymkiewicz, R. Analysis of paradoxes arising from the Chezy formula with constant roughness: I. Depth-discharge curve. Hydrol. Sci. J. 1997, 42, 659–673. [Google Scholar] [CrossRef]
- Barr, D.I.H.; Ackers, P. Hydraulic design of two-stage channels. Ice Proc. Water Marit. Energy 1992, 106, 99–101. [Google Scholar]
- Bao, W.M.; Zhang, X.Q.; Qu, S.M. Dynamic correction of roughness in the hydrodynamic model. J. Hydrodyn. Ser. B 2009, 21, 255–263. [Google Scholar] [CrossRef]
- Hsu, M.H.; Liu, W.C.; Fu, J.C. Dynamic Routing Model with Real-Time Roughness Updating for Flood Forecasting. J. Hydraul. Eng. 2006, 132, 605–619. [Google Scholar] [CrossRef]
- Bao, H.J.; Zhao, L.N. Hydraulic model with roughness coefficient updating method based on Kalman filter for channel flood forecast. Water Sci. Eng. 2011, 4, 13–23. [Google Scholar]
- Jin, Z.Q.; Han, L.X.; Zhang, J. The Inverse Problem of Roughness Parameter in Hvdraulic Calculation of Complicated River Net Work. J. Hydrodyn. 1998, 13, 280–285. [Google Scholar]
- Nikurdase, J. Strömungsgesetze in Rauhen Rohren; VDI Vera: Berlin, Germany, 1933. [Google Scholar]
- Schlichting, H. Boundary-Layer Theory, 7th ed.; McGraw-Hill: New York, NY, USA, 1979. [Google Scholar]
- Recking, A. Theoretical development on the effects of changing flow hydraulics on incipient bed load motion. Water Resour. Res. 2009, 45, 1211–1236. [Google Scholar] [CrossRef]
- Cheng, W.B.; Xie, J.H.; Zhang, R.J. River Dynamics; Wuhan University Press: Wuhan, China, 2007. [Google Scholar]
- Liu, Z.X.; Li, Z.; Sun, Z.H.; Zheng, Z.P. Calculation of Field Manning’s Roughness Coefficient. Irrig. Drain. 1998, 3, 5–9. [Google Scholar]
- Nakamura, Y.; Tomonari, Y. The effects of surface roughness on the flow past circular cylinders at high Reynolds numbers. J. Fluid Mech. 1982, 123, 363–378. [Google Scholar] [CrossRef]
- Einstein, H.A.; Banks, R.B. Fluid resistance of composite roughness. Eos Trans. Am. Geophys. Union 1950, 31, 603–610. [Google Scholar] [CrossRef]
- Rouse, H. Critical analysis of open-channel resistance. J. Hydraul. Div. 1965, 91, 1–23. [Google Scholar]
- Salem, A.M. The effects of the sediment bed thick-ness on the incipient motion of particles in a rigid rectangular channel. In Proceedings of the 17th International Water Technology, Istanbul, Turkey, 5–7 November 2013. [Google Scholar]
- Yan, X.F.; Wai, W.H.O.; Li, C.W. Characteristics of flow structure of free-surface flow in a partly obstructed open channel with vegetation patch. Environ. Fluid Mech. 2016, 16, 1–26. [Google Scholar] [CrossRef]
- Bombar, G.; Güney, M.Ş.; Tayfur, G.; Elçi, Ş. Calculation of the time-varying mean velocity by different methods and determination of the turbulence intensities. Sci. Res. Essays 2010, 5, 572–581. [Google Scholar]
- Mrokowska, M.M.; Rowiński, P.M.; Kalinowska, M.B. The Uncertainty of Measurements in River Hydraulics: Evaluation of Friction Velocity Based on an Unrepeatable Experiment. GeoPlanet-Earth Planet. Sci. 2013, 11, 195–206. [Google Scholar]
- Akossou, A.Y.J.; Palm, R. Impact of data structure on the estimators R-square and adjusted R-square in linear regression. Int. J. Math. Comput. 2013, 20, 84–93. [Google Scholar]
- Mu, J.B.; Zhang, X.F. Real-time flood forecasting method with 1-D unsteady flow model. J. Hydrodyn. Ser. B 2007, 19, 150–154. [Google Scholar] [CrossRef]

| Experimental Mode | Fence Position | |||||
|---|---|---|---|---|---|---|
| I | II | III | IV | V | VI | |
| Mode 1 | ||||||
| Mode 2 | 1 | 1 | ||||
| Mode 3 | 2 | 2 | ||||
| Mode 4 | 3 | 3 | ||||
| Mode 5 | 4 | 4 | ||||
| Mode 6 | 1 | 1 | 1 | 1 | ||
| Mode 7 | 2 | 2 | 2 | 2 | ||
| Mode 8 | 3 | 3 | 3 | 3 | ||
| Mode 9 | 4 | 4 | 4 | 4 | ||
| Mode 10 | 1 | 1 | 1 | 1 | 1 | 1 |
| Mode 11 | 2 | 2 | 2 | 2 | 2 | 2 |
| Mode 12 | 3 | 3 | 3 | 3 | 3 | 3 |
| Mode 13 | 4 | 4 | 4 | 4 | 4 | 4 |
| Experimental Mode | Linear Correlation Coefficients of Terms (X1, …, X11) and Objective Friction | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | X11 | |
| Mode 1 | 0.70 | 0.89 | −0.86 | 0.48 | −0.24 | 0.12 | 0.25 | 0.26 | −0.60 | −0.19 | −0.59 |
| Mode 2 | 0.73 | 0.81 | −0.90 | 0.45 | −0.09 | 0.01 | −0.07 | 0.11 | −0.23 | 0.11 | −0.25 |
| Mode 3 | 0.85 | 0.84 | −0.93 | 0.51 | 0.41 | −0.02 | 0.16 | 0.11 | −0.30 | −0.09 | −0.31 |
| Mode 4 | 0.72 | 0.68 | −0.89 | 0.32 | 0.75 | −0.02 | −0.88 | 0.08 | −0.15 | 0.90 | −0.26 |
| Mode 5 | 0.71 | 0.62 | −0.89 | 0.21 | 0.79 | 0.01 | 0.56 | 0.08 | −0.16 | −0.22 | −0.23 |
| Mode 6 | 0.53 | 0.50 | −0.90 | 0.19 | 0.83 | −0.03 | −0.51 | 0.01 | 0.17 | 0.74 | 0.06 |
| Mode 7 | 0.43 | 0.42 | −0.85 | 0.05 | 0.87 | −0.01 | 0.87 | 0.03 | 0.04 | 0.38 | −0.04 |
| Mode 8 | 0.35 | 0.40 | −0.82 | 0.05 | 0.86 | −0.02 | 0.29 | 0.04 | −0.01 | 0.39 | −0.25 |
| Mode 9 | 0.47 | 0.39 | −0.90 | 0.12 | 0.93 | −0.04 | 0.09 | 0.00 | 0.18 | 0.70 | −0.07 |
| Mode 10 | 0.49 | 0.34 | −0.92 | 0.10 | 0.92 | −0.05 | −0.36 | 0.00 | 0.23 | 0.89 | 0.06 |
| Mode 11 | 0.56 | 0.35 | −0.94 | 0.09 | 0.94 | −0.04 | 0.48 | 0.00 | 0.29 | 0.76 | 0.16 |
| Mode 12 | 0.48 | 0.37 | −0.90 | 0.08 | 0.92 | −0.02 | 0.90 | 0.01 | 0.17 | 0.66 | 0.05 |
| Mode 13 | 0.45 | 0.45 | −0.89 | 0.15 | 0.86 | −0.05 | 0.21 | −0.01 | 0.16 | 0.29 | 0.10 |
| Number | Best Combination |
|---|---|
| 0 | X1 |
| 1 | X1, X5 |
| 2 | X1, X2, X3 |
| 3 | X1, X2, X3, X4 |
| 4 | X1, X3, X4, X8, X10 |
| 5 | X1, X3, X4, X7, X8, X10 |
| 6 | X1, X3, X4, X7, X8, X10, X11 |
| 7 | X1, X2, X3, X4, X5, X7, X8, X10 |
| 8 | X1, X2, X3, X4, X5, X7, X8, X10, X11 |
| 9 | X1, X2, X3, X4, X5, X6, X7, X8, X10, X11 |
| 10 | X1, X2, X3, X4, X5, X6, X7, X8, X9, X10, X11 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bao, W.; Zhou, J.; Xiang, X.; Jiang, P.; Bao, M. A Hydraulic Friction Model for One-Dimensional Unsteady Channel Flows with Experimental Demonstration. Water 2018, 10, 43. https://doi.org/10.3390/w10010043
Bao W, Zhou J, Xiang X, Jiang P, Bao M. A Hydraulic Friction Model for One-Dimensional Unsteady Channel Flows with Experimental Demonstration. Water. 2018; 10(1):43. https://doi.org/10.3390/w10010043
Chicago/Turabian StyleBao, Weimin, Junwei Zhou, Xiaohua Xiang, Peng Jiang, and Muxi Bao. 2018. "A Hydraulic Friction Model for One-Dimensional Unsteady Channel Flows with Experimental Demonstration" Water 10, no. 1: 43. https://doi.org/10.3390/w10010043
APA StyleBao, W., Zhou, J., Xiang, X., Jiang, P., & Bao, M. (2018). A Hydraulic Friction Model for One-Dimensional Unsteady Channel Flows with Experimental Demonstration. Water, 10(1), 43. https://doi.org/10.3390/w10010043





