Observation and Estimation of Evapotranspiration from an Irrigated Green Roof in a Rain-Scarce Environment
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Site
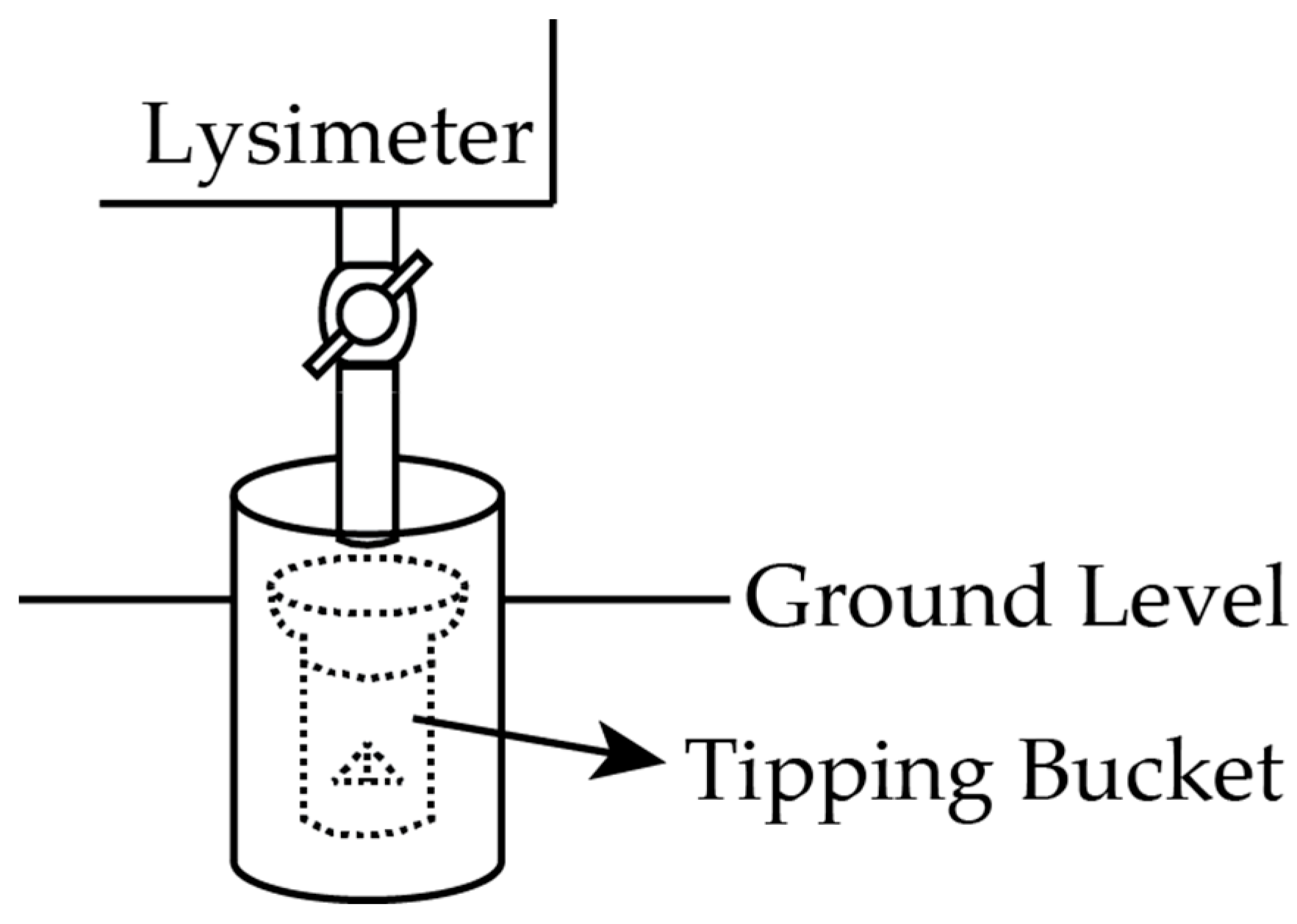
2.2. Evapotranspiration Observation
2.3. Evapotranspiration Estimation
2.4. Statistics
3. Results and Discussion
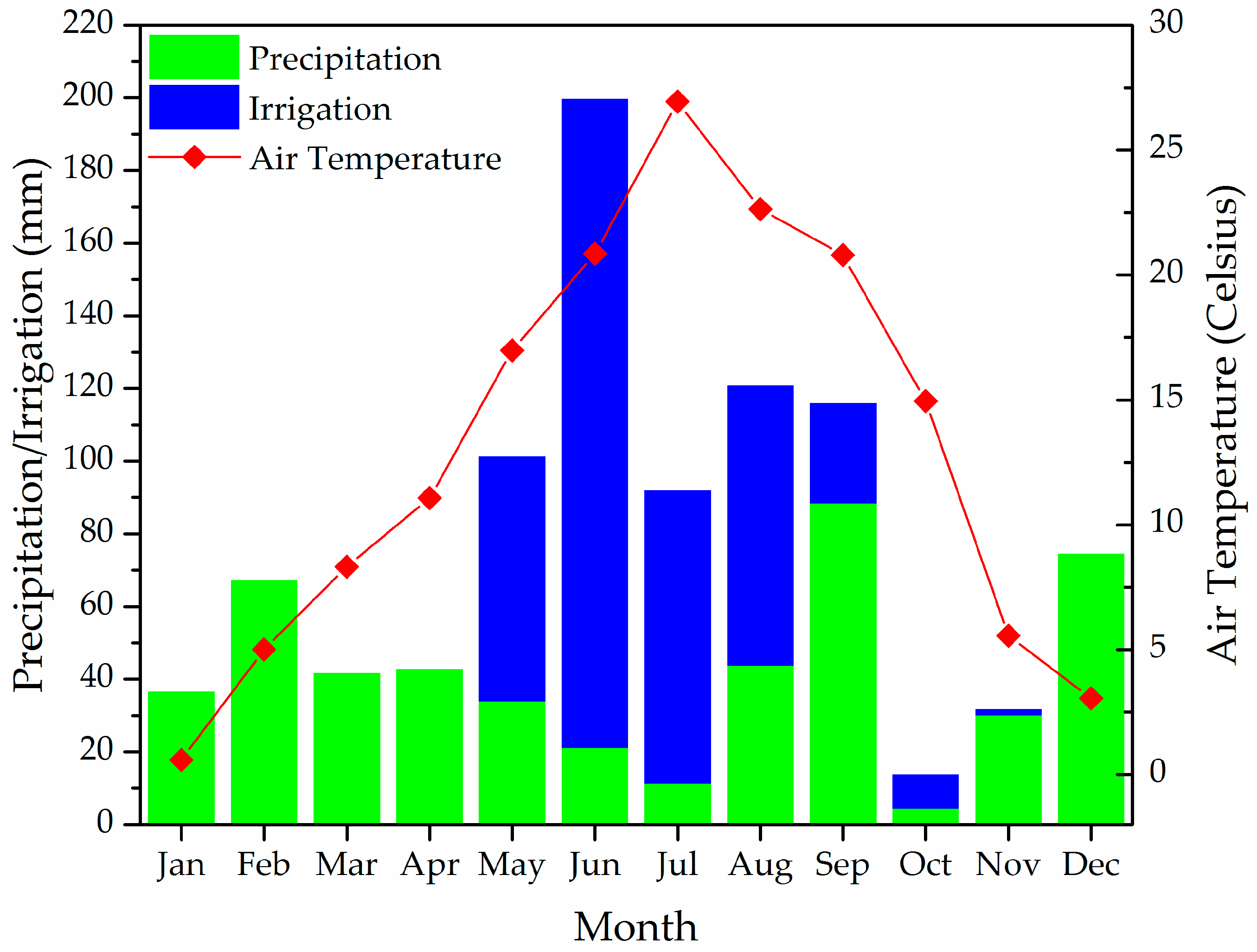
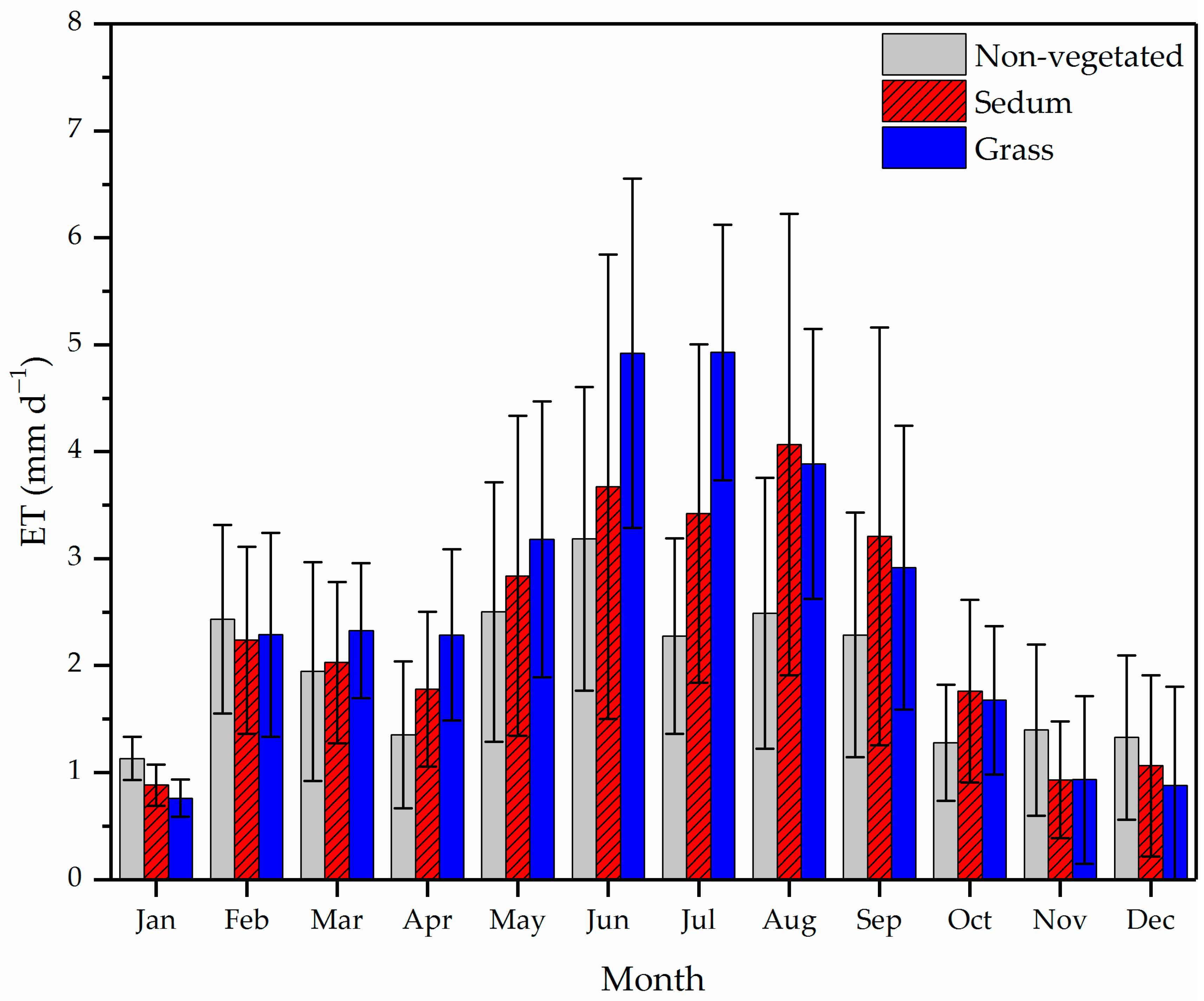
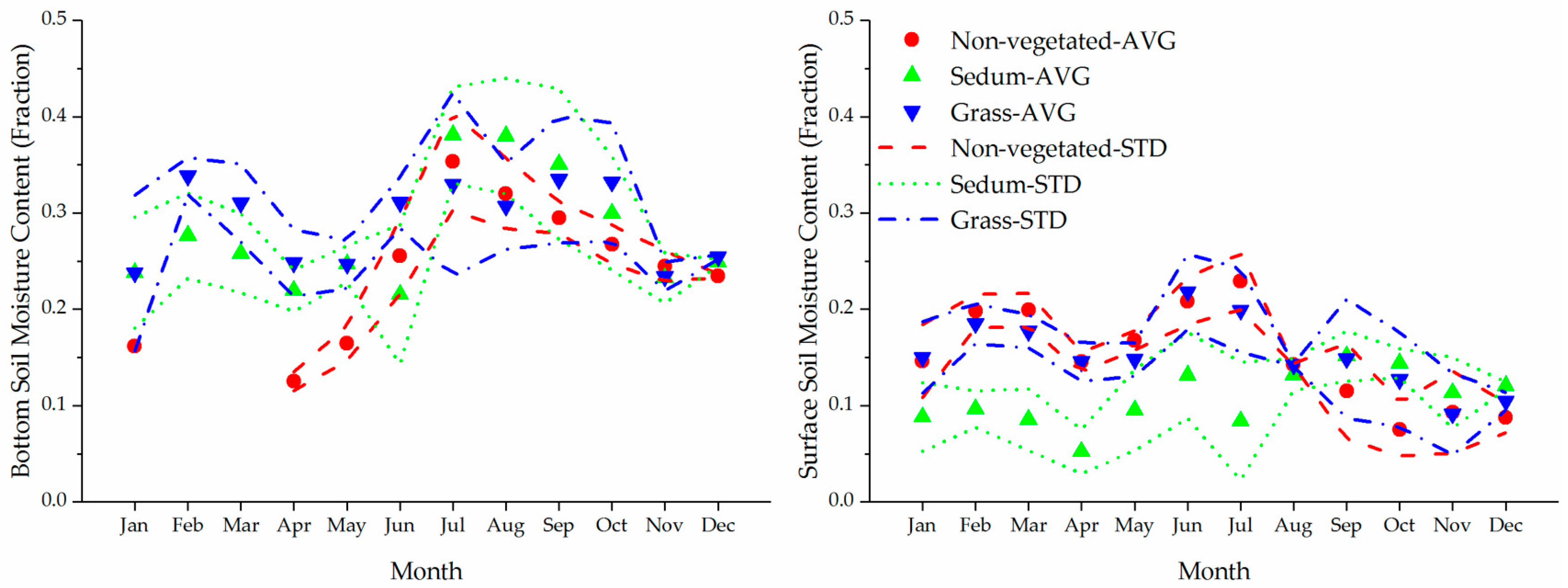
3.1. Evapotranspiration Regime
3.2. Design Considerations for Water Conservation
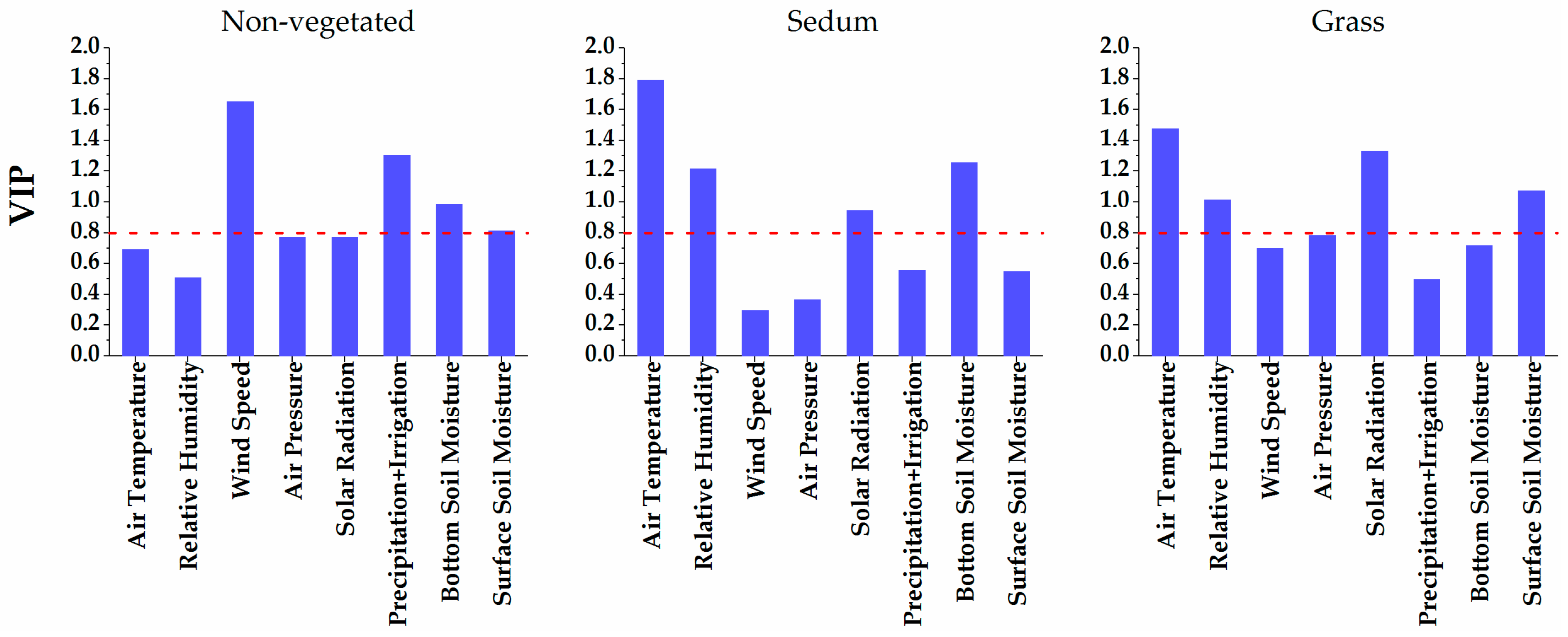
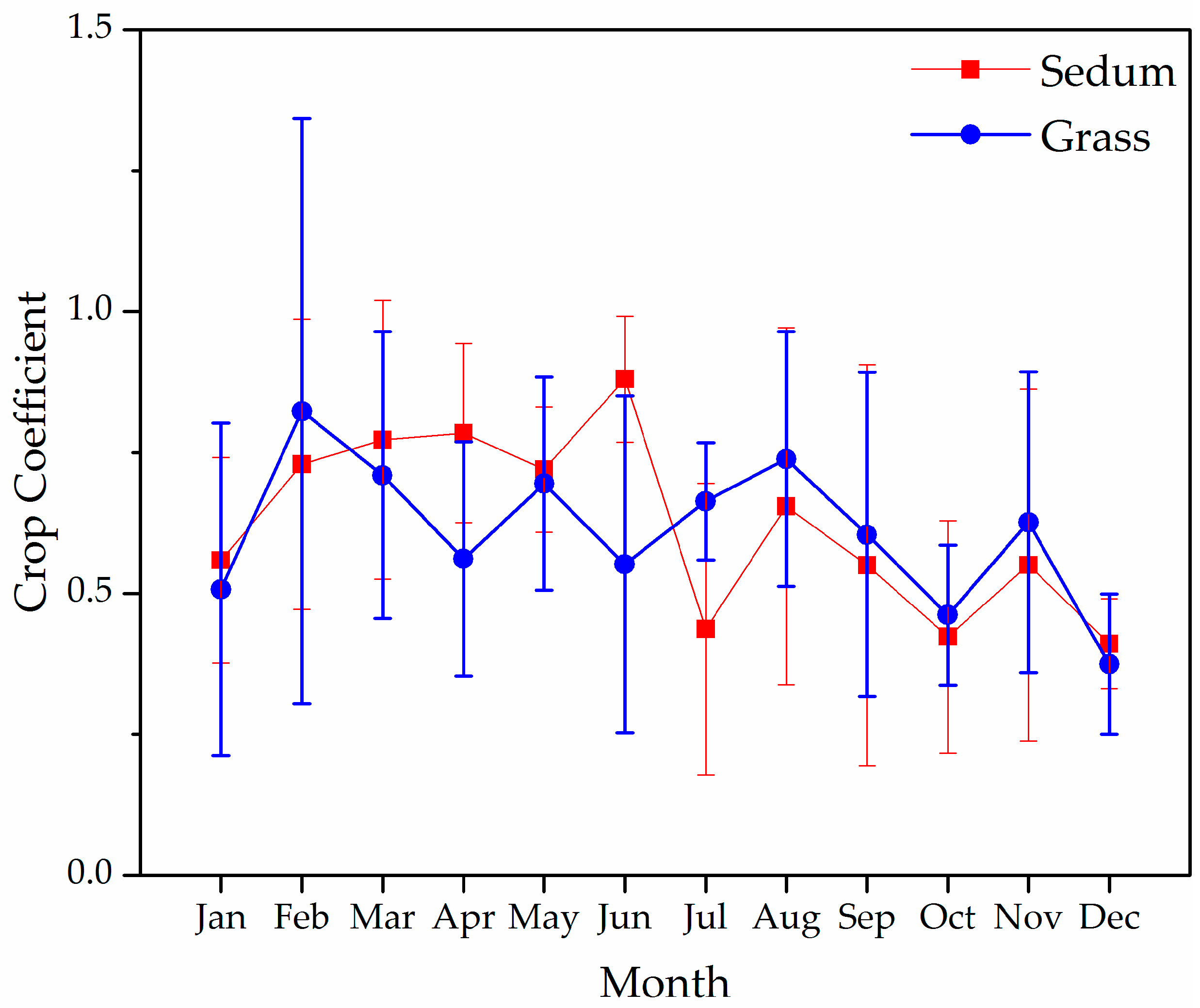
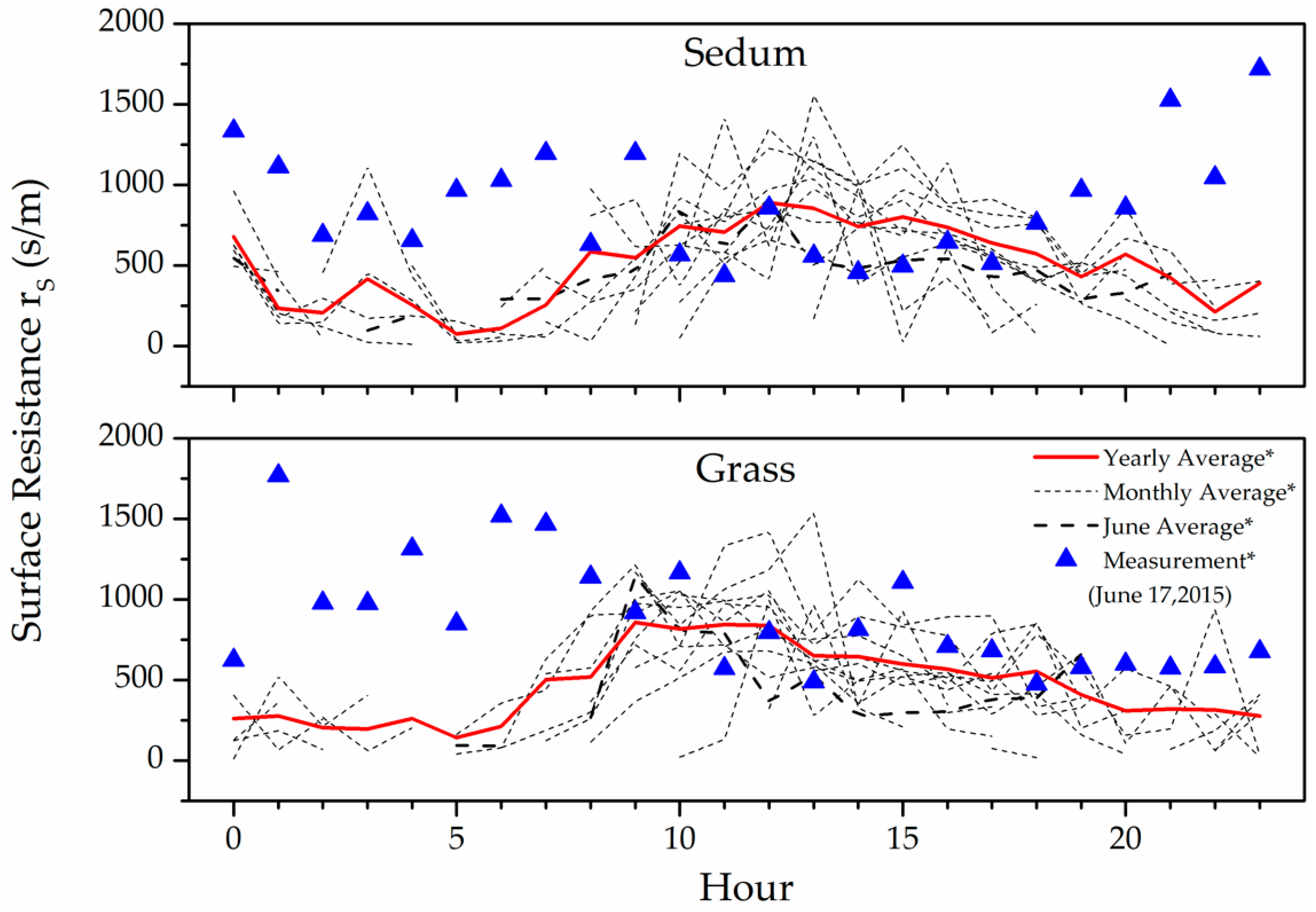
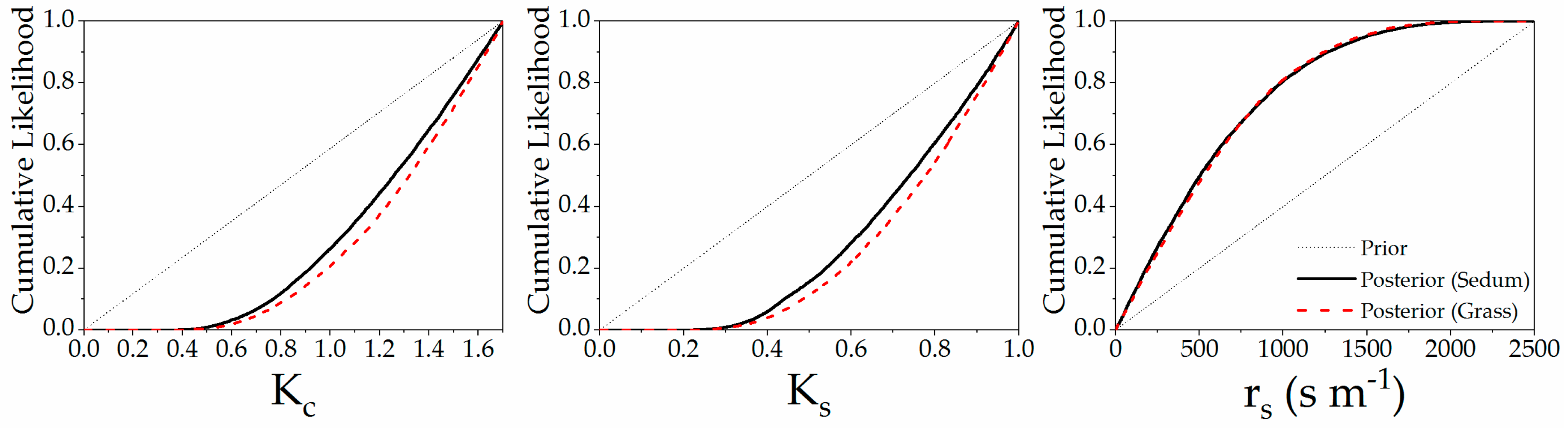
3.3. Parameterization for Evapotranspiration Modeling
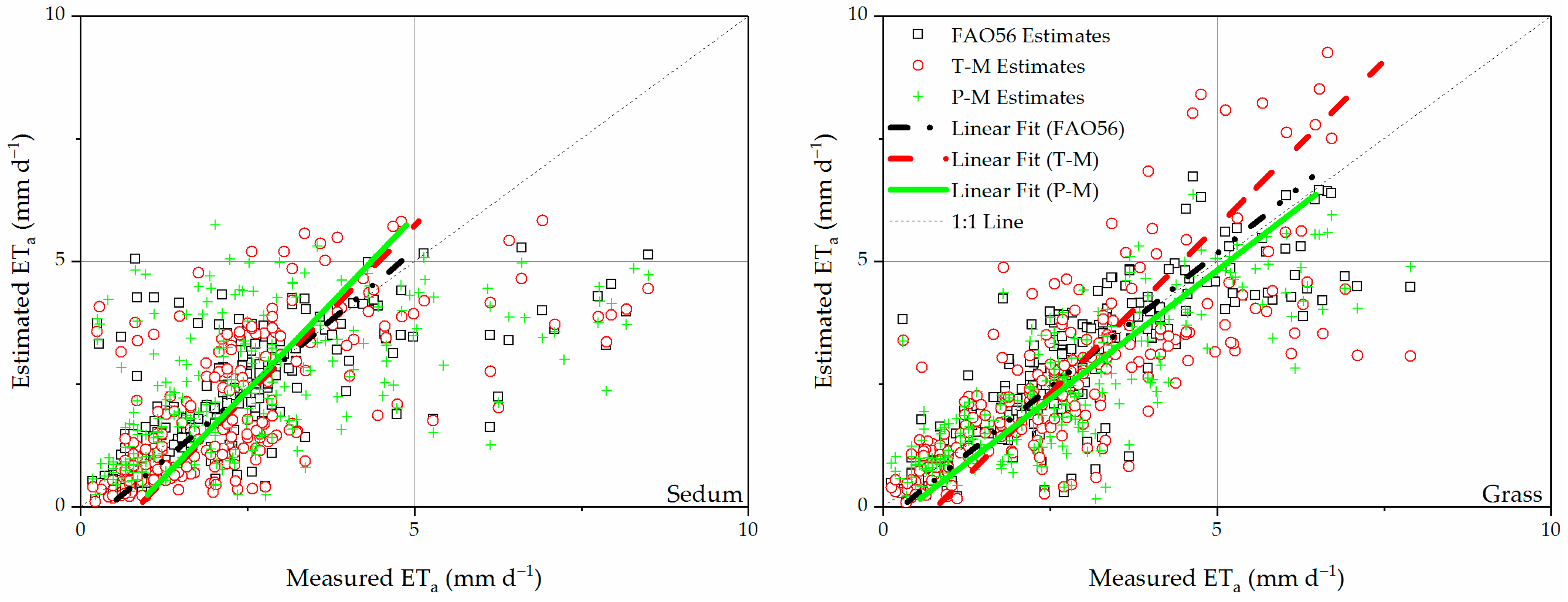
3.4. Comparison of Model Estimates
3.5. Irrigation Cost
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Askarizadeh, A.; Rippy, M.A.; Fletcher, T.D.; Feldman, D.L.; Peng, J.; Bowler, P.; Mehring, A.S.; Winfrey, B.K.; Vrugt, J.A.; AghaKouchak, A.; et al. From Rain Tanks to Catchments: Use of Low-Impact Development To Address Hydrologic Symptoms of the Urban Stream Syndrome. Environ. Sci. Technol. 2015, 49, 11264–11280. [Google Scholar] [CrossRef] [PubMed]
- Feng, Y.; Burian, S.; Pomeroy, C. Potential of green infrastructure to restore predevelopment water budget of a semi-arid urban catchment. J. Hydrol. 2016, 542, 744–755. [Google Scholar] [CrossRef]
- U.S. Environmental Protection Agency. Reducing Urban Heat Islands: Compendium of Strategies; USEPA: Washington, DC, USA, 2008.
- Fletcher, T.D.; Andrieu, H.; Hamel, P. Understanding, management and modelling of urban hydrology and its consequences for receiving waters: A state of the art. Adv. Water Resour. 2013, 51, 261–279. [Google Scholar] [CrossRef]
- Burian, S.J.; Pomeroy, C.A. Urban impacts on the water cycle and potential green infrastructure implications. In Urban Ecosystems Ecology; Aitkenhead-Peterson, J., Volder, A., Eds.; American Society of Agronomy, Crop Science Society of America, and Soil Science Society of America: Madison, WI, USA, 2010; Chapter 14. [Google Scholar]
- Levallius, J. Green roofs on municipal buildings in Lund: Modeling potential environmental benefits. In Physical Geography and Ecosystem Science; Lund University: Lund, Sweden, 2005. [Google Scholar]
- Getter, K.L.; Rowe, D.B. The role of extensive green roofs in sustainable development. HortScience 2006, 41, 1276–1285. [Google Scholar]
- VanWoert, N.D.; Rowe, D.B.; Andresen, J.A.; Rugh, C.L.; Fernandez, R.T.; Xiao, L. Green roof stormwater retention: Effects of roof surface, slope, and media depth. J. Environ. Qual. 2005, 34, 1036–1044. [Google Scholar] [CrossRef] [PubMed]
- Jarrett, A.R.; Hunt, W.F.; Berghage, R.D. Evaluating a spreadsheet model to predict green roof stormwater management. In Low Impact Development; American Society of Civil Engineers: Reston, VA, USA, 2009; pp. 252–259. [Google Scholar]
- DiGiovanni, K.; Gaffin, S.; Montalto, F. Green roof hydrology: Results from a small-scale lysimeter setup (Bronx, NY). In Low Impact Development; American Society of Civil Engineers: San Francisco, CA, USA, 2010; pp. 1328–1341. [Google Scholar]
- Berghage, R.D.; Beattie, D.; Jarrett, A.R.; Thuring, C.; Razaei, F.; O’Connor, T.P. Green Roofs for Stormwater Runoff Control; United States Environmental Protection Agency: Washington, DC, USA, 2009.
- Fassman-Beck, E.; Voyde, E.; Simcock, R.; Hong, Y.S. 4 Living roofs in 3 locations: Does configuration affect runoff mitigation? J. Hydrol. 2013, 490, 11–20. [Google Scholar] [CrossRef]
- Scherba, A.; Sailor, D.J.; Rosenstiel, T.N.; Wamser, C.C. Modeling impacts of roof reflectivity, integrated photovoltaic panels and green roof systems on sensible heat flux into the urban environment. Build. Environ. 2011, 46, 2542–2551. [Google Scholar] [CrossRef]
- Barrio, E.P.D. Analysis of the green roofs cooling potential in buildings. Energy Build. 1998, 27, 179–193. [Google Scholar] [CrossRef]
- Wong, N.H.; Chen, Y.; Ong, C.L.; Sia, A. Investigation of thermal benefits of rooftop garden in the tropical environment. Build. Environ. 2003, 38, 261–270. [Google Scholar] [CrossRef]
- Ouldboukhitine, S.-E.; Belarbi, R.; Jaffal, I.; Trabelsi, A. Assessment of green roof thermal behavior: A coupled heat and mass transfer model. Build. Environ. 2011, 46, 2624–2631. [Google Scholar] [CrossRef]
- Saadatian, O.; Sopian, K.; Salleh, E.; Lim, C.H.; Riffat, S.; Saadatian, E.; Toudeshki, A.; Sulaiman, M.Y. A review of energy aspects of green roofs. Renew. Sustain. Energy Rev. 2013, 23, 155–168. [Google Scholar] [CrossRef]
- Wong, N.H.; Cheong, D.K.W.; Yan, H.; Soh, J.; Ong, C.L.; Sia, A. The effects of rooftop garden on energy consumption of a commercial building in Singapore. Energy Build. 2003, 35, 353–364. [Google Scholar] [CrossRef]
- Kosareo, L.; Ries, R. Comparative environmental life cycle assessment of green roofs. Build. Environ. 2007, 42, 2606–2613. [Google Scholar] [CrossRef]
- Smith, K.R.; Roebber, P.J. Green roof mitigation potential for a proxy future climate scenario in Chicago, Illinois. J. Appl. Meteorol. Climatol. 2011, 50, 507–522. [Google Scholar] [CrossRef]
- Castleton, H.F.; Stovin, V.; Beck, S.B.M.; Davison, J.B. Green roofs; building energy savings and the potential for retrofit. Energy Build. 2010, 42, 1582–1591. [Google Scholar] [CrossRef]
- Voyde, E.; Fassman, E.; Simcock, R.; Wells, J. Quantifying evapotranspiration rates for New Zealand green roofs. Hydrol. Eng. 2010, 15, 395–403. [Google Scholar] [CrossRef]
- Tsang, S.W.; Jim, C.Y. Theoretical evaluation of thermal and energy performance of tropical green roofs. Energy 2011, 36, 3590–3598. [Google Scholar] [CrossRef]
- Feller, M. Quantifying Evapotranspiration in Green Infrastructure: A Green Roof Case Study. Master’s Thesis, Department of Civil and Environmental Engineering, Villanova University, Villanova, PA, USA, 2011. [Google Scholar]
- Klein, P.M.; Coffman, R. Establishment and performance of an experimental green roof under extreme climatic conditions. Sci. Total Environ. 2015, 512–513, 82–93. [Google Scholar] [CrossRef] [PubMed]
- Krebs, G.; Kuoppamäki, K.; Kokkonen, T.; Koivusalo, H. Simulation of green roof test bed runoff. Hydrol. Process. 2016, 30, 250–262. [Google Scholar] [CrossRef]
- Feng, Y.; Burian, S. Improving Evapotranspiration Mechanisms in the U.S. Environmental Protection Agency’s Storm Water Management Model. J. Hydrol. Eng. 2016, 21, 06016007. [Google Scholar] [CrossRef]
- Elliott, R.M.; Gibson, R.A.; Carson, T.B.; Marasco, D.E.; Culligan, P.J.; McGillis, W.R. Green roof seasonal variation: Comparison of the hydrologic behavior of a thick and a thin extensive system in New York City. Environ. Res. Lett. 2016, 11, 074020. [Google Scholar] [CrossRef]
- Poë, S.; Stovin, V.; Berretta, C. Parameters influencing the regeneration of a green roof’s retention capacity via evapotranspiration. J. Hydrol. 2015, 523, 356–367. [Google Scholar] [CrossRef]
- Sims, A.W.; Robinson, C.E.; Smart, C.C.; Voogt, J.A.; Hay, G.J.; Lundholm, J.T.; Powers, B.; O’Carroll, D.M. Retention performance of green roofs in three different climate regions. J. Hydrol. 2016, 542, 115–124. [Google Scholar] [CrossRef]
- Peng, Z.; Stovin, V. Independent Validation of the SWMM Green Roof Module. J. Hydrol. Eng. 2017, 22, 04017037. [Google Scholar] [CrossRef]
- Schneider, D.; Wadzuk, B.M.; Traver, R.G. Using a weighing lysimeter to determine a crop coefficient for a green roof to predict evapotranspiration with the FAO standardized Penman-Monteith equation. In World Environmental and Water Resources Congress 2011; American Society of Civil Engineers: Palm Springs, CA, USA, 2011; pp. 3629–3638. [Google Scholar]
- DiGiovanni, K.; Montalto, F.; Gaffin, S.; Rosenzweig, C. Applicability of classical predictive equations for the estimation of evapotranspiration from urban green spaces: Green roof results. J. Hydrol. Eng. 2013, 18, 99–107. [Google Scholar] [CrossRef]
- Starry, O.; Lea-Cox, J.; Ristvey, A.; Cohan, S. Parameterizing a Water-Balance Model for Predicting Stormwater Runoff from Green Roofs. J. Hydrol. Eng. 2016, 21, 04016046. [Google Scholar] [CrossRef]
- Marasco, D.E.; Culligan, P.J.; McGillis, W.R. Evaluation of common evapotranspiration models based on measurements from two extensive green roofs in New York City. Ecol. Eng. 2015, 84, 451–462. [Google Scholar] [CrossRef]
- Allen, R.G.; Pruitt, W.O.; Wright, J.L.; Howell, T.A.; Ventura, F.; Snyder, R.; Itenfisu, D.; Steduto, P.; Berengena, J.; Yrisarry, J.B.; et al. A recommendation on standardized surface resistance for hourly calculation of reference ETo by the FAO56 Penman-Monteith method. Agric. Water Manag. 2006, 81, 1–22. [Google Scholar] [CrossRef]
- Jarvis, P. The interpretation of the variations in leaf water potential and stomatal conductance found in canopies in the field. Philos. Trans. R. Soc. Lond. B Biol. Sci. 1976, 273, 593–610. [Google Scholar] [CrossRef]
- Stovin, V.; Poë, S.; Berretta, C. A modelling study of long term green roof retention performance. J. Environ. Manag. 2013, 131, 206–215. [Google Scholar] [CrossRef] [PubMed]
- Seneviratne, S.I.; Corti, T.; Davin, E.L.; Hirschi, M.; Jaeger, E.B.; Lehner, I.; Orlowsky, B.; Teuling, A.J. Investigating soil moisture–climate interactions in a changing climate: A review. Earth Sci. Rev. 2010, 99, 125–161. [Google Scholar] [CrossRef]
- Carter, T.; Keeler, A. Life-cycle cost–benefit analysis of extensive vegetated roof systems. J. Environ. Manag. 2008, 87, 350–363. [Google Scholar] [CrossRef] [PubMed]
- Sproul, J.; Wan, M.P.; Mandel, B.H.; Rosenfeld, A.H. Economic comparison of white, green, and black flat roofs in the United States. Energy Build. 2014, 71, 20–27. [Google Scholar] [CrossRef]
- Wadzuk, B.; Schneider, D.; Feller, M.; Traver, R. Evapotranspiration from a green-roof storm-water control measure. J. Irrig. Drain. Eng. 2013, 139, 995–1003. [Google Scholar] [CrossRef]
- Berretta, C.; Poë, S.; Stovin, V. Moisture content behaviour in extensive green roofs during dry periods: The influence of vegetation and substrate characteristics. J. Hydrol. 2014, 511, 374–386. [Google Scholar] [CrossRef]
- Spatari, S.; Yu, Z.; Montalto, F.A. Life cycle implications of urban green infrastructure. Environ. Pollut. 2011, 159, 2174–2179. [Google Scholar] [CrossRef] [PubMed]
- Pataki, D.E.; Carreiro, M.M.; Cherrier, J.; Grulke, N.E.; Jennings, V.; Pincetl, S.; Pouyat, R.V.; Whitlow, T.H.; Zipperer, W.C. Coupling biogeochemical cycles in urban environments: Ecosystem services, green solutions, and misconceptions. Front. Ecol. Environ. 2011, 9, 27–36. [Google Scholar] [CrossRef]
- Williams, N.S.G.; Rayner, J.P.; Raynor, K.J. Green roofs for a wide brown land: Opportunities and barriers for rooftop greening in Australia. Urban For. Urban Green. 2010, 9, 245–251. [Google Scholar] [CrossRef]
- Liu, Y.; Engel, B.A.; Flanagan, D.C.; Gitau, M.W.; McMillan, S.K.; Chaubey, I. A review on effectiveness of best management practices in improving hydrology and water quality: Needs and opportunities. Sci. Total Environ. 2017, 601–602, 580–593. [Google Scholar] [CrossRef] [PubMed]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration—Guidelines for Computing Crop Water Requirements—FAO Irrigation and Drainage Paper 56; FAO—Food and Agriculture Organization of the United Nations: Rome, Italy, 1998. [Google Scholar]
- Sun, H.; Kopp, K.; Kjelgren, R. Water-efficient Urban Landscapes: Integrating Different Water Use Categorizations and Plant Types. HortScience 2012, 47, 254–263. [Google Scholar]
- Litvak, E.; Pataki, D.E. Evapotranspiration of urban lawns in a semi-arid environment: An in situ evaluation of microclimatic conditions and watering recommendations. J. Arid Environ. 2016, 134, 87–96. [Google Scholar] [CrossRef]
- Coutts, A.M.; Tapper, N.J.; Beringer, J.; Loughnan, M.; Demuzere, M. Watering our cities: The capacity for water sensitive urban design to support urban cooling and improve human thermal comfort in the Australian context. Prog. Phys. Geogr. 2013, 37, 2–28. [Google Scholar] [CrossRef]
- Oke, T.R. Advectively-assisted evapotranspiration from irrigated urban vegetation. Bound.-Layer Meteorol. 1979, 17, 167–173. [Google Scholar] [CrossRef]
- Grimmond, C.S.B.; Oke, T.R. Urban water balance: 2. Results from a suburb of Vancouver, British Columbia. Water Resour. Res. 1986, 22, 1404–1412. [Google Scholar]
- Dimoudi, A.; Nikolopoulou, M. Vegetation in the urban environment: Microclimatic analysis and benefits. Energy Build. 2003, 35, 69–76. [Google Scholar] [CrossRef]
- Gober, P.; Brazel, A.; Quay, R.; Myint, S.; Grossman-Clarke, S.; Miller, A.; Rossi, S. Using watered landscapes to manipulate urban heat island effects: How much water will it take to cool Phoenix? J. Am. Plan. Assoc. 2009, 76, 109–121. [Google Scholar] [CrossRef]
- House-Peters, L.A.; Chang, H. Modeling the impact of land use and climate change on neighborhood-scale evaporation and nighttime cooling: A surface energy balance approach. Landsc. Urban Plan. 2011, 103, 139–155. [Google Scholar] [CrossRef]
- Oberndorfer, E.; Lundholm, J.; Bass, B.; Coffman, R.R.; Doshi, H.; Dunnett, N.; Gaffin, S.; Köhler, M.; Liu, K.K.Y.; Rowe, B. Green roofs as urban ecosystems: Ecological structures, functions, and services. BioScience 2007, 57, 823–833. [Google Scholar] [CrossRef]
- Berndtsson, J.C. Green roof performance towards management of runoff water quantity and quality: A review. Ecol. Eng. 2010, 36, 351–360. [Google Scholar] [CrossRef]
- NOAA. Salt Lake City Climate Information. 2016. Available online: http://www.wrh.noaa.gov/slc/climate/slcclimate/SLC/index.php (accessed on 23 February 2016).
- Russell, J.; Cohn, R. Climate of Salt Lake City; LENNEX Corp.: Edinburgh, UK, 2012. [Google Scholar]
- Hutchins-Cabibi, T.; Miller, B.; Hern, T.; Schwartz, A. Urban Water on the Wasatch Front: Past, Present, and Future; Western Resource Advocates: Boulder, CO, USA, 2006. [Google Scholar]
- Denich, C.; Bradford, A. Estimation of evapotranspiration from bioretention areas using weighing lysimeters. J. Hydrol. Eng. 2010, 15, 522–530. [Google Scholar] [CrossRef]
- Easlon, H.M.; Bloom, A.J. Easy Leaf Area: Automated digital image analysis for rapid and accurate measurement of leaf area. Appl. Plant Sci. 2014, 2, 1–4. [Google Scholar] [CrossRef] [PubMed]
- Priestley, C.H.B.; Taylor, R.J. On the Assessment of Surface Heat Flux and Evaporation Using Large-Scale Parameters. Mon. Weather Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Brutsaert, W.; Stricker, H. An advection-aridity approach to estimate actual regional evapotranspiration. Water Resour. Res. 1979, 15, 443–450. [Google Scholar] [CrossRef]
- Walter, I.A.; Allen, R.G.; Elliott, R.; Jensen, M.E.; Itenfisu, D.; Mecham, B.; Howell, T.A.; Snyder, R.; Brown, P.; Echings, S.; et al. ASCE’s Standardized Reference Evapotranspiration Equation. In Watershed Management and Operations Management Conferences 2000, Fort Collins, CO, USA, 20–24 June 2000; American Society of Civil Engineers: Reston, VA, USA, 2000. [Google Scholar]
- Rossman, L.; Huber, W. Storm Water Management Model Reference Manual Volume I–Hydrology (Revised); US Environmental Protection Agency: Cincinnati, OH, USA, 2016.
- Saxton, K.E.; Rawls, W.J. Soil water characteristic estimates by texture and organic matter for hydrologic solutions. Soil Sci. Soc. Am. J. 2006, 70, 1569–1578. [Google Scholar] [CrossRef]
- Monteith, J.L. Evaporation and environment. In Symposium of the Society for Experimental Biology, The State and Movement of Water in Living Organisms; Fogg, G.E., Ed.; Academic Press Inc.: Swansea, UK, 1965; pp. 205–234. [Google Scholar]
- Stull, R.B. An Introduction to Boundary Layer Meteorology; Springer: Dordrecht, The Netherlands, 1988; Volume 13. [Google Scholar]
- Jones, H. Plants and Microclimate: A Quantitative Approach to Environmental Plant Physiology; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Schulze, E.D.; Beck, E.; Müller-Hohenstein, K. Plant Ecology; Springer: Heidelberg, Germany, 2005. [Google Scholar]
- Farrés, M.; Platikanov, S.; Tsakovski, S.; Tauler, R. Comparison of the variable importance in projection (VIP) and of the selectivity ratio (SR) methods for variable selection and interpretation. J. Chemom. 2015, 29, 528–536. [Google Scholar] [CrossRef]
- Gosselin, R.; Rodrigue, D.; Duchesne, C. A Bootstrap-VIP approach for selecting wavelength intervals in spectral imaging applications. Chemom. Intell. Lab. Syst. 2010, 100, 12–21. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Beven, K.; Binley, A. The future of distributed models: Model calibration and uncertainty prediction. Hydrol. Process. 1992, 6, 279–298. [Google Scholar] [CrossRef]
- Staudt, K.; Falge, E.; Pyles, R.D.; Paw U, K.T.; Foken, T. Sensitivity and predictive uncertainty of the ACASA model at a spruce forest site. Biogeosciences 2010, 7, 3685–3705. [Google Scholar] [CrossRef]
- Prihodko, L.; Denning, A.S.; Hanan, N.P.; Baker, I.; Davis, K. Sensitivity, uncertainty and time dependence of parameters in a complex land surface model. Agric. For. Meteorol. 2008, 148, 268–287. [Google Scholar] [CrossRef]
- Schneider, D. Quantifying Evapotranspiration from a Green Roof Analytically. Master’s Thesis, Villanova University, Villanova, PA, USA, 2011. [Google Scholar]
- Hassan, A.E.; Bekhit, H.M.; Chapman, J.B. Uncertainty assessment of a stochastic groundwater flow model using GLUE analysis. J. Hydrol. 2008, 362, 89–109. [Google Scholar] [CrossRef]
- Freer, J.; Beven, K.; Ambroise, B. Bayesian Estimation of Uncertainty in Runoff Prediction and the Value of Data: An Application of the GLUE Approach. Water Resour. Res. 1996, 32, 2161–2173. [Google Scholar] [CrossRef]
- Li, Z.; Chen, Q.; Xu, Q.; Blanckaert, K. Generalized Likelihood Uncertainty Estimation Method in Uncertainty Analysis of Numerical Eutrophication Models: Take BLOOM as an Example. Math. Probl. Eng. 2013, 2013, 701923. [Google Scholar] [CrossRef]
- Poyatos, R.; Villagarcía, L.; Domingo, F.; Piñol, J.; Llorens, P. Modelling evapotranspiration in a Scots pine stand under Mediterranean mountain climate using the GLUE methodology. Agric. For. Meteorol. 2007, 146, 13–28. [Google Scholar] [CrossRef]
- Sokal, R.; Rohlf, F. Biometry; Freeman: San Francisco, CA, US, 1981; p. 859. [Google Scholar]
- Rezaei, F. Evapotranspiration Rates from Extensive Green Roof Species; Pennsylvania State University: State College, PA, USA, 2005. [Google Scholar]
- Marasco, D.E.; Hunter, B.N.; Culligan, P.J.; Gaffin, S.R.; McGillis, W.R. Quantifying Evapotranspiration from Urban Green Roofs: A Comparison of Chamber Measurements with Commonly Used Predictive Methods. Environ. Sci. Technol. 2014, 48, 10273–10281. [Google Scholar] [CrossRef] [PubMed]
- Sherrard, J.; Jacobs, J. Vegetated Roof Water-Balance Model: Experimental and Model Results. J. Hydrol. Eng. 2012, 17, 858–868. [Google Scholar] [CrossRef]
- Starry, O. The Comparative Effects of THREE SEDUM SPECies on Green Roof Stormwater Retention; University of Maryland: College Park, MA, USA, 2013. [Google Scholar]
- Lazzarin, R.M.; Castellotti, F.; Busato, F. Experimental measurements and numerical modelling of a green roof. Energy Build. 2005, 37, 1260–1267. [Google Scholar] [CrossRef]
- Voyde, E. Quantifying the complete hydrologic budget for an extensive living roof. Ph.D. Thesis, Department of Civil and Environmental Engineering, The University of Auckland, Auckland, New Zealand, 2011. [Google Scholar]
- Wolf, D.; Lundholm, J.T. Water uptake in green roof microcosms: Effects of plant species and water availability. Ecol. Eng. 2008, 33, 179–186. [Google Scholar] [CrossRef]
- Steinwand, A.L.; Harrington, R.F.; Groeneveld, D.P. Transpiration coefficients for three Great Basin shrubs. J. Arid Environ. 2001, 49, 555–567. [Google Scholar] [CrossRef]
- Dvorak, B.; Volder, A. Green roof vegetation for north american ecoregions: A literature review. Landsc. Urban Plan. 2010, 96, 197–213. [Google Scholar] [CrossRef]
- VanWoert, N.D.; Rowe, D.B.; Andresen, J.A.; Rugh, C.L.; Xiao, L. Watering regime and green roof substrate design affect sedum plant growth. HortScience 2005, 40, 659–664. [Google Scholar]
- Starry, O.; Lea-Cox, J.D.; Kim, J.; van Iersel, M.W. Photosynthesis and water use by two sedum species in green roof substrate. Environ. Exp. Bot. 2014, 107, 105–112. [Google Scholar] [CrossRef]
- Kluge, M. Is sedum acre L. a CAM plant? Oecologia 1977, 29, 77–83. [Google Scholar] [CrossRef] [PubMed]
- Gravatt, D.A.; Martin, C.E. Comparative ecophysiology of five species of sedum (crassulaceae) under well-watered and drought-stressed conditions. Oecologia 1992, 92, 532–541. [Google Scholar] [CrossRef] [PubMed]
- Mitchell, S.; Beven, K.; Freer, J. Multiple sources of predictive uncertainty in modeled estimates of net ecosystem CO2 exchange. Ecol. Model. 2009, 220, 3259–3270. [Google Scholar] [CrossRef]
- Franks, S.W.; Beven, K.J. Bayesian estimation of uncertainty in land surface-atmosphere flux predictions. J. Geophys. Res. Atmos. 1997, 102, 23991–23999. [Google Scholar] [CrossRef]
- Government, S.L.C. Salt Lake City Water Rates. Available online: http://www.slcdocs.com/utilities/PDF%20Files/UtilityRates/WaterrateswebCurrent.pdf (accessed on 8 February 2018).
- Government, S.L.C. Salt Lake City Stormwater Rates. Available online: http://www.slcdocs.com/utilities/PDF%20Files/UtilityRates/StormrateswebCurrent.pdf (accessed on 8 February 2018).



| Models | rs | Kc | Ks |
|---|---|---|---|
| FAO56 | 50 s m−1 (day); 200 s m−1 (night) | Parameterized | Measured |
| T–M | 50 s m−1 (day); 200 s m−1 (night) | 1 | Measured |
| P–M | Parameterized | 1 | 1 |
| Parameters | Min | Max | Units |
|---|---|---|---|
| Crop Coefficient (Kc) | 0 | 1.7 | - |
| Water Stress Coefficient (Ks) | 0 | 1 | - |
| Surface Resistance (rs) | 0 | 2500 | s m−1 |
| Models | Sedum | Grass | ||||||
|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | NSE | PBIAS | R2 | RMSE | NSE | PBIAS | |
| FAO56 | 0.44 | 1.25 | 0.58 | 4.97% | 0.73 | 0.88 | 0.73 | 1.82% |
| T–M | 0.42 | 1.26 | 0.52 | 9.93% | 0.59 | 1.10 | 0.52 | 4.83% |
| P–M | 0.28 | 1.52 | 0.23 | 4.79% | 0.67 | 0.97 | 0.64 | 10.69% |
| Parameters | Sedum | Grass |
|---|---|---|
| Crop Coefficient (Kc) | 0.33 | 0.39 |
| Water Stress Coefficient (Ks) | 0.33 | 0.39 |
| Surface Resistance (rs) | 0.43 | 0.41 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, Y.; Burian, S.J.; Pardyjak, E.R. Observation and Estimation of Evapotranspiration from an Irrigated Green Roof in a Rain-Scarce Environment. Water 2018, 10, 262. https://doi.org/10.3390/w10030262
Feng Y, Burian SJ, Pardyjak ER. Observation and Estimation of Evapotranspiration from an Irrigated Green Roof in a Rain-Scarce Environment. Water. 2018; 10(3):262. https://doi.org/10.3390/w10030262
Chicago/Turabian StyleFeng, Youcan, Steven J. Burian, and Eric R. Pardyjak. 2018. "Observation and Estimation of Evapotranspiration from an Irrigated Green Roof in a Rain-Scarce Environment" Water 10, no. 3: 262. https://doi.org/10.3390/w10030262
APA StyleFeng, Y., Burian, S. J., & Pardyjak, E. R. (2018). Observation and Estimation of Evapotranspiration from an Irrigated Green Roof in a Rain-Scarce Environment. Water, 10(3), 262. https://doi.org/10.3390/w10030262





