Water Resources Allocation in Transboundary River Based on Asymmetric Nash–Harsanyi Leader–Follower Game Model

Abstract

Transboundary river water resources allocation is important in water resources management. Conflicts often arise when different water users compete for a limited water supply. This study proposes a two-level asymmetric Nash–Harsanyi Leader–Follower game model to resolve conflicts of interest in transboundary river water resources allocation problems. In the proposed model, we use bankruptcy theory to derive disagreement points and determine the bargaining weights considering the principles of equity and efficiency. For comparison, a model that does not consider disagreement points and bargaining weights are also used to demonstrate the importance of disagreement points and bargaining weights. The proposed model is applied to a real case of the Huaihe River basin in China, which is facing water shortages. In the case study, the watershed management agency serves as the leader, three provinces (Henan, Anhui and Jiangsu) serve as followers, and successive linear programming is used to solve the model for followers. The results show that the proposed disagreement points can guarantee basic water demand, and the bargaining weights can better balance the economic development levels among followers.

1. Introduction

Water resources are basic resources for human survival, and water resources allocation research has attracted more and more attention [1]. Rivers follows the natural flow of the Earth’s surface, but the artificial division boundaries makes the same river flow through different administrative regions. It is difficult to allocate water resources in transboundary river basins, especially when the water resources are not enough to meet the water demand of the whole river basin, and there are inevitably water resources conflicts between the various administrative regions. Due to the differences in socio-economic, environmental and other factors, a worldwide standard for water resources conflict resolution has not been established [2].

Various methods and models have been used in water resources allocation, including simulation methods, optimization methods, water rights, game theory and complex adaptive systems [3,4,5,6,7,8]. Water resources allocation problem usually involves various rational decision-maker interactions, and water resources allocation needs to consider multiple objectives (such as economic, social, environmental and etc.), which yields multi-objective decision-making problems. This kind of allocation model solves water resources allocation problems via optimization approaches, which reflect the indirect interaction between decision-makers, but ignore the direct interaction between decision-makers, making them impractical in real-world applications [9].

Game theory is a theory of decision-making and equilibrium during the process of direct interaction between decision-makers [10]. Therefore, the water resources allocation based on game theory is a promising method for reducing this deficiency. Moreover, compared with the traditional water resources allocation, which only focuses on the interests of the whole society, using the game theory to study the conflict of water resources allocation allows full consideration of the influences of all decision-makers. It is recognized that there are different interests in decision-makers in the process of water resources allocation, and game theory can be used to maximize the benefits of all water users while achieving the rational allocation of water resources. Therefore, using the game theory to study the conflict of water resources allocation is more practical.

In recent years, water resources allocation based on game theory has been studied and extended [9,11,12,13,14,15]. Carraro et al. [11,13,14] systematically expounded the application of non-cooperative negotiation theory in water resources conflict. Parrachino et al. [12] applied cooperative game theory to water resource issues, and their results showed that cooperation over scare water resources was possible under various physical conditions and institutional arrangements. Madani et al. [9] demonstrated that the application of game theory in the field of water resources can be divided into five parts, i.e., water or benefit allocation among water users, groundwater management, transboundary water allocation, water quality management and other types of water resources management. Dinar et al. [15] divided the application of game theory in the conflict of water resources allocation into three aspects: (1) the application of non-cooperative negotiation theory in water resources allocation conflict; (2) the application of graph model in water resources allocation conflict; (3) application of Nash bargaining theory and Nash–Harsanyi bargaining theory to water resources allocation problems.

In the above water resources allocation conflict research, Rogers [16] originally applied game theory to the conflict of water resources allocation problems in transboundary river basins. In recent studies, Eleftheriadou and Mylopoulos [17] implemented game theoretical concepts in a case study of Greek–Bulgarian negotiations on the Nestos/Mesta transboundary river. Hipel et al. [18] applied the graph model of non-cooperative game to the conflict of water resources allocation, and their proposed method has been widely used. Madani and Lund [19] traced changes in Delta conflict by game theory. Kucukmehmetoglu [20] introduced a composite method that integrates both Pareto frontier and game theory in the Euphrates and Tigris River. Li et al. [21] developed a generalized uncooperative planar game theory model for water distribution in a transboundary river basin. Degefu et al. [2] proposed a cooperative bargaining approach for solving the water sharing problem in the Nile River basin.

Safari et al. [22] introduced a mathematical model which integrates both the leader–follower concept and the bargaining theory in the case of the Zarrinehrud River basin. Zarghami et al. [23] applied the nonlinear interval parameter programming combined with Nash bargaining theory to resolve competing and conflicting needs of water users from different sectors, including agriculture, domestic, industry and environment. However, the above studies ignored the solution of disagreement points and the differences of importance degree between users when solving the Nash bargaining problems, which led to unreasonable results in the water resources allocation.

This paper proposes a two-level asymmetric Nash–Harsanyi Leader–Follower game model to resolve the conflict problem of spatial water resources allocation in the Huaihe River basin. First, we propose a method to calculate the disagreement points based on bankruptcy theory and propose a calculation method for determining bargaining weights of transboundary river basins, considering equity and efficient principles. Second, we construct a two-level asymmetric Nash–Harsanyi Leader–Follower game model with a watershed management agency as the leader and Henan Province, Anhui Province and Jiangsu Province as followers and apply it to a real-world water resources allocation problem.

The rest of this paper is organized as follows: Section 2 describes the methodology of the asymmetric Nash–Harsanyi Leader–Follower game model; the determination of the disagreement points and bargaining weights is included in this section. Section 3 is a case study, in which the proposed Nash–Harsanyi Leader–Follower game model is applied to a water resources allocation problem in three provinces of the Huaihe River basin. Section 4 discusses the impact of minimum survival water demand on the disagreement points and the impact of the disagreement points on the water resources allocation, and Section 5 concludes the paper.

2. Methodology

The leader–follower game is non-cooperative; it is about how to make decision through the interaction of rational behavior if the game players cannot reach a binding cooperation agreement, and this game emphasizes individual rationality and optimal individual decision-making. In a leader–follower game, the leaders move first, and then the followers move. The asymmetric Nash–Harsanyi game is a cooperative game; it is about how the players interact with each other to achieve a binding cooperation agreement, so as to maximize the overall benefit, and this game emphasizes collective rationality. The asymmetric Nash–Harsanyi Leader–Follower game model is a combination of the leader–follower concepts and Nash–Harsanyi theory, taking into account individual and collective rationality. Water resources allocation in river basins usually involves a single leader and several followers, which is suitable for the two-level asymmetric Nash–Harsanyi Leader–Follower game model. The following section systematically describes the principles of the asymmetric Nash–Harsanyi Leader–Follower game model.

2.1. Asymmetric Nash–Harsanyi Game Model

Non-cooperative game theory studies how to make decisions so that each player obtains their own maximum income using mutual interests. In regard to cooperative game theory, Nash proposed the Nash bargaining solution, where efficiency is considered; this is known as Nash bargaining. The Nash bargaining solution maximizes the product of the grand coalition members’ additional utilities using cooperation, in contrast to non-cooperation cases [15]. Therefore, Nash bargaining solution represents the evolution from a non-cooperative game to a cooperative game. Harsanyi [24] extended the two-person Nash bargaining solution to the n-person Nash–Harsanyi bargaining solution.

In the asymmetric Nash–Harsanyi game model, it is assumed that there are $n$ decision makers, $v$ is the element of criteria space $V$, $x$ is the argument of function $u_i$, $X$ is the decision space and $u_i:X\to R$ is the objective function of decision maker $i$. The criteria space can be defined as:

$$V=\left\{v|v\in R^n,v=(v_i),v_i=u_i(x),x\in X\right\},$$

(1)

Decision makers will receive small objective function values if they are unable to reach an agreement. So, let $d=(d_1,d_2,\cdots ,d_i,\cdots ,d_n)$ be the assigned vector of the disagreement point of $n$ decision makers, let $N=\left\{1,2,\cdots ,i,\cdots ,n\right\}$ be the set of decision makers, and let $d_i$ be the disagreement point for decision maker $i$. If $V$ is a closed, bounded and convex space, then there is at least one $u\in V$ that makes $u\ge d$. When the differences in the importance degree of players are taken into account, the asymmetric Nash–Harsanyi game model can be written as the following [25]:

$$\max {\displaystyle \prod _{i=1}^n{\left(u_i-d_i\right)}^{a_i}},$$

(2)

Subject to:

Optimal solution existence constraints:

$$u_i\ge d_i,i=1,2,\dots ,n,$$

(3)

Bargaining weight constraints:

$${\displaystyle \sum _{i=1}^n{\alpha }_i=1},$$

(4)

where $u_i$ is the objective function for decision maker $i$, $d_i$ is the disagreement point for decision maker $i$, ${\alpha }_i$ is the bargaining weight for decision maker $i$, and $n$ is the number of decision makers.

The symmetric Nash–Harsanyi game is a special case of the asymmetric Nash–Harsanyi game theory, when ${\alpha }_1={\alpha }_2=\dots ={\alpha }_n$.

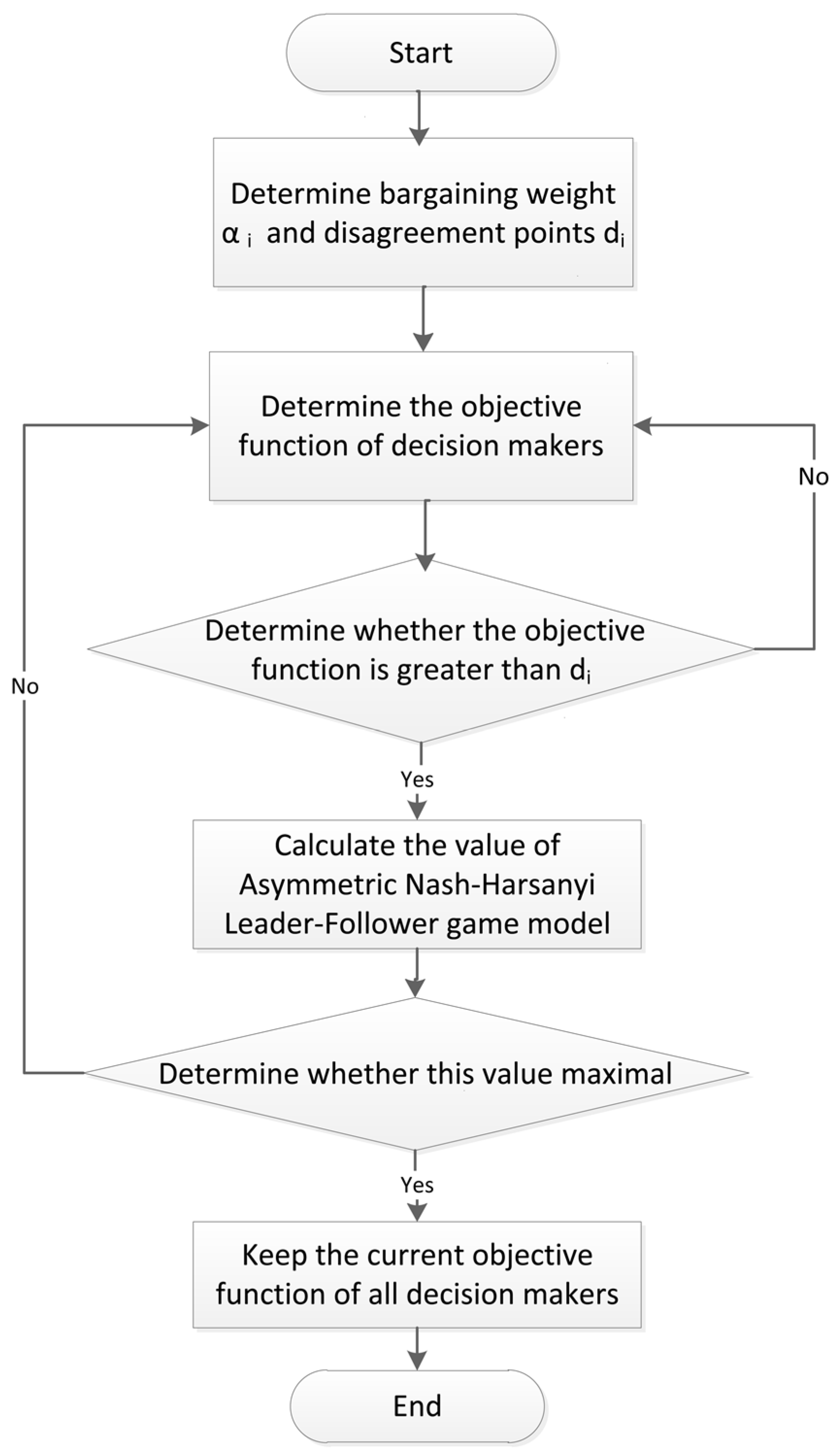
The solution steps of the asymmetric Nash–Harsanyi game model are illustrated in Figure 1.

The specific steps of the asymmetric Nash–Harsanyi bargaining process are expressed as follows:

(1)

Determine the disagreement points and bargaining weights of the decision makers;

(2)

Determine the objective function of the decision makers, if a decision maker’s objective function is less than its disagreement point, then this decision maker needs to change the objective function of other decision makers and adjust its objective function according to the requirements of other decision makers until the objective functions of all decision makers are greater than the disagreement points;

(3)

Calculate the value of ${\displaystyle \prod _{i=1}^n{\left(u_i-d_i\right)}^{a_i}}$, and judge whether this value reaches the maximum value; if not, return to (2); otherwise, keep the current objective functions of all decision makers.

2.2. Nash–Harsanyi Leader–Follower Game Model

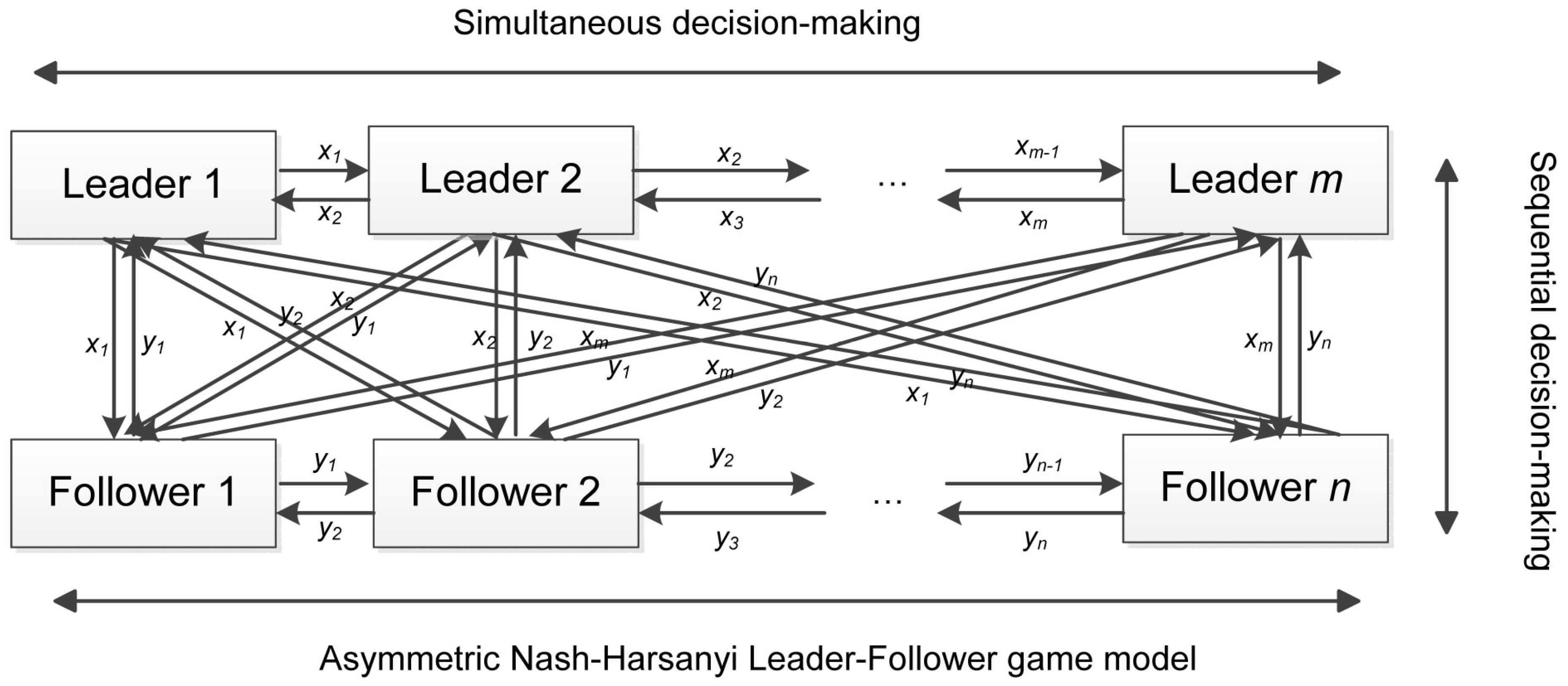
The asymmetric Nash–Harsanyi Leader–Follower game model is a combination of the leader–follower concepts and Nash–Harsanyi theory. In this model, leaders make decisions with appropriate consideration of the interests of followers, and then the followers use the asymmetric Nash–Harsanyi game after the leader makes a decision. Therefore, the asymmetric Nash–Harsanyi Leader–Follower game model can be generalized into a two-level hierarchical structure problem. Figure 2 is a two-level hierarchical structure of the asymmetric Nash–Harsanyi Leader–Follower game model, which includes multiple leaders and followers. The leaders and followers have their own objective functions and constraints. When leaders do not know the other leaders’ decisions, they make their own preferred decisions with appropriate consideration of the interests of followers. Then, after the leaders make their decisions, the followers use the asymmetric Nash–Harsanyi game model without knowing the other followers’ decisions. The solution of the followers depends on the solution of the leaders, and the leaders need to take into account the interests of the followers, which can promote bilateral cooperation and a win-win situation.

For the asymmetric Nash–Harsanyi Leader–Follower game model, assume that there are $m$ leaders and $n$ followers; the model of the leaders can be described as the following:

$$V_j=\underset{x_j}{\max F_j}(\mathit{x},\mathit{y}),$$

(5)

Subject to:

The leaders’ inequality constraints:

$$g_j(\mathit{x},\mathit{y})\ge 0,$$

(6)

The leaders’ equality constraints:

$$h_j(\mathit{x},\mathit{y})=0,$$

(7)

where $V_j$ is the objective function of leader $j$ , who makes the best decision with appropriate consideration of the interests of the followers, $\mathit{x}=\left\{x_1,x_2,\cdots ,x_m\right\}$ is the decision vector related to the leaders, $\mathit{y}=\left\{y_1,y_2,\cdots ,y_n\right\}$ is the decision vector related to the followers, $g_j(\mathit{x},\mathit{y})$ is the inequality constraints, $h_j(\mathit{x},\mathit{y})$ is the equality constraints, and $y_j^{\ast }(x)$ is the solution of the followers, $y_j=y_j^{\ast }(x)$.

The model of followers can be described as the following:

$$\max {\displaystyle \prod _{i=1}^n{(u_i(\mathit{x},\mathit{y})-d_i)}^{a_i}},$$

(8)

Subject to:

Optimal solution existence constraints:

$$u_i(\mathit{x},\mathit{y})\ge d_i,i=1,2,\cdots ,n,$$

(9)

The bargaining weight constraints:

$${\displaystyle \sum _{i=1}^n{\alpha }_i=1},$$

(10)

The followers’ inequality constraints:

$$G_i(\mathit{x},\mathit{y})\ge 0,$$

(11)

The followers’ equality constraints:

$$H_i(\mathit{x},\mathit{y})=0,$$

(12)

where $u_i(x,y)$ is the objective function of follower $i$, $G_i\left(\mathit{x},\mathit{y}\right)$ is the inequality constraints, and $H_i(\mathit{x},\mathit{y})$ is the equality constraints.

For the real-world water resources allocation problem, $d_i=u_i(I_i)$, in which $I_i$ is the minimum water allocation for follower $i$, and $u_i(I_i)$ is the benefit of minimum water allocation for follower $i$. Using the Nash–Harsanyi Leader–Follower game model, leaders need to determine the disagreement points and bargaining weights of followers in advance. The above Equations (5) and (8) show that $n$ followers make corresponding decisions according to the decisions of $m$ leaders, after the leaders have made decisions with appropriate consideration of the followers’ interests.

The real-world transboundary river water resources allocation example involves a single leader and multiple followers. In this study, a watershed management agency is considered to be the leader, who is responsible for the ecological benefits of the whole basin. Henan, Anhui and Jiangsu Provinces serve as the followers. The ecological water used by the whole basin in the allocation process is the public water. If the public water allocation is unreasonable, the ecological situation will deteriorate, and sustainable development be challenged. Therefore, it is necessary to rationally distribute public water. The transboundary river water resources allocation process can be divided into two stages. The first stage involves allocating the public water. In the second stage, followers need to allocate water resources according to the asymmetric Nash–Harsanyi game model after the decisions are given by the watershed management agency.

It is assumed that the total amount of available water that the watershed management agency can allocate is a certain value ($Q$) and the public water is $s$. The water in the $i$th follower is $w_i$, and satisfies $Q={\displaystyle \sum _{i=1}^n{w}_i}+s$. The specific generalization of water resources allocation is shown in Figure 3.

Furthermore, the disagreement point $d_i$ and bargaining weight ${\alpha }_i$ need to be determined based on the specific situation of the followers after the leader has made its decision. The calculation of the disagreement point ($d_i$) and bargaining weight (${\alpha }_i$) are described separately below.

2.2.1. Determination of the Disagreement Points

The disagreement points are not determined strictly; they can be determined by the maximum and minimum solution points, the Nash equilibrium point, the minimum benefit of each participant in non-cooperation and by other methods [26]. We define the vector of the disagreement points $(d_1,d_2,\cdots ,d_i,\cdots ,d_n)$ as the benefits of the minimum water allocation $(I_1,I_2,\cdots ,I_i,\cdots ,I_n)$ to followers, which reflects the minimum benefits that the followers can accept. Therefore, it is necessary to reflect the requirements of the individual rationality before the cooperation of the followers to satisfy the maximal and minimal solutions. Each province’s disagreement point formula is defined as follows:

$$d_i=u_i(I_i),$$

(13)

When the available water is less than the water demand, the bankruptcy theory can be used to solve the problem of the minimum water allocation of each follower. Degefu et al. [2] used the theory of bankruptcy to define the minimum water allocation. Each follower’s minimal water allocation formula is defined as follows:

$$I_i=\max (0,Q-{\displaystyle \sum _{k\ne i}{r}_i-s}),$$

(14)

Subject to:

Bankruptcy theory existence constraints:

$$Q<{\displaystyle \sum _{i=1}^n{r}_i}+s,$$

(15)

Using the above method of bankruptcy theory to solve the minimum water allocation may make the follower’s minimum water allocation zero. However, each follower requires a minimum survival water demand ${\lambda }_i$ (e.g., domestic water) in the process of the actual water resources allocation. The minimum water allocation obtained by the above theory of bankruptcy might be less than the minimum survival water demand ${\lambda }_i$. In order to avoid the case of unreasonable minimum water allocation, we propose the following formula to determine the minimum water allocation, considering minimum survival water demand:

$$I_i=\max ({\lambda }_i,Q-{\displaystyle \sum _{k\ne i}{r}_i-s}),$$

(16)

where ${\lambda }_i$ should contain the basic requirements of domestic and production water.

2.2.2. Determination of Bargaining Weight

It is important to have effective water resources allocation due to intense competition for water resources. Dinar et al. [27] showed that scarce water allocation should be based on economic efficiency, equity, flexibility, security, real opportunity cost, predictability, political and public acceptability, equity and sustainability principles. Roa-García [28] discussed the equity, efficiency and sustainability of water allocation in the Andes.

The symmetric Nash–Harsanyi Leader–Follower game model, which does not consider the bargaining weight of the followers, ignores the importance degree of each follower. However, this study applies asymmetric the Nash–Harsanyi Leader–Follower game model to the conflict of transboundary river water resources allocation, in which the watershed management agency is responsible for the ecological benefits of the basin, taking into account the principle of sustainable development. Bargaining weight in the asymmetric Nash–Harsanyi Leader–Follower game model is determined through comprehensive consideration of equity and efficiency, which reflects the equilibrium of the followers’ development levels. Since the ecological benefits of the whole basin are determined by the watershed management agency, it is no longer considered in the principle of sustainability.

The equity principle focuses on the fair use of water resources and is determined by the proportion of each follower’s water demand relative to total water demand. Since the disagreement points ensure the minimum survival needs of each follower, the minimum survival water demand should be deducted when calculating the proportion of each follower’s water demand relative to total water demand. The formula for calculating the bargaining weight of each follower when only considering the equity principle is as follows:

$${\delta }_{1i}=\frac{r_i-I_i}{{\displaystyle \sum _{i=1}^n(r_i-I_i)}},$$

(17)

where ${\delta }_{1i}$ is the bargaining weight for follower $i$ when only considering the equity principle that represents the equity of water for follower $i$, and $r_i$ is the water demand for follower $i$.

Considering the differences in water use levels between followers, the efficiency principle mainly focuses on encouraging the efficient use of water resources, increasing the water allocation for followers with high levels of water use. The bargaining weight under the principle of efficiency is determined according to the integrated water utility index method [29]. Let $D_i$ be the integrated water utility for follower $i$, and assume that each follower has $e$ water users. The integrated water utility can be calculated by Equation (18).

$$D_i={\displaystyle \sum _{k=1}^e\frac{r_{i,k}}{r_i}}{D}_{i,k},$$

(18)

where $r_{i,k}$ is the water demand of the $k$th water user in the $i$th follower, and $D_{i,k}$ is the integrated water utility of the $k$th water user in the $i$th follower.

Considering the efficiency principle, the formula for calculating the water use level correction coefficient of each follower is as follows.

$${\beta }_i=1-\frac{D_i-\frac{1}{n}{\displaystyle \sum _{i=1}^n{D}_i}}{\frac{1}{n}{\displaystyle \sum _{i=1}^n{D}_i}},$$

(19)

where ${\beta }_i$ is the water use correction coefficient for follower $i$.

The bargaining weight of each follower under the efficiency principle is calculated as follows:

$${\delta }_{2i}=\frac{{\beta }_i}{{\displaystyle \sum _{i=1}^n{\beta }_i}},$$

(20)

where ${\delta }_{2i}$ is the bargaining weight for follower $i$ when only the efficiency principle is considered; this represents the efficient use of water resources for follower $i$.

Therefore, considering equity and efficiency principles, the bargaining weight of each follower is calculated as follows:

$${\alpha }_i=\eta {\delta }_{1i}+(1-\eta ){\delta }_{2i},$$

(21)

where $\eta$ is the weight of the equity principle, and $(1-\eta )$ is the weight of the efficiency principle.

2.3. Successive Linear Programming Method

The successive linear programming method solves nonlinear optimization problems. They are particularly attractive for large, sparse nonlinear programs. Starting at some estimate of the optimal solution, the method is based on solving a sequence of first-order approximations (i.e., linearizations) of the model. The linearizations are linear programming problems, which can be solved efficiently. As the linearizations need not be bound, trust regions or similar techniques are needed to ensure convergence in theory. Palacios-Gomez et al., provided a detailed description of the successive linear programming method [30].

3. Case Study

3.1. Description of the Area

The Huaihe River basin is located between the Yellow River and Yangtze River, with a total area of 19,000 km². The Huaihe River basin includes the Huaihe drainage networks, which are located in the east (longitude from 111.9° to 121.4°) and in the north (latitude from 30.9° to 36.6°). In this study, the Huaihe River basin is divided into three regions: Henan Province, Anhui Province and Jiangsu Province. Figure 4 shows the spatial distribution and location of the administrative region of the Huaihe River basin. The study area is not international. Nevertheless, interprovincial or interstate basins are effectively equivalent to international basins as long as their boundaries do not match political boundaries, and they are managed by more than one authority [31].

3.2. The Elements and Data of Game Model

The research object of this study is Huaihe River basin, which is generalized into Henan Province, Anhui Province and Jiangsu Province. In this case study, the watershed management agency serves as the leader and the three provinces (Henan, Anhui and Jiangsu) serve as followers, $m=1$, $n=3$. The participants of the game model are Henan Province, Anhui Province, Jiangsu Province and watershed management agency.

The transboundary Huaihe River water resources allocation process can be divided into two stages. In the first stage, the watershed management agency allocates the public water. In the second stage, the three provinces allocate water resources using the asymmetric Nash–Harsanyi game model after watershed management agency has made its decision.

The utility function of the Huaihe River watershed management agency can be expressed as the public benefit $f(s)$. However, the public benefit is difficult to measure in terms of economic efficiency. Therefore, we take the negative of the square of the difference between the public water and the ideal ecological water demand as the public benefit; the public benefit formula can be obtained as follows:

$$f(s)=-{(s-s^{\ast })}^2,$$

(22)

where $s$ is the decision variable and $s^{\ast }$ is the ideal ecological water demand.

In the actual Huaihe River water resources allocation process, due to the lack of consideration of the eco-environmental water requirements, the eco-environmental water consumption is largely consumed by the production of water. This could not meet the sustainable development of the river basin, which brings about water resources and eco-environment problems. According to the current situation of the Huaihe River basin, the ideal ecological water demand is defined as follows [32]:

$$s^{\ast }=\max (\psi Q,\lambda Q),$$

(23)

where $\psi$ is the percentage of base flow in available water and $\lambda$ is the percentage of sea flow in available water. We specify $\psi$ as 0.15 based on the Tennant method and $\lambda$ as 0.26 according to the monthly guaranteed frequency method.

The utility function of the three provinces in Huaihe River basin is described by the water benefit and cost. The description of the water benefit and cost are as follows:

(1)

Let $B_i\left(w_i\right)$ be the water benefit of each province $(i=1,2,3)$. The water benefit of each province depends on the amount of water ($w_i$) allocated to the province. The water benefit increases with the total water supply; the water benefit is the largest as the water supply reaches the water demand ($r_i$). Water benefits in each province were calculated using regression analysis with data from the Statistical Yearbook [33,34,35]. The water benefit function of each province is shown in

Table 1. The water benefit function of each province. Please confirm if the lowercase is correct? Please check all cases like this in all tables.

Province	Water Demand ${\mathit{r}}_{\mathit{i}}$ (Hundred Million m3)	Water Benefit Function
Henan	126.4	$B_1(w_1)=-0.026w_1^2+11.192w_1+2.5311$
Anhui	135.2	$B_2(w_2)=-0.022w_2^2+9.153w_2+1.5002$
Jiangsu	137.3	$B_3(w_3)=-0.021w_3^2+9.521w_3+1.0414$

[32,36]. In Table 1, $w_i$ is expressed as one hundred million m³, and $B_i\left(w_i\right)$ calculated by the water benefit function, is expressed as one hundred million yuan.

(2)

Let $C_i\left(w_i\right)$ be the total cost of water supply for each province $(i=1,2,3)$. The total cost of water supply for each province is related to the amount of water ($w_i$) allocated to the province. The water supply cost increases with the total water supply. Water supply costs in each province were calculated using regression analysis with the data from the Statistical Yearbook [33,34,35].

Table 2. The total cost of water supply of each province.

Province	Total Cost of Water Supply
Henan	$C_1(w_1)=0.0042w_1^2+0.6442w_1-0.1367$
Anhui	$C_2(w_2)=0.0034w_2^2+0.5166w_2+1.3269$
Jiangsu	$C_3(w_3)=0.003w_3^2+0.5815w_3+0.9654$

shows the water supply cost of each province [36]. In Table 2, $w_i$ is expressed as one hundred million m³, and $C_i\left(w_i\right)$ calculated by the total cost of the water supply, is expressed as one hundred million yuan.

The benefit function of each province is expressed as:

$$u_i=B_i(w_i)-C_i(w_i),$$

(24)

The benefit function of the watershed management is defined as:

$$f(s)=-{(s-s^{\ast })}^2,$$

(25)

3.3. Hypothesis of the Game Model

(1)

The total amount of water allocated in this study is 400.5 hundred million m³.

(2)

In the game model, the water demand of the three provinces does not need to consider the eco-environmental water requirements, because the watershed management agency is responsible for the eco-environmental of the whole basin.

3.4. Establishment of the Game Model

The two-level asymmetric Nash–Harsanyi Leader–Follower game model is used to resolve water resources conflicts in Huaihe River basin. In this study, the watershed management agency serves as the leader; Henan, Anhui and Jiangsu provinces serve as followers. Establishment of the game model includes the establishment of the leaders and followers.

3.4.1. Establishment of the Leader Model

The model of the watershed management agency is as follows:

$$V_1=\max -{(s-s^{\ast })}^2,$$

(26)

where V₁ is the objective function of the watershed management agency.

The public water obtained by the above leader model is 100.1 hundred million m³.

3.4.2. Establishment of the Follower Model

After the watershed management agency determines that the public water is 100.1 hundred million m³, the calculation of the disagreement point (d_i) and bargaining weight (α_i) are described separately below.

According to the determination of the disagreement points in Section 2.2.1, the disagreement points ($d_1,d_2,d_3$) in this study are used as the benefits of the minimum water allocation ($I_1,I_2,I_3$) in each of the three provinces of Huaihe River basin. According to the current situation of the three provinces in Huaihe River basin, the minimum survival water demand should contain the basic requirements for domestic and production water. The domestic water proportion accounts for 100% of the domestic water demand. The basic requirements of production water mainly include industrial water and agricultural water. The proportion industrial water demand is calculated as the ratio of disposable income of urban households to real Gross Domestic Product (GDP) per capital, and agricultural water demand is calculated as the ratio of per capital consumption of food to per capital food production. The minimum survival water demand in Henan province is taken as the sum of 100% of domestic water demand, 27% of industrial water demand and 22% of agriculture water demand. The minimum survival water demand in Anhui province is taken as the sum of 100% of domestic water demand, 26% of industrial water demand and 36% of agriculture water demand. The minimum survival water demand in Jiangsu province is taken as the sum of 100% of domestic water demand, 29% of industrial water demand and 39% of agriculture water demand. The minimum survival water demands λ_i for each province are shown in

Table 3. The minimum survival water demand λ_i (hundred million m³) of each province.

Province	Domestic Water Demand (Hundred Million m3)	Industrial Water Demand (Hundred Million m3)	Agricultural Water Demand (Hundred Million m3)	Minimum Survival Water Demand λi (Hundred Million m3)
Henan	10.8	17.2	55.6	27.7
Anhui	10.4	26.8	55.2	37.0
Jiangsu	07.8	24.8	90.8	50.4

.

The minimum water allocation considering the minimum survival water demand is solved as follows:

$$I_i=\max ({\lambda }_i,400.5-{\displaystyle \sum _{k\ne i}{r}_i-100.1}),$$

(27)

According to the above formula, the minimum water allocations in Henan Province, Anhui Province and Jiangsu Province are 27.9 hundred million m³, 37.0 hundred million m³ and 50.4 hundred million m³, respectively. According to Equation (13), the disagreement points of Henan Province, Anhui Province and Jiangsu Province are 273.443 hundred million yuan, 289.476 hundred million yuan and 389.663 hundred million yuan, respectively.

The bargaining weights of the three provinces are determined by the principles of equity and efficiency. Disagreement points can guarantee the basic water requirements of the three provinces, taking into account the domestic water requirements. So, the equity principle is mainly reflected in the equity of production water.

The bargaining weights under the principle of equity are determined according to Equation (17) and are shown in

Table 4. The bargaining weights under the equity principle.

Province	Water Demand (Hundred Million m3)	Minimum Water Demand (Hundred Million m3)	Bargaining Weight
Henan	126.4	27.9	0.347
Anhui	135.2	37.0	0.346
Jiangsu	137.3	50.4	0.307

.

Taking into account the differences in water use levels among the three provinces, the efficiency principle is mainly reflected in the encouragement of efficient use of water resources. The bargaining weight of each province under the principle of efficiency is determined using the integrated water utility index method. Industry and agriculture are selected as water users. The bargaining weight of each province is calculated according to Equations (18)–(20). The bargaining weights under the efficiency principle are shown in

Table 5. The bargaining weights under the efficiency principle.

Province	Industrial Water Demand (Hundred Million m3)	Agricultural Water Demand (Hundred Million m3)	Industrial Water Utility (m3/million yuan)	Agricultural Water Utility (m3/million yuan)	Integrated Water Utility (m3/million yuan)	Bargaining Weight
Henan	17.2	55.6	153.3	825.7	666.8	0.423
Anhui	26.8	55.2	564.6	1263.6	1035.2	0.288
Jiangsu	24.8	90.8	179.8	1268.2	1034.7	0.289

.

The symmetric Nash–Harsanyi Leader–Follower game model, which does not consider the bargaining weights of the followers, ignores the importance of each follower. This model considers that the importance of each follower is equal and fails to consider the actual situation of water resources allocation. Therefore, on the basis of relative equity, the amount of water allocated to the users with high levels of water use should be appropriately increased, and the bargaining weight can be calculated using comprehensive consideration of equity and efficiency principles. According to the Analytic Hierarchy Process (AHP) calculation, the weight of the equity principle is 0.667, and the weight of the efficiency principle is 0.333. According to Equation (21), the bargaining weights of Henan Province, Anhui Province and Jiangsu Province are 0.373, 0.327 and 0.300, respectively.

According to the above calculation of the disagreement points and bargaining weights of the three provinces, the model of the three provinces is as follows:

$$\begin{array}{l}\max {(u_1-d_1)}^{{\alpha }_1}{(u_2-d_2)}^{{\alpha }_2}{(u_3-d_3)}^{{\alpha }_3}=\max ((-0.026w_1^2+11.192w_1+2.5311)-\\ (0.0042w_1^2+0.6442w_1-0.1367)-273.443{)}^{0.373}((-0.022w_2^2+9.153w_2+1.5002)\\ -(0.0034w_2^2+0.5166w_2+1.3269)-289.476{)}^{0.323}((-0.021w_3^2+9.521w_3+1.0414)\\ -(0.003w_3+0.5815w_3+0.9654)-389.663{)}^{0.300}\end{array},$$

(28)

Subject to:

Optimal solution existence constraints:

$$u_1\ge 273.443,$$

(29)

$$u_2\ge 289.476,$$

(30)

$$u_3\ge 389.663,$$

(31)

Water balance constraints:

$$w_1+w_2+w_3+s=400.5,$$

(32)

The water allocation constraint in Henan Province:

$$27.9\le w_1\le 126.4,$$

(33)

The water allocation constraint in Anhui Province:

$$37.0\le w_2\le 135.2,$$

(34)

The water allocation constraint in Jiangsu Province:

$$50.4\le w_3\le 137.3,$$

(35)

4. Results and Discussion

In this study, the asymmetric Nash–Harsanyi Leader–Follower game model was used to allocate 400.5 hundred million m³ of water in Huaihe River basin.

The amount of public water resources allocated by the watershed resources management was 100.1 hundred million m³, as determined by the asymmetric Nash–Harsanyi Leader–Follower game model. We used the successive linear programming method in LINGO software to solve the water allocation model for followers. The amount of water allocated to Henan Province, Anhui Province and Jiangsu Province was 95.5 hundred million m³, 97.5 hundred million m³ and 107.4 hundred million m³, respectively. In addition, the satisfaction rates in the corresponding provinces were 68.6%, 61.6% and 65.6%. The traditional solution of Huaihe River basin water allocation has been a multi-factor comprehensive analysis model. This model chooses relevant indictors that focus on the equality of water rights, consistency of water use benefits and food security to give the corresponding index weights and priorities. The water allocation weight of each province in Huaihe River basin is obtained by calculating the weight of various types of water indicators [37]. According to the traditional Huaihe River basin water plan [38], the eco-environmental water consumption involves water for production uses, and the satisfaction rates in the Henan Province, Anhui Province and Jiangsu Province were 58.9%, 95.8% and 46.7%. Compared to the asymmetric Nash–Harsanyi Leader–Follower game model, the traditional water plan could not meet the eco-environmental water requirements and the satisfaction rates in water demand of the three provinces were uneven. Hence, the water allocation plan using the asymmetric Nash–Harsanyi Leader–Follower game model is more reasonable than the traditional water allocation plan.

Previous studies [22,23] ignored the solution of disagreement points and the important differences between users when solving the Nash bargaining problems, which led to unreasonable results for water resources allocation. The impact of disagreement points and the influence of different degrees of importance of followers are explained in Section 4.1 and Section 4.2.

4.1. The Impact of the Minimum Survival Water Demand on Disagreement Points

The disagreement points ($d_1,d_2,d_3$) in this study are taken as the benefits of the minimum water allocation ($I_1,I_2,I_3$) in the three provinces of the Huaihe River basin. If the minimum survival water demand is not considered, the minimum water allocations in Henan Province, Anhui Province and Jiangsu Province are 27.9 hundred million m³, 36.7 hundred million m³ and 38.8 hundred million m³, respectively. In addition, the corresponding disagreement points of Henan Province, Anhui Province and Jiangsu Province are 273.443 hundred million yuan, 287.373 hundred million yuan and 293.675 hundred million yuan, respectively. However, the minimum water allocation in Henan province is higher than its minimum survival water demand, and the minimum water allocations in other two provinces are lower than their minimum survival water demands. Obviously, Anhui Province and Jiangsu Province would not meet the minimum survival water demands, so the two provinces would not accept the water allocation results. The minimum water allocation considering minimum survival water demand effectively avoids unreasonable water allocation and reflects the individual rationalities of followers. The minimum water allocations in Henan Province, Anhui Province and Jiangsu Province are 27.9 hundred million m³, 37.0 hundred million m³ and 50.4 hundred million m³. In addition, the corresponding disagreement points are 273.443 hundred million yuan, 289.476 hundred million yuan and 389.663 hundred million yuan. The minimum water allocation is more reasonable when minimum survival water demand is considered, and the disagreement point are in a reasonable range.

4.2. The Impact of Bargaining Weights on Water Resources Allocation

The symmetric Nash–Harsanyi Leader–Follower game model which does not consider the bargaining weights of the followers ignores the importance of each follower. The bargaining weights of the three provinces are determined using equity and efficiency principles, which reflect the economic development levels between the three followers.

Table 6. The water resources allocation in the three provinces of the Huaihe River basin.

Schemes	Henan Province			Anhui Province			Jiangsu Province			Total Benefit
	w1 (Hundred Million m3)	Benefit (Hundred Million yuan)	Satisfaction Rate (%)	w2 (Hundred Million m3)	Benefit (Hundred Million yuan)	Satisfaction Rate (%)	w3 (Hundred Million m3)	Benefit (Hundred Million yuan)	Satisfaction Rate (%)
Without considering the bargaining weight	90.6	710.526	63.7	98.3	603.498	62.4	111.5	698.564	70.3	2012.588
Under the principle of equity	92.4	719.298	65.5	99.7	608.879	63.9	108.3	686.700	66.6	2014.877
Under the principle of efficiency	101.3	761.280	74.5	92.9	583.256	56.9	106.2	678.775	64.2	2023.311
Using the principles of equity and efficiency	95.5	734.510	68.6	97.5	600.847	61.6	107.4	683.292	6.56	2018.649

shows the water resources allocation results for the three provinces, which mainly includes the water allocated to the three provinces, the benefits for each province, satisfaction rates regarding water demand for each province and the total benefit of the four schemes. The four schemes are as follows: no consideration of bargaining weight, consideration of the bargaining weight under the equity principle, consideration of the bargaining weight under the efficiency principle, consideration of the bargaining weight using the equity and efficiency principles. In addition, the model proposed by Safari et al. [22] is used as a comparison to the proposed Nash–Harsanyi Leader–Follower game model. The scheme that does not consider the bargaining weights uses the model proposed by Safari et al. [22].

Table 6 shows:

(1)

The importance levels of the three provinces are equal when the bargaining weights in water resources allocation are not considered, and the amounts of water allocated to Henan Province, Anhui Province and Jiangsu Province are 90.6 hundred million m³, 98.3 hundred million m³ and 111.5 hundred million m³, respectively. The satisfaction rates of Henan Province, Anhui Province and Jiangsu Province are 63.7%, 62.4% and 70.3%, respectively. In addition, the corresponding benefits are 710.526 hundred million yuan, 603.498 hundred million yuan and 698.564 hundred million yuan. The total benefit of the three provinces is 2012.588 hundred million yuan.

(2)

Although disagreement points can guarantee the basic water demands of the three provinces, they may fail to ensure the fair use of water resources. The asymmetric Nash–Harsanyi Leader–Follower game model using the equity principle can ensure the fair use of water resources. The amounts of water allocated to Henan Province, Anhui Province and Jiangsu Province are 92.4 hundred million m³, 99.7 hundred million m³ and 108.3 hundred million m³, respectively. The satisfaction rates of Henan Province, Anhui Province and Jiangsu Province are 66.5%, 63.9% and 66.6%, respectively. In addition, the corresponding benefits are 719.298 hundred million yuan, 608.879 hundred million yuan and 686.700 hundred million yuan. The total benefit of the three provinces is 201.4877 billion yuan. Compared with the scheme that does not consider the bargaining weight, the total benefit is increased, and the satisfaction rates in water demand for each province are more balanced, which reflects a fair use of water resources.

(3)

The asymmetric Nash–Harsanyi Leader–Follower game model using the equity principle provides fair water use for followers but ignores the differences in the water use levels of the followers. However, the asymmetric Nash–Harsanyi Leader–Follower game model using both equity and efficiency principles can appropriately increase the amount of water allocated by the users with high levels of relative equity, which is more in line with the actual water resources allocation. The amounts of water allocated to Henan Province, Anhui Province and Jiangsu Province are 95.5 hundred million m³, 97.5 hundred million m³ and 107.4 hundred million m³, respectively. The satisfaction rates of Henan Province, Anhui Province and Jiangsu Province are 68.6%, 61.6% and 65.6%, respectively. In addition, the corresponding benefits are 734.510 hundred million yuan, 600.847 hundred million yuan and 683.292 hundred million yuan. The total benefit of the three provinces is 2018.649 hundred million yuan. Compared with the symmetric Nash–Harsanyi Leader–Follower game model, which does not take into account the bargaining weight of each province, the total benefit is increased and the satisfaction rates in water demand for each province is more balanced, which reflects a fair use of water resources. Compared with the symmetric Nash–Harsanyi Leader–Follower game model, which considers the equity principle, the total benefit is increased, but the differences among the satisfaction rates in water demand of each province are increased as well. Compared with the symmetric Nash–Harsanyi Leader–Follower game model, which considers the efficiency principle, the total benefit is reduced, but the differences among the satisfaction rates in water demand for each province are reduced as well. Therefore, the asymmetric Nash–Harsanyi Leader–Follower game model using the equity and efficiency principles not only considers the fairness of water use, but also takes into account the differences in water use levels, which is consistent with the actual water resources allocation.

5. Conclusions

Based on the principles of equity, efficiency and sustainability, this study proposes a solution of disagreement points based on the bankruptcy theory and proposes a method to calculate the bargaining weights in a transboundary river basin with the consideration of equity and efficiency principles. The asymmetric Nash–Harsanyi Leader–Follower game model is applied to water resources allocation with the watershed management agency as the leader, and Henan, Anhui and Jiangsu Provinces as followers. This model is a combination of the asymmetric Nash–Harsanyi bargaining theory and leader–follower concept. The process consisted of two levels. First, leaders make decisions with appropriate consideration of the followers’ interests. The followers make their own preferred decisions through an asymmetric Nash–Harsanyi game after the leaders have made their decisions. In the case study model of water resources allocation involving conflict among three provinces, the status of the watershed management agency is higher than the three provinces, and benefits of the three provinces depend on the strategy of the watershed management agency. The main conclusions are as follows:

(1)

When the minimum survival water demand is considered, the disagreement points are more reasonable than when the minimum survival water demand is not considered. This method could avoid the unreasonable phenomenon in which there are disagreement points below the minimum water supply or zero.

(2)

In the process of water resources allocation, calculation of the bargaining weights using the principles of equity and efficiency can better reflect economic development levels among the followers, which could be more in line with actual water resources allocation.

(3)

The proposed disagreement points can guarantee basic water demands are met and bargaining weights can better balance the levels of economic development among the followers.