Effect of Variations in Long-Duration Rainfall Intensity on Unsaturated Slope Stability
Abstract
:1. Introduction
2. Study Area
3. Materials and Methods
3.1. Mann–Kendall Test
3.2. Theil–Sen Estimator
3.3. Rainfall Data
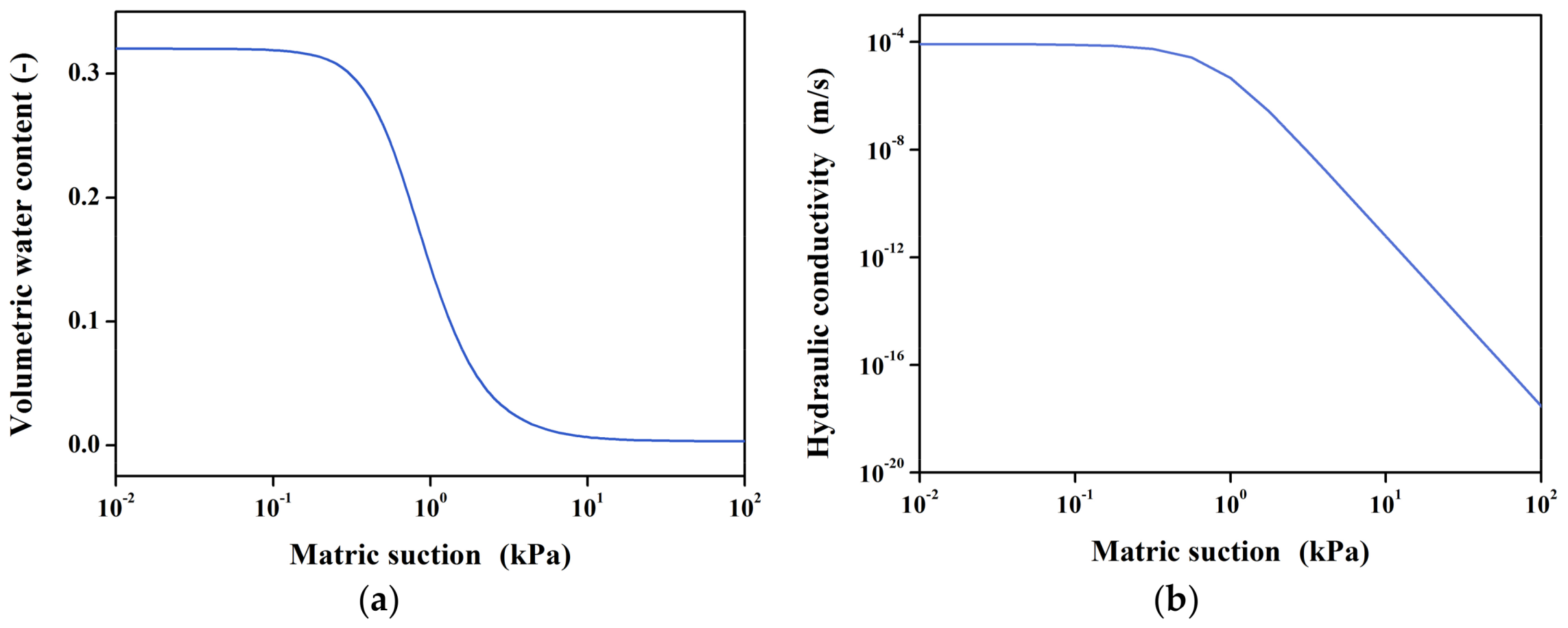
3.4. Seepage Analysis and Qualitative Analysis of Slope Stability
4. Results and Discussion
4.1. Trends in Rainfall Intensity
4.2. Seepage Analysis
4.3. Qualitative Analysis of Slope Stability
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Jemec, M.; Komac, M. Rainfall patterns for shallow landsliding in perialpine Slovenia. Nat. Hazards 2013, 67, 1011–1023. [Google Scholar] [CrossRef]
- Zhang, J.; Li, J.; Lin, H. Models and influencing factors of the delay phenomenon for rainfall on slope stability. Eur. J. Environ. Civ. Eng. 2018, 22, 122–136. [Google Scholar] [CrossRef]
- Sidle, R.C.; Bogaard, T.A. Dynamic earth system and ecological controls of rainfall-initiated landslides. Earth Sci. Rev. 2016, 159, 275–291. [Google Scholar] [CrossRef]
- Ahmadi-adli, M.; Huvaj, N.; Toker, N.K. Rainfall-triggered landslides in an unsaturated soil: A laboratory flume study. Environ. Earth Sci. 2017, 76, 735. [Google Scholar] [CrossRef]
- Kim, J.; Kim, Y.; Jeong, S.; Hong, M. Rainfall-induced landslides by deficit field matric suction in unsaturated soil slopes. Environ. Earth Sci. 2017, 76, 808. [Google Scholar] [CrossRef]
- Strauch, A.M.; MacKenzie, R.A.; Giardina, C.P.; Bruland, G.L. Climate driven changes to rainfall and streamflow patterns in a model tropical island hydrological system. J. Hydrol. 2015, 523, 160–169. [Google Scholar] [CrossRef]
- Loo, Y.Y.; Billa, L.; Singh, A. Effect of climate change on seasonal monsoon in Asia and its impact on the variability of monsoon rainfall in southeast Asia. Geosci. Front. 2015, 6, 817–823. [Google Scholar] [CrossRef]
- Kristo, C.; Rahardjo, H.; Satyanaga, A. Effect of variations in rainfall intensity on slope stability in Singapore. Int. Soil Water Conserv. Res. 2017, 5, 258–264. [Google Scholar] [CrossRef]
- Yeh, H.-F.; Wang, J.; Shen, K.-L.; Lee, C.-H. Rainfall characteristics for anisotropic conductivity of unsaturated soil slopes. Environ. Earth Sci. 2015, 73, 8669–8681. [Google Scholar] [CrossRef]
- Bogaard, T.A.; Greco, R. Landslide hydrology: From hydrology to pore pressure. Wiley Interdiscip. Rev. 2016, 3, 439–459. [Google Scholar] [CrossRef]
- Cho, S.E. Prediction of shallow landslide by surficial stability analysis considering rainfall infiltration. Eng. Geol. 2017, 231, 126–138. [Google Scholar] [CrossRef]
- Wu, Y.; Miao, F.; Li, L.; Xie, Y.; Chang, B. Time-varying reliability analysis of Huangtupo Riverside No. 2 landslide in the Three Gorges Reservoir based on water-soil coupling. Eng. Geol. 2017, 226, 267–276. [Google Scholar] [CrossRef]
- Rahimi, A.; Rahardjo, H.; Leong, E.-C. Effect of antecedent rainfall patterns on rainfall-induced slope failure. J. Geotech. Geoenviron. Eng. 2010, 137, 483–491. [Google Scholar] [CrossRef]
- Chang, J.-M.; Chen, H.; Jou, B.J.-D.; Tsou, N.-C.; Lin, G.-W. Characteristics of rainfall intensity, duration, and kinetic energy for landslide triggering in Taiwan. Eng. Geol. 2017, 231, 81–87. [Google Scholar] [CrossRef]
- Collins, B.D.; Znidarcic, D. Stability analyses of rainfall induced landslides. J. Geotech. Geoenviron. Eng. 2004, 130, 362–372. [Google Scholar] [CrossRef]
- Conte, E.; Donato, A.; Troncone, A. A simplified method for predicting rainfall-induced mobility of active landslides. Landslides 2017, 14, 35–45. [Google Scholar] [CrossRef]
- Sun, G.; Yang, Y.; Cheng, S.; Zheng, H. Phreatic line calculation and stability analysis of slopes under the combined effect of reservoir water level fluctuations and rainfall. Can. Geotech. J. 2017, 54, 631–645. [Google Scholar] [CrossRef]
- Conte, E.; Troncone, A. A performance-based method for the design of drainage trenches used to stabilize slopes. Eng. Geol. 2018, 239, 158–166. [Google Scholar] [CrossRef]
- Segoni, S.; Rosi, A.; Rossi, G.; Catani, F.; Casagli, N. Analysing the relationship between rainfalls and landslides to define a mosaic of triggering thresholds for regional-scale warning systems. Nat. Hazards Earth Syst. Sci. 2014, 14, 2637. [Google Scholar] [CrossRef]
- Rosi, A.; Lagomarsino, D.; Rossi, G.; Segoni, S.; Battistini, A.; Casagli, N. Updating EWS rainfall thresholds for the triggering of landslides. Nat. Hazards 2015, 78, 297–308. [Google Scholar] [CrossRef]
- Ciabatta, L.; Camici, S.; Brocca, L.; Ponziani, F.; Stelluti, M.; Berni, N.; Moramarco, T. Assessing the impact of climate-change scenarios on landslide occurrence in Umbria region, Italy. J. Hydrol. 2016, 541, 285–295. [Google Scholar] [CrossRef]
- Piciullo, L.; Gariano, S.L.; Melillo, M.; Brunetti, M.T.; Peruccacci, S.; Guzzetti, F.; Calvello, M. Definition and performance of a threshold-based regional early warning model for rainfall-induced landslides. Landslides 2017, 14, 995–1008. [Google Scholar] [CrossRef]
- Lin, M.L.; Lin, S.C.; Lin, Y.C. Review of landslide occurrence and climate change in Taiwan. In Slope Safety Preparedness for Impact of Climate Change; CRC Press: Boca Raton, FL, USA, 2016; pp. 409–436. [Google Scholar]
- Mann, H.B. Nonparametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Charles Griffin: London, UK, 1975. [Google Scholar]
- Longobardi, A.; Villani, P. Trend analysis of annual and seasonal rainfall time series in the Mediterranean area. Int. J. Climatol. 2010, 30, 1538–1546. [Google Scholar] [CrossRef]
- Dindang, A.; Taat, A.; Phuah, E.; Alwi, A.; Mandai, A.; Adam, S.; Othman, F.; Bima, D.A.; Lah, D. Statistical and trend analysis of rainfall data in Kuching, Sarawak from 1968–2010. J. Med. Microbiol. 2013, 6, 17. [Google Scholar]
- Yeh, C.-F.; Wang, J.; Yeh, H.-F.; Lee, C.-H. Spatial and temporal streamflow trends in northern Taiwan. Water 2015, 7, 634–651. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Lee, J.Z. The Study on the Slope Safety of Tseng-Wen Reservoir. Master Thesis, National Cheng Kung University, Tainan, Taiwan, 2005. (In Chinese). [Google Scholar]
- Geo-Slope International Ltd. Seep/W for Finite Element Seepage Analysis; Geo-Slope International Ltd.: Calgary, AB, Canada, 2004. [Google Scholar]
- Richards, L.A. Capillary conduction of liquids through porous mediums. Physics 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Carsel, R.F.; Parrish, R.S. Developing joint probability distributions of soil water retention characteristics. Water Resour. Res. 1988, 24, 755–769. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Central Geological Survey. The Investigation and Assessment Program of the Effect of Catchment Hydrogeology on Slope Stability; Central Geological Survey: Taipei, Taiwan, 2007. (In Chinese)
- Geo-Slope International Ltd. Slope/W for Slope Stability Analysis; Geo-Slope International Ltd.: Calgary, AB, Canada, 2004. [Google Scholar]
- Fredlund, D.; Morgenstern, N.R.; Widger, R. The shear strength of unsaturated soils. Can. Geotech. J. 1978, 15, 313–321. [Google Scholar] [CrossRef]
- Morgenstern, N.; Price, V.E. The analysis of the stability of general slip surfaces. Geotechnique 1965, 15, 79–93. [Google Scholar] [CrossRef]
- Water Resources Agency. Hydrological Year Book of Taiwan Republic of China; Ministry of Economic Affairs: Taipei, Taiwan, 1990. (In Chinese)
- Jung, Y.D.; Kuo, C.C.; Chen, C.S. The temporal variation of regional rainfall characteristics in Taiwan. J. Taiwan Agric. Eng. 2009, 55, 1–18. (In Chinese) [Google Scholar]
- National Science and Technology Center for Disaster Reduction. Taiwan Extreme Rainfall Events: Summary of Important Events from 1992 to 2013; National Science and Technology Center for Disaster Reduction: New Taipei, Taiwan, 2015. (In Chinese)









| Material | a (kPa) | n | m | ks (m/s) | |
|---|---|---|---|---|---|
| Sand | 0.32 | 0.7 | 2.68 | 0.63 | |
| Sandstone | 0.2 | 100 | 1.8 | 0.44 |
| Material | (kN/m3) | (kN/m3) | c’ (kN/m2) | (°) | (°) |
|---|---|---|---|---|---|
| Sand | 19.2 | 21.3 | 3 | 30 | 15 |
| Sandstone | 22.7 | 22.7 | 5100 | 63 | 30 |
| Rainfall Duration (day) | Da-Dong-Shan | Ma-To-Shan | San-Jiao-Nan-Shan | |||
|---|---|---|---|---|---|---|
| Mann–Kendall Test Result | Slope Estimator | Mann–Kendall Test Result | Slope Estimator | Mann–Kendall Test Result | Slope Estimator | |
| 1 | 0.79 | 0.13 | 0.48 | 0.09 | 1.10 | 0.08 |
| 2 | 0.63 | 0.07 | 0.42 | 0.04 | 1.31 | 0.09 |
| 3 | 0.67 | 0.05 | 0.1 | 0.00 | 1.29 | 0.08 |
| 5 | 0.25 | 0.02 | −0.17 | −0.01 | 0.71 | 0.03 |
| 7 | 0.25 | 0.01 | −1.23 | −0.05 | 0.4 | 0.01 |
| Average | - | 0.06 | - | 0.02 | - | 0.06 |
| Rainfall Station | Rainfall Intensity in 2016 (mm/h) | Rainfall Intensity in 2050 (mm/h) | Rainfall Intensity in 2100 (mm/h) | ||
|---|---|---|---|---|---|
| β | b | ||||
| Da-Dong-Shan | 0.13 | −237.5 | 14.5 | 18.8 | 25 |
| Ma-To-Shan | 0.09 | −176 | 13 | 16.2 | 20.8 |
| San-Jiao-Nan-Shan | 0.08 | −141.4 | 11.4 | 13.9 | 17.7 |
| Rainfall Station | FS Decreasing Phenomenon | 2016 | 2050 | 2100 |
|---|---|---|---|---|
| Da-Dong-Shan | FS decreasing point of time (h) | 18 | 13 | 13 |
| FS decreasing rate (%) | 37.7 | 41.7 | 41 | |
| Ma-To-Shan | FS decreasing point of time (h) | 20 | 16 | 14 |
| FS decreasing rate (%) | 35.4 | 37.8 | 42.1 | |
| San-Jiao-Nan-Shan | FS decreasing point of time (h) | 21 | 19 | 14 |
| FS decreasing rate (%) | 23.3 | 35.9 | 41 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yeh, H.-F.; Tsai, Y.-J. Effect of Variations in Long-Duration Rainfall Intensity on Unsaturated Slope Stability. Water 2018, 10, 479. https://doi.org/10.3390/w10040479
Yeh H-F, Tsai Y-J. Effect of Variations in Long-Duration Rainfall Intensity on Unsaturated Slope Stability. Water. 2018; 10(4):479. https://doi.org/10.3390/w10040479
Chicago/Turabian StyleYeh, Hsin-Fu, and Yi-Jin Tsai. 2018. "Effect of Variations in Long-Duration Rainfall Intensity on Unsaturated Slope Stability" Water 10, no. 4: 479. https://doi.org/10.3390/w10040479
APA StyleYeh, H.-F., & Tsai, Y.-J. (2018). Effect of Variations in Long-Duration Rainfall Intensity on Unsaturated Slope Stability. Water, 10(4), 479. https://doi.org/10.3390/w10040479






