Flood Risk Assessment of Global Watersheds Based on Multiple Machine Learning Models
Abstract
1. Introduction
2. Data and Methods
2.1. Data
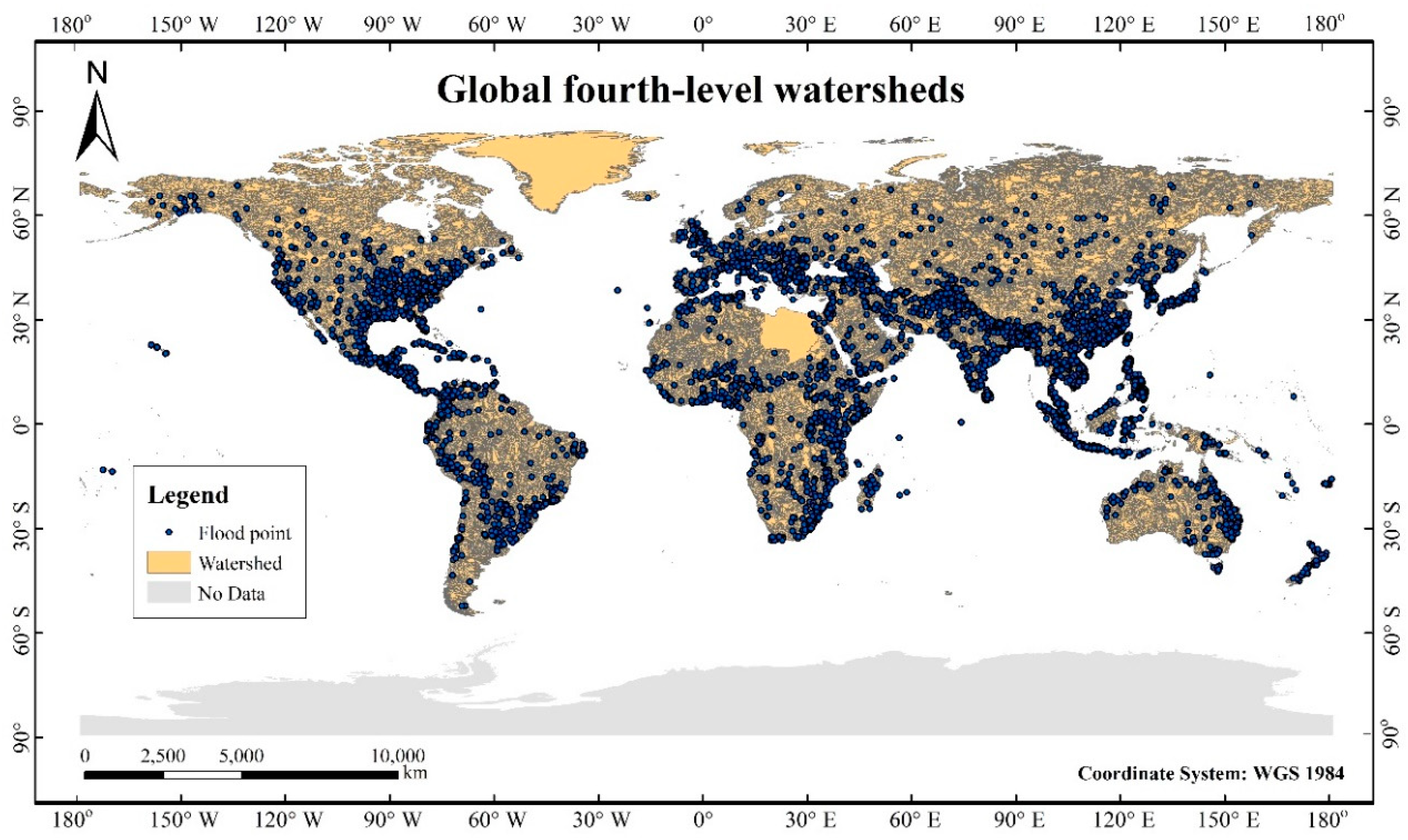
2.1.1. Global Fourth-Level Watersheds
2.1.2. Flood Disaster Inventory
2.1.3. Flood Conditioning Factors
2.2. Methods
2.2.1. Logistic Regression
2.2.2. Naive Bayes
2.2.3. AdaBoost
2.2.4. Random Forest
2.2.5. Evaluation Methods
2.2.6. Sensitivity Analysis of Conditioning Factors
3. Results
3.1. Model Analysis
3.2. Global Flood Susceptibility Map
3.3. Assessment of Sensitivity of Conditioning Factors
4. Discussions
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- UN International Strategy for Disaster Reduction (UNISDR). Reducing Disaster Risks through Science: Issues and Actions; UN International Strategy for Disaster Reduction: Geneva, Switzerland, 2009. [Google Scholar]
- Centre for Research on the Epidemiology of Disasters (CRED). The Human Cost of Weather-Related Disasters 1995–2015 Report; Centre for Research on the Epidemiology of Disasters: Brussels, Belgium, 2015. [Google Scholar]
- Hirabayashi, Y.; Mahendran, R.; Koirala, S.; Konoshima, L.; Yamazaki, D.; Watanabe, S.; Kim, H.; Kanae, S. Global flood risk under climate change. Nat. Clim. Chang. 2013, 3, 816. [Google Scholar] [CrossRef]
- Dottori, F.; Salamon, P.; Bianchi, A.; Alfieri, L.; Hirpa, F.A. Development and evaluation of a framework for global flood hazard mapping. Adv. Water Resour. 2016, 94, 87–102. [Google Scholar] [CrossRef]
- Re, M. NatCat SERVICE Database; Munich RE: Munich, Germany, 2014. [Google Scholar]
- Youssef, A.M.; Pradhan, B.; Hassan, A.M. Flash flood risk estimation along the St. Katherine road, southern Sinai, Egypt using GIS based morphometry and satellite imagery. Environ. Earth Sci. 2011, 62, 611–623. [Google Scholar] [CrossRef]
- Ahmadisharaf, E.; Tajrishy, M.; Alamdari, N. Integrating flood hazard into site selection of detention basins using spatial multi-criteria decision-making. J. Environ. Plann. Manag. 2016, 59, 1397–1417. [Google Scholar] [CrossRef]
- Schumann, G.J.P.; Bates, P.D.; Apel, H.; Aronica, G.T. Global Flood Hazard: Applications in Modeling, Mapping, and Forecasting; American Geophysical Union: Washington, DC, USA, 2018. [Google Scholar]
- Petersen, T.C.; Taylor, M.A.; Demeritte, R.; Duncombe, D.L.; Burton, S.; Thompson, F.; Porter, A.; Mercedes, M.; Villegas, E.; Martis, A.; et al. Recent changes in climate extremes in the Caribbean region. J. Geophys. Res. 2002, 107, 4601. [Google Scholar] [CrossRef]
- Griffiths, G.M.; Salinger, M.J.; Leleu, I. Trends in extreme daily rainfall across the South Pacific and relationship to the South Pacific Convergence Zone. Int. J. Climatol. 2003, 23, 847–869. [Google Scholar] [CrossRef]
- Kunkel, K.E.; Easterling, D.R.; Redmond, K.; Hubbard, K. Temporal variations of extreme precipitation events in the United States: 1895–2000. Geophys. Res. Lett. 2003, 30, 1900. [Google Scholar] [CrossRef]
- Haylock, M.R.; Goodess, C.M. Interannual variability of extreme European winter rainfall and links with mean large-scale circulation. Int. J. Climatol. 2004, 24, 759–776. [Google Scholar] [CrossRef]
- Barbosa, A.E.; Fernandes, J.N.; David, L.M. Key issues for sustainable urban stormwater management. Water Res. 2012, 46, 6787–6798. [Google Scholar] [CrossRef]
- Xu, Z.; Zhao, G. Impact of urbanization on rainfall-runoff processes: Case study in the Liangshui River Basin in Beijing, China. Proc. Int. Assoc. Hydrol. Sci. 2016, 373, 7–12. [Google Scholar] [CrossRef]
- European Commission. Directive 2007/60/EC of the European Parliament and of the Council of 23 October 2007 on the assessment and management of flood risks. Off. J. Eur. Union L 2007, 288, 27–34. [Google Scholar]
- Chen, Y.R.; Yeh, C.H.; Yu, B. Integrated application of the analytic hierarchy process and the geographic information system for flood risk assessment and flood plain management in Taiwan. Nat. Hazards 2011, 59, 1261–1276. [Google Scholar] [CrossRef]
- Tang, Z.; Zhang, H.; Yi, S.; Xiao, Y. Assessment of flood susceptible areas using spatially explicit, probabilistic multi-criteria decision analysis. J. Hydrol. 2018, 558, 144–158. [Google Scholar] [CrossRef]
- Vojtek, M.; Vojteková, J. Flood Susceptibility Mapping on a National Scale in Slovakia Using the Analytical Hierarchy Process. Water 2019, 11, 364. [Google Scholar] [CrossRef]
- Choubin, B.; Moradi, E.; Golshan, M.; Adamowski, J.; Hosseini, F.S.; Mosavi, A. An ensemble prediction of flood susceptibility using multivariate discriminant analysis, classification and regression trees, and support vector machines. Sci. Total Environ. 2019, 651, 2087–2096. [Google Scholar] [CrossRef]
- Graham, D.N.; Butts, M.B. Flexible, integrated watershed modelling with MIKE SHE. In Watershed Models; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Yamazaki, D.; Kanae, S.; Kim, H.; Oki, T. A physically based description of floodplain inundation dynamics in a global river routing model. Water Resour. Res. 2011, 47, W04501. [Google Scholar] [CrossRef]
- Sampson, C.C.; Smith, A.M.; Bates, P.D.; Neal, J.C.; Alfieri, L.; Freer, J.E. A high-resolution global flood hazard model. Water Resour. Res. 2015, 51, 7358–7381. [Google Scholar] [CrossRef]
- Hoch, J.M.; Trigg, M.A. Advancing global flood hazard simulations by improving comparability, benchmarking, and integration of global flood models. Environ. Res. Lett. 2019, 14, 034001. [Google Scholar] [CrossRef]
- Lee, S.; Kim, J.C.; Jung, H.S.; Lee, M.J.; Lee, S. Spatial prediction of flood susceptibility using random-forest and boosted-tree models in Seoul Metropolitan City, Korea. Geomat. Nat. Hazards Risk 2017, 8, 1185–1203. [Google Scholar] [CrossRef]
- Dano, U.L.; Balogun, A.L.; Matori, A.N.; Yusouf, K.W.; Abubakar, I.R.; Mohamed, M.A.S.; Aina, Y.A.; Pradhan, B. Flood Susceptibility Mapping Using GIS-Based Analytic Network Process: A Case Study of Perlis, Malaysia. Water 2019, 11, 615. [Google Scholar] [CrossRef]
- Lee, S.; Lee, S.; Lee, M.J.; Jung, H.S. Spatial Assessment of Urban Flood Susceptibility Using Data Mining and Geographic Information System (GIS) Tools. Sustainability 2018, 10, 648. [Google Scholar] [CrossRef]
- Tehrany, M.S.; Pradhan, B.; Jebur, M.N. Flood susceptibility mapping using a novel ensemble weights-of-evidence and support vector machine models in GIS. J. Hydrol. 2014, 512, 332–343. [Google Scholar] [CrossRef]
- Zhao, G.; Pang, B.; Xu, Z.X.; Peng, D.Z.; Xu, L.Y. Assessment of urban flood susceptibility using semi-supervised machine learning model. Sci. Total Environ. 2019, 659, 940–949. [Google Scholar] [CrossRef]
- Tehrany, M.S.; Pradhan, B.; Mansor, S.; Ahman, N. Flood susceptibility assessment using GIS-based support vector machine model with different kernel types. Catena 2015, 125, 91–101. [Google Scholar] [CrossRef]
- European Environment Agency (EEA). European Catchments and Rivers Network System (Ecrins); European Environment Agency: Kobenhavn, Denmark, 2012. [Google Scholar]
- World Wildlife Fund. HydroSHEDS (Hydrological Data and Maps Based on SHuttle Elevation Derivatives at Multiple Scales); World Wildlife Fund: Gland, Switzerland, 2006. [Google Scholar]
- Martz, L.W.; Garbrecht, J. The treatment of flat areas and depressions in automated drainage analysis of raster digital elevation models. Hydrol. Process. 1998, 12, 843–855. [Google Scholar] [CrossRef]
- Yan, D.H.; Wang, K.; Qin, T.L.; Weng, B.S.; Wang, H.; Bi, W.X.; Li, X.N. A Data Set of Global River Networks and Corresponding Water Resources Zones Divisions. 2019. Available online: https://doi.org/10.6084/m9.figshare.8044184.v3 (accessed on 10 May 2019).
- Rahmati, O.; Pourghasemi, H.R.; Zeinivand, H. Flood susceptibility mapping using frequency ratio and weights-of-evidence models in the Golastan Province, Iran. Geocarto Int. 2016, 31, 42–70. [Google Scholar] [CrossRef]
- Wan, Z.M.; Hong, Y.; Khan, S.; Gourley, J.; Flamig, Z.; Kirschbaum, D.; Tang, G.Q. A cloud-based global flood disaster community cyber-infrastructure: Development and demonstration. Environ. Model. Softw. 2014, 58, 86–94. [Google Scholar] [CrossRef]
- Macchione, F.; Costabile, P.; Costanzo, C.; Lorenzo, G.D. Extracting quantitative data from non-conventional information for the hydraulic reconstruction of past urban flood events. A case study. J. Hydrol. 2019, 576, 443–465. [Google Scholar] [CrossRef]
- Brakenridge, G.R. Global Active Archive of Large Flood Events. Dartmouth Flood Observatory, University of Colorado. Available online: http://floodobservatory.colorado.edu/Archives/index.html (accessed on 7 May 2019).
- NOAA Earth System Research Laboratory’s Physical Sciences Division. The NCEP/NCAR Reanalysis Project. Available online: https://www.esrl.noaa.gov/psd/data/reanalysis/reanalysis.shtml (accessed on 10 June 2019).
- Zhang, L.J.; Qian, Y.F. Annual distribution features of the yearly precipitation in China and their interannual variations. Acta Metall. Sin. 2003, 17, 146–163. [Google Scholar]
- Bui, D.T.; Pradhan, B.; Nampak, H.; Bui, Q.T.; Tran, Q.A.; Nguyen, Q.P. Hybrid artificial intelligence approach based on neural fuzzy inference model and metaheuristic optimization for flood susceptibility modeling in a high-frequency tropical cyclone area using GIS. J. Hydrol. 2016, 540, 317–330. [Google Scholar]
- Meraj, G.; Romshoo, S.A.; Yousuf, A.R.; Altaf, S.; Altaf, F. Assessing the influence of watershed characteristics on the flood vulnerability of Jhelum basin in Kashmir Himalaya. Nat. Hazards 2015, 77, 153–175. [Google Scholar] [CrossRef]
- Fischer, G.F.; Nachtergaele, S.; Prieler, H.T.; van Velthuizen, L.; Verelst, D. Wiberg. Global Agro-Ecological Zones Assessment for Agriculture (GAEZ 2008); IIASA: Laxenburg, Austria; FAO: Rome, Italy, 2008. [Google Scholar]
- Li, Z.; Zhang, J.T. Calculation of Field Manning’s Roughness Coefficient. Agric. Water Manag. 2001, 49, 153–161. [Google Scholar] [CrossRef]
- Mohamoud, Y.M. Evaluating Manning’s roughness coefficients for tilled soils. J. Hydrol. 1992, 135, 143–156. [Google Scholar] [CrossRef]
- Chen, J.; Ban, Y.; Li, S. China: Open access to Earth land-cover map. Nature 2014, 514, 434. [Google Scholar]
- Zhao, G.; Pang, B.; Xu, Z.X.; Yue, J.J.; Tu, T.B. Mapping flood susceptibility in mountainous areas on a national scale in China. Sci. Total Environ. 2018, 615, 1133–1142. [Google Scholar] [CrossRef]
- The World Bank. Population, Total Database. Available online: https://data.worldbank.org/indicator/SP.POP.TOTL (accessed on 10 June 2019).
- Yan, D.H.; Weng, B.S.; Qin, T.L.; Wang, H.; Li, X.N.; Yang, Y.H.; Wang, K. A Data Set of Distributed Global Population and Water Withdrawal from 1960 to 2017. Available online: https://figshare.com/s/fc2ca2beccf475e963cf (accessed on 10 June 2019).
- The World Bank. GDP (Current US $) Database. Available online: https://data.worldbank.org/indicator/NY.GDP.MKTP.CD (accessed on 10 June 2019).
- Cox, D.R. The regression-analysis of binary sequences. J. R. Stat. Soc. Ser. B Stat. Methodol. 1958, 20, 215–242. [Google Scholar] [CrossRef]
- Pradhan, B. Flood susceptible mapping and risk area delineation using logistic regression, GIS and remote sensing. J. Spat. Hydrol. 2010, 9, 1–18. [Google Scholar]
- George, H.J.; Pat, L. Estimating Continuous Distributions in Bayesian Classifiers. In Proceedings of the Eleventh Conference on Uncertainty in Artificial Intelligence, Montréal, QC, Canada, 18–20 August 1995; pp. 338–345. [Google Scholar]
- Das, I.; Stein, A.; Kerle, N.; Dadhwal, V.K. Landslide susceptibility mapping along road corridors in the Indian Himalayas using Bayesian logistic regression models. Geomorphology 2012, 179, 116–125. [Google Scholar] [CrossRef]
- Yoav, F.; Robert, E.S. Experiments with a new boosting algorithm. In Proceedings of the Thirteen International Conference on Machine Learning, Bari, Italy, 3–6 July 1996; pp. 148–156. [Google Scholar]
- Cao, Y.; Miao, Q.G.; Liu, J.C.; Gao, L. Advance and Prospects of AdaBoost Algorithm. Acta Autom. Sin. 2013, 39, 745–758. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Sadler, J.M.; Goodall, J.L.; Morsy, M.M.; Spencer, K. Modeling urban coastal flood severity from crowd-sourced flood reports using Poisson regression and Random Forest. J. Hydrol. 2018, 559, 43–55. [Google Scholar] [CrossRef]
- Bandos, A.I.; Guo, B.; Gur, D. Jackknife variance of the partial area under the empirical receiver operating characteristic curve. Stat. Methods Med. Res. 2017, 26, 528–541. [Google Scholar] [CrossRef]
- Chang, L.C.; Chang, F.J.; Yang, S.N.; Kao, I.F.; Ku, Y.Y.; Kuo, C.L.; Amin, I. Building an Intelligent Hydroinformatics Integration Platform for Regional Flood Inundation Warning Systems. Water 2019, 11, 9. [Google Scholar] [CrossRef]
- Tien Bui, D.; Khosravi, K.; Li, S.; Shahabi, H.; Panahi, M.; Singh, V.; Chapi, K.; Shirzadi, A.; Panahi, S.; Chen, W.; et al. New hybrids of ANFIS with Several Optimization Algorithms for flood Susceptibility Modeling. Water 2018, 10, 1210. [Google Scholar] [CrossRef]
- Chang, L.C.; Amin, M.; Yang, S.N.; Chang, F.J. Building ANN-Based Regional Multi-Step-Ahead Flood Inundation Forecast Models. Water 2018, 10, 1283. [Google Scholar] [CrossRef]






| Month | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Azimuth angle | 15 | 45 | 75 | 105 | 135 | 165 | 195 | 225 | 255 | 285 | 315 | 345 |
| Index | Logistic Regression (LR) | Naive Bayes (NB) | AdaBoost (AB) | Random Forest (RF) | ||||
|---|---|---|---|---|---|---|---|---|
| Flood | Non-Flood | Flood | Non-Flood | Flood | Non-Flood | Flood | Non-Flood | |
| Precision (P) | 0.959 | 0.868 | 0.972 | 0.728 | 0.929 | 0.867 | 0.979 | 0.927 |
| Recall (R) | 0.939 | 0.912 | 0.838 | 0.947 | 0.941 | 0.844 | 0.966 | 0.954 |
| F-score (F) | 0.948 | 0.890 | 0.900 | 0.823 | 0.935 | 0.855 | 0.972 | 0.940 |
| Time (s) | 0.6 | 1.13 | 0.4 | 1.66 | ||||
| Susceptibility Level | Number of Fourth-Level Watersheds | Percentage of Area (%) | ||||||
|---|---|---|---|---|---|---|---|---|
| LR | NB | AB | RF | LR | NB | AB | RF | |
| Lowest | 10,670 | 26,186 | 12,893 | 5952 | 17.10% | 38.80% | 18.60% | 10.30% |
| Low | 5725 | 1892 | 11,082 | 5026 | 7.40% | 2.40% | 14.50% | 8.20% |
| Medium | 5172 | 1158 | 5756 | 8101 | 7.40% | 1.70% | 7.00% | 9.40% |
| High | 6811 | 1598 | 9091 | 10,476 | 9.80% | 2.40% | 16.20% | 15.70% |
| Highest | 32,485 | 30,029 | 22,041 | 31,308 | 58.30% | 54.70% | 43.70% | 56.40% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Yan, D.; Wang, K.; Weng, B.; Qin, T.; Liu, S. Flood Risk Assessment of Global Watersheds Based on Multiple Machine Learning Models. Water 2019, 11, 1654. https://doi.org/10.3390/w11081654
Li X, Yan D, Wang K, Weng B, Qin T, Liu S. Flood Risk Assessment of Global Watersheds Based on Multiple Machine Learning Models. Water. 2019; 11(8):1654. https://doi.org/10.3390/w11081654
Chicago/Turabian StyleLi, Xiangnan, Denghua Yan, Kun Wang, Baisha Weng, Tianling Qin, and Siyu Liu. 2019. "Flood Risk Assessment of Global Watersheds Based on Multiple Machine Learning Models" Water 11, no. 8: 1654. https://doi.org/10.3390/w11081654
APA StyleLi, X., Yan, D., Wang, K., Weng, B., Qin, T., & Liu, S. (2019). Flood Risk Assessment of Global Watersheds Based on Multiple Machine Learning Models. Water, 11(8), 1654. https://doi.org/10.3390/w11081654





