Tracing Temporal Changes of Model Parameters in Rainfall-Runoff Modeling via a Real-Time Data Assimilation
Abstract
:1. Introduction
2. Methods and Data
2.1. Rainfall-Runoff Model
| Parameter | Description | Min | Max |
|---|---|---|---|
| B | Exponent of the tension water-capacity distribution curve | 0.1 | 0.6 |
| SM | Free water-storage capacity (mm) | 10 | 50 |
| WUM | Averaged soil moisture storage capacity of the upper layer (mm) | 20 | 50 |
| WLM | Averaged soil moisture storage capacity of the lower layer (mm) | 60 | 120 |
| WDM | Averaged soil moisture storage capacity of the deep layer (mm) | 10 | 40 |
2.2. EnKF with Real-Time Parameter Update
2.3. Dataset
2.4. Synthetic Experiment Design
2.4.1. Synthetic Cases
2.4.2. Uncertainty Design
| Scenarios | fr | fm | fo |
|---|---|---|---|
| Low_Level | 0.00 | 0.00 | 0.02 |
| Medial_Level | 0.05 | 0.10 | 0.10 |
| High_Level | 0.10 | 0.20 | 0.20 |
3. Results
3.1. Stationary Case

3.2. Non-Stationary Cases
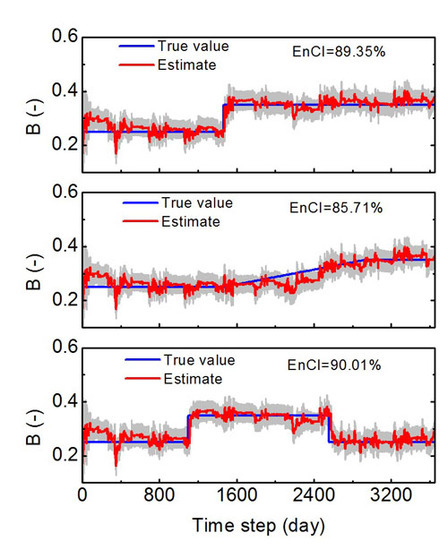
3.2.1. Tracing Changed Parameters

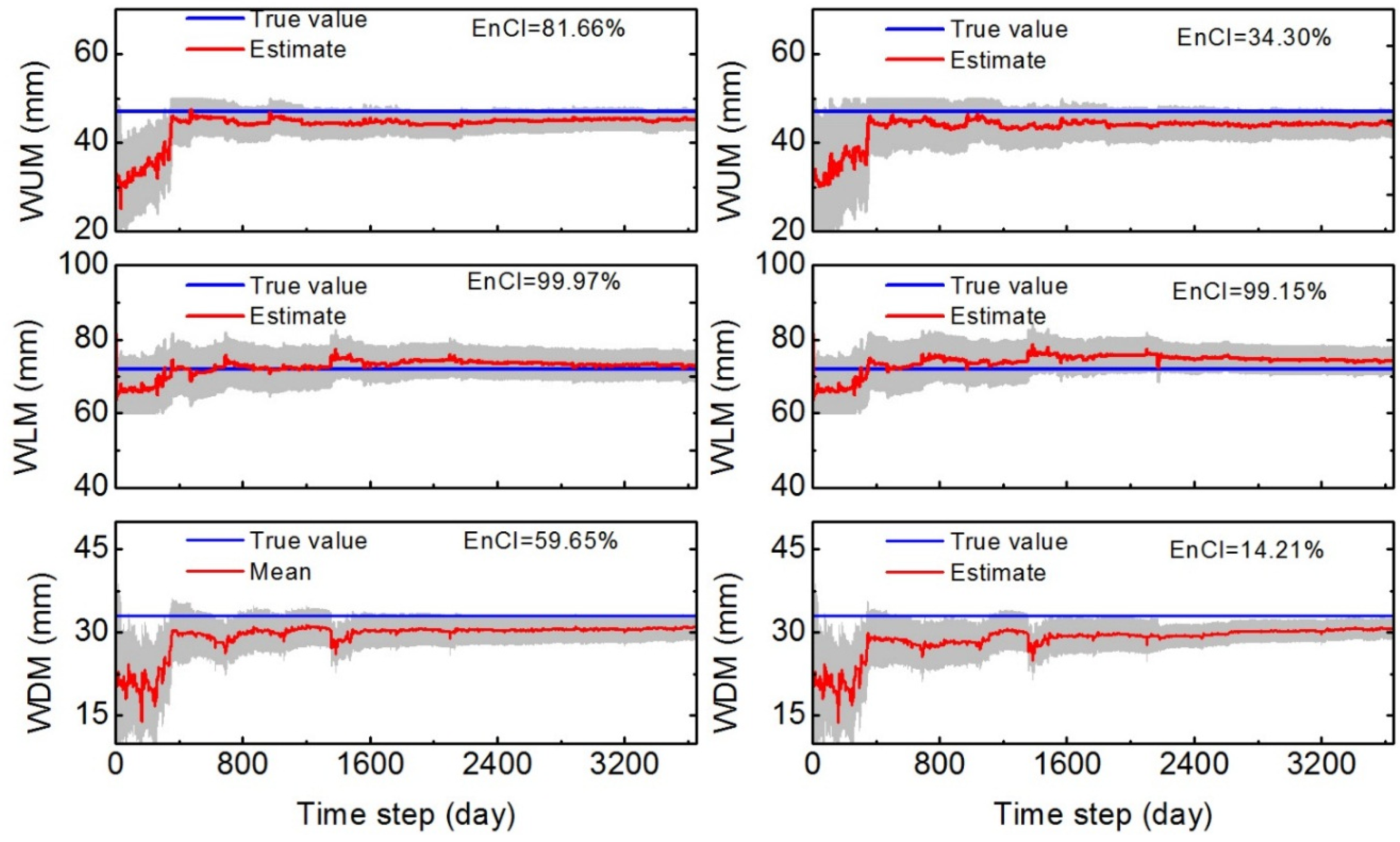
3.2.2. Estimation of Fixed Parameters
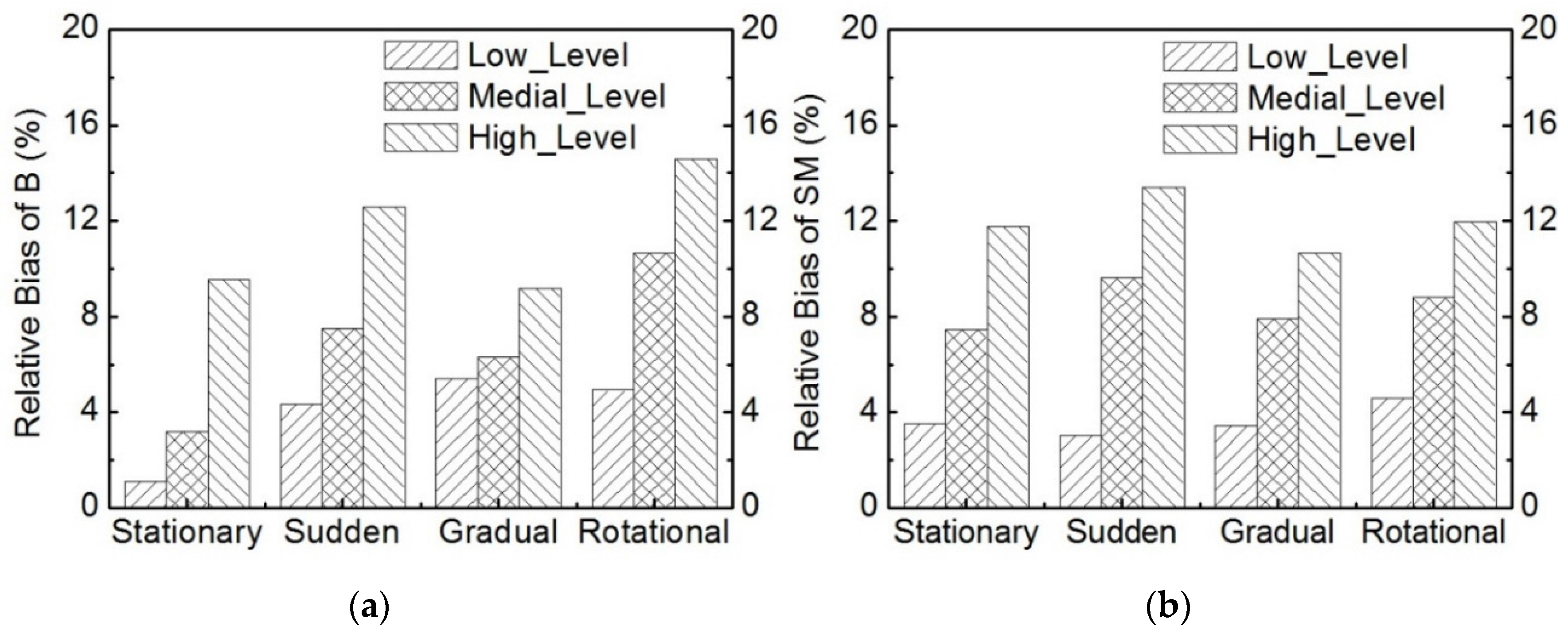
3.3. Effect of the Level of Uncertainties

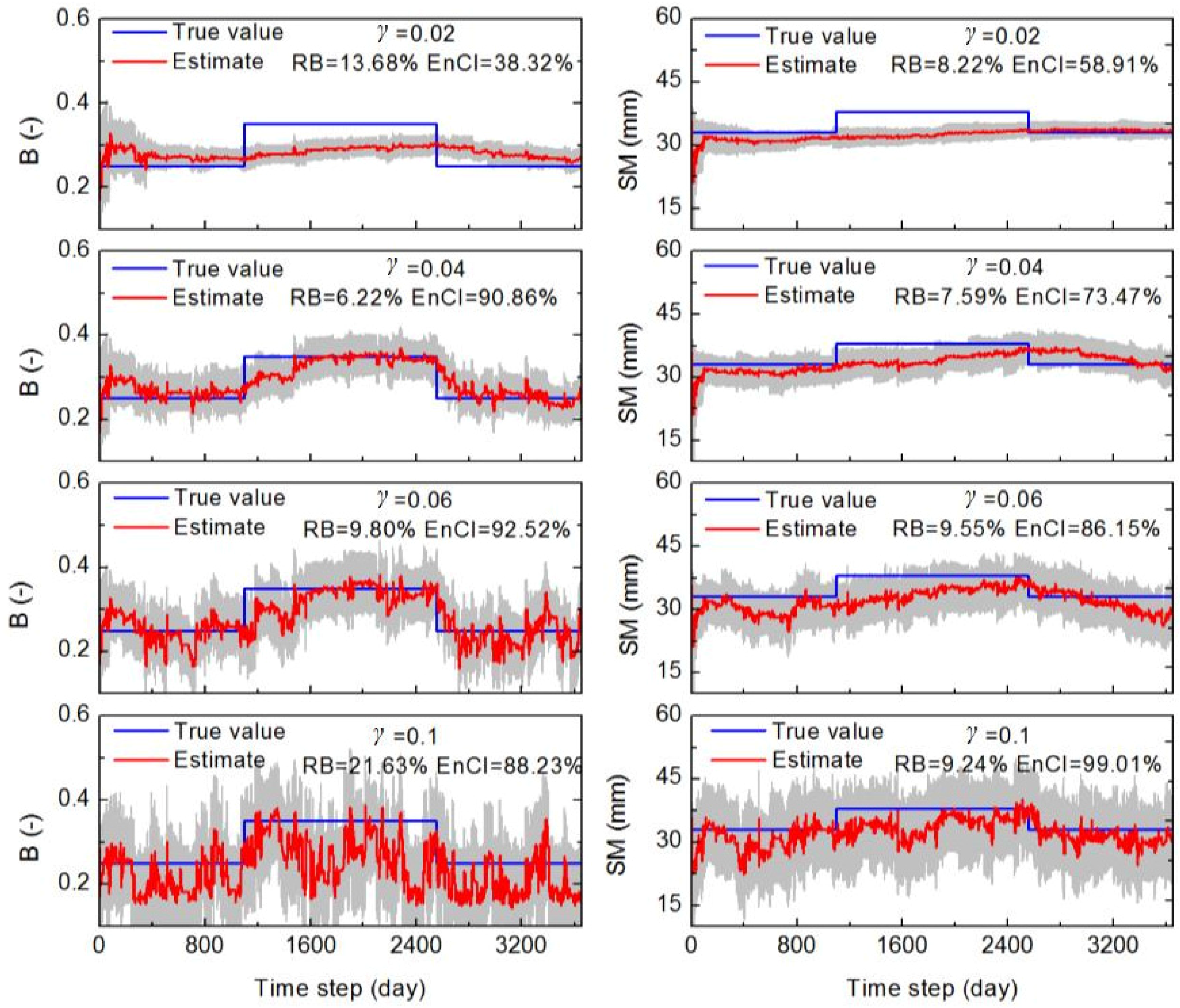
3.4. Impact of γ
4. Discussion
4.1. Comparison with SCE-UA
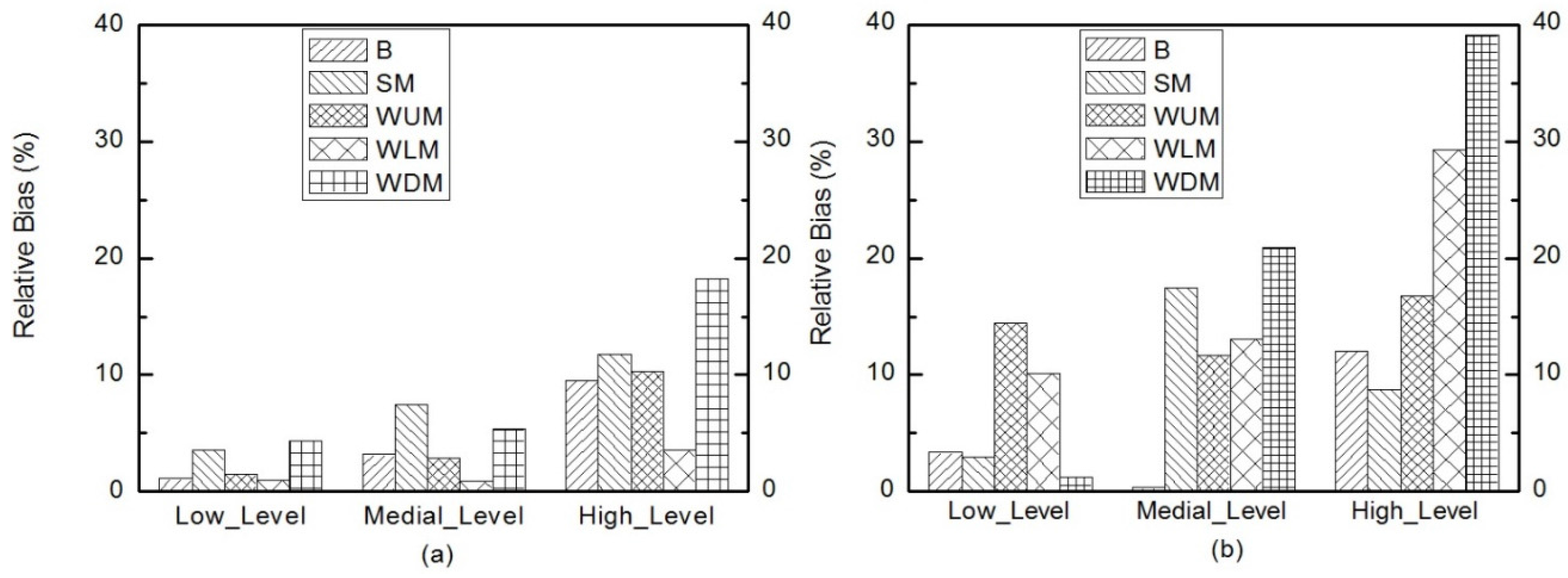
4.2. Implications for Detecting Changes in Watershed Characteristics
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wagener, T. Can we model the hydrological impacts of environmental change? Hydrol. Process. 2007, 21, 3233–3236. [Google Scholar] [CrossRef]
- Horton, P.; Schaefli, B.; Mezghani, A.; Hingray, B.; Musy, A. Assessment of climate-change impacts on alpine discharge regimes with climate model uncertainty. Hydrol. Process. 2006, 20, 2091–2109. [Google Scholar] [CrossRef]
- Huss, M.; Farinotti, D.; Bauder, A.; Funk, M. Modelling runoff from highly glacierized alpine drainage basins in a changing climate. Hydrol. Process. 2008, 22, 3888–3902. [Google Scholar] [CrossRef]
- Schaefli, B.; Harman, C.; Sivapalan, M.; Schymanski, S. Hess opinions: Hydrologic predictions in a changing environment: Behavioral modeling. Hydrol. Earth Syst. Sci. 2011, 15, 635–646. [Google Scholar] [CrossRef]
- Wang, W.; Shao, Q.; Peng, S.; Zhang, Z.; Xing, W.; An, G.; Yong, B. Spatial and temporal characteristics of changes in precipitation during 1957–2007 in the haihe river basin, China. Stoch. Environ. Res. Risk Assess. 2011, 25, 881–895. [Google Scholar] [CrossRef]
- Ghimire, S.R.; Johnston, J.M. Impacts of domestic and agricultural rainwater harvesting systems on watershed hydrology: A case study in the albemarle-pamlico river basins (USA). Ecohydrol. Hydrobiol. 2013, 13, 159–171. [Google Scholar] [CrossRef]
- Guo, B.; Zhang, J.; Gong, H.; Cheng, X. Future climate change impacts on the ecohydrology of Guishui river basin, China. Ecohydrol. Hydrobiol. 2014, 14, 55–67. [Google Scholar] [CrossRef]
- Kundzewicz, Z.W. Climate change impacts on the hydrological cycle. Ecohydrol. Hydrobiol. 2008, 8, 195–203. [Google Scholar] [CrossRef]
- Xie, X.H.; Cui, Y.L. Development and test of swat for modeling hydrological processes in irrigation districts with paddy rice. J. Hydrol. 2011, 396, 61–71. [Google Scholar] [CrossRef]
- Xie, X.; Liang, S.; Yao, Y.; Jia, K.; Meng, S.; Li, J. Detection and attribution of changes in hydrological cycle over the three-north region of China: Climate change versus afforestation effect. Agric. For. Meteorol. 2015, 203, 74–87. [Google Scholar] [CrossRef]
- Ehret, U.; Gupta, H.; Sivapalan, M.; Weijs, S.; Schymanski, S.; Blöschl, G.; Gelfan, A.; Harman, C.; Kleidon, A.; Bogaard, T. Advancing catchment hydrology to deal with predictions under change. Hydrol. Earth Syst. Sci. 2014, 18, 649–671. [Google Scholar] [CrossRef]
- Vaze, J.; Post, D.; Chiew, F.; Perraud, J.-M.; Viney, N.; Teng, J. Climate non-stationarity-validity of calibrated rainfall-runoff models for use in climate change studies. J. Hydrol. 2010, 394, 447–457. [Google Scholar] [CrossRef]
- Wagener, T.; Sivapalan, M.; Troch, P.A.; McGlynn, B.L.; Harman, C.J.; Gupta, H.V.; Kumar, P.; Rao, P.S.C.; Basu, N.B.; Wilson, J.S. The future of hydrology: An evolving science for a changing world. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Kampf, S.K.; Burges, S.J. Parameter estimation for a physics-based distributed hydrologic model using measured outflow fluxes and internal moisture states. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Xia, Y.; Yang, Z.-L.; Jackson, C.; Stoffa, P.L.; Sen, M.K. Impacts of data length on optimal parameter and uncertainty estimation of a land surface model. J. Geophys. Res. Atmos. 2004, 109. [Google Scholar] [CrossRef]
- Li, Y.; Ryu, D.; Western, A.W.; Wang, Q.J. Assimilation of stream discharge for flood forecasting: The benefits of accounting for routing time lags. Water Resour. Res. 2013, 49, 1887–1900. [Google Scholar] [CrossRef]
- Duan, Q.; Sorooshian, S.; Gupta, V. Effective and efficient global optimization for conceptual rainfall-runoff models. Water Resour. Res. 1992, 28, 1015–1031. [Google Scholar] [CrossRef]
- Duan, Q.Y.; Gupta, V.K.; Sorooshian, S. Shuffled complex evolution approach for effective and efficient global minimization. J. Optim. Theory Appl. 1993, 76, 501–521. [Google Scholar] [CrossRef]
- Peel, M.C.; Blöschl, G. Hydrological modelling in a changing world. Progress Phys. Geogr. 2011, 35, 249–261. [Google Scholar] [CrossRef]
- Milly, P.C.D.; Betancourt, J.; Falkenmark, M.; Hirsch, R.M.; Kundzewicz, Z.W.; Lettenmaier, D.P.; Stouffer, R.J. Stationarity is dead: Whither water management? Science 2008, 319, 573–574. [Google Scholar] [CrossRef] [PubMed]
- Montanari, A.; Young, G.; Savenije, H.; Hughes, D.; Wagener, T.; Ren, L.; Koutsoyiannis, D.; Cudennec, C.; Toth, E.; Grimaldi, S. “Panta rhei—Everything flows”: Change in hydrology and society—The iahs scientific decade 2013–2022. Hydrol. Sci. J. 2013, 58, 1256–1275. [Google Scholar] [CrossRef]
- Sivapalan, M. Prediction under Change (Puc): Water, Earth and Biota in the Anthropocene, In Proceedings of the AGU Fall Meeting Abstracts, San Francisco, CA, USA, 5–9 December 2011.
- Sivapalan, M.; Thompson, S.; Harman, C.; Basu, N.; Kumar, P. Water cycle dynamics in a changing environment: Improving predictability through synthesis. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Aich, V.; Liersch, S.; Vetter, T.; Andersson, J.; Müller, E.N.; Hattermann, F.F. Climate or land use?—Attribution of changes in river flooding in the sahel zone. Water 2015, 7, 2796–2820. [Google Scholar] [CrossRef]
- Merz, R.; Blöschl, G. A regional analysis of event runoff coefficients with respect to climate and catchment characteristics in Austria. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Merz, R.; Parajka, J.; Blöschl, G. Time stability of catchment model parameters: Implications for climate impact analyses. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Aronica, G.; Hankin, B.; Beven, K. Uncertainty and equifinality in calibrating distributed roughness coefficients in a flood propagation model with limited data. Adv. Water Resour. 1998, 22, 349–365. [Google Scholar] [CrossRef]
- Castaings, W.; Dartus, D.; le Dimet, F.X.; Saulnier, G.M. Sensitivity analysis and parameter estimation for distributed hydrological modeling: Potential of variational methods. Hydrol. Earth Syst. Sci. 2009, 13, 503–517. [Google Scholar] [CrossRef] [Green Version]
- Vrugt, J.A.; Gupta, H.V.; Bouten, W.; Sorooshian, S. A shuffled complex evolution metropolis algorithm for optimization and uncertainty assessment of hydrologic model parameters. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Liu, Y.; Gupta, H.V. Uncertainty in hydrologic modeling: Toward an integrated data assimilation framework. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Kumar, S.V.; Reichle, R.H.; Peters-Lidard, C.D.; Koster, R.D.; Zhan, X.; Crow, W.T.; Eylander, J.B.; Houser, P.R. A land surface data assimilation framework using the land information system: Description and applications. Adv. Water Resour. 2008, 31, 1419–1432. [Google Scholar] [CrossRef]
- Moradkhani, H.; Sorooshian, S.; Gupta, H.V.; Houser, P.R. Dual state–parameter estimation of hydrological models using ensemble kalman filter. Adv. Water Resour. 2005, 28, 135–147. [Google Scholar] [CrossRef]
- Xie, X.; Zhang, D. Data assimilation for distributed hydrological catchment modeling via ensemble kalman filter. Adv. Water Resour. 2010, 33, 678–690. [Google Scholar] [CrossRef]
- Xie, X.H.; Zhang, D.X. A partitioned update scheme for state-parameter estimation of distributed hydrologic models based on the ensemble kalman filter. Water Resour. Res. 2013, 49, 7350–7365. [Google Scholar] [CrossRef]
- Xie, X.; Meng, S.; Liang, S.; Yao, Y. Improving streamflow predictions at ungauged locations with real-time updating: Application of an enkf-based state-parameter estimation strategy. Hydrol. Earth Syst. Sci. 2014, 18, 3923–3936. [Google Scholar] [CrossRef]
- Zhao, R.J. The xinanjiang model applied in china. J. Hydrol. 1992, 135, 371–381. [Google Scholar]
- Zhao, R.; Liu, X.; Singh, V. The xinanjiang model. In Comput. Model. Watershed Hydrol; Water Resources Publications: Littleton, CO, USA, 1995; pp. 215–232. [Google Scholar]
- Ren, L.; Huang, Q.; Yuan, F.; Wang, J.; Xu, J.; Yu, Z.; Liu, X. Evaluation of the xinanjiang model structure by observed discharge and gauged soil moisture data in the hubex/game project. Iahs Publ. 2006, 303, 153–163. [Google Scholar]
- Hu, C.; Guo, S.; Xiong, L.; Peng, D. A modified xinanjiang model and its application in northern China. Nordic Hydrol. 2005, 36, 175–192. [Google Scholar]
- Bao, H.J.; Zhao, L.N.; He, Y.; Li, Z.J.; Wetterhall, F.; Cloke, H.L.; Pappenberger, F.; Manful, D. Coupling ensemble weather predictions based on tigge database with grid-xinanjiang model for flood forecast. Adv. Geosci. 2011, 29, 61–67. [Google Scholar] [CrossRef]
- Xu, H.; Xu, C.-Y.; Chen, H.; Zhang, Z.; Li, L. Assessing the influence of rain gauge density and distribution on hydrological model performance in a humid region of China. J. Hydrol. 2013, 505, 1–12. [Google Scholar] [CrossRef]
- Li, Z.J.; Xin, P.L.; Tang, J.H. Study of the Xinanjiang model parameter calibration. J. Hydrol. Eng. 2013, 18, 1513–1521. [Google Scholar]
- Zhang, D.; Zhang, L.; Guan, Y.; Chen, X.; Chen, X. Sensitivity analysis of xinanjiang rainfall-runoff model parameters: A case study in Lianghui, Zhejiang Province, China. Hydrol. Res. 2012, 43, 123–134. [Google Scholar] [CrossRef]
- Song, X.M.; Kong, F.Z.; Zhan, C.S.; Han, J.W.; Zhang, X.H. Parameter identification and global sensitivity analysis of Xin’anjiang model using meta-modeling approach. Water Sci. Eng. 2013, 6, 1–17. [Google Scholar]
- Evensen, G. Data Assimilation: The Ensemble Kalman Filter; Springer Science & Business Media: Berlin, Germany, 2009. [Google Scholar]
- Chen, H.; Yang, D.; Hong, Y.; Gourley, J.J.; Zhang, Y. Hydrological data assimilation with the ensemble square-root-filter: Use of streamflow observations to update model states for real-time flash flood forecasting. Adv. Water Resour. 2013, 59, 209–220. [Google Scholar] [CrossRef]
- Ghil, M. Data assimilation in meteorology and oceanography. Adv. Geophys. 1991, 33, 141–266. [Google Scholar]
- Shi, L.; Zeng, L.; Zhang, D.; Yang, J. Multiscale-finite-element-based ensemble kalman filter for large-scale groundwater flow. J. Hydrol. 2012, 468–469, 22–34. [Google Scholar] [CrossRef]
- Reichle, R.H.; McLaughlin, D.B.; Entekhabi, D. Hydrologic data assimilation with the ensemble kalman filter. Mon. Weather Rev. 2002, 130, 103–114. [Google Scholar] [CrossRef]
- Evensen, G. The ensemble kalman filter: Theoretical formulation and practical implementation. Ocean Dyn. 2003, 53, 343–367. [Google Scholar] [CrossRef]
- Evensen, G.; van Leeuwen, P.J. An ensemble kalman smoother for nonlinear dynamics. Mon. Weather Rev. 2000, 128, 1852–1867. [Google Scholar] [CrossRef]
- Liu, F. Bayesian Time Series: Analysis Methods Using Simulation-Based Computation. Ph.D Thesis, Institutes of Statistics and Decision Science, Duke University, Duke, NC, USA, May 2000. [Google Scholar]
- Clark, M.P.; Rupp, D.E.; Woods, R.A.; Zheng, X.; Ibbitt, R.P.; Slater, A.G.; Schmidt, J.; Uddstrom, M.J. Hydrological data assimilation with the ensemble kalman filter: Use of streamflow observations to update states in a distributed hydrological model. Adv. Water Resour. 2008, 31, 1309–1324. [Google Scholar] [CrossRef]
- Chu, W.; Gao, X.; Sorooshian, S. Improving the shuffled complex evolution scheme for optimization of complex nonlinear hydrological systems: Application to the calibration of the sacramento soil-moisture accounting model. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Evans, W.E.; Friday, E.W., Jr. Multilevel Calibration Strategy for Complex Hydrologic Simulation Models; US Department of Commerce, National Oceanic and Atmospheric Administration, National Weather Service: Washington, DC, USA, 1989. [Google Scholar]
- Sorooshian, S.; Duan, Q.; Gupta, V.K. Calibration of rainfall-runoff models: Application of global optimization to the sacramento soil moisture accounting model. Water Resour. Res. 1993, 29, 1185–1194. [Google Scholar] [CrossRef]
- Andréassian, V.; Parent, E.; Michel, C. A distribution-free test to detect gradual changes in watershed behavior. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Blazkova, S.; Beven, K. A limits of acceptability approach to model evaluation and uncertainty estimation in flood frequency estimation by continuous simulation: Skalka catchment, Czech Republic. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Calver, A.; Stewart, E.; Goodsell, G. Comparative analysis of statistical and catchment modelling approaches to river flood frequency estimation. J. Flood Risk Manag. 2009, 2, 24–31. [Google Scholar] [CrossRef]
- Grimaldi, S.; Petroselli, A.; Serinaldi, F. A continuous simulation model for design-hydrograph estimation in small and ungauged watersheds. Hydrol. Sci. J. 2012, 57, 1035–1051. [Google Scholar] [CrossRef]
- Crow, W.T.; Reichle, R.H. Comparison of adaptive filtering techniques for land surface data assimilation. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Crow, W.T.; van Loon, E. Impact of incorrect model error assumptions on the sequential assimilation of remotely sensed surface soil moisture. J. Hydrometeorol. 2006, 7, 421–432. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, S.; Xie, X.; Yu, X. Tracing Temporal Changes of Model Parameters in Rainfall-Runoff Modeling via a Real-Time Data Assimilation. Water 2016, 8, 19. https://doi.org/10.3390/w8010019
Meng S, Xie X, Yu X. Tracing Temporal Changes of Model Parameters in Rainfall-Runoff Modeling via a Real-Time Data Assimilation. Water. 2016; 8(1):19. https://doi.org/10.3390/w8010019
Chicago/Turabian StyleMeng, Shanshan, Xianhong Xie, and Xiao Yu. 2016. "Tracing Temporal Changes of Model Parameters in Rainfall-Runoff Modeling via a Real-Time Data Assimilation" Water 8, no. 1: 19. https://doi.org/10.3390/w8010019
APA StyleMeng, S., Xie, X., & Yu, X. (2016). Tracing Temporal Changes of Model Parameters in Rainfall-Runoff Modeling via a Real-Time Data Assimilation. Water, 8(1), 19. https://doi.org/10.3390/w8010019