Abstract
The impact of climate change on the hydro-climatology of the Indian subcontinent is investigated by comparing statistics of current and projected future fluxes resulting from three RCP scenarios (RCP2.6, RCP4.5, and RCP8.5). Climate projections from the CORDEX-South Asia framework have been bias-corrected using the Distribution-Based Scaling (DBS) method and used to force the HYPE hydrological model to generate projections of evapotranspiration, runoff, soil moisture deficit, snow depth, and applied irrigation water to soil. We also assess the changes in the annual cycles in three major rivers located in different hydro-climatic regions. Results show that conclusions can be influenced by uncertainty in the RCP scenarios. Future scenarios project a gradual increase in temperature (up to 7 °C on average), whilst changes (both increase and decrease) in the long-term average precipitation and evapotranspiration are more severe at the end of the century. The potential change (increase and decrease) in runoff could reach 100% depending on the region and time horizon. Analysis of annual cycles for three selected regions showed that changes in discharge and evapotranspiration due to climate change vary between seasons, whereas the magnitude of change is dependent on the region’s hydro-climatic gradient. Irrigation needs and the snow depth in the Himalayas are also affected.
1. Introduction
Climate change impacts can be particularly complex in regions which are additionally subject to other environmental and socio-economic changes, i.e., population growth, urbanization, land use change, and change in industrial and hydropower sectors [1]. India is a developing country with nearly two-thirds of the population depending directly on the climate- and water-sensitive sectors. The country already faces high risks of water shortages due to population growth, urbanization, and increasing demands in the agricultural, industrial, and hydropower sectors; hence, India offers a unique opportunity to examine the impacts of climate change, which in some areas have already been observed [2,3,4]. The region is characterised by a strong hydro-climatic gradient due to the monsoon (tropical climatic regions in the south; temperate and alpine regions in the Himalayan north, where elevated areas receive sustained winter snowfall) and the geographic features; hence, posing extraordinary scientific challenges to understand, quantify, and predict future availability of water resources. Of particular interest are the Northern Indian Himalayan plains given the sensitivity of snow and glacier melt processes to climate variability and change [5,6,7]. Arid and semi-arid regions might also experience changes in their hydrological cycle [8,9].
Assessment of future climate change impacts on water resources commonly involves climate variables (i.e. precipitation, temperature) from global circulation models (GCMs) in combination with hydrological models [10,11]. GCMs demonstrate significant skill at the continental and hemispheric spatial scales and incorporate a large proportion of the complexity of the global system; however, they are inherently unable to represent local basin-scale features and dynamics [12]. To narrow the gap between GCMs’ abilities and hydrological needs, regional climate models (RCMs) have been developed to downscale the GCM output and, thus, provide high-resolution meteorological inputs to hydrological models. To improve the confidence in regional trends of hydro-climatic key variables and increase robustness in hydrological long term predictions, the World Climate Research Programme (WCRP) has recently launched a framework, called COordinated Regional climate Downscaling EXperiment (CORDEX), to generate and evaluate fine-scale ensembles of regional climate projections for all continents globally [13]. CORDEX has several domains that are defined as regions for which the regional downscaling is taking place. In particular, the efforts in the South Asia (SA) domain aim to translate regionally-downscaled climate data into meaningful sustainable development information in the monsoon South Asia area [14]. CORDEX-SA was initiated in 2012 and the RCM outputs have only recently become available.
While RCMs transfer the large-scale information from GCMs to scales which are closer to the basin scale (10–50 km), the output often shows large bias in the magnitude and spatial distribution of precipitation and, to a lesser extent, temperature [15]. RCM data are, therefore, not considered to be directly useful for assessing hydrological impacts at the regional and/or local scale [16]. A way to tackle the problem of RCM misrepresentation is to bias correct the RCM data to make them reproduce historical observed statistics to the degree possible [17]. Different approaches to bias correction have been made, with various complexity [18]. Simpler methods include shifting long-term annual or seasonal means to agree with observations whereas more advanced methods include adjustment of the full frequency distribution. A distribution-based approach is attractive not least for precipitation, for which both bias and future change are generally found to depend on the intensity level [19]. Bias correction often includes an implicit downscaling component, in that higher-resolution reference observations are used when fitting the RCM mapping functions. Bias correction generally preserves the variability described by different climatic conditions generated by RCM projections [20]; however, the RCM may perform differently depending on the season or governing atmospheric circulation. For instance, a typically wet weather regime (e.g., pattern or season) can have a different precipitation distribution in time and space than a dry regime.
Projected hydrologic information is prone to considerable uncertainty/errors at various steps of the modelling chain, i.e., climate projection, bias correction and downscaling techniques, and hydrological simulation [21,22,23]. These errors can propagate in a very complex way (e.g., magnitude of error could vary both in space and time) which could be misinformative for management decisions [24,25]. A major source of uncertainty, among others, concerns the future emission scenarios, described by the representative concentration pathways (RCP), which further results in different climate projections. [26] showed that towards the end of the 21st century, the emission scenarios (here RCPs) are the dominant source of uncertainty in climate projections. The spatiotemporal variability of water fluxes differs between RCPs, particularly in areas with unique weather systems, i.e., monsoon [27,28]. However, the choice of GCM and RCM may also have a large impact on the results and generally an ensemble of projections—encompassing different GCMs, RCMs, and emission scenarios—is recommended in hydrological climate change impact assessments [29,30].
Conventionally, hydrologic impacts are investigated on small (~0.1–102 km2) or medium-sized basins (~102–103 km2); however, current needs require assessment on larger areas and river basins, which requires the use of large scale hydrological models [31,32]. This type of modelling has the potential to encompass many river basins, cross-regional, and international boundaries and represents a number of different geophysical and climatic zones [33]. In addition, according to [34], large scale modelling can balance “depth with breadth”, enhance process understanding, increase robustness of generalizations, facilitate catchment classification and regionalization schemes, and support better understanding of prediction uncertainty.
This paper contributes to ongoing efforts on assessing the potential impacts of climate change on water availability in the Indian subcontinent. In particular, we aim to answer the following questions: i) what is the quantified impact of climate change on India’s water resources? ii) how is the uncertainty due to RCP propagated in hydrological impact modelling? and iii) how does the potential impact vary in different climatic regions (i.e., tropical, humid subtropical, and montane)? Although previous investigations have, at least to some degree, addressed similar questions, our contribution is associated with three novel features in that we apply: 1) three recently-generated high-resolution CORDEX-SA projections (RCP2.6, RCP4.5, and RCP8.5), 2) the DBS (distribution-based scaling; [35]) method to correct biases in the climate projections, and 3) the large-scale multi-basin HYPE (HYdrological Predictions for the Environment; [36]) hydrological model, to quantify climatic as well as anthropogenic impacts of climate change on hydrology and water availability over the entire Indian subcontinent. Section 2 introduces the study area, whereas the hydrological model and methodology are presented in Section 3. Section 4 presents the results of climate change impacts, followed by a discussion in Section 5 and conclusions in Section 6.
2. Study Area and Data
2.1. Study Area
India is the seventh-largest country by area and the second-most populated country with over 1.2 billion people. The country covers an area of about 3.3 million km2 and some of its river basins extend into several neighboring countries (i.e., China, Nepal, Pakistan, and Bangladesh; see Figure 1). Major rivers of Himalayan origin that are mainly located in India include the Ganga and the Brahmaputra, both of which drain into the Bay of Bengal. Major peninsular rivers, whose steeper gradients prevent them from flooding, include the Godavari, the Mahanadi, and the Krishna, which also drain into the Bay of Bengal; and the Narmada and the Tapi, which drain into the Arabian Sea. Coastal features include the marshy Rann of Kutch of Western India and the alluvial Sundarbans delta of Eastern India; the latter is shared with Bangladesh.
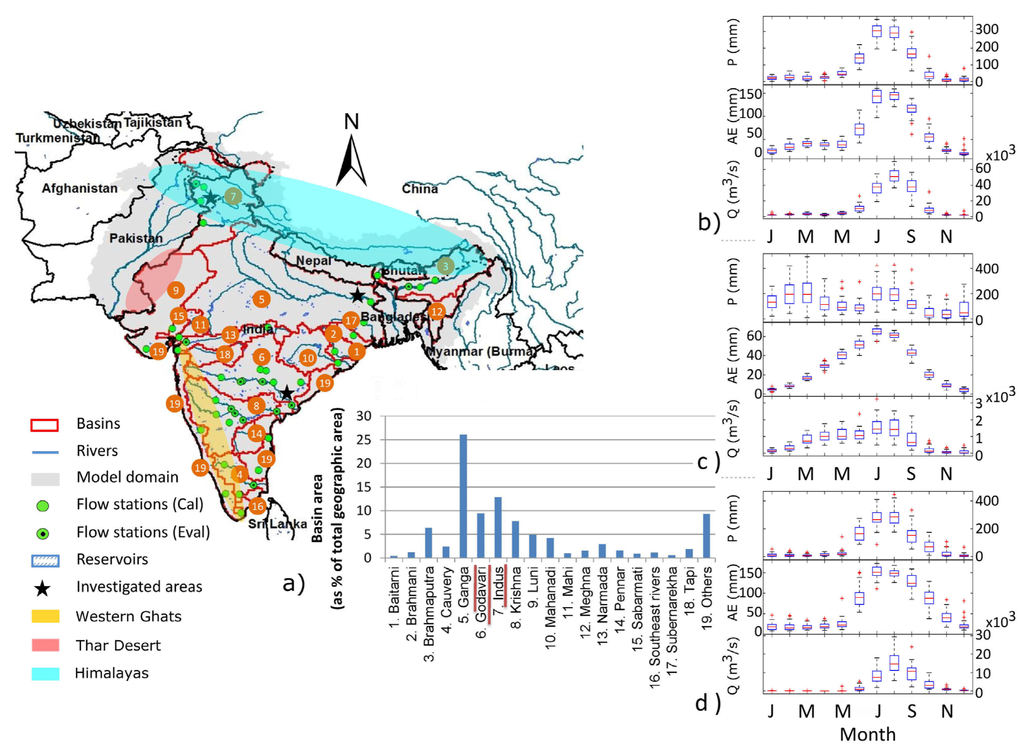
Figure 1.
(a) The Indian subcontinent (model domain)—the numbers correspond to the basins in which regional analysis is conducted. Mean annual hydro-climatic cycles (precipitation (P), actual evapotranspiration (AE), and discharge (Q)) during the period 1976–2005 for the rivers: (b) Ganga (at Farakka station), (c) Indus (Chenab at Akhnoor station), and (d) Godavari (at Polavaram station). These results are shown from investigation areas in (a) with a star.
The spatiotemporal variation in climate is perhaps greater than in any other area of similar size in the world. The climate is strongly influenced by the Himalayas and the Thar Desert in the northwest, both of which drive the summer and winter monsoons [37]. Four seasons can be distinguished: winter (January–February), pre-monsoon (March–May), monsoon (June–September), and post-monsoon (October–December). In terms of spatial variability, the rainfall pattern roughly reflects the different climate regimes of the country, which vary from humid in the northeast (precipitation is 2068 mm/year and occurs about 180 days/year), to arid in Rajasthan (precipitation is 313 mm/year and occurs about 20 days/year). Moreover, India is characterized by strong temperature variations in different seasons ranging from a mean temperature of about 10 °C in winter to about 32 °C in pre-monsoon season.
The monsoon season is very important for water resources (and in turn their use for, e.g., power generation and agriculture) in the country since 75% of the annual rainfall (877 out of 1182 mm) is received in this period [38]. In particular, India’s mean monthly rainfall during July (286.5 mm) is highest and constitutes about 24% of the annual total. The contribution in August is slightly lower (~21%) and in June and September ~14% [39]. The contribution of pre-monsoon and post-monsoon rainfall to the annual total is roughly the same (11%). Higher variation is observed during the end of post-monsoon and winter (i.e., November–February). To provide a better understanding of the system behavior, Figure 1b–d shows the annual cycles of the hydro-climatic fluxes in three different climatic regions, i.e., humid subtropical (Ganga), montane (Indus), and tropical (Godavari).
2.2. Spatial Input Data
Data availability is usually a severe constraint in the analysis of large-scale domains. To overcome such a problem, we use global datasets to extract the information required for hydrological applications (see Table 1 in [40]).

Table 1.
The three CORDEX-SA climate projections used in this study.
2.3. Meteorological Reference Data
Daily precipitation inputs for the period 1971–2005 are obtained from the Asian Precipitation—Highly-Resolved Observational Data Integration Towards Evaluation of Water Resources (APHRODITE) project [41,42] at 0.25° resolution (Table 1). Similarly, AphroTEMP [43] provides daily temperature inputs for the same period at 0.5° resolution. APHRODITE and AphroTEMP (in the following jointly denoted APHRODITE) are the only long-term continental-scale gridded datasets that are based on a dense network of daily data for Asia including the Himalayas. Therefore, the datasets have contributed to studies including among others water resources, climate change analysis, and statistical downscaling [28]. In this study, as a reference period we have chosen the 30-year period 1976–2005. The APHRODITE dataset fully covers this reference period and the period does not overlap with the future climate projections that start in 2006.
2.4. Climate Projections
Our ensemble of three climate projections consists of modelling chains that use the same GCM (EC-EARTH; [44]) and RCM (RCA4; [45]), but three different representative concentration pathways, RCPs (see ). RCPs are numbered after their increased radiative forcing until year 2100 (+2.6, +4.5, and +8.5 W/m2, respectively; [46]). Note that more climate projections are becoming available over the South Asian domain through the CORDEX initiative (e.g., [47]).
A total of 129 years of hydrological simulations have been conducted for each climate scenario (1971–2099). However, the analysis is based on three 30-year periods: reference period (1976–2005), mid-century period (2021–2050), and end-century period (2070–2099). Note that in here we only analyze three projections from the CORDEX-SA ensemble; the CORDEX experiment is ongoing and more projections are being generated but these were the only ones available at the time of the study.
3. Methodology
3.1. India-HYPE: Description, Setup, and Calibration
The Hydrological Predictions for the Environment, HYPE, model [36] is a semi-distributed rainfall-runoff model capable of describing the hydrological processes at the basin scale. The model represents processes for snow and ice accumulation and melting, evapotranspiration, soil moisture, discharge generation, groundwater recharge, and routing through rivers and lakes. HYPE simulates the water flow paths in soil, which is divided into three layers with a fluctuating groundwater table. Parameters are linked to physiographical characteristics in the landscape, such as hydrological response units (HRUs) linked to soil type and depths and vegetation. Elevation is used to get temperature variations within a sub-basin for estimating the snow cover dynamics.
Lakes are defined as classes with specified areas and receive the local runoff and the river flow from upstream sub-basins. Precipitation falls directly on lake surfaces and lake water evaporates at the potential rate until the lake is dry. Each lake has a defined depth below an outflow threshold. The outflow from lakes is determined by a general rating curve, unless a specific one is given or if the lake is regulated. Lakes and man-made reservoirs are not separated in the simulation. A simple regulation rule can be used, in which the outflow is constant or follows a seasonal function for water levels above the threshold. A rating curve for the spillways can be used when the reservoir is full.
Irrigation in HYPE is simulated based on crop water demands calculated either with the FAO-56 crop coefficient method [48] or relative to a reference flooding level for submerged crops (e.g., rice). The demands are withdrawn from rivers, lakes, reservoirs, and/or groundwater within and/or external to the sub-basin where the demands originated. The demands are constrained by the water availability at these sources. After subtraction of conveyance losses, the withdrawn water is applied as additional infiltration to the irrigated soils from which the demands originated (in here named as applied irrigation water to soil (AIW)).
The HYPE model is set up for the entire Indian subcontinent (4.9 million km2) divided into 6010 sub-basins, i.e., with an average size of 810 km2, and is referred to as India-HYPE. The model runs at a daily time step using APHRODITE as input data, but due to lack of daily discharge observations it was calibrated and evaluated (both in space and time) against monthly observations from 42 stations in the GRDC (Global Runoff Data Centre) database. For the Indian subcontinent, GRDC data are limited to monthly discharge for chosen river basins in the period 1971–1979. More discharge data are held in the Indian government agencies, but are not released to the public domain due to confidentiality; this generally sets a constraining factor for a model setup. Many of the parameters in the model are coupled to soil type or land use, while others are assumed to be general to a larger region. This approach fosters the potential of parameter transferability within reasonably homogeneous regions. In applications of HYPE, we generally consider the parameter identifiability and their regionalization to ungauged regions to be acceptable if the model performs adequately in the gauged basins over the entire model domain.
The HYPE model was spatiotemporally calibrated and evaluated in a multi-basin approach by considering the median performance in selected stations; 30 stations were selected for model calibration and 12 “blind” stations for spatial evaluation. The years 1969–1970 were used as a model warm-up period, the next five years for model calibration (1971–1975) and the final four years for temporal performance evaluation (1976–1979). The model’s predictability was tested using various performance measures (i.e., objective functions and flow signatures) and additional data sources (i.e., remote sensing potential evapotranspiration records); see details in [40]. Here, we assess the model’s predictability based on the Nash-Sutcliffe Efficiency, NSE [49] and relative error, RE (defined as the difference between the mean modelled value and the mean observed value divided by the mean observed value). The former has been widely applied in hydrology as a benchmark measure of fit. It can also be interpreted as a classic skill score, where skill is interpreted as the comparative ability with regards to a baseline model (here taken to be the “mean of the observations”; i.e., NSE < 0 indicates that the mean of the observed time series provides, on average, a better prediction than the model). NSE ranges between 1 (perfect fit) and −∞ whereas RE ranges between −∞ and +∞, with the “ideal” value being 0.
3.2. Bias Correction of RCM Data
The RCM projections (mean daily precipitation and temperature) were bias corrected against the APHRODITE dataset using the distribution based scaling, DBS, statistical method [35]. In brief, DBS aims to map the quantile distributions of precipitation and temperature in the RCM data to those of the reference data. For precipitation, a two-step procedure is applied: 1) correction of the wet-day frequency by applying a wet-day cut-off threshold (in case of wet frequency bias) or by adding wet-days to pre-existing wet-spells (if dry frequency bias), and 2) quantile-mapping of the precipitation data using a double-gamma distribution to accurately represent both normal and extreme precipitation intensity ranges. For temperature, a quantile-mapping correction based on a Gaussian distribution is used. The temperature correction model is dependent on the wet/dry state of the corresponding precipitation. This means that DBS takes into account different biases on wet and dry days (see details in [35]). The bias-corrected projections were used to force the hydrological model for the assessment of climate change impacts on water resources. DBS was used for bias-correcting GCM projections over India (Mumbai region) by [50].
3.3. Climate Change Impact Assessment
For the present climate, water availability in space and time was simulated using the reference APHRODITE dataset as input. The same framework is then used to project the impact of climate change on the water resources with the assumption that the land use shall not change over time.
3.3.1. Long-Term Averages
Firstly, we assess the impact of climate change on the hydro-climatic variables, i.e., long-term means of precipitation (P, in mm), temperature (T, in C), actual evapotranspiration (AE, in mm), runoff (R, in mm), soil moisture deficit (SMD, in mm), snow depth (SD, in cm), and applied irrigation water to soil (AIW, in Mm3). The daily series for each 30-year period (reference, mid- and end-century) is used to extract the statistics. The relative future change in the long-term average (%) between two periods (mid- or end-century versus reference period) due to climate change is estimated for each sub-basin. Positive (negative) change indicates increase (decrease) from the average value in the reference period. Note that for T we calculate absolute differences between future and reference periods; hence, we can express properly also changes in the sign of T.
The spatial variability of change at the basin scale is further summarized (here presented as a boxplot) allowing comparison of the overall change between basins; note that this analysis is only presented for P and R.
3.3.2. Annual Cycles
To complement the above assessment, we investigate the changes in the annual cycles in different locations and governing climatic conditions. We, therefore, compare the annual cycles of P, E, and discharge (Q, in m3/s) for the Ganga (at Farakka station), Indus (Chenab at Akhnoor station), and Godavari (at Polavaram station) basins (see annual cycles of the present climate in Figure 1b–d). The climate in these basins is characterized as humid subtropical, montane, and tropical, respectively; hence, the analysis can capture the sensitivity to the dominant climatic gradients in the subcontinent.
4. Results
4.1. Model Evaluation
Here, we investigate the model’s reliability (which involves measures sensitive to high flows, timing, variability, and volume), and present performances for the benchmark objective functions, i.e., NSE and RE. The NSE and RE for all calibration and evaluation stations and periods are presented in Table 2. Overall, the India-HYPE model achieved an acceptable performance for our purpose and is, therefore, considered adequate to describe the dominant hydrological processes in the region (median NSE and RE for the calibration period is 0.76 and −5.26%, respectively, while for the evaluation period the values are 0.68 and +8.01%, respectively). However, as expected, the performance decreased when the model is validated both in space and time (NSE and RE equal 0.40 and 16.81%, respectively); the model is not “trained” to capture the flow conditions at independent areas and time periods. A more detailed analysis during the evaluation period showed that the model could not fully capture the variability (e.g., standard deviation) of the observed data in the validation stations. The ratio of the standard deviation of modelled over the standard deviation of observed data decreases during the evaluation period at the evaluation stations from 0.78 to 0.58 which consequently affects the NSE values; see the discussion on the decomposition of the NSE and the importance of its decomposed terms (dealing with timing, variability, and volume) on the overall NSE in [51]. However other flow characteristics, i.e. timing and volume, are better represented than variability during the evaluation period. Further analysis and discussion on model performance and consistency can be found in [40].

Table 2.
Median model performance for calibration and evaluation stations and periods.
4.2. Bias Correction
The effect of bias-correction using the DBS methodology is illustrated here for the case of mean P (Figure 2). The highest P amounts are measured along the mountain ridges, e.g., on the western side of the Western Ghats, Southwest India, and at the foothills of the Himalaya in the northern part of the study region. Those wet regions are strongly associated with atmospheric flows during the monsoon season. Dry regions are located in the northwestern part and on the eastern side of the Western Ghats. The projections employed in this study all share the same historical run, thus Figure 2 is representative for all three projections. The historical projection shows large positive and negative biases in mean P, with sharp gradients between regions of positive and negative biases. The regions with sharp gradients coincide very well with regions of complex topography (e.g., in the Himalaya or on the lee and luv side of the Western Ghats). DBS is able to correct for most of the bias although some remaining dry bias is apparent in regions where the historical projection strongly underestimates mean precipitation. This is related to a dry frequency bias, i.e., too few wet days in the projection. DBS is not able to fully correct for the pronounced deficits in rain days, but can only correct moderate dry frequency bias by adding wet-days to existing wet-spells. Such a limitation of bias-correction methods in case of dry frequency biases is a general limitation of current quantile-mapping bias-correction methods [35,52].
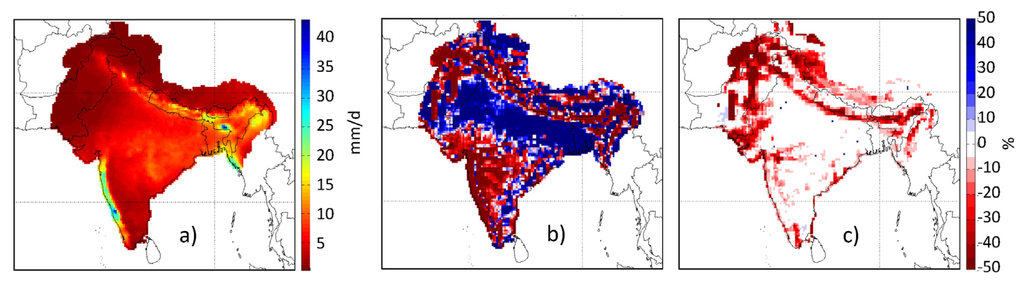
Figure 2.
Observed precipitation and RCM bias in the period 1976–2005: (a) mean daily precipitation in APHRODITE; (b) relative bias in uncorrected historical GCM-RCM projection, and (c) relative bias in bias-corrected historical GCM-RCM projection.
Concerning T, in most parts of India it was underestimated by 1–2 C in the historical GCM-RCM projection (not shown). After the DBS bias-correction, only a negligible bias remained and the spatial pattern became essentially identical to the observations (see Figure 3c).
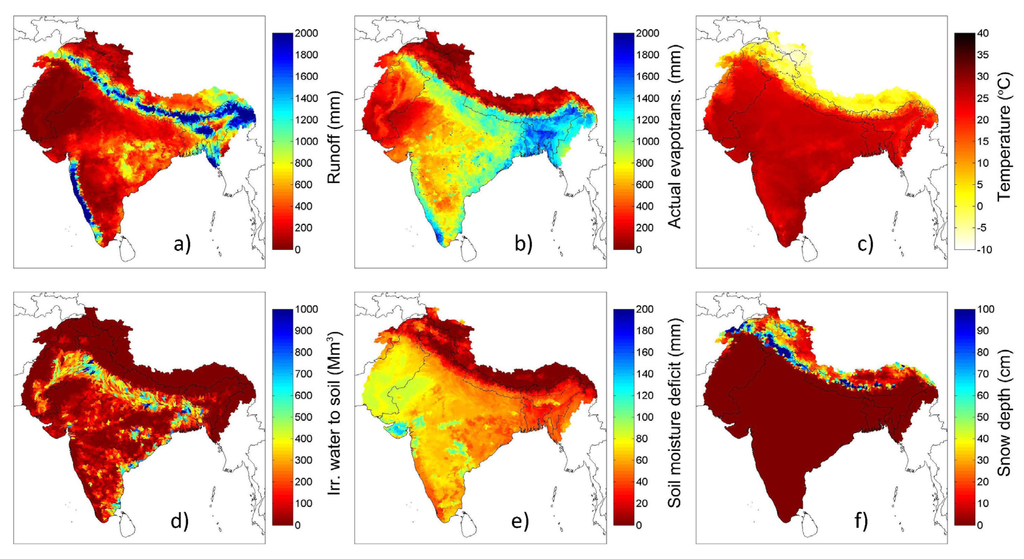
Figure 3.
Annual averages (period 1976–2005) for the variables: (a) runoff, R; (b) actual evapotranspiration, AE; (c) temperature, T; (d) applied irrigation water to soil, AIW; (e) soil moisture deficit, SMD; and (f) snow depth, SD.
4.3. Reference Data Analysis
To infer a quantitative understanding of the magnitude of the climate change impact on the hydro-climatic components (P was analyzed in Section 4.2), it is necessary to estimate the long-term averages of India-HYPE driven by APHRODITE for the entire reference period (Figure 3). Long-term average R is controlled by the spatial patterns of P and AE; consequently high R is generated at the southwestern rivers and at the Himalayan mountain range. AE, which in this model is controlled by water availability and T, shows similar spatial patterns to P but lower than the latter by almost 25%; hence, indicating that most precipitated water is evaporated back to the atmosphere. Note, also, the high temperatures which are almost homogeneously distributed over the region (average T is about 25 °C); however, the T gradient is very strong at the Himalayan mountain range (average T varies between −5 and 2 °C). The AIW varies between 100 and 900 Mm3 per year with high spatial variability in the region (note that the spatial pattern of this variable is subject to the GMIA irrigation map). The SMD is between 0 and 140 mm/year, with the Himalayas exhibiting very low values and the Thar Desert exhibiting high values; note the presence of wetlands covering this northwest region. Finally, SD can reach 100 cm in the Himalayas with large local variability.
4.4. Climate Change Impacts
As outlined in Section 3.3, we analyze the effects of climate change for various variables in two different scenario periods. We firstly present changes in the variables which control the hydro-climatic conditions and continue with the applied irrigation water to soil which is more “end-user related”. We then investigate the changes in the annual cycles of three regions.
4.4.1. Long-Term Averages
All projections show an increase of T for both scenario periods and in the whole modelling domain (Figure 4). In RCP2.6, the increase in T is limited to ranges below +1.5 °C until the end of the 21st century. For the same scenario period and RCP4.5, the increase in T is projected to fall into the range of +1.0 to +2.0 °C over most of the domain, but is higher—up to +3.0 °C—in the mountainous parts in the north. The same spatial pattern is seen in RCP8.5 in which T is projected to increase between 1.5 and 6.0 °C with the highest increase also occurring in the mountainous regions. This elevation dependency could be due to the snow albedo effect which leads to higher increases in T when the snow cover duration decreases [53].
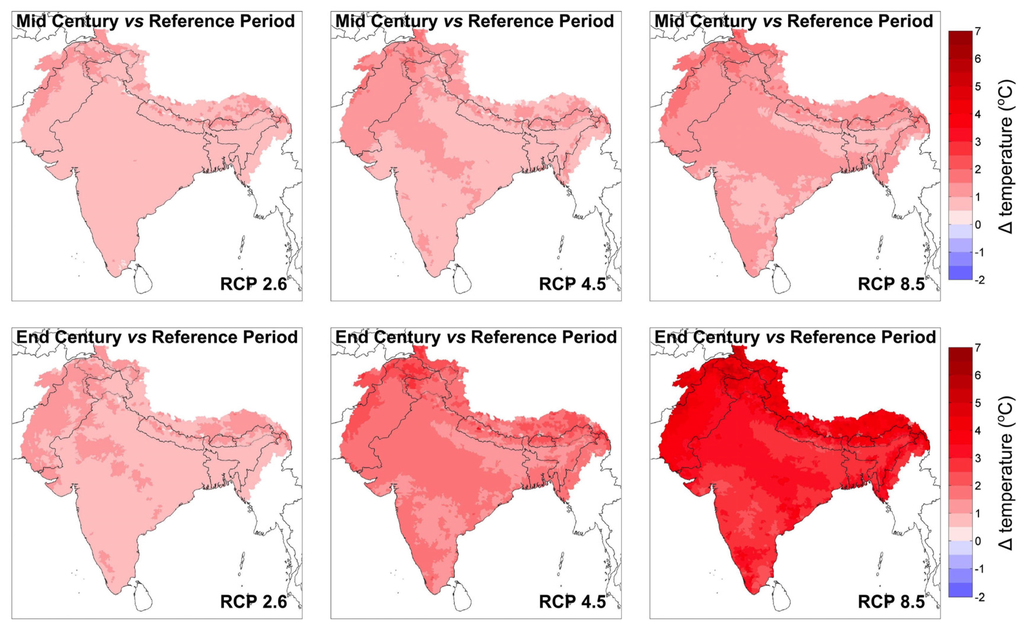
Figure 4.
Change in temperature T for each climate projection (columns 1–3) and period (top and bottom row for the mid- and end-century, respectively).
Regarding P, the projections show strongly increasing mean P over most of the region (Figure 5). This also includes areas where present day P is already very high (e.g. along the Western Ghats and the southern side of the Himalayan mountain range). The signal is stronger towards the end of the 21st century than in mid-century and the higher the RCP is, with the exception of RCP2.6 for which there is no intensification of the signal from the mid- to the end-century period. The clear dependency of the change signal on the period and the RCP is true for all variables discussed below. The dry regions in the northwestern and central parts, including e.g., the Indus, Luni, Sabarmati, and parts of the Ganga River, are projected to receive less P. Additionally, the spatial variability of the changes within the major river basins (see boxplots in Figure 5) is generally increasing towards the end of the century. The above-mentioned river basins include sub-basins with a very heterogeneous pattern of P changes, ranging from decreases to increases for all projections except for the RCP8.5 end-century evaluation. Those basins are located in a zone where slight changes in the spatial patterns of P decrease or increase might lead to a pronounced effect on the basin-wide qualitative changes (i.e., decrease or increase of mean P).
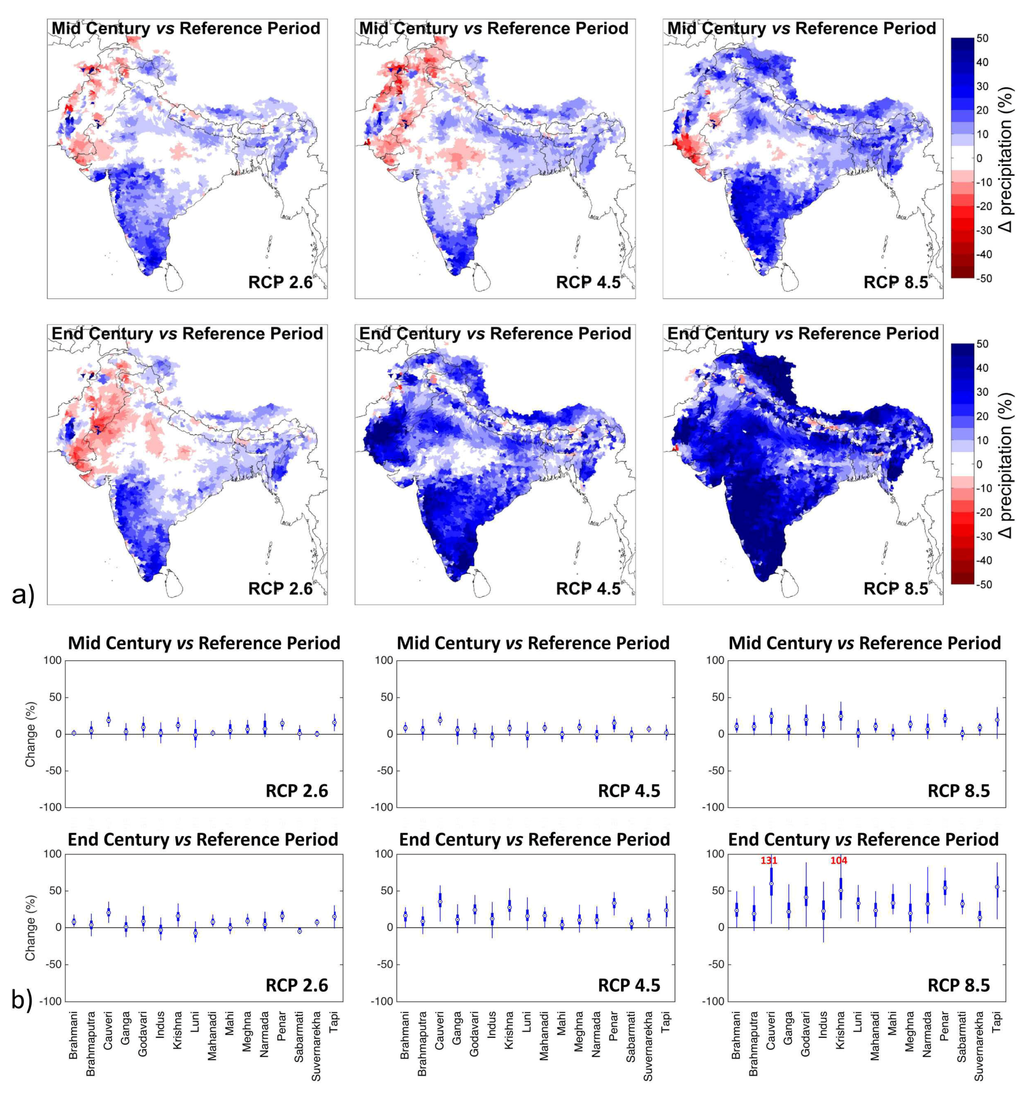
Figure 5.
(a) Relative change in precipitation P for each climate projection (columns 1–3) and period (top and bottom row for the mid- and end-century, respectively); and (b) variability of the change at the basin scale for each climate projection (columns 1–3) and period (rows 1–2).
AE generally either remains essentially unchanged or increases. In areas with a pronounced decrease in P, such as in the northwest, a slight decrease of AE may, however, occur (see Figure 6). The increase of evaporation in the south is due to decrease in SMD (see Figure 8). Over the Himalayan mountain range, strong increases are projected in all RCPs and both scenario periods. In that area, the increase of potential evapotranspiration (not shown) due to increased temperature and a shortened period of snow cover (see Figure 8 for snow depth changes as an indicator of snow cover changes) both contribute to higher AE.
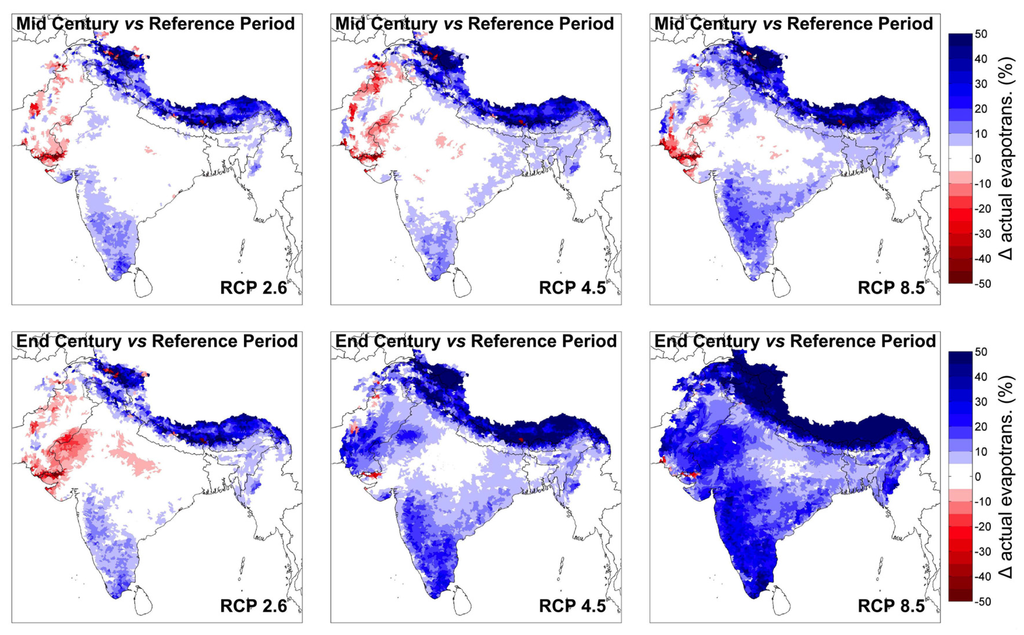
Figure 6.
Same as Figure 5a for actual evapotranspiration AE.
The pattern of R changes follows the one of P but the magnitudes of the relative changes are larger than for P (Figure 7). Consequently, the spatial variability within the major river basins is also much larger than for P, shown by the wider boxplots in the Figure 7. Thus, the basins, which are susceptible to small spatial changes of areas with increasing and decreasing P, are even more sensitive to spatial changes when it comes to R.
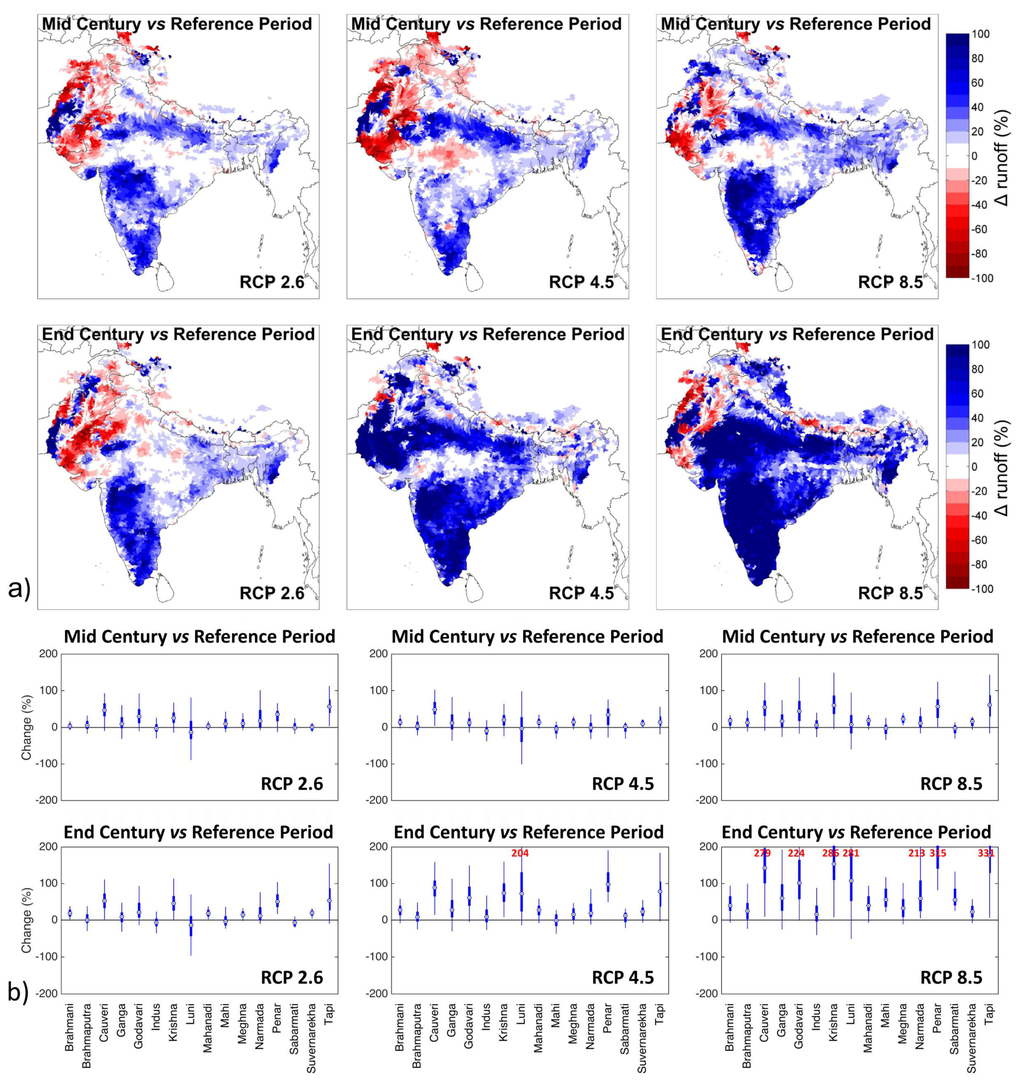
Figure 7.
(a) Same as Figure 5a for runoff R. Maximum values for the regions in which change is greater than 200% are presented in red and (b) variability of the change at the basin scale for each climate projection (columns 1–3) and period (rows 1–2).
Within the model domain, snow only occurs in the Himalayas (Figure 3). For a large fraction of that area, SD is projected to decrease strongly, a change which is already apparent in the mid-century period (Figure 8). Only in some high-elevated areas is T cold enough to make SD increase due to increased mean P.
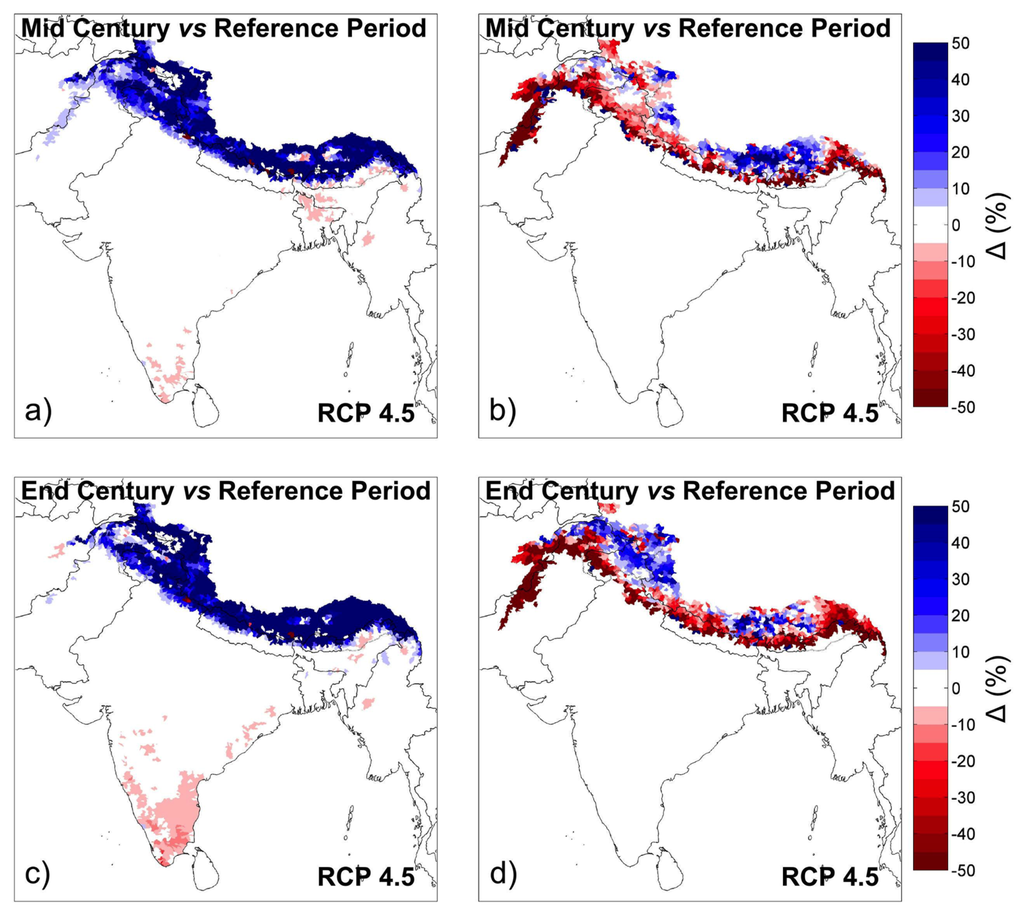
Figure 8.
Relative change in soil moisture deficit SMD (column 1) and snow depth SD (column 2) for climate projection RCP4.5 until mid-century (row 1) and end-century (row 2). Only RCP4.5 is shown; the spatial pattern of changes is very similar for the other RCPs. (a) SMD change for mid-century; (b) SD change for mid-century; (c) SMD change for end-century, and (d) SD change for end-century. See the results for all RCPs and future periods in Figures S1 and S2 in the Supplement.
The changes in irrigated water to soil (Figure 9) should be interpreted in a way that they represent the changes in future demand for irrigation. Wherever irrigation is projected to increase, a higher demand for irrigation is implied. In that sense, the results indicate that the demand for irrigation will increase in the Northwestern and central regions in all RCPs and both scenario periods. Towards the end of the century in RCP8.5, the region with increased irrigation demand is enlarged and encompasses the whole Indus and Ganga river basins. Decreases in irrigation needs are projected for the southern part of the model domain.
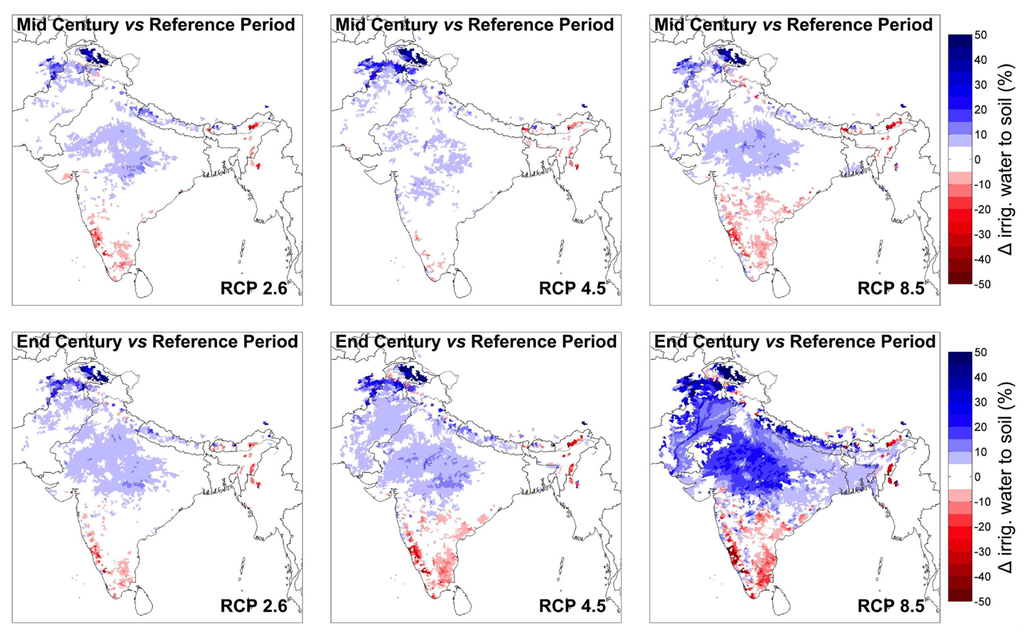
Figure 9.
Same as Figure 5a for applied irrigation water to soil AIW.
4.4.2. Annual Cycles
Whereas in Section 4.4.1 we presented spatially detailed maps of changes in annual mean quantities, we show here the results of changes in the annual cycle at three selected gauges (see stars in Figure 1) in order to provide more details about the seasonal dynamics.
The Ganga River has clear Q seasonality with peak Q in the monsoon season and very little Q in the remaining months (Figure 1b). P is projected to increase during the monsoon period, and little change happens in the rest of the year (Figure 10a). This trend is stronger for the end-century than for the mid-century changes in RCP4.5 and RCP8.5, while RCP2.6’s changes remain on a low level even at the end of the century. For the end-century period, RCP8.5 also shows a longer season of increasing P, lasting until the start of the post-monsoon season in October. The seasonal pattern of changes in AE closely follows the one of P, but the magnitudes of the changes are smaller. Thus, the increases in P partly become runoff effective, which is seen as increasing Q in the monsoon season. The largest increases in Q towards the end of the century are projected to range from 5000 to 20,000 m3/s depending on the chosen RCP, corresponding to a 12 to 50 % increase compared to the reference period.
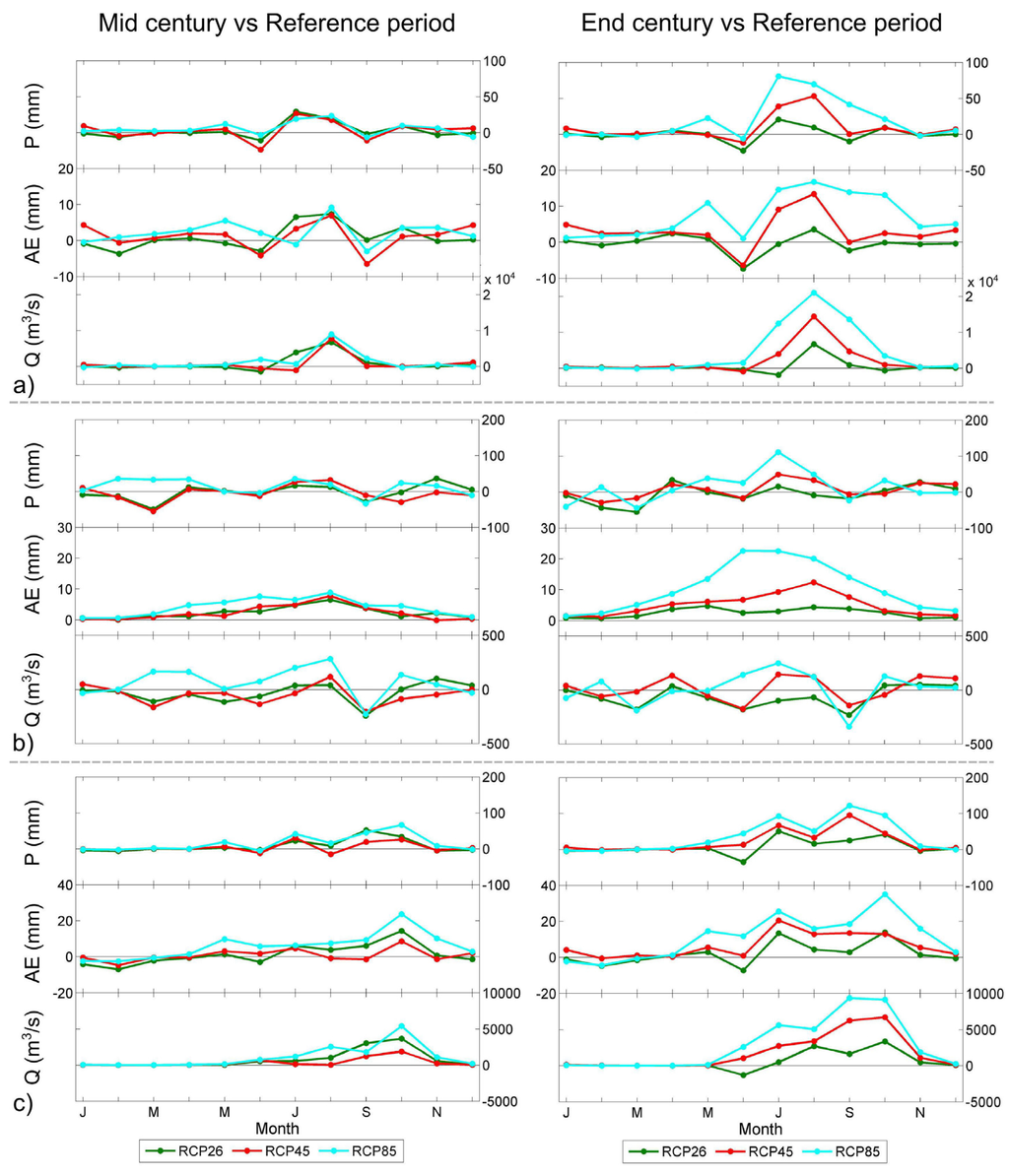
Figure 10.
Absolute changes in the annual cycles of precipitation P, actual evapotranspiration AE and discharge Q for each climate scenario and period (column 1 and 2 for the mid- and end-century, respectively) for the rivers: (a) Ganga (at Farakka station); (b) Indus (Chenab at Akhnoor station), and (c) Godavari (at Polavaram station).
The gauge in the Indus catchment lies close to the Himalayas. In present day conditions, the seasonal cycle of P shows a two-peak pattern with one peak in March and the second one in July/August (Figure 1c). The three projections do not agree on the change signal (Figure 10b). For the end-century period, a slight tendency towards increasing P in summer and decreasing P in March is noticeable. This would mean that the first P peak weakens, whereas the second one in summer gets stronger. AE increases throughout the year, with the largest increases being projected for the summer. There is no clear link between the P and the AE change signal, indicating that the soil moisture is not the limiting factor for AE in that area. The change signal in Q is associated with more uncertainty and small projected changes switch sign several times in the course of the annual cycle. This is also reflected in the boxplots in Figure 7 where the Indus River shows a large spatial variability of runoff changes around the no-change level. Small changes in some sub-basins might lead to a switch of the sign of change in the response on the aggregated basin level. Overall, it seems that the climate change signal of discharge is small.
Under the current conditions, the Godavari River has a clear seasonal discharge regime with a peak in the monsoon season and low discharge in the rest of the year (Figure 1d). Compared to the Ganga River, the seasonality is even more pronounced due to the lack of snow-melt from the Himalayas during the pre- and post-monsoon season. Additionally, the seasonal pattern of changes in all variables looks similar to the ones in the Ganga River; however, the magnitudes are larger (Figure 10c). For total Q in the monsoon and post-monsoon period, the changes amount to +10% to +80%.
5. Discussion
5.1. Enhancing Understanding of Future Climate Change Impacts
Our study contributes to the previously reported assessments of future climatic patterns (which in most cases are driven by projections from different GCMs and RCMs) in India and their impact on water resources. Overall our results support previous findings that climate projections reveal an increase in monsoon precipitation in the mid-century [54,55] and a possible extension of the monsoon period [56,57,58]. Our results over Northern and Western India and the southeastern coastline differ from previous projections based on the CGCM3.1-PRECIS model chain and the A1B emission scenario [31,59]. According to [59], in those regions precipitation is expected to decrease both in the mid- and end-century. Moreover, analysis (not shown here) on the number of wet spells was consistent with the general trends of previous finding, showing a higher frequency of wet spells from the 2060s and beyond, mostly in northern and coastal regions [14,60].
[61] define the river basins of Kutch, Saurashtra, Luni, and Indus in the northwest and Pennar in the southeast as physically water-scarce, most of the rest of India as economically water-scarce, and only Brahmaputra, Meghna, Brahmani, Mahanadi, and some smaller basins along the east coast as non-water-scarce (Figure 1). Our results support this regional classification, however attention is needed in results for R in the northwestern basins due to their pronounced spatial variability (although overall results point at decreasing runoff). The overall decreasing future trend of water availability in the northwestern basins with a high spatial variability agrees with the results in [31]. In our results river Pennar will clearly become less water-scarce by the end of the century, which is in contrast to [31] who found a reduced water yield in this basin on this time horizon.
A key component for assessing water scarcity is the evapotranspiration. Similarly to P, AE in our results exhibit a pronounced spatial variability in the northwest and overall an increase is projected for the Indian subcontinent. This can be contrasted with recent findings of observed decreasing trends in temperature (and consequently evaporation and water scarcity) over Northeastern India [62], the Godavari basin [63], as well as many regions world-wide [64,65]. For India, this finding has been attributed to mainly a reduction of wind speeds (‘stilling’) and an increase of atmospheric humidity [63]. These impacts cannot be simulated with the purely T-based relationship for AE used here.
In the Himalayan region, we found a generally consistent increase in runoff for different projections and future periods, which agrees with the general trend in the literature [5,6,66,67,68]; however this increase varies significantly in space (following the topographic pattern). In addition, it is generally expected that the changes in the Ganga and Meghna rivers will be larger than in the Brahmaputra river, probably due to the impact of melted water from snow and glaciers [2]. This conclusion is consistent with our results. Change in runoff in the Krishna river is ambiguous with studies showing both a future increase [32,69], as here, and a decrease [31].
5.2. Limitations of This Study
Reliability of the input data used to drive large-scale multi-basin hydrological models, particularly those derived from global datasets, has been questioned [70]. Although a preliminary comparison of the applied climatic and physiographic data against national data did not show significant discrepancies (e.g., when comparing the APHRODITE data against P and T observations from the Indian Meteorological Department), some inconsistencies were generally observed at the local scale.
Here, we have only focused on the uncertainty from the RCP scenario. This was motivated by previous findings indicating that towards the end of the 21st century, generally the emission scenario (here, RCP) is the dominant source of uncertainty in climate projections (e.g., [26]). However, it is clear that also the other sources may substantially contribute to the uncertainty, e.g., the choice of GCMs, RCMs, bias-correction method, hydrological model structure, and parameterization can have a substantial impact [71,72].
Climate change impact results are subject to the impact model’s predictability and consistency, here assessed by the model’s performance in the present climate. The India-HYPE model can adequately represent the long-term average fluxes and their seasonal variation (see details in [40]); however, it is expected that a larger number of discharge gauges (representing different hydro-climatic systems) and/or temporally extended time series (in terms of length and resolution) and/or additional variables (e.g., evapotranspiration, snow cover area etc.) would provide additional information to drive the parameterization of the model and guide towards model structural improvements.
Finally, our study is limited by the assumed stationarity in the investigated hydrological systems. It is recognized that non-stationarity exists as a characteristic of the natural world due to various environmental changes (land use and other man-made alterations) [73].
6. Conclusions
We have explored the potential impact of climate change on the hydrology and water resources of the Indian subcontinent, based on an RCP-ensemble of regional climate projections from the CORDEX-SA framework. Climate projections with GCM EC-EARTH and RCM RCA4 based on three RCP scenarios (RCP2.6, RCP4.5, and RCP8.5) are bias-corrected and introduced into the HYPE hydrological model to assess average changes in various hydro-climatic fluxes for two future periods (mid- and end-century). Additionally, the intra-annual variability of key fluxes (precipitation, evapotranspiration, and discharge) in three river systems.
Overall, the distribution of change in runoff varies considerably with both hydro-climatic region and climate projection. In particular, the following future changes were indicated:
- Temperature will increase in the entire subcontinent, with the highest increase in the mountainous regions.
- An increase in long-term average precipitation and evapotranspiration in wet regions; however, less precipitation and evapotranspiration are expected at the dry regions.
- Average snow depth in the Himalayan region will be reduced; this is consistent in all projections and time horizons.
- A general increase in the need for irrigation; however, the need is reduced in the south.
- Large relative changes in runoff, and large spatial variability at the basin scale, particularly towards the end of the century.
- Changed seasonality in discharge, with more pronounced changes in the tropical and subtropical zones than in the mountainous regions.
Overall, the conclusions support previous findings in most parts of India (including the Himalayas), with respect to future trends in runoff. This study, however, indicates larger changes under the severe emission scenario RCP8.5. Regionally, some differences are found in comparison with existing results, e.g., for precipitation and evapotranspiration in northern and western India and the southeastern coastline and for runoff changes in the Krishna river. These differences highlight the need for further studies focusing on climate change impacts on hydrology in India. In addition to pure climate impact modelling, as performed here, we believe more efforts are needed to better understand and quantify the sensitivity of the river systems to climate changes, as well as other changes (e.g., land-use and population). This work should preferably include multiple scenarios of all considered changes used in combination with multiple hydrological models. Work in this direction is ongoing and will be reported elsewhere.
Supplementary Materials
The following are available online at www.mdpi.com/2073-4441/8/5/177/s1. Figure S1: Relative change in soil moisture deficit (SMD) for each climate projection (columns 1–3) and period (top and bottom row for mid- and end-century respectively), Figure S2: Relative change in snow depth (SD) for each climate projection (columns 1–3) and period (top and bottom row for mid- and end-century, respectively).
Acknowledgements
This work was funded mainly by the Swedish International Development Cooperation Agency (SIDA; grant no. AKT-2012-022) with additional support from the Swedish Research Council Formas (grant No. 2010-121) and the Swedish Secretariat for Environmental Earth System Sciences (SSEESS; grant No. KVA/2015/111/75). We would also like to acknowledge David Gustafsson, Kean Foster, Kristina Isberg, Jörgen Rosberg, Jafet Andersson and Sian de Koster for assistance with background material for this study and manuscript checks.
Author Contributions
Ilias G. Pechlivanidis led the project-related activities on setting up the hydrological model, conducting the analyses, and writing the manuscript. Jonas Olsson assisted on the manuscript writing and supervised the efforts on bias-correction of the climate projections. Thomas Bosshard led the activities on bias-correcting the climate projections and assisted on writing the manuscript. Devesh Sharma and K.C. Sharma provided local knowledge during the hydrological model setup and made improvements to the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Buytaert, W.; De Bièvre, B. Water for cities: The impact of climate change and demographic growth in the tropical Andes. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Mirza, M.; Warrick, R.; Ericksen, N. The implications of climate change on floods of the Ganges, Brahmaputra and Meghna rivers in Bangladesh. Clim. Chang. 2003, 57, 287–318. [Google Scholar] [CrossRef]
- Neupane, R.P.; Yao, J.; White, J.D. Estimating the effects of climate change on the intensification of monsoonal-driven stream discharge in a Himalayan watershed. Hydrol. Process. 2014, 28, 6236–6250. [Google Scholar] [CrossRef]
- Singh, P.; Kumar, N. Impact assessment of climate change on the hydrological response of a snow and glacier melt runoff dominated Himalayan river. J. Hydrol. 1997, 193, 316–350. [Google Scholar] [CrossRef]
- Pervez, M.S.; Henebry, G.M. Assessing the impacts of climate and land use and land cover change on the freshwater availability in the Brahmaputra River basin. J. Hydrol. Reg. Stud. 2014, 3, 285–311. [Google Scholar] [CrossRef]
- Singh, P.; Bengtsson, L. Impact of warmer climate on melt and evaporation for the rainfed, snowfed and glacierfed basins in the Himalayan region. J. Hydrol. 2005, 300, 140–154. [Google Scholar] [CrossRef]
- Singh, P.; Arora, M.; Goel, N.K. Effect of climate change on runoff of a glacierized Himalayan basin. Hydrol. Process. 2006, 20, 1979–1992. [Google Scholar] [CrossRef]
- Gosain, A.; Rao, S.; Basuray, D. Climate change impact assessment on hydrology of Indian river basins. Curr. Sci. 2006, 90, 346–353. [Google Scholar]
- Pechlivanidis, I.G.; Olsson, J.; Sharma, D.; Bosshard, T.; Sharma, K.C. Assessment of the climate change impacts on the water resources of the Luni region, India. Glob. NEST J. 2015, 17, 29–40. [Google Scholar]
- Graham, L.P.; Hagemann, S.; Jaun, S.; Beniston, M. On interpreting hydrological change from regional climate models. Clim. Chang. 2007, 81, 97–122. [Google Scholar] [CrossRef]
- Pechlivanidis, I.G.; Jackson, B.; McIntyre, N.; Wheater, H.S. Catchment scale hydrological modelling: A review of model types, calibration approaches and uncertainty analysis methods in the context of recent developments in technology and applications. Glob. NEST J. 2011, 13, 193–214. [Google Scholar]
- Fowler, H.J.; Blenkinsop, S.; Tebaldi, C. Linking climate change modelling to impacts studies : Recent advances in downscaling techniques for hydrological. Int. J. Climatol. 2007, 27, 1547–1578. [Google Scholar] [CrossRef]
- Giorgi, F.; Jones, C.; Asrar, G.R. Addressing climate information needs at the regional level: The CORDEX framework. WMO Bull. 2009, 58, 175–183. [Google Scholar]
- Chaturvedi, R.; Joshi, J.; Jayaraman, M.; Bala, G.; Ravindranath, N. Multi-model climate change projections for India under representative concentration pathways. Curr. Sci. 2012, 103, 1–12. [Google Scholar]
- Foley, A. Uncertainty in regional climate modelling: A review. Prog. Phys. Geogr. 2010, 34, 647–670. [Google Scholar] [CrossRef]
- Haylock, M.R.; Cawley, G.C.; Harpham, C.; Wilby, R.L.; Goodess, C.M. Downscaling heavy precipitation over the United Kingdom: A comparison of dynamical and statistical methods and their future scenarios. Int. J. Climatol. 2006, 26, 1397–1415. [Google Scholar] [CrossRef]
- Wetterhall, F.; Pappenberger, F.; He, Y.; Freer, J.; Cloke, H.L. Conditioning model output statistics of regional climate model precipitation on circulation patterns. Nonlinear Process. Geophys. 2012, 19, 623–633. [Google Scholar] [CrossRef]
- Teutschbein, C.; Seibert, J. Bias correction of regional climate model simulations for hydrological climate-change impact studies: Review and evaluation of different methods. J. Hydrol. 2012, 456–457, 12–29. [Google Scholar] [CrossRef]
- Déqué, M. Frequency of precipitation and temperature extremes over France in an anthropogenic scenario: Model results and statistical correction according to observed values. Glob. Planet. Change 2007, 57, 16–26. [Google Scholar] [CrossRef]
- Lenderink, G.; Buishand, A.; van Deursen, W. Estimates of future discharges of the river Rhine using two scenario methodologies: Direct versus delta approach. Hydrol. Earth Syst. Sci. 2007, 11, 1145–1159. [Google Scholar] [CrossRef]
- Chen, H.; Xu, C.-Y.; Guo, S. Comparison and evaluation of multiple GCMs, statistical downscaling and hydrological models in the study of climate change impacts on runoff. J. Hydrol. 2012, 434–435, 36–45. [Google Scholar] [CrossRef]
- Minville, M.; Brissette, F.; Leconte, R. Uncertainty of the impact of climate change on the hydrology of a nordic watershed. J. Hydrol. 2008, 358, 70–83. [Google Scholar] [CrossRef]
- Preston, B.L.; Jones, R.N. Evaluating sources of uncertainty in Australian runoff projections. Adv. Water Resour. 2008, 31, 758–775. [Google Scholar] [CrossRef]
- Chiew, F.H.S.; Teng, J.; Vaze, J.; Kirono, D.G.C. Influence of global climate model selection on runoff impact assessment. J. Hydrol. 2009, 379, 172–180. [Google Scholar] [CrossRef]
- Jones, R.N.; Chiew, F.H.S.; Boughton, W.C.; Zhang, L. Estimating the sensitivity of mean annual runoff to climate change using selected hydrological models. Adv. Water Resour. 2006, 29, 1419–1429. [Google Scholar] [CrossRef]
- Hawkins, E.; Sutton, R. The potential to narrow uncertainty in regional climate predictions. Bull. Am. Meteorol. Soc. 2009, 90, 1095–1107. [Google Scholar] [CrossRef]
- Bueh, C.; Cubasch, U.; Hagemann, S. Impacts of global warming on changes in the East Asian monsoon and the related river discharge in a global time-slice experiment. Clim. Res. 2003, 24, 47–57. [Google Scholar] [CrossRef]
- Lucas-Picher, P.; Christensen, J.H.; Saeed, F.; Kumar, P.; Asharaf, S.; Ahrens, B.; Wiltshire, A.J.; Jacob, D.; Hagemann, S. Can regional climate models represent the Indian monsoon? J. Hydrometeorol. 2011, 12, 849–868. [Google Scholar] [CrossRef]
- Aich, V.; Liersch, S.; Vetter, T.; Huang, S.; Tecklenburg, J.; Hoffmann, P.; Koch, H.; Fournet, S.; Krysanova, V.; Müller, E.N.; Hattermann, F.F. Comparing impacts of climate change on streamflow in four large African river basins. Hydrol. Earth Syst. Sci. 2014, 18, 1305–1321. [Google Scholar] [CrossRef]
- Huang, S.; Krysanova, V.; Hattermann, F. Projections of climate change impacts on floods and droughts in Germany using an ensemble of climate change scenarios. Reg. Environ. Chang. 2014, 15, 461–473. [Google Scholar] [CrossRef]
- Gosain, A.; Rao, S.; Arora, A. Climate change impact assessment of water resources of India. Curr. Sci. 2011, 101, 356–371. [Google Scholar]
- Raje, D.; Priya, P.; Krishnan, R. Macroscale hydrological modelling approach for study of large scale hydrologic impacts under climate change in Indian river basins. Hydrol. Process. 2013, 28, 1874–1889. [Google Scholar] [CrossRef]
- Blöschl, G.; Sivapalan, M.; Wagener, T.; Viglione, A.; Savenije, H. Runoff Prediction in Ungauged Basins. Synthesis across Processes, Places and Scales; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Gupta, H.V.; Perrin, C.; Blöschl, G.; Montanari, A.; Kumar, R.; Clark, M.; Andréassian, V. Large-sample hydrology: A need to balance depth with breadth. Hydrol. Earth Syst. Sci. 2014, 18, 463–477. [Google Scholar] [CrossRef]
- Yang, W.; Andréasson, J.; Graham, P.L.; Olsson, J.; Rosberg, J.; Wetterhall, F. Distribution-based scaling to improve usability of regional climate model projections for hydrological climate change impacts studies. Hydrol. Res. 2010, 41, 211–229. [Google Scholar] [CrossRef]
- Lindström, G.; Pers, C.; Rosberg, J.; Strömqvist, J.; Arheimer, B. Development and testing of the HYPE (Hydrological Predictions for the Environment) water quality model for different spatial scales. Hydrol. Res. 2010, 41, 295–319. [Google Scholar] [CrossRef]
- Attri, S.D.; Tyagi, A. Climate Profile of India; Government of India Ministry of Earth Sciences: New Delhi, India, 2010; p. 129.
- Mall, R.K.; Singh, R.; Gupta, A.; Srinivasan, G.; Rathore, L.S. Impact of Climate Change on Indian Agriculture: A Review. Clim. Change 2006, 78, 445–478. [Google Scholar] [CrossRef]
- Li, L.; Xu, C.-Y.; Zhang, Z.; Jain, S.K. Validation of a new meteorological forcing data in analysis of spatial and temporal variability of precipitation in India. Stoch. Environ. Res. Risk Assess. 2013, 28, 239–252. [Google Scholar] [CrossRef]
- Pechlivanidis, I.G.; Arheimer, B. Large-scale hydrological modelling by using modified PUB recommendations: the India-HYPE case. Hydrol. Earth Syst. Sci. 2015, 19, 4559–4579. [Google Scholar] [CrossRef]
- Yatagai, A.; Kamiguchi, K.; Arakawa, O.; Hamada, A.; Yasutomi, N.; Kitoh, A. APHRODITE: Constructing a long-term daily gridded precipitation dataset for Asia based on a dense network of rain gauges. Bull. Am. Meteorol. Soc. 2012, 93, 1401–1415. [Google Scholar] [CrossRef]
- Yatagai, A.; Arakawa, O.; Kamiguchi, K. A 44-year daily gridded precipitation dataset for Asia based on a dense network of rain gauges. Sola 2009, 5, 137–140. [Google Scholar] [CrossRef]
- Yasutomi, N.; Hamada, A.; Yatagai, A. Development of a long-term daily gridded temperature dataset and its application to rain/snow discrimination of daily precipitation. Glob. Environ. Res. 2011, 3, 165–172. [Google Scholar]
- Hazeleger, W.; Wang, X.; Severijns, C.; Ştefănescu, S.; Bintanja, R.; Sterl, A.; Wyser, K.; Semmler, T.; Yang, S.; van den Hurk, B.; van Noije, T.; van der Linden, E.; van der Wiel, K. EC-Earth V2.2: Description and validation of a new seamless earth system prediction model. Clim. Dyn. 2012, 39, 2611–2629. [Google Scholar] [CrossRef]
- Samuelsson, P.; Collin, G.J.; Willén, U.; Ullerstig, A.; Gollvik, S.; Hansson, U.; Jansson, C.; Kjellström, E.; Nikulin, G.; Wyser, K. The Rossby Centre Regional Climate model RCA3: Model description and performance. Tellus 2011, 63A, 4–23. [Google Scholar] [CrossRef]
- Moss, R.H.; Edmonds, J.A.; Hibbard, K.A.; Manning, M.R.; Rose, S.K.; van Vuuren, D.; Carter, T.R.; Emori, S.; Kainuma, M.; Kram, T.; et al. The next generation of scenarios for climate change research and assessment. Nature 2010, 463, 747–756. [Google Scholar] [CrossRef] [PubMed]
- Ghimire, S.; Choudhary, A.; Dimri, A.P. Assessment of the performance of CORDEX‑South Asia experiments for monsoonal precipitation over the Himalayan region during present climate: Part I. Clim. Dyn. 2015. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration, Guidelines for Computing Crop Water Requirements-FAO Irrigation and Drainage Paper 56; Food and Agriculture Organization of the United Nations (FAO): Rome, Italy, 1998. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Rana, A.; Foster, K.; Bosshard, T.; Olsson, J.; Bengtsson, L. Impact of climate change on rainfall over Mumbai using Distribution-based Scaling of Global Climate Model projections. J. Hydrol. Reg. Stud. 2014, 1, 107–128. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Themeßl, M.J.; Gobiet, A.; Heinrich, G. Empirical-statistical downscaling and error correction of regional climate models and its impact on the climate change signal. Clim. Change 2012, 112, 449–468. [Google Scholar] [CrossRef]
- Kotlarski, S.; Bosshard, T.; Lüthi, D.; Pall, P.; Schär, C. Elevation gradients of European climate change in the regional climate model COSMO-CLM. Clim. Change 2012, 112, 189–215. [Google Scholar] [CrossRef]
- Cherchi, A.; Alessandri, A.; Masina, S.; Navarra, A. Effects of increased CO2 levels on monsoons. Clim. Dyn. 2010, 37, 83–101. [Google Scholar] [CrossRef]
- Kripalani, R.H.; Oh, J.H.; Kulkarni, A.; Sabade, S.S.; Chaudhari, H.S. South Asian summer monsoon precipitation variability: Coupled climate model simulations and projections under IPCC AR4. Theor. Appl. Climatol. 2007, 90, 133–159. [Google Scholar] [CrossRef]
- Goswami, B.N.; Venugopal, V.; Sengupta, D.; Madhusoodanan, M.S.; Xavier, P.K. Increasing trend of extreme rain events over India in a warming environment. Science 2006, 314, 1442–1445. [Google Scholar] [CrossRef] [PubMed]
- Kumar, K.K.; Patwardhan, S.K.; Kulkarni, A.; Kamala, K.; Rao, K.K.; Jones, R. Future projection of Indian summer monsoon variability under climate change scenario: An assessment from CMIP5 climate models. Curr. Sci. 2011, 101, 312–326. [Google Scholar]
- Sharmila, S.; Joseph, S.; Sahai, A.K.; Abhilash, S.; Chattopadhyay, R. Future projection of Indian summer monsoon variability under climate change scenario: An assessment from CMIP5 climate models. Glob. Planet. Chang. 2014, 124, 62–78. [Google Scholar] [CrossRef]
- Salvi, K.; Kannan, S.; Ghosh, S. High-resolution multisite daily rainfall projections in India with statistical downscaling for climate change impacts assessment. J. Geophys. Res. Atmos. 2013, 118, 3557–3578. [Google Scholar] [CrossRef]
- Ojha, R.; Kumar, D.N.; Sharma, A.; Mehrotra, R. Assessing severe drought and wet events over India in a future climate using a nested bias-correction approach. J. Hydrol. Eng. 2013, 18, 760–772. [Google Scholar] [CrossRef]
- Amarasinghe, U.A.; Sharma, B.R.; Aloysius, N.; Scott, C.; Smakhtin, V.; de Fraiture, C. Spatial Variation in Water Supply and Demand across River Basins of India; Research Report 83; International Water Management Institute: Colombo, Sri Lanka, 2004. [Google Scholar] [CrossRef]
- Jhajharia, D.; Shrivastava, S.K.; Sarkar, D.; Sarkar, S. Temporal characteristics of pan evaporation trends under the humid conditions of northeast India. Agric. For. Meteorol. 2009, 149, 763–770. [Google Scholar] [CrossRef]
- Jhajharia, D.; Dinpashoh, Y.; Kahya, E.; Choudhary, R.R.; Singh, V.P. Trends in temperature over Godavari River basin in Southern Peninsular India. Int. J. Climatol. 2014, 34, 1369–1384. [Google Scholar] [CrossRef]
- McVicar, T.R.; Roderick, M.L.; Donohue, R.J.; Li, L.T.; van Niel, T.G.; Thomas, A.; Grieser, J.; Jhajharia, D.; Himri, Y.; Mahowald, N.M.; et al. Global review and synthesis of trends in observed terrestrial near-surface wind speeds: Implications for evaporation. J. Hydrol. 2012, 416–417, 182–205. [Google Scholar] [CrossRef]
- Schewe, J.; Heinke, J.; Gerten, D.; Haddeland, I.; Arnell, N.W.; Clark, D.B.; Dankers, R.; Eisner, S.; Fekete, B.M.; Colón-González, F.J.; et al. Multimodel assessment of water scarcity under climate change. PNAS 2014, 111, 3245–3250. [Google Scholar] [CrossRef] [PubMed]
- Immerzeel, W.W.; Droogers, P.; de Jong, S.M.; Bierkens, M.F.P. Large-scale monitoring of snow cover and runoff simulation in Himalayan river basins using remote sensing. Remote Sens. Environ. 2009, 113, 40–49. [Google Scholar] [CrossRef]
- Masood, M.; Yeh, P.J.-F.; Hanasaki, N.; Takeuchi, K. Model study of the impacts of future climate change on the hydrology of Ganges–Brahmaputra–Meghna (GBM) basin. Hydrol. Earth Syst. Sci. Discuss. 2014, 11, 5747–5791. [Google Scholar] [CrossRef]
- Mukhopadhyay, B. Signature and hydrologic consequences of climate change within the upper-middle Brahmaputra Basin. Hydrol. Process. 2013, 27, 2126–2143. [Google Scholar] [CrossRef]
- Meenu, R.; Rehana, S.; Mujumdar, P. Assessment of hydrologic impacts of climate change in Tunga–Bhadra river basin, India with HEC-HMS and SDSM. Hydrol. Process. 2013, 27, 1572–1589. [Google Scholar] [CrossRef]
- Kauffeldt, A.; Halldin, S.; Rodhe, A.; Xu, C.-Y.; Westerberg, I.K. Disinformative data in large-scale hydrological modelling. Hydrol. Earth Syst. Sci. 2013, 17, 2845–2857. [Google Scholar] [CrossRef]
- Hagemann, S.; Chen, C.; Haerter, J.O.; Heinke, J.; Gerten, D.; Piani, C. Impact of a statistical bias correction on the projected hydrological changes obtained from three GCMs and two hydrology models. J. Hydrometeorol. 2011, 12, 556–578. [Google Scholar] [CrossRef]
- Pechlivanidis, I.G.; Arheimer, B.; Donnelly, C.; Hundecha, Y.; Huang, S.; Aich, V.; Samaniego, L.; Eisner, S.; Shi, P. Analysis of hydrological extremes at different hydro-climatic regimes under present and future conditions. Clim. Chang. 2016. submitted. [Google Scholar]
- Wagner, P.D.; Kumar, S.; Schneider, K. An assessment of land use change impacts on the water resources of the Mula and Mutha Rivers catchment upstream of Pune, India. Hydrol. Earth Syst. Sci. 2013, 17, 2233–2246. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).