SPI Based Meteorological Drought Assessment over a Humid Basin: Effects of Processing Schemes
Abstract
:1. Introduction
2. Materials and Methods
2.1. Methods
2.1.1. Standardized Precipitation Index
2.1.2. Thiessen Polygon Approach
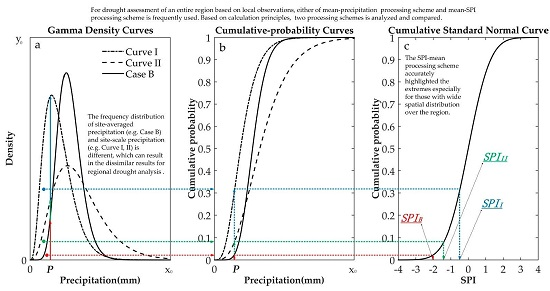
2.1.3. Two Processing Schemes for Regional SPI
2.1.4. Metrics for Comparison
2.2. Study Area and Data Sources
3. Results
3.1. Areal Weights Obtained from the Thiessen Polygons Approach
3.2. Frequency Distribution of Site-Scale and Site-Averaged Precipitation
3.3. Comparison of Case A and Case B for Drought Identification
3.4. Difference in Drought Identification between Two Processing Schemes
4. Discussion
5. Conclusions
- (1)
- Both processing schemes could express the similar monitoring trends, number of drought events, and drought duration as well. However, the drought severity in the case of the precipitation-mean scheme was generally smaller than that of the SPI-mean scheme.
- (2)
- The difference from two processing schemes had a significantly positive correlation with the number of stations monitoring drought (p < 0.005). Moreover, sometimes, the difference was so large that it could change meteorological drought levels.
- (3)
- The precipitation-mean scheme reduced the extent of precipitation deficits and made the precipitation more clustered in some certain. Meanwhile, it made less precipitation deviate from the precipitation-mean series farther when the less precipitation has wide spatial distribution over the region. However, the SPI-mean scheme can accurately highlight the relatively serious and universal dry situations occurred over the region. Therefore, on regional meteorological drought monitored effectively basis, for representing regional meteorological drought reliably, the SPI-mean scheme is more likely to satisfy the physical.
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Rossi, G.; Benedini, M.; Tsakiris, G.; Giakoumakis, S. On regional drought estimation and analysis. Water Resour. Manag. 1992, 6, 249–277. [Google Scholar] [CrossRef]
- Obasi, G.O.P. Wmo’s role in the international decade for natural disaster reduction. Bull. Am. Meteorol. Soc. 1994, 75, 1655–1661. [Google Scholar] [CrossRef]
- Spinoni, J.; Naumann, G.; Carrao, H.; Barbosa, P.; Vogt, J. World drought frequency, duration, and severity for 1951–2010. Int. J. Climatol. 2014, 34, 2792–2804. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. A review of drought concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- Mpelasoka, F.; Hennessy, K.; Jones, R.; Bates, B. Comparison of suitable drought indices for climate change impacts assessment over australia towards resource management. Int. J. Climatol. 2008, 28, 1283–1292. [Google Scholar] [CrossRef]
- Kallis, G. Droughts. Annu. Rev. Environ. Resour. 2008, 33, 85–118. [Google Scholar] [CrossRef]
- Gumbel, E.J. Statistical forecast of droughts. Int. Assoc. Sci. Hydrol. Bull. 1963, 8, 5–23. [Google Scholar] [CrossRef]
- Palmer, W.C. Meteorological Drought; US Department of Commerce, Weather Bureau: Washington, DC, USA, 1965.
- Dracup, J.A.; Lee, K.S.; Paulson, E.G., Jr. On the definition of droughts. Water Resour. Res. 1980, 16, 297–302. [Google Scholar] [CrossRef]
- Wilhite, D.; Glantz, M. Understanding: The drought phenomenon: The role of definitions. Water Int. 1985, 10, 111–120. [Google Scholar] [CrossRef]
- Stanley, A.; Changnon, J.; Easterllng, W.E. Measuring drought impacts the illinois case. Water Resour. Bull. 1989, 25, 27–42. [Google Scholar]
- Hao, Z.C.; Singh, V.P. Drought characterization from a multivariate perspective: A review. J. Hydrol. 2015, 527, 668–678. [Google Scholar] [CrossRef]
- Society, A.M. Policy statement: Meteorological drought. Bull. Am. Meteorol. Soc. 1997, 78, 847–849. [Google Scholar]
- Peters, E. Propagation of Drought through Groundwater Systems: Illustrated in the Pang (UK) and Upper-guadiana (es) Catchments. Ph.D. Thesis, Wageningen University, Wageningen, The Netherlands, 2003. [Google Scholar]
- Zargar, A.; Sadiq, R.; Naser, B.; Khan, F.I. A review of drought indices. Environ. Rev. 2011, 19, 333–349. [Google Scholar] [CrossRef]
- Eltahir, E.A.B.; Yeh, P.J.F. On the asymmetric response of aquifer water level to floods and droughts in illinois. Water Resour. Res. 1999, 35, 1199–1217. [Google Scholar] [CrossRef]
- Peters, E.; Torfs, P.J.J.F.; van Lanen, H.A.J.; Bier, G. Propagation of drought through groundwater—A new approach using linear reservoir theory. Hydrol. Process. 2003, 17, 3023–3040. [Google Scholar] [CrossRef]
- Van Loon, A.F.; van Lanen, H.A.J.; Tallaksen, L.M.; Hanel, M.; Fendeková, M.; Machlica, A.; Sapriza, G.; Koutroulis, A.; van Huijgevoort, M.H.J.; Jódar Bermúdez, J.; et al. Propagation of Drought through the Hydrological Cycle; WATCH Technical Report 31; Wageningen University: Wageningen, The Netherlands, 2011. [Google Scholar]
- Potop, V. Evolution of drought severity and its impact on corn in the republic of moldova. Theor. Appl. Climatol. 2011, 105, 469–483. [Google Scholar] [CrossRef]
- Al-Faraj, F.A.M.; Scholz, M.; Tigkas, D.; Boni, M. Drought indices supporting drought management in transboundary watersheds subject to climate alterations. Water Policy 2015, 17, 865–886. [Google Scholar] [CrossRef]
- Akhtari, R.; Morid, S.; Mahdian, M.H.; Smakhtin, V. Assessment of areal interpolation methods for spatial analysis of spi and edi drought indices. Int. J. Climatol. 2009, 29, 135–145. [Google Scholar] [CrossRef]
- Zhang, Q.; Sun, P.; Li, J.; Xiao, M.; Singh, V.P. Assessment of drought vulnerability of the Tarim River basin, Xinjiang, China. Theor. Appl. Climatol. 2014, 121, 337–347. [Google Scholar] [CrossRef]
- Pei, W.; Fu, Q.; Liu, D.; Li, T.-X.; Cheng, K. Assessing agricultural drought vulnerability in the Sanjiang plain based on an improved projection pursuit model. Nat. Hazards 2016, 82, 683–701. [Google Scholar] [CrossRef]
- Tallaksen, L.M.; Hisdal, H.; Lanen, H.A.J.V. Space-time modelling of catchment scale drought characteristics. J. Hydrol. 2009, 375, 363–372. [Google Scholar] [CrossRef]
- Vrochidou, A.E.K.; Tsanis, I.K.; Grillakis, M.G.; Koutroulis, A.G. The impact of climate change on hydrometeorological droughts at a basin scale. J. Hydrol. 2013, 476, 290–301. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology; American Meteorological Society: Boston, MA, USA, 1993; Volume 17, pp. 179–183. [Google Scholar]
- Byun, H.-R.; Wilhite, D.A. Objective quantification of drought severity and duration. J. Clim. 1999, 12, 2747–2756. [Google Scholar] [CrossRef]
- Tsakiris, G.; Vangelis, H. Establishing a drought index incorporating evapotranspiration. Eur. Water 2005, 9, 3–11. [Google Scholar]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A multiscalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Hayes, M.J.; Svoboda, M.D.; Wilhite, D.A.; Vanyarkho, O.V. Monitoring the 1996 drought using the standardized precipitation index. Bull. Am. Meteorol. Soc. 1999, 80, 429–438. [Google Scholar] [CrossRef]
- Livada, I.; Assimakopoulos, V.D. Spatial and temporal analysis of drought in greece using the standardized precipitation index (SPI). Theor. Appl. Climatol. 2007, 89, 143–153. [Google Scholar] [CrossRef]
- Shiau, J.T.; Modarres, R. Copula-based drought severity-duration-frequency analysis in iran. Meteorol. Appl. 2009, 16, 481–489. [Google Scholar] [CrossRef]
- Qian, B.; Zhang, X.; Chen, K.; Feng, Y.; O’Brien, T. Observed long-term trends for agroclimatic conditions in Canada. J. Appl. Meteorol. Climatol. 2010, 49, 604–618. [Google Scholar] [CrossRef]
- Bonsal, B.R.; Aider, R.; Gachon, P.; Lapp, S. An assessment of canadian prairie drought: Past, present, and future. Clim. Dyn. 2013, 41, 501–516. [Google Scholar] [CrossRef]
- Jenkins, K.; Warren, R. Quantifying the impact of climate change on drought regimes using the standardised precipitation index. Theor. Appl. Climatol. 2015, 120, 41–54. [Google Scholar] [CrossRef] [Green Version]
- Merino, A.; López, L.; Hermida, L.; Sánchez, J.L.; García-Ortega, E.; Gascón, E.; Fernández-González, S. Identification of drought phases in a 110-year record from western mediterranean basin: Trends, anomalies and periodicity analysis for iberian peninsula. Glob. Planet. Chang. 2015, 133, 96–108. [Google Scholar] [CrossRef]
- Svoboda, M.D.; Fuchs, B.A.; Poulsen, C.C.; Nothwehr, J.R. The drought risk atlas: Enhancing decision support for drought risk management in the United States. J. Hydrol. 2015, 526, 274–286. [Google Scholar] [CrossRef]
- Hayes, M.; Svoboda, M.; Wall, N.; Widhalm, M. The lincoln declaration on drought indices: Universal meteorological drought index recommended. Bull. Am. Meteorol. Soc. 2011, 92, 485–488. [Google Scholar] [CrossRef]
- Zhai, J.; Su, B.; Krysanova, V.; Vetter, T.; Gao, C.; Jiang, T. Spatial variation and trends in PDSI and SPI indices and their relation to streamflow in 10 large regions of China. J. Clim. 2010, 23, 649–663. [Google Scholar] [CrossRef]
- Gao, L.; Zhang, Y. Spatio-temporal variation of hydrological drought under climate change during the period 1960–2013 in the Hexi Corridor, China. J. Arid Land 2016, 8, 157–171. [Google Scholar] [CrossRef]
- Dash, B.K.; Rafiuddin, M.; Khanam, F.; Islam, M.N. Characteristics of meteorological drought in Bangladesh. Nat. Hazards 2012, 64, 1461–1474. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P.; Desai, V.R. Drought characterization: A probabilistic approach. Stoch. Environ. Res. Risk Assess. 2007, 23, 41–55. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M. Differences in spatial patterns of drought on different time scales: An analysis of the iberian peninsula. Water Resour. Manag. 2006, 20, 37–60. [Google Scholar] [CrossRef]
- The Ramsar Convention. The List of Wetlands of International Importance. Available online: http://www.ramsar.org/document/the-list-of-wetlands-of-international-importance-the-ramsar-list (accessed on 3 May 2016).
- Liu, Y.; Wu, G. Hydroclimatological influences on recently increased droughts in China’s largest freshwater lake. Hydrol. Earth Syst. Sci. 2016, 20, 93–107. [Google Scholar] [CrossRef]
- Liu, Y.B.; Wu, G.; Guo, R.F.; Wang, R.G. Changing landscapes by damming: The three gorges dam causes downstream lake shrinkage and severe droughts. Landsc. Ecol. 2016. [Google Scholar] [CrossRef]
- Thom, H.C.S. A note on the gamma distribution. Mon. Weather Rev. 1958, 86, 117–122. [Google Scholar] [CrossRef]
- Milton, A.; Stegun, I.A. Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables; Courier Corporation: New York, NY, USA, 1965. [Google Scholar]
- Johnson, D.; Smith, M.; Koren, V.; Finnerty, B. Comparing mean areal precipitation estimates from nexrad and rain gauge networks. J. Hydrol. Eng. 1999, 4, 117–124. [Google Scholar] [CrossRef]
- Fiedler, F. Simple, practical method for determining station weights using thiessen polygons and isohyetal maps. J. Hydrol. Eng. 2003, 8, 219–221. [Google Scholar] [CrossRef]
- Squires, G.L. Practical Physics; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Gosset, M.; Viarre, J.; Quantin, G.; Alcoba, M. Evaluation of several rainfall products used for hydrological applications over west africa using two high-resolution gauge networks. Q. J. R. Meteorol. Soc. 2013, 139, 923–940. [Google Scholar] [CrossRef]
- Hu, Q.; Feng, S.; Guo, H.; Chen, G.; Jiang, T. Interactions of the yangtze river flow and hydrologic processes of the Poyang Lake, China. J. Hydrol. 2007, 347, 90–100. [Google Scholar] [CrossRef]
- Canadell, J.G.; Steffen, W.L.; White, P.S. Igbp_gcte terrestrial transects dynamics ofterrestrial ecosystems under environmental change. J. Veg. Sci. 2002, 13, 297–450. [Google Scholar]
- Liu, Y.; Wu, G.; Zhao, X. Recent declines in China’s largest freshwater lake: Trend or regime shift? Environ. Res. Lett. 2013, 8, 014010. [Google Scholar] [CrossRef]
- Janga Reddy, M.; Ganguli, P. Application of copulas for derivation of drought severity-duration-frequency curves. Hydrol. Process. 2012, 26, 1672–1685. [Google Scholar] [CrossRef]
- Tao, H.; Fischer, T.; Zeng, Y.; Fraedrich, K. Evaluation of TRMM 3B43 precipitation data for drought monitoring in Jiangsu Province, China. Water 2016, 8, 221. [Google Scholar] [CrossRef]








| SPI Range | Drought Classes |
|---|---|
| [2.0, +) | Extremely wet |
| [1.5, 2.0) | Very wet |
| [1.0, 1.5) | Moderate wet |
| (−1.0, 1.0) | Near normal |
| (−1.5, −1.0] | Moderate drought |
| (−2.0, −1.5] | Severe drought |
| (−, −2.0] | Extreme drought |
| Station Code | Area of Corresponding Thiessen Polygon (km2) | Weighting Value |
|---|---|---|
| 57598 | 12,509 | 0.0772 |
| 57793 | 11,323 | 0.0699 |
| 57799 | 12,993 | 0.0802 |
| 57896 | 11,587 | 0.0715 |
| 57993 | 25,241 | 0.1558 |
| 58519 | 9797 | 0.0605 |
| 58527 | 12,417 | 0.0767 |
| 58606 | 11,966 | 0.0739 |
| 58608 | 11,324 | 0.0699 |
| 58626 | 10,472 | 0.0646 |
| 58634 | 8448 | 0.0522 |
| 58715 | 10,220 | 0.0631 |
| 58813 | 13,683 | 0.0845 |
| Station Code | Jan. | Feb. | Mar. | Apr. | May | Jun. | Jul. | Aug. | Sep. | Oct. | Nov. | Dec. |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 57598 | 3.60 | 3.12 | 5.77 | 4.81 | 6.18 | 5.48 | 2.13 | 3.05 | 2.18 | 1.96 | 1.46 | 1.61 |
| 57793 | 2.81 | 4.68 | 6.83 | 8.52 | 4.80 | 4.77 | 2.17 | 2.35 | 2.28 | 1.70 | 1.56 | 1.20 |
| 57799 | 2.45 | 3.15 | 6.02 | 7.76 | 4.58 | 4.68 | 2.22 | 1.49 | 1.39 | 1.04 | 1.22 | 1.20 |
| 57896 | 1.97 | 2.12 | 4.25 | 6.42 | 8.77 | 5.26 | 1.86 | 2.53 | 2.84 | 1.00 | 1.24 | 1.15 |
| 57993 | 1.41 | 1.70 | 4.02 | 5.12 | 6.10 | 4.09 | 1.98 | 2.86 | 1.89 | 0.75 | 1.11 | 1.29 |
| 58519 | 2.64 | 3.32 | 5.41 | 5.67 | 4.09 | 3.84 | 2.04 | 1.52 | 0.97 | 1.64 | 1.39 | 1.35 |
| 58527 | 2.91 | 3.14 | 5.19 | 5.81 | 6.09 | 4.49 | 1.73 | 1.59 | 1.72 | 1.33 | 1.32 | 1.47 |
| 58606 | 2.61 | 3.04 | 6.06 | 5.57 | 4.17 | 5.26 | 2.12 | 1.71 | 1.23 | 1.60 | 1.19 | 1.23 |
| 58608 | 2.46 | 3.70 | 6.08 | 8.33 | 4.83 | 4.30 | 2.06 | 1.67 | 1.89 | 1.36 | 1.31 | 1.32 |
| 58626 | 2.95 | 3.77 | 6.63 | 6.80 | 5.55 | 4.02 | 2.24 | 2.13 | 2.07 | 1.61 | 1.33 | 1.40 |
| 58634 | 3.44 | 3.53 | 5.87 | 6.49 | 5.47 | 4.29 | 1.39 | 1.97 | 2.47 | 1.58 | 1.23 | 1.23 |
| 58715 | 2.37 | 3.60 | 5.96 | 6.64 | 6.04 | 4.85 | 1.65 | 2.51 | 1.65 | 1.07 | 1.21 | 1.27 |
| 58813 | 1.87 | 2.76 | 4.93 | 5.75 | 5.89 | 3.94 | 1.90 | 3.02 | 1.62 | 0.73 | 1.12 | 1.38 |
| Case B | 2.65 | 4.52 | 8.31 | 9.96 | 9.22 | 10.53 | 4.34 | 4.82 | 4.35 | 1.37 | 1.68 | 1.51 |
| No. of Drought Events | Drought Duration (Months) Mean ± SD (max) | Drought Severity Mean ± SD (Max) | |
|---|---|---|---|
| Case A | 161 | 2.13 ± 1.72 (11) | 1.36 ± 1.33 (9.63) |
| Case B | 162 | 2.13 ± 1.69 (11) | 1.70 ± 1.65 (12.26) |
| ΔSPI | ≥7 Stations | ≥9 Stations | ≥10 Stations |
|---|---|---|---|
| Extreme droughts | 0.616 ± 0.559 | 0.675 ± 0.658 | 0.759 ± 0.761 |
| Severe droughts and above | 0.412 ± 0.409 | 0.462 ± 0.499 | 0.496 ± 0.510 |
| Moderate droughts and above | 0.305 ± 0.313 | 0.339 ± 0.360 | 0.368 ± 0.365 |
| Month | Slope | Intercept | R2 | Min (SPIA, SPIB) | Max (SPIA, SPIB) |
|---|---|---|---|---|---|
| January | 1.1037 | 0.0004 | 0.9882 | (−2.31, −3.25) | (2.37, 2.49) |
| February | 1.1736 | −0.0067 | 0.9899 | (−2.19, −2.64) | (2.24, 2.72) |
| March | 1.2272 | −0.0003 | 0.9964 | (−1.76, −2.10) | (2.78, 3.39) |
| April | 1.2631 | 0.0004 | 0.9971 | (−2.17, −2.62) | (1.35, 1.88) |
| May | 1.2879 | −0.0010 | 0.9943 | (−2.03, −2.57) | (1.53, 1.97) |
| June | 1.5625 | 0.0002 | 0.9816 | (−1.45, −2.37) | (1.60, 2.48) |
| July | 1.4022 | −0.0045 | 0.9752 | (−1.79, −2.33) | (1.45, 2.10) |
| August | 1.4210 | −0.0052 | 0.9912 | (−1.88, −2.55) | (1.60, 2.50) |
| September | 1.3862 | −0.0104 | 0.9798 | (−1.75, −2.59) | (1.88, 2.75) |
| October | 1.1900 | 0.0002 | 0.9318 | (−2.04, −4.20) | (1.63, 1.94) |
| November | 1.1235 | −0.0057 | 0.9956 | (−2.31, −2.58) | (1.80, 2.02) |
| December | 1.0925 | −0.0032 | 0.9965 | (−2.27, −2.65) | (1.80, 1.97) |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, H.; Liu, Y. SPI Based Meteorological Drought Assessment over a Humid Basin: Effects of Processing Schemes. Water 2016, 8, 373. https://doi.org/10.3390/w8090373
Zhou H, Liu Y. SPI Based Meteorological Drought Assessment over a Humid Basin: Effects of Processing Schemes. Water. 2016; 8(9):373. https://doi.org/10.3390/w8090373
Chicago/Turabian StyleZhou, Han, and Yuanbo Liu. 2016. "SPI Based Meteorological Drought Assessment over a Humid Basin: Effects of Processing Schemes" Water 8, no. 9: 373. https://doi.org/10.3390/w8090373
APA StyleZhou, H., & Liu, Y. (2016). SPI Based Meteorological Drought Assessment over a Humid Basin: Effects of Processing Schemes. Water, 8(9), 373. https://doi.org/10.3390/w8090373