A New Method for Evaluating Riverside Well Locations Based on Allowable Withdrawal

Abstract

This study aims to derive the optimal solution for well locations based on the allowable withdrawal. To demonstrate the proposed technique, a numerical model of a typical well field at the Qinbei Power Plant was constructed and 20 possible drawdown scenarios were simulated for each of three different arrangements of pumping wells. The concept of the Unit Increased Drawdown Value (UIDV) was used as a basis to select the location of pumping wells, where the UIDV is defined as the increase in drawdown associated with the addition of a unit of extraction. Results showed that for modeled well fields with the same number of wells and rates of exploitation, drawdown will reach the maximum and minimum when the well field is located in the recharge zone and discharge zone, respectively, because of the specific relationships between groundwater and surface water. This paper considered a pumping program with maximum exploitation and minimum costs corresponding to allowable withdrawals of 2.44 m³/s and 1.07 m³/s, respectively, and the relationship between groundwater and surface water was elucidated. The study results provide a theoretical basis for the layout of wells. The solution takes economic factors into consideration and describes the best solution for well locations to meet drawdown limitations during pumping applications.

1. Introduction

Construction and use of riverside groundwater well fields is advantageous for several reasons including the good recharge conditions and excellent opportunities for centralized exploitation and management compared to surface water [1,2]. With the treatment of water as it passes through the unsaturated zone, the quality of riverside groundwater is generally better and more stable than that of surface water. Additionally, owing to the close interaction between aquifers and river water, riverside aquifers typically have higher storage capacities than other types of aquifers [3]. For these reasons, exploitation near a river has become one of the main attributes of optimal groundwater resource utilization.

However, despite the above benefits, inappropriate exploitation of groundwater during practical work may have deleterious consequences. For example, if the upstream water cycle changes (such as during reservoir construction) or human activities change, the river flow may be affected, and thus, the supply to pumping wells would also be affected; declines in groundwater levels can directly threaten ecosystems and agriculture in surrounding areas, and excessive capture of river water may even cause reductions in stream flows, which can damage downstream ecosystems. Therefore, how to carry on a reasonable groundwater extraction project along a river has become an important problem addressed in recent years.

Pumping wells play an important role during groundwater extraction. The literature about groundwater pumping wells is diverse. In the early 1960s, there was much research and discussion into the problems involved with the construction and arrangement of extraction wells. Lerner [4] predicted pumping water levels in single and multiple wells by using regional groundwater models and derived methods that could adjust data according to changes in the water table; these methods were deemed applicable for partially penetrating wells. Székely [5] presented a computing method to estimate the drawdown and the development of flow in wells with multiple or long screens. Jiao and Rushton [6] conducted a sensitivity analysis of the drawdown’s response to various parameters and studied the influence of parameter estimation on pumping tests in large-diameter wells. Singh [7] discussed the well storage effect during pumping tests in a low permeability aquifer. Singh [8] proposed an optimization method for estimating the transmissivity, storage coefficient, and effective well radius from drawdown data for large-diameter wells. Székely [9] evaluated pumping-induced flow in observation wells during aquifer testing. In a coastal zone, Saeed et al. [10] discussed hydraulic and hydro-salinity behaviors of skimming wells under different pumping regimes (the term skimming well refers to any technique employed with the intention of extracting relatively fresh water from the upper zone of fresh–saline aquifers). Rao and Manju [11] determined the optimal pumping locations of skimming wells by using simulated annealing and an artificial neural network. The model results suggested that the skimming wells should be operated from optimal locations staggered in space and time to obtain the least saline water. However, most of these studies were designed to consider quantitative data from a single extraction well. Some were directed at improving pumping efficiency with process technology, while others had an emphasis on describing the features of water movement in a single well systematically. A suitable evaluation method for multiple well locations with regard to the allowable withdrawal has not yet been proposed.

Location evaluation for other types of wells has received some research attention. Zhao et al. [12] proposed a method for determining the minimum safe distance between a relief well and blowout well, and this was accomplished by analyzing the factors that had the most influence on deepwater relief well location selection. Salmachi et al. [13] developed a workflow scheme to find potential locations for well placement within a reservoir; this work consisted of reservoir simulations and statistical analyses. Rodrigues et al. [14] proposed a 0–1 Linear Programming Model that minimizes the development costs for a given oil field as a whole. The model seeks to define the ideal numbers, locations, and capacities of production platforms, as well as the numbers and positions of wells. These methods can be very helpful in regard to research-based evaluations of pumping well locations.

As we can see from the above research progress, while some studies have focused on the problem of evaluation with other types of wells, research on well evaluation for groundwater pumping wells located close to a riverside source is lacking.

For a particular area, if groundwater supplies are required for long periods of time, a rational method of organizing well locations is required. If over-extraction occurs, groundwater levels will decline rapidly, thus leading to the enhanced risks during droughts and other environmental and geological problems. In addition, interactions between wells will impact drawdown during pumping. This study develops a new method to evaluate the well locations with regard to the allowable withdrawals, and this method is applied to a particular area with multiple wells along a river. A MODFLOW model was developed for simulating groundwater flow, and the impact of drawdown changes with regard to the complex interactions between groundwater and surface water was investigated. Many researchers have chosen MODFLOW to simulate the interactions between surface water and groundwater within various types of packages [15,16,17,18]. For example, Ou et al. [17] developed a new MODFLOW technique to improve the computational efficiency and reduce the noise for each simulation during linearized stream depletion analyses; furthermore, Guzman et al. [18] combined the SWAT and MODFLOW models together to simulate the interactions between surface water and groundwater. In MODFLOW modeling, various approaches exist for representing a surface water body, such as a head dependent boundary derived with the river package [19]. In our study, dynamic variations of the drawdown caused by varying locations of wells were analyzed. This was done to establish the evaluation criteria for the best location arrangement and to deliver the best solution for pumping well locations and pumping rates.

It is worth mentioning that, after decades of climate change, it is expected to have very limited effects on a particular aquifer. Iyalomhe [20] proposed a Regional Risk Assessment methodology integrated with a chain of numerical models to evaluate potential climate change-related impacts on aquifers and linked natural and human systems (i.e., wells, river, agricultural areas, lakes, forests and semi-natural environments). The results show that it has limited effects on a particular aquifer in Italy with no consequences on the considered natural and human systems. Goderniaux [21] calculated and compared the uncertainties on groundwater reserves around impact projections from several sources (climate models, natural variability of the weather, hydrological model calibration) in a study area in Belgium. Results show that, with the condition of climate changes, the uncertainty becomes smaller than the predicted decline in groundwater levels. These conclusions indicated that it was appropriate to choose the last period of data to do the research related to a representative aquifer.

Moreover, a new concept called Unit Increased Drawdown Value (UIDV) was proposed, and the method that used UIDV to evaluate the allowable withdrawal proved to be effective and reliable.

2. Methodology

2.1. Groundwater Flow Model

MODFLOW, which is a widely used numerical groundwater flow computer code developed by the United States Geological Survey, has previously been used in investigations of river–aquifer interactions [22,23,24]; thus, MODFLOW was selected to simulate the flow movement in this research.

The hydrogeologic system was modeled as a one-layer unconfined aquifer with two-dimensional (2D) horizontal flow in the particular study area, and the unconfined aquifer consisted of porous media. A recent study based on stochastic MODFLOW simulations showed that conceptualizing an aquifer as a 2D one-layer flow system would be adequate for describing subsurface flow within the aquifer.

According to the hydrogeological conceptual model mentioned above, the governing equation for saturated flow in porous media implemented in MODFLOW is as follows [21,25]:

$$\frac{\partial }{\partial \mathrm{x}}\left(K\frac{\partial \mathrm{h}}{\partial \mathrm{x}}\right)+\frac{\partial }{\partial \mathrm{y}}\left(K\frac{\partial \mathrm{h}}{\partial \mathrm{y}}\right)+W=s_{\mathrm{s}}\frac{\partial \mathrm{h}}{\partial \mathrm{t}},\left(x,y\right)\in D$$

(1)

where h denotes the potentiometric head (L); K denotes the hydraulic conductivity (L/T); $s_{\mathrm{s}}$ denotes the specific storage of the porous material (L⁻¹); W denotes the volumetric flux per unit volume representing sources and/or sinks of water (T⁻¹); and D denotes the model domain.

The uncertainties in hydraulic conductivity were considered. Local sensitivity analysis was used to analyze the sensitivity of drawdown at the maximum drawdown point to the model parameters. Generally, sensitivity of a model output can be expressed as a partial derivative of the input parameters:

$$X_{\mathrm{i},\mathrm{k}}=\frac{\partial {\mathrm{y}}_{\mathrm{i}}}{\partial {\mathsf{\alpha }}_{\mathrm{k}}}$$

(2)

where $X_{\mathrm{i},\mathrm{k}}$ is the sensitivity coefficient of the k^th input parameter of the model at the i^th observation point.

To calculate the sensitivity of a model drawdown output to the k^th parameter, all other parameters were kept constant. Assuming the k^th parameter was changed from ${\mathsf{\alpha }}_{\mathrm{k}}$ to ${\mathsf{\alpha }}_{\mathrm{k}}+\mathrm{\Delta }{\mathsf{\alpha }}_{\mathrm{k}}$ and the model output changed from $y_{\mathrm{i}}\left({\mathsf{\alpha }}_{\mathrm{k}}\right)$ to $y_{\mathrm{i}}\left({\mathsf{\alpha }}_{\mathrm{k}}+\mathrm{\Delta }{\mathsf{\alpha }}_{\mathrm{k}}\right)$, sensitivity could be estimated by using the following equation:

$$X_{\mathrm{i},\mathrm{k}}=\frac{\partial {\mathrm{y}}_{\mathrm{i}}}{\partial {\mathsf{\alpha }}_{\mathrm{k}}}\approx \left[y_{\mathrm{i}}({\mathsf{\alpha }}_{\mathrm{k}}+\mathrm{\Delta }{\mathsf{\alpha }}_{\mathrm{k}})-y_{\mathrm{i}}({\mathsf{\alpha }}_{\mathrm{k}})\right]/\mathrm{\Delta }{\mathsf{\alpha }}_{\mathrm{k}}$$

(3)

For the purpose of comparisons, the relative sensitivity was calculated as follows:

$$X_{\mathrm{i},\mathrm{k}}=\frac{\partial {\mathrm{y}}_{\mathrm{i}}}{\partial {\mathsf{\alpha }}_{\mathrm{k}}}\approx \{\frac{\left[y_{\mathrm{i}}({\mathsf{\alpha }}_{\mathrm{k}}+\mathrm{\Delta }{\mathsf{\alpha }}_{\mathrm{k}})-y_{\mathrm{i}}({\mathsf{\alpha }}_{\mathrm{k}})\right]}{y_{\mathrm{i}}}\}/(\frac{\mathrm{\Delta }{\mathsf{\alpha }}_{\mathrm{k}}}{{\mathsf{\alpha }}_{\mathrm{k}}})$$

(4)

2.2. Arrangement of Well Locations

Under the premise of ensuring proper functioning in the existing agricultural wells, our purpose was to determine the most suitable locations to establish new wells. In order to calculate the impact that changing well positions would have on the drawdown, three different arrangements of pumping wells were evaluated. These arrangements represented pumping wells in the recharge zone, transition zone, and discharge zone in an aquifer near a river. Drawdown of the aquifer was compared across the three different arrangements for a ten-year simulation period. Distances between zones were varied by about 8 km.

In each case, based on extraction needs, ten wells were spaced at 100 m intervals along the river. The pumping rates were varied between 0.2 m³/s up to 4 m³/s (with 0.2 m³/s as the basic unit), and this setup thus resulted in a total of 20 extraction scenarios (i.e., 0.2 m³/s, 0.4 m³/s, 0.6 m³/s, …, 4 m³/s). For ease of comparisons, the lateral distances from the river to the pumping wells were set to be the same. For each arrangement, the center core of the pumping wells was defined as the observation location in the model.

2.3. Unity Increased Drawdown Value (UIDV)

When the extraction increased by a basic unit, drawdown at the end of the simulation would increase. In this study, we defined the UIDV as follows: the increase in drawdown compared to the drawdown of a previous extraction when extraction is increased by the unit value. Obviously, UIDV is a value that changes with the amount of extraction. This definition refers to every point within a particular place, though this study only focused on the maximum UIDV point for comparison purposes. The mathematical representation of the formula is as follows:

$${\mathsf{\mu }}_{\mathrm{D}}=\frac{\mathrm{\Delta }D}{\mathrm{\Delta }Q}=\frac{D_y-D_{y-1}}{Q_y-Q_{y-1}}$$

(5)

where ${\mathsf{\mu }}_{\mathrm{D}}$ denotes the UIDV; $\mathrm{\Delta }D$ denotes the change in drawdown; $\mathrm{\Delta }Q$ denotes the change in the extraction rate; $D_{\mathrm{y}}$ denotes the drawdown in the y^th scenario; and $Q_{\mathrm{y}}$ denotes the extraction in the y^th scenario. Figure 1 shows a schematic diagram of the definition of UIDV.

Investigations of UIDV can help us to more accurately predict the changes in drawdown under different exploitation conditions. As the volume extracted increased within a certain range, the range of the variation of drawdown was able to be estimated, and the data remained in a predictable and controllable state. For these reasons, we consider the development of UIDV as a particularly important procedure.

To evaluate the merits of UIDV, two main points need to be considered. The first point involves the value of UIDV. If the UIDV is small in each given extraction scenario, this means that the rate of change in drawdown caused by the increased extraction is small. Such results indicate that the aquifer is stable and conducive to exploitation. The second point involves the stability of UIDV. If the UIDV varies in a predictable manner for each extraction scenario, it is more likely that changes in drawdown will be predictable and occur in a controllable manner.

2.4. Method for Evaluating the Well Location Arrangement

The general criterion used to evaluate the arrangement of wells in this study was whether changes to drawdown were considered small and stable for a given exploitation. Specifically, the results in this study were assessed against these following points:

• Low observed drawdown;
• A low value of UIDV;
• A stable UIDV.

Under the three arrangements tested in this study, the most desirable solution would be the one that produces these results.

Economic considerations for the different arrangements were also taken into account, as the most appropriate pumping location may not necessarily be economically feasible. For example, if the well field is too far away from the water user, the benefits associated with pumping at the location would be overshadowed by the cost associated with transporting water.

In this study, the relationship between well location and the maximum allowable withdrawal could be found. We defined the cost of extraction as a value proportional to the distance from the upper reaches to the pumping wells. The closer the pumping wells were to the upper reaches, the smaller the cost of transporting the water, and vice versa.

Thus, the problem of the economic cost can be resolved using the distance from the upper reaches of the river to the simulated wells. Mathematically, the relationship between the distance and the pumping volume can be expressed as follows:

$$\max Z=\mathrm{f}\left(Y\right)$$

(6)

where Z denotes the pumping volume and Y denotes the distance from the upper stream to the wells.

Accordingly, the restrictions involved in the exploitation process were:

$$\{\begin{array}{c}D\le D_{\mathrm{r}}\\ {\mathsf{\mu }}_{\mathrm{D}}\le {\mathsf{\mu }}_{\mathrm{Dr}}\end{array}$$

(7)

where $D_{\mathrm{r}}$ denotes the permitted maximum drawdown and ${\mathsf{\mu }}_{\mathrm{Dr}}$ denotes the permitted maximum UIDV.

These limits were determined based on the results of previous research [26] and the findings of the authors of this paper. In this paper, the maximum permitted drawdown was determined to be half the minimum thickness of the aquifer, namely:

$$D_{\mathrm{r}}=\frac{1}{2}\min H$$

(8)

where H denotes the thickness of the aquifer.

Currently, there is no correlation identification method for the permitted maximum UIDV. Based on practical experience, the standard was set as follows:

• Maximum value of UIDV: this is used to evaluate whether the magnitude of change in drawdown is appropriate. Based on the maximum drawdown, the standard value of UIDV is set to be the minimum thickness of the aquifer (26.7 m/(m³/s)).
• Stability standard of UIDV: this parameter is used to evaluate whether the sequence of UIDV has recursive relationships. We determined that the sequence should be monotonic, or close to it. If the sequence of UIDV is monotonically increasing (or decreasing), it is possible to predict that the trend in drawdown would increase (or decrease) when a basic unit value was added in any extraction scenario.

Conversely, if the sequence is not monotonic, the effect of a change in drawdown would not be predictable, thus reducing capacity to make objective decisions about a given arrangement. This study developed specific standards to find the best solutions for well locations and to identify the maximum pumping rate for each well location.

3. Application and Discussion

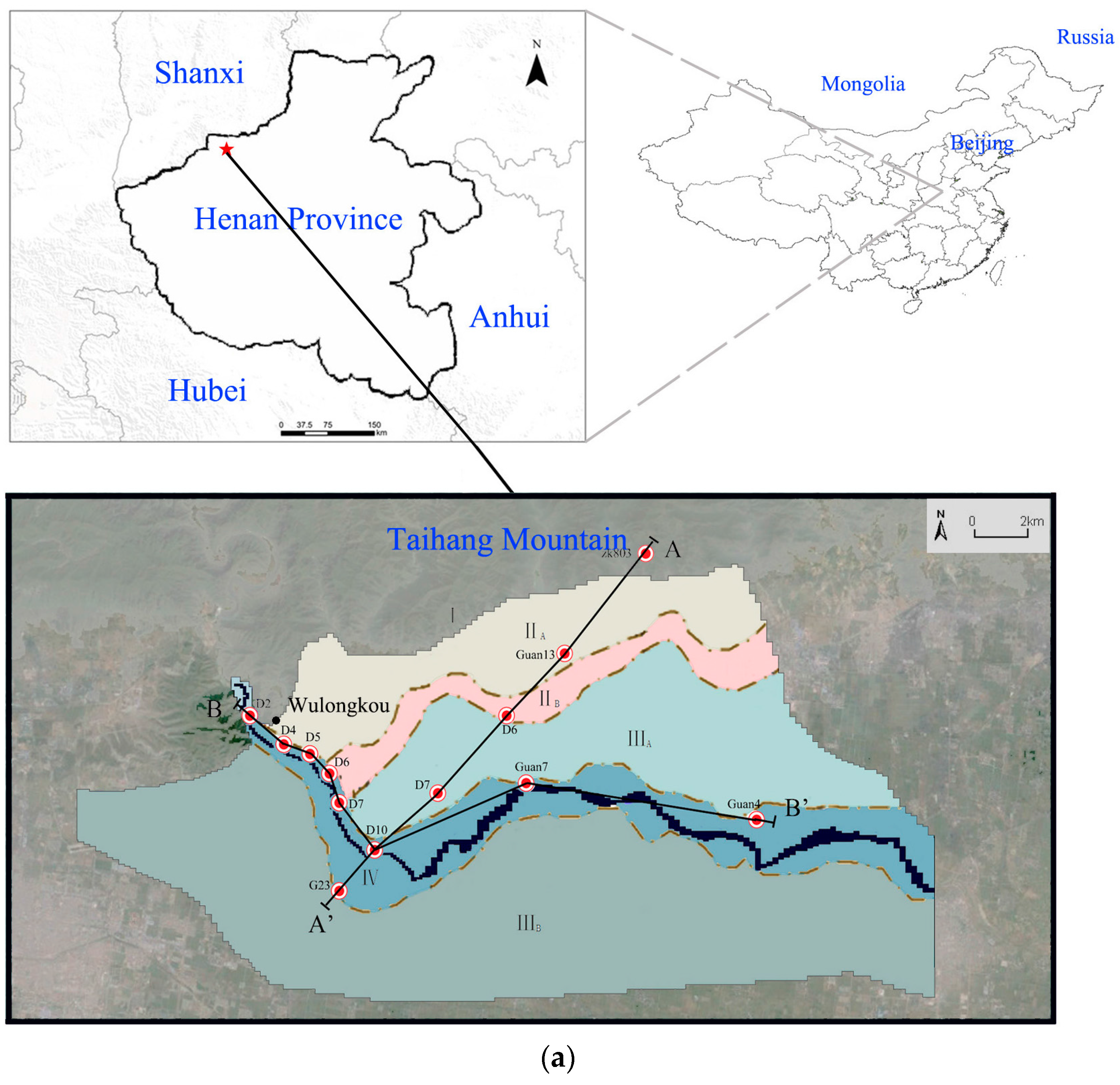
3.1. Study Area

The study area, i.e., the Qinbei Power Plant well field, is located in Wulongkou, Jiyuan City, China (Figure 2). It stretches west to the village of Dongxu, east beyond the village of Qinguduo, north to the Taihang Mountains, and south to the Kwong Lee main canal region. The total area simulated was 28,494 m².

The general drainage through the terrain of this area is from the Taihang Mountains in the north towards the alluvial plain of the Qin River in the south. The study site has a warm temperate monsoon climate with an average annual precipitation amount of about 644 mm (based on data from the Wulongkou Hydrological Station from 1956 to 2000). The maximum and minimum precipitation is about 1027 mm and 311 mm, respectively. More than 70% of the total precipitation occurs from June to September.

The highly permeable Qinbei aquifer system is comprised of rocks (primarily limestone) and sediments. The hydrogeological system of the Qinbei aquifer consists of four main parts (Figure 2b):

• Mountainous area (part I): this area consists of the Taihang Mountains. This part contains terrain that is 250–750 m higher than that at the well field, and a distinct topography is present in the southern region.
• Alluvial area (part II): this area is located near the Taihang Mountains, and it can be divided into two sub-parts according to the topography, namely:

  • Part II_A: a zonal distribution from west to east. The width from north to south is about 3–4 km. The length from west to east is about 8–9 km. The lithology consists of stone and pebble.
  • Part II_B: a fringe along the alluvial area. The width from north to south is about 1–2 km. The length from west to east is about 8–9 km. The lithology consists of pebble and gravel.
• Low-lying area (part III): this area can be divided into two sub-parts according to the topography, namely:

  • Part III_A: an area located along the left bank of the Qin River. The width from north to south is about 3–5 km. The ground elevation ranges from 135 to 142 m (from west to east). The lithology consists of round gravel.
  • Part III_B: an area located along the right bank of the Qin River. The width from north to south is about 5–7 km. The length from west to east is about 20 km. The lithology consists of loam.
• Valley area (part IV): this area is located in the valley of the Qin River. The width of the floodplain ranges from 200 to 500 m. Gravel is distributed around the valley, and sand covers the ground in the downstream reaches of the Qin River.

The main river in the study area, the Qin River, originates in the Shanxi Province, and it flows from north to south through the Henan Province. The aquifer in the study area contains predominately unconsolidated sand, which is distributed along the Qin River. The thinnest part of the aquifer is 53.3 m. To identify the relationships between groundwater and surface water in the study area, seven river cross-sections (from Shengzhuang to Longquannan) were chosen for observations of the flow conditions for a duration of two hydrological years (Figure 3). The changes in flow regimes are presented in

Table 1. Changes in flow regimes from Shengzhuang to Longquannan.

Section	Interval Distance	Recharge Item	Discharge Item	Amount of Infiltration
No. 1 (Shengzhuang)–No. 6 (Shagou)	7.80 km	Qin River	Aquifer	0.35 m3/s
No. 6 (Shagou)–No. 7 (Longquannan)	14.40 km	Aquifer	Qin River	2.09 m3/s

.

Observations from the sections show that the relationships between groundwater and surface water in the study area vary spatially. The reach from Wulongkou to Shagou (about 7800 m) is a recharge reach that supplies water to the local groundwater system. In this area, groundwater flows are in the downstream direction of the Qin River. Where the river level is higher than the local groundwater level, the groundwater receives seepage from the Qin River at all times. Using two years of observation data, the average annual recharge in this area was calculated to be 0.35 m³/s.

When groundwater flows eastward to the reach below Shagou where the riverbed elevation is lower than local groundwater levels and the groundwater upward gradient increases, the aquifer recharges the river flow. In the reach from Shagou to Longquannan, the amount of recharge to the river was estimated at 0.89 m³/s.

The local people have extracted groundwater in the study area for many years. The only other water source for the Qinbei Power Plant, the Qin River, is too shallow for extraction purposes, and it cannot recharge the local groundwater when well fields are in operation. Additionally, there are about 90 irrigation wells distributed throughout the area surrounding the Qinbei Power Plant (Figure 4). The main use of groundwater is for irrigation over an area of 6063.4 ha, and 3350.0 ha of this total amount are located along the left bank of the river. No groundwater contamination has been reported up to this date. The purpose of this research, which was conducted under the premise of ensuring the existing agricultural wells, was to evaluate different cases to find out where it would be feasible to establish new wells.

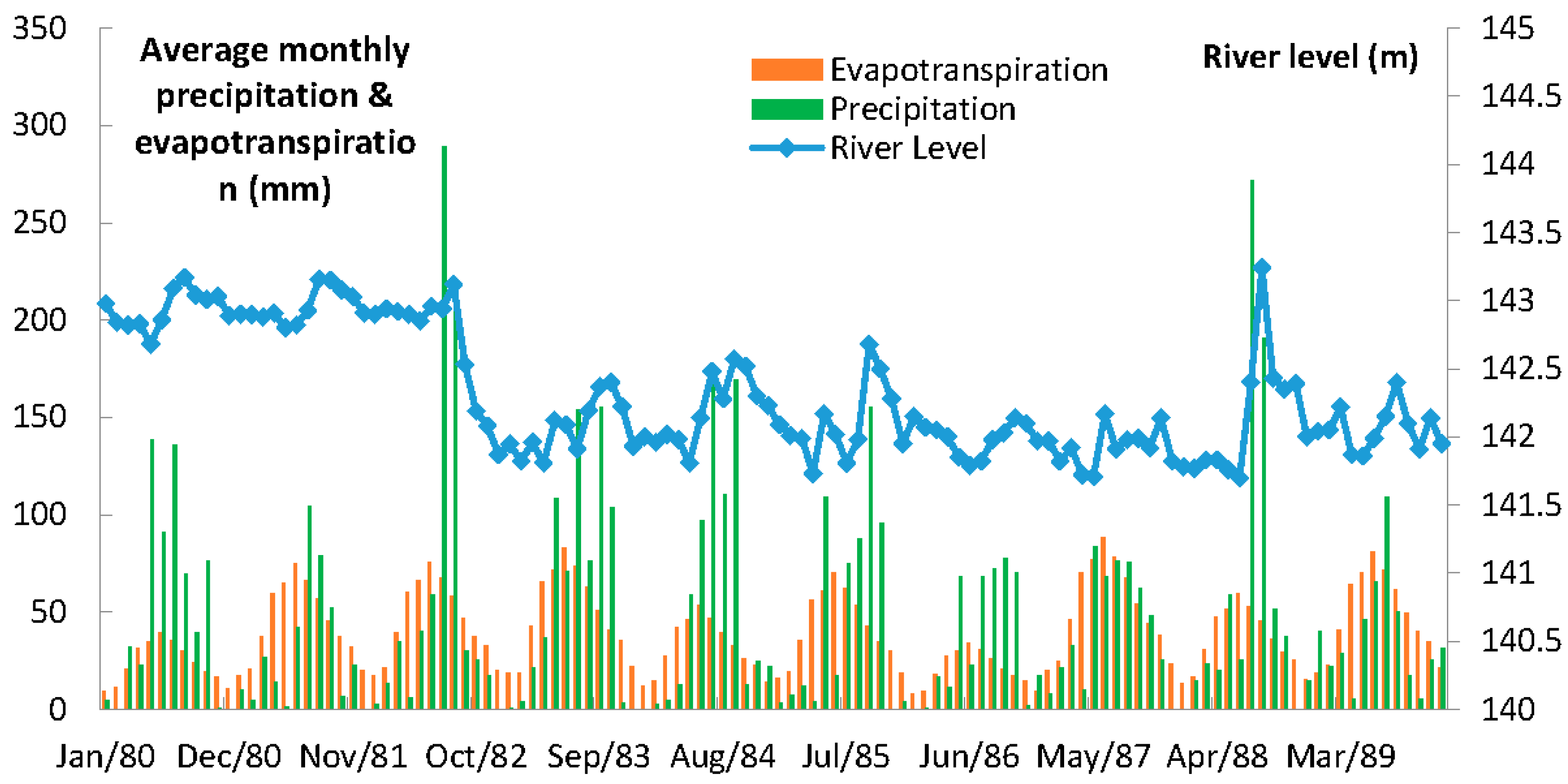
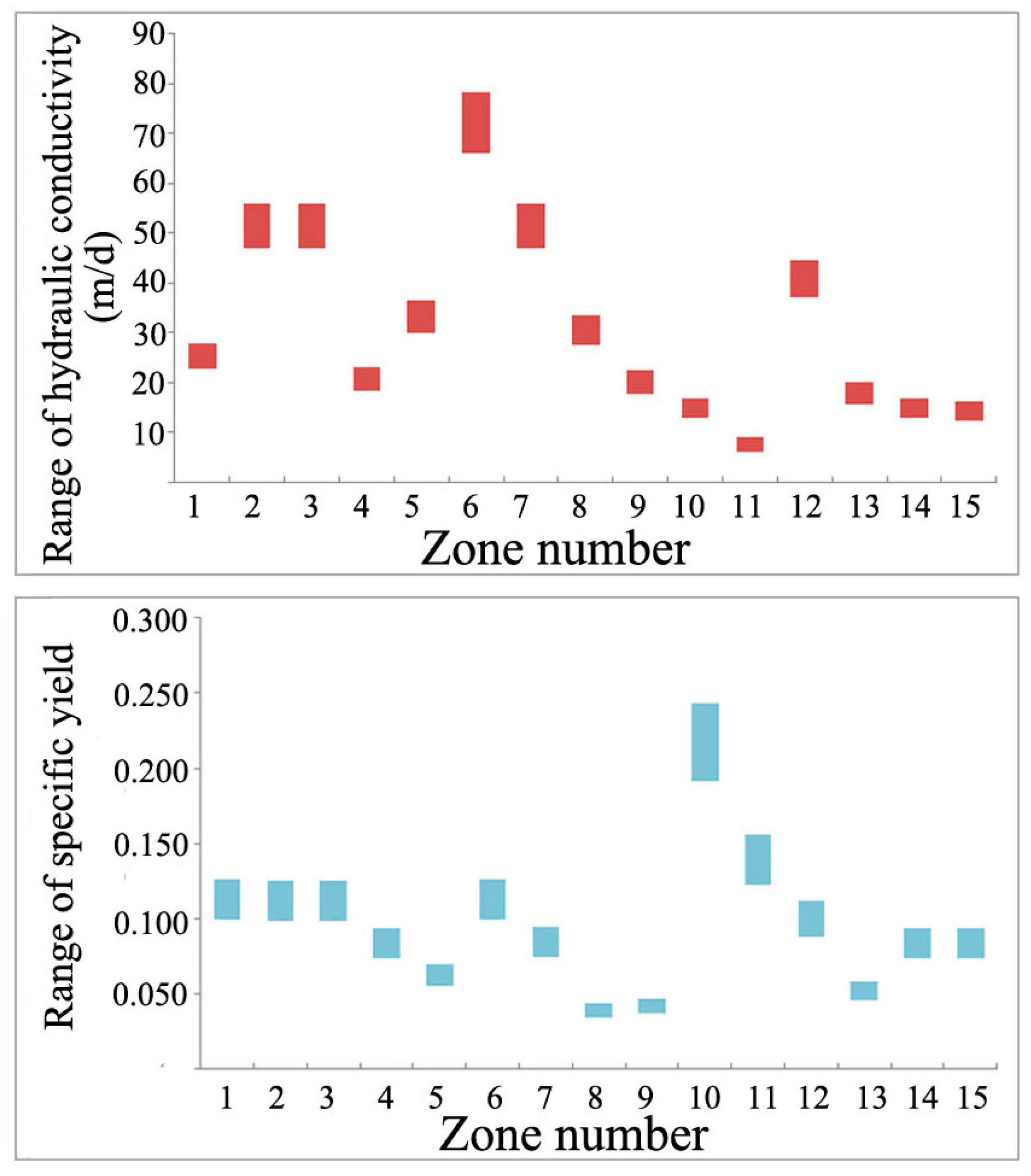
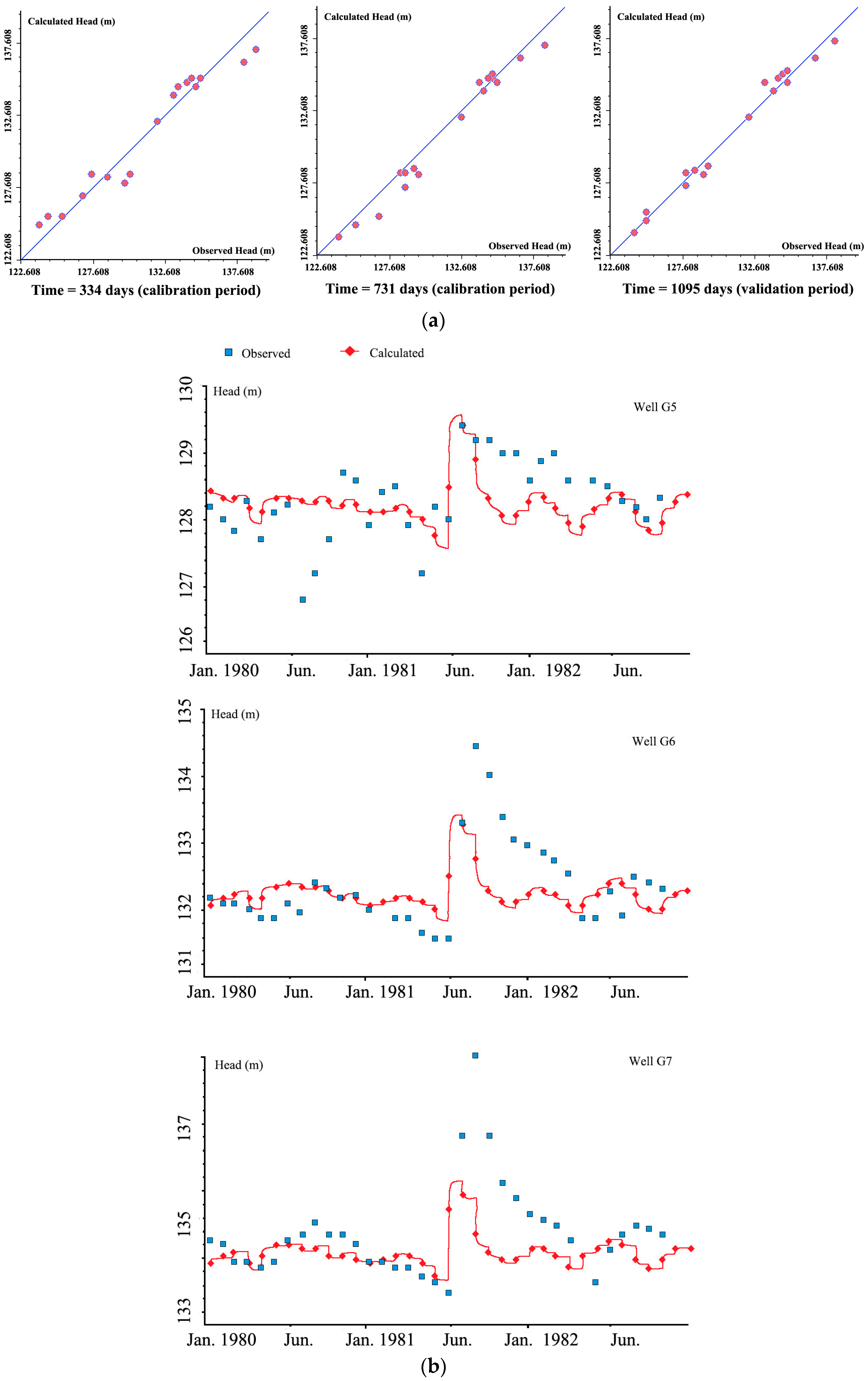
3.2. Establishment of the Groundwater Flow Model

Based on long-term hydrological gauging data, abundant hydrogeological test data, and numerical simulation results for the study area (Qinbei Power Plant riverside well field), a MODFLOW numerical model was established to simulate the hydrodynamic conditions.

The model boundaries were defined as general-head boundaries (GHBs). Transient groundwater data showed that the groundwater level fluctuates under non-steady state conditions. The aquifer in the model was considered isotropic but heterogeneous. The following boundary conditions were used in the simulation: river level, evapotranspiration, and recharge. The bottom boundary was described as a no-flow boundary consistent with the observed 2D horizontal flow in the study area. Based on the differences in geohydrology, the Taihang Mountains were used to set the western, eastern, and northern boundaries of the flow domain. Simulation time of the model was from January 1980 to December 1989.

Surface water–groundwater interactions were simulated by using the RIVER (RIV) package. The RIV package was selected because it is capable of producing a simple and adequate representation of the interactions between the Qin River and the Qinbei aquifer. It was assumed that the river level did not change during each stress period, which was set to be one month. Figure 5 shows the monthly river level conditions during 1980–1989 (data were based on the information obtained from the Wulongkou Hydrological Station).

Evapotranspiration was simulated by using observation data that were collected during 1980–1989. The extinction depth of evapotranspiration was set as 5 m. If the thickness of the unsaturated zone exceeded this value, the evapotranspiration of groundwater was not incorporated into the model calculation. Recharge to the aquifer was simulated by using the RCH package. The recharge amount entering groundwater was calculated by using the difference between rainfall and evapotranspiration. A recharge value was assigned to each stress period.

The finite difference grid consisted of a single layer covering approximately 28,494 m². The model layer was discretized into 184 columns and 146 rows with a grid size that was 198 m long and 144 m wide. In order to accurately simulate the groundwater flow in the study area, part of the mesh was then further refined as shown in Figure 6.

The aquifer in the study area was divided into 15 zones based on the lithology of the aquifer and pumping test results. The initial parameters of each zone were obtained from previous work in this area.

The data from January 1980 to December 1981 were used to calibrate the model, while the data from January 1982 to December 1982 were used to validate the model. Initial conditions over the model domain were obtained from observation well data at the start of the simulation and data that were interpolated over the model domain.

Calibration results (January 1980 to December 1981, as well as day 1 to day 731) reproduced the observed water table elevations at 17 observation wells. The relationship between the calculated head and observed head could be found through a comparison. Over a period of 365 days, the average error₃₆₅ between the calculated head and observed head was 0.868 m, while the RMS₃₆₅ (root mean square) was 1.09 m and the standardized RMS₃₆₅ was 7.14%. Over a period of 731 days, the average error₇₃₁ was 0.657 m, the RMS₇₃₁ was 0.812 m, and the standardized RMS₇₃₁ was 5.68%.

The parameters such as hydraulic conductivity and specific yield were firstly determined based on hydrogeological pumping tests. All of the parameters were put into the MODFLOW model, and according to the calibration and validation of the output results, the final parameter values were determined. The results of the parameter calibration were distributed as shown in Figure 6 (parameter partitioning) and

Table 2. Simulated values for the hydraulic conductivity and specific yield.

Zone	1	2	3	4	5	6	7	8
K (m/d)	25	50	50	20.5	32.6	70	50	30
Zone	9	10	11	12	13	14	15	–
K (m/d)	20	15	8	39.9	17.9	15	14.5	–
Zone	1	2	3	4	5	6	7	8
μ	0.113	0.112	0.112	0.084	0.062	0.113	0.085	0.039
Zone	9	10	11	12	13	14	15	–
μ	0.042	0.217	0.139	0.1	0.052	0.084	0.084	–

(value of hydraulic conductivity and specific yield in each zone). The range of each parameter was determined by the 3σ method [27], where the possibility of deviation from the value of 3σ is very small in a normal distribution. According to previous studies [28,29], the hydraulic conductivity was assumed to be normally distributed in an aquifer. In this paper, we also assumed that the distribution of the specific yield was a normal distribution. Therefore, the range of each parameter was (A − 3σ, A + 3σ). The standard deviation of each parameter was determined by a large number of hydrogeological tests. The range of each parameter is shown in Figure 7.

The validation of the model at all the observation wells was performed for the time period of January 1982 to December 1982 (day 731 to day 1095). As we can see from the results, over a period of 1095 days, the average error₁₀₉₅ was 0.518 m, the RMS₁₀₉₅ was 0.629 m, and the standardized RMS₁₀₉₅ was 4.43%. Figure 8a shows the details of the relationships between the calculated head and observed head in the calibration and validation. Figure 8b shows the change process for the calculated head and observation head within the time series for well G5, G6, and G7.

Sensitivity analysis enables the determination of the response of the model drawdown output to the model parameters. It was necessary to determine the sensitivity ranges of the different parameters to understand how they respectively affected the groundwater drawdown at the Qinbei Power Plant. Figure 9 shows the results of the sensitivity analyses for 15 aquifer hydraulic conductivities. It can be seen that K13 (13 is the zone number, which was assigned as in Figure 6) was the most sensitive aquifer parameter that affected the groundwater drawdown, followed by K14, K10, K7, and K9, with K5 being the least sensitive. Three parameters, namely, K3, K8, and K15, were negatively correlated with the drawdown. This was because of the flow of the groundwater from west to east and the locations of the three corresponding zones, which were positioned far away from the maximum drawdown point; this caused them to be recharged from the western part. As the hydraulic conductivities of these three zones increased, the movement of the groundwater from the west accelerated, thus resulting in an increase in the drawdown at the maximum drawdown point.

The distribution of drawdown is shown in Figure 10 based on the numerical model with only exploitation from irrigation wells (i.e., without the influence of any Qinbei pumping wells) after ten simulation years.

The results show that drawdown in the recharge zone and transition zone were larger than that in the discharge zone. This was probably due to the following reasons:

• The terrain to the west of the study area is higher, and groundwater flows here from west to east, which makes the discharge of the upper reaches of the river in the study area larger.
• The aquifer materials of the upper reaches of the river in the study area were mostly boulders and gravels, with high permeability, thus resulting in high hydraulic conductivity. Therefore, larger changes in drawdown can occur as groundwater in this area is more easily exploited.

However, because there was a close relationship between the drawdown and the location of wells, further pumping wells should be set in different places to simulate the situation in more detail.

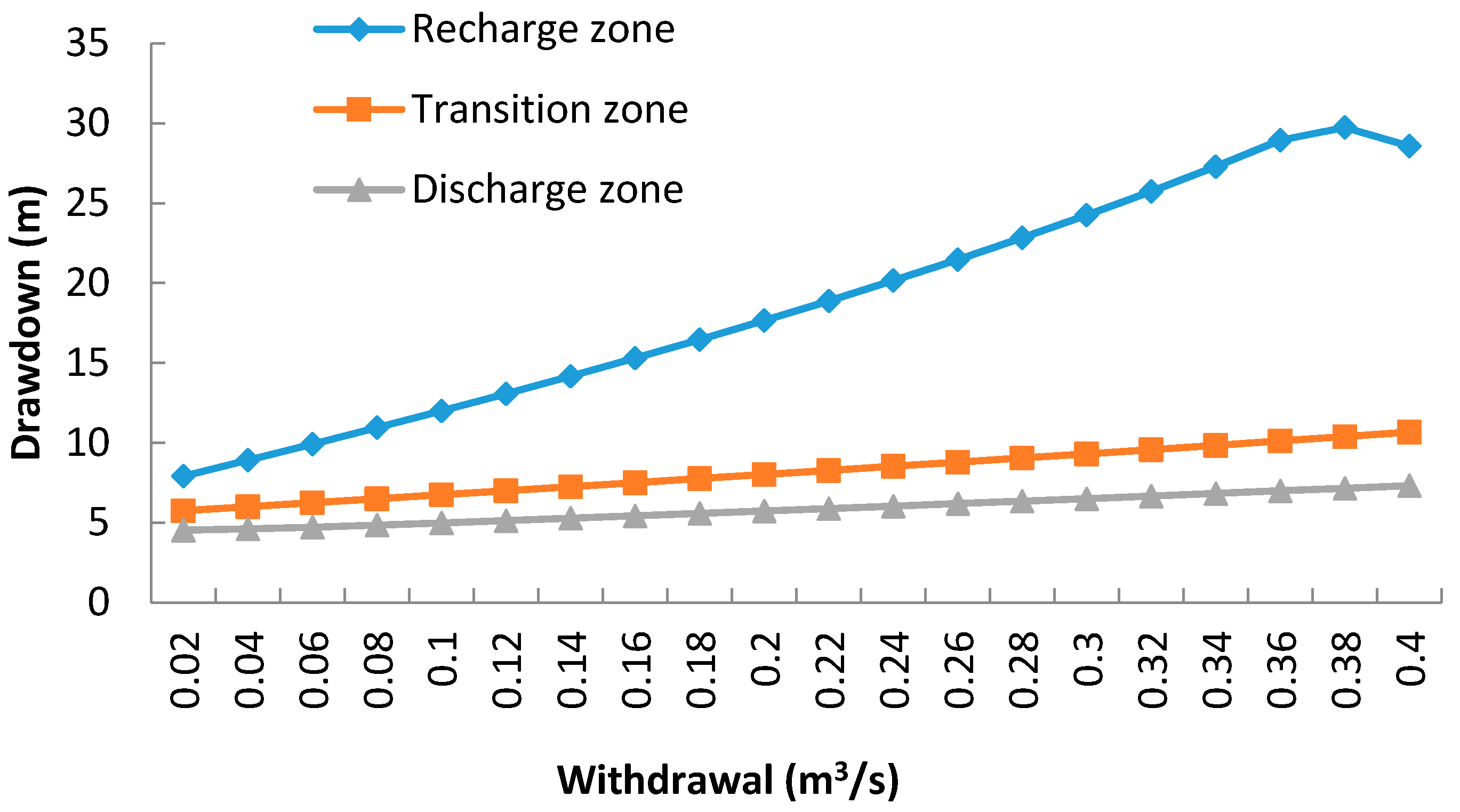
3.3. Drawdown Changes under Different Cases

Three cases were simulated with 20 scenarios each. Drawdown data versus pumping rates are shown for each case in Figure 11.

As can be seen from the results above, the maximum drawdown was produced in the case where the well field was located in the recharge zone, and the values ranged from 7.9 m to 28.6 m. The second largest drawdown values were seen in the transition zone, and the values ranged from 5.7 m to 10.7 m. The discharge zone showed the lowest values of drawdown, and the values were only in the range of 4.5 m to 7.3 m.

It is noteworthy that in the 18th scenario involving the recharge zone case (withdrawal rate of 3.6 m³/s), the groundwater level appeared to be below the confining bed of the aquifer. While in the 19th scenario, the drawdown displayed a decreasing trend in the center core of the exploitation area. This situation presents a new problem: namely, if the withdrawal continues to increase until the groundwater level is consistently lower than the confining bed of the aquifer, it would be prudent to discuss whether certain rules should be implemented in accordance with the drawdown change conditions.

In order to investigate this issue, a detailed study of the recharge zone well field arrangement was conducted. Starting from an extraction volume of 0.4 m³/s, pumping rates were increased by 0.02 m³/s intervals for 20 scenarios, i.e., the extraction volume was set as follows: 0.42 m³/s, 0.44 m³/s, 0.46 m³/s, …, 0.8 m³/s. These different scenarios were input into MODFLOW, and the results of these simulations are shown in Figure 12.

As shown above, although drawdown generally increased with the increasing withdrawal, the changes were not regular and thus not conducive to the actual exploitation work.

3.4. Unit Increased Drawdown Value (UIDV) Changes under Different Cases

Using the drawdown associated with different well field arrangements, the UIDV was calculated (Figure 13).

From Figure 13 we can make the following observations:

• In the recharge zone case, UIDV increased with increases in the withdrawal, and the values ranged from 49.4 m/(m³/s) to 82.2 m/(m³/s) (Figure 13a). This trend continued until the 19th and 20th scenario, where UIDV dropped sharply and displayed negative values. These results suggest that with the trend of increasing withdrawal, the groundwater level decreased and presented an upward decreasing trend until the moment when the groundwater level fell below the confining bed of the aquifer (which is consistent with the drawdown conditions). This implies that when the withdrawal forces the groundwater level to be lower than the confining bed of the aquifer, neither drawdown nor UIDV were calculated properly by the model. Moreover, according to the familiar trend between UIDV and drawdown conditions, the data imply that UIDV expresses the same physical meaning as the drawdown to some extent.
• In the transition zone case, UIDV ranged from 12.4 m/(m³/s) to 13.7 m/(m³/s), as shown in Figure 13b. We could assume from the modeling results that the UIDV in the transition zone would always be smaller than that in the recharge zone, but obviously the change in UIDV in the transition zone is not monotonic according to the model.
• In the discharge zone case, UIDV ranged from 4.41 m/(m³/s) to 8.37 m/(m³/s) (Figure 13c). The value of UIDV in the discharge zone was the smallest and most stable, with a monotonically increasing trend, which was similar to the trend for the drawdown conditions. However, a key difference between UIDV and drawdown was as follows: UIDV reflects the increasing rate of drawdown, and thus, the value of UIDV could better reflect the situation of drawdown changes.

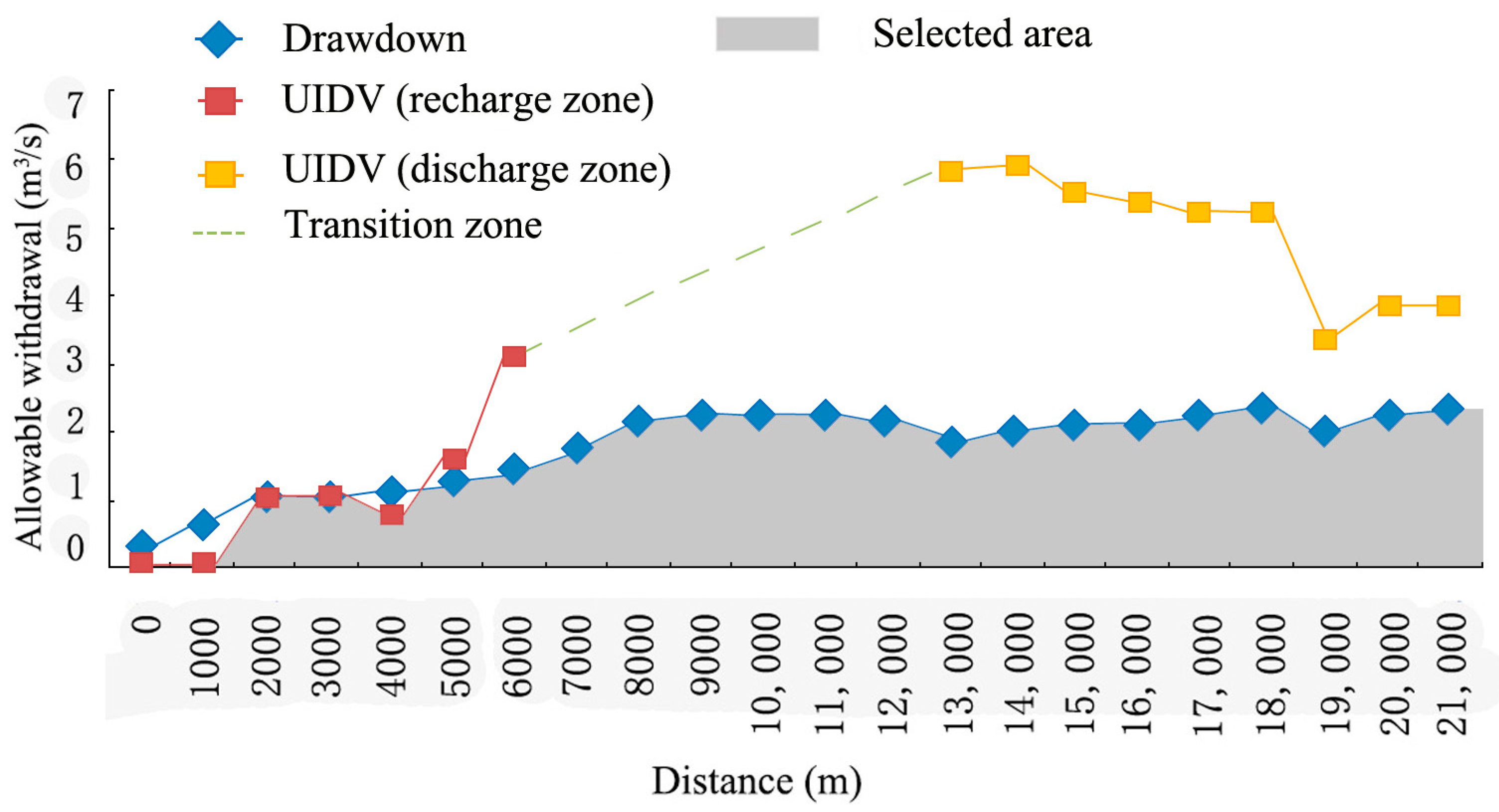
3.5. Results for the Pumping Well Location Selection

According to the drawdown and UIDV series, pumping wells located in the discharge zone give a lower risk for over-exploitation. However, the distance from the Qinbei site to the discharge zone is large and would result in impractical economic costs.

Considering the restrictions to drawdown and UIDV limits as well as long computational times associated with numerical simulations, the results for the maximum permitted withdrawal related to the distance from the upper reaches of the Qin River are shown in Figure 14. Here, the distance from the upper reaches in the study area is shown on the horizontal axis, with the river recharge area in the upper reaches at the axis origin.

As can be seen from either the drawdown or UIDV data, there was an increasing trend along the river upstream, which means that the recharge zone appeared to show a larger drawdown than the discharge zone during the extraction; these results indicate that there is a need to re-examine the recharge and discharge relationships between groundwater and surface water. When the pumping wells are located in the recharge zone of the study area, groundwater recharge cannot be completely reliant on the river as a source, even though the river water level is higher than the groundwater level. Conversely, when the pumping wells are located in the discharge zone, even though groundwater also contributes to the baseflow of the river, with the low elevation of the aquifer in this zone, groundwater in the discharge zone can accept supplies from the west side of the groundwater system, and changes in drawdown can be inconspicuous. Therefore, the decisions about riverside groundwater exploitation not only depend on whether wells are located near the river, but also on the aquifer characteristics and overall water balance for each case of exploitation.

When the two curves of drawdown and UIDV were superimposed, the selected area considering both drawdown and UIDV can be plotted as shown in the shaded area in Figure 14. This shaded area demonstrates that withdrawal cannot be greater than the minimum allowable withdrawal related by the two curves.

This study does not consider the viability of locating wells at distances between 7000 and 12,000 m from the upstream reaches since the UIDV data were not stable. If it is decided that this area is needed for groundwater extraction, further study is needed.

According to the preferred well criteria shown as a shaded area in Figure 14:

• To maximize exploitation, wells should be set in the area 18 km from the upstream reaches, and the pumping rates should not exceed 2.44 m³/s. This area was classified as the river discharge zone. Due to the lower elevation, local groundwater could also be recharged from upstream. Drawdown in this zone changes slowly and steadily.
• To minimize costs, wells should be set in the area with a distance of 2000 m from the upstream reaches of the Qin River, and withdrawal should not exceed 1.07 m³/s. This area is known as the river recharge zone. Because of the higher terrain in the study area, the aquifer is underdeveloped. Drawdown changes will thus likely be larger for extraction in this area. If wells are located in the area less than 2 km from the upstream reaches, this will lead to excessive drawdown even at low pumping rates.
• In the area at a distance between 7000 and 12,000 m from the upstream area (this area belongs to the transition zone), the relationships between groundwater and surface water were unstable, and this caused the UIDV to be highly variable. During the pumping scenarios, the trend of increasing drawdown per unit withdrawal could not be estimated, and therefore, this paper does not consider the viability of locating wells in this area.

The proposed method simplifies consideration of the relationship between economic costs and allowable withdrawal. Using distance from the upper reaches instead of the cost could easily solve the complex problem. Decision makers do have flexibility to set well locations according to the demands on water yield. This makes it possible to minimize costs while meeting the required yields.

4. Summary and Conclusions

This paper proposed a new concept called the Unit Increased Drawdown Value (UIDV), and the method that uses UIDV to evaluate the allowable withdrawal was proven to be effective and reliable. On this basis, problems associated with the decision-making process for situating wells in optimal locations were discussed. Although joint management of groundwater resources and surface water resources, as well as interactions between surface water and groundwater, have been largely addressed in the literature, we have suggested a new method to find the best locations for groundwater wells, and the proposed method was used to evaluate the water supply in the study area; this method is applicable to other areas as well. The main results obtained in this study are described below:

• A numerical groundwater model was built to represent a particular study area, the Qinbei Power Plant well field. Calibration and validation of the model were performed, and the results demonstrated the reliability of this model in simulating practical problems. Based on a ten-year numerical model simulation that only considered the withdrawal of the aquifer from existing irrigation wells, drawdown for the existing withdrawal in the recharge zone and transition zone were found to be larger than in the discharge zone.
• Three cases of pumping well locations (recharge zone, transition zone, and discharge zone) were evaluated. Each case was simulated by using 20 different scenarios (with different withdrawal values) to calculate the associated drawdown. The results showed that with the same extraction volume, locating the well field in the recharge zone will produce the maximum drawdown. The well field in the transition zone had the second largest drawdown, while extraction from the discharge zone showed the minimum drawdown. Among the cases evaluated, if the groundwater level is lower than the confining bed of the aquifer, the calculated drawdown does not change monotonously with the extraction. These results indicate that groundwater recharge cannot be completely reliant on the river as a source, even though the river water level is higher than the groundwater level.
• The concept of the UIDV was introduced. Based on the drawdown results calculated in this study, UIDVs for the three cases were presented. The results showed that for the same extraction volume, well fields in the recharge zone, transition zone, and discharge zone produced the maximum, moderate, and minimum UIDVs, respectively. These results also showed that the calculated value of UIDV produced trends that were similar to drawdown, and further, that the zone of larger drawdown is likely to occur where there is a larger increasing rate of drawdown when extraction is increased by a unit value. Thus, the UIDV was useful for revealing the uncontrollability of excessive drawdown. According to the familiar trend between UIDV and drawdown conditions, the data imply that UIDV expresses the same physical meaning as the drawdown to some extent. However, a key difference between UIDV and drawdown was that UIDV reflects the increasing rate of drawdown, and thus, the value of UIDV could better reflect the situation of drawdown changes.
• The selection of a well field location was done based on the results of the allowable withdrawal evaluation. For maximum exploitation, wells should be in the area 18 km from the upstream reaches, and the allowable withdrawal should not exceed 2.44 m³/s. For a program with minimum costs, wells should be in the area at a distance of 2000 m from the upstream reaches, with the allowable withdrawal not exceeding 1.07 m³/s. In the area with a distance between 7000 and 12,000 m from the upstream reaches, the relationships between groundwater and surface water were unstable, and we considered this area as an unsuitable location for a well field. The aquifer of study area, the Qinbei Power Plant, belongs to an unconfined aquifer consisting of porous media, which is a ubiquitous type around China and even all over the world. Based on the representativeness of the study area, this proposed method can be applied to other sites in China as well as in regions outside of China where there are similar issues about jointly managing groundwater and surface water resources.