The Spatial and Temporal Contribution of Glacier Runoff to Watershed Discharge in the Yarkant River Basin, Northwest China
Abstract
:1. Introduction
2. Materials and Methods
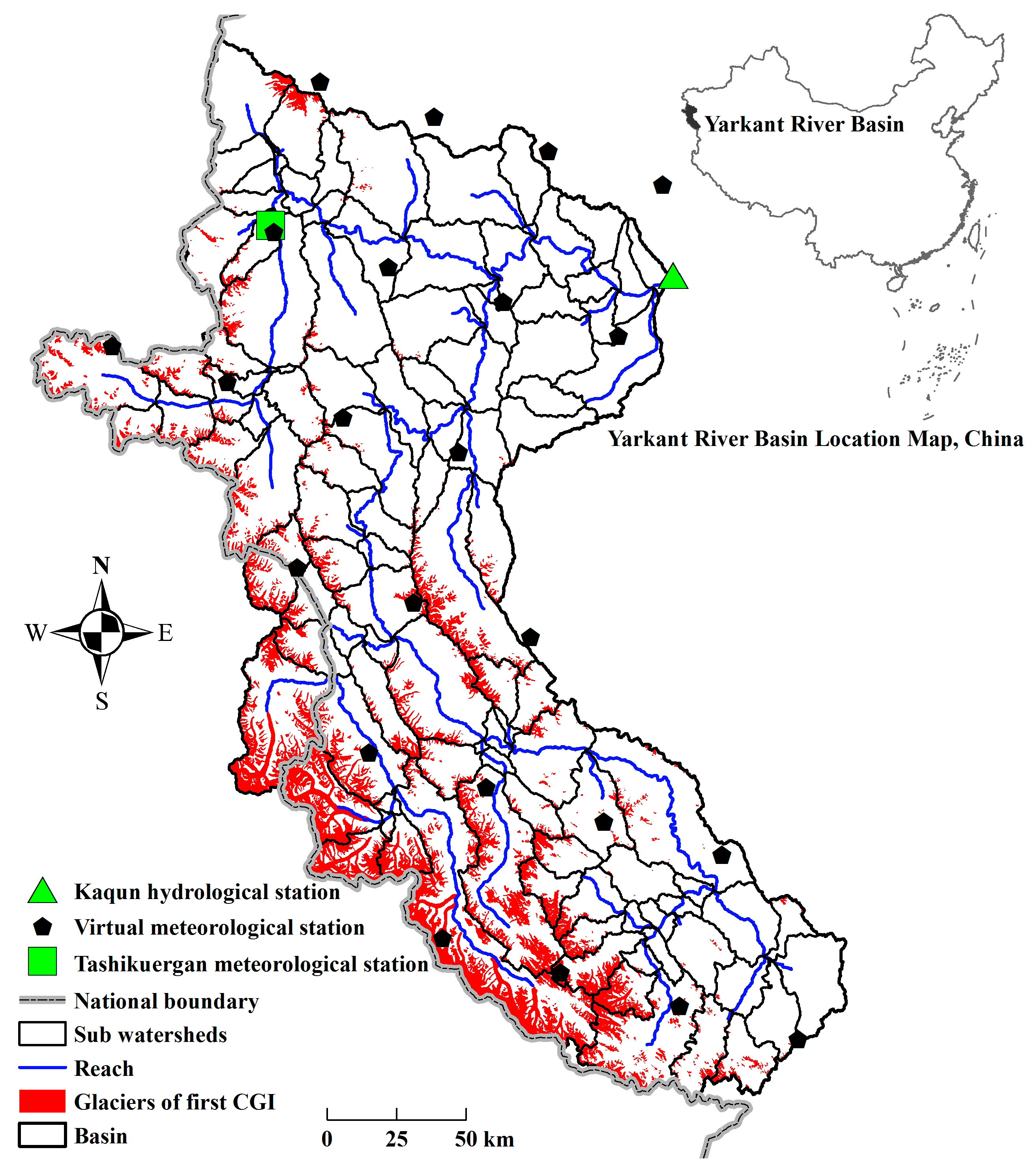
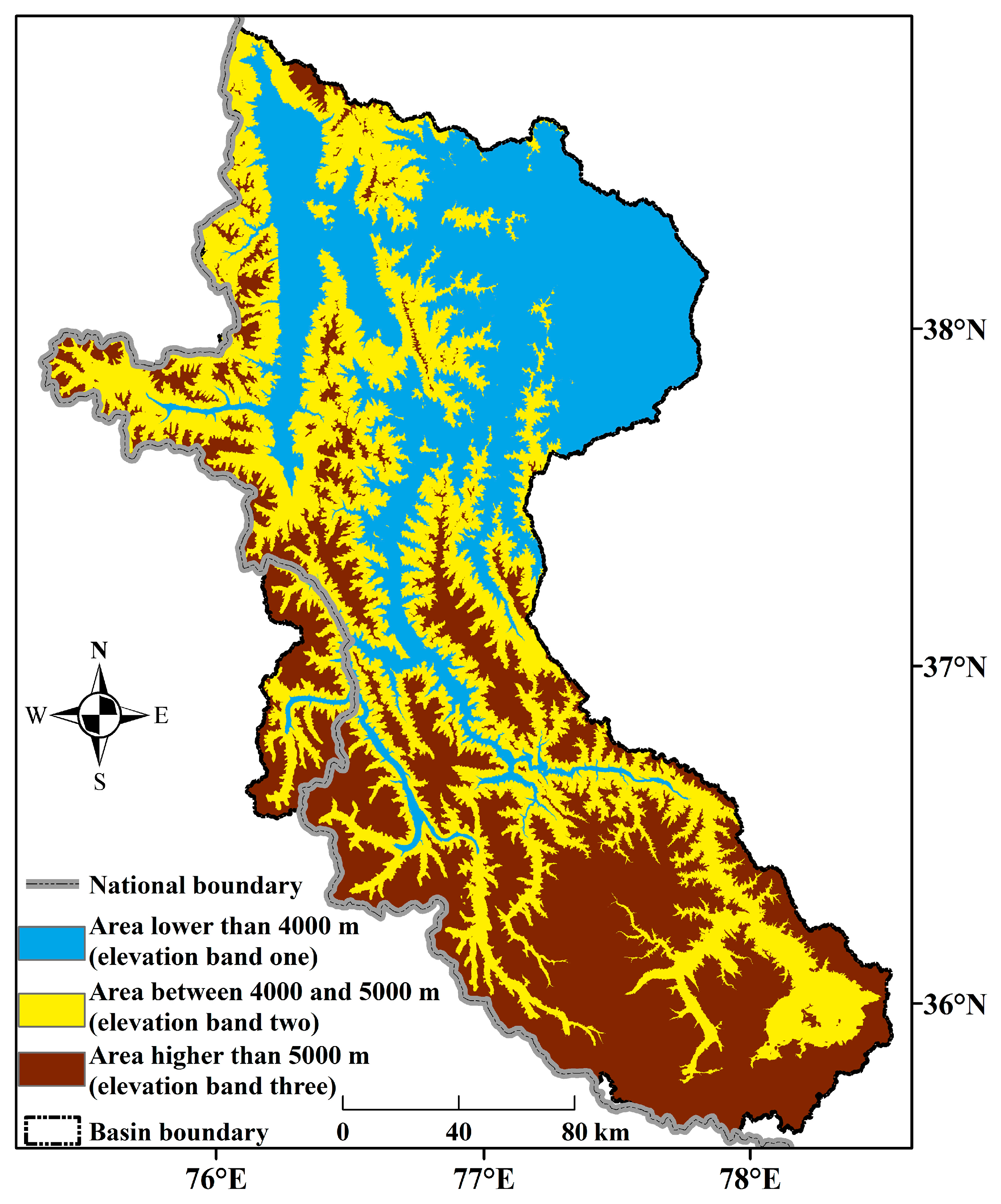
2.1. Study Area
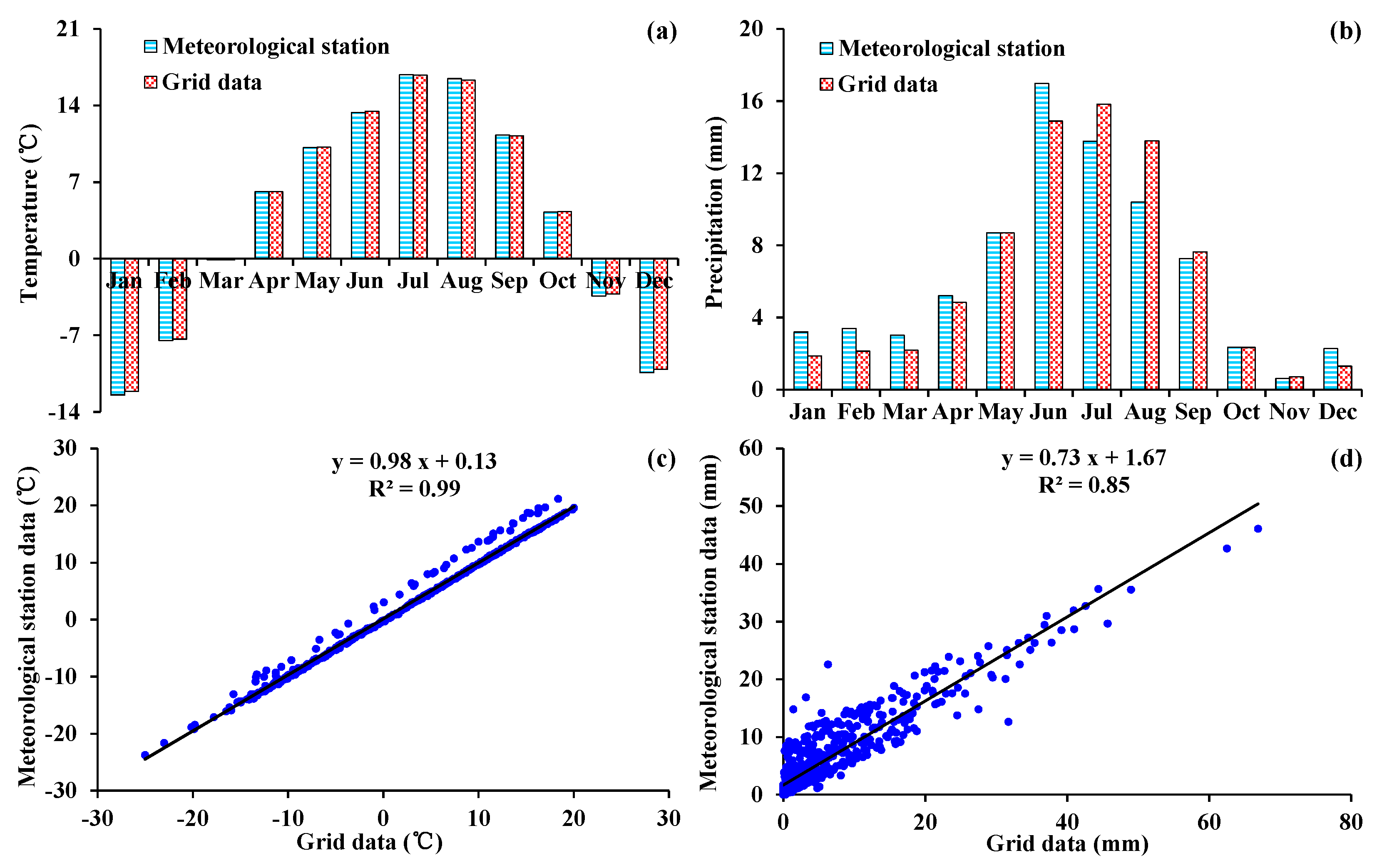
2.2. Meteorological and Hydrological Data
2.3. Underlying GIS-Referenced Data
2.4. Glacier Data
2.5. Description of SWAT
2.6. Glacier and Snow Melt Algorithm
2.6.1. Snow Melt Algorithm
2.6.2. Glacier Melt Algorithm
2.6.3. Glacier Area Changes
2.6.4. Glacier Accumulation Rate
2.7. Model Performance Evaluation
3. Results and Discussion
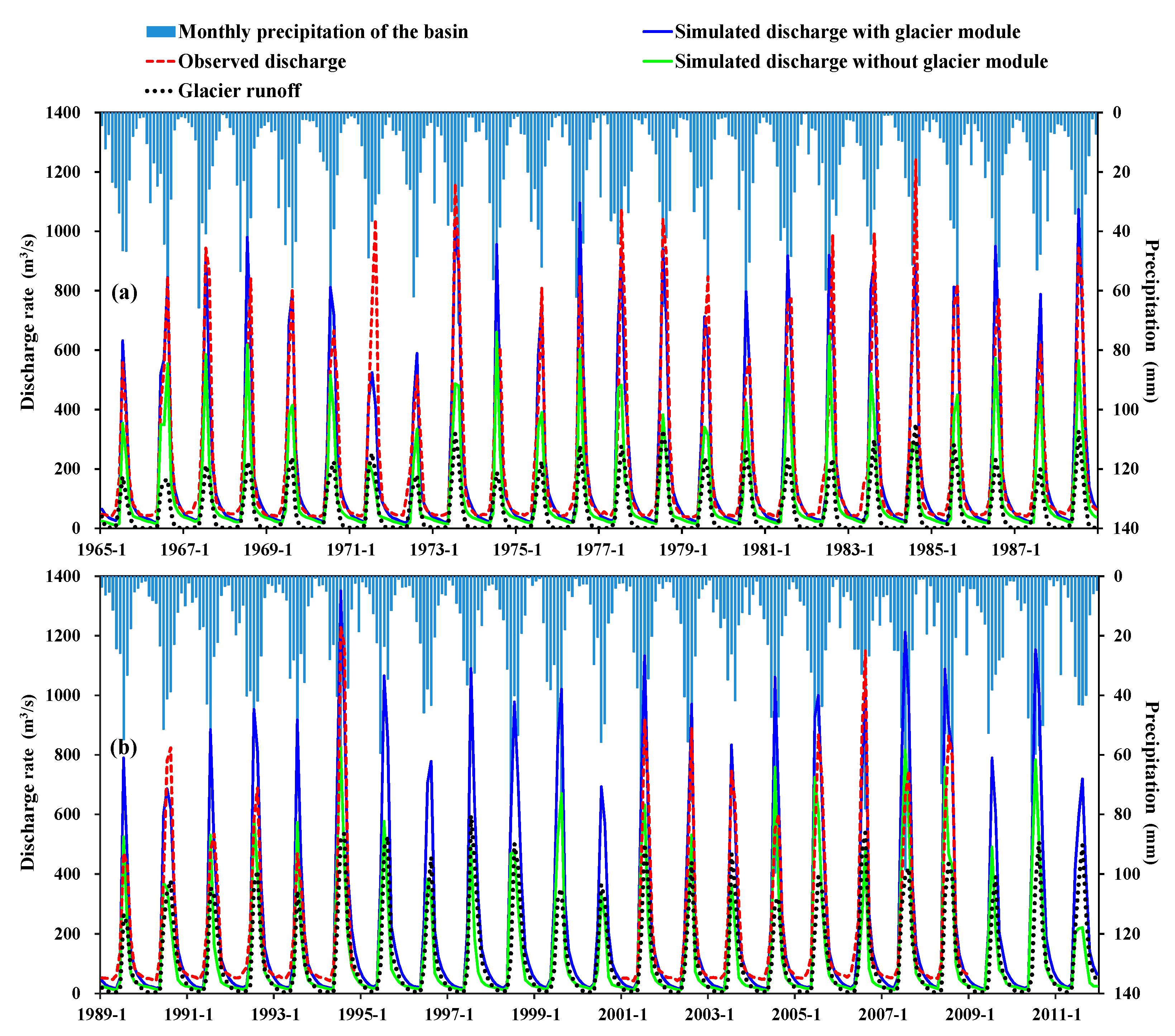
3.1. Calibration
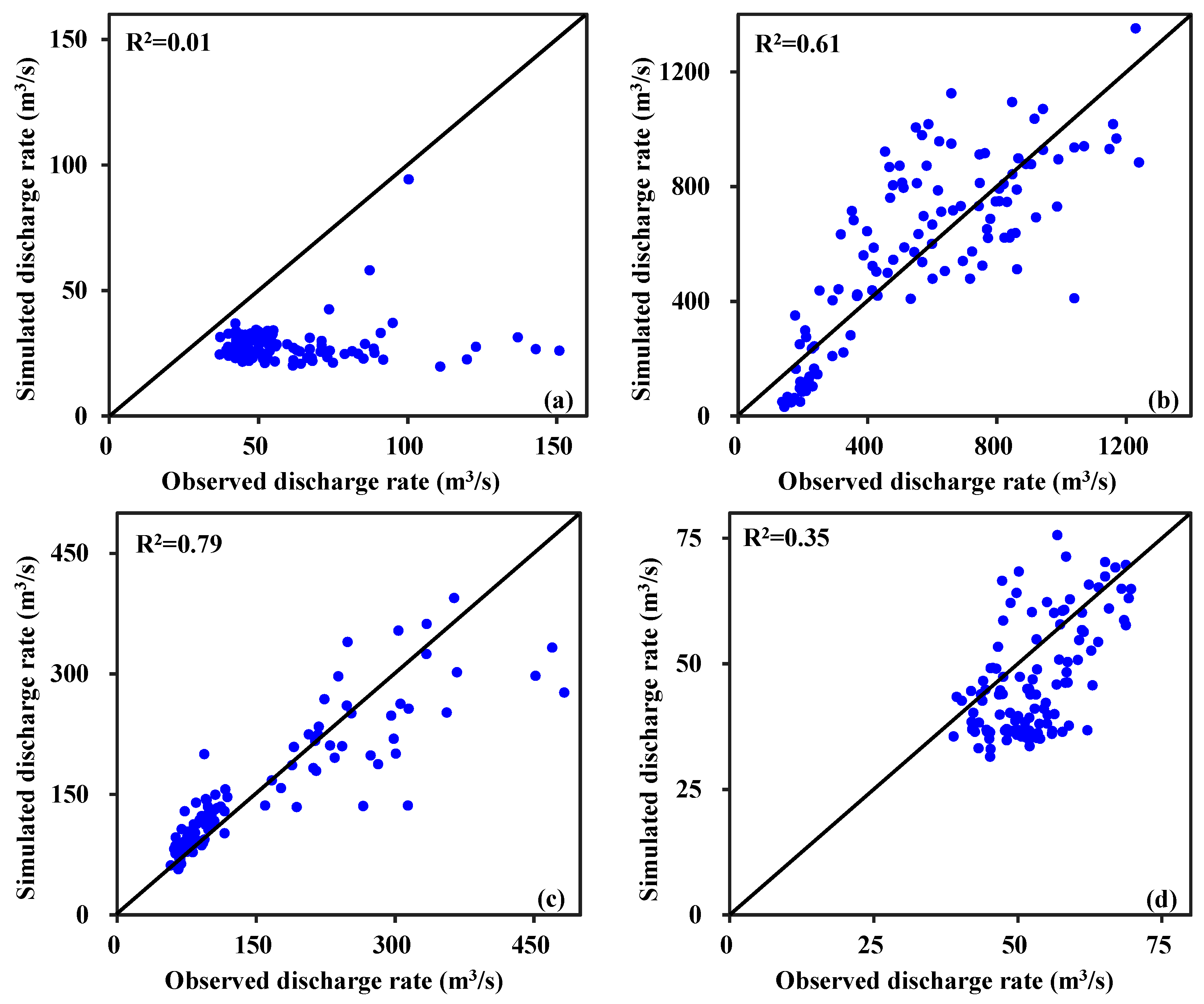
3.2. Model Performance
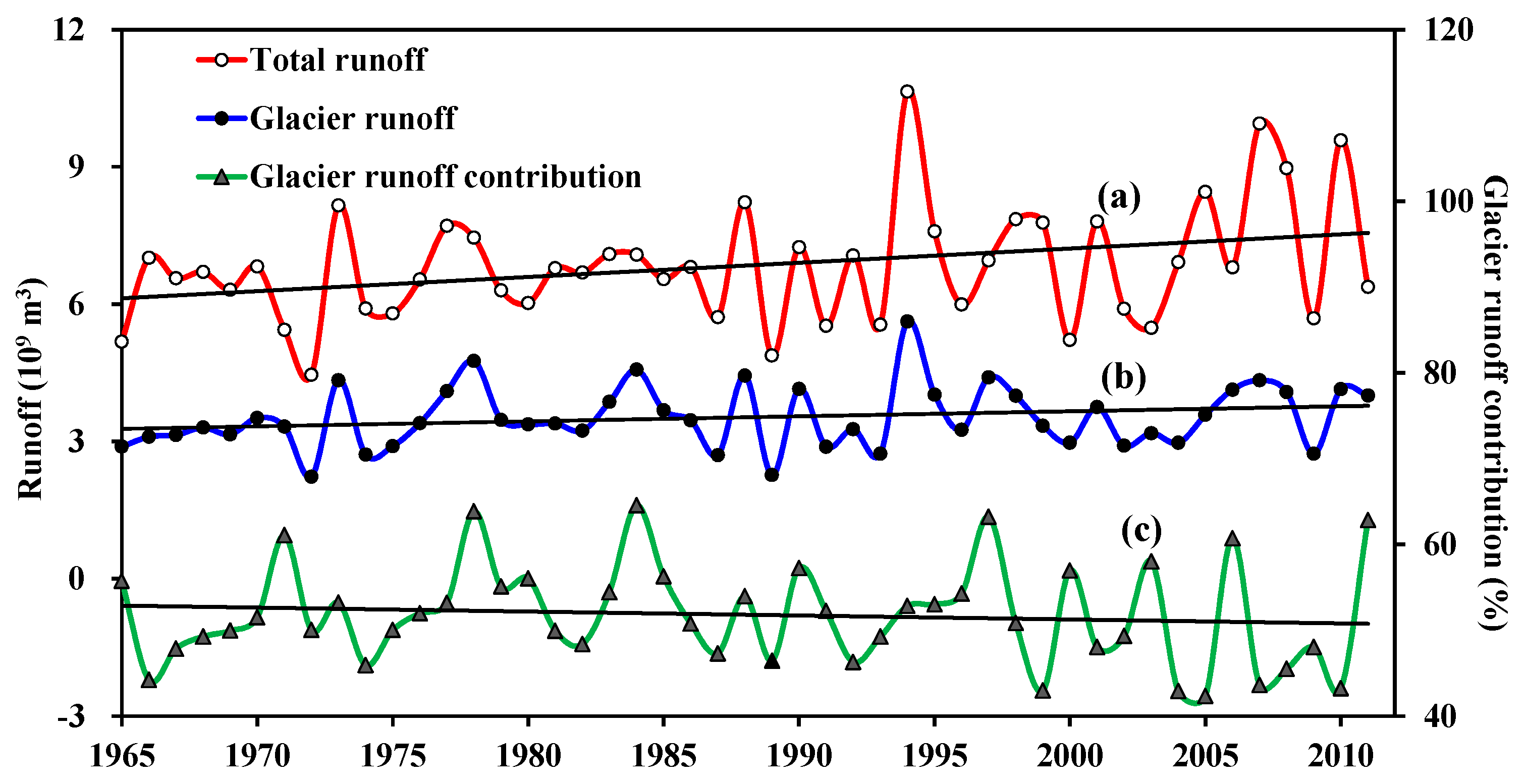
3.3. Annual Glacier Runoff Variation and Contribution
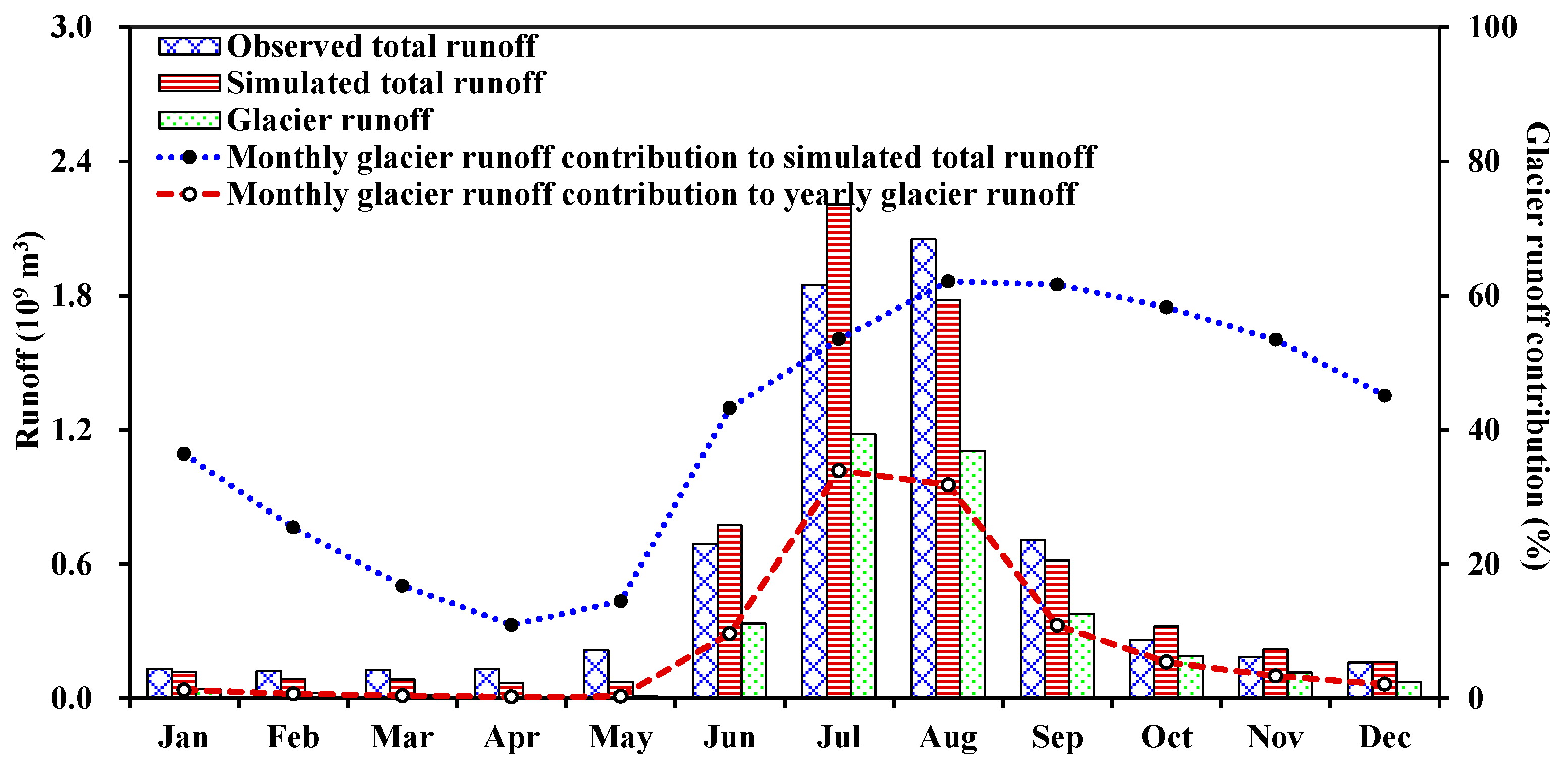
3.4. Multi-Year Monthly Average Glacier Runoff Contribution
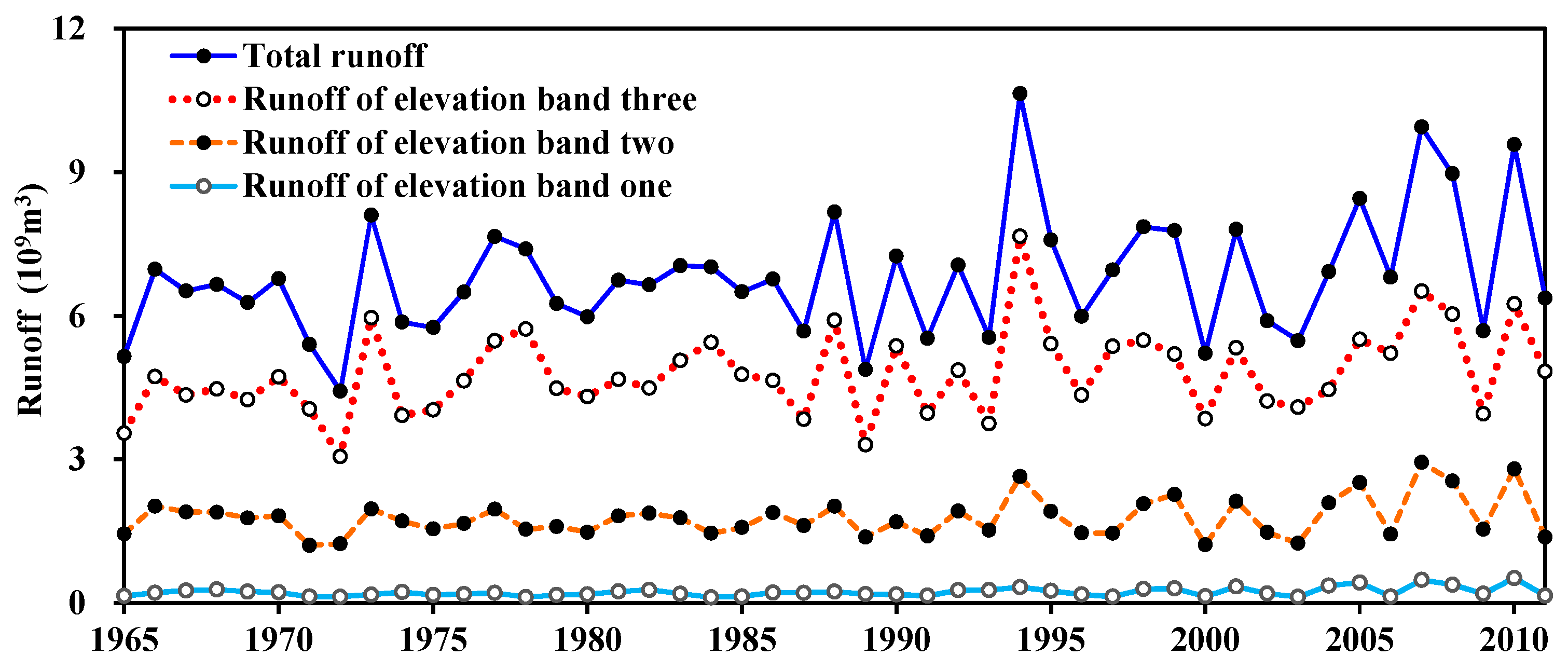
3.5. Glacier Runoff Contribution of Different Elevation Bands
4. Summary
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Morán-Tejeda, E.; Zabalza, J.; Rahman, K.; Gago-Silva, A.; López-Moreno, J.I.; Vicente-Serrano, S.; Lehmann, A.; Tague, C.L.; Beniston, M. Hydrological impacts of climate and land-use changes in a mountain watershed: Uncertainty estimation based on model comparison. Ecohydrology 2014, 8, 1396–1416. [Google Scholar] [CrossRef]
- Ivy-Ochs, S. Glacier variations in the European Alps at the end of the last glaciation. Cuad. Investig. Geogr. 2015, 41, 295. [Google Scholar] [CrossRef]
- Fischer, A. Glaciers and climate change: Interpretation of 50 years of direct mass balance of hintereisferner. Glob. Planet. Chang. 2010, 71, 13–26. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; van Beek, L.P.; Bierkens, M.F. Climate change will affect the asian water towers. Science 2010, 328, 1382–1385. [Google Scholar] [CrossRef] [PubMed]
- Huss, M.; Farinotti, D.; Bauder, A.; Funk, M. Modelling runoff from highly glacierized alpine drainage basins in a changing climate. Hydrol. Process. 2008, 22, 3888–3902. [Google Scholar] [CrossRef]
- Piao, S.; Ciais, P.; Huang, Y.; Shen, Z.; Peng, S.; Li, J.; Zhou, L.; Liu, H.; Ma, Y.; Ding, Y.; et al. The impacts of climate change on water resources and agriculture in China. Nature 2010, 467, 43–51. [Google Scholar] [CrossRef] [PubMed]
- Feng, Q.; Miao, Z.; Li, Z.; Li, J.; Si, J.; S, Y.; Chang, Z. Public perception of an ecological rehabilitation project in inland river basins in northern China: Success or failure. Environ. Res. 2015, 139, 20–30. [Google Scholar] [CrossRef] [PubMed]
- Oliva, M.; Antoniades, D.; Giralt, S.; Granados, I.; Pla-Rabes, S.; Toro, M.; Liu, E.J.; Sanjurjo, J.; Vieira, G. The holocene deglaciation of the Byers Peninsula (Livingston Island, Antarctica) based on the dating of lake sedimentary records. Geomorphology 2016, 261, 89–102. [Google Scholar] [CrossRef]
- Huss, M. Present and future contribution of glacier storage change to runoff from macroscale drainage basins in Europe. Water Resour. Res. 2011, 47, W07511. [Google Scholar] [CrossRef]
- Baraer, M.; Mark, B.G.; McKenzie, J.M.; Condom, T.; Bury, J.; Huh, K.-I.; Portocarrero, C.; Gómez, J.; Rathay, S. Glacier recession and water resources in Peru’s Cordillera Blanca. J. Glaciol. 2012, 58, 134–150. [Google Scholar] [CrossRef]
- Pellicciotti, F.; Buergi, C.; Immerzeel, W.W.; Konz, M.; Shrestha, A.B. Challenges and uncertainties in hydrological modeling of remote Hindu Kush–Karakoram–Himalayan (HKH) basins: Suggestions for calibration strategies. Mt. Res. Dev. 2012, 32, 39–50. [Google Scholar] [CrossRef]
- Feng, Q.; Wen, X.H.; Li, J.G. Wavelet analysis-support vector machine coupled models for monthly rainfall forecasting in arid regions. Water Resour. Manag. 2015, 29, 1049–1065. [Google Scholar] [CrossRef]
- Schaner, N.; Voisin, N.; Nijssen, B.; Lettenmaier, D.P. The contribution of glacier melt to streamflow. Environ. Res. Lett. 2012, 7, 034029. [Google Scholar] [CrossRef]
- Yin, Z.L.; Feng, Q.; Zou, S.B.; Yang, L.S. Assessing variation in water balance components in mountaious inland river basin experiencing climate change. Water 2016, 8, 472. [Google Scholar] [CrossRef]
- Koboltschnig, G.R.; Schöner, W.; Zappa, M.; Kroisleitner, C.; Holzmann, H. Runoff modelling of the glacierized alpine upper Salzach Basin (Austria): Multi-criteria result validation. Hydrol. Process. 2008, 22, 3950–3964. [Google Scholar] [CrossRef]
- Moors, E.J.; Groot, A.; Biemans, H.; van Scheltinga, C.T.; Siderius, C.; Stoffel, M.; Huggel, C.; Wiltshire, A.; Mathison, C.; Ridley, J.; et al. Adaptation to changing water resources in the Ganges Basin, northern India. Environ. Sci. Policy 2011, 14, 758–769. [Google Scholar] [CrossRef]
- Bolch, T.; Kulkarni, A.; Kaab, A.; Huggel, C.; Paul, F.; Cogley, J.G.; Frey, H.; Kargel, J.S.; Fujita, K.; Scheel, M.; et al. The state and fate of Himalayan glaciers. Science 2012, 336, 310–314. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Oliva, M.; Serrano, E.; Gómez-Ortiz, A.; González-Amuchastegui, M.J.; Nieuwendam, A.; Palacios, D.; Pérez-Alberti, A.; Pellitero-Ondicol, R.; Ruiz-Fernández, J.; Valcárcel, M.; et al. Spatial and temporal variability of periglaciation of the Iberian Peninsula. Quat. Sci. Rev. 2016, 137, 176–199. [Google Scholar] [CrossRef]
- Kaser, G.; Grosshauser, M.; Marzeion, B. Contribution potential of glaciers to water availability in different climate regimes. Proc. Natl. Acad. Sci. USA 2010, 107, 20223–20227. [Google Scholar] [CrossRef] [PubMed]
- Gascoin, S.; Kinnard, C.; Ponce, R.; Lhermitte, S.; MacDonell, S.; Rabatel, A. Glacier contribution to streamflow in two headwaters of the Huasco river, Dry Andes of Chile. Cryosphere 2011, 5, 1099–1113. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.; Gao, X.; Ye, B.; Zhang, X.; Hagemann, S. A modified monthly degree-day model for evaluating glacier runoff changes in China. Part II: Application. Hydrol. Process. 2012, 26, 1697–1706. [Google Scholar] [CrossRef]
- Liu, S.Y.; Zhang, Y.; Zhang, Y.S.; Ding, Y.J. Estimation of glacier runoff and future trends in the Yangtze River source region, China. J. Glaciol. 2009, 55, 353–362. [Google Scholar]
- Kong, Y.; Pang, Z. Evaluating the sensitivity of glacier rivers to climate change based on hydrograph separation of discharge. J. Hydrol. 2012, 434–435, 121–129. [Google Scholar] [CrossRef]
- Li, Z.X.; Feng, Q.; Liu, W.; Wang, T.T.; Cheng, A.F.; Gao, Y.; Guo, X.Y.; Pan, Y.H.; Li, J.G.; Guo, R. Study on the contribution of cryosphere to runoff in the cold alpine basin: A case study of Hulugou River Basin in the Qilian Mountains. Glob. Planet. Chang. 2014, 122, 345–361. [Google Scholar]
- Rahman, K.; Besacier-Monbertrand, A.L.; Castella, E.; Lods-Crozet, B.; Ilg, C.; Beguin, O. Quantification of the daily dynamics of streamflow components in a small alpine watershed in Switzerland using end member mixing analysis. Environ. Earth Sci. 2015, 74, 1–11. [Google Scholar] [CrossRef]
- Nolin, A.W.; Phillippe, J.; Jefferson, A.; Lewis, S.L. Present-day and future contributions of glacier runoff to summertime flows in a Pacific Northwest watershed: Implications for water resources. Water. Resour. Res. 2010, 46, W12509. [Google Scholar] [CrossRef]
- Prasch, M.; Mauser, W.; Weber, M. Quantifying present and future glacier melt-water contribution to runoff in a central Himalayan river basin. Cryosphere 2013, 7, 889–904. [Google Scholar] [CrossRef]
- Boscarello, L.; Ravazzani, G.; Rabuffetti, D.; Mancini, M. Integrating glaciers raster-based modelling in large catchments hydrological balance: The Rhone case study. Hydrol. Process. 2014, 28, 496–508. [Google Scholar] [CrossRef]
- La Frenierre, J.; Mark, B.G. A review of methods for estimating the contribution of glacial meltwater to total watershed discharge. Prog. Phys. Geogr. 2014, 38, 173–200. [Google Scholar] [CrossRef]
- Debele, B.; Srinivasan, R.; Gosain, A.K. Comparison of process-based and temperature-index snowmelt modeling in SWAT. Water Resour. Manag. 2009, 24, 1065–1088. [Google Scholar] [CrossRef]
- Gao, H.; He, X.; Ye, B.; Pu, J. Modeling the runoff and glacier mass balance in a small watershed on the central Tibetan Plateau, China, from 1955 to 2008. Hydrol. Process. 2012, 26, 1593–1603. [Google Scholar] [CrossRef]
- Jost, G.; Moore, R.D.; Menounos, B.; Wheate, R. Quantifying the contribution of glacier runoff to streamflow in the upper Columbia River Basin, Canada. Hydrol. Earth Syst. Sci. 2012, 16, 849–860. [Google Scholar] [CrossRef] [Green Version]
- Farinotti, D.; Usselmann, S.; Huss, M.; Bauder, A.; Funk, M. Runoff evolution in the Swiss Alps: Projections for selected high-alpine catchments based on ensembles scenarios. Hydrol. Process. 2012, 26, 1909–1924. [Google Scholar] [CrossRef]
- Gabbi, J.; Farinotti, D.; Bauder, A.; Maurer, H. Ice volume distribution and implications on runoff projections in a glacierized catchment. Hydrol. Earth Syst. Sci. 2012, 16, 4543–4556. [Google Scholar] [CrossRef] [Green Version]
- Nepal, S.; Krause, P.; Flügel, W.A.; Fink, M.; Fischer, C. Understanding the hydrological system dynamics of a glaciated alpine catchment in the Himalayan region using the J2000 hydrological model. Hydrol. Process. 2014, 28, 1329–1344. [Google Scholar] [CrossRef]
- Verbunt, M.; Gurtz, J.; Jasper, K.; Lang, H.; Warmerdam, P.; Zappa, M. The hydrological role of snow and glaciers in alpine river basins and their distributed modeling. J. Hydrol. 2003, 282, 36–55. [Google Scholar] [CrossRef]
- Finger, D.; Heinrich, G.; Gobiet, A.; Bauder, A. Projections of future water resources and their uncertainty in a glacierized catchment in the Swiss Alps and the subsequent effects on hydropower production during the 21st century. Water Resour. Res. 2012, 48, W02521. [Google Scholar] [CrossRef]
- Luo, Y.; Arnold, J.; Liu, S.; Wang, X.; Chen, X. Inclusion of glacier processes for distributed hydrological modeling at basin scale with application to a watershed in Tianshan Mountains, northwest China. J. Hydrol. 2013, 477, 72–85. [Google Scholar] [CrossRef]
- Rahman, K.; Maringanti, C.; Beniston, M.; Widmer, F.; Abbaspour, K.; Lehmann, A. Streamflow modeling in a highly managed mountainous glacier watershed using SWAT: The upper Rhone river watershed case in Switzerland. Water Resour. Manag. 2012, 27, 323–339. [Google Scholar] [CrossRef]
- Hock, R. Temperature index melt modelling in mountain areas. J. Hydrol. 2003, 282, 104–115. [Google Scholar] [CrossRef]
- Hock, R. A distributed temperature-index ice- and snowmelt model including potential direct solar radiation. J. Glaciol. 1999, 45, 101–111. [Google Scholar] [CrossRef]
- Pellicciotti, F.; Brock, B.; Strasser, U.; Burlando, P.; Funk, M.; Corripio, J. An enhanced temperature-index glacier melt model including the shortwave radiation balance: Development and testing for Haut Glacier d’Arolla, Switzerland. J. Glaciol. 2005, 51, 573–587. [Google Scholar] [CrossRef]
- Zappa, M.; Pos, F.; Strasser, U.; Warmerdam, P.M.M.; Gurtz, J. Seasonal water balance of an alpine catchment as evaluated by different methods for spatially distributed snowmelt modelling. Hydrol. Res. 2003, 34, 179–202. [Google Scholar]
- Rahman, K.; Etienne, C.; Gago-Silva, A.; Maringanti, C.; Beniston, M.; Lehmann, A. Streamflow response to regional climate model output in the mountainous watershed: A case study from the Swiss Alps. Environ. Earth Sci. 2014, 72, 4357–4369. [Google Scholar] [CrossRef]
- Radić, V.; Hock, R. Glaciers in the earth’s hydrological cycle: Assessments of glacier mass and runoff changes on global and regional scales. Surv. Geophys. 2013, 35, 813–837. [Google Scholar] [CrossRef]
- Wang, X.; Sun, L.; Zhang, Y.; Luo, Y. Rationalization of altitudinal precipitation profiles in a data-scarce glacierized watershed simulation in the Karakoram. Water 2016, 8, 186. [Google Scholar] [CrossRef]
- Huang, S.; Krysanova, V.; Zhai, J.; Su, B. Impact of intensive irrigation activities on river discharge under agricultural scenarios in the semi-arid Aksu River Basin, northwest China. Water Resour. Manag. 2015, 29, 1–15. [Google Scholar] [CrossRef]
- Chen, Y.; Xu, C.; Chen, Y.; Li, W.; Liu, J. Response of glacial-lake outburst floods to climate change in the Yarkant River Basin on northern slope of Karakoram Mountains, China. Quatern. Int. 2010, 226, 75–81. [Google Scholar] [CrossRef]
- Liu, S.Y.; Yao, X.J.; Guo, W.Q.; Xu, J.L.; Shangguan, D.H.; Wei, J.F.; Bao, W.J.; Wu, L.Z. The contemporary glaciers in China based on the Second Chinese Glacier Inventory. Acta Geogr. Sin. 2015, 70, 3–16. (In Chinese) [Google Scholar]
- Yang, H.A.; An, R.Z. Glacier Inventory of China, V: Karakorum Mountains (Drainage Basin of the Yarkant River); Science Press: Bejing, China, 1989. [Google Scholar]
- Zhang, X.S.; Zhou, Y.C. Study on the Glacier Lake Outburst Floods of the Yarkant River, Karakorum Mountains; Science Press: Beijing, China, 1990. [Google Scholar]
- Liu, J.; Liu, T.; Bao, A.; De Maeyer, P.; Kurban, A.; Chen, X. Response of hydrological processes to input data in high alpine catchment: An assessment of the Yarkant River Basin in China. Water 2016, 8, 181. [Google Scholar] [CrossRef]
- Xu, Y.; Gao, X.; Shen, Y.; Xu, C.; Shi, Y.; Giorgi, F. A daily temperature dataset over China and its application in validating a RCM simulation. Adv. Atmos. Sci. 2009, 26, 763–772. [Google Scholar] [CrossRef]
- Zhao, Y.F.; Zhu, J. Assessing quality of grid daily precipitation datasets in China in recent 50 years. Plateau Meteorol. 2015, 34, 50–58. (In Chinese) [Google Scholar]
- Guo, D.; Wang, H. Simulation of permafrost and seasonally frozen ground conditions on the Tibetan Plateau, 1981–2010. J. Geophys. Res. Atmos. 2013, 118, 5216–5230. [Google Scholar] [CrossRef]
- Arnold, J.G.; Srinivasan, R.; Williams, J.R. Large area hydrologic modeling and assessment. Part I: Model development. J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil and Water Assessment Tool Theoretical Documentation: Version 2005; USDA-ARS Grassland, Soil and Water Research Laboratory: Temple, TX, USA, 2005. [Google Scholar]
- Gassman, P.W.; Reyes, M.R.; Green, C.H.; Arnold, J.G. The soil and water assessment tool: Historical development, applications, and future research directions. Trans. Asabe 2007, 50, 1211–1250. [Google Scholar] [CrossRef]
- Wang, X.; Melesse, A.M. Evaluation of the SWAT model’s snowmelt hydrology in a northwestern minnesota watershed. Trans. ASABE 2005, 48, 1359–1376. [Google Scholar] [CrossRef]
- Zhang, X.; Srinivasan, R.; Debele, B.; Hao, F. Runoff simulation of the headwaters of the Yellow River using the SWAT model with three snowmelt algorithms. J. Am. Water Resour. Assoc. 2008, 44, 48–61. [Google Scholar] [CrossRef]
- Zhang, W.; Zha, X.; Li, J.; Liang, W.; Ma, Y.; Fan, D.; Li, S. Spatiotemporal change of blue water and green water resources in the headwater of Yellow River Basin, China. Water Resour. Manag. 2014, 28, 4715–4732. [Google Scholar] [CrossRef]
- Zhang, Y.; Fujita, K.; Liu, S.; Liu, Q.; Nuimura, T. Distribution of debris thickness and its effect on ice melt at Hiluogou glacier, southeastern Tibetan Plateau, using in situ surveys and ASTER imagery. J. Glaciol. 2011, 57, 1147–1157. [Google Scholar] [CrossRef]
- Garnier, B.J.; Ohmura, A. A method of calculating the direct shortwave radiation income of slopes. J. Appl. Meteorol. 1968, 7, 796–800. [Google Scholar] [CrossRef]
- Jiang, X.; Wang, N.; He, J.; Wu, X.; Song, G. A distributed surface energy and mass balance model and its application to a mountain glacier in China. Chin. Sci. Bull. 2010, 55, 2079–2087. [Google Scholar] [CrossRef]
- Liu, S.Y.; Sun, W.X.; Shen, Y.P.; Li, G. Glacier changes since the Little Ice Age maximum in the western Qilian Shan, northwest China, and consequences of glacier runoff for water supply. J. Glaciol. 2003, 49, 117–124. [Google Scholar]
- Meier, M.F.; Bahr, D.B. Counting Glaciers: Use of Scaling Methods to Estimate the Number and Size Distribution of the Glaciers of the World; U.S. Army: Hanover, NH, USA, 1996. [Google Scholar]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, S.; Ding, Y. Observed degree-day factors and their spatial variation on glaciers in western China. Ann. Glaciol. 2006, 43, 301–306. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, S.; Xu, J.; Shangguan, D. Glacier change and glacier runoff variation in the Tuotuo River basin, the source region of Yangtze River in western China. Environ. Geol. 2008, 56, 59–68. [Google Scholar] [CrossRef]
- Peng, D.Z.; Xu, Z.X. Simulating the impact of climate change on streamflow in the Tarim River Basin by using a modified semi-distributed monthly water balance model. Hydrol. Process. 2010, 24, 209–216. [Google Scholar] [CrossRef]
- Shangguan, D.; Liu, S.; Ding, Y.; Ding, L.; Xu, J.; Jing, L. Glacier changes during the last forty years in the Tarim interior River Basin, northwest China. Prog. Nat. Sci. 2009, 19, 727–732. [Google Scholar] [CrossRef]
- Chen, Y.N.; Xu, C.C.; Hao, X.M.; Li, W.H.; Chen, Y.P.; Zhu, C.G.; Ye, Z.X. Fifty-year climate change and its effect on annual runoff in the Tarim River Basin, China. Quat. Int. 2009, 208, 53–61. [Google Scholar]
- Gao, X.; Ye, B.; Zhang, S.; Qiao, C.; Zhang, X. Glacier runoff variation and its influence on river runoff during 1961–2006 in the Tarim River Basin, China. Sci. China Earth Sci. 2010, 53, 880–891. [Google Scholar] [CrossRef]
- Fan, Y.; Chen, Y.; Li, W.; Wang, H.; Li, X. Impacts of temperature and precipitation on runoff in the Tarim River during the past 50 years. J. Arid Land 2011, 3, 220–230. [Google Scholar] [CrossRef]
- Hock, R. Glacier melt: A review of processes and their modelling. Prog. Phys. Geogr. 2002, 27, 362–391. [Google Scholar] [CrossRef]
- Comeau, L.E.L.; Pietroniro, A.; Demuth, M.N. Glacier contribution to the North and South Saskatchewan Rivers. Hydrol. Process. 2009, 23, 2640–2653. [Google Scholar] [CrossRef]
- Ling, H.; Xu, H.; Fu, J. Changes in intra-annual runoff and its response to climate change and human activities in the headstream areas of the Tarim River Basin, China. Quat. Int. 2014, 336, 158–170. [Google Scholar] [CrossRef]
- Xu, Z.; Liu, Z.; Fu, G.; Chen, Y. Trends of major hydroclimatic variables in the Tarim River Basin during the past 50 years. J. Arid Environ. 2010, 74, 256–267. [Google Scholar] [CrossRef]

| Watershed | Glacier | Ice Temperature Melt Factor (mm·d−1·°C−1) | Altitude (m) | Observation Period |
|---|---|---|---|---|
| Yarkant River | Batura | 3.4 | 2780 | June–August 1975 |
| Teram Kangri | 5.9 | 4630 | 25 June–7 September 1987 | |
| 6.4 | 4650 | 6 June–7 September 1987 | ||
| Tailan River | Qirbulake | 2.6 | 4750 | 6 June–30 July 1960 |
| Yangbulake | 4.3 | 4800 | 1–5 July 1987 | |
| Qiongtailan | 4.5 | 3675 | 17 June–13 July 1978 | |
| 7.3 | 4100 | 25 June–31 July 1978 | ||
| 8.6 | 4200 | 21 June–31 July 1978 | ||
| Aksu River | Keqicar Baxi | 4.5 | 3347 | 28 June–12 September 2003 |
| 7.0 | 4216 | 11 July–13 September 2003 |
| Model Routine | Parameter | Description | Range | Optimized Value |
|---|---|---|---|---|
| Snow | SMFMX | Melt factor for snow, 21 June (mm/°C-day) | 0, 10 | 6.5 |
| SMFMN | Melt factor for snow, 21 December (mm/°C-day) | 0, 10 | 1.0 | |
| SFTMP | Snowfall temperature (°C) | −5, +5 | 1.0 | |
| SMTMP | Snow melt base temperature (°C) | −5, +5 | 0.5 | |
| TIMP | Snow pack temperature lag factor | 0.1, 2.0 | 1.0 | |
| Glacier | FM | Melt factor for ice (mm/°C-day) | 2.6, 13 | 5.5 |
| rice | Radiation factor for ice | 0, 0.1 | 14.4 × 10−6 | |
| β0 | Basal accumulation coefficient | 0.001, 0.006 | 0.003 | |
| Runoff | ESCO | Soil evaporation compensation factor | 0.01, 1.0 | 0.55 |
| ALPHA_BF | Baseflow alpha factor (days) | 0.1, 1.0 | 0.036 | |
| CN2 | Initial SCS CN II value | 50, 80 | Multiply 70% | |
| CH_K2 | Effective hydraulic conductivity in channel (mm/h) | 0, 50 | 4 | |
| GWQMN | Threshold depth of water in shallow aquifer (mm) | 1, 200 | 100 | |
| GW_DELAY | Groundwater delay (days) | 0, 180 | 45 |
| Periods | NSE | RSR | PBIAS (%) |
|---|---|---|---|
| Calibration (January 1965–December 1988) | 0.86 | 0.37 | −4.51 |
| Validation (January 1989–December 2011) | 0.82 | 0.42 | 2.38 |
| Overall (January 1965–December 2011) | 0.85 | 0.39 | −1.75 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, Z.; Feng, Q.; Liu, S.; Zou, S.; Li, J.; Yang, L.; Deo, R.C. The Spatial and Temporal Contribution of Glacier Runoff to Watershed Discharge in the Yarkant River Basin, Northwest China. Water 2017, 9, 159. https://doi.org/10.3390/w9030159
Yin Z, Feng Q, Liu S, Zou S, Li J, Yang L, Deo RC. The Spatial and Temporal Contribution of Glacier Runoff to Watershed Discharge in the Yarkant River Basin, Northwest China. Water. 2017; 9(3):159. https://doi.org/10.3390/w9030159
Chicago/Turabian StyleYin, Zhenliang, Qi Feng, Shiyin Liu, Songbing Zou, Jing Li, Linshan Yang, and Ravinesh C. Deo. 2017. "The Spatial and Temporal Contribution of Glacier Runoff to Watershed Discharge in the Yarkant River Basin, Northwest China" Water 9, no. 3: 159. https://doi.org/10.3390/w9030159
APA StyleYin, Z., Feng, Q., Liu, S., Zou, S., Li, J., Yang, L., & Deo, R. C. (2017). The Spatial and Temporal Contribution of Glacier Runoff to Watershed Discharge in the Yarkant River Basin, Northwest China. Water, 9(3), 159. https://doi.org/10.3390/w9030159










