Multivariate Analysis of Joint Probability of Different Rainfall Frequencies Based on Copulas
Abstract
:1. Introduction
2. Data and Method
2.1. Methodology
2.1.1. Concept of Copulas
2.1.2. Copula Fitting
2.1.3. Recurrence Interval
2.2. Catchment and Data
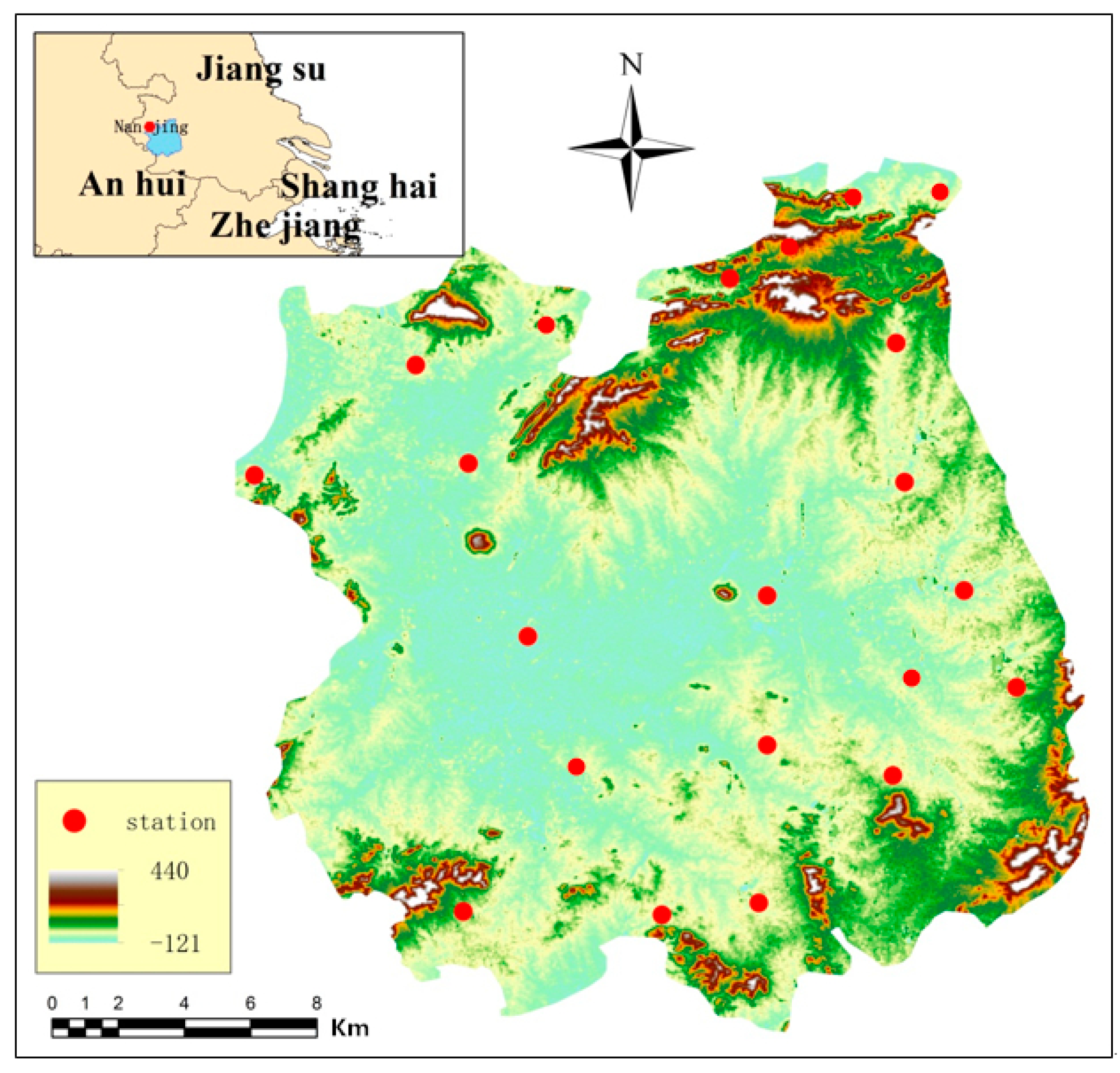
2.2.1. The Catchment
2.2.2. Rainfall Data
3. Results and Discussion
3.1. Data Analysis
3.2. Marginal Distributions
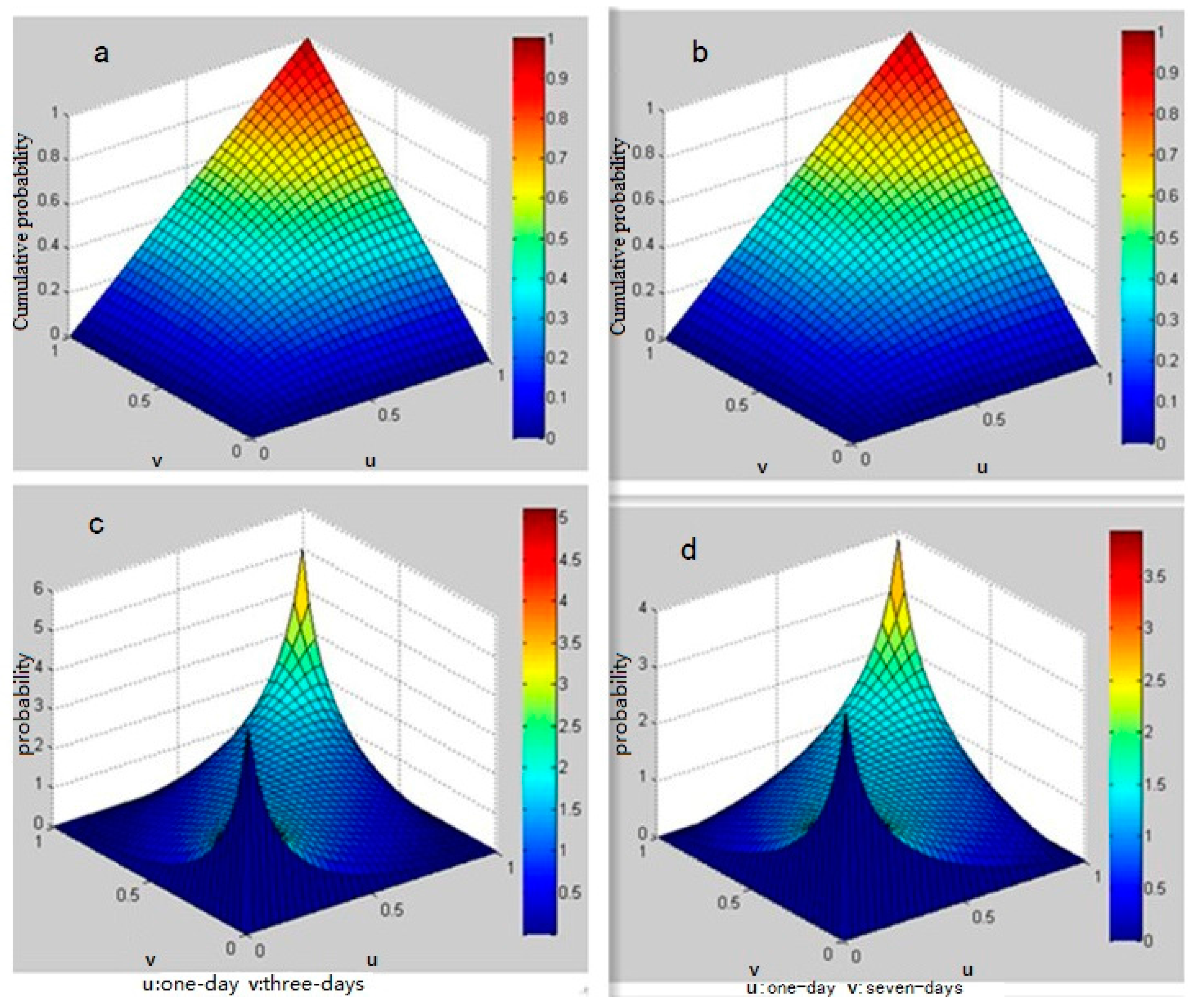
3.3. Dependence Structure
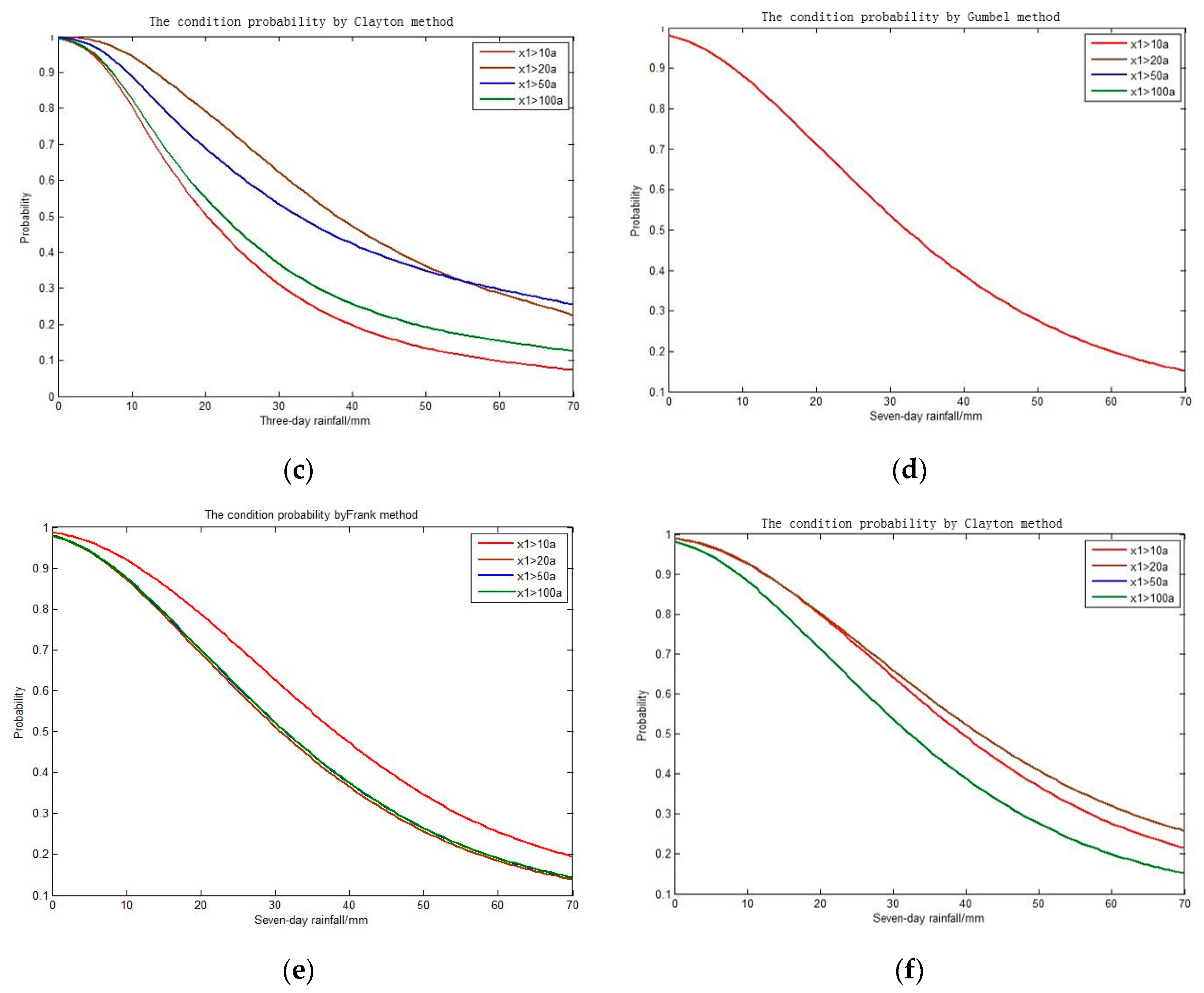
3.4. Conditional Probability
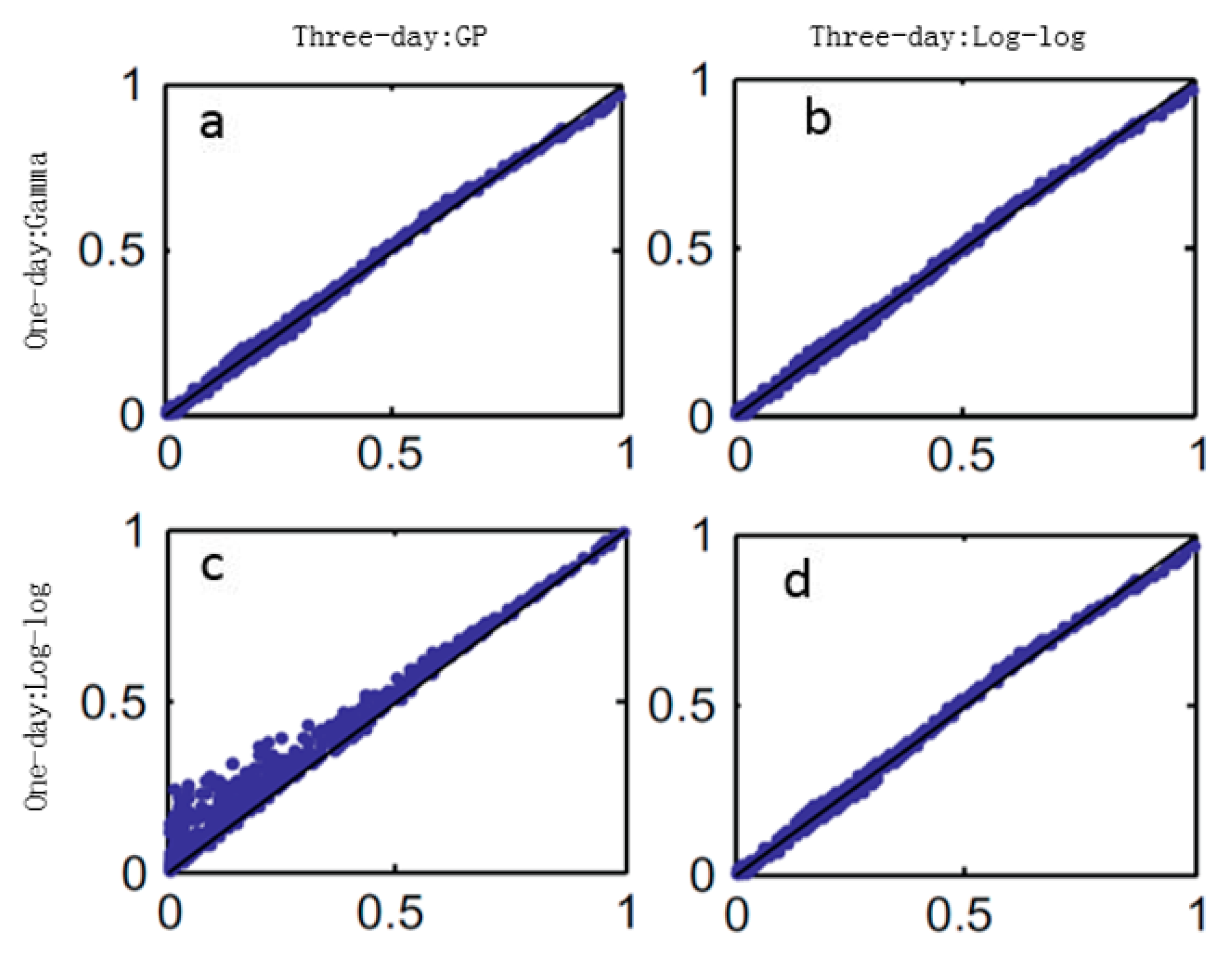
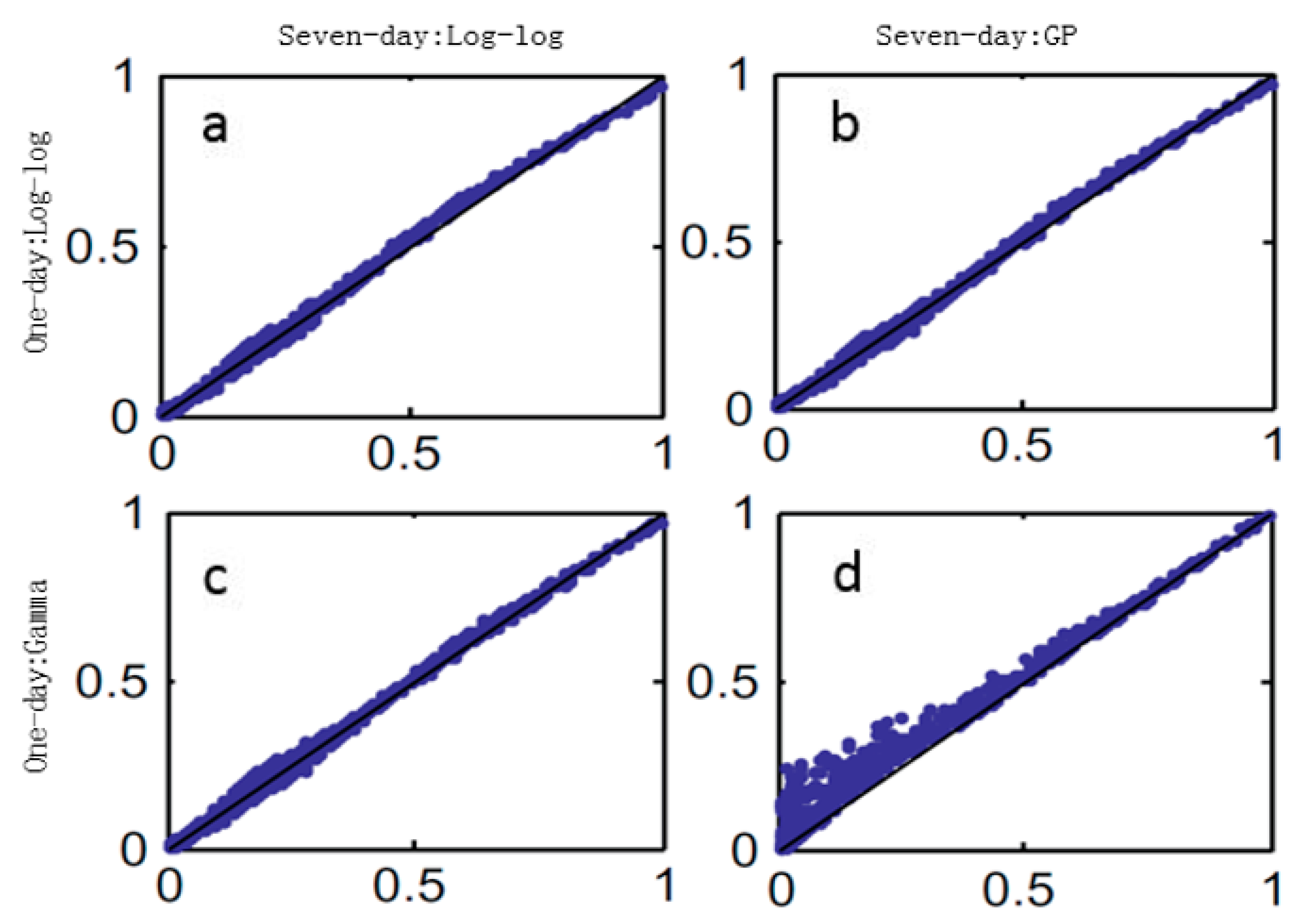
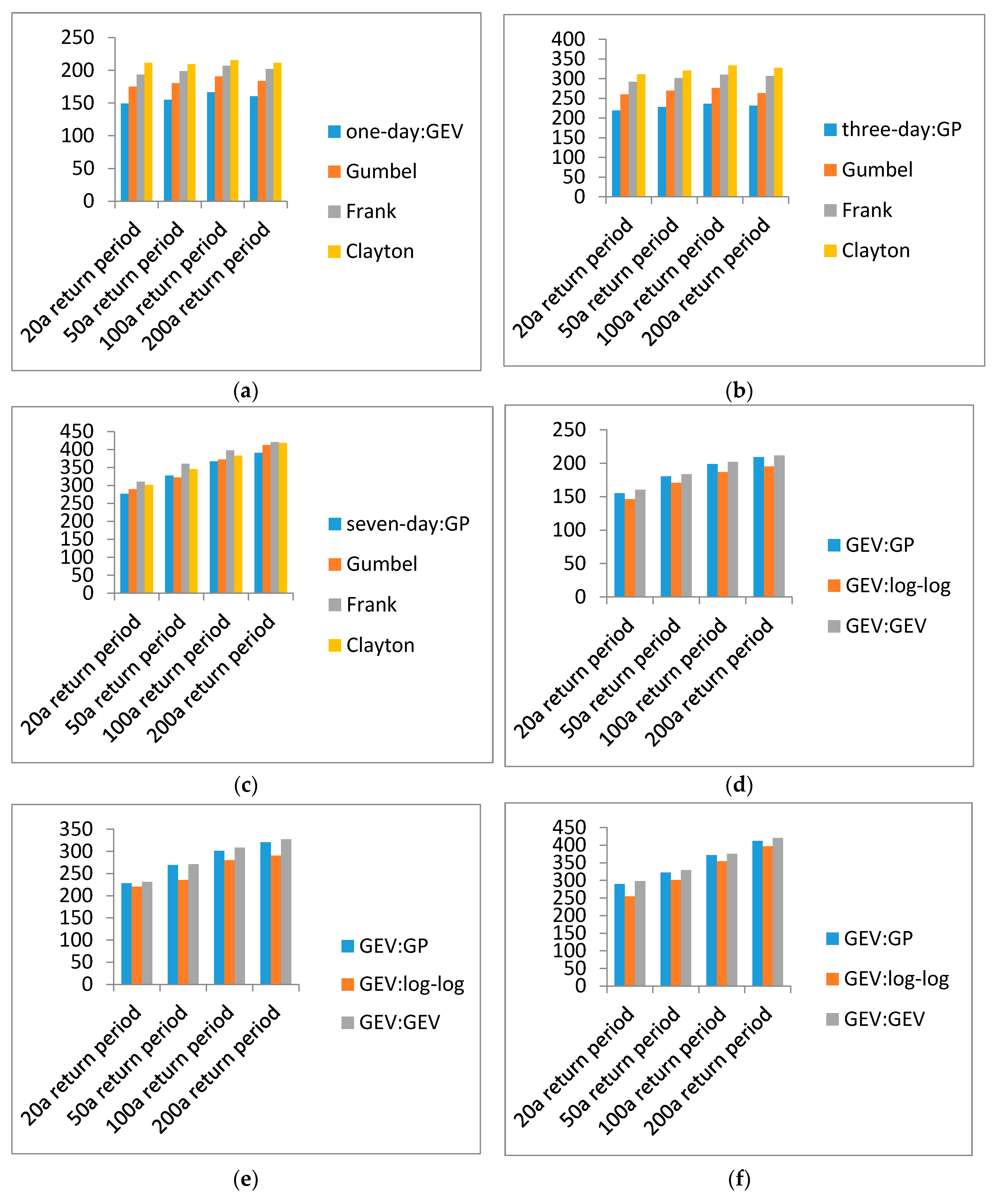
3.5. Impacts of Copulas and Marginal Distributions
4. Conclusions
- (1)
- It is necessary to consider different marginal distributions that cannot be rejected by statistical tests for copula fitting rather than choosing the best ranked distributions. As revealed using bivariate copulas, the pair of the best fitted marginal distributions for the one-day and multi-day rainfall cannot produce the best overall performance during construction of the joint distribution of one-day and multi-day events.
- (2)
- Several different measures should be used to consider the best fit copula identification, including statistics, graphical approaches, tail dependence analysis and comparison to empirical copulas. Different measures can reflect different characteristics of copulas. A single measure may identify inappropriate copulas, leading to an overestimate or underestimate of the probability of a flood.
- (3)
- The copula method has flexibility and provides notable advantages in constructing complex, bivariate probability distributions for one-day and multi-day rainfall for system performance analysis. The results provide a more accurate probabilistic evaluation of precipitation for flood control based on the characterisation of the dependence structure for one-day and multi-day rainfall.
- (4)
- The designed maximum one-day precipitation and maximum three-day precipitation are important when we think about a city’s flood control system. However, it is meaningful to take the probabilistic relationships between the first day rainfall and the overall rainfall using multivariable joint distribution into account. This provides crucial information for more accurate estimation of storm designs and the associated risks.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Liu, P.; Li, L.; Guo, S.; Xiong, L.; Zhang, W.; Zhang, J.; Xu, C.Y. Optimal design of seasonal flood limited water levels and its application for the Three Gorges Reservoir. J. Hydrol. 2015, 527, 1045–1053. [Google Scholar] [CrossRef]
- Seo, B.C.; Krajewski, W.F. Correcting temporal sampling error in radar-rainfall: Effect of advection parameters and rain storm characteristics on the correction accuracy. J. Hydrol. 2015, 531, 272–283. [Google Scholar] [CrossRef]
- Huang, S.; Hou, B.; Chang, J.; Huang, Q.; Chen, Y. Copulas-based probabilistic characterization of the combination of dry and wet conditions in the Guanzhong Plain, China. J. Hydrol. 2014, 519, 3204–3213. [Google Scholar] [CrossRef]
- Balistrocchi, M.; Grossi, G.; Bacchi, B. Deriving a practical analytical-probabilistic method to size flood routing reservoirs. Adv. Water Resour. 2013, 62, 37–46. [Google Scholar] [CrossRef]
- Molina, J.L.; Zazo, S.; Rodríguez-Gonzálvez, P.; González-Aguilera, D. Innovative Analysis of Runoff Temporal Behavior through Bayesian Networks. Water 2016, 8, 35–56. [Google Scholar] [CrossRef]
- Thorndahl, S.; Willems, P. Probabilistic modelling of overflow, surcharge and flooding in urban drainage using the first-order reliability method and parameterization of local rain series. Water Res. 2008, 42, 455–466. [Google Scholar] [CrossRef] [PubMed]
- Stephenson, A.G.; Lehmann, E.A.; Phatak, A. A max-stable process model for rainfall extremes at different accumulation durations. Weather Clim. Extrem. 2016, 13, 44–53. [Google Scholar] [CrossRef]
- Van de Vyver, H. Bayesian estimation of rainfall intensity–duration–frequency relationships. J. Hydrol. 2015, 529, 1451–1463. [Google Scholar] [CrossRef]
- Ma, T.; Li, C.; Lu, Z.; Bao, Q. Rainfall intensity—Duration thresholds for the initiation of landslides in Zhejiang Province, China. Geomorphology 2015, 245, 193–206. [Google Scholar] [CrossRef]
- Huang, Y.F.; Mirzaei, M.; Amin, M.Z.M. Uncertainty Quantification in Rainfall Intensity Duration Frequency Curves Based on Historical Extreme Precipitation Quantiles. Procedia Eng. 2016, 154, 426–432. [Google Scholar] [CrossRef]
- Favre, A.C.; El Adlouni, S.; Perreault, L.; Thiémonge, N.; Bobée, B. Multivariate hydrological frequency analysis using copulas. Water Resour. Res. 2004, 40, 67–79. [Google Scholar] [CrossRef]
- Li, F.; Zheng, Q. Probabilistic modelling of flood events using the entropy copula. Probabilistic modelling of flood events using the entropy copula. Adv. Water Resour. 2016, 97, 233–240. [Google Scholar] [CrossRef]
- Durocher, M.; Chebana, F.; Ouarda, T.B. On the prediction of extreme flood quantiles at ungauged locations with spatial copula. J. Hydrol. 2015, 533, 523–532. [Google Scholar] [CrossRef]
- Fu, G.; Butler, D.; Khu, S.T. Multiple objective optimal control of integrated urban wastewater systems. Environ. Model. Softw. 2008, 23, 225–234. [Google Scholar] [CrossRef]
- Frahm, G.; Junker, M.; Schmidt, R. Estimating the tail dependence coefficient: Properties and pitfalls. Insur. Math. Econ. 2005, 37, 80–100. [Google Scholar] [CrossRef]
- Nazemi, A.; Elshorbagy, A. Application of copula modelling to the performance assessment of reconstructed watersheds. Stoch. Environ. Res. Risk Assess. 2012, 26, 189–205. [Google Scholar] [CrossRef]
- Targino, R.S.; Peters, G.W.; Shevchenko, P.V. Sequential Monte Carlo Samplers for capital allocation under copula-dependent risk models. Insur. Math. Econ. 2015, 61, 206–226. [Google Scholar] [CrossRef]
- Meintanis, S.G.; Ngatchou-Wandji, J.; Taufer, E. Goodness-of-fit tests for multivariate stable distributions based on the empirical characteristic function. J. Multivar. Anal. 2015, 140, 171–192. [Google Scholar] [CrossRef]
- Aghakouchak, A.; Ciach, G.; Habib, E. Estimation of tail dependence coefficient in rainfall accumulation fields. Adv. Water Res. 2010, 33, 1142–1149. [Google Scholar] [CrossRef]
- Fu, G.; Butler, D. Copula-based frequency analysis of overflow and flooding in urban drainage systems. J. Hydrol. 2014, 510, 49–58. [Google Scholar] [CrossRef] [Green Version]
- Ma, M.W.; Ren, L.L.; Song, S.B.; Song, J.L.; Jiang, S.H. Goodness-of-fit tests for multi-dimensional copulas: Expanding application to historical drought data. Water Sci. Eng. 2013, 6, 18–30. [Google Scholar]
- Villarini, G.; Serinaldi, F.; Krajewski, W.F. Modeling radar-rainfall estimation uncertainties using parametric and non-parametric approaches. Adv. Water Res. 2008, 31, 1674–1686. [Google Scholar] [CrossRef]
- Montes-Iturrizaga, R.; Heredia-Zavoni, E. Reliability analysis of mooring lines using copulas to model statistical dependence of environmental variables. Appl. Ocean Res. 2016, 59, 564–576. [Google Scholar] [CrossRef]
- Joe, H. Multivariate Models and Dependence Concepts; Chapman and Hall: London, UK, 1997. [Google Scholar]
- Bazargani, N.; Nosratinia, A. Joint maximum likelihood estimation of activation and Hemodynamic Response Function for FMRI. Med. Image Anal. 2014, 18, 711–724. [Google Scholar] [CrossRef] [PubMed]
- Kao, S.C.; Govindaraju, R.S. Probabilistic structure of storm surface runoff considering the dependence between average intensity and storm duration of rainfall events. Water Sci. Eng. 2007, 430, 491–496. [Google Scholar] [CrossRef]
- Genest, C.; Favre, A.C. Everything You Always Wanted to Know about Copula Modeling but Were Afraid to Ask. J. Hydrol. Eng. 2007, 12, 347–368. [Google Scholar] [CrossRef]
- Chatzithomas, C.D.; Alexandris, S.G. Solar radiation and relative humidity based, empirical method, to estimate hourly reference evapotranspiration. Agric. Water Manag. 2015, 152, 188–197. [Google Scholar] [CrossRef]
- Genest, C.; Rivest, L.P. Statistical Inference Procedures for Bivariate Archimedean Copulas. J. Am. Stat. Assoc. 1993, 88, 1034–1043. [Google Scholar] [CrossRef]
- Vandenberghe, S.; Verhoest, N.E.C.; De Baets, B. Fitting bivariate copulas to the dependence structure between storm characteristics: A detailed analysis based on 105 year 10 min rainfall. Water Resour. Res. 2010, 46, 489–496. [Google Scholar] [CrossRef]
- Basinger, M.; Montalto, F.; Lall, U. A rainwater harvesting system reliability model based on nonparametric stochastic rainfall generator. J. Hydrol. 2010, 392, 105–188. [Google Scholar] [CrossRef]
- Di Bernardino, E.; Rulliere, D. On tail dependence coefficients of transformed multivariate Archimedean copulas. Fuzzy Sets Syst. 2016, 284, 89–112. [Google Scholar] [CrossRef]
- Hua, L.; Joe, H. Strength of tail dependence based on conditional tail expectation. J. Multivar. Anal. 2014, 123, 143–159. [Google Scholar] [CrossRef]
- Keylock, C.J. Describing the recurrence interval of extreme floods using nonextensive thermodynamics and Tsallis statistics. Adv. Water Resour. 2005, 28, 773–778. [Google Scholar] [CrossRef]
- Zhang, J.; Lin, X.; Guo, B. Multivariate Copula-Based Joint Probability Distribution of Water Supply and Demand in Irrigation District. Water Resour. Manag. 2016, 30, 2361–2375. [Google Scholar] [CrossRef]
- Nelsen, R.B. An Introduction to Copulas; Springer: New York, NY, USA, 2006. [Google Scholar]


| NO. | Name of Rain Station | Date Series |
|---|---|---|
| 1 | qinhuai new river sluice | 1967–1968, 1981–1982, 1987–2010 |
| 2 | wudingmen sluice | 1961–2010 |
| 3 | tiansheng bridge sluice | 1953–2010 |
| 4 | qianhan village | 1965–1969, 1978–2010 |
| 5 | east mountain | 1953–2010 |
| 6 | jurong | 1953–2010 |
| 7 | zhaocun reservoir | 1955–1960, 1962–2010 |
| 8 | anjishan reservoir | 1953–1910 |
| 9 | linchang | 1965–2001 |
| 10 | tingzi | 1967–2001 |
| 11 | xixie | 1967–2001 |
| 12 | aiyuan | 1967–2001 |
| 13 | chishan new sluice | 1960–2010 |
| 14 | tianwangsi | 1953–1961, 1963–1999 |
| 15 | qilin | 1967–1968, 1978–1999 |
| 16 | north mountain reservoir | 1960–1988, 1991, 1996–2010 |
| 17 | ershengqiao reservoir | 1962–1988, 2000–2010 |
| 18 | maoshan reservoir | 1978–1988, 2004–2010 |
| 19 | fangbian reservoir | 1954, 1957, 1958, 1960–1966, 1991, 1996–2010 |
| 20 | wolongshan reservoir | 2004–2010 |
| 21 | zhongshan reservoir | 1977–1979, 2004–2010 |
| Date Series | Distribution | K–S | p-Value |
|---|---|---|---|
| Kn | |||
| one-day rainfall | GEV | 0.017 | 0.833 |
| Gamma | 0.023 | 0.510 | |
| Log-Log | 0.036 | 0.429 | |
| GP | 0.049 | 0.065 | |
| three-day rainfall | GP | 0.019 | 0.910 |
| Log-Log | 0.025 | 0.176 | |
| GEV | 0.038 | 0.091 | |
| Gamma | 0.042 | 0.091 |
| Date Series | Distribution | K–S | p-Value |
|---|---|---|---|
| Kn | |||
| one-day rainfall | GEV | 0.022 | 0.072 |
| Log-Log | 0.032 | 0.047 | |
| Gamma | 0.043 | 0.037 | |
| GP | 0.054 | 0.006 | |
| seven-day rainfall | GP | 0.019 | 1.003 |
| Log-Log | 0.031 | 0.194 | |
| GEV | 0.048 | 0.103 | |
| Gamma | 0.056 | 0.111 |
| One-Day Rainfall | Three-Day Rainfall | Gumbel | Confidence Interval | Frank | Confidence Interval | Clayton | Confidence Interval |
|---|---|---|---|---|---|---|---|
| GEV | GP | 1.375 | [1.285, 1.466] | 2.472 | [1.971, 2.974] | 0.443 | [0.317, 0.570] |
| Log-Log | 1.399 | [1.309, 1.489] | 2.412 | [1.916, 2.909] | 0.393 | [0.273, 0.513] | |
| GEV | 1.372 | [1.280, 1.465] | 2.546 | [2.032, 3.059] | 0.413 | [0.288, 0.539] | |
| Gamma | GP | 1.377 | [1.280, 1.465] | 2.509 | [1.997, 3.021] | 0.375 | [0.257, 0.494] |
| Log-Log | 1.403 | [1.284, 1.470] | 2.447 | [1.940, 2.953] | 0.340 | [0.227, 0.453] | |
| GEV | 1.375 | [1.311, 1.496] | 2.591 | [2.067, 3.114] | 0.354 | [0.237, 0.471] | |
| Log-Log | GP | 1.382 | [1.281, 1.470] | 2.845 | [2.290, 3.400] | 0.507 | [0.344, 0.671] |
| Log-Log | 1.403 | [1.288, 1.476] | 2.447 | [1.940, 2.953] | 0.340 | [0.227, 0.453] | |
| GEV | 1.385 | [1.311, 1.496] | 3.063 | [2.502, 3.623] | 0.473 | [0.323, 0.623] |
| One-Day Rainfall | Seven-Day Rainfall | Gumbel | Confidence Interval | Frank | Confidence Interval | Clayton | Confidence Interval |
|---|---|---|---|---|---|---|---|
| GEV | GP | 1.100 | [1.028, 1.173] | 2.101 | [1.964, 2.240] | 0.399 | [0.373, 0.425] |
| Log-Log | 1.119 | [1.046, 1.193] | 2.050 | [1.916, 2.186] | 0.354 | [0.331, 0.377] | |
| GEV | 1.098 | [1.026, 1.170] | 2.164 | [2.032, 2.307] | 0.372 | [0.347, 0.396] | |
| Log-Log | GP | 1.102 | [1.029, 1.175] | 2.133 | [1.993, 2.274] | 0.338 | [0.315, 0.360] |
| Log-Log | 1.122 | [1.049, 1.197] | 2.080 | [1.944, 2.218] | 0.306 | [0.286, 0.326] | |
| GEV | 1.100 | [1.028, 1.173] | 2.202 | [2.058, 2.348] | 0.319 | [0.298, 0.340] | |
| Gamma | GP | 1.106 | [1.033, 1.179] | 2.418 | [2.260, 2.578] | 0.456 | [0.426, 0.486] |
| Log-Log | 1.122 | [1.049, 1.197] | 2.080 | [1.944, 2.218] | 0.306 | [0.286, 0.326] | |
| GEV | 1.108 | [1.035, 1.181] | 2.604 | [2.433, 2.776] | 0.426 | [0.398, 0.454] |
| One-Day Rainfall | Three-Day Rainfall | Gumbel | Frank | Clayton | |||
|---|---|---|---|---|---|---|---|
| RMSE | Tn | RMSE | Tn | RMSE | Tn | ||
| GEV | GP | 0.014 | 0.111 | 0.015 | 0.119 | 0.013 | 0.102 |
| Log-Log | 0.016 | 0.147 | 0.016 | 0.140 | 0.013 | 0.099 | |
| GEV | 0.015 | 0.138 | 0.020 | 0.212 | 0.016 | 0.166 | |
| Gamma | GP | 0.011 | 0.062 | 0.014 | 0.103 | 0.016 | 0.168 |
| Log-Log | 0.013 | 0.091 | 0.015 | 0.127 | 0.017 | 0.169 | |
| GEV | 0.014 | 0.102 | 0.019 | 0.208 | 0.020 | 0.242 | |
| Log-Log | GP | 0.061 | 2.078 | 0.074 | 3.041 | 0.048 | 1.421 |
| Log-Log | 0.013 | 0.091 | 0.015 | 0.127 | 0.017 | 0.169 | |
| GEV | 0.059 | 2.017 | 0.079 | 3.481 | 0.048 | 1.458 | |
| One-Day Rainfall | Seven-Day Rainfall | Gumbel | Frank | Clayton | |||
|---|---|---|---|---|---|---|---|
| RMSE | Tn | RMSE | Tn | RMSE | Tn | ||
| GEV | GP | 0.013 | 0.111 | 0.012 | 0.124 | 0.011 | 0.102 |
| Log-Log | 0.014 | 0.147 | 0.013 | 0.121 | 0.011 | 0.099 | |
| GEV | 0.014 | 0.138 | 0.016 | 0.201 | 0.014 | 0.166 | |
| Log-Log | GP | 0.010 | 0.062 | 0.011 | 0.204 | 0.014 | 0.168 |
| Log-Log | 0.011 | 0.091 | 0.012 | 0.205 | 0.015 | 0.169 | |
| GEV | 0.012 | 0.102 | 0.015 | 0.293 | 0.018 | 0.242 | |
| Gamma | GP | 0.052 | 1.918 | 0.060 | 1.726 | 0.042 | 1.421 |
| Log-Log | 0.011 | 0.091 | 0.012 | 0.205 | 0.015 | 0.169 | |
| GEV | 0.053 | 2.017 | 0.064 | 1.771 | 0.042 | 1.458 | |
| One-Day | GEV | Gamma | Log-Log | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Three-day | GP | Log-Log | GEV | GP | Log-Log | GEV | GP | Log-Log | GEV |
| ƛu | 0.337 | 0.352 | 0.336 | 0.339 | 0.354 | 0.337 | 0.342 | 0.354 | 0.344 |
| u | 0.344 | 0.363 | 0.345 | 0.349 | 0.361 | 0.346 | 0.347 | 0.360 | 0.350 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Li, C.; Liu, J.; Yu, F.; Qiu, Q.; Tian, J.; Zhang, M. Multivariate Analysis of Joint Probability of Different Rainfall Frequencies Based on Copulas. Water 2017, 9, 198. https://doi.org/10.3390/w9030198
Wang Y, Li C, Liu J, Yu F, Qiu Q, Tian J, Zhang M. Multivariate Analysis of Joint Probability of Different Rainfall Frequencies Based on Copulas. Water. 2017; 9(3):198. https://doi.org/10.3390/w9030198
Chicago/Turabian StyleWang, Yang, Chuanzhe Li, Jia Liu, Fuliang Yu, Qingtai Qiu, Jiyang Tian, and Mengjie Zhang. 2017. "Multivariate Analysis of Joint Probability of Different Rainfall Frequencies Based on Copulas" Water 9, no. 3: 198. https://doi.org/10.3390/w9030198
APA StyleWang, Y., Li, C., Liu, J., Yu, F., Qiu, Q., Tian, J., & Zhang, M. (2017). Multivariate Analysis of Joint Probability of Different Rainfall Frequencies Based on Copulas. Water, 9(3), 198. https://doi.org/10.3390/w9030198






