Abstract
The design of hydraulic structures and flood risk management is often based on instantaneous peak flow (IPF). However, available flow time series with high temporal resolution are scarce and of limited length. A correct estimation of the IPF is crucial to reducing the consequences derived from flash floods, especially in Mediterranean countries. In this study, empirical methods to estimate the IPF based on maximum mean daily flow (MMDF), artificial neural networks (ANN), and adaptive neuro-fuzzy inference system (ANFIS) have been compared. These methods have been applied in 14 different streamflow gauge stations covering the diversity of flashiness conditions found in Peninsular Spain. Root-mean-square error (RMSE), and coefficient of determination (R2) have been used as evaluation criteria. The results show that: (1) the Fuller equation and its regionalization is more accurate and has lower error compared with other empirical methods; and (2) ANFIS has demonstrated a superior ability to estimate IPF compared to any empirical formula.
1. Introduction
Flash floods are one of the most significant natural hazards in Europe, especially in the Mediterranean countries [1]. In recent years, flash floods have caused many economic losses and loss of life throughout Peninsular Spain. As can be seen in Barredo (2007) [2], Spain is the country in Europe that has been the most affected by flash floods from 1950 to 2005. Estimation of the frequency and magnitude of the instantaneous peak flow (IPF) is crucial for the design of hydraulic structures and floodplain management [3]. As happens in many countries, Spanish basin management agencies record data relating to mean daily flow (MDF) while the availability of IPF time series is less frequent. The application of techniques that reduce uncertainties associated with IPF estimations is needed because of the damage that flash floods cause.
Several methods for estimating IPF based on MDF have been developed. From an empirical point of view, there are two types of approaches to estimating IPF based on MDF. The first type of approach establishes a relationship between IPF and MDF using the physiographic characteristics of the basin and the second type of approach calculates IPF using the sequence of mean daily flow. In the first group, the method by Fuller (1914) [4] is included; he conducted one of the first studies related to obtaining the IPF from the maximum MDF (MMDF) using drainage area. Other studies, such as those by Silva (1997) [5] and Silva and Tucci (1998) [6], also used the physiographic characteristics to estimate the IPF. Taguas et al. (2008) [7] proposed an equation to estimate IPF from MMDF, drainage area and mean annual rainfall in Southeastern Spain. Among the methods that use the second approach, there are two pioneering methods [8,9] described by Linsley et al. (1949) [10] and the Sangal (1983) [11]. Many studies adjusted Fuller’s formula for use in their regions. Fill and Steiner (2013) [12] summarized many of these regional formulas in their research. In Spain, the Spanish Centre for Public Works Studies and Experimentation CEDEX [13] adjusted the Fuller formula to obtain thirteen regional equations, which cover Peninsular Spain. In this research, four of these empirical methods were evaluated. Two of them, Fuller’s (1914) [4] and the regionalized formula obtained by CEDEX, are included in the first approach group and Sangal (1983) [11] and the Fill and Steiner (2013) [12] methodologies are included in the second group.
According to recent studies [14], new methods have increased the accuracy associated with estimating IPF through the application of data-driven techniques, such as adaptive neuro-fuzzy inference systems (ANFIS) and artificial neural networks (ANN). Therefore, in this work, we have also employed the ANN and ANFIS, which are machine-learning methods used widely in order to compare the results obtained by applying the empirical formula. ANNs reproduce the learning process of the human brain [15]. An ANN is a powerful and efficient mathematical model for linear and nonlinear approximations and is often known as a universal approximator [16]. Mustafa et al. (2012) [17] examined the effectiveness of ANNs in solving different hydrologic problems and concluded that appropriate ANN modelling is advantageous compared with conventional modelling techniques. Generalizability and forecast accuracy are some advantages of ANNs [18]. These properties make ANNs suitable for solving problems of estimation and prediction in hydrology [19]. ANNs have the capability of obtaining the relationship between the predictor variables (in this case, MMDF) and the estimated variables (here, IPF) of a process [16,19]. We have also used the ANFIS model to estimate IPF from MMDF. ANFIS is another powerful technique for modeling a nonlinear system and it integrates fuzzy logic into neural networks. Therefore, ANFIS has the ANN learning ability [20]. The ANFIS model is a fusion of ANN and a Fuzzy Inference System (FIS) and possesses the advantages of both systems. The benefit of ANNs is that it learns independently and adapts itself to changing environments and the advantage of FIS is that it systematically generates unknown fuzzy rules from given information (inputs/outputs) [21]. Therefore, this combination allows a FIS to learn from the data to create models. This is an efficient model for determining the behaviour of imprecisely defined complex dynamical systems [22]. This model has also been accepted as an efficient alternative technique for modeling and prediction in hydrology [23]. Some researchers who have applied ANFIS in hydrological modelling are Dastorani et al. (2010) [24] and Seckin (2011) [25].
Although ANN and ANFIS have great advantages, there are also certain disadvantages [26,27], such as: (1) Neural networks are a black box and do not clarify the functional relationship between the input and output values; (2) a neural network has to be trained for each problem to obtain the adequate architecture, and this requires greater computational resources; and (3) ANFIS is more complicated than FIS and is not available for all FIS options.
Many hydrological studies have shown that ANFIS was more efficient than other models as recurrent neural networks or fuzzy logic [28,29]. Shabani et al. (2012) [30] and Dastorani et al. (2013) [31] applied ANFIS and ANNs to estimate IPF from MMDF and compared their results with the methods of Fuller [4], Sangal [11], and Fill-Steiner [12]. They found that ANFIS increased the accuracy of the estimation of the IPF. The aim of this study is to identify a method to estimate IPF with greater accuracy in fourteen watersheds covering the diversity of flashiness conditions found in Peninsular Spain. In those basins, longer MDF data series exist, but the IPF data series are shorter. Nevertheless, at least 30 years of IPF data are available in the selected basins in order to compare the performance between estimated and measured IPF.
2. Materials and Methods
2.1. Study Area and Data
Spain shows a wide range of climatic characteristics due to its position between the European temperature zone and the subtropical zone. It also includes some of the rainiest areas in Europe in the northeast as well as the driest ones in the southeast, with a marked long drought period in summer. A set of 14 flow gauging stations distributed over peninsular Spain was selected to serve as a case study. The basins were selected based on several criteria. It was intended to have (1) a wide diversity of various flow regimes representative of the diversity of the conditions across Peninsular Spain; (2) a sufficiently long time series (more than 30 years) from gauging stations located in near-natural basins; (3) basin areas not exceeding 1000 km2. As shown in Figure 1, the basins used in this study are well distributed over Peninsular Spain, covering the three main climatic zones distinguished in Peninsular Spain: the Mediterranean climate, which is characterised by dry and warm summers and cool to mild, wet winters; the oceanic climate, which is located in the northern part of the country; and the semiarid climate, which is present in the centre and southeastern parts of the country, where in contrast to the Mediterranean climate, the dry season continues beyond the end of summer.
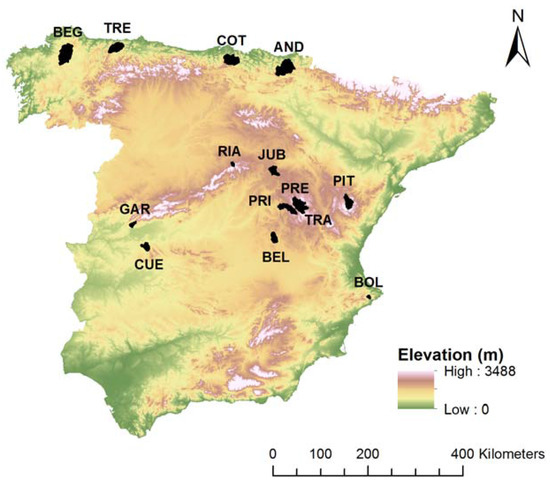
Figure 1.
Location of the selected basins.
Table 1 lists the set of 14 basins, showing basin areas ranging from 29 to 837 km2 with an average area of 307 km2, altitudes vary from 16 to 1278 m and streamflow data covering a period ranging from 38 to 70 years. According to the Koppen climate classification system [32], among the fourteen studied basins, six of them are considered warm-summer Mediterranean climates (Csb), four of them are considered oceanic climates (Cfb), three of them are considered hot-summer Mediterranean climates (Csa), and there is only one basin representing semi-arid climate (Bsk). There is no south-western basin in this study due to the lack of data in this area, which has been studied for less than ten years in most gauging stations. Besides, according to Senent-Aparicio et al. (2016) [33], Southern Spain is one of the most water-stressed regions of Europe, and this is why it is very difficult to find near-natural basins in this part of Spain. In order to evaluate the flashiness of the basins selected, the Richards-Baker Flashiness Index (R-B Index) [34] has been obtained. This index reflects the velocity and frequency of short term changes in streamflow in response to storm events and can be calculated as shown in Equation (1).
where, i is the time step, n is the total number of time step and q is the daily flow.

Table 1.
Summary of the main characteristics of the selected basins.
As shown in Table 1, the R-B Index in the basins selected range from 0.08 to 0.47, covering the diversity of flashiness conditions found in Peninsular Spain. Higher values for this index indicate higher flashiness (flashy streams), whereas lower values indicate stable streams. Climates, topography, geology, percentages of forest cover, catchment area and shape, land use and other catchment attributes influence the streamflow regime and, hence, the flashiness index [34]. Depending on the case study, different correlations between flashiness index and catchment attributes can be found. We have found a negative correlation with the mean catchment elevation, and this is similar to results obtained by Holko et al. (2011) [35]. The daily flow data and streamflow gauging stations were collected from the CEDEX [36].
2.2. Empirical Formulas
The only way to obtain instantaneous flows accurately is to measure them. If these have not been measured, any attempt to obtain the instantaneous flow afterwards will result in an approximate value. Although the relationship between MDF and IPF is logically variable from one flood to another, in most watersheds, this relationship is usually more or less constant or, at least, it fluctuates within a relatively narrow range of values [13]. This has led to the application of empirical formulas to calculate the unknown values of IPF from the known values of MDF. The following are the different empirical methods used in this study.
2.2.1. Fuller
Fuller [4] studied flood data of 24 watersheds in The United States with basin areas between 3.06 and 151,592 km2 and suggested an equation where IPF is calculated from MMDF as a function of the drainage area. Fuller formula (Equation (2)) is the most important and widely accepted due to its simplicity [11].
where IPF is the estimated instantaneous peak flow (m3/s), MMDF is the maximum observed mean daily flow (m3/s), and A is the drainage area (km2). The coefficients present in Equation (2) are regression coefficients that were obtained in Fuller’s study [4].
2.2.2. CEDEX Regionalization of Fuller´s Formula
In 2011, CEDEX [13] published a technical report about methodologies used in maximum streamflow mapping of the different river basin districts of Spain. CEDEX proposed twelve regional formulas to transform MMDF data into the corresponding IPF based on Fuller’s method. Each formula corresponds to a river basin district; these are shown in Table 2. In these regional formulas, IPF is the estimated instantaneous peak flow (m3/s), MMDF is the maximum observed mean daily flow (m3/s), A is the drainage area (km2) and the coefficients have been obtained by regression for each region.

Table 2.
Regional formulas of CEDEX [13].
2.2.3. Sangal
In his study, Sangal [11] realised several calculations based on a triangular hydrograph and proposed the following formula (Equation (3)) where the variables are the mean daily flow of three consecutive days.
where IPF is the estimated instantaneous peak flow (m3/s), MMDF is the maximum observed mean daily flow (m3/s), Q1 is the mean daily flow on the preceding day (m3/s), and Q3 is the mean daily flow on the following day.
Sangal tested his method using data from 387 gauging stations in Ontario (Canada) for basin areas measuring less than 1 km2 to more than 100,000 km2. He obtained good estimations in the majority of basins, although in small basins the peak flow could be underestimated.
2.2.4. Fill and Steiner
Fill and Steiner [12] created a study based on Sangal’s formula and obtained values of estimated IPF that were higher than the observed values in basin areas greater than 1000 km2. This problem of overestimating instantaneous peak flow led Fill and Steiner to propose an improvement to Sangal’s method. They used data from 14 stations of basins with drainage areas between 84 and 687 km2 in Brazil and developed a simple formula (Equation (4)), suitable for drainage areas from 50 to 700 km2, similar to Sangal’s (Equation (3)) to obtain the IPF from the mean daily flow of three consecutive days.
where IPF is the estimated instantaneous peak flow (m3/s), MMDF is the maximum observed mean daily flow (m3/s), Q1 is the mean daily flow on preceding day (m3/s) and Q3 is the mean daily flow on posterior day. Further details about Equation (4) are available in Fill and Steiner (2003) [12].
2.3. Artificial Neural Network (ANN)
To estimate IPF data, we used the feedforward multilayer perceptron network (MLP), the most popular ANN in hydrology [37]. The MLP network includes an input layer, an output layer, and one or more hidden layers. The first layer receives the input data, the hidden layers process data, and the last layer obtains the output data [38]. Each layer contains one or more neurons connected with all neurons of the next immediate layer through vertically aligned interconnections. The output y of a neuron j is obtained by computing the following Equation (5) [39]:
where, f is an activation function, X is a vector of inputs, Wj is a vector of connection weights from neurons in the preceding layer to neuron j, and bj is a bias associated with neuron j.
During the training process with a backpropagation algorithm, the output errors are repeatedly fed back into the network to adjust connection weights and biases until optimal values are obtained [40]. The number of hidden neurons and the number of hidden layers is often determined by trial and error [41,42]. In this study, one or two hidden layers with a number of neurons between two and twenty are considered. The optimal network configuration has been determined using an iterative process, evaluating the performance for different network structures. In this process, the data sets are randomly divided into three subsets: training set (70%), validation set (15%), and test set (15%). The number of maximum training iterations (epochs) was 1000 and the Levenberg-Marquardt backpropagation algorithm [43,44] is applied to adjust the appropriate weights and minimize error.
The ANN structure used in this work is shown in Figure 2, where the input data is the maximum mean daily flow and the output data is the instantaneous peak flow. The tangent sigmoid transfer function in the hidden layers and linear transfer function in the output layer were used. We implemented and built the ANNs using MATLAB® software (version 8.2.0.701 (R2013b), The Mathworks, MA, USA).
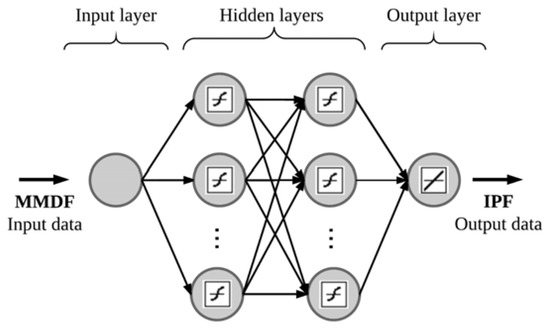
Figure 2.
Structure of feedforward multilayer perceptron network (MLP) network used in this research.
2.4. Adaptive Neuro-Fuzzy Inference System (ANFIS)
ANFIS models nonlinear functions and makes a nonlinear map from input space to output space using fuzzy if-then rules, with each rule describing the local behaviour of the mapping. The parameters of these rules determine the efficiency of the FIS [45] and describe the shape of the Membership Functions (MF).
In this study, the Sugeno-type FIS [46,47] was used. In this learning process, a hybrid learning algorithm—a combination of the least-squares method and the backpropagation gradient descent method—is used to emulate a given training data set and estimate the parameters of the FIS. The ANFIS architecture is based on the work of Jang (1993) [48] and it is composed of five layers. In the first layer, every node is an adaptive node and acts as an MF. Different MFs were used in this study and the models with the generalized bell and sigmoidal membership function obtained the more accurate results in the testing phase. MMDF was used as input data.
2.5. Evaluation Criteria
In this work, the performance of the different methods was evaluated using three evaluation tools. Firstly, coefficient of determination (R2) (Equation (6)) was used to describe the degree of collinearity between estimated and observed data and the proportion of variance in observed data explained by the model [49].
where is the ith observed data, is the mean of the observed data, is the ith estimated data, is the mean of the estimated data, n is the total number of observations, is the variance of the observed data and is the variance of the estimated data.
Secondly, root mean square error (RMSE) (Equation (7)) was used. RMSE is an error index commonly used for quantifying the estimation error and is useful in assessing the errors in the units of the data [49].
Finally, an analysis of observed-estimated plot with the identity line (1:1 line) was used.
3. Results and Discussion
As shown in Table 3, to compare the results of the empirical formulas, R2 and RMSE values were calculated for the fourteen gauge stations studied. The best results for each basin are highlighted in black in Table 3. The estimation with a higher R2 value and a lower RMSE value is the best. According to the results obtained, in most of the stations, Fuller or the regionalization of Fuller’s equation (CEDEX) have the higher coefficient of determination and the lowest amount of error. It can also be concluded that the regionalization of the Fuller equation improves the estimation of the IPF, especially in basins with a high flashiness index, as demonstrated in the results obtained in AND, COT, TRE, GAR, and CUE. Besides, the Fill and Steiner formula obtained more accurate results in PER and PIT, basins characterized by a low flashiness index. The Sangal formula exhibits very regular behaviour in general, with more accurate results compared with Fill and Steiner but worse results compared with the Fuller equation or its regionalization. With regard to climate zones, a clear pattern is not observed indicating a preference of one method over another.

Table 3.
Evaluation of the results of empirical formulas based on R2 and root mean square error (RMSE) criteria.
Results obtained by ANN, ANFIS, and the best empirical formula in each basin are shown in Table 4. The best results for each basin are highlighted in black. In order to construct the ANN and its accurate training, data was entered into the MATLAB software in the form of 80% training data and 20% test data. An ANN structure with two hidden layers and two hidden neurons in each layer was the optimal structure for most basins, while the second most used structure had one hidden layer with two hidden neurons. ANN, ANFIS, and empirical formulas were applied to the same gauge stations under similar conditions and compared using R2 and RMSE as evaluation criteria. From the data in Table 4, it is evident that the highest R2 and the lowest RMSE between simulated and observed results in most of the stations were obtained using the ANFIS method. These results support outcomes of Dastorani et al. (2013) [31] and Fathzadeh et al. (2016) [14]. With respect to the ANN method, the accuracy of ANN outputs is, in general, higher than the outputs obtained using empirical formulas, but lower compared to ANFIS results. As shown in the RIA basin data, estimations obtained using ANN are more accurate when the flow data series used as input data is longer. In general, the results obtained by machine-learning techniques (ANN and ANFIS) are clearly more accurate than those obtained by empirical formulas. Only in AND and BEG basins do the empirical formulas improve the results obtained by these techniques.

Table 4.
Statistics of artificial neural networks (ANN), adaptive neuro-fuzzy inference (ANFIS) versus the best empirical formula.
Moreover, according to the plots in Figure 3, where line slope and correlation coefficient between observed and measured values of IPF obtained with ANN and ANFIS techniques are compared, ANFIS seems to be slightly better in most of the gauge stations studied because those results concentrate closer to the identity line (perfect line) and the correlation coefficient is closer to 1. However, the differences between the techniques increase when the RMSE results are analysed, as shown in Table 4.
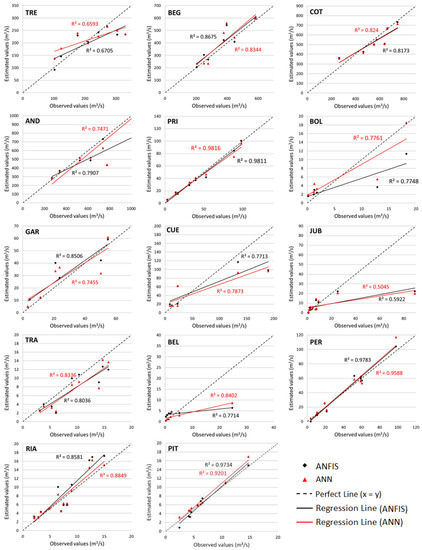
Figure 3.
Scatter plots of observed instantaneous peak flow (IPF) (m3/s) and the estimated IPF (m3/s) obtained with ANN versus ANFIS for basins (test phase). The letters on the top left of each subfigure show the basin codes (see Table 1).
4. Conclusions
Estimation of instantaneous peak flow is essential for flood management and the design of hydraulic structures, especially in countries like Spain, where flash floods are a common occurrence and can cause significant damage. In this research, empirical formulas found in the literature and some learning-machine algorithms that have been used recently to estimate many different hydrological variables were applied to estimate IPF from MMDF. Our results show that the use of machine-learning models of the fuzzy type, such as ANFIS, are more accurate in general than ANN. These conclusions suggest that ANFIS is the more accurate method for increasing the accuracy of the estimation of IPF when a long-time series of MDF is available but the availability of IPF is shorter. The machine-learning method is superior to empirical formulas due to the data used from the basins in the case study, and future extensive studies with more data would be needed to obtain better estimators. On the other hand, the nonlinear dynamics of the relationship between IPF and MDF justifies the results obtained by the ANFIS method.
The main drawback of these machine-learning methods was the time consumed to model them. Finding the optimal structure of a neural network, the appropriate MF, and the shape of each variable in ANFIS is difficult and is determined through the process of trial and error. So, they require long tests and much greater computational resources than empirical formulas.
Acknowledgments
The first author was supported by the Catholic University of Murcia (UCAM) research scholarship program. The authors gratefully acknowledge support from the UCAM through the project “PMAFI/06/14”. This research was also partially supported by the GESINHIMPADAPT project (CGL2013-48424-C2-2-R) and by the HETEROLISTIC project (TIN2016-78799-P) with Spanish MINECO funds. We acknowledge Papercheck Proofreading & Editing Services.
Author Contributions
All authors contributed significantly to the development of the methodology applied in this study. Patricia Jimeno-Sáez and Javier Senent-Aparicio designed the experiments and wrote the manuscript; Julio Pérez-Sánchez and José María Cecilia helped to perform the experiments and reviewed and helped to prepare this paper for publication; David Pulido-Velázquez as the supervisor of Patricia Jimeno-Sáez provided many important advices on the concept of methodology and structure of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gaume, E.; Bain, V.; Bernardara, P.; Newinger, O.; Barbuc, M.; Bateman, A.; Blaškovičová, L.; Blöschl, G.; Borga, M.; Dumitrescu, A.; et al. A compilation of data on European flash floods. J. Hydrol. 2009, 367, 70–78. [Google Scholar] [CrossRef]
- Barredo, J.I. Major flood disasters in Europe: 1950–2005. Nat. Hazards 2007, 42, 125–148. [Google Scholar] [CrossRef]
- Ding, J.; Haberlandt, U. Estimation of instantaneous peak flow from maximum mean daily flow by regionalization of catchment model parameters. Hydrol. Process. 2017, 31, 612–626. [Google Scholar] [CrossRef]
- Fuller, W.E. Flood flows. Trans. ASCE 1914, 77, 564–617. [Google Scholar]
- Silva, E.A. Estimativa Regional da Vazao Máxima Instantânea em Algumas Bacias Brasileiras. Master’s Thesis, Universidade Federal do Rio Grande do Sul, Porto Alegre, Brazil, 1997. [Google Scholar]
- Silva, E.A.; Tucci, C.E.M. Relaçao entre as vazoes máximas diárias e instantáneas. Rev. Bras. Recur. Hídr. 1998, 3, 133–151. [Google Scholar] [CrossRef]
- Taguas, E.V.; Ayuso, J.L.; Pena, A.; Yuan, Y.; Sanchez, M.C.; Giraldez, J.V.; Pérez, R. Testing the relationship between instantaneous peak flow and mean daily flow in a Mediterranean Area Southeast Spain. Catena 2008, 75, 129–137. [Google Scholar] [CrossRef]
- Jarvis, C.S. Floods in United States. In Water Supply Paper; US Geological Survey: Reston, VA, USA, 1936. [Google Scholar]
- Langbein, W.B. Peak discharge from daily records. Water Resour. Bull. 1944, 145. [Google Scholar]
- Linsley, R.K.; Kohler, M.A.; Paulhus, J.L.H. Applied Hydrology; McGraw-Hill: New York, NY, USA, 1949. [Google Scholar]
- Sangal, B.P. Practical method of estimating peak flow. J. Hydraul. Eng. 1983, 109, 549–563. [Google Scholar] [CrossRef]
- Fill, H.D.; Steiner, A.A. Estimating instantaneous peak flow from mean daily flow data. J. Hydrol. Eng. 2003, 8, 365–369. [Google Scholar] [CrossRef]
- Centre for Public Works Studies and Experimentation (CEDEX). Mapa de Caudales Máximos. Memoria Técnica (In Spanish). 2011. Available online: http://www.mapama.gob.es/es/agua/temas/gestion-de-los-riesgos-de-inundacion/memoria_tecnica_v2_junio2011_tcm7–162773.pdf (accessed on 5 January 2017).
- Fathzadeh, A.; Jaydari, A.; Taghizadeh-Mehrjardi, R. Comparison of different methods for reconstruction of instantaneous peak flow data. Intell. Autom. Soft Comput. 2017, 23, 41–49. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks: A Comprehensive Foundation, 2nd ed.; Macmillan: New York, NY, USA, 1994; ISBN 81-7808-300-0. [Google Scholar]
- Ajmera, T.K.; Goyal, M.K. Development of stage-discharge rating curve using model tree and neural networks: An application to Peachtree Creek in Atlanta. Expert Syst. Appl. 2012, 39, 5702–5710. [Google Scholar] [CrossRef]
- Mustafa, M.R.; Isa, M.H.; Rezaur, R.B. Artificial neural networks modelling in water resources engineering: Infrastructure and applications. World Acad. Sci. Eng. Technol. 2012, 62, 341–349. [Google Scholar]
- Cheng, C.T.; Feng, Z.K.; Niu, W.J.; Liao, S.L. Heuristic Methods for Reservoir Monthly Inflow Forecasting: A Case Study of Xinfengjiang Reservoir in Pearl River, China. Water 2015, 7, 4477–4495. [Google Scholar] [CrossRef]
- Govindaraju, R.S. Artificial neural networks in hydrology. II: Hydrological applications. J. Hydrol. Eng. 2000, 5, 124–137. [Google Scholar] [CrossRef]
- Hamaamin, Y.A.; Nejadhashemi, A.P.; Zhang, Z.; Giri, S.; Woznicki, S.A. Bayesian Regression and Neuro-Fuzzy Methods Reliability Assessment for Estimating Streamflow. Water 2016, 8, 287. [Google Scholar] [CrossRef]
- Abraham, A.; Köppen, M.; Franke, K. Design and Application of Hybrid Intelligent Systems; IOS Press: Amsterdam, The Netherlands, 2003; ISBN 978-1-58603-394-1. [Google Scholar]
- Kim, J.; Kasabov, N. HyFIS: Adaptive neuro-fuzzy inference systems and their application to nonlinear dynamical systems. Neural Netw. 1999, 12, 1301–1319. [Google Scholar] [CrossRef]
- Emamgholizadeh, S.; Moslemi, K.; Karami, G. Prediction the groundwater level of Bastam Plain (Iran) by artificial neural network (ANN) and adaptive neuro-fuzzy inference system (ANFIS). Water Resour. Manag. 2014, 28, 5433–5446. [Google Scholar] [CrossRef]
- Dastorani, M.; Moghadamnia, A.; Piri, J.; Rico-Ramirez, M. Application of ANN and ANFIS models for reconstructing missing flow data. Environ. Monit. Assess. 2010, 166, 421–434. [Google Scholar] [CrossRef] [PubMed]
- Seckin, N. Modeling flood discharge at ungauged sites across Turkey using neuro-fuzzy and neural networks. J. Hydroinform. 2011, 13, 842–849. [Google Scholar] [CrossRef]
- Tu, J.V. Advantages and disadvantages of using artificial neural networks versus logistic regression for predicting medical outcomes. J. Clin. Epidemiol. 1996, 49, 1225–1231. [Google Scholar] [CrossRef]
- Rezaei, H.; Rahmati, M.; Modarress, H. Application of ANFIS and MLR models for prediction of methane adsorption on X and Y faujasite zeolites: Effect of cations substitution. Neural Comput. Appl. 2015, 28, 301–312. [Google Scholar] [CrossRef]
- Bisht, D.; Mohan-Raju, M.; Joshi, M. Simulation of water table elevation fluctuation using fuzzy-logic and ANFIS. Comput. Model. New Technol. 2009, 13, 16–23. [Google Scholar]
- Guldal, V.; Tongal, H. Comparison of recurrent neural network, adaptive neuro-fuzzy inference system and stochastic models in Egirdir lake level forecasting. Water Resour. Manag. 2010, 24, 105–128. [Google Scholar] [CrossRef]
- Shabani, M.; Shabani, N. Application of artificial neural networks in instantaneous peak flow estimation for Kharestan Watershed, Iran. J. Resour. Ecol. 2012, 3, 379–383. [Google Scholar] [CrossRef]
- Dastorani, M.T.; Koochi, J.S.; Darani, H.S.; Talebi, A.; Rahimian, M.H. River instantaneous peak flow estimation using daily flow data and machine-learning-based models. J. Hydroinform. 2013, 15, 1089–1098. [Google Scholar] [CrossRef]
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World Map of the Köppen-Geiger climate classification updated. Meteorol. Z. 2006, 15, 259–263. [Google Scholar] [CrossRef]
- Senent-Aparicio, J.; Pérez-Sánchez, J.; Bielsa-Artero, A.M. Asessment of Sustainability in Semiarid Mediterranean Basins: Case Study of the Segura Basin, Spain. Water Technol. Sci. 2016, 7, 67–84. [Google Scholar]
- Baker, D.B.; Richards, R.P.; Loftus, T.T.; Kramer, J.W. A new flashiness index: Characteristics and applications to Midwestern rivers and streams. J. Am. Water Resour. Assoc. 2004, 40, 503–522. [Google Scholar] [CrossRef]
- Holko, L.; Parajka, J.; Kostka, Z.; Škoda, P.; Blöschl, G. Flashiness of mountain streams in Slovakia and Austria. J. Hydrol. 2011, 405, 392–401. [Google Scholar] [CrossRef]
- Centre for Public Works Studies and Experimentation (CEDEX). Anuario de Aforos (In Spanish). Available online: http://ceh-flumen64.cedex.es/anuarioaforos/default.asp (accessed on 4 January 2017).
- Maier, R.H.; Jain, A.; Graeme, C.D.; Sudheer, K.P. Methods used for the development of neural networks for the prediction of water resource variables in river systems: Current status and future directions. Environ. Model. Softw. 2010, 25, 891–909. [Google Scholar] [CrossRef]
- Hasanpour Kashani, M.; Daneshfaraz, R.; Ghorbani, M.; Najafi, M.; Kisi, O. Comparison of different methods for developing a stage–discharge curve of the Kizilirmak River. J. Flood Risk Manag. 2015, 8, 71–86. [Google Scholar] [CrossRef]
- Govindaraju, R.S. Artificial neural networks in hydrology. I: Preliminary concepts. J. Hydrol. Eng. 2000, 5, 115–123. [Google Scholar] [CrossRef]
- Wang, J.; Shi, P.; Jiang, P.; Hu, J.; Qu, S.; Chen, X.; Chen, Y.; Dai, Y.; Xiao, Z. Application of BP Neural Network Algorithm in Traditional Hydrological Model for Flood Forecasting. Water 2017, 9, 48. [Google Scholar] [CrossRef]
- Meng, C.; Zhou, J.; Tayyab, M.; Zhu, S.; Zhang, H. Integrating Artificial Neural Networks into the VIC Model for Rainfall-Runoff Modeling. Water 2016, 8, 407. [Google Scholar] [CrossRef]
- Wolfs, V.; Willems, P. Development of discharge-stage curves affected by hysteresis using time varying models, model trees and neural networks. Environ. Model. Softw. 2014, 55, 107–119. [Google Scholar] [CrossRef]
- Levenberg, K. A Method for the Solution of Certain Problems in Least Squares. Appl. Math. 1944, 2, 164–168. [Google Scholar]
- Marquardt, D. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Nayak, P.C.; Sudheer, K.P.; Rangan, D.M.; Ramasastri, K.S. A neuro-fuzzy computing technique for modeling hydrological time series. J. Hydrol. 2004, 291, 52–66. [Google Scholar] [CrossRef]
- Takagi, T.; Sugeno, M. Fuzzy Identification of Systems and Its Applications to Modeling and Control. IEEE Trans. Syst. Man Cybern. 1985, 15, 116–132. [Google Scholar] [CrossRef]
- Sugeno, M.; Kang, G.T. Structure identification of fuzzy model. Fuzzy Sets Syst. 1988, 28, 15–33. [Google Scholar] [CrossRef]
- Jang, J.S.R. ANFIS: Adaptive-network-based fuzzy inference system. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Liew, M.W.; Binger, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–890. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).