A Semi-Infinite Interval-Stochastic Risk Management Model for River Water Pollution Control under Uncertainty
Abstract
:1. Introduction
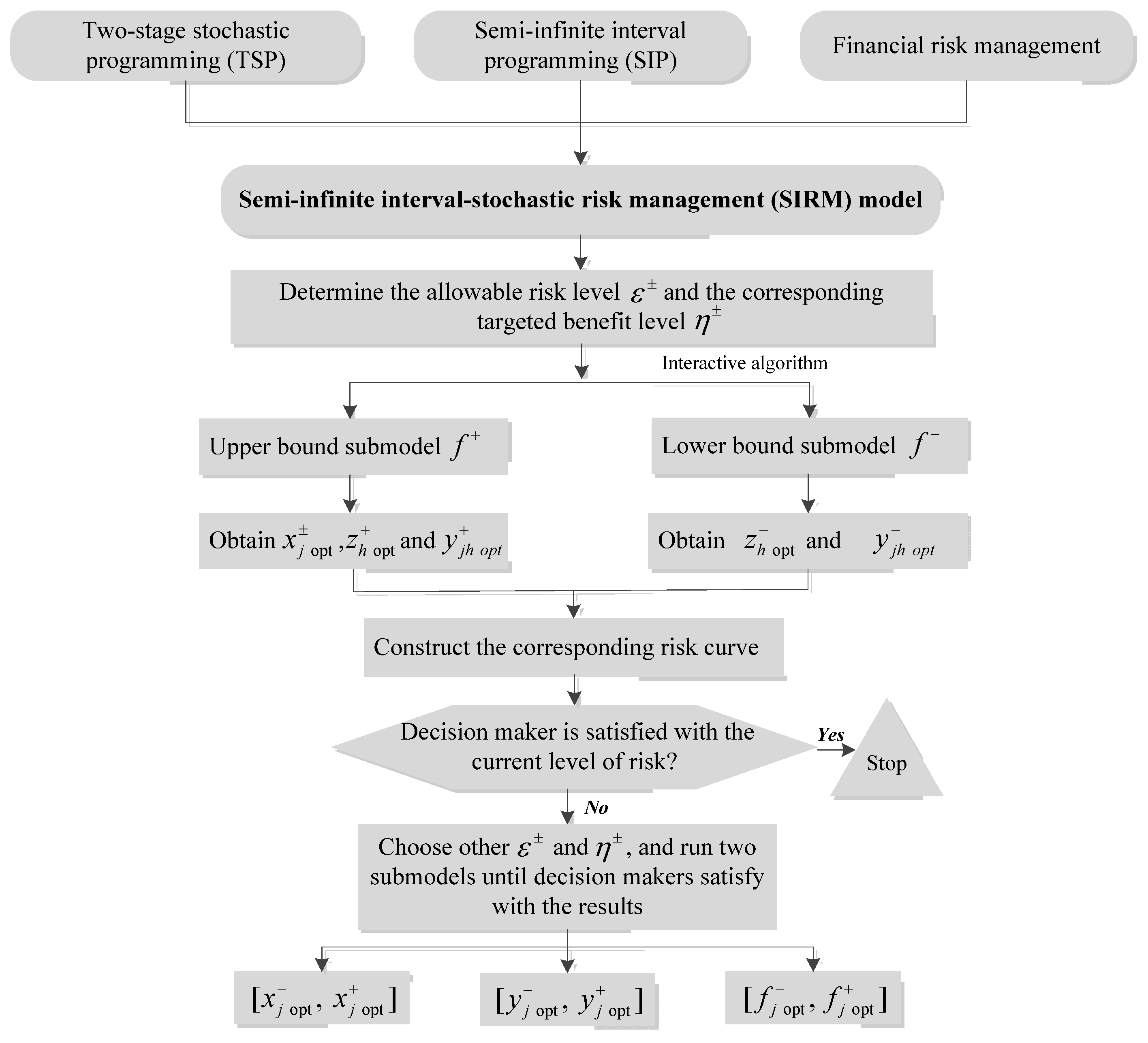
2. Methodology
3. Case Study
3.1. Study Area
3.2. Modelling Formulation
- (1)
- Wastewater treatment capacity constraints:
- (2)
- BOD discharge constraints:
- (3)
- Nitrogen discharge constraints:
- (4)
- Phosphorus discharge constraints:
- (5)
- Soil loss constraints:
- (6)
- Financial risk management:
- (7)
- Cropland resources constraints:
- (8)
- Industrial production scale constraints:
- (9)
- Non-negative constraints:
3.3. Data Analysis
4. Results and Discussion
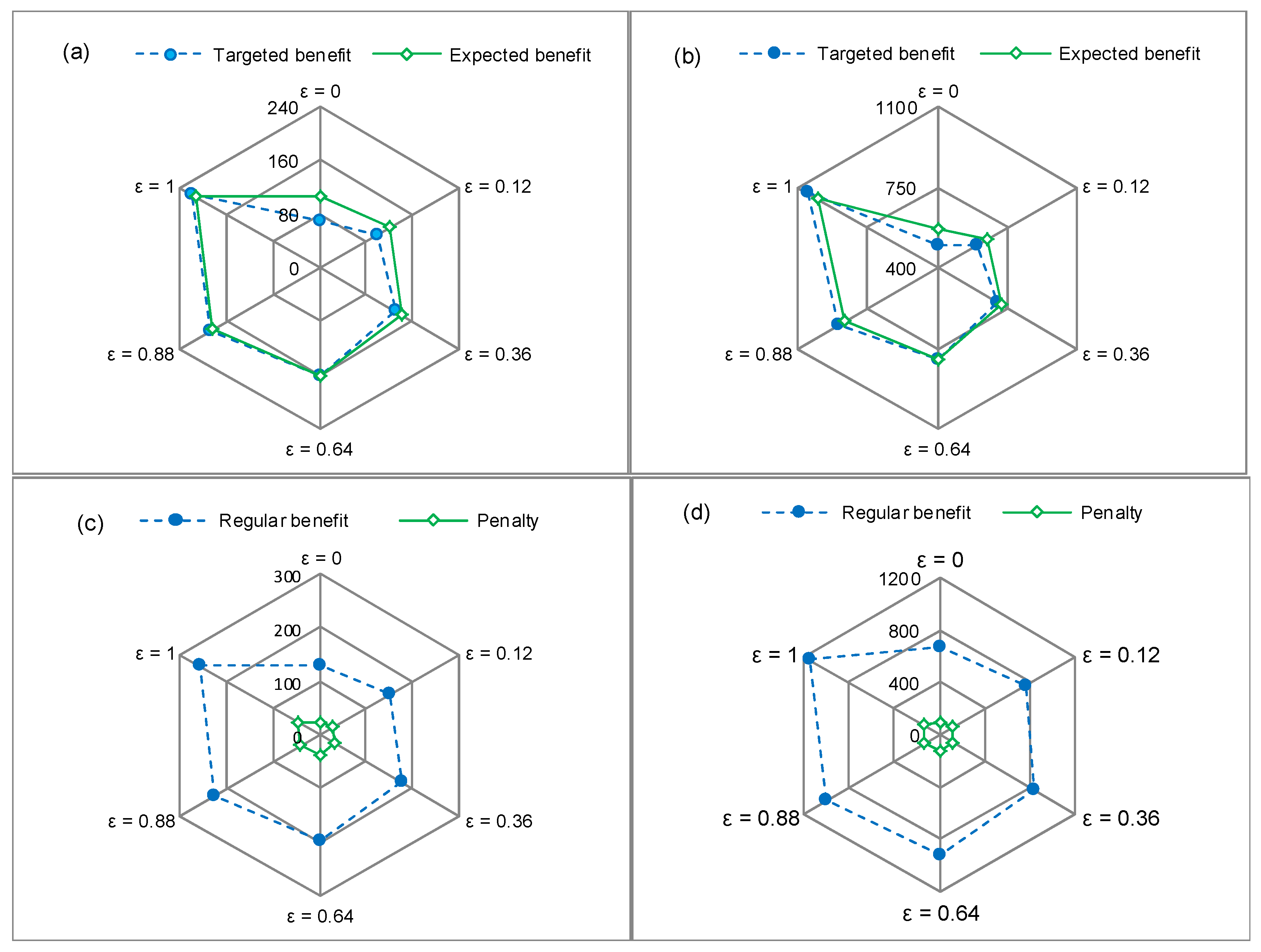
4.1. Benefit and Cost
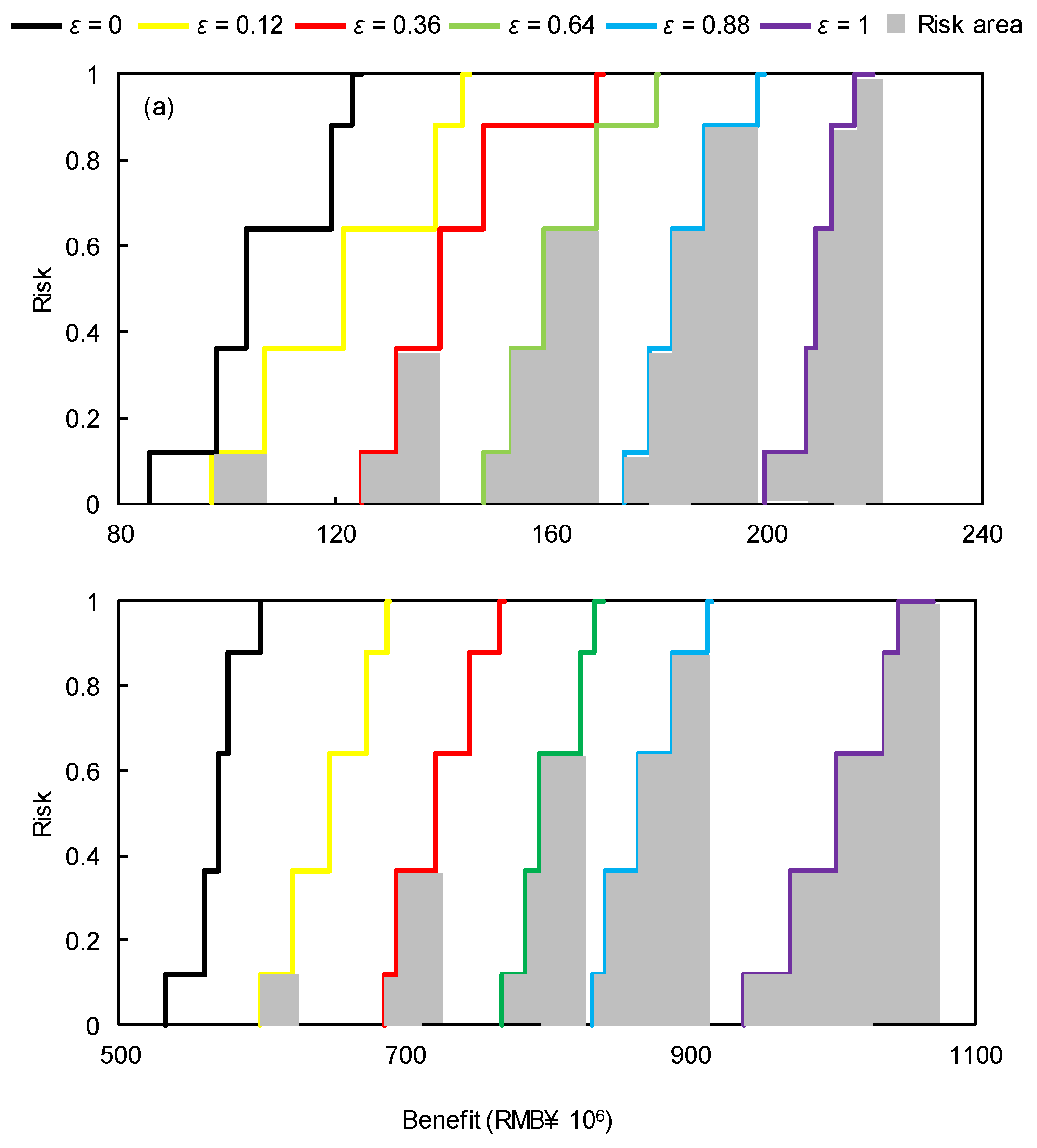
4.2. Risk Analysis
4.3. Proportion of Benefit under Different Scenarios
4.4. Optimal Production Target and Actual Production Level
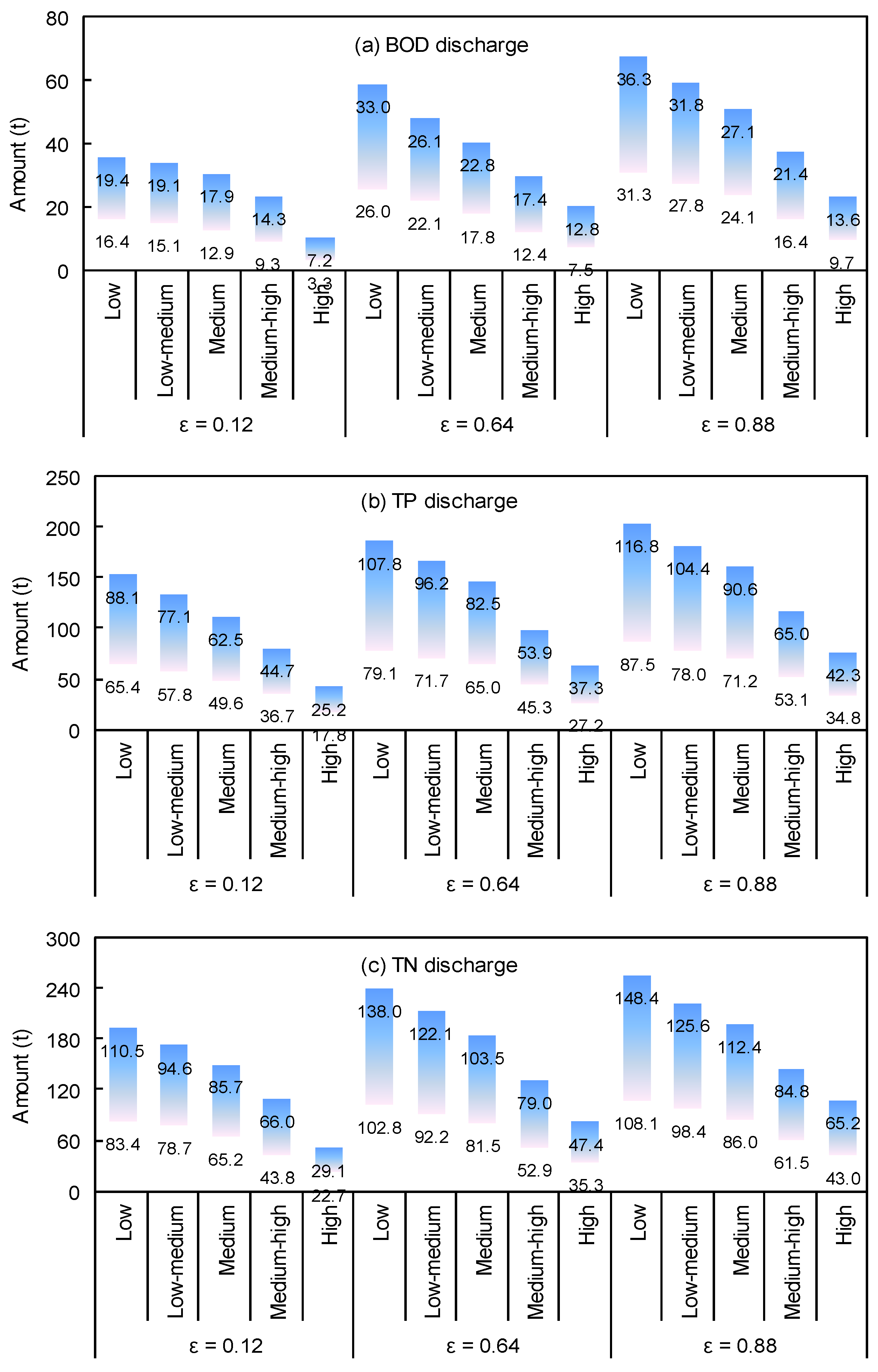
4.5. Excess Pollutant Discharge
5. Conclusions
Acknowledgements
Author Contributions
Conflicts of Interest
Appendix A. Solution Method
Appendix B. Nomenclatures of SIRM Model
| i | chemical plant, 1 = Gufu (GF), 2 = Baishahe (BSH), 3 = Pingyikou (PYK), 4 = Liucaopo (LCP), 5 = Xiangjinlianying (XJLY) |
| j | agricultural zone, and j = 1, 2, 3, 4 |
| k | main crop, 1 = citrus, 2 = tea, 3 = wheat, 4 = potato, 5 = rapeseed, 6 = alpine rice, 7 = second rice, 8 = maize, 9 = vegetables |
| n | phosphorus mining company; 1 = Xinglong (XL), 2 = Xinghe (XH), 3 = Xingchang (XC), 4 = Geping (GP), 5 = Jiangjiawan (JJW), 6 = Shenjiashan (SJS) |
| s | town, 1 = Gufu, 2 = Nanyang, 3 = Gaoyang, 4 = Xiakou |
| t | planning time period, 1 = dry season, 2 = wet season |
| Lt | length of period (day) |
| l | independent variable representing time with the range of [0, 180] |
| h | allowable pollutant discharge scenario; h = 1, 2, 3 |
| probability of occurrence allowable pollutant discharge level h (%); | |
| net benefit from chemical plant i in period t (RMB¥/t); | |
| production level of chemical plant i in period t (t/day); | |
| average benefit for per unit phosphate ore (RMB¥/t); | |
| production level of phosphorus mining company n during period t (t/day); | |
| net benefit from water supply to municipal uses (RMB¥/m3); | |
| quantity of water supply to town s in period t (m3/day); | |
| average benefit for agricultural product (RMB¥/t); | |
| planning area of crop k in agricultural zone j during period t (ha); | |
| economic cost when the production targets from plant i in period t are not met (RMB¥/t); | |
| actual production level of plant i under scenario h in period t (t/day); | |
| economic cost when the production targets from company n in period t are not met (RMB¥/t); | |
| actual production level of company n under scenario h in period t (t/day); | |
| economic cost when the water supply targets for town s in period t are not met (RMB¥/m3); | |
| actual water supply level of town s under scenario h in period t (m3/day); | |
| economic cost when the plant targets of crop farm j in period t are not met (RMB¥/ha); | |
| actual plant area of crop farm j under scenario h in period t (ha); | |
| wastewater generation rate of chemical plant i during period t (m3/t) | |
| wastewater generation rate at town s during period t (m3/m3) | |
| capacity of wastewater treatment capacity (WTPs) (m3/day) | |
| capacity of wastewater treatment capacity (chemical plants) (m3/day) | |
| BOD concentration of raw wastewater from chemical plant i in period t (kg/m3) | |
| BOD treatment efficiency in chemical plant i during period t (%) | |
| allowable BOD discharge for chemical plant i under scenario h in period t (kg/day) | |
| BOD concentration of municipal wastewater at town s during period t (kg/m3) | |
| BOD treatment efficiency of WTPs at town s during period t (%) | |
| allowable BOD discharge for WTPs at town s during period t (kg/day) | |
| nitrogen content of soil in agricultural zone j planted with crop k (%) | |
| average soil loss from agricultural zone j planted with crop k in period t (t/ha) | |
| runoff from agricultural zone j with crop k in period t (mm) | |
| dissolved nitrogen concentration in runoff from agricultural zone j planted with crop k in period t (mg/L) | |
| maximum allowable nitrogen loss in agricultural zone j under scenario h during period t (t) | |
| phosphorus concentration of raw wastewater from chemical plant i in period t (kg/m3) | |
| phosphorus treatment efficiency in chemical plant i in period t (%) | |
| amount of slag discharged by chemical plant i in period t (kg/t) | |
| slag loss rate due to rain wash in chemical plant i during period t (%) | |
| phosphorus content in slag generated by chemical plant i in period t (%) | |
| allowable phosphorus discharge for chemical plant i under scenario h in period t (kg/day) | |
| phosphorus concentration of municipal wastewater at town s in period t (kg/m3) | |
| phosphorus treatment efficiency of WTP at town s in period t (%) | |
| allowable phosphorus discharge for WTP at town s under scenario h in period t (kg/day) | |
| wastewater generation from phosphorus mining company n in period t (m3/t) | |
| phosphorus concentration of wastewater from mining company n in period t (kg/ m3) | |
| phosphorus treatment efficiency in mining company n (%) | |
| amount of slag discharged by mining company n during period t (kg/t) | |
| phosphorus content in generated slag (%) | |
| slag loss rate due to rain wash (%) | |
| allowable phosphorus discharge for mining company n under scenario h during period t (kg/day) | |
| phosphorus content of soil in agricultural zone j planted with crop k (%) | |
| average soil loss from agricultural zone j planted with crop k in period t (t/ha) | |
| dissolved phosphorus concentration in runoff from agricultural zone j with crop k (mg/L) | |
| maximum allowable phosphorus loss in agricultural zone j under scenario h in period t (t/ha) | |
| maximum allowable soil loss agricultural zone j under scenario h in period t (t) | |
| targeted benefit level of economic activities (RMB¥) | |
| integer variable, which would take a value of zero if the benefit for each economic activity under scenario h is greater than or equal to the target level () and a value of one otherwise | |
| upper bound benefit under each scenario h (RMB¥) | |
| desired risk exposure level of economic activity | |
| the government requirement for minimum area of farmland during period t (ha); | |
| minimum production level of chemical plant i in period t (t/day) | |
| maximum production level of chemical plant i in period t (t/day) | |
| minimum quantity of water supply to town s in period t (m3/day) | |
| maximum quantity of water supply to town s in period t (m3/day) | |
| minimum production level of phosphorus mining company n during period t (t/day) | |
| maximum production level of phosphorus mining company n during period t (t/day) |
References
- Ministry of Water Resources, People’s Republic of China. China Water Resources Bulletin; China Water Power Press: Beijing, China, 2017.
- Cederkvist, K.; Jensen, M.B.; Ingvertsen, S.T.; Holm, P.E. Controlling stormwater quality with filter soil—Event and dry weather testing. Water 2016, 8, 349. [Google Scholar] [CrossRef]
- He, J. Probabilistic evaluation of causal relationship between variables for water pollution control. J. Environ. Inform. 2016, 28, 110–119. [Google Scholar] [CrossRef]
- Toyosada, K.; Otani, T.; Shimizu, Y.; Managi, S. Water quality study on the hot and cold water supply systems at Vietnamese Hotels. Water 2017, 9, 251. [Google Scholar] [CrossRef]
- Li, Y.P.; Zhang, N.; Huang, G.H.; Liu, J. Coupling fuzzy-chance constrained program with minimax regret analysis for water pollution control. Stoch. Environ. Res. Risk Assess. 2014, 28, 1769–1784. [Google Scholar] [CrossRef]
- Li, Y.P.; Huang, G.H. Fuzzy-stochastic-based violation analysis method for planning water resources management systems with uncertain information. Inf. Sci. 2009, 179, 4261–4276. [Google Scholar] [CrossRef]
- Li, Y.P.; Huang, G.H. Two-stage planning for sustainable water-quality management under uncertainty. J. Environ. Manag. 2009, 90, 2402–2413. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Li, Y.P.; Huang, G.H.; Nie, S. Development of a fuzzy-boundary interval programming method for water pollution control under uncertainty. Water Resour. Manag. 2014, 29, 1169–1191. [Google Scholar] [CrossRef]
- Kerachian, R.; Karamouz, M. A stochastic conflict resolution model for water pollution control in reservoir-river systems. Adv. Water Resour. 2007, 30, 866–882. [Google Scholar] [CrossRef]
- Li, Y.P.; Huang, G.H.; Yang, Z.F.; Nie, S.L. IFMP: Interval-fuzzy multistage programming for water resources management under uncertainty. Resour. Conserv. Recycl. 2008, 52, 800–812. [Google Scholar] [CrossRef]
- Ocampo-Duque, W.; Osorio, C.; Piamba, C.; Schuhmacher, M.; Domingo, J.L. Water quality analysis in rivers with non-parametric probability distributions and fuzzy inference systems: Application to the Cauca River, Colombia. Environ. Int. 2013, 52, 17–18. [Google Scholar] [CrossRef] [PubMed]
- Mohammad, R.N.; Najmeh, M. Water quality zoning using probabilistic support vector machines and self-organizing maps. Water Resour. Manag. 2013, 27, 2577–2594. [Google Scholar] [CrossRef]
- Chen., C.F.; Tsai, L.Y.; Fan, C.H.; Lin, J.Y. Using exceedance probability to determine total maximum daily loads for reservoir water pollution control. Water 2016, 8, 541. [Google Scholar] [CrossRef]
- Hwang, S.A.; Hwang, S.J.; Park, S.R.; Lee, S.W. Examining the relationships between water shed urban land use and stream water quality using linear and generalized additive models. Water 2016, 8, 155. [Google Scholar] [CrossRef]
- Ji., Y.; Huang, G.H.; Sun, W.; Li, Y.F. Water pollution control in a wetland system using an inexact left-hand-side chance-constrained fuzzy multi-objective approach. Stoch. Environ. Res. Risk Assess 2016, 30, 621–633. [Google Scholar] [CrossRef]
- Zolfagharipoor, M.A.; Ahmadi, A. A decision-making framework for river water pollution control under uncertainty: Application of social choice rules. J. Environ. Manag. 2016, 183, 152–163. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Zou, R.; Han, S.; Bai, S.; Faizullabhoy, M.; Wu, Y.Y.; Guo, H.C. Development of an integrated water quality and macroalgae simulation model for Tidal Marsh eutrophication control decision support. Water 2017, 9, 277. [Google Scholar] [CrossRef]
- Li, Y.P.; Huang, G.H.; Huang, Y.F.; Zhou, H.D. A multistage fuzzy-stochastic programming model for supporting sustainable water resources allocation and management. Environ. Model. Softw. 2009, 24, 786–797. [Google Scholar] [CrossRef]
- Nematian, J. An extended two-stage stochastic programming approach for water resources management under uncertainty. J. Environ. Inform. 2016, 27, 72–84. [Google Scholar] [CrossRef]
- Huang, G.H.; Loucks, D.P. An inexact two-stage stochastic programming model for water resources management under uncertainty. Civ. Eng. Environ. Syst. 2000, 17, 95–118. [Google Scholar] [CrossRef]
- Zhang, N.; Li, Y.P.; Huang, W.W.; Liu, J. An inexact two-stage water pollution control model for supporting sustainable development in a rural system. J. Environ. Inform. 2014, 24, 52–64. [Google Scholar] [CrossRef]
- Luo, B.; Li, J.B.; Huang, G.H.; Li, H.L. A simulation-based interval two-stage stochastic model for agricultural non-point source pollution control through land retirement. Sci. Total Environ. 2006, 361, 38–56. [Google Scholar] [CrossRef] [PubMed]
- Harrison, K.W. Two-stage decision-making under uncertainty and stochasticity: Bayesian Programming. Adv. Water Resour. 2007, 30, 641–664. [Google Scholar] [CrossRef]
- Tavakoli, A.; Nikoo, M.R.; Kerachian, R.; Soltani, M. River water pollution control considering agricultural return flows: Application of a nonlinear two-stage stochastic fuzzy programming. Environ. Monit. Assess. 2015, 187, 158. [Google Scholar] [CrossRef] [PubMed]
- Hu, X.H.; Li, Y.P.; Huang, G.H.; Zhuang, X.W.; Ding, X.W. A Bayesian-based two-stage inexact optimization method for supporting stream water pollution control in the three gorges reservoir region. Environ. Sci. Pollut. Res. 2016, 23, 9164–9182. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, S.; Sahinidis, N.V. Robust process planning under uncertainty. Ind. Eng. Chem. Res. 1998, 37, 1883–1892. [Google Scholar] [CrossRef]
- Li, Y.P.; Huang, G.H. Interval-parameter robust optimization for environmental management under uncertainty. Can. J. Civ. Eng. 2009, 36, 592–606. [Google Scholar] [CrossRef]
- Khan, U.T.; Valeo, C. Short-term peak flow rate prediction and flood risk assessment using fuzzy linear regression. J. Environ. Inform. 2016, 28, 71–89. [Google Scholar] [CrossRef]
- Koppol, A.P.R.; Bagajewicz, M.J. Financial risk management in the design of water utilization systems in process plants. Ind. Eng. Chem. Res. 2004, 42, 5249–5255. [Google Scholar] [CrossRef]
- Barbaro, A.; Bagajewicz, M.J. Managing financial risk in planning under uncertainty. Process Syst. Eng. 2004, 50, 963–989. [Google Scholar] [CrossRef]
- Liu, Z.F.; Huang, G.H. Dual-interval two-stage optimization for flood management and risk analyses. Water Resour. Manag. 2009, 23, 2141–2162. [Google Scholar] [CrossRef]
- Ahmed, S.; Elsholkami, M.; Elkamel, A.; Du, J.; Ydstie, E.B.; Douglas, P.L. Financial risk management for new technology integration in energy planning under uncertainty. Appl. Energy 2014, 128, 75–81. [Google Scholar] [CrossRef]
- Zhu, Y.; Li, Y.P.; Huang, G.H. Planning carbon emission trading for Beijing’s electric power systems under dual uncertainties. Renew. Sustain. Energy Rev. 2013, 23, 113–128. [Google Scholar] [CrossRef]
- Felfel, H.; Ayadi, O.; Masmoudi, F. Multi-objective stochastic multi-site supply chain planning under demand uncertainty considering downside risk. Comput. Ind. Eng. 2016, 102, 268–279. [Google Scholar] [CrossRef]
- McCray, A.W. Petroleum Evaluations and Economic Decisions; Prentice Hall: Englewood Cliffs, NJ, USA, 1975; ISBN 0136622136. [Google Scholar]
- Chen, H.W.; Chang, N.B. Decision support for allocation of watershed pollution load using grey fuzzy multobjective programming. J. Am. Water Resour. Assoc. 2006, 42, 725–745. [Google Scholar] [CrossRef]


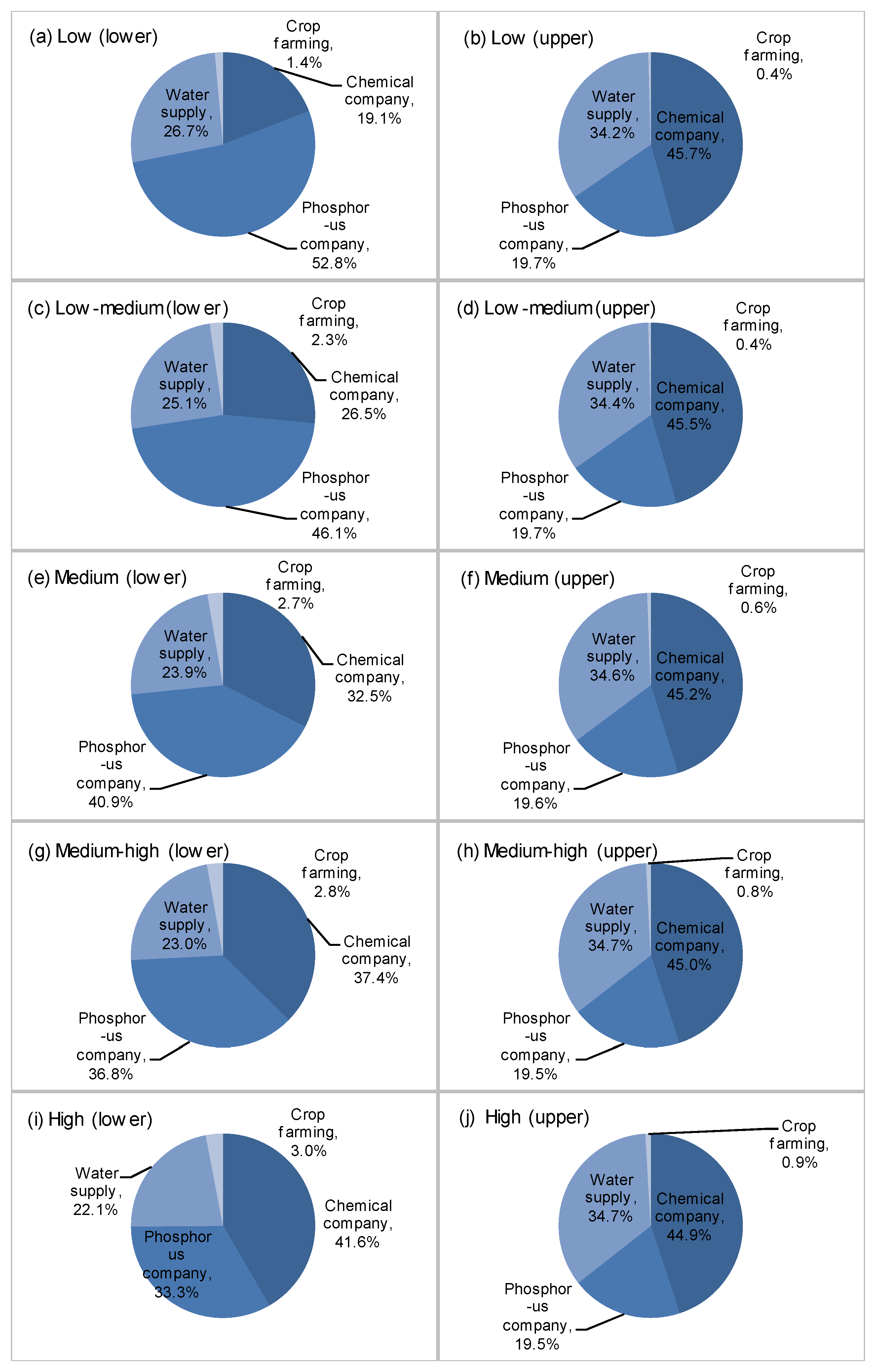

| Industrial Activities | Net Benefit | Penalty | ||
|---|---|---|---|---|
| Period 1 | Period 2 | |||
| Chemical plant (RMB¥/t) | ||||
| Gufu (GF) | [791.3, 832.4] | [803.2, 864.7] | [823.6, 891.5] | [833.1, 910.4] |
| Baishahe (BSH) | [1217.4, 1493.8] | [1532.3, 1682.4] | [1357.4, 1634.1] | [1723.7, 1841.6] |
| Pingyikou (PYK) | [832.8, 912.4] | [943.5, 1032.4] | [861.5, 943.8] | [993.5, 1145.7] |
| Liucaopo (LCP) | [1532.6, 1843.5] | [1682.2, 1942.5] | [1735.7, 2011.1] | [1835.3, 2113.5] |
| Xiangjinlianying (XJLY) | [1843.3, 2174.3] | [1932.4, 2243.5] | [1992.3, 2294.5] | [2014.5, 2385.3] |
| Water supply (RMB¥/m3) | ||||
| Gufu | [45.4, 52.7] | [58.8, 61.4] | [52.4, 58.9] | [63.7, 68.2] |
| Nanyang | [32.4, 38.5] | [41.4, 46.7] | [39.5, 43.1] | [47.2, 53.4] |
| Gaoyang | [48.3, 52.4] | [56.4, 59.4] | [55.5, 58.7] | [63.7, 70.1] |
| Xiakou | [42.1, 46.2] | [48.3, 53.4] | [49.2, 54.5] | [53.8, 59.1] |
| Phosphorus mining company (RMB¥/t) | ||||
| Xinglong (XL) | [167.3, 185.3] | [167.3, 194.2] | [196.7, 213.5] | [196.7, 221.3] |
| Xinghe (XH) | [154.5, 164.9] | [163.4, 173.4] | [178.4, 197.3] | [182.1, 207.3] |
| Xingchang (XC) | [161.5, 178.4] | [161.5, 178.4] | [188.4, 204.5] | [188.4, 204.5] |
| Geping (GP) | [166.4, 174.7] | [168.3, 179.4] | [189.2, 201.3] | [191.2, 207.3] |
| Jiangjiawan (JJW) | [161.4, 178.6] | [166.4, 181.4] | [188.3, 204.6] | [189.2, 211.3] |
| Shenjiashan (SJS) | [161.4, 183.4] | [171.9, 191.5] | [188.3, 211.3] | [198.2, 201.4] |
| Industrial Activities | Period 1 | Period 2 |
|---|---|---|
| Allowable phosphorus discharge for each chemical plant (kg/day) | ||
| Gufu (GF) | [0.60 + 0.002l, 1.05 + 0.002l] | [0.70 + 0.001l, 1.15 + 0.001l] |
| Baishahe (BSH) | [195.63 + 0.089l, 432.56 + 0.089l] | [162.64 + 0.086l, 407.87+ 0.086l] |
| Pingyikou (PYK) | [30.49 + 0.09l, 70.71+ 0.09l] | [50.03 + 0.013l, 90.30 + 0.013l] |
| Liucaopo (LCP) | [124.7 + 0.046l, 294.7 + 0.046l] | [213.40 + 0.043l, 409.5 + 0.043l] |
| Xiangjinlianying (XJLY) | [126.22 + 0.042l, 321.76 + 0.042l] | [174.4 + 0.039l, 364.8 + 0.039l] |
| Allowable phosphorus discharge for each mine company (kg/m3) | ||
| Xinglong (XL) | [47.41 + 0.043l, 123.49 + 0.043l] | [78.31 + 0.41l, 191.59 + 0.041l] |
| Xinghe (XH) | [23.68 + 0.044l, 86.87 + 0.044l] | [39.19 + 0.42l, 86.87 + 0.042l] |
| Xingchang (XC) | [30.54 + 0.038l], 62.75, + 0.038l] | [52.74 + 0.034l, 115.76 + 0.034l] |
| Geping (GP) | [48.39 + 0.012l, 109.36 + 0.012l] | [70.03 + 0.011l, 173.95 + 0.011l] |
| Jiangjiawan (JJW) | [25.91 + 0.014l, 40.13 + 0.014l] | [38.49 + 0.013l, [87.51 + 0.013l] |
| Shenjiashan (SJS) | [20.23 + 0.011l, 42.3l + 0.011l] | [28.19 + 0.009l, [82.6l + 0.009l] |
| Allowable BOD discharge for each WTP (kg/day) | ||
| Gufu | [70 + 0.003l, 110 + 0.003l] | [75 + 0.002l, 115 + 0.002l] |
| Nanyang | [3 + 0.0001l, 8 + 0.0001l] | [4 + 0.0009l, 9 + 0.0009l] |
| Gaoyang | [10 + 0.0003l, 25 + 0.0003l] | [12 + 0.0002l, 27 + 0.0002l] |
| Xiakou | [15 + 0.0002l, 28 + 0.0002l] | [17 + 0.0001l, 30 + 0.0001l] |
| Activity | Designed Target | ε = 0 | ε = 1 | |||
|---|---|---|---|---|---|---|
| t = 1 | t = 2 | t = 1 | t = 2 | t = 1 | t = 2 | |
| Production level of chemical plants (t/day) | ||||||
| i = 1 | [21.8, 28.6] | [17.6, 28.3] | 28.6 | 28.3 | 28.6 | 28.3 |
| i = 2 | [457.5, 573.7] | [461.6, 625.6] | 573.7 | 461.6 | 573.7 | 625.6 |
| i = 3 | [69.5, 112.6] | [62.8, 110.5] | 69.5 | 110.5 | 112.6 | 110.5 |
| i = 4 | [347.2, 526.8] | [327.6, 552.4] | 347.2 | 552.4 | 526.8 | 552.4 |
| i = 5 | [260.4, 376.8] | [256.7, 373.7] | 260.4 | 256.7 | 376.8 | 373.7 |
| Production level of phosphorus mining companies (t/day) | ||||||
| n = 1 | [679.4, 1435.6] | [736.5, 1324.5] | 679.4 | 736.5 | 1435.6 | 1324.5 |
| n = 2 | [246.7, 424.5] | [194.6, 412.5] | 424.5 | 412.5 | 424.5 | 412.5 |
| n = 3 | [257.4, 436.4] | [227.5, 415.3] | 436.4 | 415.3 | 436.4 | 415.3 |
| n = 4 | [385.3, 783.5] | [325.6, 704.5] | 783.5 | 704.5 | 783.5 | 704.5 |
| n = 5 | [348.6, 568.4] | [287.4, 503.5] | 568.4 | 503.5 | 568.4 | 503.5 |
| n = 6 | [495.6, 689.4] | [437.8,612.7] | 689.4 | 437.8 | 689.4 | 612.7 |
| Quantity of water supply to towns (m3/day) | ||||||
| s = 1 | [9921.5, 17533.5] | [10385.7, 21756.4] | 9921.5 | 10385.7 | 17533.5 | 21756.4 |
| s = 2 | [729.5, 1232.7] | [798.5, 1463.6] | 1232.7 | 1463.6 | 1232.7 | 1463.6 |
| s = 3 | [2804.5, 3424.5] | [2964.5, 3853.7] | 3424.5 | 3853.7 | 3424.5 | 3853.7 |
| s = 4 | [1428.7, 2104.7] | [1564.6, 2746.4] | 2104.7 | 2746.4 | 2104.7 | 2746.4 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Li, Y.; Huang, G.; Fan, Y. A Semi-Infinite Interval-Stochastic Risk Management Model for River Water Pollution Control under Uncertainty. Water 2017, 9, 351. https://doi.org/10.3390/w9050351
Liu J, Li Y, Huang G, Fan Y. A Semi-Infinite Interval-Stochastic Risk Management Model for River Water Pollution Control under Uncertainty. Water. 2017; 9(5):351. https://doi.org/10.3390/w9050351
Chicago/Turabian StyleLiu, Jing, Yongping Li, Guohe Huang, and Yurui Fan. 2017. "A Semi-Infinite Interval-Stochastic Risk Management Model for River Water Pollution Control under Uncertainty" Water 9, no. 5: 351. https://doi.org/10.3390/w9050351
APA StyleLiu, J., Li, Y., Huang, G., & Fan, Y. (2017). A Semi-Infinite Interval-Stochastic Risk Management Model for River Water Pollution Control under Uncertainty. Water, 9(5), 351. https://doi.org/10.3390/w9050351








