A Simple Method for Measuring the Bilateral Symmetry of Leaves
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
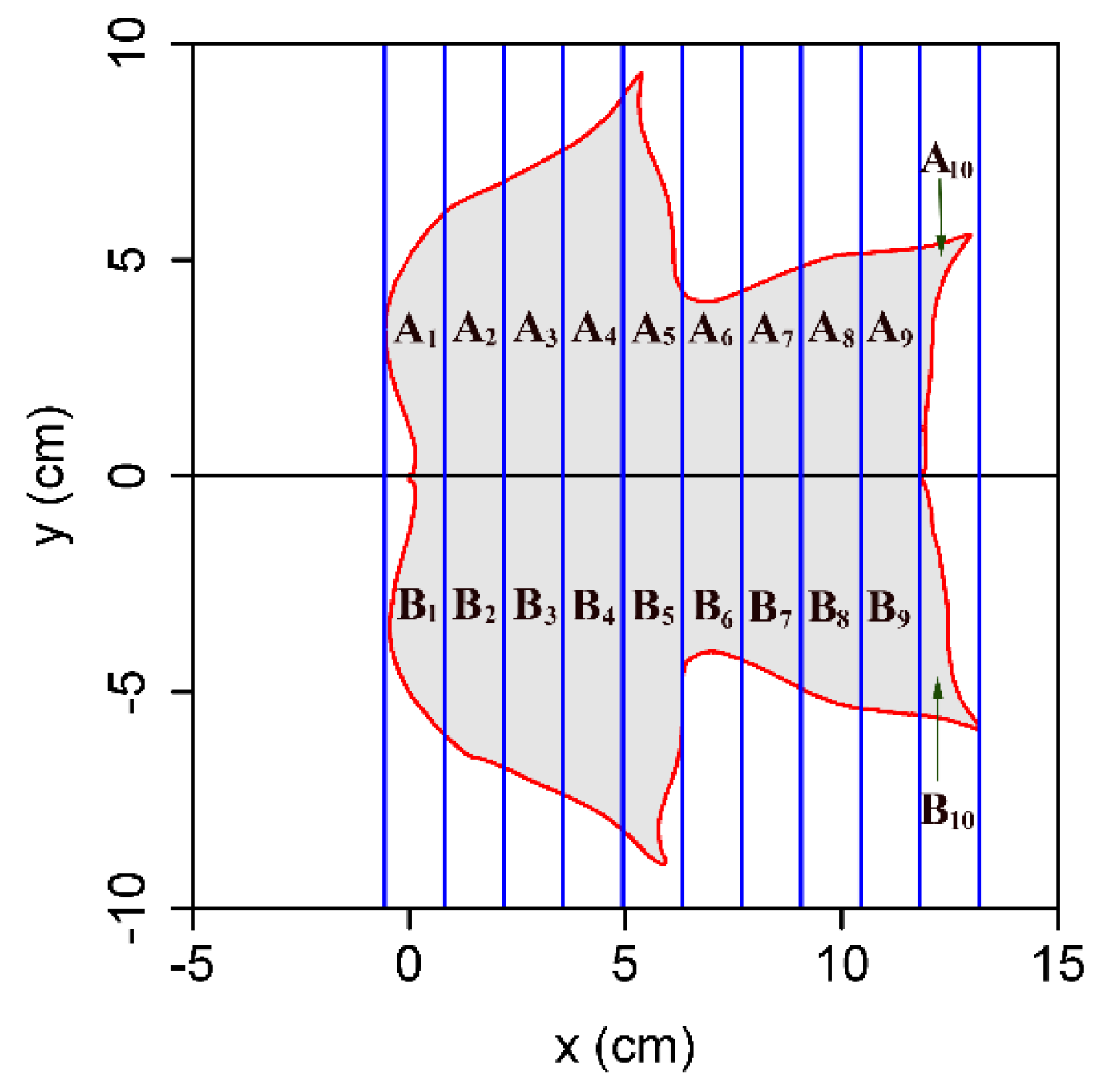
2.2. Methods
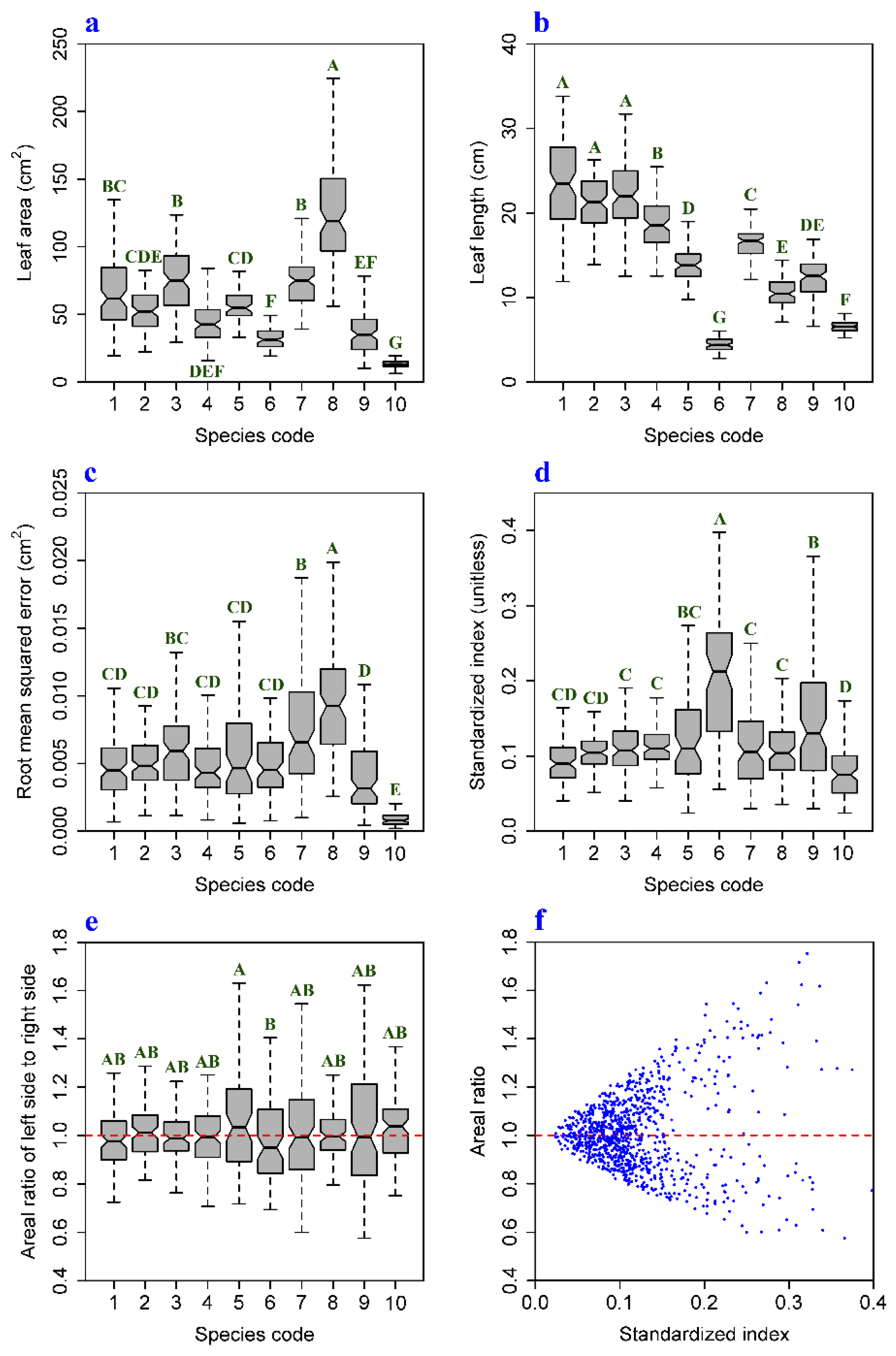
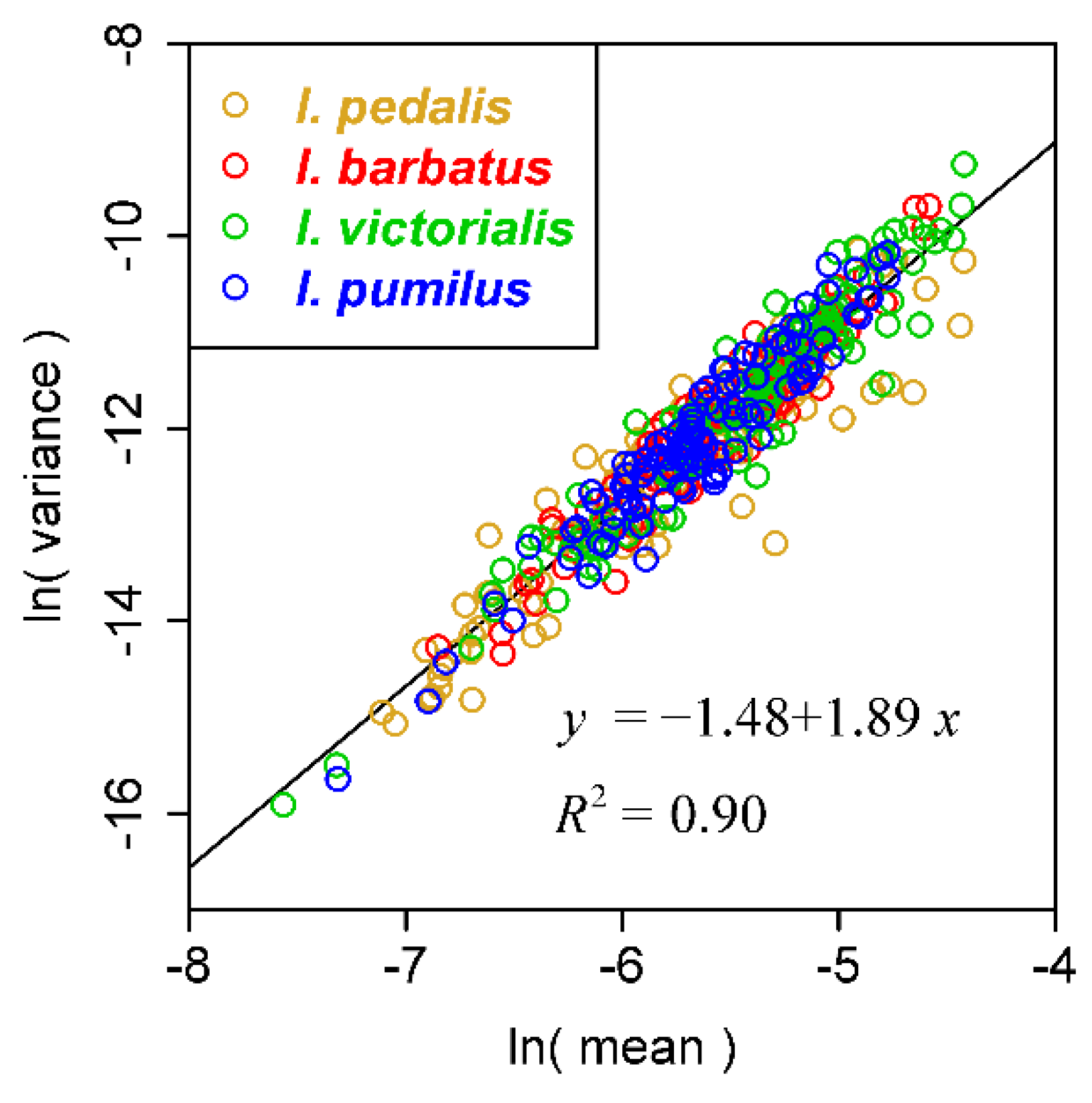
3. Results and Discussion
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Thompson, D.W. On Growth and Form; Cambridge University Press: London, UK, 1917. [Google Scholar]
- Van Valen, L. A study of fluctuating asymmetry. Evolution 1961, 16, 125–142. [Google Scholar] [CrossRef]
- Palmer, A.R.; Strobeck, C. Fluctuating asymmetry: Measurement, analysis, patterns. Ann. Rev. Ecol. Syst. 1986, 17, 391–421. [Google Scholar] [CrossRef]
- Fischer, C.; Neuhaus, G. Influence of auxin on the establishment of bilateral symmetry in monocots. Plant J. 1996, 9, 659–669. [Google Scholar] [CrossRef]
- Mardia, K.V.; Bookstein, F.L.; Moreton, I.J. Statistical assessment of bilateral symmetry of shapes. Biometrika 2000, 87, 285–300. [Google Scholar] [CrossRef]
- Klingenberg, C.P.; Barluenga, M.; Meyer, A. Shape analysis of symmetric structures: quantifying variation among individuals and asymmetry. Evolution 2002, 56, 1909–1920. [Google Scholar] [CrossRef] [PubMed]
- Klingenberg, C.P. Analyzing fluctuating asymmetry with geometric morphometrics: Concepts, methods, and applications. Symmetry 2015, 7, 843–934. [Google Scholar] [CrossRef]
- Gielis, J. The Geometrical Beauty of Plants; Atlantis Press: Paris, France, 2017. [Google Scholar] [CrossRef]
- Tucić, B.; Budečević, S.; Jovanović, S.M.; Vuleta, A.; Klingenberg, C.P. Phenotypic plasticity in response to environmental heterogeneity contributes to fluctuating asymmetry in plants: first empirical evidence. J. Evol. Biol. 2018, 31, 197–210. [Google Scholar] [CrossRef] [PubMed]
- Nicotra, A.B.; Cosgrove, M.J.; Cowling, A.; Schlichting, C.D.; Jones, C.S. Leaf shape linked to photosynthetic rates and temperature optima in South African Pelargonium species. Oecologia 2008, 154, 625–635. [Google Scholar] [CrossRef] [PubMed]
- Barabé, D.; Daigle, S.; Brouillet, L. On the interpretation of the asymmetrical leaf of Begonia by D’Arcy Thompson. Acta Biotheor. 1992, 40, 329–332. [Google Scholar] [CrossRef]
- Shi, P.J.; Huang, J.G.; Hui, C.; Grissino-Mayer, H.D.; Tardif, J.; Zhai, L.H.; Wang, F.S.; Li, B.L. Capturing spiral radial growth of conifers using the superellipse to model tree-ring geometric shape. Front. Plant Sci. 2015, 6, 856. [Google Scholar] [CrossRef] [PubMed]
- Wright, I.J.; Dong, N.; Maire, V.; Prentice, C.; Westoby, M.; Díaz, S.; Gallagher, R.V.; Jacobs, B.F.; Kooyman, R.; Law, E.A.; et al. Global climatic derivers of leaf size. Science 2017, 357, 917–921. [Google Scholar] [CrossRef] [PubMed]
- R Core Team. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing. 2015. Available online: https://www.R-project.org/ (accessed on 17 April 2018).
- Baddeley, A.; Rubak, E.; Turner, R. Spatial Point Patterns: Methodology and Applications with R; Chapman and Hall/CRC Press: London, UK, 2015. [Google Scholar]
- De Mendiburu, F. Agricolae: Statistical Procedures for Agricultural Research. R Package Version 1.2-4. Available online: https://CRAN.R-project.org/package=agricolae (accessed on 17 April 2018).
- Lin, S.; Zhang, L.; Reddy, G.V.P.; Hui, C.; Gielis, J.; Ding, Y.; Shi, P. A geometrical model for testing bilateral symmetry of bamboo leaf with a simplified Gielis equation. Ecol. Evol. 2016, 6, 6798–6806. [Google Scholar] [CrossRef] [PubMed]
- Milla, R.; Reich, P.B. The scaling of leaf area and mass: The cost of light interception increases with leaf size. Proc. R. Soc. Lond. B Biol. Sci. 2007, 274, 2109–2114. [Google Scholar] [CrossRef] [PubMed]
- Lin, S.; Shao, L.; Hui, C.; Song, Y.; Reddy, G.V.P.; Gielis, J.; Li, F.; Ding, Y.; Wei, Q.; Shi, P. Why does not the leaf weight-area allometry of bamboos follow the 3/2-power law? Fron. Plant Sci. 2018, in press. [Google Scholar] [CrossRef]
- Oren, R.; Schulze, E.-D.; Matyssek, R.; Zimmermann, R. Estimating photosynthetic rate and annual carbon gain in conifer from specific leaf weight and leaf biomass. Oecologia 1986, 70, 187–193. [Google Scholar] [CrossRef] [PubMed]
- Niinemets, Ü.; Kull, K. Leaf weight per area and leaf size of 85 Estonian woody species in relation to shade tolerance and light availability. For. Ecol. Manag. 1994, 70, 1–10. [Google Scholar] [CrossRef]
- Smith, W.K.; Vogelmann, T.C.; DeLucia, E.H.; Bell, D.T.; Shepherd, K.A. Leaf form and photosynthesis: Do leaf structure and orientation interact to regulate internal light and carbon dioxide? BioScience 1997, 47, 785–793. [Google Scholar] [CrossRef]
- Semiarti, E.; Ueno, Y.; Tsukaya, H.; Iwakawa, H.; Machida, C.; Machida, Y. The ASYMMETRIC LEAVES2 gene of Arabidopsis thaliana regulates formation of a symmetric lamina, establishment of venation and repression of meristem-related homeobox genes in leaves. Development 2001, 128, 1771–1783. [Google Scholar]
- Sandhu, H.S.; Shi, P.; Kuang, X.; Xue, F.; Ge, F. Applications of the bootstrap to insect physiology. Fla. Entomol. 2011, 94, 1036–1041. [Google Scholar] [CrossRef]
- Taylor, L.R. Aggregation, variance and the mean. Nature 1961, 189, 732–735. [Google Scholar] [CrossRef]
- Cohen, J.E.; Xu, M. Random sampling of skewed distributions implies Taylor’s power law of fluctuation scaling. Proc. Natl. Acad. Sci. USA 2015, 112, 7749–7754. [Google Scholar] [CrossRef] [PubMed]
- Cohen, J.E.; Lai, J.; Coomes, D.A.; Allen, R.B. Taylor’s law and related allometric power laws in New Zealand mountain beech forests: The roles of space, time and environment. Oikos 2016, 125, 1342–1357. [Google Scholar] [CrossRef]
- Shi, P.J.; Sandhu, H.S.; Reddy, G.V.P. Dispersal distance determines the exponent of the spatial Taylor’s power law. Ecol. Model. 2016, 335, 48–53. [Google Scholar] [CrossRef]
- Cheng, L.; Hui, C.; Reddy, G.V.P.; Ding, Y.-L.; Shi, P.-J. Internode morphometrics and allometry of Tonkin Cane Pseudosasa amabilis McClure. Front. Ecol. Evol. 2017, 7, 9651–9660. [Google Scholar] [CrossRef] [PubMed]
- Valladares, F.; Brites, D. Leaf phyllotaxis: Does it really affect light capture? Plant Ecol. 2004, 174, 11–17. [Google Scholar] [CrossRef]
- Jurik, T.W. Temporal and spatial patterns of specific leaf weight in successional northern hardwood trees species. Am. J. Bot. 1986, 73, 1083–1092. [Google Scholar] [CrossRef]

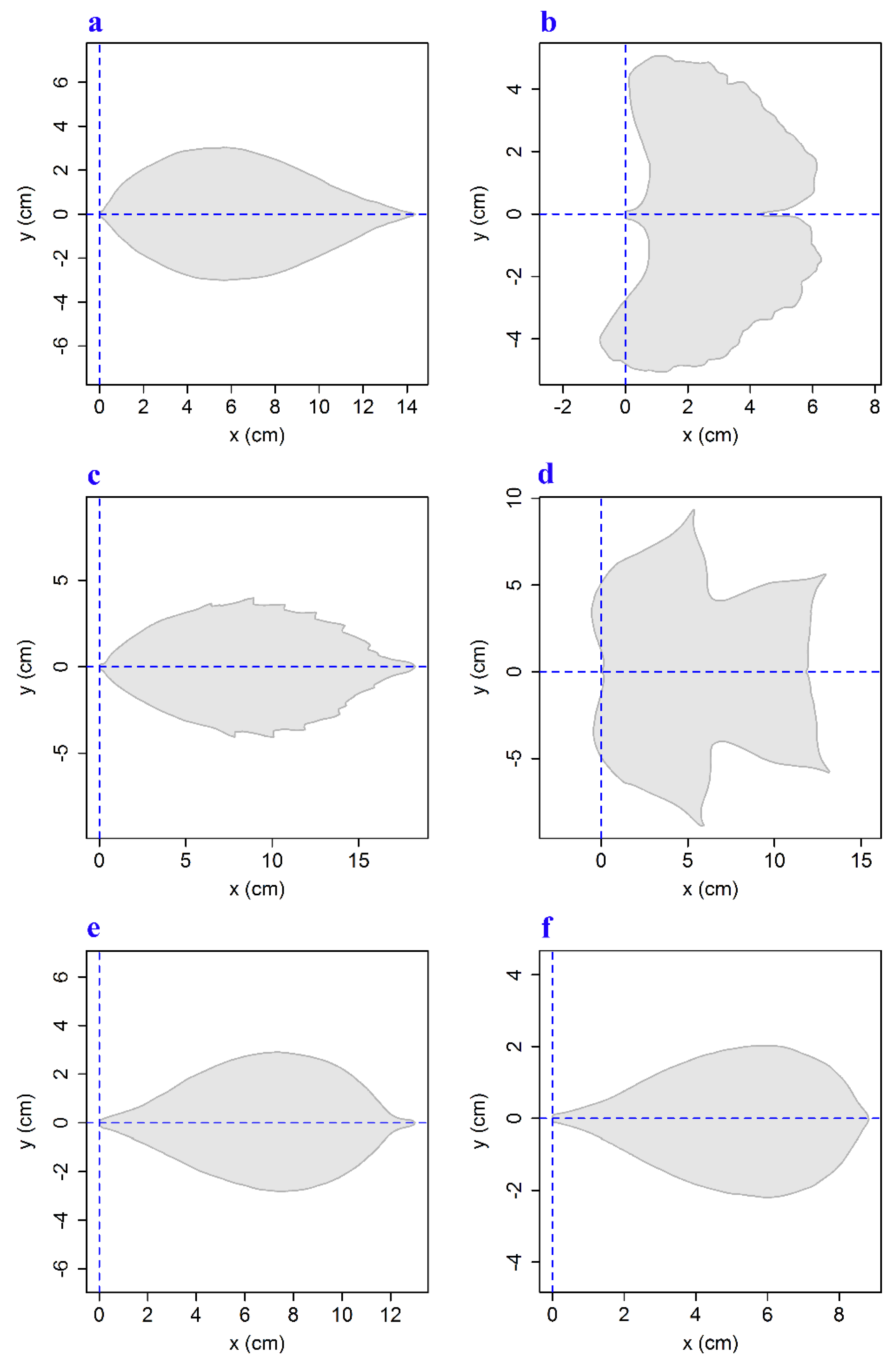
| Species Code | Latin Name | Family | Leaves | Sampling Time |
|---|---|---|---|---|
| 1 | Indocalamus pedalis (Keng) P. C. Keng | Poaceae | 100 | early July 2014 |
| 2 | Indocalamus barbatus McClure | Poaceae | 100 | early July 2014 |
| 3 | Indocalamus victorialis P. C. Keng | Poaceae | 100 | early July 2014 |
| 4 | Indocalamus pumilus Q. H. Dai et C. F. Keng | Poaceae | 100 | early July 2014 |
| 5 | Chimonanthus praecox (Linn.) Link | Calycanthaceae | 72 | 20 October 2017 |
| 6 | Ginkgo biloba L. | Ginkgoaceae | 84 | 20 October 2017 |
| 7 | Aucuba japonica Thunb. var. variegata D’ombr. | Cornaceae | 100 | 20 October 2017 |
| 8 | Liriodendron tulipifera L. | Magnoliaceae | 100 | 11 October 2017 |
| 9 | Phoebe sheareri (Hemsl.) Gamble | Lauraceae | 100 | 26 October 2017 |
| 10 | Pittosporum tobira (Thunb.) Ait. | Pittosporaceae | 100 | 27 October 2017 |
| Species | r (RMSE 1, LA 2) | r (SI 3, LA) | r (AR 4, LA) | CVRMSE | CVSI | CVAR |
|---|---|---|---|---|---|---|
| 1 | 0.686 (p < 0.01) | 0.013 (p > 0.05) | −0.182 (p > 0.05) | 52.3% | 37.2% | 12.1% |
| 2 | 0.786 (p < 0.01) | 0.192 (p > 0.05) | −0.025 (p > 0.05) | 40.2% | 21.8% | 9.9% |
| 3 | 0.500 (p < 0.01) | −0.21 (p = 0.036) | −0.139 (p > 0.05) | 50.4% | 35.8% | 10.7% |
| 4 | 0.753 (p < 0.01) | 0.132 (p > 0.05) | 0.172 (p > 0.05) | 43.4% | 24.1% | 12.0% |
| 5 | 0.263 (p < 0.05) | −0.071 (p > 0.05) | −0.053 (p > 0.05) | 65.2% | 54.2% | 20.9% |
| 6 | 0.467 (p < 0.01) | 0.119 (p > 0.05) | −0.160 (p > 0.05) | 47.7% | 42.4% | 17.2% |
| 7 | 0.345 (p < 0.01) | −0.048 (p > 0.05) | 0.041 (p > 0.05) | 59.8% | 51.4% | 21.3% |
| 8 | 0.545 (p < 0.01) | −0.101 (p > 0.05) | −0.008 (p > 0.05) | 48.2% | 42.4% | 10.9% |
| 9 | 0.472 (p < 0.01) | −0.143 (p > 0.05) | −0.090 (p > 0.05) | 69.5% | 54.3% | 24.7% |
| 10 | 0.290 (p < 0.01) | −0.027 (p > 0.05) | −0.008 (p > 0.05) | 55.6% | 46.5% | 12.6% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, P.; Zheng, X.; Ratkowsky, D.A.; Li, Y.; Wang, P.; Cheng, L. A Simple Method for Measuring the Bilateral Symmetry of Leaves. Symmetry 2018, 10, 118. https://doi.org/10.3390/sym10040118
Shi P, Zheng X, Ratkowsky DA, Li Y, Wang P, Cheng L. A Simple Method for Measuring the Bilateral Symmetry of Leaves. Symmetry. 2018; 10(4):118. https://doi.org/10.3390/sym10040118
Chicago/Turabian StyleShi, Peijian, Xiao Zheng, David A. Ratkowsky, Yang Li, Ping Wang, and Liang Cheng. 2018. "A Simple Method for Measuring the Bilateral Symmetry of Leaves" Symmetry 10, no. 4: 118. https://doi.org/10.3390/sym10040118
APA StyleShi, P., Zheng, X., Ratkowsky, D. A., Li, Y., Wang, P., & Cheng, L. (2018). A Simple Method for Measuring the Bilateral Symmetry of Leaves. Symmetry, 10(4), 118. https://doi.org/10.3390/sym10040118






