Pursuit and Evasion Linear Differential Game Problems with Generalized Integral Constraints

Abstract

In this paper, we study pursuit and evasion differential game problems of one pursuer/one evader and many pursuers/one evader, respectively, in the space ${\mathbb{R}}^n$. In both problems, we obtain sufficient conditions that guarantee the completion of a pursuit and an evasion. We construct the players’ optimal strategies in both problems, and we estimate the possible distance that an evader can preserve from pursuers. Lastly, we illustrate our results via some numerical examples.

1. Introduction

In differential games, pursuit and evasion conflicts represent challenging problems with important applications in the fields of aerospace and robotics. In pursuit–evasion problems, the synthesis of intelligent actions must consider the adversary’s potential strategies. Differential game theory provides an adequate framework to analyze possible outcomes of a conflict without assuming particular behaviors by the opponent [1].

The problems usually involve two key players (namely, pursuer and evader) or autonomous agents with conflicting objectives; generalizations are typical in the sense of multiple players divided into two teams—the pursuer team and the evader team. The main purpose is to construct strategies and provide sufficient conditions that enable an autonomous agent to perform a set of actions against the opponent; for instance, the pursuer aims at determining a strategy that will result in the capture or interception of the evader. The dynamics of the players are often described by system ordinary (partial) differential equations. The players’ control functions or strategies are usually subjected to integral, geometric, and mixed (that is, both integral and geometric) constraints. In this work, we are interested in pursuit and evasion differential game problems where players’ dynamics are governed by ordinary differential equations and control functions subject to integral constraints.

2. Preliminaries

Among the early works on linear differential games is the work of Pshennichnyi and Onopchuk [2], where the dynamics of the game are described by the linear equation

$$\stackrel{·}{z}\left(t\right)=Az\left(t\right)+bu\left(t\right)-cv\left(t\right),$$

where the coefficients A and b (as well as c) are a constant $n\times n$ matrix and an n dimensional vector, respectively, and the control functions of the pursuer and the evader, $u(·)$ and $v(·)$, are subject to the integral constraints

$${\int }_0^{\infty }{\left|u\left(t\right)\right|}^{2}dt\le {\rho }^2,{\int }_0^{\infty }{\left|v\left(t\right)\right|}^{2}dt\le {\sigma }^2,$$

respectively, where $\rho$ and $\sigma$ are given positive numbers (usually interpreted as the maximum energy resources of the pursuer and the evader, respectively). The authors [2] obtained some conditions for the completion of a pursuit. To this end, they proposed a formula for the optimal pursuit time and constructed optimal strategies for the pursuer.

Motivated by the results in [2], some authors [3,4,5,6,7,8,9,10,11,12,13,14] studied this class of problem and proposed various methods of solving the pursuit and evasion problems with integral or other form of the aforementioned constraints on the players’ control functions. For instance, Rakhmanov et al. [3] studied a linear pursuit differential game of one pursuer and one evader. Controls of the pursuer and the evader are subjected to integral and geometric constraints, respectively. Conditions of completion of a pursuit in the game from all initial points of players are obtained. Ibragimov et al. [4] recently studied an evasion differential game of one evader and many pursuers with players’ dynamics described by linear differential equations. The control functions of players are subjected to integral constraints. They solved the evasion problem under the assumption that the total energy of pursuers does not exceed the energy of an evader. The rest of the papers [11,13,14] are concerned with a pursuit and evasion problem where geometric constraints are imposed on the players’ control functions. A generalized case of the geometric constraints (that is, Gronwall–Bellman-type constraints) was proposed in the work of Samatov [5], where a simple pursuit differential game was considered. Here, we are more interested in differential game problems with integral constraints.

In [6], the authors obtained sufficient conditions that guarantee a pursuit and also an evasion in a differential game with integral constraints. To this end, pursuers’ and evader’s optimal strategies are constructed. The results are demonstrated with some illustrative examples.

Chikrii and Belousov [7] proposed a scheme that uses the ideas of the method of resolving functions and established sufficient conditions for the termination of a pursuit in some guaranteed time.

Azimov [8] studied the evasion version of the pursuit problem in [7] with integral constraints on players’ control functions, and obtained sufficient conditions for an evasion from any given point in the phase space.

Ibragimov et al. [15] considered both pursuit and evasion problems with the control function of the players subject to integral constraints. The case where the control resources of the pursuer are less than or equal to that of the evader is studied. For this case, the authors proposed a new method for solving the evasion problem. For construction, the strategy of the evader information about the state of the system and the control resources of the players is used.

Ibragimov and Hasim [16] studied a pursuit–evasion differential game in the space ${\mathsf{\ell }}_2$ with the dynamic equation of the players described by

$$\begin{array}{c}\hfill {\stackrel{.}{z}}_k\left(t\right)=-{\lambda }_k{z}_k\left(t\right)+w_k\left(t\right),w_k\left(t\right)=v_k\left(t\right)-u_k\left(t\right),\end{array}$$

(1)

where ${\lambda }_k$ is a scalar, $z_k(·),w_k(·)\in {\mathsf{\ell }}_2$; integral constraints were imposed on the players’ controls and solved an evasion problem when the total resource of the pursuers was less than that of the evader. Ibragimov et al. [9] also examined a pursuit–evasion differential game in the space ${\mathbb{R}}^n$ with players’ motion described by

$$\begin{array}{c}\hfill \stackrel{.}{z}\left(t\right)=A\left(t\right)z+B\left(t\right)\left(v\left(t\right)-u\left(t\right)\right)z\left(0\right)=z_0,z(·),z_0,u(·),v(·)\in {\mathbb{R}}^n,\end{array}$$

(2)

where $A\left(t\right)$ and $B\left(t\right)$ are $n\times n$ matrices; players’ control functions were subject to integral constraints. The authors constructed optimal strategies of the players (pursuer and evader) when the control resource of the pursuer was greater than that of the evader and obtained the optimal pursuit time.

Recently, Ahmed et al. [10] studied a pursuit differential game on a closed convex subset K of ${\mathbb{R}}^n$ with dynamic equations of the players described by

$$\stackrel{.}{x}\left(t\right)=\eta \left(t\right)u\left(t\right)x\left(0\right)=x_0\stackrel{.}{y}\left(t\right)=\eta \left(t\right)v\left(t\right)y\left(0\right)=y_0,$$

where $\eta \left(t\right)$ is a scalar function, $t\ge 0$; control functions of the players were subject to the more general integral constraints

$$\begin{array}{c}\hfill {\int }_0^{\infty }{\left|u\left(s\right)\right|}^{p}ds<{\rho }^p,{\int }_0^{\infty }{\left|v\left(s\right)\right|}^{p}ds<{\sigma }^p,\end{array}$$

(3)

where $p\ge 1,\rho$ and $\sigma$ are given positive numbers. The authors [10] obtained a sufficient condition for the completion of a pursuit. Rilwan et al. [6] also studied an evasion version of the problem [10] with $p=2$ and obtained sufficient conditions that guaranteed the avoidance of contact of the evader from the pursuers. To this end, they constructed the evader’s optimal strategy.

It is worth mentioning that the dynamic equations in [10] above can be transformed to the form (2) by simply letting $A\left(t\right)=0$ and $B\left(t\right)$=$\eta \left(t\right)$ be scalars. This transformation and also the fact that the integral constraints (3) generalize the existing integral constraints in the literature motivated the following research question: is it possible to solve a pursuit and evasion problem with players’ dynamics described in [9] with the integral constraints (3) imposed on players’ control function? Answering this question will indeed generalize some results on pursuit and evasion problems in the literature (see, for example, [3,4,5,6,8,9,10,11,12,14,16,17]).

Players’ dynamics in pursuit and evasion problems are not always restricted to the linear differential Equation (2). Badakaya et al. [18] investigated a pursuit–evasion differential game involving a countable number of pursuers and one evader with players’ dynamics described by certain $n^{th}$-order differential equations and the constructed players’ optimal strategies. Jamilu et al. [19] also studied a pursuit–evasion differential game problem in which countably many pursuers chase one evader in the Hilbert space ${\mathsf{\ell }}_2$ for a fixed period of time. The control function for each of the players satisfies an integral constraint; the dynamic equations of the pursuers and evader were governed by first- and second-order differential equations, respectively, and constructed optimal strategies for the players and found the value of the game. Azimov et al. [20] studied a differential game of many pursuers and one evader, where all the players moved only along the one-skeleton graph of an orthoplex of the dimension $d+1$. The authors obtained the optimal number of pursuers in the game. In [21], a two-player pursuit evasion differential game and a time optimal zero control problem in ${\mathsf{\ell }}_2$ were considered. The optimal control for the corresponding zero control problem was found. A strategy for the pursuer that guaranteed a solution for the pursuit problem was constructed.

In summary, the main objective of this paper is to address the above research question. More precisely, we find sufficient conditions for the completion of a pursuit and also for an evasion in the differential game described as in (2) with the integral constraints (3) imposed on players’ control function.

The rest of this paper is organized as follows: In Section 3, we present the players’ dynamics and the definitions of some basic terms. This is followed by the main results in Section 4, which comprises two subsections: one of the sections, Section 4.1, is concerned with pursuit problems where we give sufficient conditions for the completion of the pursuit, while Section 4.2 presents sufficient conditions that guarantee evasion. Section 5 presents examples to illustrate our results, and Section 6 concludes the paper.

3. Statement of the Problem

Consider the space ${\mathbb{R}}^n$ with the norm $\left|\right|·\left|\right|:{\mathbb{R}}^n\to [0,+\infty )$ defined as

$$∥\alpha ∥={\left(\sum _{k=1}^n{\left|{\alpha }_k\right|}^p\right)}^{\frac{1}{p}},\alpha \in {\mathbb{R}}^n.$$

The dynamic equations of pursuers and an evader are given by

$$\begin{array}{cc}\hfill {\stackrel{.}{x}}_j\left(t\right)=& A\left(t\right)x_j\left(t\right)+B\left(t\right)u_j\left(t\right),x_j\left(0\right)=x_j^{0}j=1,2,3,\cdots ,m\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill \stackrel{.}{y}\left(t\right)=& A\left(t\right)y\left(t\right)+B\left(t\right)v\left(t\right),y\left(0\right)=y^0,\hfill \end{array}$$

(5)

where $x_j\left(t\right),y\left(t\right)\in {\mathbb{R}}^n$ is the state of the pursuers and the evader at time t, and $u_j\left(t\right)$ and $v\left(t\right)$ are the control functions of the pursuer and evader, respectively. The dynamic Equations (4) and (5) can be expressed in closed form as

$$\begin{array}{c}\hfill {\stackrel{.}{z}}_j\left(t\right)=A\left(t\right)z_j\left(t\right)+B\left(t\right)w_j\left(t\right),z_j\left(0\right)=z_j^0,\end{array}$$

(6)

where $z_j\left(t\right)=y\left(t\right)-x_j\left(t\right)$, $w_j\left(t\right)=v\left(t\right)-u_j\left(t\right)$, $A\left(t\right)$, and $B\left(t\right)$ are continuous $n\times n$ matrices, and $u_j\left(t\right),j=1,2,\cdots ,m$ and $v\left(t\right)$ are the control functions of the pursuers and the evader, respectively. The pursuers’ aim at any point in time is to to force the state towards the origin of the space ${\mathbb{R}}^n$ (that is, $z_j\left(t\right)=0$ for all $t\ge 0$) against any action of the evader who, on the other hand, tries to avoid this. We find the possibilities/conditions for which the conflicting players can achieve their aims in this work.

Definition 1

([22], p. 43). Let $(X,\mathcal{M})$ be a measurable space. A real- or complex-valued function f is said to be $\mathcal{M}$-measurable, or just measurable, if it is $(\mathcal{M},{\mathcal{B}}_{\mathbb{R}})$ or $(\mathcal{M},{\mathcal{B}}_{\mathbb{C}})$ measurable, where ${\mathcal{B}}_{\mathbb{R}}$ and ${\mathcal{B}}_{\mathbb{C}}$ are the σ-algebra in the range space unless otherwise specified. In particular, $f:\mathbb{R}\to \mathbb{C}$ is Lebesgue (resp. Borel) measurable if it is $(\mathcal{L},{\mathcal{B}}_{\mathbb{C}})$ (resp. $({\mathcal{B}}_{\mathbb{R}},{\mathcal{B}}_{\mathbb{C}}))$ measurable: likewise, $f:\mathbb{R}\to \mathbb{R}.$

Let $L_p(0,\infty )$ be the set of Lebesgue measurable functions and $(1\le p,q<\infty )$ be such that $\frac{1}{p}+\frac{1}{q}=1$. Then

$$\begin{array}{c}\hfill ∥f∥={\left({\int }_0^{\infty }{∥f\left(t\right)∥}^{p}dt\right)}^{\frac{1}{p}}<\infty \end{array}$$

for any $f\in L_p(0,\theta )$.

Definition 2.

A function $u_j(·),u_j:[0,\infty )\to {\mathbb{R}}^n$ (resp. $v(·),v:[0,\infty )\to {\mathbb{R}}^n$) with measurable coordinates $(u_{j1}(·),u_{j2}(·),\dots ,u_{jn}(·))(resp.(v_1(·),v_2(·),\dots ,v_n(·))$ such that

$${\int }_0^{\infty }\left|\right|u_j\left(t\right){\left|\right|}^{p}dt\le {\rho }_j^p,j=1,2,\cdots ,m\left(resp.{\int }_0^{\infty }{\left|\right|v\left(t\right)\left|\right|}^{p}dt\le {\sigma }^p\right),$$

(7)

where ${\rho }_j,j=1,2,\cdots ,m$ (and also σ) are positive numbers, is called the admissible control of the $j^{th}$ pursuer (evader, respectively).

Definition 3.

A function $U_j(t,v),U_j:[0,\infty )\times {\mathbb{R}}^n\to {\mathbb{R}}^n$, is called a strategy of the jth pursuer if the system (6) has a solution $z_j\left(t\right)=z_j(t,z_j^0,U_j,v(·)),t\ge 0$, at $u_j=U_j(t,v)$ for every admissible control of the evader v(·). If each control generated by this strategy is admissible, then the pursuer’s strategy is admissible.

Definition 4

([16]). A function $V(u_1,u_2,\cdots ,u_m)$, $V:{\mathbb{R}}^n\times {\mathbb{R}}^n\times \cdots \times {\mathbb{R}}^n\to {\mathbb{R}}^n,$ is referred to as the strategy of the evader if

• For any admissible control of the pursuers, $u_j=u_j\left(t\right),j=1,2,\cdots ,m,t\ge 0$, the system (6) has a unique solution at $v=V(u_1\left(t\right),u_2\left(t\right),\cdots ,u_m\left(t\right)),t\ge 0;$
• The inequality

  $${\int }_0^{\infty }{\parallel V(u_1\left(t\right),u_2\left(t\right),\cdots ,u_m\left(t\right))\parallel }^{p}dt\le {\sigma }^p$$

  (8)

  holds.

Definition 5.

Pursuit is said to be completed at some time $\tau \ge 0$ in the games (6) and (7) if there exists an admissible strategy of the $j^{th}$ pursuer that guarantees $z_j\left(\tau \right)=0$.

Definition 6

([6]). Evasion is possible in the games (6) and (7) with the initial position $z_j^0$ if there exists a strategy V of the evader such that for all admissible controls of the pursuers $u_j(·)$, $j=1,2,\cdots ,m,$ the relation $z_j\left(t\right)\ne 0,0\le t\le \infty$ holds for all $j=1,2,\cdots ,m$.

According to Definition 6, we have $x_j\left(t\right)\ne y\left(t\right)$, since $z_j(·)=y(·)-x_j(·)$. That is, the state variable of the $j^{th}$ pursuer and evader does not coincides at all times $t\ge 0$.

Problems:

i. 

Find sufficient conditions that guarantee the completion of the pursuit in the games (9) and (10).

ii. 

Find sufficient conditions that guarantee the possibility of evasion in the games (9) and (10).

iii. 

Estimate the least possible distance the evader can preserve from the pursuers in the games (9) and (10).

4. Main Results

In this section, we address the research problems stated in Section 3. To this end, we will construct the respective players’ admissible strategies and find the conditions required in the problems i and $ii$, and then estimate the distance in the problem $iii$.

4.1. Conditions That Guarantee Completion of Pursuit

By dropping the index j in (4), we consider the differential game problem of one pursuer and one evader in this section. That is, the players’ dynamics (4) now reduce to

$$\begin{array}{c}\hfill \stackrel{.}{z}\left(t\right)=A\left(t\right)z\left(t\right)+B\left(t\right)w\left(t\right),z\left(0\right)=z^0,\end{array}$$

(9)

where $z\left(t\right)=y\left(t\right)-x\left(t\right)$, $w\left(t\right)=v\left(t\right)-u\left(t\right)$, $A\left(t\right)$, and $B\left(t\right)$ are continuous $n\times n$ matrices, and $u\left(t\right)$ and $v\left(t\right)$ are the control functions of the pursuer and the evader subject to

$${\int }_0^{\infty }\left|\right|u{\left(t\right)\left|\right|}^{p}dt\le {\rho }^{p}and{\int }_0^{\infty }{\left|\right|v\left(t\right)\left|\right|}^{p}dt\le {\sigma }^p,$$

(10)

respectively; $\frac{1}{p}+\frac{1}{q}=1$, $\left(1\le p,q<\infty \right)$.

Assumption 1.

The matrix $A(·)$ is diagonal.

Lemma 1.

The following properties hold for all square matrices A, B, and C.

i. 

$e^A{e}^B=e^{A+B}$;

ii. 

$A\left(BC\right)=\left(AB\right)C$;

iii. 

$AB=BA$, for all diagonal matrices $A,B$.

It follows from Assumption 1 and Lemma 1 that the solution of Equation (9) is

$$z\left(t\right)=e^{{\int }_0^{t}A\left(s\right)ds}\left(z^0+{\int }_0^t{e}^{-{\int }_0^{s}A\left(r\right)dr}B\left(s\right)\left(v\left(s\right)-u\left(s\right)\right)ds\right).$$

(11)

It is worth mentioning that in this problem, q belongs to the set of natural numbers and the matrix $B(·)$ is not necessarily a diagonal matrix.

Let

$$\eta \left(t\right):=z^0+{\int }_0^{t}C\left(s\right)\left(v\left(s\right)-u\left(s\right)\right)ds$$

(12)

and

$${\Lambda }^q\left(t\right):={\int }_0^t{C}^q\left(s\right)ds,t>0,$$

(13)

where

$$C\left(s\right):=e^{-{\int }_0^{s}A\left(r\right)dr}B\left(s\right).$$

Assumption 2.

The matrix ${\Lambda }^q\left(t\right)$ is nonsingular for all $t>0.$

Lemma 2.

For any square matrix function $Q:[0,\infty )\to {\mathbb{R}}^{n\times n}$ and a constant vector $\overline{v}\in {\mathbb{R}}^n$, we have

$$\begin{array}{c}\hfill {\int }_0^{t}Q\left(s\right)\overline{v}ds=\left({\int }_0^{t}Q\left(s\right)ds\right)\overline{v},t\in [0,\infty ).\end{array}$$

(14)

Lemma 3.

In ${\mathbb{R}}^n,{∥x∥}_q\le {∥x∥}_p$ whenever $p\le q$.

Lemma 4.

Let A be an $n\times n$ matrix and $\overline{v}$ be an n-vector with the norm $\parallel ·\parallel :{\mathbb{R}}^{n\times n}\to \mathbb{R}$ and $\parallel ·\parallel :{\mathbb{R}}^n\to [0,\infty )$, respectively, defined by

$$\begin{array}{c}\hfill \parallel A\parallel :={\left(\sum _{i=1}^n\sum _{j=1}^n{\left|a_{ij}\right|}^p\right)}^{\frac{1}{p}}and\parallel \overline{v}\parallel :={\left(\sum _{k=1}^n{\left|v_k\right|}^p\right)}^{\frac{1}{p}},\end{array}$$

respectively, then

$$\begin{array}{c}\hfill \parallel A\overline{v}\parallel \le \parallel A\parallel \parallel \overline{v}\parallel .\end{array}$$

Lemma 5.

The exponential of a diagonal matrix M is equal to the exponential of its entries.

In view of Lemmas (2)–(5), we state sufficient conditions for the completion of a pursuit in the games (6) and (7) as follows.

Theorem 1.

Let Assumptions 1 and 2 hold. Suppose $\rho >\sigma$, then a pursuit is possible in the games (9) and (10) at the time θ, satisfying

$$\begin{array}{c}\hfill {\int }_0^{\theta }{∥C^{q-1}\left(s\right)∥}^{p}ds\le {\left(\frac{\rho -\sigma }{∥{\Lambda }^{-q}\left(\theta \right)z_0∥}\right)}^p,\end{array}$$

where ρ and σ are the energy resources of the pursuer and evader, respectively.

Proof. 

Let the hypotheses of the theorem hold. We construct a pursuer’s strategy as follows:

$$u\left(t\right)=\left\{\begin{array}{c}{\displaystyle C^{q-1}\left(t\right){\Lambda }^{-q}\left(\theta \right)z_0+v\left(t\right),0\le t\le \theta ,}\hfill \\ \\ {\displaystyle 0,t>\theta .}\hfill \end{array}\right.$$

(15)

To employ the strategy (15) for showing a completion pursuit, we first establish its admissibility as follows:

$$\begin{array}{cc}\hfill {\left({\int }_0^{\infty }{∥u\left(t\right)∥}^{p}dt\right)}^{\frac{1}{p}}=& {\left({\int }_0^{\theta }{∥C^{q-1}\left(t\right){\Lambda }^{-q}\left(\theta \right)z_0+v\left(t\right)∥}^{p}dt+0\right)}^{\frac{1}{p}}\hfill \\ \hfill \le & {\left({\int }_0^{\theta }{∥C^{q-1}\left(t\right){\Lambda }^{-q}\left(\theta \right)z_0∥}^{p}dt\right)}^{\frac{1}{p}}+{\left({\int }_0^{\theta }{∥v\left(t\right)∥}^{p}dt\right)}^{\frac{1}{p}}\hfill \\ \hfill \le & {\left({\int }_0^{\theta }{∥C^{q-1}\left(t\right){\Lambda }^{-q}\left(\theta \right)z_0∥}^{p}dt\right)}^{\frac{1}{p}}+\sigma .\hfill \\ \hfill {\left({\int }_0^{\infty }{∥u\left(t\right)∥}^{p}dt\right)}^{\frac{1}{p}}\le & {\left({\int }_0^{\theta }{∥C^{q-1}\left(t\right){\Lambda }^{-q}\left(\theta \right)z_0∥}^{p}dt\right)}^{\frac{1}{p}}+\sigma .\hfill \end{array}$$

(16)

By applying Lemma 4, the inequality (16) becomes

$$\begin{array}{cc}\hfill {\left({\int }_0^{\infty }{∥u\left(t\right)∥}^{p}dt\right)}^{\frac{1}{p}}\le & {\left({\int }_0^{\theta }{∥C^{q-1}\left(t\right)∥}^p{∥{\Lambda }^{-q}\left(\theta \right)z_0∥}^{p}dt\right)}^{\frac{1}{p}}+\sigma \hfill \\ \hfill =& {\left({∥{\Lambda }^{-q}\left(\theta \right)z_0∥}^p{\int }_0^{\theta }{∥C^{q-1}\left(t\right)∥}^{p}dt\right)}^{\frac{1}{p}}+\sigma \hfill \\ \hfill =& ∥{\Lambda }^{-q}\left(\theta \right)z_0∥{\left({\int }_0^{\theta }{∥C^{q-1}\left(t\right)∥}^{p}dt\right)}^{\frac{1}{p}}+\sigma \hfill \\ \hfill \le & ∥{\Lambda }^{-q}\left(\theta \right)z_0∥{\left({\left(\frac{\rho -\sigma }{∥{\Lambda }^{-q}\left(\theta \right)z_0∥}\right)}^p\right)}^{\frac{1}{p}}+\sigma \hfill \\ \hfill =& \rho .\hfill \end{array}$$

This implies that

$$\begin{array}{cc}\hfill {\left({\int }_0^{\infty }{∥u\left(t\right)∥}^{p}dt\right)}^{\frac{1}{p}}\le & \rho .\hfill \end{array}$$

Hence, it follows from Definition 2 that the strategy (15) is admissible.

Suppose that the pursuer employs the admissible strategy (15) on the interval $[0,\theta ]$, then from Equation (12), we have

$$\begin{array}{cc}\hfill \eta \left(\theta \right)=& z^0+{\int }_0^{\theta }C\left(s\right)\left(v\left(s\right)-C^{q-1}\left(s\right){\Lambda }^{-q}\left(\theta \right)z_0-v\left(s\right)\right)ds\hfill \\ \hfill =& z^0+{\int }_0^{\theta }C\left(s\right)\left(-C^{q-1}\left(s\right){\Lambda }^{-q}\left(\theta \right)z_0\right)ds\hfill \\ \hfill =& z^0-{\int }_0^{\theta }{C}^q\left(s\right){\Lambda }^{-q}\left(\theta \right)z_{0}ds.\hfill \end{array}$$

That is,

$$\begin{array}{cc}\hfill \eta \left(\theta \right)=& z^0-{\int }_0^{\theta }{C}^q\left(s\right)ds{\Lambda }^{-q}\left(\theta \right)z_0.\hfill \end{array}$$

(17)

Note that the equality (17) follows from (14).

This implies

$$\eta \left(\theta \right)=z^0-{\Lambda }^q\left(\theta \right){\Lambda }^{-q}\left(\theta \right)z_0=0.$$

Consequently, from (11), we have

$$z\left(\theta \right)=0.$$

This implies $x\left(\theta \right)=y\left(\theta \right)$. Hence, the conclusion of Theorem 1 follows. That is, a pursuit is completed at the time $\theta$ as long as Assumptions 1 and 2 hold, and the total energy resources of the pursuer $\rho$ are greater than that of the evader $\sigma$. □

Remark 1.

As mentioned earlier, we note here that if the matrices $A\left(t\right)=0$ and $B\left(t\right)=\eta \left(t\right)$ (some scalar function), the result obtained here reduces to that of Ahmed et al. [10]. Additionally, if $A\left(t\right)=1,B\left(t\right)=-{\lambda }_i$, where ${\lambda }_i>0,i=1,2,\cdots ,m,\cdots$ and $p=2$, the pursuit problem considered here reduces to that of Ibragimov and Hasim [16]. The authors [16] solved the pursuit problem by partitioning the time interval and established the completion of the pursuit problem by induction, which is a bit tedious. Here, we solve a more general case via a comprehensive and straightforward method of proof. Moreover, the symmetric conditions on the matrices $A(·)$ and $B(·)$ play an important role in the construction of the pursuer’s strategies in this section.

In the next section, Section 4.2, which concerns an evasion problem, we consider the case of m pursuers and one evader with players’ dynamics and constraints on players’ control functions as stated in (6) and (7), respectively.

4.2. Conditions That Guarantee Evasion

Consider the differential game problems (6) and (7). Let $B(·)$ be a diagonal matrix and

$$C\left(s\right):=e^{-{\int }_0^{s}A\left(r\right)dr}B\left(s\right).$$

It follows from Assumption 1 that $C(·)$ is also diagonal with the entries $\left(c_{ii}(·)\right)$, $i=1,2,3,\dots ,n$.

Observe that the vector $z_j\left(t\right)=(z_{j1}\left(t\right),z_{j2}\left(t\right),\cdots ,z_{jn}\left(t\right))$ has the coordinates

$$\begin{array}{c}\hfill z_{ji}\left(t\right)=e^{{\int }_0^t{a}_{ii}\left(s\right)ds}\left(z_{ji}^0+{\int }_0^t{c}_{ii}\left(s\right)w_{ji}\left(s\right)ds\right),i=1,2,3,\cdots ,n.\end{array}$$

(18)

Let

$$\rho :={\left(\sum _{j=1}^m{\rho }_j^p\right)}^{\frac{1}{p}}and{\lambda }_j\left(t\right):={\int }_0^t\parallel C\left(s\right)w_j\left(s\right)\parallel ds.$$

(19)

We now state the following sufficient conditions that guarantee evasion in the differential game problems (6) and (7) below.

Theorem 2.

If Assumption 1 holds and ${\sigma }^p>{\rho }^p$, then an evasion is possible in the games (6) and (7) with initial positions of the players $z^0=\left\{z_1^0,z_2^0,z_3^0,\cdots ,z_m^0\right\}$.

Proof. 

The proof will be presented in three parts, namely, construction of an evader’s strategy, evasion, and estimation of the distance between the evader and the pursuers.

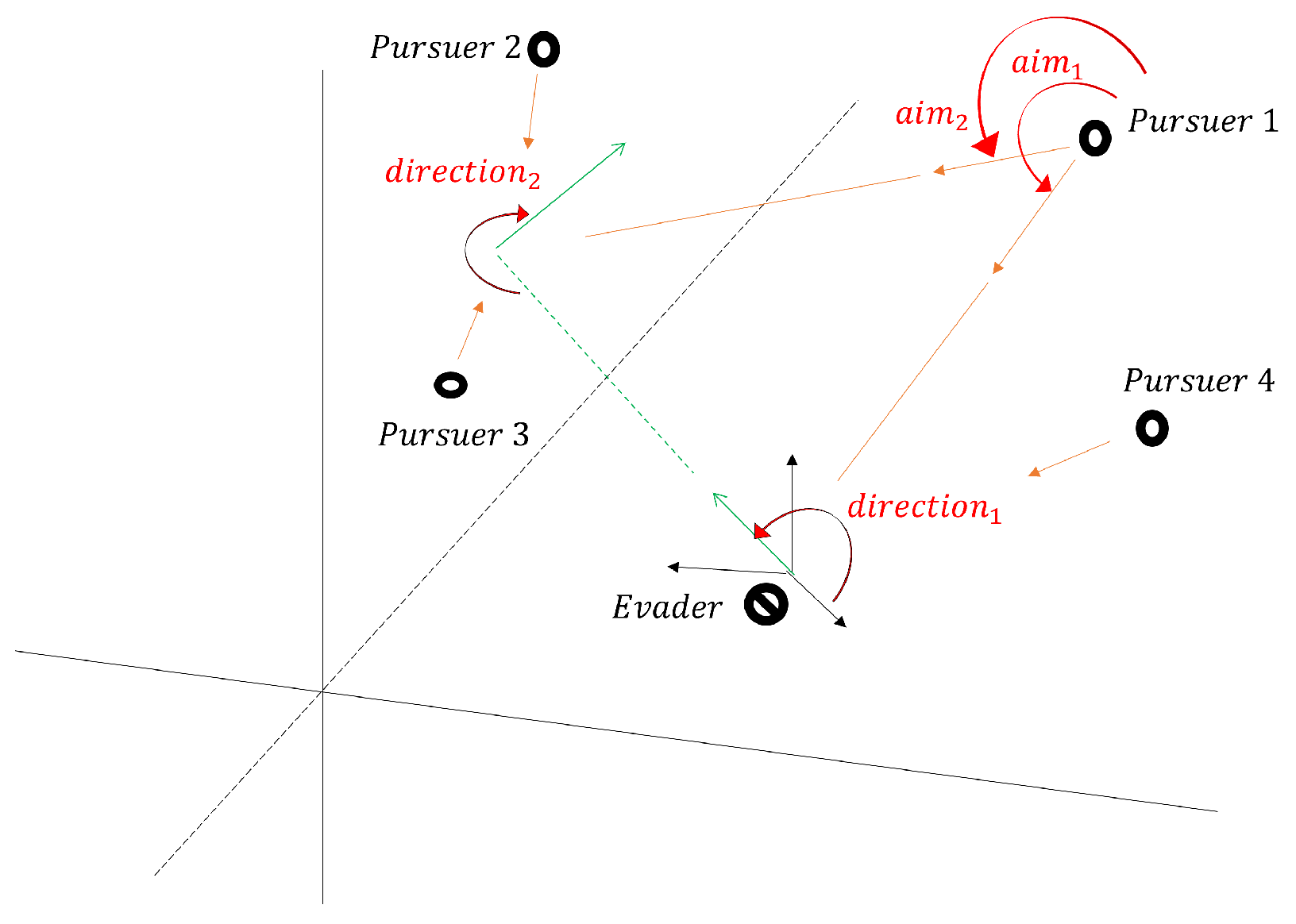
• Construction of evader’s strategy
  Consider the $k^{th}$ octant (that is, a coordinate axis that divides an n dimensional space into $2^n$ regions) in ${\mathbb{R}}^n$ given by

  $${\mathcal{O}}_k:=\left\{({\delta }_1,{\delta }_2,{\delta }_3,\cdots ,{\delta }_n,)\in {\mathbb{R}}^n|{\delta }_i=0orsign\left({\delta }_i\right)={\beta }_{ki}if{\delta }_i\ne 0,i=1,2,\cdots ,n\right\},$$

  where ${\beta }_{ki}=sign\left({\left(-1\right)}^{\lfloor \frac{k-1}{2^{i-1}}\rfloor }\right)fori=1,2,3,\cdots ,n.$
  Let

  $$\begin{array}{c}\hfill {\mathcal{O}}_{\omega }=\left\{({\delta }_1,{\delta }_2,{\delta }_3,\cdots ,{\delta }_n,)\in {\mathbb{R}}^n|{\delta }_i<0,i=1,2,\cdots ,n\right\}\end{array}$$

  be the octant with negative coordinates. Since there are $2^n$ octants in the space ${\mathbb{R}}^n$, then there exists an octant that does not contain $z_j^0$. Let ${\mathcal{O}}_{\omega }$ be the octant that does not contain $z_j^0$; that is, $z_j^0=(z_{j1}^0,z_{j2}^0,z_{j3}^0,·,z_{jn}^0)$ is a vector in a region with at least one non-negative coordinate.
  Let the evader use the following strategy, $v(·)=(v_1(·),v_2(·),\cdots ,v_n(·))$, where the coordinates

  $$v_i\left(t\right)=\left\{\begin{array}{c}{\displaystyle {\left(\sum _{j=1}^m{\left|u_{ji}\left(t\right)\right|}^p+\frac{({\sigma }^p-{\rho }^p)}{(2^i-2^{i-n})\theta }\right)}^{\frac{1}{P}},0\le t\le \theta ,}\hfill \\ \\ {\displaystyle 0,t>\theta ,}\hfill \end{array}\right.$$

  (20)

  for all $i=1,2,\cdots ,n$.
  According to the strategy (20), for each $i^{th}$ coordinate, the evader applies a control which allows keeping its distance on this coordinate from any of the pursuers moving in the direction of the $i^{th}$ coordinate. This is further illustrated in the space ${\mathbb{R}}^3$ as in the Figure 1 below.
  Next, we show the admissibility of the strategy (20):

  $$\begin{array}{cc}\hfill {\int }_0^{\infty }{\parallel v\left(s\right)\parallel }^{p}ds=& {\int }_0^{\theta }\sum _{i=1}^n{\left|v_i\left(s\right)\right|}^{p}ds\hfill \\ \hfill =& {\int }_0^{\theta }\sum _{i=1}^n\left|\sum _{j=1}^m{\left|u_{ji}\left(s\right)\right|}^p+\frac{({\sigma }^p-{\rho }^p)}{(2^i-2^{i-n})\theta }\right|ds\hfill \\ \hfill \le & {\int }_0^{\theta }\sum _{i=1}^n\left(\left|\sum _{j=1}^m{\left|u_{ji}\left(s\right)\right|}^p\right|+\left|\frac{({\sigma }^p-{\rho }^p)}{(2^i-2^{i-n})\theta }\right|\right)ds\hfill \\ \hfill \le & {\int }_0^{\theta }\sum _{i=1}^n\left(\sum _{j=1}^m{\left|u_{ji}\left(s\right)\right|}^p+\frac{({\sigma }^p-{\rho }^p)}{(2^i-2^{i-n})\theta }\right)ds\hfill \\ \hfill =& \sum _{j=1}^m{\int }_0^{\theta }\sum _{i=1}^n{\left|u_{ji}\left(s\right)\right|}^{p}ds+\frac{({\sigma }^p-{\rho }^p)}{(1-2^{-n})\theta }\sum _{i=1}^n\frac{1}{2^i}{\int }_0^{\theta }ds\hfill \\ \hfill =& \sum _{j=1}^m{\int }_0^{\theta }{\parallel u_j\left(s\right)\parallel }^{p}ds+\frac{({\sigma }^p-{\rho }^p)}{(1-2^{-n})\theta }\sum _{i=1}^n\frac{1}{2^i}{\int }_0^{\theta }ds\hfill \\ \hfill \le & \sum _{j=1}^m{\rho }_j^p+{\sigma }^p-{\rho }^p={\sigma }^p.\hfill \end{array}$$
  That is

  $$\begin{array}{c}\hfill {\int }_0^{\theta }{\parallel v\left(s\right)\parallel }^{p}ds\le {\sigma }^p.\end{array}$$
  Hence, the strategy is admissible.
• Evasion
  Here, we show that evasion is possible for any given initial position of the players $z^0$=$\left\{z_1^0,z_2^0,\cdots ,z_m^0\right\}$, $z_j^0\in {\mathbb{R}}^n$, $j=1,2,3,\cdots ,m$. That is, $z_j\left(t\right)\ne 0$ holds for all $t\in [0,\theta ]$, $j=1,2,3,\cdots ,m$.
  Let

  $$\begin{array}{c}\hfill I_i=\left\{j:z_{jk}^0<0,k=1,2,3,\cdots ,i-1;z_{jl}^0\ge 0,l=i,i+1,i+2,\cdots ,n\right\}\end{array}$$

  be the set of octants with at least one non-negative coordinate. That is, if, for instance, $h\in I_3$, then $z_h^0=(z_{h1}^0,z_{h2}^0,z_{h3}^0,\cdots ,z_{hn}^0)$: $z_{hk}^0<0,$ for all $k<3$ and $z_{hk}^0\ge 0,k\ge 3$.
  Now consider the point $z_g\left(t\right)\in {\mathbb{R}}^n$, where $g\in I_i$ and i is chosen in such a way that $z_g^0$ has coordinates $z_{gi}^0\ge 0$. It is easy to see that

  $$\sum _{j=1}^m{\left|u_{ji}\left(s\right)\right|}^p\ge \sum _{j\in I_i}{u}_{ji}^p\left(s\right)\ge u_{gi}^p\left(s\right).$$

  (21)
  We now show that evasion is guaranteed if the evader’s strategy (20) is employed. To this end, we substitute (20) in (18) and use the inequality (21) as follows:

  $$\begin{array}{cc}\hfill z_{gi}\left(t\right)=& e^{{\int }_0^t{a}_{ii}\left(s\right)ds}\left(z_{gi}^0+{\int }_0^t{c}_{ii}\left(s\right)w_{gi}\left(s\right)ds\right)\hfill \\ \hfill =& e^{{\int }_0^t{a}_{ii}\left(s\right)ds}\left(z_{gi}^0+{\int }_0^t{c}_{ii}\left(s\right)\left(v_i\left(s\right)-u_{gi}\left(s\right)\right)ds\right)\hfill \\ \hfill \ge & e^{{\int }_0^t{a}_{ii}\left(s\right)ds}\left({\int }_0^t{c}_{ii}\left(s\right)\left({\left(\sum _{j=1}^m{\left|u_{ji}\left(s\right)\right|}^p+\frac{({\sigma }^p-{\rho }^p)}{(2^i-2^{i-n})\theta }\right)}^{\frac{1}{P}}-u_{gi}\left(s\right)\right)ds\right)\hfill \\ \hfill \ge & e^{{\int }_0^t{a}_{ii}\left(s\right)ds}\left({\int }_0^t{c}_{ii}\left(s\right)\left({\left(u_{gi}^p\left(s\right)+\frac{({\sigma }^p-{\rho }^p)}{(2^i-2^{i-n})\theta }\right)}^{\frac{1}{P}}-u_{gi}\left(s\right)\right)ds\right)\hfill \\ \hfill >& e^{{\int }_0^t{a}_{ii}\left(s\right)ds}\left({\int }_0^t{c}_{ii}\left(s\right)\left({\left(u_{gi}^p\left(s\right)\right)}^{\frac{1}{P}}-u_{gi}\left(s\right)\right)ds\right)=0.\hfill \end{array}$$
  That is, $z_g\left(t\right)>0$, which implies $z_g\left(t\right)\ne 0$, for all $t\ge 0$. Since the point $z_g\left(t\right)$ is arbitrary, then it follows from Definition 6 that evasion is possible for the evader in the games (6) and (7). This completes the proof of Theorem 2.
  The smallest possible distance the evader can maintain from any of the m pursuers is estimated in the section below.
• Estimation of the distance of the evader from the pursuers
  We already have $z_j\left(t\right)\ne 0$ for all $j=1,2,3,\cdots ,m$ and for all $t\in [0,\theta ]$. Let $\parallel z_j^0\parallel$ denote the initial distance of the evader from the $j^{th}$ pursuer; then

  $$\begin{array}{cc}\hfill \parallel z_j\left(t\right)\parallel =& ∥z_j^0+{\int }_0^{t}C\left(s\right)w_j\left(s\right)ds∥\hfill \\ \hfill \ge & \parallel z_j^0\parallel -∥{\int }_0^{t}C\left(s\right)w_j\left(s\right)ds∥\hfill \\ \hfill \ge & \parallel z_j^0\parallel -{\int }_0^t∥C\left(s\right)w_j\left(s\right)∥ds\hfill \\ \hfill \ge & \parallel z_j^0\parallel -{\lambda }_j\left(\theta \right).\hfill \end{array}$$
  Note that $\parallel z_j\left(t\right)\parallel \ge |z_{ji}\left(t\right)|$ for all $t\in [0,\theta ]$ and for all $i=1,2,3,\cdots ,n$.
  Since $z_j^0\notin {\mathcal{O}}_{\omega }$ for all j, then we have

  $$\begin{array}{cc}\hfill z_{ji}\left(t\right)=& z_{ji}^0+{\int }_0^t{c}_{ii}\left(s\right)w_{ji}\left(s\right)ds\hfill \\ \hfill \ge & z_{ji}^0.\hfill \end{array}$$
  This implies

  $$\parallel z_j\left(t\right)\parallel \ge |z_{ji}^0|$$

  for all $t\in [0,\theta ]$.
  Set

  $$d_j=\left\{\begin{array}{c}{\displaystyle |z_{ji}^0|,if\parallel z_j^0\parallel -{\lambda }_j\left(\theta \right)\le 0,}\hfill \\ \\ {\displaystyle min\left\{|z_{ji}^0|,\parallel z_j^0\parallel -{\lambda }_j\left(\theta \right)\right\},if\parallel z_j^0\parallel -{\lambda }_j\left(\theta \right)>0,}\hfill \end{array}\right.$$

  for all $i=1,2,3,\cdots ,n$; then we have $\parallel z_j\left(t\right)\parallel \ge d_j$, $0\le t\le \theta$. That is, the smallest distance the evader can maintain from the $j^{th}$ pursuer is the value $d_j$.

□

Figure 1. Illustration of the evader’s strategy (20).

Remark 2.

It is worth noting that if the matrices $A\left(t\right)=0$ and $B\left(t\right)=\eta \left(t\right)$ (some scalar function), the result obtained here for an evasion problem reduces to that of Rilwan et al. [6] irrespective of the space considered. Additionally, if $A\left(t\right)=1,B\left(t\right)=-{\lambda }_i$ where ${\lambda }_i>0,i=1,2,\cdots ,m$ and $p=2$, the evasion problem considered here reduces to that of Ibragimov and Hasim [16] and also Ibragimov et al. [4]. We employ a similar method of proof as in [16], but with more general dynamic equations and also constraints in our work. The method of proof employed in this section is indeed an improvement of the proposed method of solving an evasion problem in [9], where a similar dynamic equation is considered with $p=2$.

5. Illustrative Examples

This section presents examples to illustrate our results. Numerical values are assigned to the players’ initial positions and also to all the parameters employed. In addition, the matrix functions $A(·)$ and $B(·)$ are specified.

5.1. Example (Pursuit Problem)

Consider a differential game with the initial positions of the pursuer and evader given as $x_0=(1,0)$ and $y_0=(1,1)$, respectively, and a fixed time $\theta =1$ with a dynamic equation described by

$$\begin{array}{c}\stackrel{·}{z}\left(t\right)=A\left(t\right)z\left(t\right)+B\left(t\right)\left(v\left(t\right)-u\left(t\right)\right),z\left(0\right)=z_0,\hfill \end{array}$$

(22)

where

$$\begin{array}{c}\hfill A\left(t\right)=\left[\begin{array}{cc}-2t& 0\\ 0& -2t\end{array}\right],B\left(t\right)=\left[\begin{array}{cc}\sqrt{t}& \sqrt{t}\\ 2\sqrt{t}& 0\end{array}\right].\end{array}$$

Then from the definition of $C\left(t\right)$ in (14),

$$\begin{array}{cc}\hfill C\left(t\right)=& e^{-{\int }_0^{t}A\left(r\right)dr}B\left(t\right)\hfill \\ \hfill =& \left[\begin{array}{cc}{e}^{t^2}& 0\\ 0& e^{t^2}\end{array}\right]\left[\begin{array}{cc}\sqrt{t}& \sqrt{t}\\ 2\sqrt{t}& 0\end{array}\right]\hfill \\ \hfill =& \left[\begin{array}{cc}\sqrt{t}{e}^{t^2}& \sqrt{t}{e}^{t^2}\\ 2\sqrt{t}{e}^{t^2}& 0\end{array}\right].\hfill \end{array}$$

The control functions of players are subject to

$$\begin{array}{c}\hfill {\left({\int }_0^{\infty }{\left|u\left(s\right)\right|}^{2}ds\right)}^{\frac{1}{2}}\le 20,{\left({\int }_0^{\infty }{\left|v\left(s\right)\right|}^{2}ds\right)}^{\frac{1}{2}}\le 11.\end{array}$$

This implies that $\rho =20,\sigma =11,p=q=2$.

First, we verify the hypothesis of Theorem 1 as follows, since it is required that

$$\begin{array}{c}\hfill {\int }_0^{\theta }{∥C^{q-1}\left(s\right)∥}^{p}ds\le {\left(\frac{\rho -\sigma }{∥{\Lambda }^{-q}\left(\theta \right)z_0∥}\right)}^p.\end{array}$$

(23)

L.H.S.

$$\begin{array}{cc}\hfill \parallel C^{q-1}{\left(t\right)\parallel }^p=& \parallel C^{2-1}{\left(t\right)\parallel }^2\hfill \\ \hfill =& |\sqrt{t}{e}^{t^2}{|}^2+|\sqrt{t}{e}^{t^2}{|}^2+{\left|2\sqrt{t}{e}^{t^2}\right|}^2\hfill \\ \hfill =& t{e}^{2t^2}+t{e}^{2t^2}+4t{e}^{2t^2}\hfill \\ \hfill =& 6t{e}^{2t^2}\hfill \\ \hfill {\int }_0^1{\parallel C\left(t\right)\parallel }^{2}dt=& {\int }_0^{1}6t{e}^{2t^2}dt\hfill \\ \hfill =& \frac{3}{2}{e}^{2{\left(1\right)}^2}-\frac{3}{2}{e}^{2{\left(0\right)}^2}\hfill \\ \hfill {\int }_0^1{\parallel C\left(t\right)\parallel }^{2}dt=& 10.08.\hfill \end{array}$$

(24)

R.H.S.

$$\begin{array}{cc}\hfill {\Lambda }^{-2}\left(\theta \right)={\left({\Lambda }^2\left(1\right)\right)}^{-1}=& {\left({\int }_0^1{C}^2\left(t\right)dt\right)}^{-1}\hfill \\ \hfill =& {\left({\int }_0^1\left[\begin{array}{cc}3t{e}^{2t^2}& t{e}^{2t^2}\\ 2t{e}^{2t^2}& 2t{e}^{2t^2}\end{array}\right]\right)}^{-1}\hfill \end{array}$$

$$\begin{array}{cc}\hfill =& {\left(\left[\begin{array}{cc}4.79& 1.6\\ 3.19& 3.19\end{array}\right]\right)}^{-1}\hfill \\ \hfill {\Lambda }^{-2}\left(1\right)=& \left[\begin{array}{cc}0.31& -0.16\\ -0.31& 0.47\end{array}\right].\hfill \\ \hfill \parallel {\Lambda }^{-2}\left(1\right)z_0\parallel =& ∥\left[\begin{array}{cc}0.31& -0.16\\ -0.31& 0.47\end{array}\right]\left[\begin{array}{c}0\\ 1\end{array}\right]∥\hfill \\ \hfill =& ∥\left[\begin{array}{c}-0.16\\ 0.47\end{array}\right]∥\hfill \\ \hfill =& 0.4965.\hfill \\ \hfill {\left(\frac{\rho -\sigma }{∥{\Lambda }^{-q}\left(\theta \right)z_0∥}\right)}^p=& {\left(\frac{20-11}{0.4965}\right)}^2\hfill \\ \hfill =& {\left(\frac{9}{0.4965}\right)}^2\hfill \\ \hfill =& 328.58.\hfill \end{array}$$

(25)

Thus,

$$\begin{array}{c}\hfill {\int }_0^{\theta }{∥C^{q-1}\left(s\right)∥}^{p}ds<{\left(\frac{\rho -\sigma }{∥{\Lambda }^{-q}\left(\theta \right)z_0∥}\right)}^p.\end{array}$$

Hence, a pursuit is possible at time $\theta =1$ since the hypothesis in Theorem 1 is satisfied.

From Equation (11), we have

$$z\left(t\right)=e^{{\int }_0^{t}A\left(s\right)ds}\left(z^0+{\int }_0^t{e}^{-{\int }_0^{s}A\left(r\right)dr}B\left(s\right)\left(v\left(s\right)-u\left(s\right)\right)ds\right)=e^{{\int }_0^{t}A\left(s\right)ds}\left(\eta \left(t\right)\right),$$

where

$$\begin{array}{cc}\hfill \eta \left(t\right)=& z^0+{\int }_0^{t}C\left(s\right)\left(v\left(s\right)-u\left(s\right)\right)ds.\end{array}$$

Now $\eta \left(t\right)=0$ is equivalent to $z\left(t\right)=0$.

Applying the following strategy,

$$u\left(t\right)=\left\{\begin{array}{c}{\displaystyle C\left(t\right){\Lambda }^{-2}\left(1\right)z_0+v\left(t\right),0\le t\le 1,}\hfill \\ \\ {\displaystyle 0,t>1,}\hfill \end{array}\right.$$

we have

$$\begin{array}{cc}\hfill \eta \left(t\right)=& z^0+{\int }_0^{t}C\left(s\right)\left(v\left(s\right)-u\left(s\right)\right)ds\hfill \\ \hfill \eta \left(1\right)=& z_0+{\int }_0^{1}C\left(s\right)\left(-C\left(s\right){\Lambda }^{-2}\left(1\right)z_0\right)ds\hfill \\ \hfill =& \left[\begin{array}{c}0\\ 1\end{array}\right]-{\int }_0^1\left[\begin{array}{cc}3t{e}^{2t^2}& t{e}^{2t^2}\\ 2t{e}^{2t^2}& 2t{e}^{2t^2}\end{array}\right]\left[\begin{array}{cc}0.31& -0.16\\ -0.31& 0.47\end{array}\right]\left[\begin{array}{c}0\\ 1\end{array}\right]dt\hfill \\ \hfill =& \left[\begin{array}{c}0\\ 1\end{array}\right]-{\int }_0^1\left[\begin{array}{c}-0.01t{e}^{2t^2}\\ 0.62t{e}^{2t^2}\end{array}\right]dt\hfill \\ \hfill =& \left[\begin{array}{c}0\\ 1\end{array}\right]-{\left[\begin{array}{c}\frac{-0.01}{4}{e}^{2t^2}\\ \frac{0.62}{4}{e}^{2t^2}\end{array}\right]}_0^1\hfill \\ \hfill =& \left[\begin{array}{c}0\\ 1\end{array}\right]-\left(\left[\begin{array}{c}-0.018\\ 1.145\end{array}\right]-\left[\begin{array}{c}-0.003\\ 0.155\end{array}\right]\right)\hfill \\ \hfill =& \left[\begin{array}{c}0\\ 1\end{array}\right]-\left[\begin{array}{c}-0.015\\ 0.99\end{array}\right]=\left[\begin{array}{c}0.015\\ 0.01\end{array}\right]\approx \left[\begin{array}{c}0\\ 0\end{array}\right],\hfill \end{array}$$

which shows that a pursuit is completed.

5.2. Example (Evasion Problem)

Consider the motions of countably many pursuers $p_j$, $j\in \left\{1,2,3,\cdots ,m\right\}$ and an evader E in the space ${\mathbb{R}}^3$ governed by the equation

$$\begin{array}{c}\hfill \stackrel{.}{z}\left(t\right)=A\left(t\right)z_j\left(t\right)+B\left(t\right)w_j\left(t\right),z_j\left(0\right)=z_j^0,\end{array}$$

(26)

where

$$\begin{array}{c}\hfill A\left(t\right)=\left[\begin{array}{ccc}1& 0& 0\\ 0& -2t& 0\\ 0& 0& -3t^2\end{array}\right],B=\left[\begin{array}{ccc}2t& 0& 0\\ 0& t& 0\\ 0& 0& e^{t^3}\end{array}\right].\end{array}$$

$$\begin{array}{cc}\hfill C\left(t\right)=& e^{-{\int }_0^{t}A\left(r\right)dr}B\left(t\right)\hfill \\ \hfill =& \left[\begin{array}{ccc}2t{e}^{-t}& 0& 0\\ 0& t{e}^{t^2}& 0\\ 0& 0& e^{2t^3}\end{array}\right]\hfill \end{array}$$

where $c_{11}\left(t\right)=2t{e}^{-t},c_{22}\left(t\right)=t{e}^{t^2},c_{33}\left(t\right)=e^{2t^3}$. The control functions $u_j(·)$ and $v(·)$ are subject to

$${\int }_0^{\infty }\left|\right|u_j{\left(t\right)\left|\right|}^{3}dt\le {\left(\frac{3}{\left(2^j-2^{j-3m}\right)}\right)}^{3}and{\int }_0^{\infty }{\left|\right|v\left(t\right)\left|\right|}^{3}dt\le 8,$$

respectively.

Given the initial position of the pursuers and evader as $x_j^0=\left(2^1,2^2,-2^3\right)$ and $y^0=\left(0,0,0\right)$, respectively, observe that $z_j^0=y^0-x_j^0=\left(-2,-2^2,2^3\right)$ is not contained in the octant ${\mathcal{O}}_{\omega }$ for each $j\in I_i$ and

$$\begin{array}{cc}\hfill \rho =& \sqrt[3]{\sum _{j=1}^m{\left(\frac{3}{\left(2^j-2^{j-3m}\right)}\right)}^3}\hfill \\ \hfill =& \frac{3}{\left(1-2^{-3m}\right)}\sqrt[3]{\sum _{j=1}^m\frac{1}{2^{3j}}}\hfill \\ \hfill =& \frac{3}{\left(1-2^{-3m}\right)}\sqrt[3]{\frac{1}{7}\left(1-2^{-3m}\right)}\hfill \\ \hfill =& \frac{3}{7\left(1-2^{-3m}\right)}.\hfill \end{array}$$

Let $\theta =4$ since $\rho <\sigma =\sqrt[3]{8}=2$; then by Theorem 2, if the evader adopts the admissible strategy $v\left(t\right)=(v_1\left(t\right),v_2\left(t\right),v_3\left(t\right)$, where

$$v_i\left(t\right)=\left\{\begin{array}{c}{\displaystyle {\left(\sum _{j=1}^m{\left|u_{ji}\left(t\right)\right|}^3+\frac{(\sigma -\rho )}{(2^i-2^{i-3})4}\right)}^{\frac{1}{3}},0\le t\le 4,}\hfill \\ \\ {\displaystyle 0,t>4,}\hfill \end{array}\right.$$

(27)

avoidance of contact from all the pursuers is guaranteed for all $t>0$. That is, for any arbitrary point $z_g\left(t\right)=(z_{g1}\left(t\right),z_{g2}\left(t\right),z_{g3}\left(t\right))$, $g\in I_i$, we have

$$\begin{array}{cc}\hfill z_{gi}\left(t\right)=& e^{{\int }_0^t{a}_{ii}\left(s\right)ds}\left(z_{gi}^0+{\int }_0^t{c}_{ii}\left(s\right)w_{gi}\left(s\right)ds\right)\hfill \\ \hfill =& e^{{\int }_0^t{a}_{ii}\left(s\right)ds}\left(z_{gi}^0+{\int }_0^t{c}_{ii}\left(s\right)\left(v_i\left(s\right)-u_{gi}\left(s\right)\right)ds\right)\hfill \\ \hfill \ge & e^{{\int }_0^t{a}_{ii}\left(s\right)ds}\left({\int }_0^t{c}_{ii}\left(s\right)\left({\left(\sum _{j=1}^m{\left|u_{ji}\left(t\right)\right|}^3+\frac{(\sigma -\rho )}{(2^i-2^{i-1})4}\right)}^{\frac{1}{3}}-u_{gi}\left(s\right)\right)ds\right)\hfill \\ \hfill \ge & e^{{\int }_0^t{a}_{ii}\left(s\right)ds}\left({\int }_0^t{c}_{ii}\left(s\right)\left({\left(u_{gi}^3\left(s\right)+\frac{(\sigma -\rho )}{(2^i-2^{i-1})4}\right)}^{\frac{1}{3}}-u_{gi}\left(s\right)\right)ds\right)\hfill \\ \hfill >& e^{{\int }_0^t{a}_{ii}\left(s\right)ds}\left({\int }_0^t{c}_{ii}\left(s\right)\left({\left(u_{gi}^3\left(s\right)\right)}^{\frac{1}{3}}-u_{gi}\left(s\right)\right)ds\right)=0.\hfill \end{array}$$

Hence, $z_g\left(t\right)\ne 0$, ∀$t\ge 0$.

6. Conclusions

We have studied the pursuit and evasion differential game of many pursuers and one evader in ${\mathbb{R}}^n$, with generalized integral constraints imposed on the players’ control functions. Given some sufficient conditions and a finite time $\theta$, we solved the pursuit problem through the construction of an admissible pursuer’s strategy and showed that, indeed, the strategy guarantees a completion of a pursuit at time $\theta$. To solve the evasion problem, we constructed a coordinate-wise evader’s strategy in such a way that for each coordinate, the evader keeps its distance away from any of the pursuers on the coordinate. We further estimated the smallest possible distance the evader can preserve from any of the pursuers at a given finite time. Compared with some of the problems studied in the literature [2,4,6,7,10,12,14,16,23], which are actually particular cases of the problems in this paper, we have solved both pursuit and evasion problems described by more general dynamic equations and more general integral constraints via a comprehensive and straightforward method of proof.

Following this research, we propose the following interesting problems for future study: the first is to construct the guaranteed pursuit time, and the second is to estimate the value of the game with respect to the game dynamics and constraints considered in this work.