Abstract
Due to the loosely coupled property of cloud computing environments, no node has complete knowledge of the system. For this reason, detecting a Sybil attack in cloud computing environments is a non-trivial task. In such a dynamic system, the use of algorithms based on tree or ring structures for collecting the global state of the system has unfortunate downsides, that is, the structure should be re-constructed in the presence of node joining and leaving. In this paper, we propose an unstructured Sybil attack detection algorithm in cloud computing environments. Our proposed algorithm uses one-to-one communication primitives rather than broadcast primitives and, therefore, the message complexity can be reduced. In our algorithmic design, attacker nodes forging multiple identities are effectively detected by normal nodes with the fail-stop signature scheme. We show that, regardless of the number of attacker nodes, our Sybil attack detection algorithm is able to reach consensus.
1. Introduction
A Sybil attack [1] is a well-known attack in peer-to-peer (P2P) systems. To subvert the P2P systems, an attacker node generates non-existent pseudonymous identities and colludes with other attacker nodes to hinder or delay the objectives of normal nodes. It has been proven that large-scale Sybil attacks can be easily carried out in distributed hash tables (DHTs) of the peer-to-peer file sharing protocol (BitTorrent) [2,3] and several solutions to the Sybil attacks in various environments have been studied [4,5,6,7,8,9].
In dynamic computing systems such as cloud computing, detecting Sybil attacks is a non-trivial task because the network topology is not fully connected due to the loosely coupled property. For instance, in cloud computing environments, virtualized resources (virtual machines) are provided over the Internet on demand [10,11,12]. As the use of cloud computing is expanding rapidly, security protection and threats mitigating mechanisms for healthcare, privacy-preserving, and intrusion detection has been proposed [13,14,15,16,17,18,19]. However, the existing research work for detecting a Sybil attack is heavily based on routing tables, and the message complexity of the work is sub-optimal.
In this paper, we propose an efficient algorithm for detecting Sybil attacks in cloud computing environments. Unlike the previous work, our algorithm does not rely on broadcast primitives and, therefore, the message complexity can be reduced from O(n2) to O(n), where n is the number of nodes in the system. To deal with attacker nodes, we use a randomized approach, where each node maintains small membership information, called local view, instead of full membership information, and each local view can be constructed by sampling random nodes in the system. To effectively detect a Sybil attack, we use the fail-stop signature scheme [20]. The objective of employing the fail-stop signature scheme is to remove attacker nodes’ information in the local view. How to detect attacker nodes in the system and how to realize such local view maintenance using the fail-stop signature scheme is at the core of our algorithmic design.
The remainder of the paper is organized as follows. In Section 2, we describe preliminaries and related work including our system model and problem definition. The two-phase algorithm for detecting Sybil nodes in loosely-coupled networks are presented in Section 3. Section 4 presents the performance evaluation with realistic scenarios and a formal proof of the proposed Sybil attack detection algorithm. Finally, Section 5 concludes the paper.
2. Preliminaries and Related Work
2.1. Sybil Attack
In a Sybil attack, a malicious or a Sybil node counterfeits a large number of identities to subvert the reputation system of a peer-to-peer (P2P) network. When the Sybil attack is successfully launched, the Sybil nodes are able to gain the control of the network because a number of logical nodes in an overlay network are controlled by Sybil nodes. The Sybil attack has been a thread to network security in many forms, and a small number of Sybil nodes can compromise the network by making benign nodes isolated in membership management [21].
The Sybil attack can be formulated as follows [22]. The set of participants in the network is denoted as N = {node1, node2, node3, … , noden}, and the set of users in the network is denoted as U = {user1, user2, user3, … , userm}, where n ≥ m. The set of logical nodes controlled by a user ui is denoted by Ni. It follows Ni ⋂ Nj, where ∀ i, j: i ≠ j and N1 ⋃ N2 ⋃ … ⋃ Nm = N. Then, the Sybil attack is characterized by useri as |Ni| > c, where c is a certain threshold.
Figure 1 depicts the Sybil nodes and the Sybil attack. In the bottom layer, there are physical or logical nodes. When a node is provisioned as a virtual machine in cloud computing environments, the node can be regarded as a logical node. In the top layer, there is an overlay network. The Sybil node in the bottom layer has multiple identities and, therefore, it can have more control capabilities of the network even the number of Sybil nodes is small.
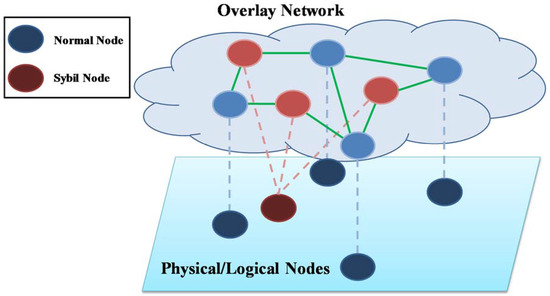
Figure 1.
Illustration of Sybil nodes and the Sybil attack.
In Figure 1, there are four normal nodes and one Sybil node in the bottom layer. However, in the top layer, there are three Sybil nodes because the Sybil node has multiple identities in the overlay network. In this circumstance, the Sybil node can gain the control of the network. For instance, the Sybil node spreads the wrong commands to sleep forever, sends malicious programs to perform a distributed denial of service (DDOS) attack, or informs erroneous results of computation to hinder the normal nodes.
2.2. Related Work
There are three broad categories of Sybil threats [23] (i.e., routing attacks, storage and retrieval attacks, and miscellaneous attacks) and four categories for their countermeasures [24] (i.e., use of diverse routing schemes, limitation on the number of peers, verification of some types of requirements, and periodical refresh of the routing tables or of the IDs). The first category of Sybil threats can have various forms including polluted lookup routing with forged identities, incorrect routing update operations for routing tables, and partition into a non-existent network. The second type of threats can be represented by denying notifications for delivered data or pretending to have resources that are not actually owned by providing fake resources or data. The third one is comprised of different malicious attitudes and attributes that cannot be classified in the two categories; that is, exhibiting inconsistent behavior, overload of target nodes, frequent churning, or flooding unsolicited messages to the network.
In [25], the authors proposed a diversity routing ID lookup and trust profile technique for a distributed hash table (DHT). To avoid incorrect routing for finding nodes or values, they use a redundancy-based zig-zag routing mechanism. In [26], the authors proposed a secure routing primitives by providing failure tests for high probability of message delivery with two routing tables: one for exploiting network proximity and the other for exploiting a constraint on closeness. For trust management of P2P systems, a scalable overlay network creation technique has been proposed based on a reputation model [27].
SybilGuard [4] uses a randomized routing algorithm with a predefined number of hops and performs identity verification based on routing information. Since SybilGuard relies on the predefined parameter, it is essential to choose the proper value of the parameter. Newsome et al. [28] designed countermeasures for various types of Sybil threats in sensor networks. For incorrect routing update operations, they employ periodic identity legitimacy checks for neighbor nodes, and provide randomized key-sets to each node in order to test coinciding keys in sets of different nodes in the network.
Rowaihy et al. [29] proposed a signature-based scheme with hierarchical structures based on bootstrap graphs. Borisov [30] incorporated computational puzzles with locally-generated challenges. The approach uses a combining function to generate certificates that can be used to prove that each node's challenge was delivered. Steiner et al. [31] explored DHT traffics by analyzing false ID creations and proposed a double-key encryption scheme for new IP addresses by a central agent. Several important issues need to be addressed in this literature are: (i) no single point of failure; (ii) efficient solution in terms of the number of messages; (iii) effective reduction of Sybil nodes in the network; and (iv) no false errors (false positives or false negatives). In this paper, we propose a Sybil attack detection scheme that resolves the above issues. More specifically, our approach does not rely on a centralized authority and is efficient in terms of the number of messages since it uses one-to-one message communication rather than broadcast primitives. To effectively diminish Sybil nodes in the network, we employ the fail-stop signature scheme and, therefore, false errors can be eliminated for detecting Sybil nodes.
2.3. System Model
We assume that the cloud computing infrastructure that consists of a collection of n nodes, node1, node2, node3, ···, noden, and each node is functionally equal to another node. To achieve a common goal, individual nodes process arbitrary programs. Each node has no global information of the system and the nodes communicate solely by passing messages. Message sending and receiving are done in an asynchronous way and all decisions are made by local information. Messages are delivered reliably with finite and arbitrary time delay. For message exchange, each node maintains partial neighbor information in local view and constructing local view can be done by the peer sampling service [32]. The attacker nodes have unlimited computational power to produce the same signature and match the public key of other nodes based on the fail-stop signature scheme [12].
2.4. Problem Definition
We consider a cloud computing environment in which the network topology is not fully connected due to the loosely-coupled property. Since it is almost impossible for each node to have the full membership information of the dynamic network, individual nodes maintain a small membership information called local view. Under this assumption, message propagation or aggregation can be done with a round based one-to-one communication mechanism. At each round, a node selects f (fanout) neighbors and communicates with the neighbors in push, pull, or push-pull mode. This type of communication patterns is also known as gossip. Among nodes, a Sybil node produces multiple identities to control the network with unlimited computational resources. The problem is to detect Sybil nodes and defend the Sybil attack in the cloud computing environment satisfying the following properties.
- Safety: If a normal node (nodei) encounters a Sybil node (nodej) performing the Sybil attack by generating multiple identities, nodei can determine whether nodej is a Sybil node of the network or not.
- Liveness: If a Sybil node (nodej) starts the Sybil attack, normal nodes eventually detect nodej as a Sybil node.
The informal definitions of safety and liveness in distributed algorithms are nothing bad happening and something good eventually happening, respectively. More specifically, the safety property in our algorithm is to make sure that if a normal node (nodei) tests a Sybil node (nodej), nodei always confirms that nodej is, indeed, a Sybil node. Likewise, the liveness property in our algorithm is to make sure that when a Sybil node (nodej) exists in the network, nodej is detected by normal nodes eventually. The safety property is reducible to the proof of the fail-stop signature scheme [33] and the liveness property is reducible to the proof of the gossip protocol [34].
3. The Proposed Sybil Attack Detection Algorithm
This section describes how to detect Sybil nodes and defend the Sybil attack under loosely-coupled networks. We employ the fail-stop signature scheme, where a signer who has a secret key produces a signature and many other keys can be used to produce the same signature matching the public key. Therefore, there is a high probability that the key computed or guessed by Sybil nodes will be different from the one held by normal nodes. How to apply the fail-stop signature to the loosely-coupled network for detecting Sybil nodes and defending the Sybil attack is at the core of our approach.
Basically, there are two threads for message exchange between nodes: active thread and passive thread [32]. Algorithm 1 shows pseudocode of active thread for the basic communication protocol. At each round, each node selects one of neighbors from its local view randomly, and then sends its own node information to the target in push mode. In pull mode, a node tries to receive a target’s node information, in turn, it updates the local information accordingly. The push-pull mode is considered as a combination of the push mode and the pull mode of the communication protocol.
At passive thread side, it waits for messages from other nodes for communication. When a node sends a message to a target node, the passive thread of the target node is triggered. As shown in Algorithm 2, it receives the target node’s information in push mode and updates with its own local information, then it sends the local information to the target in pull mode. Note that the fanout parameter is set to 1 for simplicity in Algorithms 1 and 2.
| Algorithm 1. Basic Communication Protocol (Active Thread) | |
| 1: | begin at each round |
| 2: | nodetarget ← selectNode(); |
| 3: | if push mode then |
| 4: | send (informationlocal, nodetarget); |
| 5: | end if |
| 6: | if pull mode then |
| 7: | informationtarget ← receive (nodetarget); |
| 8: | updateInformation (informationlocal, informationtarget); |
| 9: | end if |
| 10: | end |
| Algorithm 2. Basic Communication Protocol (Passive Thread) | |
| 1: | repeat |
| 2: | nodetarget ← waitForNode(); |
| 3: | if push mode then |
| 4: | informationtarget ← receive (nodetarget); |
| 5: | updateInformation (informationlocal, informationtarget); |
| 6: | end if |
| 7: | if pull mode then |
| 8: | send (informationlocal, nodetarget); |
| 9: | end if |
| 10: | until forever; |
The summary of the fail-stop signature scheme, where signers enjoy unconditional unforgeability and verifiers bear the risk of forged signatures, is as follows [20]: A trusted third party (TTP) chooses a prime modulus p satisfying p – 1 = 2q, where q is a prime number, g ∈ Zp, and r ∈ Z*q, then it computes R = gr and sends (p, q, g, R) to a node, while r is kept secret by the TTP. A node chooses x = (a1, a2, b1, b2) ∈ Zq and computes R ≡ gr (mod p), A ≡ ga1 Ra2 (mod p), and B ≡ gb1 Rb2 (mod p).
Next, the node sends K = (g, p, R, A, B) to the registry while x is kept secret by itself. For signing message m, a node produce s = SGx(m) = (β1, β2), where β1 ≡ a1 + mb1 (mod q) and β2 ≡ a2 + mb2 (mod q). For verification of signature s’ = (β1’, β2’), message m’, and public key K, it checks whether VK(m’, s’) = (ABm’ ≡ g β1’R β2’ (mod p)). For forged signature s’ = (β1’, β2’) on message m, it computes P(s’) ≡ (β1 − β1’)(β2’ − β2,)−1 (mod q), where s = (β1, β2) is the original signature for m.
Algorithm 3 shows our two-phase Sybil node detection algorithm integrated with the fail-stop signature scheme. Two data structures are used for checking Sybil nodes, that is, sybilNodes[] for the first phase and conflictCheck[] for the second phase. In each round, nodei performs the checkSybil() function to check whether nodetarget exists in sybilNodes[]. If this first checking procedure is passed, it proceeds to the second checking procedure. Otherwise, it does not perform local information update operations with the Sybil node. The checkConflict() function is performed for the second phase to detect Sybil nodes. In the checkConflict() function, it checks whether there is conflict information with nodetarget’s identity.
This conflict verification procedure is performed to reduce unnecessary signature verification operations. Without the conflict verification, it will always perform the signature verification procedure provided that nodetarget is not in sybilNodes[]. After the conflict verification procedure, the verifySignature() function based on the fail-stop signature scheme is performed. If the nodetarget’s message is forged, nodei will not perform message exchange operations with nodetarget and the Sybil node’s information is stored in sybilNodes[]. Thereby, whenever the same Sybil node is encountered, the Sybil node is filtered in the first phase with sybilNodes[].
For computational complexity of the proposed algorithm, a node should perform the discrete logarithm computation for the fail-stop signature scheme. However, this discrete logarithm computation is executed only when messages are forged. In other words, when no Sybil nodes exist and no Sybil attack is launched, the computation will not be performed according to the specification of the proposed algorithm. Hence, the computational complexity is proportional to the number of Sybil nodes activating the attack in the network. Furthermore, as Sybil nodes are detected, the computation that needs to compute decreases.
The fail-stop signature scheme is integrated to Algorithm 3 as follows: Before sending a message, each node signs the message producing s = SGx(m) = (β1, β2). To verify the signature, a node checks VK(m’, s’) = (ABm’ ≡ g β1’R β2’ (mod p)) (Line 31). The message signing and signature verification procedures are omitted in Algorithm 3 for simplicity.
| Algorithm 3. Sybil Node Detection Algorithm with the Fail-Stop Signature for nodei | |
| 1: | begin initialization |
| 2: | sybilNodes[j] ← null, ∀j∈ {1 … maxnode}; |
| 3: | conflictCheck[j] ← null, ∀j∈ {1 … maxnode}; |
| 4: | end |
| 5: | begin at each round |
| 6: | if checkSybil() then |
| 7: | return; |
| 8: | end if |
| 9: | if checkConflict() then |
| 10: | if verifySignature() then |
| 11: | sybilNodes[nodetarget] ← informationtarget; |
| 12: | return; |
| 13: | end if |
| 14: | end if |
| 15: | update local information according to Algorithms 1 and 2; |
| 16: | end |
| 17: | function checkSybil() |
| 18: | if ∃ nodetarget ∈ sybilNodes[j], ∀j ∈ {1 … maxnode} then |
| 19: | return true; |
| 20: | else |
| 21: | return false; |
| 22: | end if |
| 23: | end function |
| 24: | function checkConflict() |
| 25: | if conflictCheck[nodetarget] != informationtarget then |
| 26: | return true; |
| 27: | else |
| 28: | return false; |
| 29: | end function |
| 30: | function verifySignature() |
| 31: | verify nodetarget‘s signature based on the fail-stop signature |
| 32: | if nodetarget‘s message is forged then |
| 33: | return true; |
| 34: | else |
| 35: | return false; |
| 36: | end if |
| 37: | end function |
4. Proof and Performance Evaluation of the Algorithm
In this section, we formally prove the proposed Sybil attack detection algorithm in terms of safety and liveness. Then, we present experimental results that demonstrate the performance of our two-phase Sybil nodes detection algorithm based on the fail-stop signature scheme described in Algorithm 3.
4.1. Proof of the Algorithm
We prove the proposed Sybil attack detection algorithm based on the fail-stop signature by showing the satisfaction of the safety and liveness properties. For message complexity, refer to [35], which formally proved that the message complexity of one-to-one communication used in our algorithm is O(n).
Theorem 1.
The proposed Sybil attack detection algorithm based on the fail-stop signature satisfies the safety property.
Proof of Theorem 1.
The proof is by contradiction. Suppose nodei is a normal node and nodej is a Sybil node in the network. Since nodej is a Sybil node, nodej will pretend it is another node by generating a forged identity. Suppose nodek is a normal node and nodej tries to forge nodek’s identity. If nodei finds nodej imposing nodek’s identity, nodei performs the specification of Algorithm 3 and will be informed about nodek’s information. Since nodej is checked by either the checkSybil() function or the checkConflict() function, nodei knows nodej is a Sybil node. If nodej is checked by the checkSybil() function, the signature of nodej is already verified confirming that nodej is a Sybil node. If nodej is checked by the checkConflict() function, the verifySignature() function is performed inside the checkConflict() function. Then, the information of nodej is stored in sybilNodes[]. Once this procedure is performed, nodej is regarded as a Sybil node by the checkSybil() function without performing a signature verifying computation. Either way, the verification step based on the fail-stop signature scheme is performed. More precisely, for forged signature s’ = (β1’, β2’) on message m, it computes P(s’) ≡ (β1 – β1’)( β2’ – β2,)−1 (mod q), where s = (β1, β2) is the original signature for m. Since the fail-stop signature scheme is based on the discrete logarithm problem, it is impossible for nodej to deny the challenge (non-repudiation). This is a contradiction. Therefore, the proposed Sybil attack detection algorithm based on the fail-stop signature satisfies the safety property. ☐
Theorem 2.
The proposed Sybil attack detection algorithm based on the fail-stop signature satisfies the liveness property.
Proof of Theorem 2.
The proof is by induction.
Basis: There is one Sybil node in the network.
Let nodej be the Sybil node in the network. Since there is one Sybil node in the network, nodej should generate a very large number of identities to control network. In this case, there is a high probability to be detected by normal nodes and the Sybil node’s information will be propagated rapidly. If nodej tries to generate only one forged identity (i.e., nodek’s identity), there are two cases. One is that nodej is detected by nodek. The other case is that nodej is detected by another normal node. Once nodek encounters nodej, nodej is regarded as a Sybil node. In the latter case, nodej is detected when another normal node called nodel encounters nodej by performing Algorithm 3. Therefore, the proposed Sybil attack detection algorithm based on the fail-stop signature satisfies the liveness property when there is one Sybil node in the network.
Induction step (1): There are k Sybil nodes in the network.
Let nodei be a normal node in the network. Suppose that nodei detects one of k Sybil nodes in the network based on the basis step. Then, the number of Sybil nodes that remain undetected is k − 1. Likewise, another Sybil node will be detected as the communication round goes on and, therefore, the number of detected Sybil nodes will increase. After launching the Sybil attack, the Sybil node is detected because of the non-repudiation property of the fail-stop signature scheme. If a Sybil node does not launch the Sybil attack, it will act as a normal node. However, because of the definition of a Sybil node, a Sybil node eventually will launch the Sybil attack. Therefore, the proposed Sybil attack detection algorithm based on the fail-stop signature satisfies the liveness property when there are k Sybil nodes in the network.
Induction step (2): There are k + 1 Sybil nodes in the network.
Let nodek+1 be the (k + 1)-th Sybil node in the network. Since k Sybil nodes are detected based on induction step (1), there is one Sybil node that remains undetected in the network. In this case, the situation is same as the basis case. Since the basis step is proved, it also proves the induction step (2). Therefore, the proposed Sybil attack detection algorithm based on the fail-stop signature satisfies the liveness property. ☐
4.2. Experimental Results
Table 1 shows experimental parameters used in our evaluation. We assume that numerous nodes exist in the network and the communication mode is the push-pull mode. Rather than maintaining the full membership information, each node stores 20 neighbors’ information at maximum with the peer sampling service and, therefore, the complexity of the overlay network is greatly simplified. We vary percentages of Sybil nodes from 0.1 to 0.4. The percentages of Sybil nodes are not configured to higher than 0.5 since we require at least n/2 + 1 normal nodes for consensus [10]. We show the effectiveness of our Sybil nodes detection algorithm under this constrained circumstance.

Table 1.
Experimental parameters and their values.
A Sybil node is eager to spread malicious or incorrect information to normal nodes by selecting one or more neighbors from its local view. In this regard, the selected target node from the Sybil node can be either a normal node or a Sybil node. When the Sybil node selects a normal node, the attack can proceed.
Figure 2 shows the number of Sybil nodes encountered by normal nodes. Note that the numbers of the graphs are averaged over the number of normal nodes in the network. Obviously, as the number of rounds increases, the number of Sybil nodes encountered by normal nodes increases. For higher than the 90th percentile of cumulative distribution function (CDF), the proposed algorithm require at least four rounds and five rounds when percentages of Sybil nodes are less than or equal to 0.2 and greater than or equal to 0.3, respectively. To reach the 100th percentile of CDF, more rounds are required as the percentage of Sybil nodes increases.
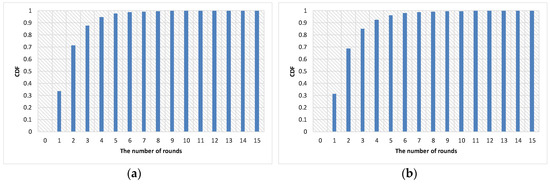
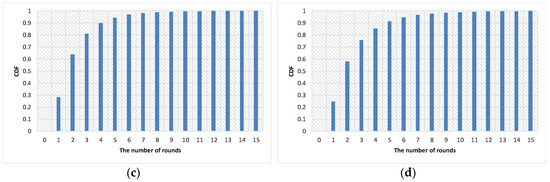
Figure 2.
The number of Sybil nodes encountered by normal nodes. (a) Percentage of Sybil nodes: 0.1; (b) percentage of Sybil nodes: 0.2; (c) percentage of Sybil nodes: 0.3; and (d) percentage of Sybil nodes: 0.4.
Figure 3 shows the standard deviation for the number of Sybil nodes encountered by normal nodes. At early stages, the standard deviation is relatively high regardless of the percentages of Sybil nodes. However, as the number of rounds goes on, the standard deviation approaches to 0. The peak value of the standard deviation appears at round 1 since there is a great deal of uncertainty for a node to encounter a Sybil node.
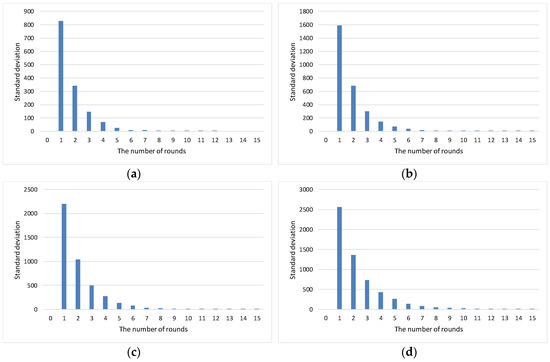
Figure 3.
Standard deviation for the number of Sybil nodes encountered by normal nodes. (a) Percentage of Sybil nodes: 0.1; (b) percentage of Sybil nodes: 0.2; (c) percentage of Sybil nodes: 0.3; (d) and percentage of Sybil nodes: 0.4.
Figure 4 shows the number of active Sybil nodes in the network. With our proposed Sybil nodes detection algorithm based on the fail-stop signature scheme, the number of active Sybil nodes logarithmically decreases. This signifies that our algorithm is effective in terms of reducing the number of Sybil nodes in the network. Moreover, because our algorithm does not rely on broadcast primitives, the message complexity is also greatly reduced.
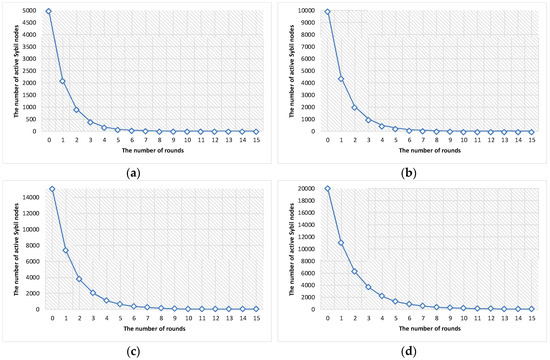
Figure 4.
The number of active Sybil nodes. (a) Percentage of Sybil nodes: 0.1; (b) PERCENTAGE of Sybil nodes: 0.2; (c) Percentage of Sybil nodes: 0.3; and (d) percentage of Sybil nodes: 0.4.
5. Conclusions
In this paper, we proposed a Sybil attack detection algorithm in cloud computing environments based on the fail-stop signature scheme. Despite the attacker nodes that have unlimited computational power and can generate forged signatures for messages, our algorithm is able to detect the attacker nodes effectively in dynamic environments. Therefore, normal nodes in the system can reach consensus regardless of the number of attacker nodes by removing attacker nodes’ information in local view. Since the proposed algorithm does not rely on broadcast primitives, the message complexity of our algorithm is O(n). Future work includes the optimization of the proposed algorithm for efficiency in terms of the required rounds and uniformity of neighbor information in the local view for normal nodes.
Acknowledgments
This research was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (NRF-2014R1A1A2055463 and NRF-2015R1D1A1A01061373).
Author Contributions
All the authors contributed equally to the work. All authors read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Douceur, J.R. The sybil attack. In Peer-to-Peer Systems: First International Workshop, IPTPS 2002, Cambridge, MA, USA, March 7–8, 2002 Revised Papers; Druschel, P., Kaashoek, F., Rowstron, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; pp. 251–260. [Google Scholar]
- Wang, L.; Kangasharju, J. Real-world sybil attacks in bittorrent mainline DHT. In Proceedings of the 2012 IEEE Global Communications Conference (GLOBECOM), Anaheim, CA, USA, 3–7 December 2012; pp. 826–832.
- Wang, L.; Kangasharju, J. Measuring large-scale distributed systems: Case of bittorrent mainline DHT. In Proceedings of the 2013 IEEE Thirteenth International Conference on Peer-to-Peer Computing (P2P), Trento, Italy, 9–11 September 2013; pp. 1–10.
- Yu, H.; Kaminsky, M.; Gibbons, P.B.; Flaxman, A.D. Sybilguard: Defending against sybil attacks via social networks. IEEE/ACM Trans. Netw. 2008, 16, 576–589. [Google Scholar] [CrossRef]
- Ssu, K.-F.; Wang, W.-T.; Chang, W.-C. Detecting sybil attacks in wireless sensor networks using neighboring information. Comput. Netw. 2009, 53, 3042–3056. [Google Scholar] [CrossRef]
- Yu, B.; Xu, C.-Z.; Xiao, B. Detecting sybil attacks in vanets. J. Parallel Distrib. Comput. 2013, 73, 746–756. [Google Scholar] [CrossRef]
- Chang, S.; Qi, Y.; Zhu, H.; Zhao, J.; Shen, X. Footprint: Detecting sybil attacks in urban vehicular networks. IEEE Trans. Parallel Distrib. Syst. 2012, 23, 1103–1114. [Google Scholar] [CrossRef]
- Abbas, S.; Merabti, M.; Llewellyn-Jones, D.; Kifayat, K. Lightweight sybil attack detection in manets. IEEE Syst. J. 2013, 7, 236–248. [Google Scholar] [CrossRef]
- Wang, G.; Musau, F.; Guo, S.; Abdullahi, M.B. Neighbor similarity trust against sybil attack in P2P e-commerce. IEEE Trans. Parallel Distrib. Syst. 2015, 26, 824–833. [Google Scholar] [CrossRef]
- Lim, J.; Suh, T.; Gil, J.; Yu, H. Scalable and leaderless byzantine consensus in cloud computing environments. Inf. Syst. Front. 2014, 16, 19–34. [Google Scholar] [CrossRef]
- Hsu, C.-H.; Ma, J.; Obaidat, M.S. Dynamic intelligence towards merging cloud and communication services. Inf. Syst. Front. 2014, 16, 1–5. [Google Scholar] [CrossRef]
- Javanmardi, S.; Shojafar, M.; Amendola, D.; Cordeschi, N.; Liu, H.; Abraham, A. Hybrid job scheduling algorithm for cloud computing environment. In Proceedings of the Fifth International Conference on Innovations in Bio-Inspired Computing and Applications IBICA 2014; Kömer, P., Abraham, A., Snášel, V., Eds.; Springer International Publishing: Cham, Switzerland, 2014; pp. 43–52. [Google Scholar]
- Zhu, W.; Lee, C. A security protection framework for cloud computing. J. Inf. Process. Syst. 2016, 12, 538–547. [Google Scholar]
- Kar, J.; Mishra, M.R. Mitigating threats and security metrics in cloud computing. J. Inf. Process. Syst. 2016, 12, 226–233. [Google Scholar]
- Hanen, J.; Kechaou, Z.; Ayed, M.B. An enhanced healthcare system in mobile cloud computing environment. Viet. J. Comput. Sci. 2016, 3, 267–277. [Google Scholar] [CrossRef]
- Alharbi, F.; Atkins, A.; Stanier, C. Understanding the determinants of cloud computing adoption in saudi healthcare organisations. Complex Intell. Syst. 2016, 2, 155–171. [Google Scholar] [CrossRef]
- Salam, M.I.; Yau, W.-C.; Chin, J.-J.; Heng, S.-H.; Ling, H.-C.; Phan, R.C.-W.; Poh, G.S.; Tan, S.-Y.; Yap, W.-S. Implementation of searchable symmetric encryption for privacy-preserving keyword search on cloud storage. Hum.-Centric Comput. Inf. Sci. 2015, 5, 19. [Google Scholar] [CrossRef]
- Keegan, N.; Ji, S.-Y.; Chaudhary, A.; Concolato, C.; Yu, B.; Jeong, D.H. A survey of cloud-based network intrusion detection analysis. Hum.-Centric Comput. Inf. Sci. 2016, 6, 19. [Google Scholar] [CrossRef]
- Baker, T.; Mackay, M.; Shaheed, A.; Aldawsari, B. Security-oriented cloud platform for soa-based scada. In Proceedings of the 2015 15th IEEE/ACM International Symposium on Cluster, Cloud and Grid Computing, Shenzhen, China, 4–7 May 2015; pp. 961–970.
- Pfitzmann, B.; Hildesheim, U. Fail-stop signatures; principles and applications. In Proceedings of the Eighth World Conference on Computer Security, Audit, and Control, COMPUSEC ’91, London, UK, 30 October–1 November 1991; Elsevier: London, UK; pp. 125–134.
- Lim, J.B.; Jung, D.; Suh, T.; Yu, H. Unstructured membership management for byzantine fault tolerance in clouds. In Proceedings of the 2014 Workshop Proceedings on Architecture of Computing Systems, ARCS 2014, Lübeck, Germany, 25–28 February 2014; pp. 1–8.
- Dinger, J.; Hartenstein, H. Defending the sybil attack in P2P networks: Taxonomy, challenges, and a proposal for self-registration. In Proceedings of the First International Conference on Availability, Reliability and Security (ARES ’06), Vienna, Austria, 20–22 April 2006; pp. 756–763.
- Sit, E.; Morris, R. Security considerations for peer-to-peer distributed hash tables. In Peer-to-Peer Systems: First Internationalworkshop, IPTPS 2002 Cambridge, MA, USA, 7–8 March 2002 Revised Papers; Druschel, P., Kaashoek, F., Rowstron, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; pp. 261–269. [Google Scholar]
- Pecori, R. S-kademlia: A trust and reputation method to mitigate a sybil attack in kademlia. Comput. Netw. 2016, 94, 205–218. [Google Scholar] [CrossRef]
- Danezis, G.; Lesniewski-Laas, C.; Kaashoek, M.F.; Anderson, R. Sybil-resistant dht routing. In Proceedings of the 10th European conference on Research in Computer Security, Milan, Italy, 12–14 September 2005; Springer: Milan, Italy, 2005; pp. 305–318. [Google Scholar]
- Castro, M.; Druschel, P.; Ganesh, A.; Rowstron, A.; Wallach, D.S. Secure routing for structured peer-to-peer overlay networks. SIGOPS Oper. Syst. Rev. 2002, 36, 299–314. [Google Scholar] [CrossRef]
- Javanmardi, S.; Shojafar, M.; Shariatmadari, S.; Ahrabi, S.S. Fr trust: A fuzzy reputation-based model for trust management in semantic P2P grids. Int. J. Grid Util. Comput. 2015, 6, 57–66. [Google Scholar] [CrossRef]
- Newsome, J.; Shi, E.; Song, D.; Perrig, A. The sybil attack in sensor networks: Analysis & defenses. In Proceedings of the 3rd International Symposium on Information Processing in Sensor Networks, Berkeley, CA, USA, 26–27 April 2004; ACM: Berkeley, CA, USA, 2004; pp. 259–268. [Google Scholar]
- Rowaihy, H.; Enck, W.; McDaniel, P.; Porta, T.L. Limiting sybil attacks in structured P2P networks. In Proceedings of the IEEE INFOCOM 2007—26th IEEE International Conference on Computer Communications, Anchorage, AK, USA, 6–12 May 2007; pp. 2596–2600.
- Borisov, N. Computational puzzles as sybil defenses. In Proceedings of the Sixth IEEE International Conference on Peer-to-Peer Computing (P2P ’06), Cambridge, UK, 6–8 September 2006; pp. 171–176.
- Steiner, M.; En-Najjary, T.; Biersack, E.W. Exploiting kad: Possible uses and misuses. SIGCOMM Comput. Commun. Rev. 2007, 37, 65–70. [Google Scholar] [CrossRef]
- Jelasity, M.; Guerraoui, R.; Kermarrec, A.-M.; Steen, M.V. The peer sampling service: Experimental evaluation of unstructured gossip-based implementations. In Proceedings of the Middleware 2004: ACM/IFIP/USENIX International Middleware Conference, Toronto, ON, Canada, 18–22 October 2004; Jacobsen, H.-A., Ed.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 79–98. [Google Scholar]
- Bleumer, G. Fail-stop signature. In Encyclopedia of Cryptography and Security; van Tilborg, H.C.A., Jajodia, S., Eds.; Springer: Boston, MA, USA, 2011; pp. 446–447. [Google Scholar]
- Allavena, A.; Demers, A.; Hopcroft, J.E. Correctness of a gossip based membership protocol. In Proceedings of the Twenty-Fourth Annual ACM Symposium on Principles of Distributed Computing, Las Vegas, NV, USA, 17–20 July 2005; ACM: Las Vegas, NV, USA, 2005; pp. 292–301. [Google Scholar]
- Lim, J.; Suh, T.; Yu, H. Unstructured deadlock detection technique with scalability and complexity-efficiency in clouds. Int. J. Commun. Syst. 2014, 27, 852–870. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).