Analysis of a Similarity Measure for Non-Overlapped Data

Abstract

A similarity measure is a measure evaluating the degree of similarity between two fuzzy data sets and has become an essential tool in many applications including data mining, pattern recognition, and clustering. In this paper, we propose a similarity measure capable of handling non-overlapped data as well as overlapped data and analyze its characteristics on data distributions. We first design the similarity measure based on a distance measure and apply it to overlapped data distributions. From the calculations for example data distributions, we find that, though the similarity calculation is effective, the designed similarity measure cannot distinguish two non-overlapped data distributions, thus resulting in the same value for both data sets. To obtain discriminative similarity values for non-overlapped data, we consider two approaches. The first one is to use a conventional similarity measure after preprocessing non-overlapped data. The second one is to take into account neighbor data information in designing the similarity measure, where we consider the relation to specific data and residual data information. Two artificial patterns of non-overlapped data are analyzed in an illustrative example. The calculation results demonstrate that the proposed similarity measures can discriminate non-overlapped data.

1. Introduction

1.1. Background and Motivation

A fuzzy set was defined and summarized with respect to an ordinary set [1,2]; the fuzzy set theory provides a fundamental background for controller design, signal processing, pattern recognition, and other related areas [3,4,5]. Among the research on the fuzzy set theory, the analysis of data uncertainties has been carried out by numerous researchers through fuzzy data sets [6,7,8]. Of those researches based on fuzzy data sets, the similarity measure design problem—i.e., the design of a measure evaluating the degree of similarity between two data sets [8,9,10,11,12,13,14,15]—has been attracting an increasing amount of attention from the research community due to the increasing number of applications, including data mining, pattern recognition, and clustering [16,17]. The design of the similarity measure based on fuzzy numbers is convenient, but it can only use triangular or trapezoidal fuzzy membership functions [11,12]. If we design a similarity measure based on a distance measure, we can use a general fuzzy membership function without any limit on its shape [13,14,15].

Note that most conventional similarity measures—whether based on fuzzy number or distance measure—can be applied to overlapped data sets only [8,11,13,14,18,19,20,21]. By “overlapped data sets” we mean data sets with the same support. Similarity measure design and investigations of its relation to dissimilarity have been carried out in the literature. Some similarity measure results are designed based on fuzzy numbers [11,12], and axiomatic similarity measures have been defined [18,19]. In addition, some similarity measures have been designed to work with non-overlapped data sets as well [22,23,24]. However, research on non-overlapped data sets is increasingly becoming important in big data analysis, especially in atypical data analysis [23,24].

In our previous research, analysis was carried out on overlapped and non-overlapped data, and intuitionistic fuzzy sets were introduced with artificial data [20]. Similarity measure design based on fuzzy numbers and similarity measure applications to intuitionistic fuzzy sets have also been studied [21]. The obtained results were summarized in a follow-up paper, in which similarity measures on intuitionistic fuzzy sets were proposed and proved [22].

In this paper, we present a methodology for the analysis of the similarity of non-overlapped data distributions. If conventional similarity measures are applied, there is no discrimination on different non-overlapped data distribution pairs, which results in the same value. We preprocessed non-overlapped data distributions to obtain information relations as a new measure between neighbor information. This represents information on how distributions are related to each other, and it allows conventional similarity to be applied. This procedure is also effective for similarity measures on overlapped data distributions. Another approach is to consider neighbor information, where a similarity measure is derived and verified with an illustrative example.

The results of the similarity of non-overlapped data suggest that the measure can be applicable to atypical data analysis. The approach is extensible to big data analysis based on the rationale that the neighbor information of each data is closely related to the similarity of each data.

1.2. Data Description

We considered a sequence of data, each element of which can take either a continuous or a discrete value. A data sequence provides information on facts. For each data sequence, its data distribution is represented by various structures. We designed similarity measures for data that have been shown as overlapped data in previous works [13,14,15]. In the following, we explain several types of data with examples:

• Two data, $\mathit{f}({\mathit{x}}_{\mathit{i}})$ and $\mathit{g}({\mathit{y}}_{\mathit{j}})$ for ${\mathit{x}}_{\mathit{i}}, {\mathit{y}}_{\mathit{j}}ϵ \mathit{X}$, $\mathit{X}$ denotes a universe of discourse. $\mathit{f}({\mathit{x}}_{\mathit{i}})$ and $\mathit{g}({\mathit{y}}_{\mathit{j}})$ have values at the same support ${\mathit{x}}_{\mathit{i}}={\mathit{y}}_{\mathit{j}}$ whether it is same or not. It means direct operation such as summation or subtract is possible between two values.
• On the other hand, they are classified as non-overlapped data. It is rather difficult to attain operation results between two data in different supports. In this paper, we propose a similarity design for such non-overlapped data with the help of preprocessing.
• Atypicality is one of the characteristics in big data [23,24]. Huge amount of data constitute different types of structure. Hence, it is challenging to analyze the similarity between different structures of data, even though they have the same meaning and fact.
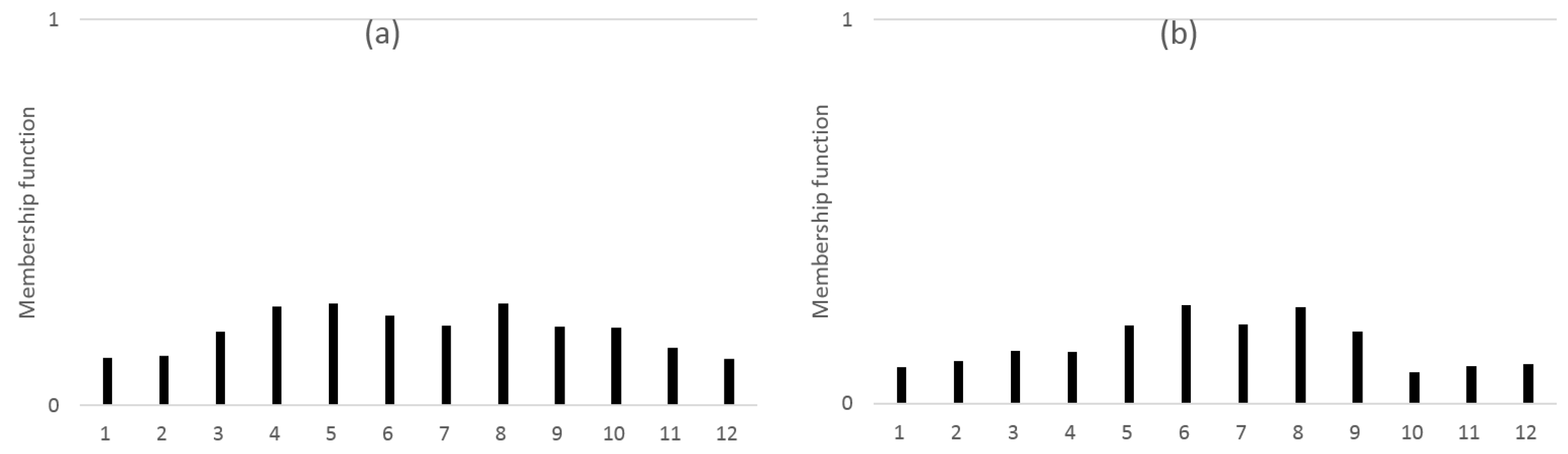
• In general, data—especially big data—provide a large amount of information, and groups of data are located close to or far from each other geometrically. The information analysis on neighbor data is used to design the non-overlapped data in this paper.

In this paper, we illustrate the usefulness of the proposed similarity measure on the non-overlapped data with the example data. Data distribution can be continuous or discrete; in this paper, however, only discrete data are considered for the ease of explanation of the computational procedure.

We begin with the review of the preliminary results on the similarity measure and distance measure using two discrete data sets in Section 2. In Section 3, the similarity measure for non-overlapped data is designed with neighbor information, and an explicit similarity measure is proposed and proved. In order to illustrate the usefulness of the proposed similarity measure, example data distributions are introduced and analyzed. Section 4 concludes our work in this paper.

2. Preliminaries on Similarity Measure

The axiomatic definition of a similarity measure is given by Liu [8]; based on this definition, a similarity measure can be designed explicitly using a distance measure such as the Manhattan distance. From the definition, numerous properties for a similarity measure between data sets can be derived.

Definition 1.

[8] A real function $s$: $F^2\to R^{+}$ is called a similarity measure if $s$ satisfies the following properties:

(S1) 

$s(A,B)=s(B,A)$, for $\forall A, B\in F(X)$

(S2) 

$s(D,D^C)=0$, if and only if $D\in P(X)$

(S3) 

$s(C,C)=ma{x}_{A,B\in F}s(A,B)$, for $\forall C\in F(X)$

(S4) 

$A,B,C\in F(X)$, if $A\subset B\subset C$, then $s(A,B)\ge s(A,C)$ and $s(B,C)\ge s(A,C)$

where $R^{+}=[0,\infty )$, $X$ is the universal set, $F(X)$ denotes the class of all fuzzy sets of $X$, $P(X)$ is the class of all crisp sets of $X$, and $D^C$ is the complement of $D$. From Definition 2.1, numerous similarity measures can be derived.

Distance is needed to represent the similarity measure explicitly; Liu also introduced the distance measure with axiomatic definition in [8].

Definition 2.

[8] A real function $d$: $F^2\to R^{+}$ is called a distance measure on $F$ if $d$ satisfies the following properties:

(D1) 

$d(A,B)=d(B,A)$, for $\forall A,B\in F(X)$

(D2) 

$d(A,A)=0$, $A\in F(X)$

(D3) 

$d(D,D^C)=ma{x}_{A,B\in F}d(A,B)$, $D\in F(X)$

(D4) 

$A,B,C\in F(X)$, if $A\subset B\subset C$, then $d(A,B)\le d(A,C)$ and $d(B,C)\le d(A,C)$.

Generally, Manhattan distance is commonly used as a distance measure between fuzzy sets $A$ and $B$ [22]:

$$d(A,B)=\frac{1}{n}{{\displaystyle \sum }}_{i=1}^n|{\mu }_A(x_i)-{\mu }_B(x_i)|$$

where $X=\{x_1,x_2, \cdots , x_n\}$, $|k|$ is the absolute value of $k$, and ${\mu }_A(x)$ denotes the membership function of $A\in F(X)$. Conventional similarity measures are illustrated in the following theorems. Theorem 1 is a similarity measure equation with Manhattan distance [22].

Theorem 1.

∀$A,B\in F(X)$, if $d$ is the Manhattan distance measure, then:

$$s(A,B)=1-d(A,A{\displaystyle \cap }B)-d(B,A{\displaystyle \cap }B)$$

(1)

is a normalized similarity measure between sets $A$ and $B$.

Proof. 

The proof of Theorem 1 is given in Appendix A. ☐

Besides the similarity measure given by Theorem 1, other similarity measures can be defined as well, which is illustrated in Theorem 2.

Theorem 2.

$\forall A,B\in F(X)$ if $d$ satisfies the Manhattan distance measure, then:

$$s(A,B)=2-d((A{\displaystyle \cap }B),[1{]}_X)-d((A{\displaystyle \cap }B),[0{]}_X)$$

(2)

is another normalized similarity measure between sets $A$ and $B$; note that given sets A and B, Equation (2) results in the same measure value as Equation (1).

Proof. 

The proof of Theorem 2 is given in Appendix B. ☐

Now we consider the overlapped discrete data distributions shown in Figure 1, where two data sets $X$ and $Y$ are distributed over the same support in the universe of discourse with 12 data, each with different magnitudes: $X=$ {$x(i)$: 0.5, 0.8, 0.6, 0.3, 0.5, 0.3, 0.2, 0.4, 0.4, 1.0, 0.6, 0.4} and $Y=$ {$y(i)$: 0.2, 0.2, 0.4, 0.4, 0.3, 0.6, 0.7, 0.2, 0.5, 0.8, 0.8, 0.6}, for $i=1,2,\dots ,12$. The similarity calculation between diamond and circle data is carried out with Equations (1) and (2). We explain the computation results in the following. For more details of the computation, readers are referred to [25].

Applying the similarity measure Equation (1) to the data distributions in Figure 1, we obtain:

$$\begin{array}{cc}\hfill s(X,Y)& =1-d(X,X{\displaystyle \cap }Y)-d(Y,X{\displaystyle \cap }Y)\hfill \\ & \hspace{0.17em}=1-\frac{1}{12}(2.9)=0.758\hfill \end{array}$$

(3)

With the similarity measure in Equation (2), we obtain the same result as follows:

$$\begin{array}{cc}\hfill s(X,Y)& =2-d((X{\displaystyle \cap }Y),[1{]}_X)-d((X{\displaystyle \cup }Y),[0{]}_X)\hfill \\ & =2-\frac{1}{12}(7.5+7.4)=0.758\hfill \end{array}$$

(4)

The computational procedures are clear.

Hence, similarity measures in Equations (1) and (2) show their effectiveness.

For comparison, example non-overlapped data distributions are shown in Figure 2. Each of twelve-member sets X and Y has six non-zero membership values, which are distributed differently and without any overlap, but they have the same magnitude distributions as those in Figure 1.

Now, the similarity measure is applied to calculate similarity for non-overlapped data. We demonstrate the usefulness of the similarity measure with examples. Consider the discrete data shown in Figure 2, where two data sets $X$ and $Y$ are illustrated with different combinations as follows:

-

Figure 2a: $X=$ {$x(i)$: 0.5, 0.8, 0.6, 0.0, 0.5, 0.0, 0.0, 0.4, 0.0, 1.0, 0.0, 0.0} and $Y=$ {$y(i)$: 0.0, 0.0, 0.0, 0.4, 0.0, 0.6, 0.7, 0.0, 0.5, 0.0, 0.8, 0.6}

-

Figure 2b: $X=$ {$x(i)$: 0.5, 0.8, 0.6, 0.4, 0.5, 0.0, 0.0, 0.4, 0.0, 0.0, 0.0, 0.0} and $Y=$ {$y(i)$: 0.0, 0.0, 0.0, 0.0, 0.0, 0.6, 0.7, 0.0, 0.5, 1.0, 0.8, 0.6}

where there are no overlaps in positions between non-zero elements of $X$ and $Y$. Next, the conventional similarity measures in Equations (1) and (2) are applied to calculate the similarity between $X$ and $Y$ in Figure 2.

For the data shown in Figure 2a, the similarity calculation between $X$ and $Y$ is derived with Equation (1) as follows:

$$\begin{gathered} s(X,Y)=1-d(X, X{\displaystyle \cap }Y)-d(Y, X{\displaystyle \cap }Y) \\ =1-d(X,{[0]}_X)-d(Y,[0{]}_X) \\ =1-\frac{1}{12}{\displaystyle \sum }_{i}height(x(i))-\frac{1}{12}{\displaystyle \sum }_{i}height(y(i)) \end{gathered}$$

(5)

Note that the similarity calculation for the data shown in Figure 2b results in the same value as that obtained for Figure 2a as long as the data magnitudes are the same.

Because there is no intersection between the two distributions, $X{\displaystyle \cap }Y={[0]}_X$, the similarity measure calculations using Equation (2) for the data shown in Figure 2 are the same as shown below:

$$\begin{array}{cc}\hfill s(X,Y)=2-d& ((X{\displaystyle \cap }Y),[1{]}_X)+d((X{\displaystyle \cap }Y),[0{]}_X)\hfill \\ & =2-d({[0]}_X,[1{]}_X)+d((X{\displaystyle \cap }Y),[0{]}_X)=2-1-d((X{\displaystyle \cap }Y),[0{]}_X)\hfill \\ & =1-\frac{1}{12}{\displaystyle {\displaystyle \sum }_i}height(x(i)+y(i))\hfill \end{array}$$

(6)

Results in Equations (5) and (6) suggest that the similarity between the two non-overlapped data sets is related to the summation of their magnitudes and the independence of their distributions.

Note that the similarity measures in Equations (1) and (2) do not discriminate between the two different non-overlapping data distributions shown in Figure 2. This is because the operations in the definitions of the similarity measures are based on minimum/maximum value comparison in the same support such as $A{\displaystyle \cap }B$ or $A{\displaystyle \cup }B$. Therefore, the design of the similarity measures on non-overlapped data distributions requires a different approach.

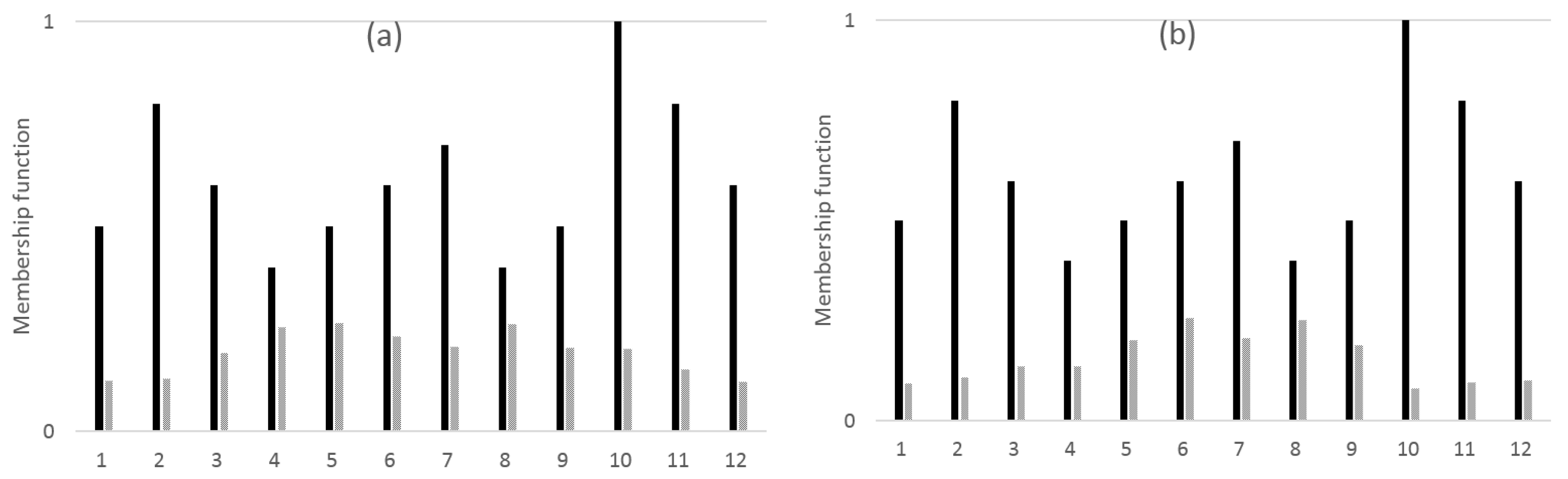
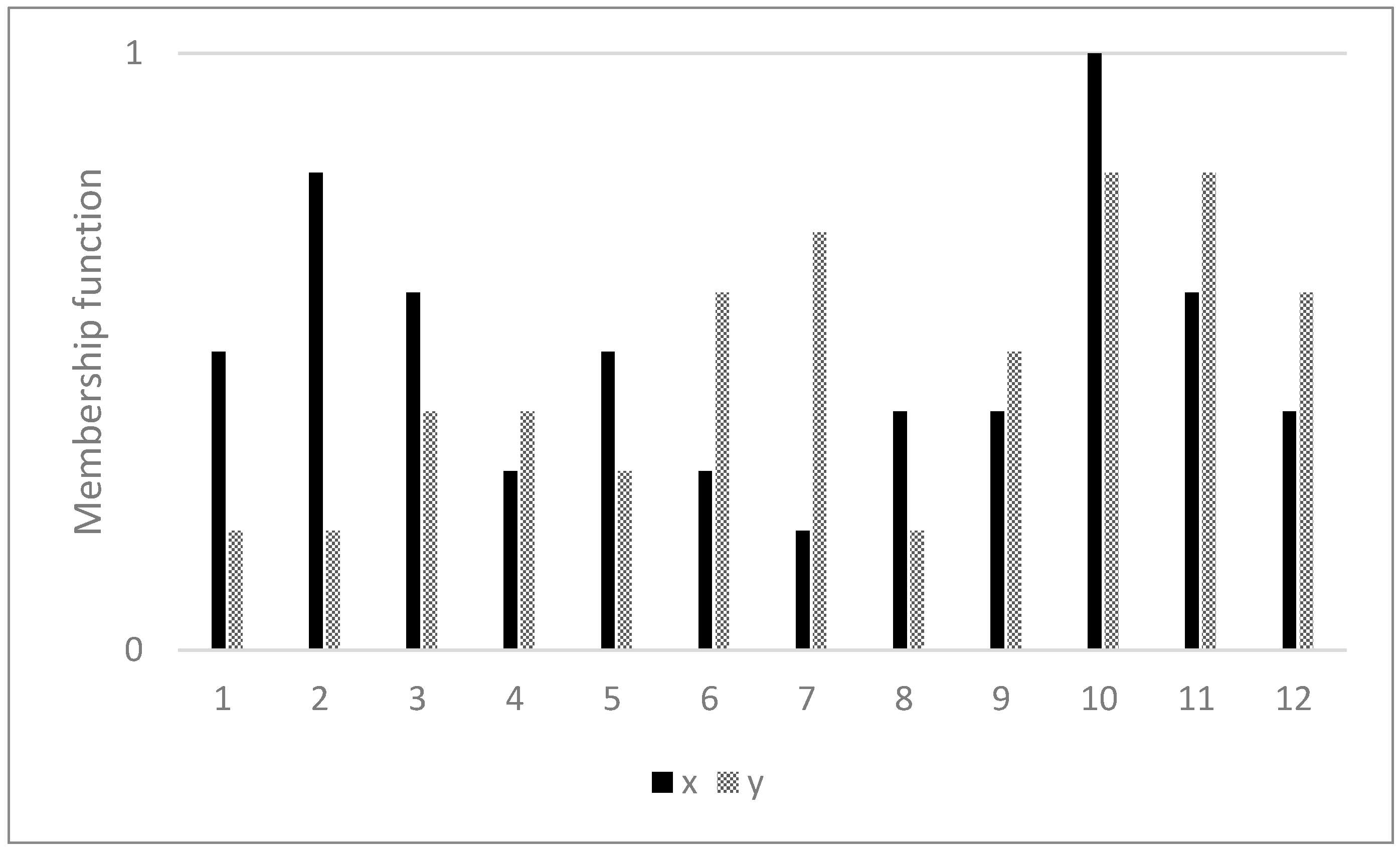
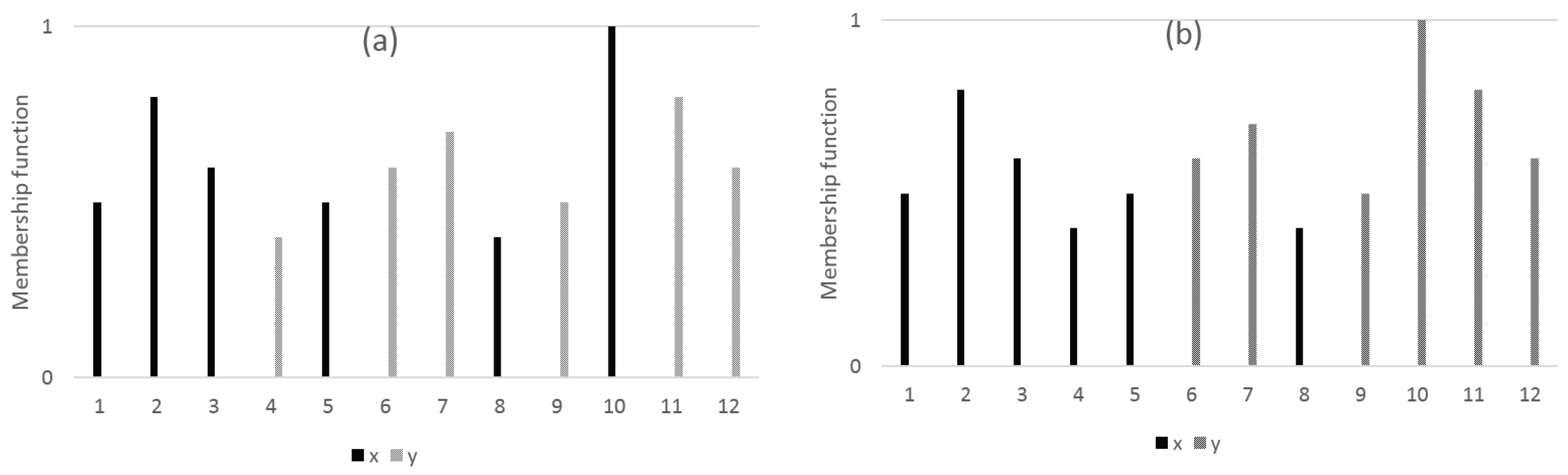
3. Similarity Measure on Non-Overlapped Data

Two approaches for the similarity measure on non-overlapped data distributions are now proposed. First, a conventional similarity measure approach is applied in a novel way to non-overlapping data. In order to apply similarity measures given in Equations (1) or (2) to non-overlapped data distribution (Figure 2), the original data distribution is expressed as an information-related diagram with the proposed measure. Having obtained the information-related graph, we can find the similarity measure between this and the original data distribution.

Second, a new design of a similarity measure on non-overlapping data is carried out. It is based on neighbor information.

3.1. Data Transformation and Application to Similarity Measure

In order to apply a conventional similarity measure to non-overlapped data, we consider both the distance between two different patterns and the difference between two membership values, i.e., for each $x(i)>0, i=1, 2, \dots , 12$:

$${\displaystyle \sum }_{\forall j\in [1,2,\cdots ,12] s.t. y(j)>0}\frac{1}{|i-j|+1}(1-|x(i)-y(i)|)$$

(7)

and for each $y(i)>0,i=1,2,\dots ,12:$

$${\displaystyle \sum }_{\forall j\in [1,2,\cdots 12] s.t. x(j)>0}\frac{1}{|i-j|+1}(1-|x(j)-y(i)|)$$

(8)

where each difference should be satisfied between different patterns. From calculations of the proposed preprocessing, six data are obtained from Equations (7) and (8), respectively.

Following the calculation process described and applying it to each pattern in turn, we obtain the information relationships between different patterns shown in Figure 3.

Next, we apply the similarity measure between the previous pattern of Figure 2 and preprocessing results of Figure 3. Here, the previous pattern is considered in terms of the whole distribution.

Now, conventional similarity measures given in Equations (1) and (2) can be applied to the newly derived data distributions shown in Figure 4, i.e., the union of $X$ and $Y$ (i.e., the black bars in the figure and denoted $\mathit{d}$ below) and the preprocessing results from Figure 3 (i.e., the gray bars in the figure and denoted $p$ below). Equations (1) and (2) become Equations (9) and (10) as follows:

$$s(\mathit{d},p)=1-d(\mathit{d},\mathit{d}{\displaystyle \cap }p)-d(p,\mathit{d}{\displaystyle \cap }p)$$

(9)

$$s(\mathit{d},p)=2-d((\mathit{d}{\displaystyle \cap }p),[1{]}_X)+d((\mathit{d}{\displaystyle \cap }p),[0{]}_X)$$

(10)

The calculation results of Equations (9) and (10) for Figure 4a are given by:

$$\begin{gathered} s(\mathit{d},p)=1-d(\mathit{d},\mathit{d}{\displaystyle \cap }p)+d(p,\mathit{d}{\displaystyle \cap }p) \\ =1-\frac{1}{12}(|0.5-0.1232|+|0.8-0.1284|+|0.6-0.1912|+|0.4-0.2554| \\ +|0.5-0.2632|+|0.6-0.2328|+|0.7-0.206|+|0.4-0.2628|+|0.5-0.2045| \\ +|1.0-0.2004|+|0.8-0.1504|+|0.6-0.12|) \\ =0.5782 \end{gathered}$$

$$\begin{gathered} s(\mathit{d},p)=2-d((\mathit{d}{\displaystyle \cap }p),[1{]}_X)+d((\mathit{d}{\displaystyle \cap }p),[0{]}_X) \\ =2-\frac{1}{12}(0.8768+0.8716+0.8088+0.7446+0.7368+0.7672+0.794+0.7372+0.7955+0.7996+0.8496+0.88) \\ -\frac{1}{12}(0.5+0.8+0.6+0.4+0.5+0.6+0.7+0.4+0.5+1.0+0.8+0.6) \\ =0.5782 \end{gathered}$$

The same result is obtained for both cases.

Applying Equations (9) and (10), we obtain the similarity measure for Figure 4b as follows:

$$\begin{gathered} s(\mathit{d},p)=1-d(\mathit{d},\mathit{d}{\displaystyle \cap }p)-d(p,\mathit{d}{\displaystyle \cap }p) \\ =1-\frac{1}{12}(|0.5-0.094|+|0.8-0.1099|+|0.6-0.1371|+|0.4-0.1354|+|0.5-0.2021|+|0.6-0.2572| +|0.7-0.206|+|0.4-0.2517|+|0.5-0.1879|+|1.0-0.0813|+|0.8-0.0963|+|0.6-0.1015|) \\ =0.5384 \end{gathered}$$

$$\begin{gathered} s(\mathit{d},p)=2-d((\mathit{d}{\displaystyle \cap }p),[1{]}_X)+-d((\mathit{d}{\displaystyle \cup }p),[0{]}_X) \\ =2-\frac{1}{12}(0.906+0.8901+0.8629+0.8646+0.7979+0.7428+0.794+0.7483+0.8121+0.9187+0.9037+0.8985)-\frac{1}{12}(0.5+0.8+0.6+0.4+0.5+0.6+0.7+0.4+0.5+1.0+0.8+0.6) \\ =0.5384 \end{gathered}$$

From a heuristic point of view, it is clear that the similarity between X and Y in Figure 2a is higher than that in Figure 2b. The calculation results clearly show this similarity.

3.2. Similarity Measure Design Using Neighbor Information

Here, we give a brief introduction of the similarity measure on non-overlapped data proposed in [21,22] and compare its results with those obtained in Section 3.1. We assume that the similarity measure is affected from neighbor data information as in Section 3.1. Theorem 3 provides a similarity measure on non-overlapped data, which has been proved in [21,22].

Theorem 3.

Given fuzzy sets $A$ and $B$, let $\tilde{A}$ and $\tilde{B}$ be their supports, respectively. If $d$ is the Manhattan distance measure, then:

$$s(A,B)=1-|s_{\tilde{A}}-s_{\tilde{B}}|$$

(11)

is a similarity measure between set $A$ and $B$, where:

$$S_{\tilde{A}}=d\left(\left(\tilde{A}{\displaystyle \cap }(A{\displaystyle \cup }B)\right),{[1]}_X\right)$$

and:

$$S_{\tilde{B}}=d\left(\left(\tilde{B}{\displaystyle \cap }(A{\displaystyle \cup }B)\right),{[1]}_X\right)$$

The similarity measure given in Equation (10) is designed using a distance measure. Equation (10) is applied to the non-overlapped data in Figure 2, and calculation results are given below.

For the data distribution shown in Figure 2a:

$$s(A,B) =1-\left|d\left(\left(\tilde{A}{\displaystyle \cap }(A{\displaystyle \cup }B)\right),{[1]}_X\right)-d\left(\left(\tilde{B}{\displaystyle \cap }(A{\displaystyle \cup }B)\right),{[1]}_X\right)\right|=0.967$$

(12)

For the data distribution shown in Figure 2b:

$$s(A,B) =1-\left|d\left(\left(\tilde{A}{\displaystyle \cap }(A{\displaystyle \cup }B)\right),{[1]}_X\right)-d\left(\left(\tilde{B}{\displaystyle \cap }(A{\displaystyle \cup }B)\right),{[1]}_X\right)\right|=0.833$$

(13)

The calculation results show that the similarity measure designed for non-overlapped data gives similar results; the value of the similarity measure on the data shown in Figure 4a is higher than that on the data shown in Figure 4b, i.e., 0.967 versus 0.833. Calculation results are shown in Appendix C. Therefore, the similarity measure given in Equation (10) enables the comparison of similarity on non-overlapped data. Note that the first distribution pair shows a higher similarity even when we decide it heuristically.

4. Conclusions

In this paper, we have designed similarity measures on non-overlapped data and demonstrated their effectiveness with illustrative examples.

First, we presented conventional similarity measures on overlapped data and shown their usefulness with an overlapped data distribution. Calculation results have shown that they are effective for overlapped data. However, similarity calculation results on non-overlapped data are the same even for different distribution pairs, which means that they cannot provide discrimination on non-overlapped data. From the example, therefore, we have concluded that we cannot directly apply those similarity measures designed for overlapped data to non-overlapped data.

Second, in order to utilize conventional similarity measures, we proposed a new measure with nearest information and derived information relation. The result is illustrated in Figure 3. This makes it possible to apply conventional similarity measures to non-overlapped data. Calculation results show the difference for data distributions shown in Figure 2. We have also proposed another similarity measure based on neighbor information. Its effectiveness is also demonstrated through an illustrative example. Note that, even though the calculation results are not identical to those of the first approach, they show a similar pattern in discriminating between two different data distributions.

The results from this paper show that it is possible to design a similarity measure applicable to both overlapped and non-overlapped data, which can discriminate between two different data distributions even in the case of non-overlapped data.

Note that our work reported in this paper could be extended for applications in the analysis of big data in the future.