A Mathematical Model of Gas and Water Flow in a Swelling Geomaterial—Part 1. Verification with Analytical Solution
Abstract
:1. Introduction
2. Mathematical Model
2.1. Study Overview
- derivation of analytical solutions for 1D steady-state and 1D transient single-phase gas flow (i.e., assuming immobile liquid phase) through a low-permeable geomaterial problem based on the linear poro-elastic hydromechanical mathematical model proposed in Dagher et al. [9].
- verification of the numerical model by comparing the results of the numerical simulations performed in COMSOL® Multiphysics® finite element method (FEM) software (Version 5.4a, COMSOL AB, Boston, MA, USA) to the results of the analytical steady-state and transient solutions.
2.2. Assumptions for Poromechanical Behaviour
2.2.1. Bishop’s Modified Effective Stress Principle
- is the effective stress tensor (Pa)
- is the Kronecker delta (identity tensor) (adimensional) and
- is the porefluid pressure (Pa)
- is the poregas pressure (Pa)
- is the porewater pressure (Pa)
- is the net normal stress (Pa)
- is the matric suction (Pa)
- is a parameter related to the degree of saturation of the soil (unitless)
2.2.2. Poro-Elastic Stress-Strain Relation
2.3. Constitutive Relations for the Hydraulic Behaviour
- van Genuchten equation for the soil-water characteristic curve [9].
- Huang et al. [21] equation depicting the relationship between the AEV and void ratio.
- Darcy’s law for two-phase flow.
- Equation for the effective diffusivity for gas dissolved in water through porous media, utilizing the Millington and Quirk model to define the tortuosity as a function of the degree of saturation, and the porosity, [22].
2.4. Governing Equations for Two-Phase Flow through a Linear Elastic Geomaterial
2.4.1. Conservation of Water Mass
- density of water phase (kg m−3)
- is the porewater pressure (Pa)
- intrinsic permeability tensor of the porous medium (m2)
- relative permeability of the water phase (unitless)
- dynamic viscosity of the water phase (Pa s or kg m−1 s−1)
- is the acceleration due to gravity (m s−2)
- porosity (m3 voids · m−3 total)
- is the degree of saturation of water
- is the matric suction (Pa)
- is the bulk modulus of the water phase (Pa s or kg m−1 s−1)
- is the volumetric strain (unitless)
- is the displacement (m)
- is time (s).
2.4.2. Conservation of Gas Mass
- density of the gas phase (kg m−3)
- is the poregas pressure (Pa)
- relative permeability of the gas phase (unitless)
- dynamic viscosity of the gas phase (Pa s or kg m−1 s−1)
- is Henry’s coefficient (kg species A m−3 in aqueous phase kg−1 species A m3 in gas phase)
- is the effective diffusivity of gas dissolved in water through porous media (m2 s−1)
- is the bulk modulus of the gas phase (Pa)
2.4.3. Conservation of Momentum (Quasi-Static Equilibrium)
- is the stress tensor (Pa)
- is the volumetric body force tensor (kg m−2 s−2)
- represents the change in normal and shear stresses across the soil element (kg m−2 s−2)
3. Verification Study Analysis
3.1. Analysis Overview
- immobile liquid phase
- no dissolution of gas into and no diffusion gas through the porewater
- constant gas permeability
- constant gas density
- constant fluid viscosity
- constant degree of saturation of water
- role of suction ignored
- role of gravity ignored
- isothermal process
- constant volume boundary condition
3.2. Analytical Solutions for Two-Phase Flow through a Linear Poro-Elastic Geomaterial
3.2.1. One-Dimensional (1D) Steady-State Gas Flow Problem
- is atmospheric pressure (Pa)
- is the length of the soil specimen (m)
3.2.2. 1D Transient Gas Flow Problem
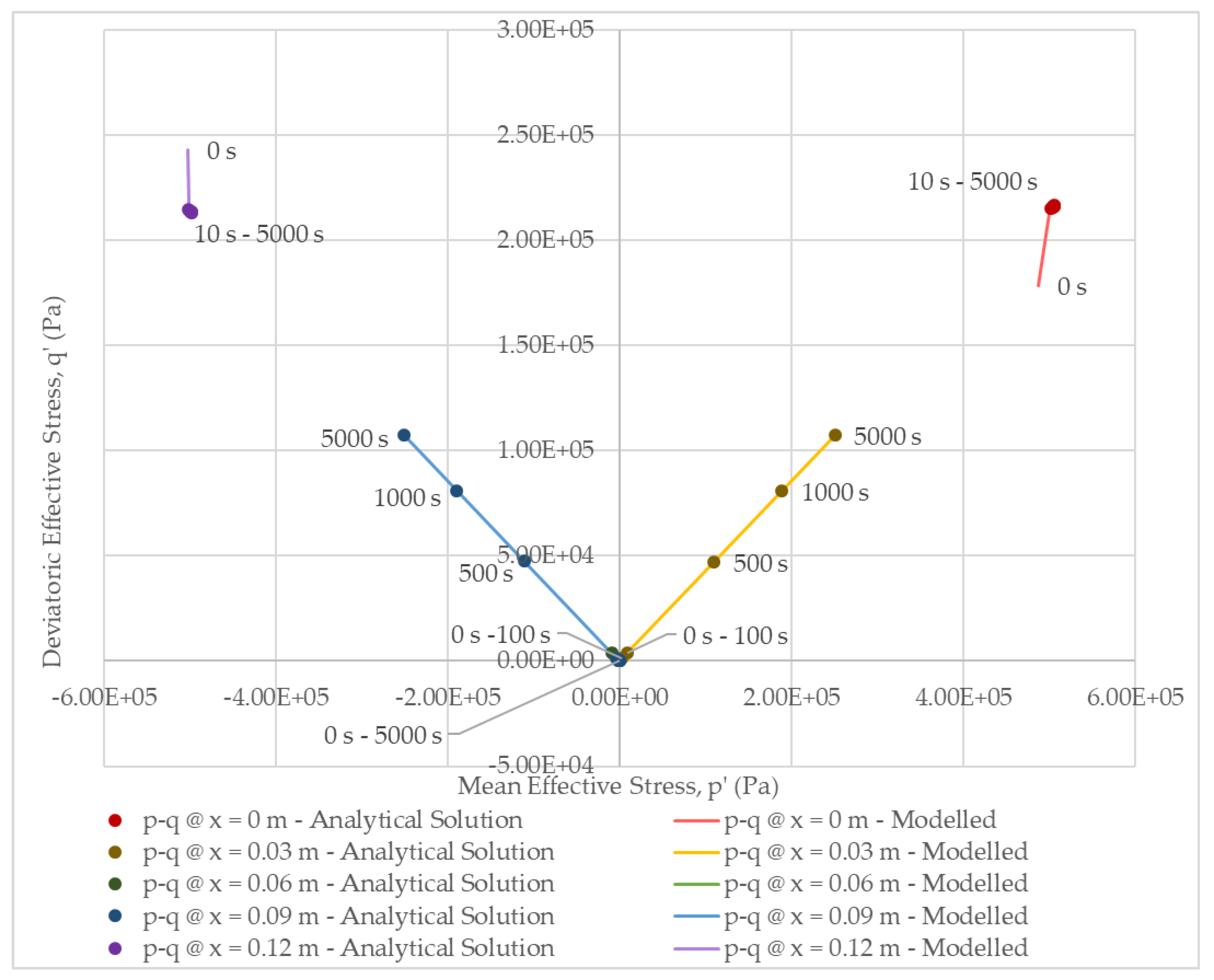
3.2.3. Mean Stress and Deviatoric Stress
3.3. Numerical Model Description
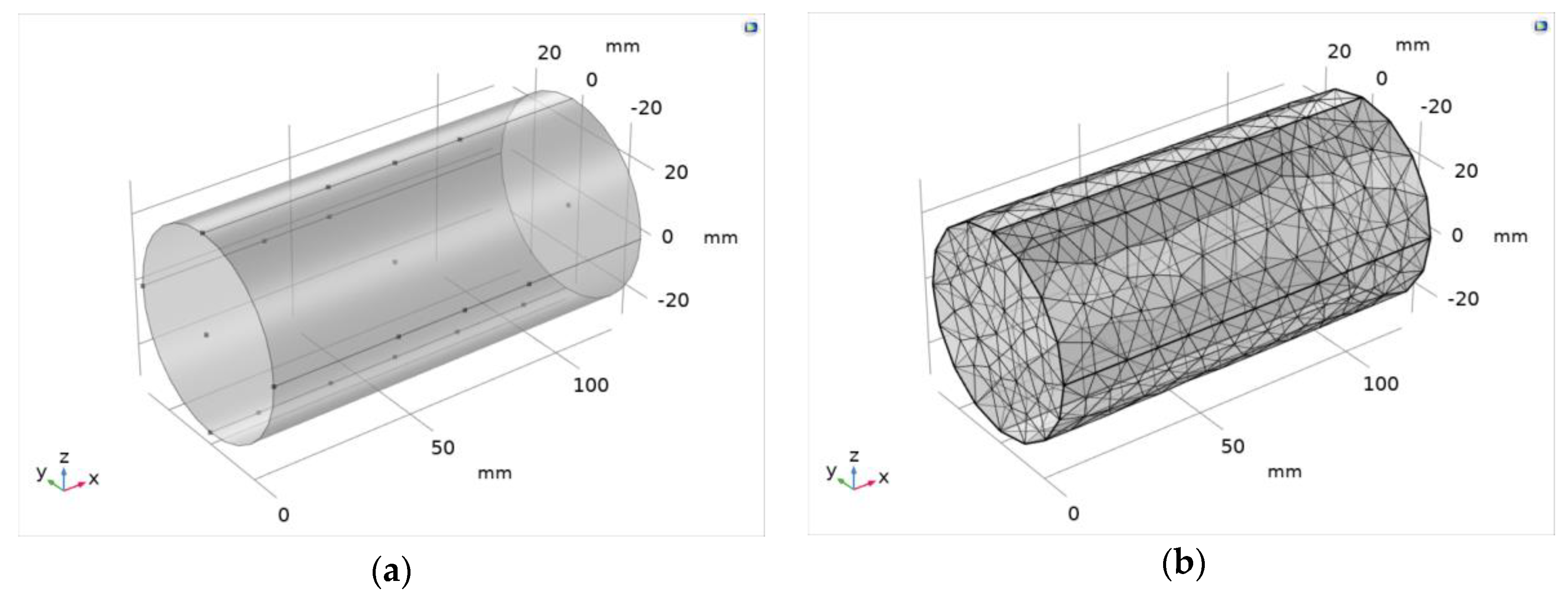
Model Geometry and Mesh
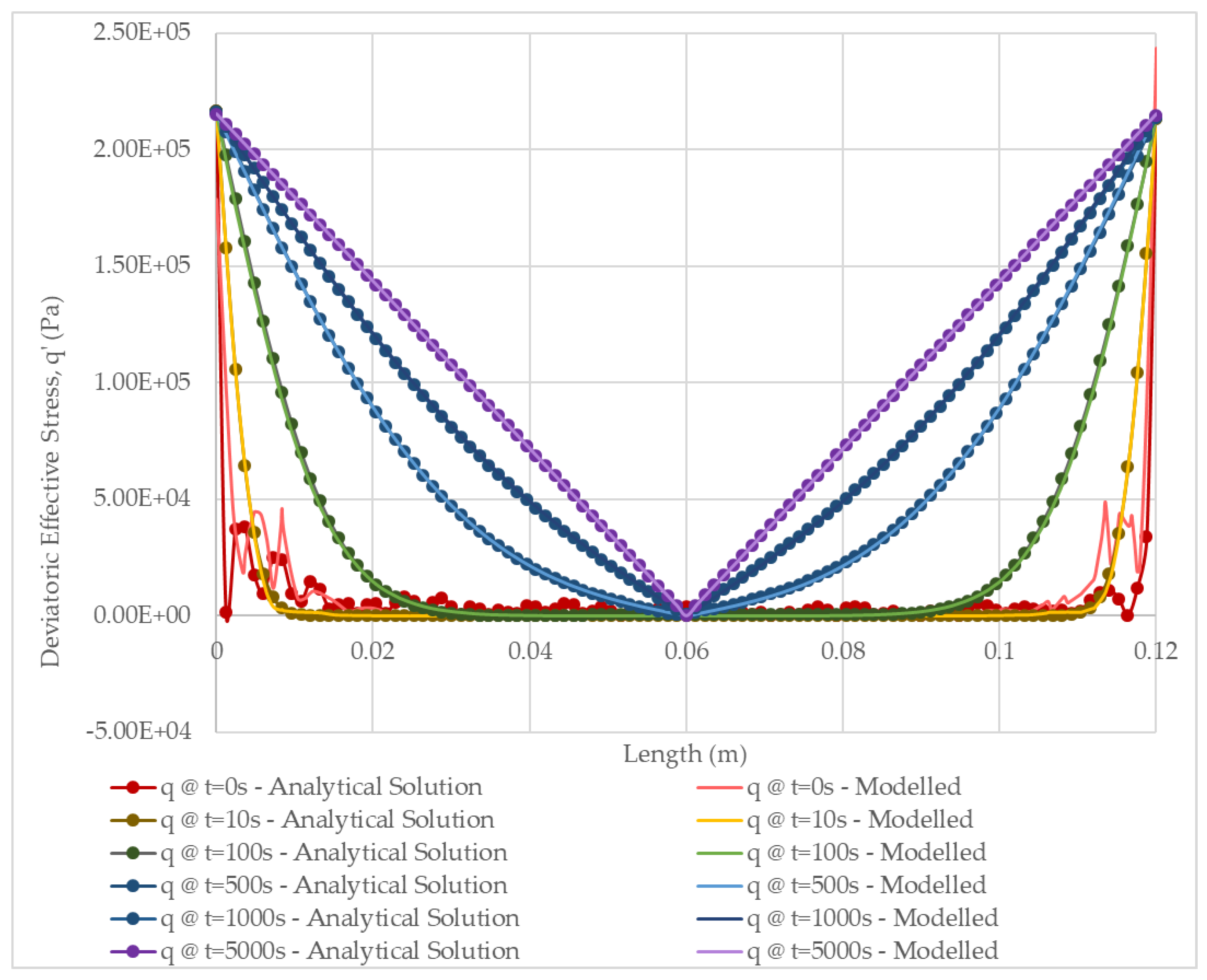
3.4. Results and Discussion
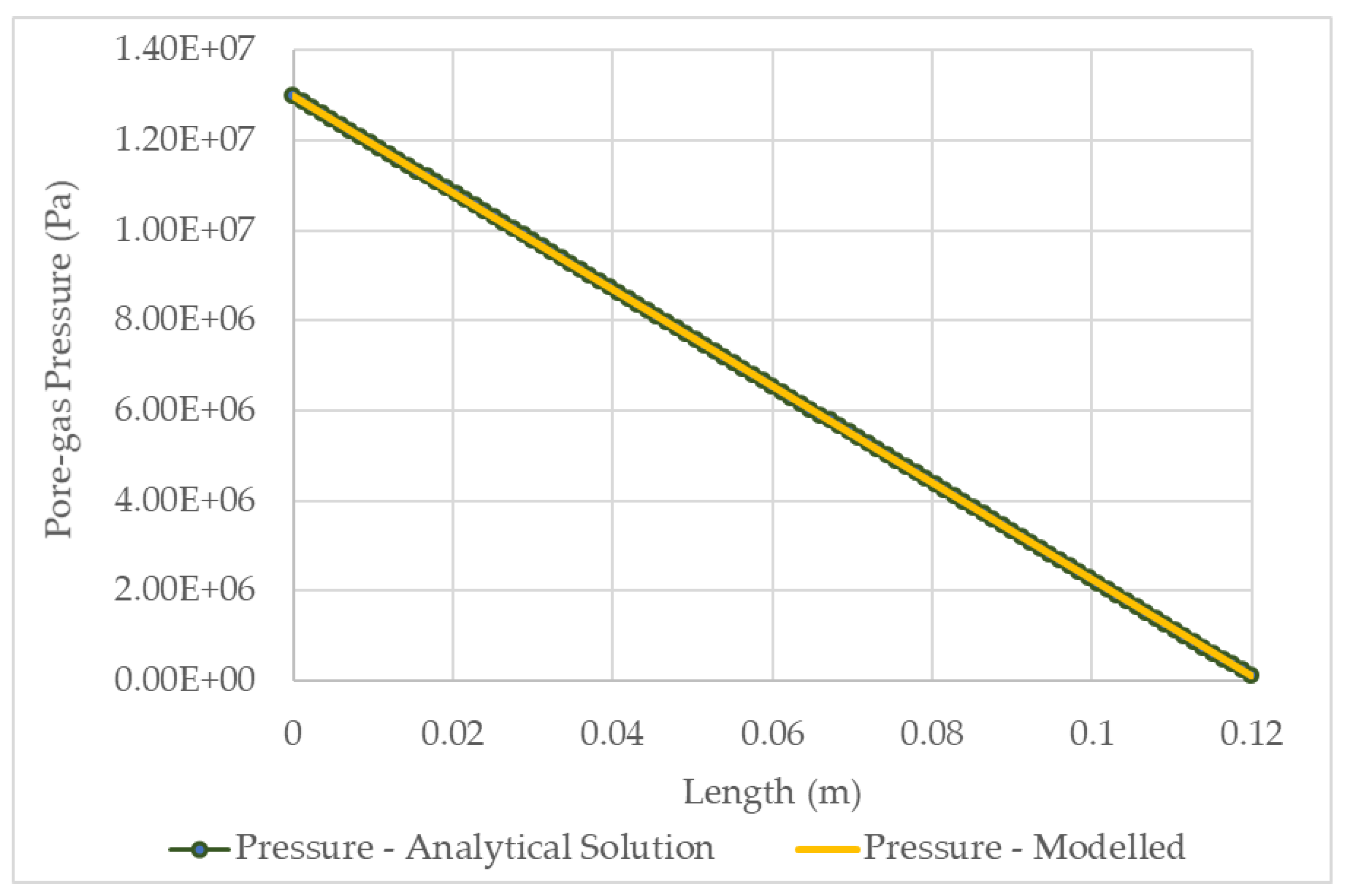
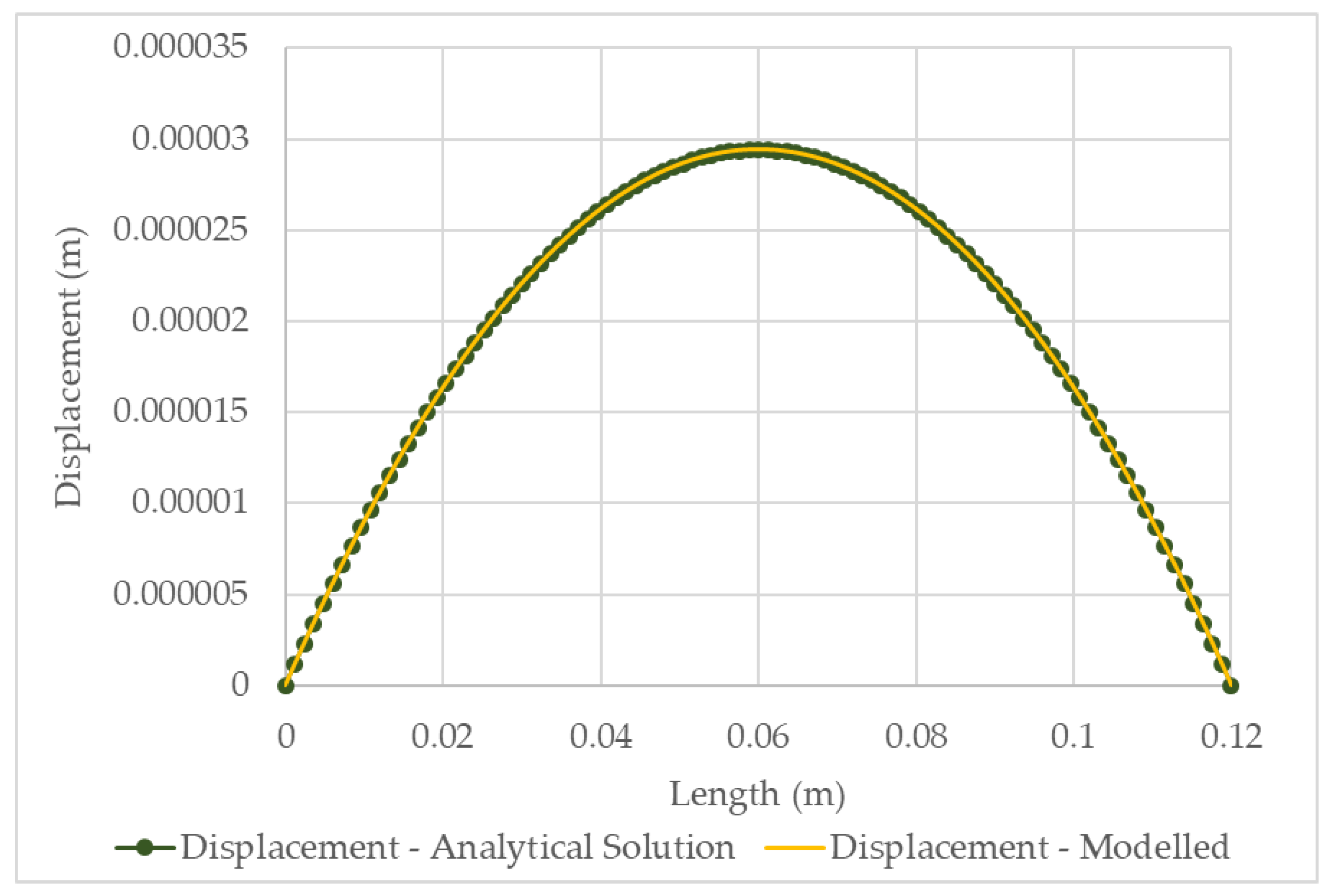
3.4.1. Steady-State Solution
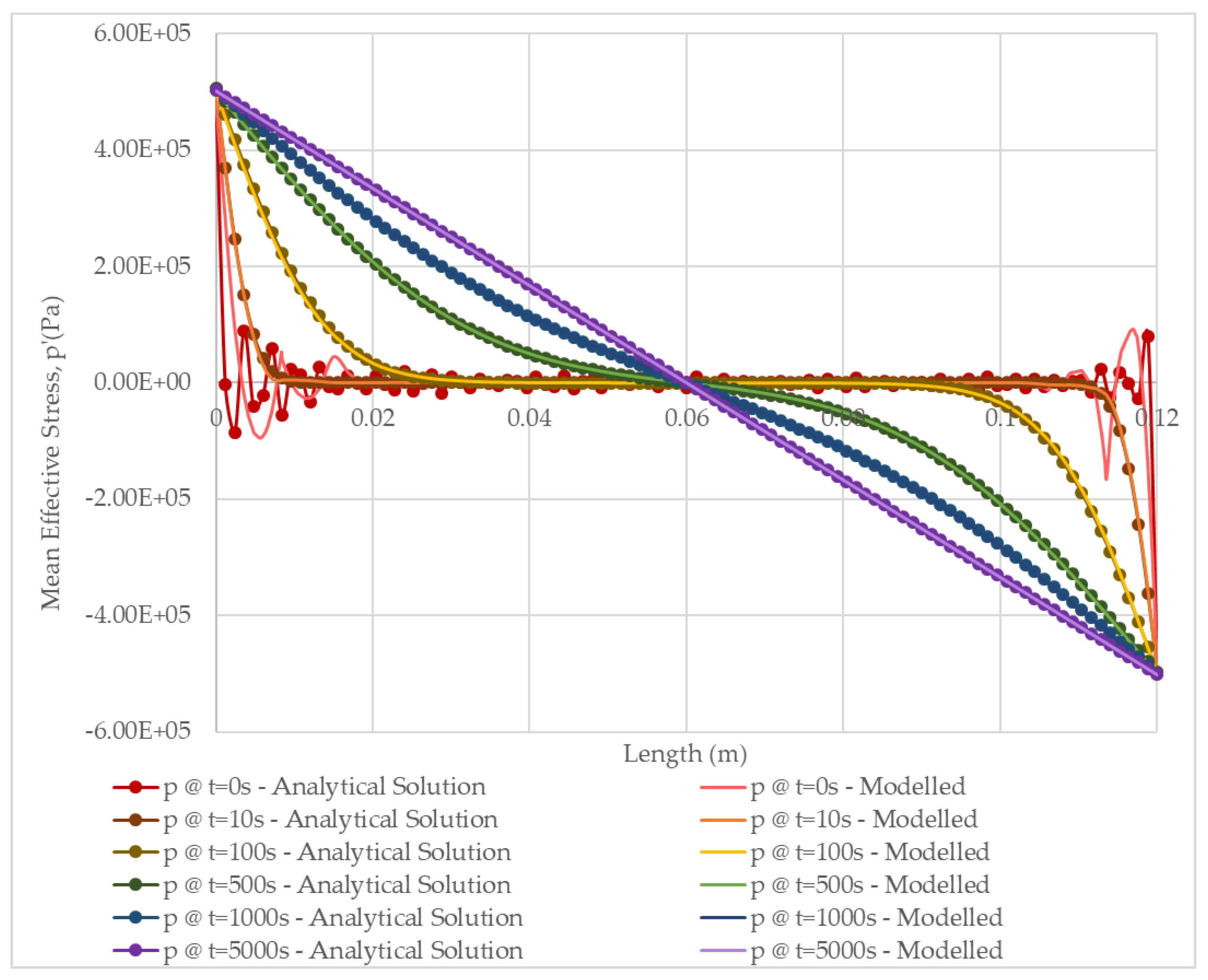
3.4.2. Transient Solution
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Analytical Solutions for 1-Dimensional Gas Flow in a Linear Elastic Porous Media
A.1. Problem Statement

- immobile liquid phase
- no dissolution of gas into and no diffusion gas through the porewater
- constant gas permeability
- constant gas density
- constant degree of saturation of water
- role of suction ignored
- role of gravity ignored
- isothermal process
- constant volume boundary condition
A.2. Steady-State Solution
A.2.1. Governing Equations
A.2.2. Formulation of the Analytical Solution to the Conservation of Mass Equation
A.2.3. Formulation of the Analytical Solution to the Conservation of Momentum Equation
A.2.4. Final Analytical Solution
A.3. Analytical Solution for 1-Dimensional Transient Gas Flow in a Linear Elastic Porous Media
A.3.1 Governing Equations
A.3.2 Formulation of the Analytical Solution to the Conservation of Mass Equation
- C1 is the concentration at boundary x = 0
- C2 is the concentration at boundary x = L
- C0 is the initial uniform concentration
A.3.3 Formulation of the Analytical Solution to the Conservation of Momentum Equation
A.3.4. Final Analytical Solution
References
- CNSC. Regulatory Guide G-320, Assessing the Long Term Safety of Radioactive Waste Management; CNSC: Ottawa, ON, Canada, 2006.
- Norris, S. EC FORGE project: Updated consideration of gas generation and migration in the safety case. In Gas Generation and Migration in Deep Geological Radioactive Waste Repositories; Shaw, R.P., Ed.; Geological Society: London, UK, 2015; Special Publications; Volume 415, pp. 241–258. [Google Scholar]
- Shaw, R.P. The Fate of Repository Gases (FORGE) project. In Gas Generation and Migration in Deep Geological Radioactive Waste Repositories; Shaw, R.P., Ed.; Geological Society: London, UK, 2015; Special Publications, 415; pp. 1–7. [Google Scholar]
- Cuss, R.; Harrington, J.; Giot, R.; Auvray, C. Experimental observations of mechanical dilation at the onset of gas flow in Callovo-Oxfordian claystone. In Clays in Natural and Engineered Barriers for Radioactive Waste Confinement; Norris, S., Bruno, J., Cathelineau, M., Delage, P., Fairhurst, C., Gaucher, E.C., Höhn, E.H., Kalinichev, A., Lalieux, P., Sellin, P., Eds.; Geological Society: London, UK, 2014; Volume 400, pp. 507–519. [Google Scholar]
- Ahusborde, E.; Amaziane, B.; Jurak, M. Three-dimensional numerical simulation by upscaling of gas migration through engineered and geological barriers for a deep repository for radioactive waste. In Gas Generation and Migration in Deep Geological Radioactive Waste Repositories; Shaw, R.P., Ed.; Geological Society: London, UK, 2015; Special Publication, 415; pp. 123–141. [Google Scholar]
- Horseman, S.T.; Harrington, J.F.; Sellin, P. Gas migration in clay barriers. Eng. Geol. 1999, 54, 139–149. [Google Scholar] [CrossRef]
- Sellin, P.; Leupin, O.X. The use of Clay as an Engineered Barrier in Radioactive-Waste Management—A Review. Clays Clay Miner. 2013, 61, 477–498. [Google Scholar] [CrossRef]
- Sellin, P. Experiments and Modelling on the behaviour of EBS. Reprot D 2014, 3, 38. [Google Scholar]
- Dagher, E.E.; Nguyen, T.S.; Sedano, J.A.I. Development of a mathematical model for gas migration (two-phase flow) in natural and engineered barriers for radioactive waste disposal. In Multiple Roles of Clays in Radioactive Waste Confinement; Norris, S., Neeft, E., van Geet, M., Eds.; Geological Society: London, UK, 2018; Special Publications. [Google Scholar]
- Nash, P.J.; Swift, B.T.; Goodfield, M.; Rodwell, W.R. Modelling Gas Migration in Compacted Bentonite: A Report Produced for the GAMBIT Club; POSIVA: Helsinki, Finland, 1998. [Google Scholar]
- Hoch, R.; Cliffe, K.A.; Swift, B.T.; Rodwell, W.R. Modelling Gas Migrationin Compacted Bentonite: GAMBIT Club Phase 3 Final Report; POSIVA: Olkiluoto, Finland, 2004. [Google Scholar]
- Fall, M.; Nasir, O.; Nguyen, T. A coupled hydro-mechanical model for simulation of gas migration in host sedimentary rocks for nuclear waste repositories. Eng. Geol. 2014, 176, 24–44. [Google Scholar] [CrossRef] [Green Version]
- Harrington, J.F.; Horseman, S.T. Gas transport properties of clays and mudrocks. In Muds and Mudstones: Physical and Fluid Flow Properties; Aplin, A.C., Fleet, A.J., MacQuaker, J.H., Eds.; The Geological Society of London: London, UK, 1999; Volume 158, pp. 107–124. [Google Scholar]
- Horseman, S.T.; Harrington, J.F.; Sellin, P. Water and Gas Movement in Mx80 Bentonite Buffer Clay. Symposium on the Scientific Basis for Nuclear Waste Management XXVII (Kalmar). Mater. Res. Soc. 2003, 807, 715–720. [Google Scholar] [CrossRef]
- Harrington, J.F.; de la Vaissiére, R.; Noy, D.J.; Cuss, R.J.; Talandier, J. Gas flow in Callovo-Oxfordian claystone (COx): results from laboratory and field-scale measurements. Mineral. Mag. 2012, 76, 3303–3318. [Google Scholar] [CrossRef] [Green Version]
- Graham, C.C.; Harrington, J.F.; Cuss, R.J.; Sellin, P. Gas migration experiments in bentonite: implications for numerical modelling. Mineral. Mag. 2012, 76, 3279–3292. [Google Scholar] [CrossRef] [Green Version]
- Bennett, D.P.; Cuss, R.J.; Vardon, P.J.; Harrington, J.F.; Sedighi, M.; Thomas, R.H. Exploratory data analysis of the Large Scale Gas Injection Test (Lasgit) dataset, focusing on ’second-order’ events around macro-scale gas flows. In Gas Generation and Migration in Deep Geological Radioactive Waste Repositories; Shaw, R.P., Ed.; Geological Society: London, UK, 2015; Special Publications, 415; pp. 225–239. [Google Scholar]
- Marschall, P.; Horseman, S.; Gimmi, T. Characterisation of Gas Transport Properties of the Opalinus Clay, a Potential Host Rock Formation for Radioactive Waste Disposal. Oil Gas Sci. Technol. Rev. IFP 2005, 60, 121–139. [Google Scholar] [CrossRef] [Green Version]
- Khalili, N.; Khabbaz, M.H. A unique relatiship for χ for the determination of the shear strength of unsaturated soils. Géotechnique 1998, 48, 681–687. [Google Scholar] [CrossRef]
- Nguyen, T.; Le, A. Simultaneous gas and water flow in a damage-susceptible bedded argillaceous rock. Can. Geotech. J. 2015, 52, 18–32. [Google Scholar] [CrossRef]
- Huang, S.; Barbour, S.L.; Fredlund, D.G. Development and verification of a coefficient of permeability function for a deformable unsaturated soil. Candian Geotech. J. 1998, 35, 411–425. [Google Scholar] [CrossRef]
- Ho, C.K.; Webb, S.W. (Eds.) Gas Transport in Porous Media; Springer: Dordrecht, The Netherlands, 2006. [Google Scholar]
- Pall, R.; Moshenin, N.N. Permeability of Porous Media as a Function of Porosity and Particle Size Distribution. Trans. Asae 1980, 23, 742–745. [Google Scholar] [CrossRef]
- Carman, P.C. Flow of Gases Through Porous Media; Academic Press Inc.: New York, NY, USA, 1956. [Google Scholar]
- Crank, J. The Mathematics of Diffusion, 2nd ed.; Clarendon Press: Oxford, UK, 1975. [Google Scholar]
- Daniels, K.A.; Harrington, J.F. The Response of Compact Bentonite during a 1D Gas. Flow Test., British Geological Survey Open Report, OR/17/067; British Geological Survey: Nottingham, UK, 2017. [Google Scholar]





| Parameter Name | Symbol | Value | Units |
|---|---|---|---|
| Length | 0.12 | m | |
| Injection poregas pressure boundary condition | 1.30 × 107 | Pa | |
| Atmospheric gas pressure boundary condition | 1.01 × 105 | Pa | |
| Initial uniform pore-gas pressure (for transient gas flow problem) | 6.55 × 106 | Pa | |
| Density of bentonite | 1526 | kg m−3 | |
| Young’s Modulus | 3.07 × 108 | Pa | |
| Poisson’s ratio (nu) | 0.4 | - | |
| Porosity | 0.44 | - | |
| Intrinsic permeability | 3.40 × 10−21 | m2 | |
| Dynamic viscosity | 2.00 × 10−5 | Pa s | |
| Degree of saturation | 0.9 | - | |
| Air-entry value | 1 × 107 | Pa | |
| Constant porewater pressure 1 | 1.0 × 106 | Pa | |
| Relative gas permeability 1 | 0.03 | - | |
| Chi factor 1 | 0.9 | - |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dagher, E.E.; Infante Sedano, J.Á.; Nguyen, T.S. A Mathematical Model of Gas and Water Flow in a Swelling Geomaterial—Part 1. Verification with Analytical Solution. Minerals 2020, 10, 30. https://doi.org/10.3390/min10010030
Dagher EE, Infante Sedano JÁ, Nguyen TS. A Mathematical Model of Gas and Water Flow in a Swelling Geomaterial—Part 1. Verification with Analytical Solution. Minerals. 2020; 10(1):30. https://doi.org/10.3390/min10010030
Chicago/Turabian StyleDagher, Elias Ernest, Julio Ángel Infante Sedano, and Thanh Son Nguyen. 2020. "A Mathematical Model of Gas and Water Flow in a Swelling Geomaterial—Part 1. Verification with Analytical Solution" Minerals 10, no. 1: 30. https://doi.org/10.3390/min10010030





