Mixture of Akash Distributions: Estimation, Simulation and Application

Abstract

In this paper, we propose a two-component mixture of Akash model (TC-MAM). The behavior of TC-MAM distribution has been presented graphically. Moment-based measures, including skewness, index of dispersion, kurtosis, and coefficient of variation, have been determined and hazard rate functions are presented graphically. The probability generating function, Mills ratio, characteristic function, cumulants, mean time to failure, and factorial moment generating function are all statistical aspects of the mixed model that we explore. Furthermore, we figure out the relevant parameters of the mixture model using the most suitable methods, such as least square, weighted least square, and maximum likelihood mechanisms. Findings of simulation experiments to examine behavior of these estimates are graphically presented. Finally, a set of data taken from the real world is examined in order to demonstrate the new model’s practical perspectives. All of the metrics evaluated favor the new model and the superiority of proposed distribution over mixture of Lindley, Shanker, and exponential distributions.

1. Introduction

In most reliability scenarios, data are modelled using a single parametric model. However, in certain circumstances, a population can be split into many subgroups, each showing a particular category of collapse. Finite mixture models serve a significant role in modelling such diverse data. Biology, business, engineering, healthcare, genetics, marketing, real-world applications, and social sciences all benefit from finite mixture models. Mixture models are created by varying the proportions of two or more models to generate a new distribution with novel properties. Consequently, it is essential to examine the statistical characteristics of the suggested mixture model and employ the suitable methods for estimating the unexplained parameters. Mixture models are used in a diversity of applications, such as clustering and classification [1,2,3,4]. Sultan et al. [5] proposed a mix of inverse Weibull models and utilized density and hazard function graphs to study some of its features. The conventional characteristics of the concoction of Burr XII and Weibull distributions were examined by [6]. Recently, the authors [7,8], Ateya [9], Mohammadi et al. [10], and Al-Moisheer et al. [11] are among the scientists who study mixture modelling in a variety of contexts.

Many applied sciences, including medical, engineering, insurance, and finance, rely on lifetime data modelling and analysis. Some of the continuous distributions used to explain lifetime data are Weibull, gamma, exponential, lognormal, and Lindley, as well as their generalizations. Since many investigators have employed Lindley distribution to predict lifetime data, and Hussain [12] has demonstrated that Lindley model is effective for stress-strength dependability modelling, Lindley model may not be suitable for describing real-world data in many cases. Shanker [13] developed a novel model by using a two-component concoction of an exponential model $\left(\vartheta \right)$ and a gamma model $\left(3,\vartheta \right)$ to have a unique distribution that is more flexible than Lindley and exponential distribution for modelling lifespan data in terms of dependability and hazard rate shapes. Shanker et al. [14] have devised and addressed the concept of modelling lifetime data using one parameter families of distributions, such as Akash, exponential, and Lindley distributions. Many lifetime datasets are employed to exhibit its adaptability over the exponential distribution. Shanker and Shukla [15] examined the two-parameter Akash model and determined its statistical characteristic, estimation problem, and application to it. As a reason, the Akash distribution can be used as an alternate lifetime model in reliability analysis.

The maximal likelihood estimation (MLE) is well-known estimation approach. Despite the fact that MLE is efficient and has strong conceptual features, there is confirmation that it does not work well, especially with small samples. As a result, different estimation approaches have been offered in the studies as options to conventional method. The weighted least-squares estimation (WLSE), L-moments estimator (LME), percentile estimator (PCE) and least squares estimator (LSE) are among the most frequently recommended. These approaches, in general, do not possess desirable theoretical features, but they can offer better estimates of unknown parameters in specific instances than the MLE. Various estimating approaches for many models have been investigated in the studies, as illustrations [16,17,18,19,20,21]. The goal of this research is to give a mechanism for expert statisticians to choose the best evaluation method for the Two-Component Mixture of Akash Model (TC-MAM). In this investigation, we estimate the TC-MAM using LSE and WLSE, in conjunction to MLE.

Our goal in this investigation is to develop a novel mixture model for modeling real lifespan datasets from various disciplines of knowledge that is better fitting than mixture of Shanker, exponential and Lindley distributions. The TC-MAM model has an advantage over the Shanker and exponential models because the exponential distribution has a constant hazard rate function and the Shanker model has an increasing hazard rate function, whereas the failure rate function for a TC-MAM model exhibits monotonically increasing, modified declining, decreasing–increasing–decreasing (DID), declining–increasing (DI), and upside-down bathtub behavior. The novel TC-MAM is being developed in particular to offer a novel flexible parametric model for modeling complex data that emerges in dependability research, investigation of lifespan, quality control, statistical mechanics, economics, biological investigations, and other fields. The purpose is to provide a novel model for lifespan analysis that can handle various types of failure rates, as well as various close form features of novel model with simple physical interpretations.

The originality of this research is due to the fact that we present a thorough explanation of the statistical aspects of TC-MAM in the hopes of attracting more applications in lifespan analysis. Additionally, as far as we know, no investigation has been performed to evaluate all of these estimators of the TC-MAM, as well as their mathematical and statistical features and assessment methods to estimate of unexplained parameters of TC-MAM. For various sample sizes and parametric values, we demonstrate how alternative frequentist estimators of the suggested distribution work.

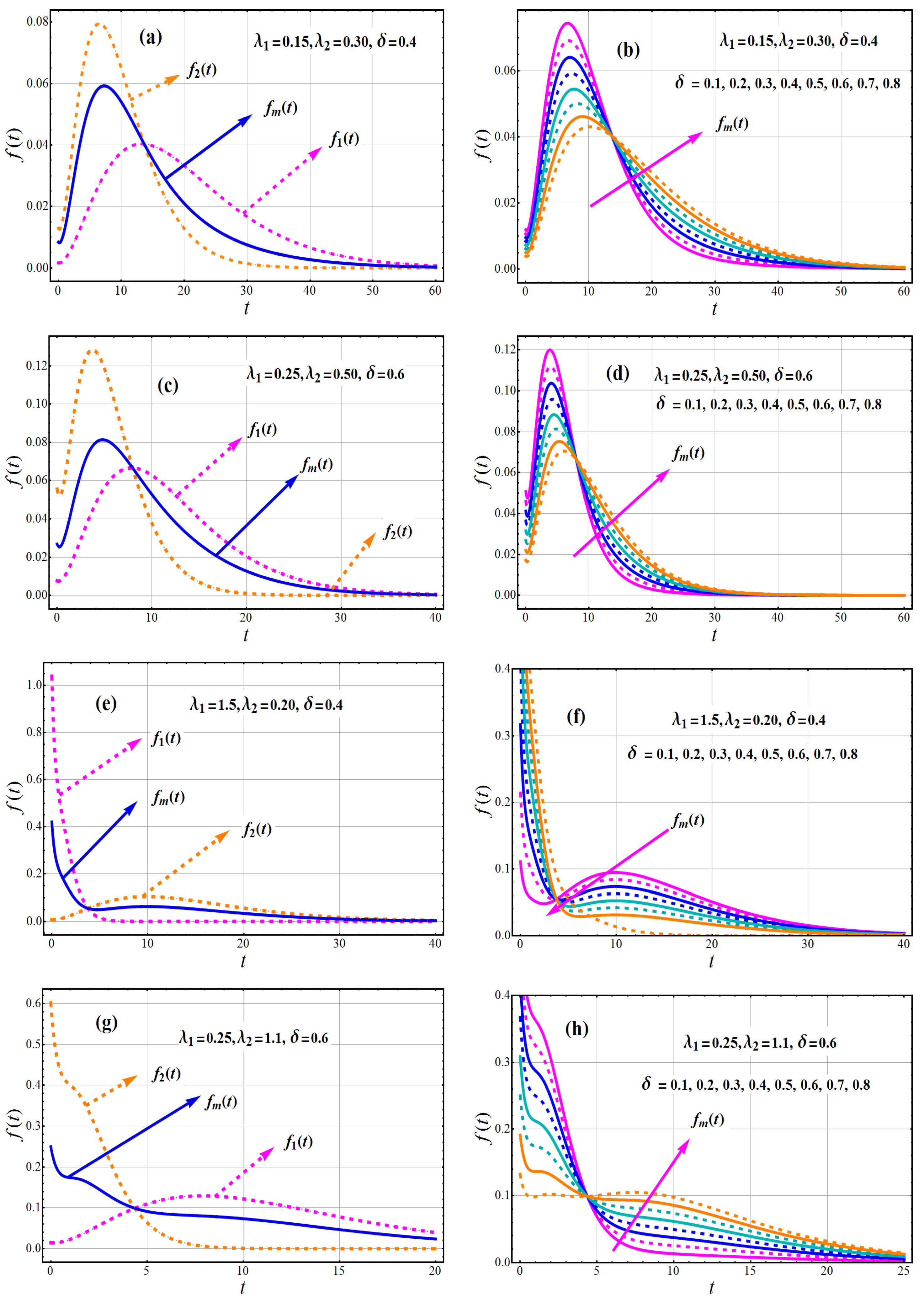
2. The Two-Component Mixture of Akash Model

A $r.v.$ T is stated to have a TC-MAM if its PDF and CDF can be integrated as:

$$\begin{array}{ccc}\hfill f\left(\left.t\right|\varpi \right)& =& \delta f_1\left(\left.t\right|{\lambda }_1\right)+\tilde{\delta }{f}_2\left(\left.t\right|{\lambda }_2\right),\tilde{\delta }=1-\delta ,t,{\lambda }_i>0,i=1,2.\hfill \end{array}$$

(1)

$$\begin{array}{ccc}\hfill f\left(\left.t\right|\varpi \right)& =& \delta \frac{{\lambda }_1^3}{{\lambda }_1^2+2}(1+t^2)\exp \left(-{\lambda }_{1}t\right)+\tilde{\delta }\frac{{\lambda }_2^3}{{\lambda }_2^2+2}(1+t^2)\exp \left(-{\lambda }_{2}t\right),\hfill \end{array}$$

(2)

and

$$\begin{array}{ccc}\hfill F\left(\left.t\right|\varpi \right)& =& \delta F_1\left(\left.t\right|{\lambda }_1\right)+\tilde{\delta }{F}_2\left(\left.t\right|{\lambda }_2\right),\hfill \end{array}$$

(3)

$$\begin{array}{ccc}\hfill F\left(\left.t\right|\varpi \right)& =& \delta \left\{1-\left(1+\frac{{\lambda }_{1}t\left({\lambda }_{1}t+2\right)}{{\lambda }_1^2+2}\right)\exp \left(-{\lambda }_{1}t\right)\right\}\hfill \\ & & +\tilde{\delta }\left\{1-\left(1+\frac{{\lambda }_{2}t\left({\lambda }_{2}t+2\right)}{{\lambda }_2^2+2}\right)\exp \left(-{\lambda }_{2}t\right)\right\},\hfill \end{array}$$

(4)

where $\varpi =\left({\lambda }_1,{\lambda }_2,\delta \right)$ and $\delta$ is a positive mixing parameter, whereas ${\lambda }_i$ are positive scale parameters.

2.1. Mode

By tackling the given non-linear equation with respect to t, the mode of the TC-MAM($\varpi$) is derived

$$\delta \frac{{\lambda }_1^3}{{\lambda }_1^2+2}\left[\exp \left(-{\lambda }_{1}t\right)\left\{t(2-{\lambda }_{1}t)-{\lambda }_1\right\}\right]+\tilde{\delta }\frac{{\lambda }_2^3}{{\lambda }_2^2+2}\left[\exp \left(-{\lambda }_{2}t\right)\left\{t(2-{\lambda }_{2}t)-{\lambda }_2\right\}\right]=0.$$

(5)

2.2. Median

The median of TC-MAM$\left(\varpi \right)$ is given here. Let $F(\left.t\right|$$\varpi )$ be CDF of TC-MAM$\left(\varpi \right)$ the median is at 50th quantiles that is $Q_{0.5}$. The median ($t^{*}$) can, therefore, be determined by resolving given equation for t.

$$\begin{array}{c}\delta \left\{1-\left(1+\frac{{\lambda }_{1}t\left({\lambda }_{1}t+2\right)}{{\beta }_1^2+2}\right)\exp \left(-{\lambda }_{1}t\right)\right\}+\tilde{\delta }\left\{1-\left(1+\frac{{\lambda }_{2}t\left({\lambda }_{2}t+2\right)}{{\lambda }_2^2+2}\right)\exp \left(-{\lambda }_{2}t\right)\right\}=0.5,\hfill \end{array}$$

(6)

$$\delta \left(1+\frac{{\lambda }_{1}t\left({\lambda }_{1}t+2\right)}{{\beta }_1^2+2}\right)\exp \left(-{\lambda }_{1}t\right)+\tilde{\delta }\left(1+\frac{{\lambda }_{2}t\left({\lambda }_{2}t+2\right)}{{\lambda }_2^2+2}\right)\exp \left(-{\lambda }_{2}t\right)=0.5,$$

(7)

Numerical strategies like Newton–Raphson approach can be utilised to find $t^{*}$ from Equation (7).

Several graphs of PDF and CDF of TC-MAM, as well as both component densities, for various parametric values are shown in Figure 1 and Figure 2. It should be indicated that input parameters were selected at random until a wide range of patterns could be examined. The PDF exemplifies its adaptability. The PDF curves of TC-MAM($\varpi$) indicate that it can be monotonically decreasing, positively skewed, inverted U, and declining–increasing–decreasing (DID), as well as modified monotonically decreasing with platykurtic, mesokurtic, and leptokurtic curves. As a result, it can be used to model a diverse set of data.

Figure 1. Behavior of $f_1\left(\left.t\right|{\lambda }_1\right)$ (first component density), $f_2\left(\left.t\right|{\lambda }_2\right)$ (second component density) and density of TC-MAM $f_m\left(\left.t\right|\varpi \right)$ with $\delta$ against t.

Figure 2. Behavior of $F_1\left(\left.t\right|{\lambda }_1\right)$ (first component CDF), $F_2\left(\left.t\right|{\lambda }_2\right)$ (second component CDF) and CDF of TC-MAM $(F_m\left(\left.t\right|\varpi \right)$) with $\delta$ against t.

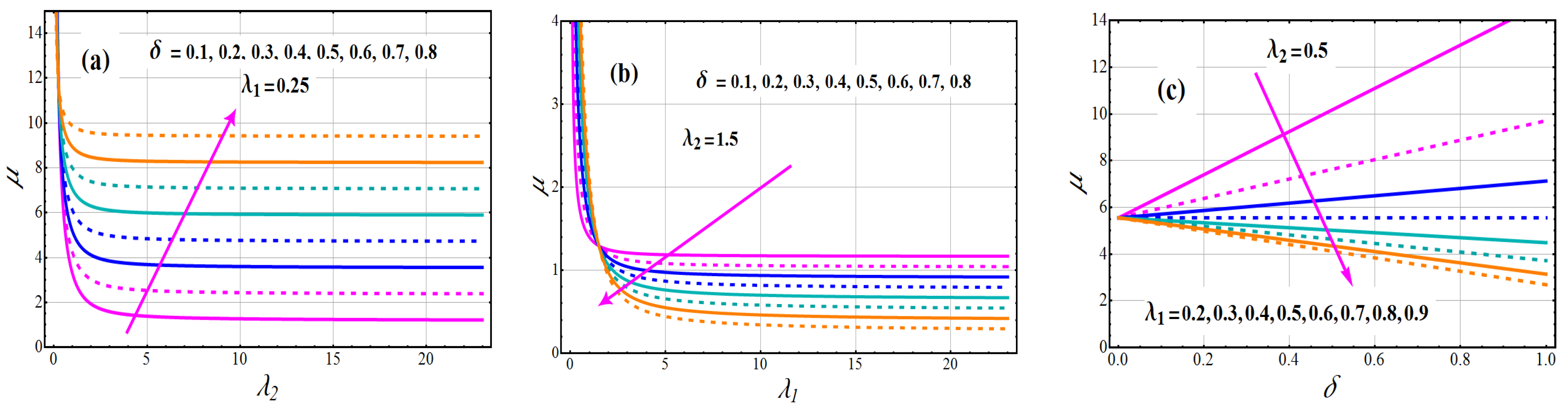
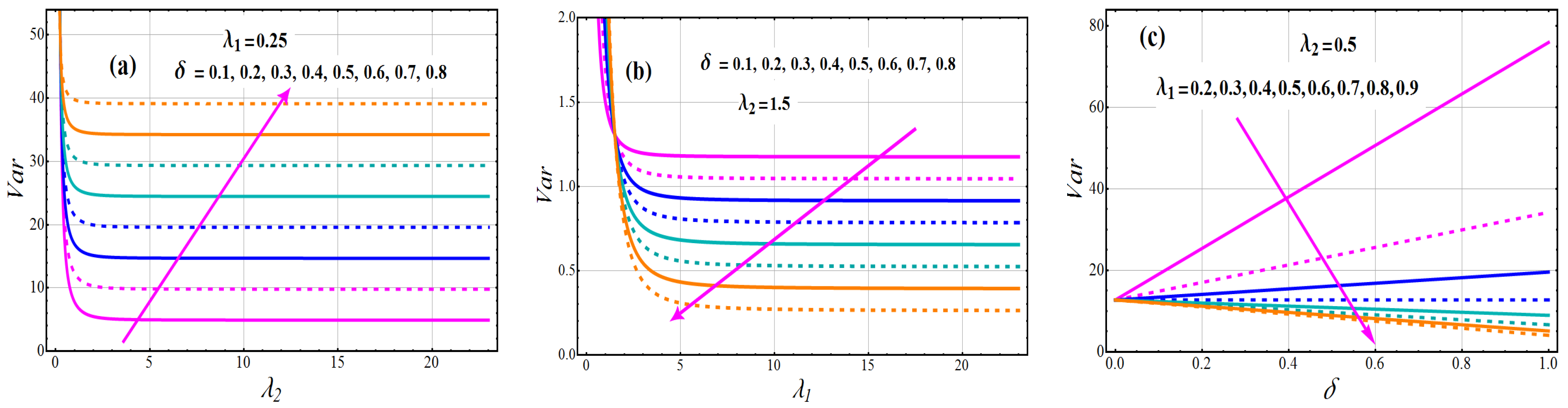
2.3. mth Moments about Origin

For a r.v. T, the mth moments of TC-MAM$\left(\varpi \right)$ are as:

$${\breve{\mu }}_m=E\left(T^m\right)=\underset{0}{\overset{\infty }{\int }}{t}^{m}f(\left.t\right|\breve{\Delta })dt=\underset{0}{\overset{\infty }{\int }}{t}^m\left\{\delta \frac{(1+t^2){\lambda }_1^3}{{\lambda }_1^2+2}\exp \left(-{\lambda }_{1}t\right)+\tilde{\delta }\frac{(1+t^2){\lambda }_2^3}{{\lambda }_2^2+2}\exp \left(-{\lambda }_{2}t\right)\right\}dt,$$

(8)

$$E\left(T^m\right)=\delta \frac{m!\left({\lambda }_1^2+\left(m+1\right)\left(m+2\right)\right)}{{\lambda }_1^m\left({\lambda }_1^2+2\right)}+\tilde{\delta }\frac{m!\left({\lambda }_2^2+\left(m+1\right)\left(m+2\right)\right)}{{\lambda }_2^m\left({\lambda }_2^2+2\right)},m=1,2\dots .$$

(9)

The mean of the TC-MAM$\left(\varpi \right)$ is:

$${\breve{\mu }}_1=\delta \frac{\left({\lambda }_1^2+6\right)}{{\lambda }_1\left({\lambda }_1^2+2\right)}+\tilde{\delta }\frac{\left({\lambda }_1^2+6\right)}{{\lambda }_1\left({\lambda }_1^2+2\right)}=\mu ,$$

(10)

while the variance is given by

$${\breve{\sigma }}^2=\delta \frac{\left({\lambda }_1^4+16{\lambda }_1^2+12\right)}{{\lambda }_1^2{\left({\lambda }_1^2+2\right)}^2}+\tilde{\delta }\frac{\left({\lambda }_2^4+16{\lambda }_2^2+12\right)}{{\lambda }_2^2{\left({\lambda }_2^2+2\right)}^2}.$$

(11)

Graphs of the mean and variance of TC-MAM ($\varpi$) for a variety of parameter values that can be identified in Figure 3 and Figure 4. The mean of TC-MAM ($\varpi$), shows a monotonically decreasing behavior for fixed value of ${\lambda }_1$ and $\delta$ and varying values of ${\lambda }_2$ (see Figure 3a). The escalating changes of mixing parameter $\delta$ enhanced the mean concentration, according to this analysis. We draw mean graphs (see Figure 3b) to demonstrate the behavior of the mean for fixed values of ${\lambda }_2$ and $\delta$ and varying values of ${\lambda }_1$. It reveals the characteristics of component parameter ${\lambda }_1$ in relation to a mean profile. The boosting attitude of $\delta$ reduce the concentration of mean for the all varying values of ${\lambda }_1$. The significances of the mixing parameter versus the mean profile are defined in Figure 3c for various levels of ${\lambda }_1$. From these drawn lines, it can be deduced that the concentration of the mean profile is a deteriorating function for parameter ${\lambda }_1$. The variance exhibits the same behavior as the mean in all scenarios (see Figure 4a–c).

Figure 3. Variations of Mean of TC-MAM.

Figure 4. Variations of Variance of TC-MAM.

In particular moments about origin

$${\breve{\mu }}_2=\delta \frac{2\left({\lambda }_1^2+12\right)}{{\lambda }_1^2\left({\lambda }_1^2+2\right)}+\tilde{\delta }\frac{2\left({\lambda }_2^2+12\right)}{{\lambda }_2^2\left({\lambda }_2^2+2\right)},$$

(12)

$${\breve{\mu }}_3=\delta \frac{6\left({\lambda }_1^2+20\right)}{{\lambda }_1^3\left({\lambda }_1^2+2\right)}+\tilde{\delta }\frac{6\left({\lambda }_2^2+20\right)}{{\lambda }_2^3\left({\lambda }_2^2+2\right)},$$

(13)

$${\breve{\mu }}_4=\delta \frac{24\left({\lambda }_1^2+30\right)}{{\lambda }_1^4\left({\lambda }_1^2+2\right)}+\tilde{\delta }\frac{24\left({\lambda }_2^2+30\right)}{{\lambda }_2^4\left({\lambda }_2^2+2\right)},$$

(14)

and the moments about mean of the TC-MAM$\left(\varpi \right)$ are:

$${\mu }_2=\delta \frac{\left({\lambda }_1^4+16{\lambda }_1^2+12\right)}{{\lambda }_1^2{\left({\lambda }_1^2+2\right)}^2}+\tilde{\delta }\frac{\left({\lambda }_2^4+16{\lambda }_2^2+12\right)}{{\lambda }_2^2{\left({\lambda }_2^2+2\right)}^2},$$

(15)

$${\mu }_3=\delta \frac{2\left({\lambda }_1^6+30{\lambda }_1^4+36{\lambda }_1^2+24\right)}{{\lambda }_1^3{\left({\lambda }_1^2+2\right)}^3}+\tilde{\delta }\frac{2\left({\lambda }_2^6+30{\lambda }_2^4+36{\lambda }_2^2+24\right)}{{\lambda }_2^3{\left({\lambda }_2^2+2\right)}^3},$$

(16)

$${\mu }_4=\delta \frac{3\left(3{\lambda }_1^8+128{\lambda }_1^6+408{\lambda }_1^4+576{\lambda }_1^2+240\right)}{{\lambda }_1^4{\left({\lambda }_1^2+2\right)}^4}+\tilde{\delta }\frac{3\left(3{\lambda }_2^8+128{\lambda }_2^6+408{\lambda }_2^4+576{\lambda }_2^2+240\right)}{{\lambda }_2^4{\left({\lambda }_2^2+2\right)}^4}.$$

(17)

The ${\breve{\phi }}_{CV}$ (Coefficient of Variation), ${\breve{\Psi }}_{Sk}$ (Skewness) and ${\breve{\psi }}_K$ (Kurtosis) of TC-MAM$\left(\varpi \right)$ are:

$${\breve{\phi }}_{CV}=\frac{\sqrt{\delta \frac{\left({\lambda }_1^4+16{\lambda }_1^2+12\right)}{{\lambda }_1^2{\left({\lambda }_1^2+2\right)}^2}+\tilde{\delta }\frac{\left({\lambda }_2^4+16{\lambda }_2^2+12\right)}{{\lambda }_2^2{\left({\lambda }_2^2+2\right)}^2}}}{\delta \frac{\left({\lambda }_1^2+6\right)}{{\lambda }_1\left({\lambda }_1^2+2\right)}+\tilde{\delta }\frac{\left({\lambda }_1^2+6\right)}{{\lambda }_1\left({\lambda }_1^2+2\right)}},$$

(18)

$${\Psi }_{Sk}=\frac{\delta \frac{2\left({\lambda }_1^6+30{\lambda }_1^4+36{\lambda }_1^2+24\right)}{{\lambda }_1^3{\left({\lambda }_1^2+2\right)}^3}+\tilde{\delta }\frac{2\left({\lambda }_2^6+30{\lambda }_2^4+36{\lambda }_2^2+24\right)}{{\lambda }_2^3{\left({\lambda }_2^2+2\right)}^3}}{{\left(\delta \frac{\left({\lambda }_1^4+16{\lambda }_1^2+12\right)}{{\lambda }_1^2{\left({\lambda }_1^2+2\right)}^2}+\tilde{\delta }\frac{\left({\lambda }_2^4+16{\lambda }_2^2+12\right)}{{\lambda }_2^2{\left({\lambda }_2^2+2\right)}^2}\right)}^{3/2}},$$

(19)

$${\breve{\psi }}_K=\frac{\delta \frac{3\left(3{\lambda }_1^8+128{\lambda }_1^6+408{\lambda }_1^4+576{\lambda }_1^2+240\right)}{{\lambda }_1^4{\left({\lambda }_1^2+2\right)}^4}+\tilde{\delta }\frac{3\left(3{\lambda }_2^8+128{\lambda }_2^6+408{\lambda }_2^4+576{\lambda }_2^2+240\right)}{{\lambda }_2^4{\left({\lambda }_2^2+2\right)}^4}}{{\left(\delta \frac{\left({\lambda }_1^4+16{\lambda }_1^2+12\right)}{{\lambda }_1^2{\left({\lambda }_1^2+2\right)}^2}+\tilde{\delta }\frac{\left({\lambda }_2^4+16{\lambda }_2^2+12\right)}{{\lambda }_2^2{\left({\lambda }_2^2+2\right)}^2}\right)}^2},$$

(20)

and Index of Dispersion $\left(ID\right)$ is

$$ID=\frac{\left(\delta \frac{\left({\lambda }_1^4+16{\lambda }_1^2+12\right)}{{\lambda }_1^2{\left({\lambda }_1^2+2\right)}^2}+\tilde{\delta }\frac{\left({\lambda }_2^4+16{\lambda }_2^2+12\right)}{{\lambda }_2^2{\left({\lambda }_2^2+2\right)}^2}\right)}{\delta \frac{\left({\lambda }_1^2+6\right)}{{\lambda }_1\left({\lambda }_1^2+2\right)}+\tilde{\delta }\frac{\left({\lambda }_1^2+6\right)}{{\lambda }_1\left({\lambda }_1^2+2\right)}}.$$

(21)

The TC-MAM$\left(\varpi \right)$ is readily explained to be over-distributed when ${\mu }_2>\mu$, equi-dispersed ${\mu }_2=\mu ,$ as well as under-dispersed ${\mu }_2<\mu .$

Graphs of the ID of TC-MAM ($\varpi$) for various parameter settings are illustrated in Figure 5. The boosting attitude of $\delta$ rise the concentration of mean for the all varying values of ${\lambda }_2$ (see Figure 5a). However, boosting attitude of $\delta$ reduces the concentration of mean for the all varying values of ${\lambda }_1$ (see Figure 5b). The effects of $\delta$ against the concentration of the mean profile are shown in Figure 5c. The concentration of the mean profile is a decreasing function for parameter ${\lambda }_1$ according to these depicted lines. Figure 6 and Figure 7 explain the nature of ${\Psi }_{Sk}$ and ${\breve{\psi }}_K$ in relation to ${\lambda }_1$, ${\lambda }_2$ and $\delta .$ The coefficient of skewness and kurtosis of TC-MAM ($\varpi$), shows a decreasing behavior for fixed value of ${\lambda }_1$ and $\delta$ and varying values of ${\lambda }_2$ (see Figure 6a and Figure 7a).

Figure 5. Variations of index of dispersion of TC-MAM$\left(\varpi \right)$.

Figure 6. Variations of coefficient of skewness $SK$, of TC-MAM$\left(\varpi \right)$.

Figure 7. Behavior of coefficient of kurtosis $\left(K\right)$ of TC-MAM$\left(\varpi \right)$.

To expose the behavior of ${\Psi }_{Sk}$ and ${\breve{\psi }}_K$ for fixed value of ${\lambda }_2$ and $\delta$ and varying values of ${\lambda }_1$(see Figure 6b and Figure 7b). The escalating changes of mixing parameter $\delta$ enhanced ${\Psi }_{Sk}$ and ${\breve{\psi }}_K$ concentration, according to this analysis. The significances of the mixing parameter versus the coefficient of skewness and kurtosis profile are defined in Figure 6c and Figure 7c for various levels of ${\lambda }_1$. From these drawn lines, it can be deduced that the concentration of the skewness and kurtosis profile is a deteriorating function for parameter ${\lambda }_1$.

2.4. Moment Generating Function

The MGF of TC-MAM$\left(\varpi \right)$ is specified as:

$${\tilde{M}}_t\left(\upsilon \right)=E\left(e^{t\upsilon }\right)=\underset{0}{\overset{\infty }{\int }}{e}^{t\upsilon }\left\{\delta \frac{{\lambda }_1^3}{{\lambda }_1^2+2}(1+t^2)\exp \left(-{\lambda }_{1}t\right)+\tilde{\delta }\frac{{\lambda }_2^3}{{\lambda }_2^2+2}(1+t^2)\exp \left(-{\lambda }_{2}t\right)\right\}dt,$$

(22)

$${\tilde{M}}_t\left(\upsilon \right)=\delta \left[\frac{{\lambda }_1^3}{{\lambda }_1^2+2}\left(\frac{1}{{\lambda }_1-\upsilon }+\frac{2}{{\left({\lambda }_1-\upsilon \right)}^3}\right)\right]+\tilde{\delta }\left[\frac{{\lambda }_2^3}{{\lambda }_2^2+2}\left(\frac{1}{{\lambda }_2-\upsilon }+\frac{2}{{\left({\lambda }_2-\upsilon \right)}^3}\right)\right].$$

(23)

$${\tilde{M}}_t\left(\upsilon \right)=\delta \left[\sum _{k=0}^{\infty }\frac{{\lambda }_1^2+\left(k+1\right)\left(k+2\right)}{{\lambda }_1^2+2}{\left(\frac{\upsilon }{{\lambda }_1}\right)}^k\right]+\tilde{\delta }\left[\sum _{k_1=0}^{\infty }\frac{{\lambda }_2^2+\left(k_1+1\right)\left(k_1+2\right)}{{\lambda }_2^2+2}{\left(\frac{\upsilon }{{\lambda }_2}\right)}^{k_1}\right].$$

(24)

2.5. Cumulants

The cumulants (CF), $\breve{\xi }\left(\upsilon \right)=E\left[\exp \left(i\upsilon t\right)\right]$ of TC-MAM$\left(\varpi \right)$ is derived by plugging $\upsilon$ with ‘$i\upsilon$’ in Equation (22), the following formula can be used to obtain the CF:

$$\breve{\xi }\left(\upsilon \right)=\delta \left[\sum _{k=0}^{\infty }\frac{{\lambda }_1^2+\left(k+1\right)\left(k+2\right)}{{\lambda }_1^2+2}{\left(\frac{i\upsilon }{{\lambda }_1}\right)}^k\right]+\tilde{\delta }\left[\sum _{k_1=0}^{\infty }\frac{{\lambda }_2^2+\left(k_1+1\right)\left(k_1+2\right)}{{\lambda }_2^2+2}{\left(\frac{i\upsilon }{{\lambda }_2}\right)}^{k_1}\right],$$

(25)

where the complex unit $i=\sqrt{-1}$.

2.6. Probability Generating Function (PGF)

In Equation (22), the PGF by plugging $\upsilon$ with “ln($\omega$)” is:

$$P_t\left(\omega \right)=E\left({\omega }^t\right)=\delta \left[\sum _{k=0}^{\infty }\frac{{\lambda }_1^2+\left(k+1\right)\left(k+2\right)}{{\lambda }_1^2+2}{\left(\frac{ln\left(\omega \right)}{{\lambda }_1}\right)}^k\right]+\tilde{\delta }\left[\sum _{k_1=0}^{\infty }\frac{{\lambda }_2^2+\left(k_1+1\right)\left(k_1+2\right)}{{\lambda }_2^2+2}{\left(\frac{ln\left(\omega \right)}{{\lambda }_2}\right)}^{k_1}\right].$$

(26)

2.7. Factorial Moment Generating Function

By plugging $\upsilon$ with ‘ln$\left(1+\varphi \right)$’ in Equation (22), the FMGF can be shown as

$$\begin{array}{cc}\hfill {\breve{F}}_t\left(\omega \right) =& E\left(e^{t\ln \left(1+\varphi \right)}\right)=\delta \left[\sum _{k=0}^{\infty }\frac{{\lambda }_1^2+\left(k+1\right)\left(k+2\right)}{{\lambda }_1^2+2}{\left(\frac{ln\left(1+\varphi \right)}{{\lambda }_1}\right)}^k\right]\hfill \\ & +\tilde{\delta }\left[\sum _{k_1=0}^{\infty }\frac{{\lambda }_2^2+\left(k_1+1\right)\left(k_1+2\right)}{{\lambda }_2^2+2}{\left(\frac{ln\left(1+\varphi \right)}{{\lambda }_2}\right)}^{k_1}\right].\hfill \end{array}$$

(27)

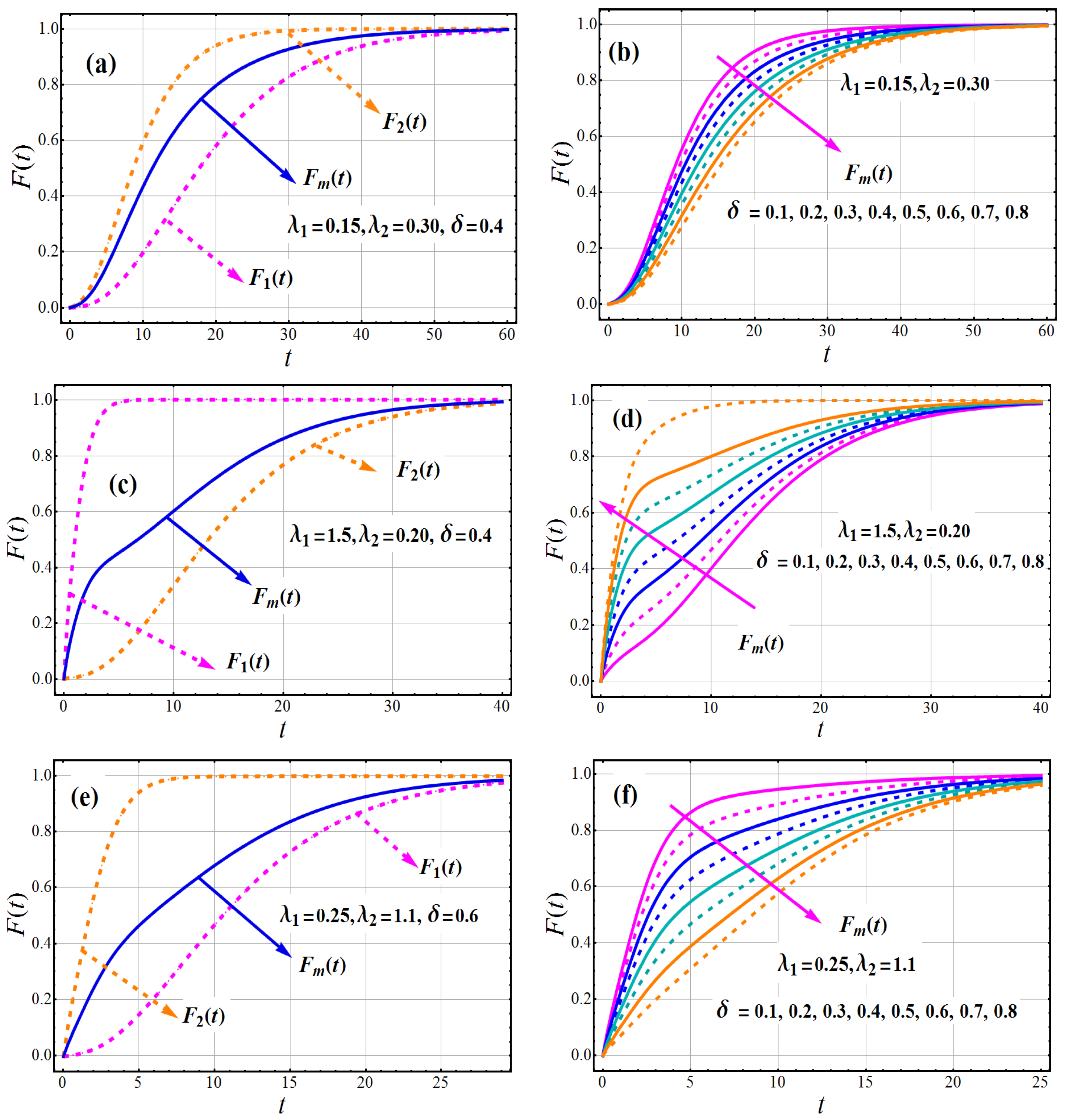
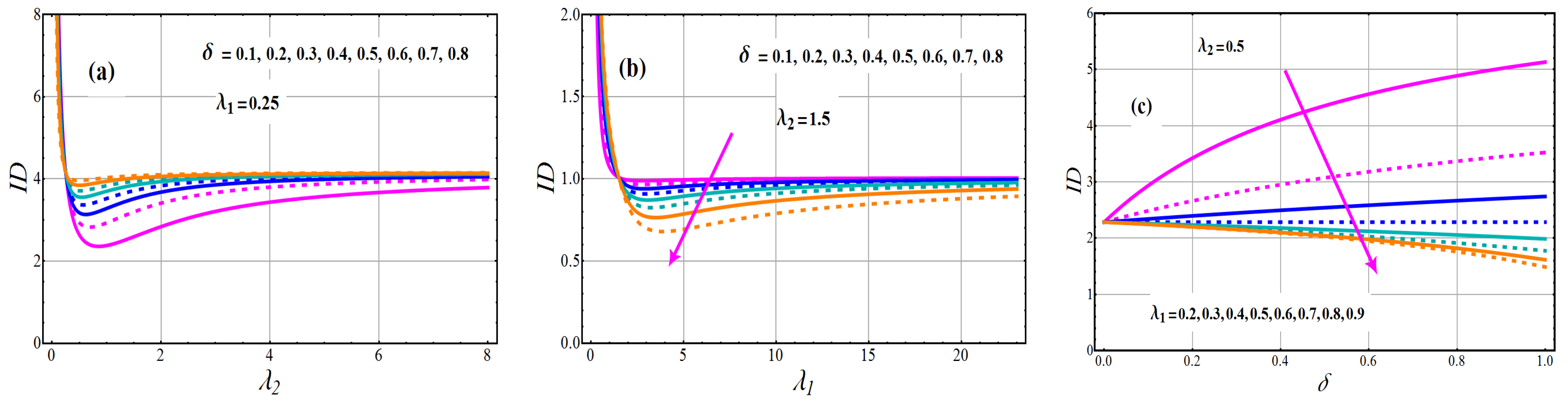
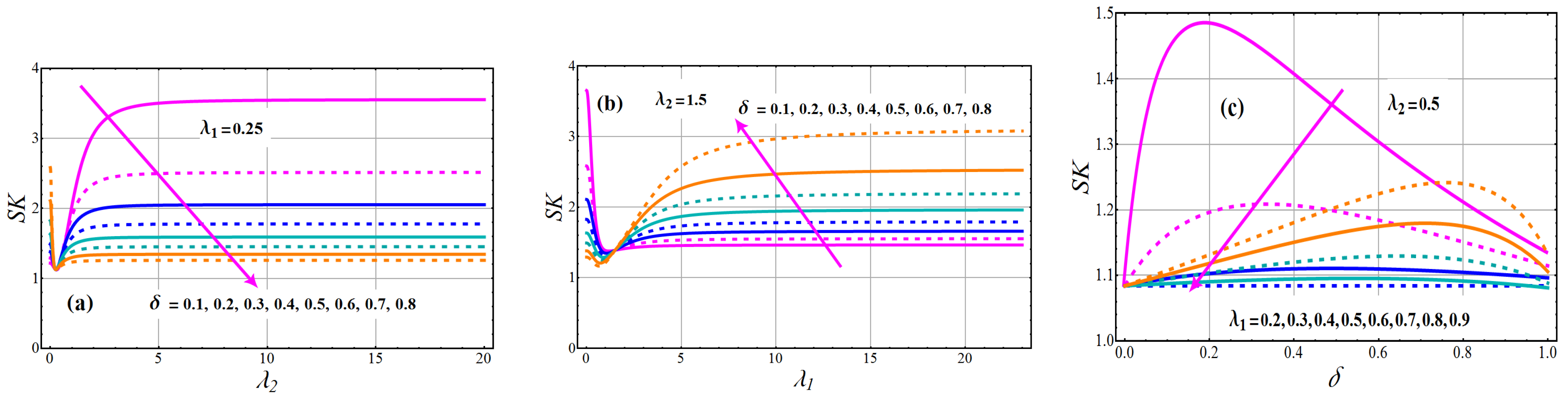
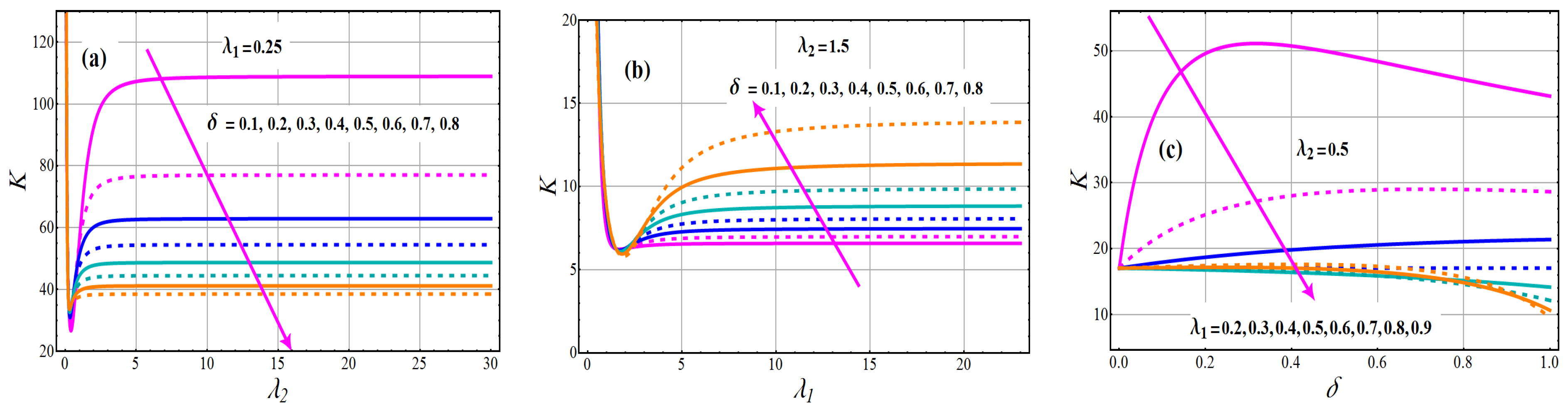
3. Reliability Measures

In reliability framework, lifetime models are classified using the reliability/survival function and the failure/hazard rate function. TC-MAM$\left(\varpi \right)$ is currently being studied for its reliability properties.

3.1. Reliability Function

The reliability function $\left(R\left(\left.t\right|\varpi \right)\right)$ of TC-MAM$\left(\varpi \right)$ is.

$$R\left(\left.t\right|\varpi \right)=\delta \left(1+\frac{{\lambda }_{1}t\left({\lambda }_{1}t+2\right)}{{\lambda }_1^2+2}\right)\exp \left(-{\lambda }_{1}t\right)+\tilde{\delta }\left(1+\frac{{\lambda }_{2}t\left({\lambda }_{2}t+2\right)}{{\lambda }_2^2+2}\right)\exp \left(-{\lambda }_{2}t\right)$$

(28)

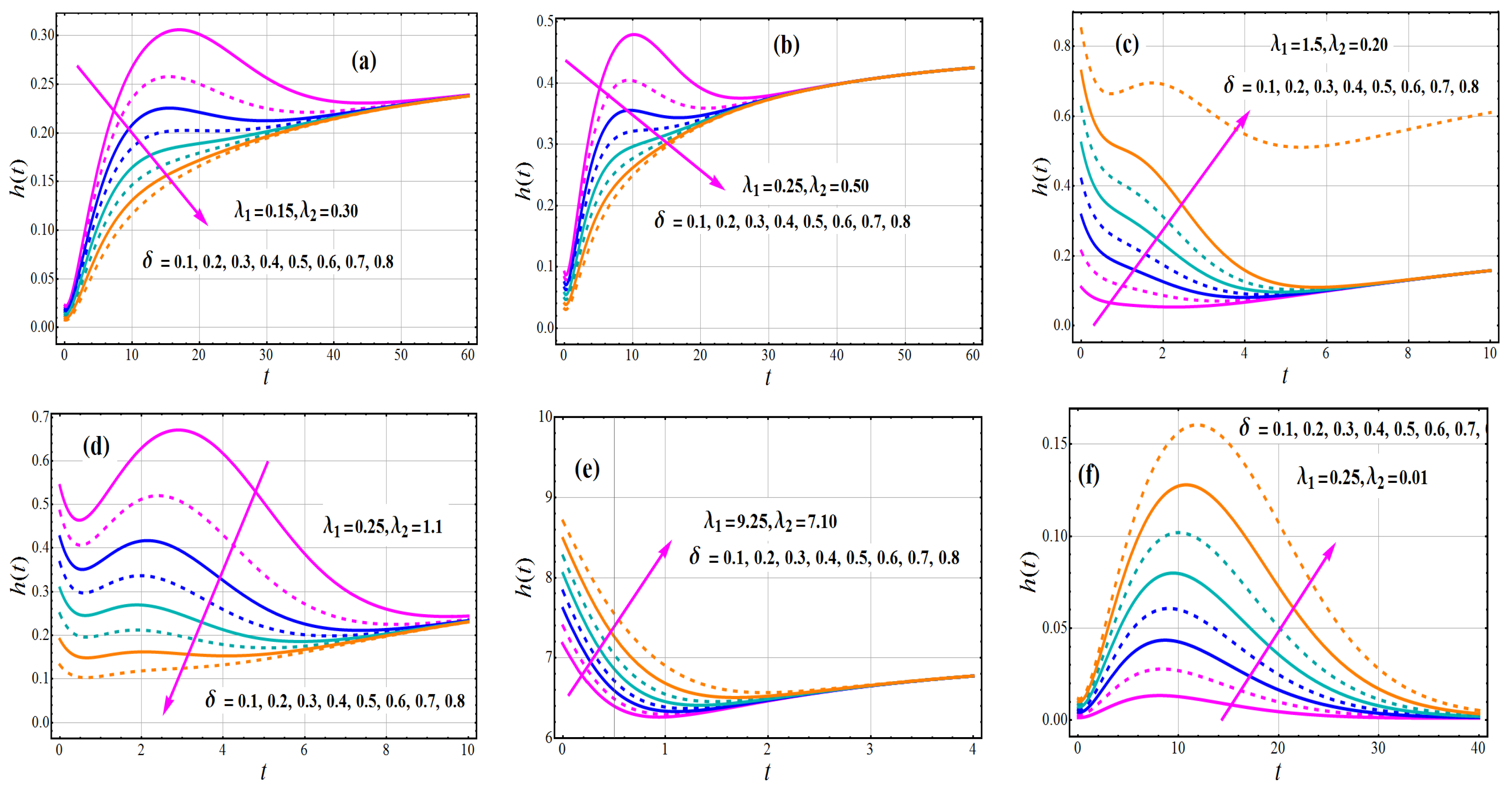
3.2. Hazard Function

The failure rate function $h(\left.t\right|$$\varpi )$ of the TC-MAM($\varpi$) is described as follows.

$$h\left(\left.t\right|\varpi \right)=\frac{\delta \frac{{\lambda }_1^3}{{\lambda }_1^2+2}(1+t^2)\exp \left(-{\lambda }_{1}t\right)+\tilde{\delta }\frac{{\lambda }_2^3}{{\lambda }_2^2+2}(1+t^2)\exp \left(-{\lambda }_{2}t\right)}{\delta \left(1+\frac{{\lambda }_{1}t\left({\lambda }_{1}t+2\right)}{{\lambda }_1^2+2}\right)\exp \left(-{\lambda }_{1}t\right)+\tilde{\delta }\left(1+\frac{{\lambda }_{2}t\left({\lambda }_{2}t+2\right)}{{\lambda }_2^2+2}\right)\exp \left(-{\lambda }_{2}t\right)}.$$

(29)

In Figure 8, the HRF of TC-MAM$\left(\varpi \right)$ shows monotonically increasing, modified decreasing, decreasing–increasing–decreasing (DID), decreasing–increasing (DI), and upside down bathtub behavior. Figure 8a,b,d signifies that the reduction in failure rate function profile and is noted by enlarging the value of mixing parameter $\delta ,$ and for ${\lambda }_1<{\lambda }_2$. Figure 8c,e,f exhibits the diversion in the failure rate function for various values of $\delta$. It is found in Figure 8 that the failure rate distribution is expanding due to higher the value of mixing parameter $\delta ,$ and for ${\lambda }_1>{\lambda }_2.$

Figure 8. Variations in $h(\left.t\right|$$\varpi )$ for ${\lambda }_1,$ ${\lambda }_1$ and $\delta$.

3.3. Mills Ratio

Mills ratio is an another method of quantifying reliability due to its relation to failure rate. Mills ratio $\check{\mathsf{{\rm Y}}}\left(\left.t\right|\varpi \right)$ of TC-MAM($\varpi$) is

$$\check{\mathsf{{\rm Y}}}\left(\left.t\right|\varpi \right)=\frac{R\left(\left.t\right|\varpi \right)}{f\left(\left.t\right|\varpi \right)}=\frac{\delta \left(1+\frac{{\lambda }_{1}t\left({\lambda }_{1}t+2\right)}{{\lambda }_1^2+2}\right)\exp \left(-{\lambda }_{1}t\right)+\tilde{\delta }\left(1+\frac{{\lambda }_{2}t\left({\lambda }_{2}t+2\right)}{{\lambda }_2^2+2}\right)\exp \left(-{\lambda }_{2}t\right)}{\delta \frac{{\lambda }_1^3}{{\lambda }_1^2+2}(1+t^2)\exp \left(-{\lambda }_{1}t\right)+\tilde{\delta }\frac{{\lambda }_2^3}{{\lambda }_2^2+2}(1+t^2)\exp \left(-{\lambda }_{2}t\right)}.$$

(30)

3.4. Cumulative Hazard Rate Function

The CHRF of TC-MAM$\left(\varpi \right)$ is

$$H\left(\left.t\right|\varpi \right)=\underset{0}{\overset{t}{\int }}h\left(\left.y\right|\varpi \right)dy=-\log \left[R\left(\left.t\right|\varpi \right)\right].$$

(31)

It is a risk indicator: the stronger the $H\left(\left.t\right|\varpi \right)$ estimate, the greater the chance of failure by t-time. It must be stated that

$$R\left(\left.t\right|\varpi \right)=e^{-H\left(\left.t\right|\varpi \right)}\mathrm{and}f\left(\left.t\right|\varpi \right)=h\left(\left.t\right|\varpi \right)e^{-H\left(\left.t\right|\varpi \right)}.$$

(32)

So,

$$H\left(\left.t\right|\varpi \right)=-\log \left[\delta \left(1+\frac{{\lambda }_{1}t\left({\lambda }_{1}t+2\right)}{{\lambda }_1^2+2}\right)\exp \left(-{\lambda }_{1}t\right)+\tilde{\delta }\left(1+\frac{{\lambda }_{2}t\left({\lambda }_{2}t+2\right)}{{\lambda }_2^2+2}\right)\exp \left(-{\lambda }_{2}t\right)\right].$$

(33)

3.5. Reversed Hazard Rate Function

The RHRF of a random life of TC-MAM$\left(\varpi \right)$ is defined as

$$\breve{h}\left(\left.t\right|\varpi \right)=\frac{\delta \frac{{\lambda }_1^3}{{\lambda }_1^2+2}(1+t^2)\exp \left(-{\lambda }_{1}t\right)+\tilde{\delta }\frac{{\lambda }_2^3}{{\lambda }_2^2+2}(1+t^2)\exp \left(-{\lambda }_{2}t\right)}{1-\delta \left(1+\frac{{\lambda }_{1}t\left({\lambda }_{1}t+2\right)}{{\lambda }_1^2+2}\right)\exp \left(-{\lambda }_{1}t\right)-\tilde{\delta }\left(1+\frac{{\lambda }_{2}t\left({\lambda }_{2}t+2\right)}{{\lambda }_2^2+2}\right)\exp \left(-{\lambda }_{2}t\right)}.$$

(34)

3.6. Mean Time to Failure (MTTF)

The expected time for which the device performs efficiently is given by the mean time to failure (MTTF). If TC-MAM$\left(\varpi \right)$ then reliability function is used to express MTTF, which is as follows:

$$\breve{M}\left(\left.t\right|\varpi \right)=\underset{0}{\overset{+\infty }{\int }}R\left(\left.t\right|\varpi \right)dt,$$

(35)

and $R\left(t\right)$ is provided in Equation (28). Thus

$$\breve{M}\left(\left.t\right|\varpi \right)=\delta \frac{\left({\lambda }_1^2+6\right)}{{\lambda }_1\left({\lambda }_1^2+2\right)}+\tilde{\delta }\frac{\left({\lambda }_1^2+6\right)}{{\lambda }_1\left({\lambda }_1^2+2\right)}.$$

(36)

4. Estimation Inference via Simulation

Given that the parametric vector $\varpi$ is undetermined, certain statistical properties of the TC-MAM($\varpi$) are presented to this section. The evaluation of parametric vector $\varpi$ is accomplished by three widely known estimation mechanisms, such as MLE, LSE, and WLSE. From now, $t_1,t_2,\dots ,t_n$ signify n determined values from T and their ascending sorting values $t_{\left(1\right)}\le t_{\left(2\right)}\le \dots \le t_{\left(n\right)}.$

4.1. Maximum Likelihood Estimation (MLE)

The MLE method is the best methodology for parameter assessment. The popularity of the approach stems from its many advantageous characteristics, such as consistency, normality, and asymptotic efficiency. Let $t_1,t_2,\dots ,t_n$ be n determined values from the Equation (2) and $\varpi$ be the vector of undetermined parameters. The evaluations of MLEs of $\varpi$ can be given by optimizing the likelihood function with respect to ${\lambda }_1,$${\lambda }_2,$ and $\delta$ given by $L\left(\left.\mathbf{t}\right|\varpi \right)={\displaystyle \prod _{i=1}^n}f(t_i;$$\varpi )$ or likewise the log-likelihood function for $\varpi$ is

$$l\left(\left.\mathbf{t}\right|\varpi \right)=\ln \prod _{i=1}^{n}f(t_i;\varpi )$$

(37)

$$l\left(\left.\mathbf{t}\right|\varpi \right)=\sum _{i=1}^n\ln \left\{\delta \frac{{\lambda }_1^3}{{\lambda }_1^2+2}(1+t_i^2)\exp \left(-{\lambda }_1{t}_i\right)+\tilde{\delta }\frac{{\lambda }_2^3}{{\lambda }_2^2+2}(1+t_i^2)\exp \left(-{\lambda }_2{t}_i\right)\right\}.$$

(38)

So, by partially differentiating $l\left(\left.\mathbf{t}\right|\varpi \right)$ in terms of each parameter (${\lambda }_1,$${\lambda }_2,$$\delta$) and placing the results to zero, the MLEs of the relevant parameters are determined as

$$\frac{\partial l\left(\left.\mathbf{t}\right|\varpi \right)}{\partial {\lambda }_1}=\sum _{i=1}^n\frac{\delta (1+t_i^2){\lambda }_1^2\exp \left(-{\lambda }_1{t}_i\right)\left\{\frac{3}{\left({\lambda }_1^2+2\right)}-\frac{{\lambda }_1{t}_i}{\left({\lambda }_1^2+2\right)}-\frac{2{\lambda }_1^2}{{\left({\lambda }_1^2+2\right)}^2}\right\}}{\left\{\delta \frac{{\lambda }_1^3}{{\lambda }_1^2+2}(1+t_i^2)\exp \left(-{\lambda }_1{t}_i\right)+\tilde{\delta }\frac{{\lambda }_2^3}{{\lambda }_2^2+2}(1+t_i^2)\exp \left(-{\lambda }_2{t}_i\right)\right\}},$$

(39)

$$\frac{\partial l\left(\left.\mathbf{t}\right|\varpi \right)}{\partial {\lambda }_2}=\sum _{i=1}^n\frac{\tilde{\delta }(1+t_i^2){\lambda }_2^2\exp \left(-{\lambda }_2{t}_i\right)\left\{\frac{3}{\left({\lambda }_2^2+2\right)}-\frac{{\lambda }_2{t}_i}{\left({\lambda }_2^2+2\right)}-\frac{2{\lambda }_2^2}{{\left({\lambda }_2^2+2\right)}^2}\right\}}{\left\{\delta \frac{{\lambda }_1^3}{{\lambda }_1^2+2}(1+t_i^2)\exp \left(-{\lambda }_1{t}_i\right)+\tilde{\delta }\frac{{\lambda }_2^3}{{\lambda }_2^2+2}(1+t_i^2)\exp \left(-{\lambda }_2{t}_i\right)\right\}},$$

(40)

$$\frac{\partial l\left(\left.\mathbf{t}\right|\varpi \right)}{\partial \delta }=\sum _{i=1}^n\frac{\frac{{\lambda }_1^3}{{\lambda }_1^2+2}(1+t_i^2)\exp \left(-{\lambda }_1{t}_i\right)-\frac{{\lambda }_2^3}{{\lambda }_2^2+2}(1+t_i^2)\exp \left(-{\lambda }_2{t}_i\right)}{\left\{\delta \frac{{\lambda }_1^3}{{\lambda }_1^2+2}(1+t_i^2)\exp \left(-{\lambda }_1{t}_i\right)+\tilde{\delta }\frac{{\lambda }_2^3}{{\lambda }_2^2+2}(1+t_i^2)\exp \left(-{\lambda }_2{t}_i\right)\right\}}.$$

(41)

As a consequence, the MLE is found by evaluating this non-linear set of equations. However such equations cannot be handled analytically, we can use statistical software to solve them using an iterative methodology namely the Newton method or fixed point iteration methods.

4.2. Least Square Estimators (LSE)

The ordinary least square approach [22] is widely used for assessing undetermined parameters. The LSEs of ${\lambda }_1,$ ${\lambda }_2,$ and $\delta$, indicated by ${\tilde{\lambda }}_{1LSE},$ ${\tilde{\lambda }}_{2LSE},$ and ${\tilde{\delta }}_{LSE}$, can be determined by minimizing Equation (42)

$$LS\left(\varpi \right)=\sum _{i=1}^n{\left[F\left(\left.t_{\left(i\right)}\right|\varpi \right)-\frac{i}{n+1}\right]}^2,$$

(42)

with respect to ${\lambda }_1,$ ${\lambda }_2,$ and $\delta$, where $F($·)is given by Equation(4). They may be determined in the similar way by solving the non-linear equations below:

$$\frac{\partial LS\left(\varpi \right)}{\partial {\lambda }_1}=\sum _{i=1}^n\left[F\left(\left.t_{\left(i\right)}\right|\varpi \right)-\frac{i}{n+1}\right]{\breve{\Psi }}_1\left(\left.t_{\left(i\right)}\right|{\lambda }_1\right)=0,$$

(43)

$$\frac{\partial LS\left(\varpi \right)}{\partial {\lambda }_2}=\sum _{i=1}^n\left[F\left(\left.t_{\left(i\right)}\right|\varpi \right)-\frac{i}{n+1}\right]{\breve{\Psi }}_2\left(\left.t_{\left(i\right)}\right|{\lambda }_2\right)=0,$$

(44)

and

$$\frac{\partial LS\left(\varpi \right)}{\partial \delta }=\sum _{i=1}^n\left[F\left(\left.t_{\left(i\right)}\right|\varpi \right)-\frac{i}{n+1}\right]{\breve{\Psi }}_3\left(\left.t_{\left(i\right)}\right|\delta \right)=0,$$

(45)

where

$${\tilde{\Psi }}_1\left(\left.t_{\left(i\right)}\right|{\lambda }_1\right)=\frac{\delta t_{\left(i\right)}{\lambda }_1^2\exp \left(-{\lambda }_1{t}_{\left(i\right)}\right)\left\{6+{\lambda }_1^2+2{\lambda }_1{t}_{\left(i\right)}+\left(2+{\lambda }_1^2\right)t_{\left(i\right)}\right\}}{{\left({\lambda }_1^2+2\right)}^2},$$

(46)

$${\tilde{\Psi }}_2\left(\left.t_{\left(i\right)}\right|{\lambda }_2\right)=\frac{\tilde{\delta }{t}_{\left(i\right)}{\lambda }_2^2\exp \left(-{\lambda }_2{t}_{\left(i\right)}\right)\left\{6+{\lambda }_2^2+2{\lambda }_2{t}_{\left(i\right)}+\left(2+{\lambda }_2^2\right)t_{\left(i\right)}\right\}}{{\left({\lambda }_2^2+2\right)}^2},$$

(47)

$${\tilde{\Psi }}_3\left(\left.t_{\left(i\right)}\right|\delta \right)=\left\{1+\frac{{\lambda }_2{t}_{\left(i\right)}\left(2+{\lambda }_2{t}_{\left(i\right)}\right)}{{\lambda }_2^2+2}\right\}\exp \left(-{\lambda }_2{t}_{\left(i\right)}\right)-\left\{1+\frac{{\lambda }_1{t}_{\left(i\right)}\left(2+{\lambda }_1{t}_{\left(i\right)}\right)}{{\lambda }_1^2+2}\right\}\exp \left(-{\lambda }_1{t}_{\left(i\right)}\right).$$

(48)

4.3. Weighted Least Squares Estimators (WLSE)

Take a look at the following weighted function (see [23])

$${\breve{\kappa }}_i=\frac{{\left(n+1\right)}^2\left(n+2\right)}{i\left(n-i+1\right)}.$$

(49)

The WLSEs ${\tilde{\lambda }}_{1WLSE},$ ${\tilde{\lambda }}_{2WLSE},$ and ${\tilde{\delta }}_{WLSE}$, can be obtained by minimizing Equation (50)

$$WLS\left(\varpi \right)=\sum _{i=1}^n\frac{{\left(n+1\right)}^2\left(n+2\right)}{i\left(n-i+1\right)}{\left[F\left(\left.t_{\left(i\right)}\right|\varpi \right)-\frac{i}{n+1}\right]}^2,$$

(50)

One can also obtain these estimators by solving:

$$\frac{\partial WLS\left(\varpi \right)}{\partial {\lambda }_1}=\sum _{i=1}^n\frac{{\left(n+1\right)}^2\left(n+2\right)}{i\left(n-i+1\right)}\left[F\left(\left.t_{\left(i\right)}\right|\varpi \right)-\frac{i}{n+1}\right]{\breve{\Psi }}_1\left(\left.t_{\left(i\right)}\right|{\lambda }_1\right)=0,$$

(51)

$$\frac{\partial WLS\left(\varpi \right)}{\partial {\lambda }_2}=\sum _{i=1}^n\frac{{\left(n+1\right)}^2\left(n+2\right)}{i\left(n-i+1\right)}\left[F\left(\left.t_{\left(i\right)}\right|\varpi \right)-\frac{i}{n+1}\right]{\breve{\Psi }}_2\left(\left.t_{\left(i\right)}\right|{\lambda }_2\right)=0,$$

(52)

and

$$\frac{\partial WLS\left(\varpi \right)}{\partial \delta }=\sum _{i=1}^n\frac{{\left(n+1\right)}^2\left(n+2\right)}{i\left(n-i+1\right)}\left[F\left(\left.t_{\left(i\right)}\right|\varpi \right)-\frac{i}{n+1}\right]{\breve{\Psi }}_3\left(\left.t_{\left(i\right)}\right|\delta \right)=0,$$

(53)

where ${\tilde{\Psi }}_1\left(\left.t_{\left(i\right)}\right|{\lambda }_1\right),$${\tilde{\Psi }}_2\left(\left.t_{\left(i\right)}\right|{\lambda }_2\right)$ and ${\tilde{\Psi }}_3\left(\left.t_{\left(i\right)}\right|\delta \right)$ are given in Equations (46)–(48).

4.4. Simulation Study

The simulation study is used to evaluate the various estimating methodologies outlined in the preceding subsection. Monte Carlo simulations are performed with a variety of mixing proportion $\delta$ and distribution parameters. The performance of MLE, LSEs, and WLSEs of the TC-MAM($\varpi$) parameters is evaluated using four simulation experiments. The proficiency of the MLEs, LSEs, and WLSEs is discussed using the bias and MSE indicators. In terms of n, the efficiency of each parameter estimation strategy for the TC-MAM($\varpi$) model is examined. The simulation algorithm is subdivided into six steps:

• By adjusting the mixing proportion and model parameters $\left({\lambda }_1,{\lambda }_2,\delta \right)=$Set-I$\left(0.15,0.30,0.40\right),$ Set-II$\left(0.25,0.5,0.6\right)$ and Set-III$\left(0.5,0.2,0.6\right)$, generate random samples of sizes $25,30,\dots ,500$ from TC-MAM($\varpi$). The random samples for the simulation are obtained as specified in the upcoming stage.
• Generate a random variable u from uniform distribution $U(0,1)$, employing R uniform generator (runif).
• If $u\le \delta$, then generate a random variable from the first component, which is a Akash distribution $\left({\lambda }_1\right)$. If $u>\delta$, the second component, Akash distribution $\left({\lambda }_2\right)$, is utilized to produce a random variate.
• Follow (2 and 3) till you have the prescribed sample size n.
• Employing 1000 iterations, continue steps 1–4 each time. Evaluate MLEs, LSEs, and WLSEs for the 1000 samples, say ${\tilde{\kappa }}_j$ for $j=1,2,\dots ,1000,$ having optima function and the Nelder–Mead technique in R to compute estimates.
• Determine biases and MSEs. The two metrics are utilized to meet these targets:

  $$Bia{s}_{\kappa }\left(n\right)=\frac{1}{1000}\sum _{j=1}^{1000}\left({\tilde{\kappa }}_j-\kappa \right),$$

  $$MS{E}_{\kappa }\left(n\right)=\frac{1}{1000}\sum _{j=1}^{1000}{\left(\tilde{\kappa }-\kappa \right)}^2,$$

  where $\kappa =\left({\lambda }_1,{\lambda }_2,\delta \right).$

The empirical findings are depicted in Figure 9, Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14. These results suggest that the proposed estimation methods are effective at estimating the TC-MAM parameters. We can deduce that the estimators display asymptotic unbiasedness because the bias goes to zero as n rises. On the other hand, MSE behavior implies consistency because the errors trend to zero as n increases. The following conclusions can be drawn from Figure 9, Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14.

Figure 9. Behavior of bias of estimators with different methods under parametric set I against n.

Figure 10. Behavior of MSE of estimators with different methods under parametric set I against n.

Figure 11. Behavior of bias of estimators with different methods under parametric set II against n.

Figure 12. Behavior of MSE of estimators with different methods under parametric set II against n.

Figure 13. Behavior of bias of estimators with different methods under parametric set III against n.

Figure 14. Behavior of MSE of estimators with different methods under parametric set III against n.

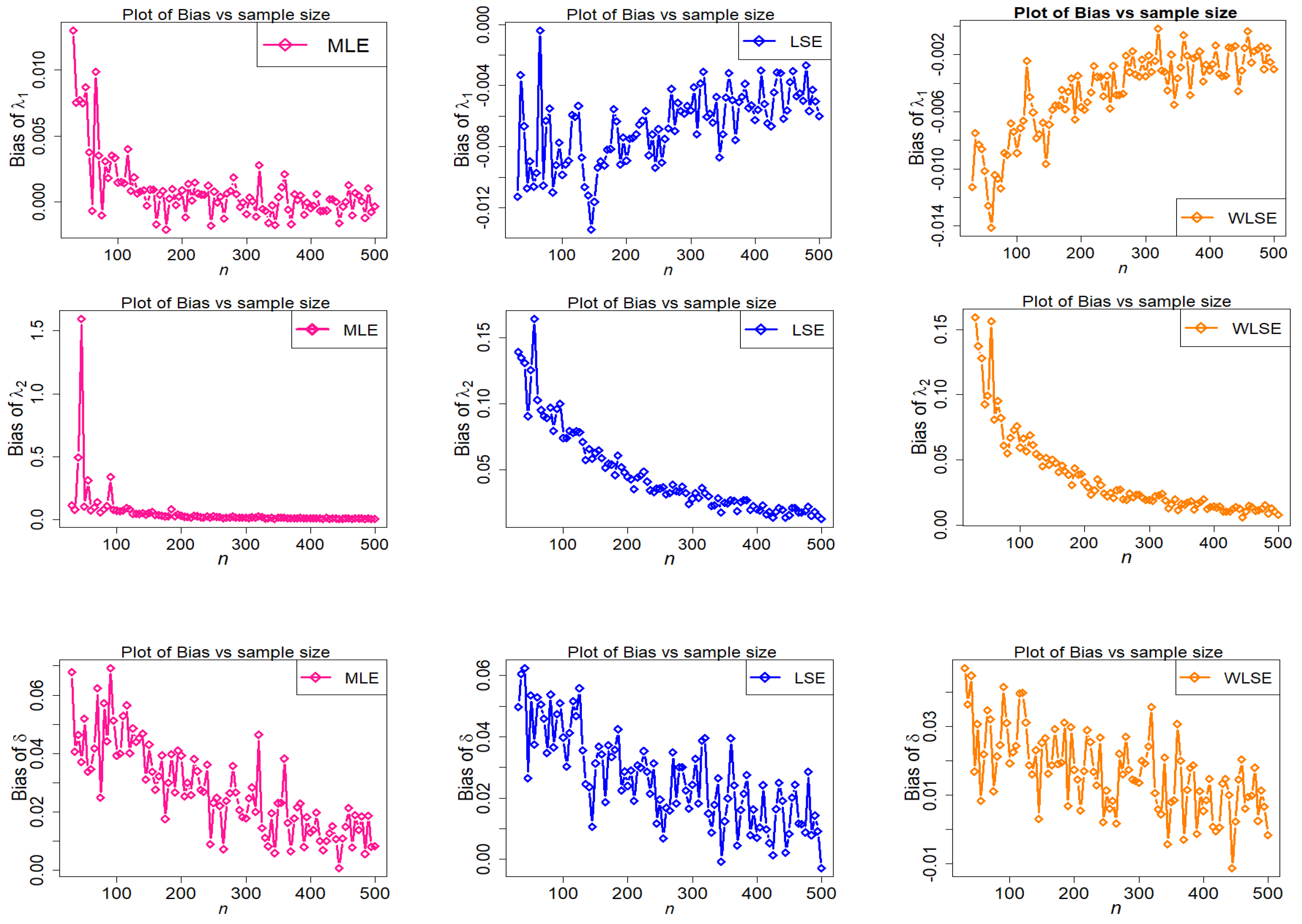
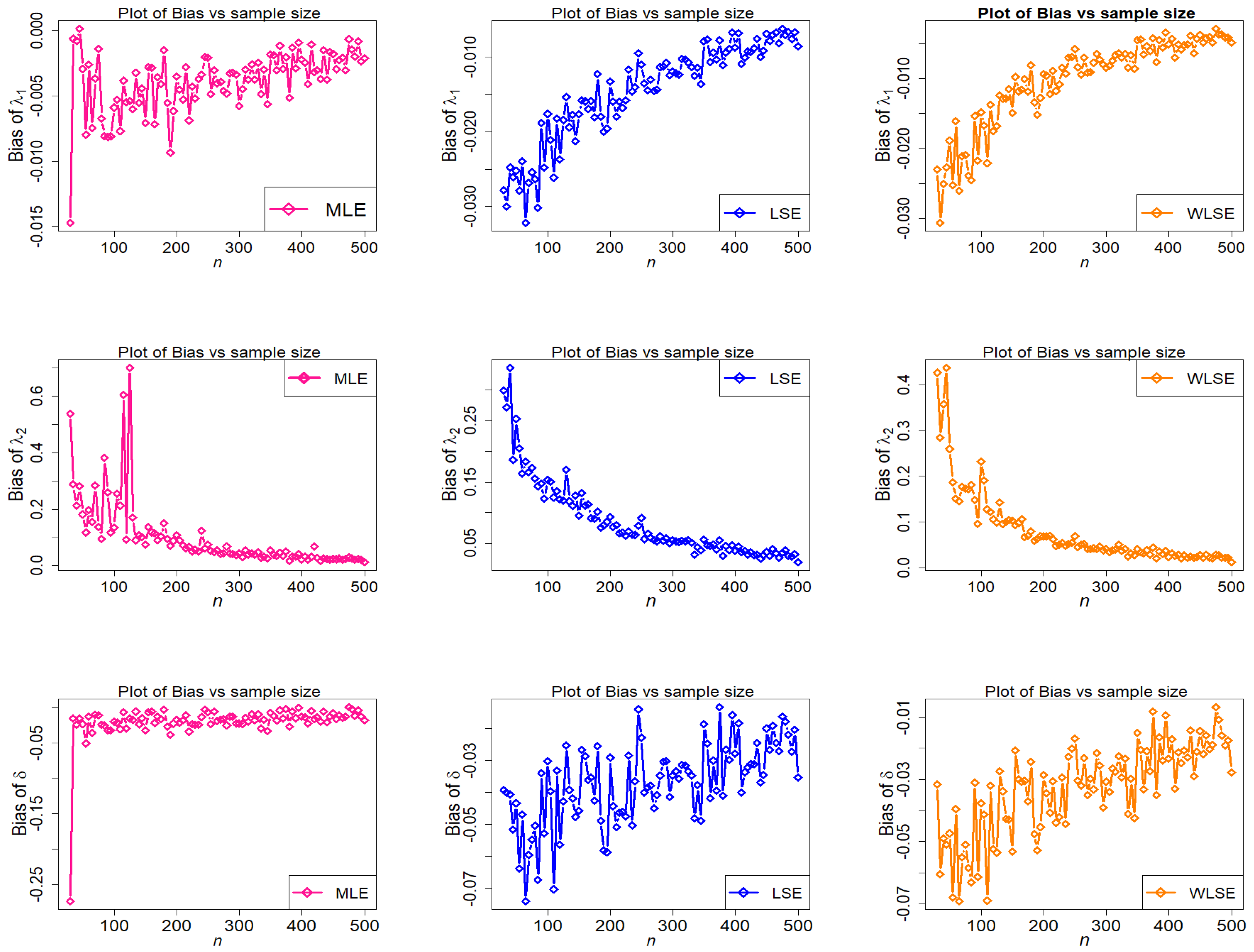
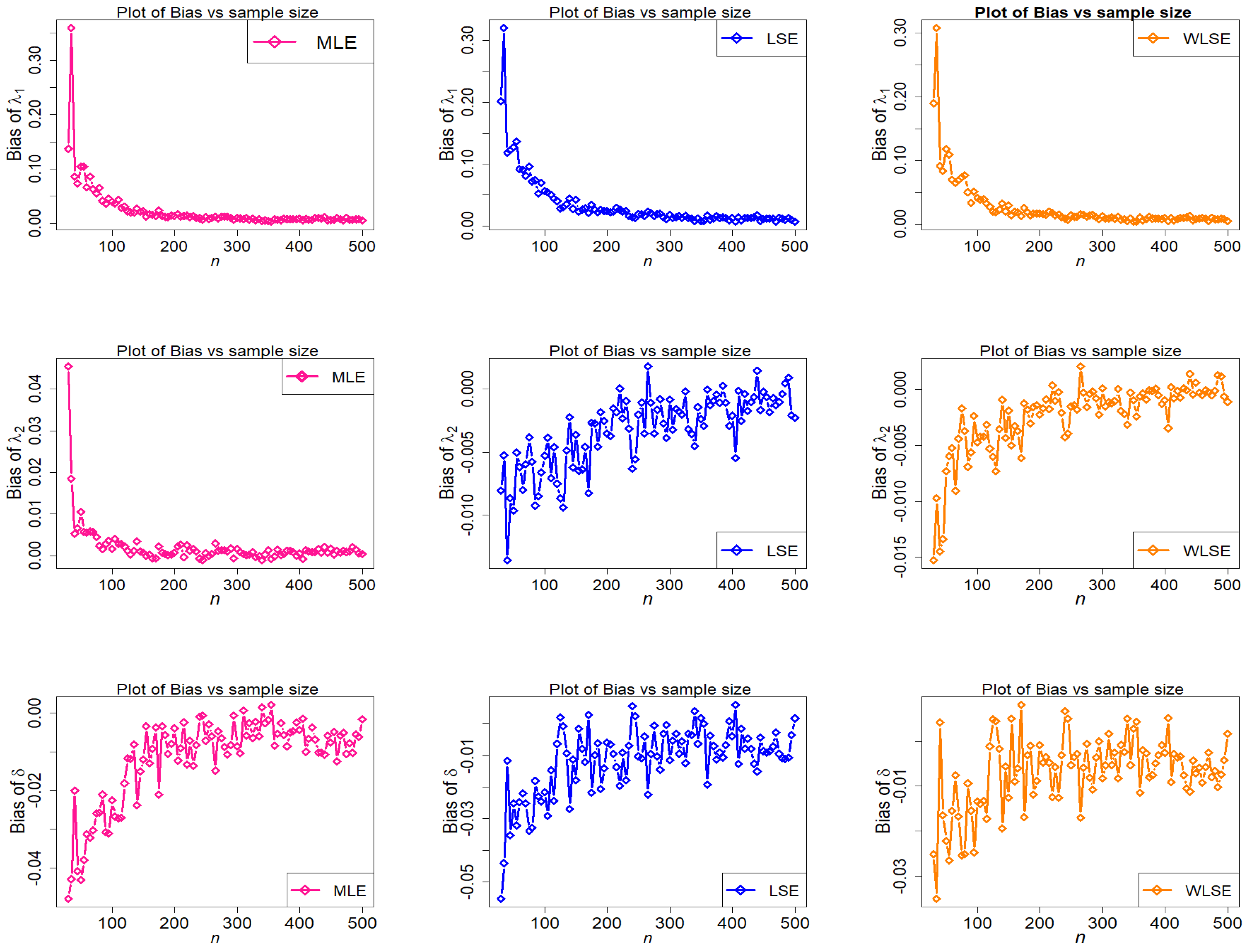
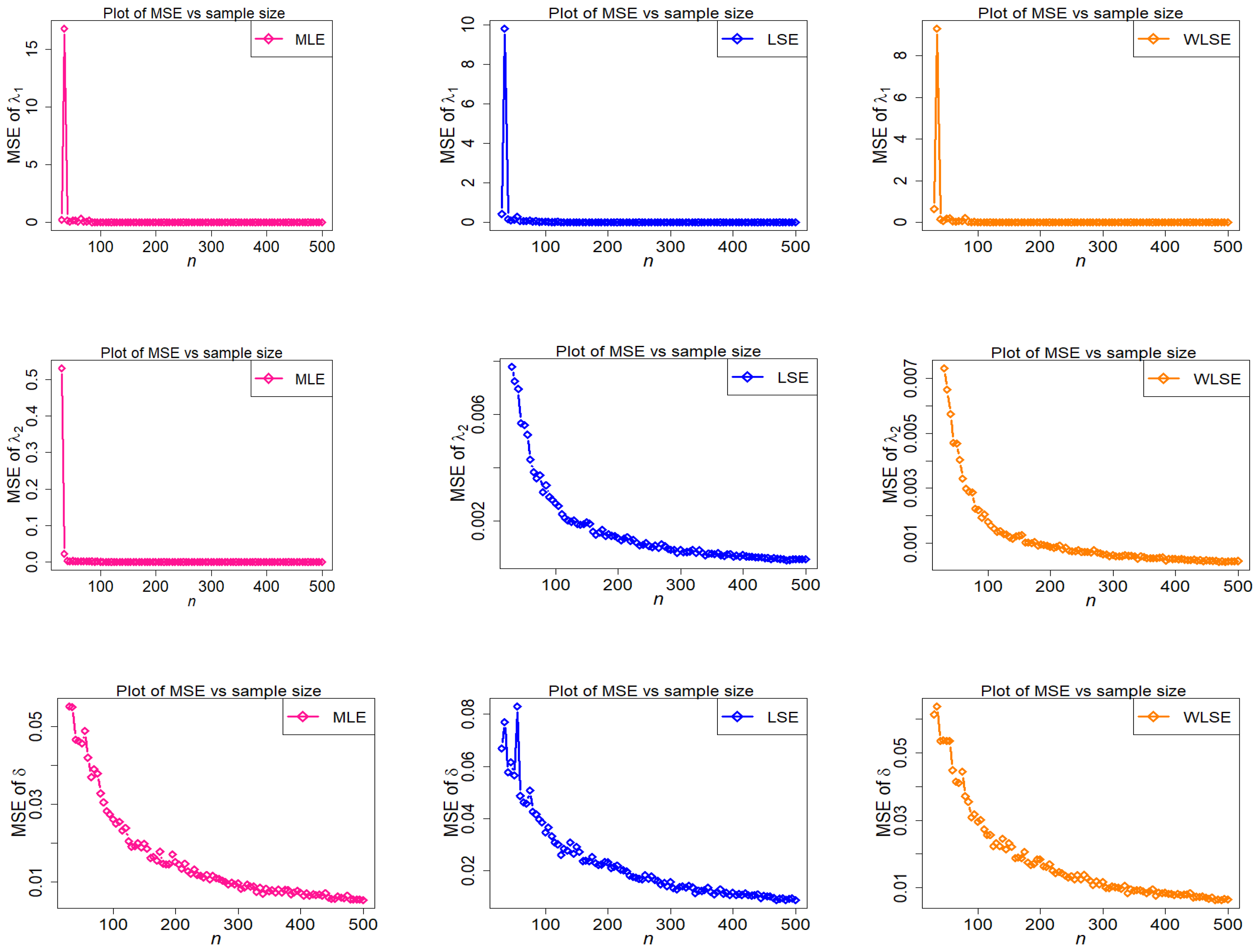
• Under all three estimation procedures, the estimated bias of parameters ${\lambda }_1,{\lambda }_2,\delta$ reduces as n grows.
• For parametric set-I, the estimated bias of parameter ${\lambda }_1$ under LSE, WLSE is negative, for Set II ${\lambda }_1$ and $\delta$ under all three estimation methods and for set III, the estimated bias of parameter $\delta$ is negative (see Figure 9, Figure 11 and Figure 13).
• Figure 9 and Figure 10 show the bias and MSE of ${\tilde{\lambda }}_1,{\tilde{\lambda }}_2,$ and $\tilde{\delta }$, for parametric Set-I and the WLSE always has the smallest value of bias and MSE of all estimators.
• In the second scenario, the MLE estimators of ${\lambda }_2$ is over-estimated, while MSE of ${\lambda }_2$ is highest among the three considered estimators (see Figure 11 and Figure 12).
• The estimators of ${\lambda }_1$ are over-estimated in the third scenario, however the over and under estimation of ${\lambda }_2$ and $\delta$ are seen among the three investigated estimators, and the WLSE always has the minimum value of bias of all estimators (see Figure 13).
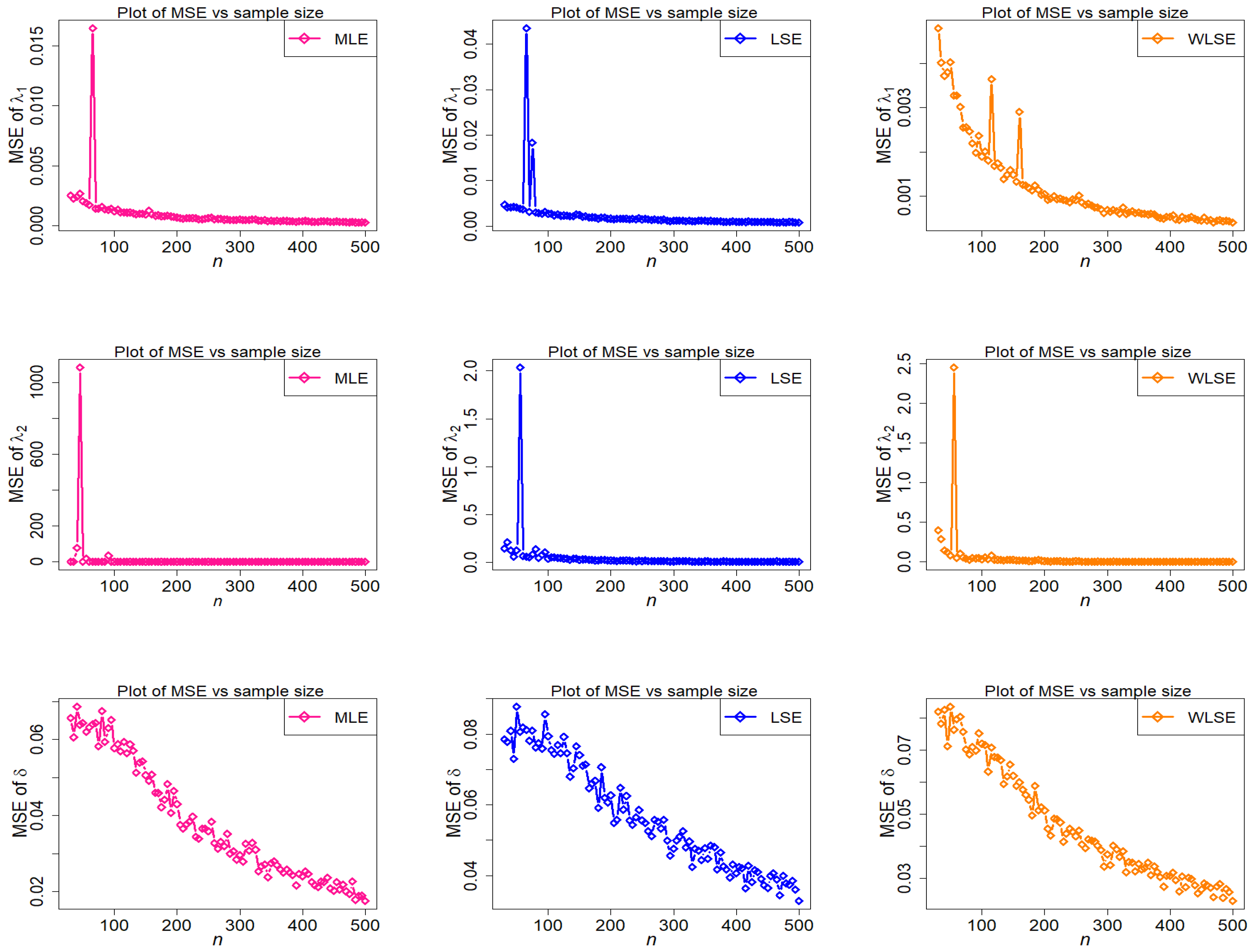
• Among the three estimators evaluated, the MSE of ${\lambda }_1$ is the greatest (see Figure 14).
• The MSE of ${\tilde{\lambda }}_2$ is strongly stimulated and higher under MLE and LSE estimation methods when $n<50$ (see Figure 10).
• Figure 13 and Figure 14 demonstrate the influence of choice of parameters on the estimation approaches, here bias and MSEs are comparatively low among the selected set of parameters.
• Some big shifts in MSEs of considered estimators under MLE, LSE, and WLSE are observed when $n<50$.
• In terms of bias, the WLSE’s performance is relatively favorable.
• Furthermore, when n increases, the MSE for all three estimating strategies decreases, satisfying the consistency criteria (Figure 10, Figure 12 and Figure 14).
• In all estimating methodologies, the difference between estimates and stated parameters reduces as n rises.
• As n approaches infinity, WLSE estimation is frequently better in terms of bias and MSE when likened to other estimation methods for all given parameter values.
• The estimated MSEs of parameters ${\tilde{\lambda }}_1,{\tilde{\lambda }}_2,$ and $\tilde{\delta }$ under the MLE estimation technique decrease quickly as n increases, demonstrating the effectiveness of the MLE procedure.

The final conclusion drawn from the foregoing figures is that, as n rises, estimated bias and MSE graphs for estimators ${\tilde{\lambda }}_1$, ${\tilde{\lambda }}_2$, and $\tilde{\delta }$ finally approach zero for all estimating methods. This demonstrates the accuracy of both the estimating methods and the numerical computations for the TC-MAM parameters.

5. Applications

We demonstrate the flexibility of the TC-MAM in this section by examining a real dataset. The TC-MAM distribution is compared to competing models, such as the two component mixture of Shanker distribution (2C-MSM), the two component mixture of exponential model (2-CMEM), and the two component mixture of Lindley distribution (2C-MLM) using the R function maxLik(). The -Log-likelihood (-LL), the AIC, BIC, and AICC have all been used to compare these models. The model having the least quantities of above-mentioned goodness-of-fit (GoF) measures may be the best fit for the real dataset.

Dataset: There are 56 observations in this dataset pertaining to the burning velocity of various chemical substances. The laminar flame speed at the specified composition, temperature, and pressure circumstances is the burning speed/velocity. It lowers as the inhibitor concentration rises, and it may be observed directly by analysing the pressure distribution in the spherical vessel and monitoring the flame propagation. We consider a real-life dataset which represents the burning velocity (cm/s) of several chemical compounds to show the TC-MAM distribution’s suitability. This dataset is extracted from https://www.cheresources.com/mists.pdf (accessed on 4 September 2022) and the data are as follows: 68, 61, 64, 55, 51, 68, 44, 50, 82, 60, 89, 61, 54, 166, 66, 50, 87, 48, 42, 58, 46, 67, 46, 46, 44, 48, 56, 47, 54, 47, 89, 38, 108, 46, 40, 44, 312, 41, 31, 40, 41, 40, 56, 45, 43, 46, 46, 46, 46, 52, 58, 82, 71, 48, 39, and 41 [24,25,26,27] contains further data applications. The MLEs for the TC-MAM and GoF measures are shown in Table 1. The TC-MAM clearly outperforms the 2-CMSM, 2-CMEM, and 2-CMLM, as shown in Table 1. The profiles of the log-likelihood function (PLLF) based on the dataset that confirm the conclusions of Table 1 are shown in Figure 15. Figure 15 and Figure 16 show a graphical illustration of MLE existence and uniqueness, respectively. To summarize, the TC-MAM emerges as the better model for the dataset, indicating its usefulness in a real-world setting. We can deduce from this graphical representation and results obtain from Table 1 that the TC-MAM is a better fit for the dataset in consideration.

Table 1. MLEs, and GoF statistics for the Dataset I.

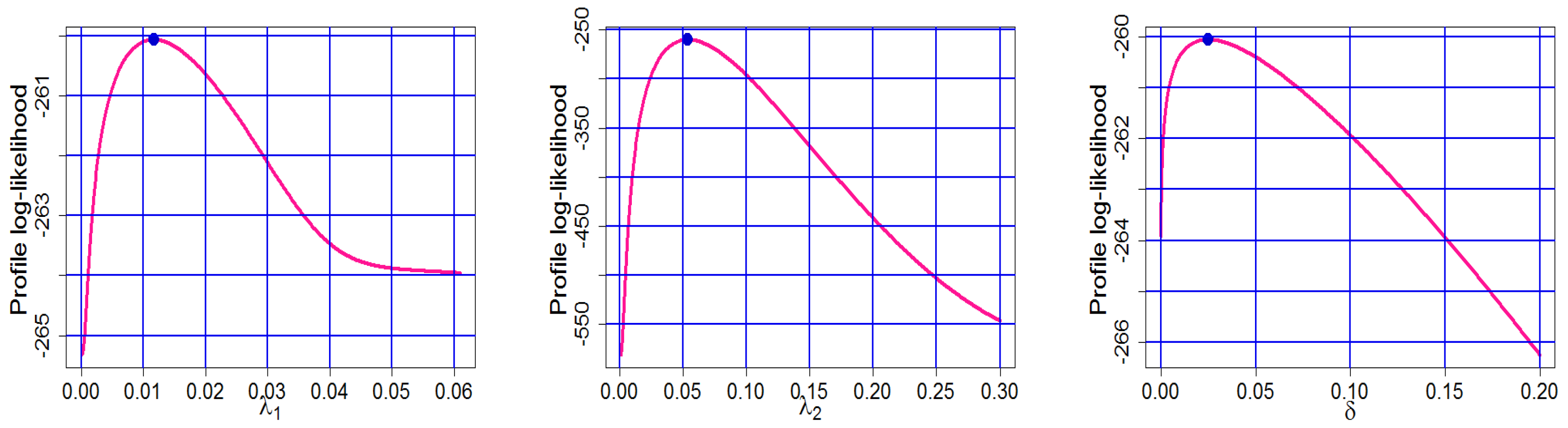
Distributions		MLEs	$-\mathit{L}\mathit{L}$	AIC	BIC	AICC
TC-MAM	${\tilde{\lambda }}_1$	0.011647	260.0557	526.1114	532.1875	526.5729
	${\tilde{\lambda }}_2$	0.053562
	$\tilde{\delta }$	0.024836
2C-MSM	${\tilde{\lambda }}_1$	0.008656	269.2051	544.4102	550.4863	544.8717
	${\tilde{\lambda }}_2$	0.035161
	$\tilde{\delta }$	0.023762
2C-MLM	${\tilde{\lambda }}_1$	0.008684	270.0022	546.0045	552.0805	546.4659
	${\tilde{\lambda }}_2$	0.034539
	$\tilde{\delta }$	0.023282
2C-MEM	${\tilde{\lambda }}_1$	0.016401	286.1761	578.3523	584.4283	578.8137
	${\tilde{\lambda }}_2$	0.016396
	$\tilde{\delta }$	0.746712

Figure 15. The plots of PLLF for Dataset.

Figure 16. The graphs of score functions cross the horizontal axis at ${\tilde{\lambda }}_1,{\tilde{\lambda }}_2,$ and $\tilde{\delta }$ of Dataset.

6. Conclusions

In this investigation, we used three estimated techniques: MLE, LSE, and WLSE to work on two component mixtures of Akash models. In particular, the Akash mixing model’s statistical and reliability features were achieved, such as central moments, Cumulants, Cumulant Generating Function, Probability Generating Function, Mean Time to Failure, Factorial Moment Generating Function, Coefficient of variation, Mills ratio, skewness and kurtosis, Reversed Hazard Rate Function, and Mean Residual Life. To investigate and assess the estimating approaches’ performance, a simulation study with 1000 iterations was performed and it was noted that when n increases, the estimated MSEs of parameters ${\tilde{\lambda }}_1,{\tilde{\lambda }}_2,$ and $\tilde{\delta }$ under the MLE estimation technique rapidly decrease, illustrating the efficiency of the MLE procedure. As a result, we found that estimating model unknown parameters with regards of accuracy and consistency, the MLE approach surpassed the rest. Furthermore, we used real datasets to explain the utility of the underlying mixture model.