A Comparative Study of Several Classical, Discrete Differential and Isogeometric Methods for Solving Poisson’s Equation on the Disk
Abstract
:1. Introduction
- a qualitative comparison between classical finite elements, a DDG approach and four isogeometric constructions;
- an investigation of quadrature formulas for subdivision IgA finite elements;
- implementation of an IgA method for functions on complex domains that is based on constructions and yields convergence, also at irregular points; this improved convergence is confirmed for an L-shaped domain and for an elastic plate with a circular hole;
- implementation of an IgA method with singular parameterization at irregular points that yields convergence also at irregular points.
Overview
2. Classical Finite and DDG Elements
2.1. Quadratic Triangular Elements
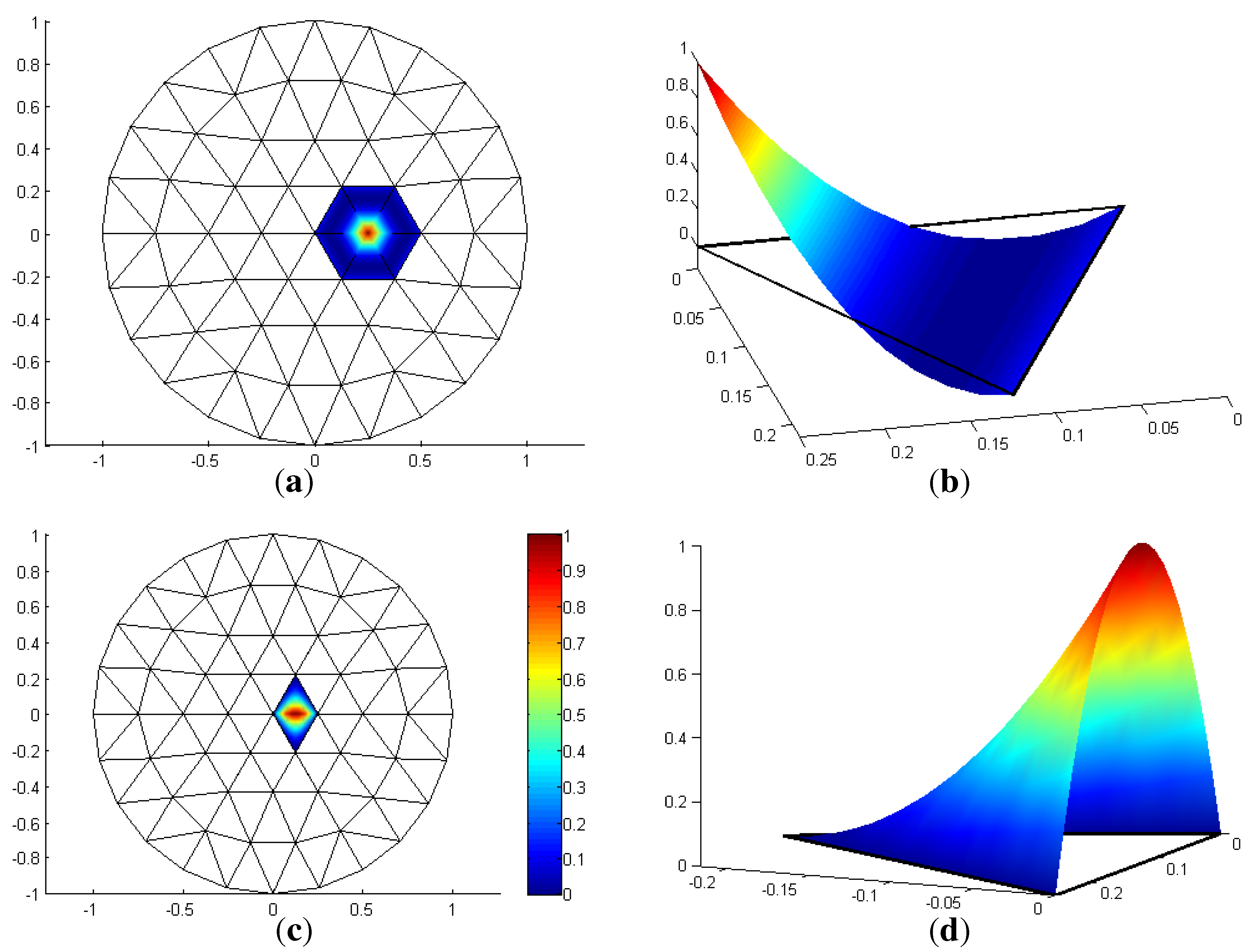
2.2. Hsieh–Clough–Tocher Elements
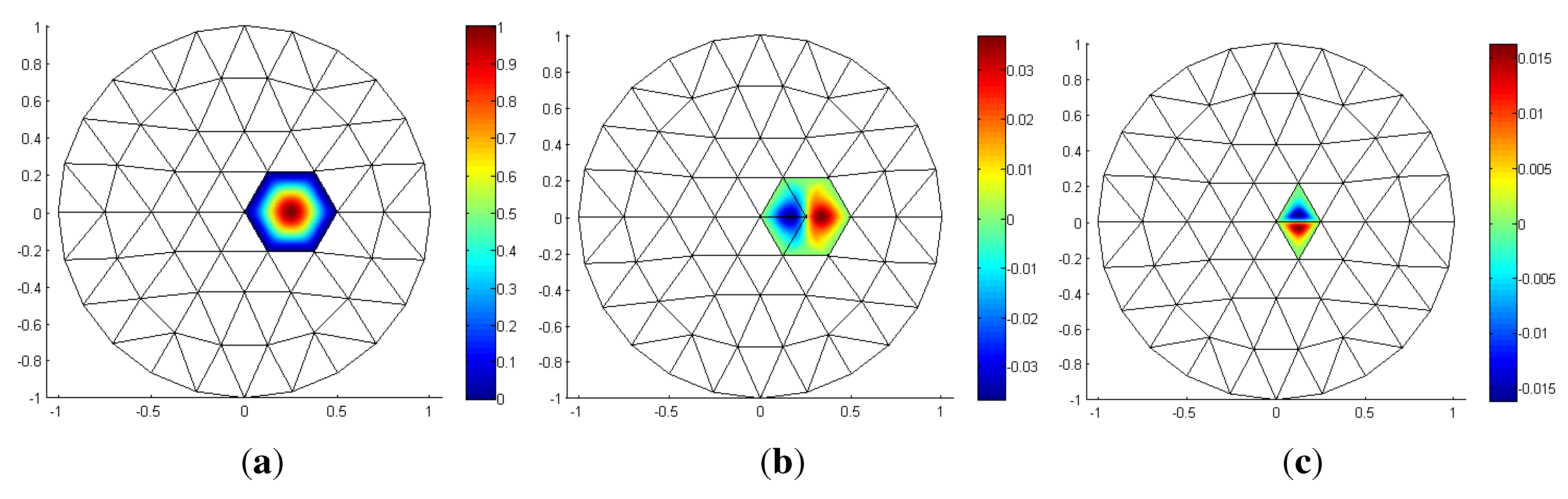
2.3. The Discrete Differential Geometry Approach
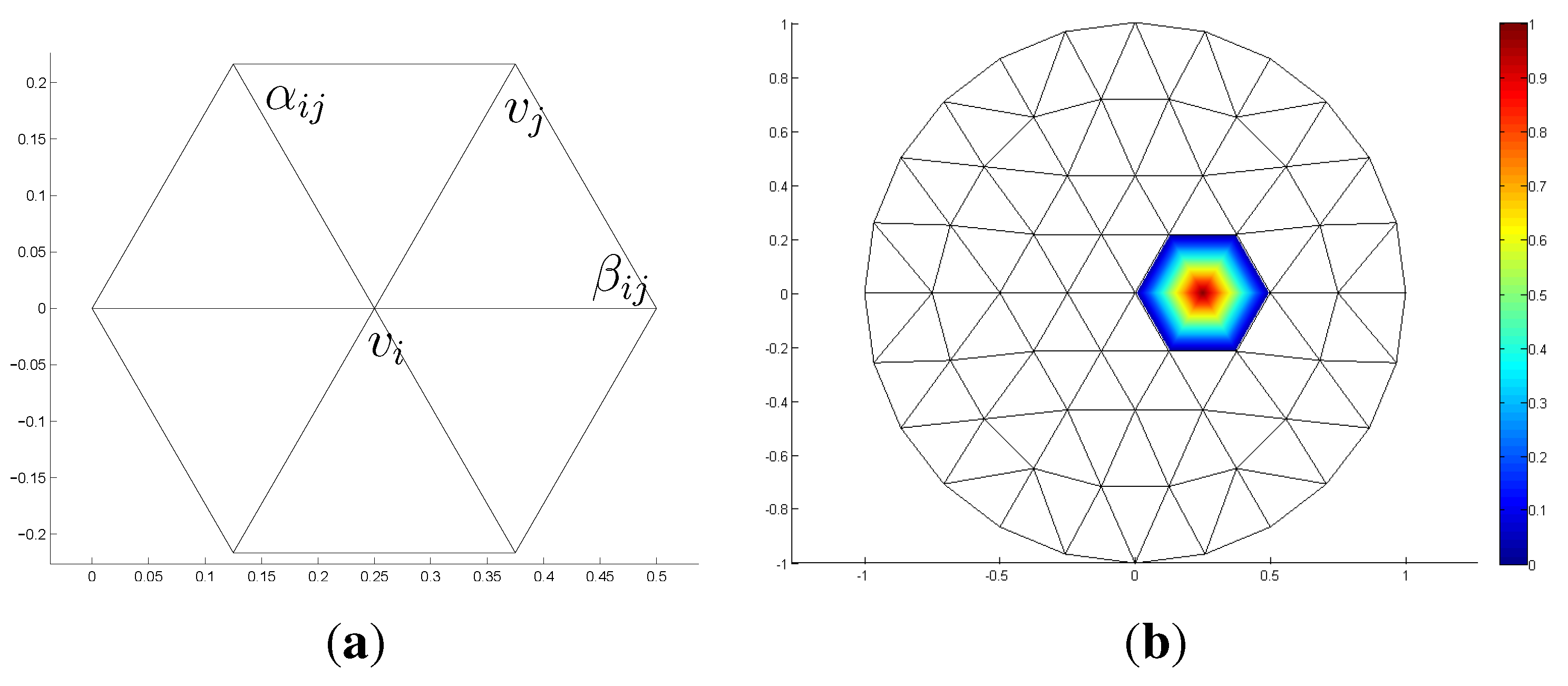
3. The Isogeometric Approach

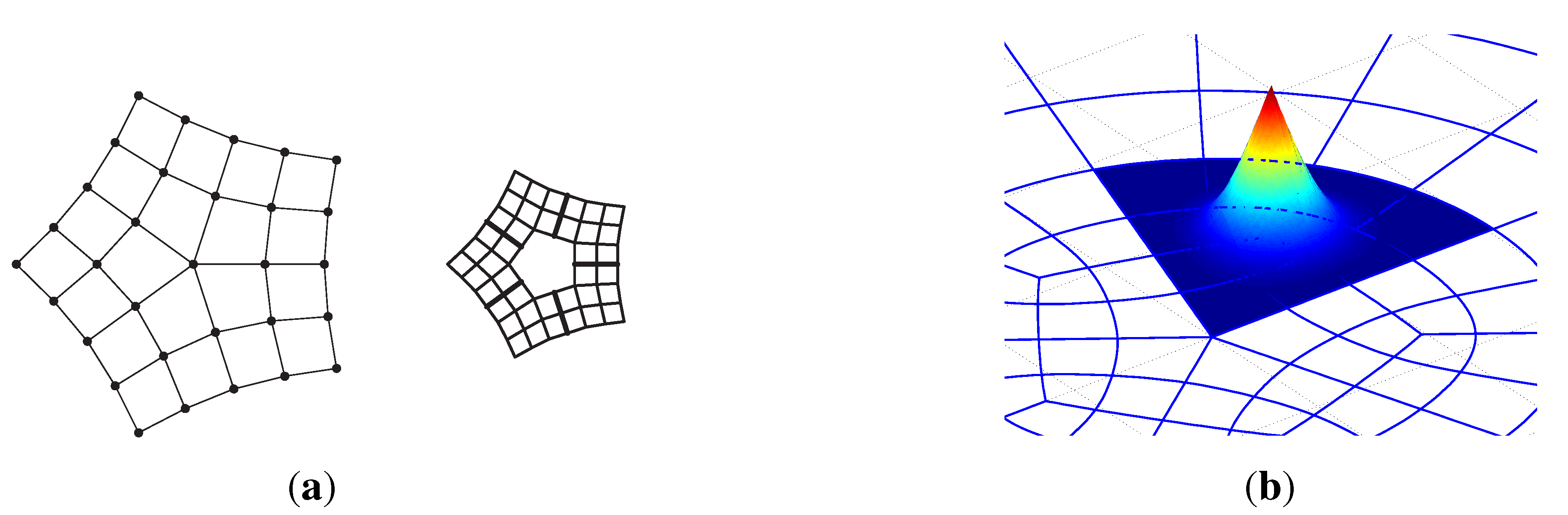
3.1. Bi-3 Elements That Are at Extraordinary Points
3.2. Catmull–Clark Elements

| Depth | ||
|---|---|---|
| 3 | 893.063 | 476.26 |
| 5 | 100.44 | 81.193 |
| 7 | 70.395 | 47.004 |
| 9 | 70.073 | 43.992 |
3.3. Higher-Order Elements
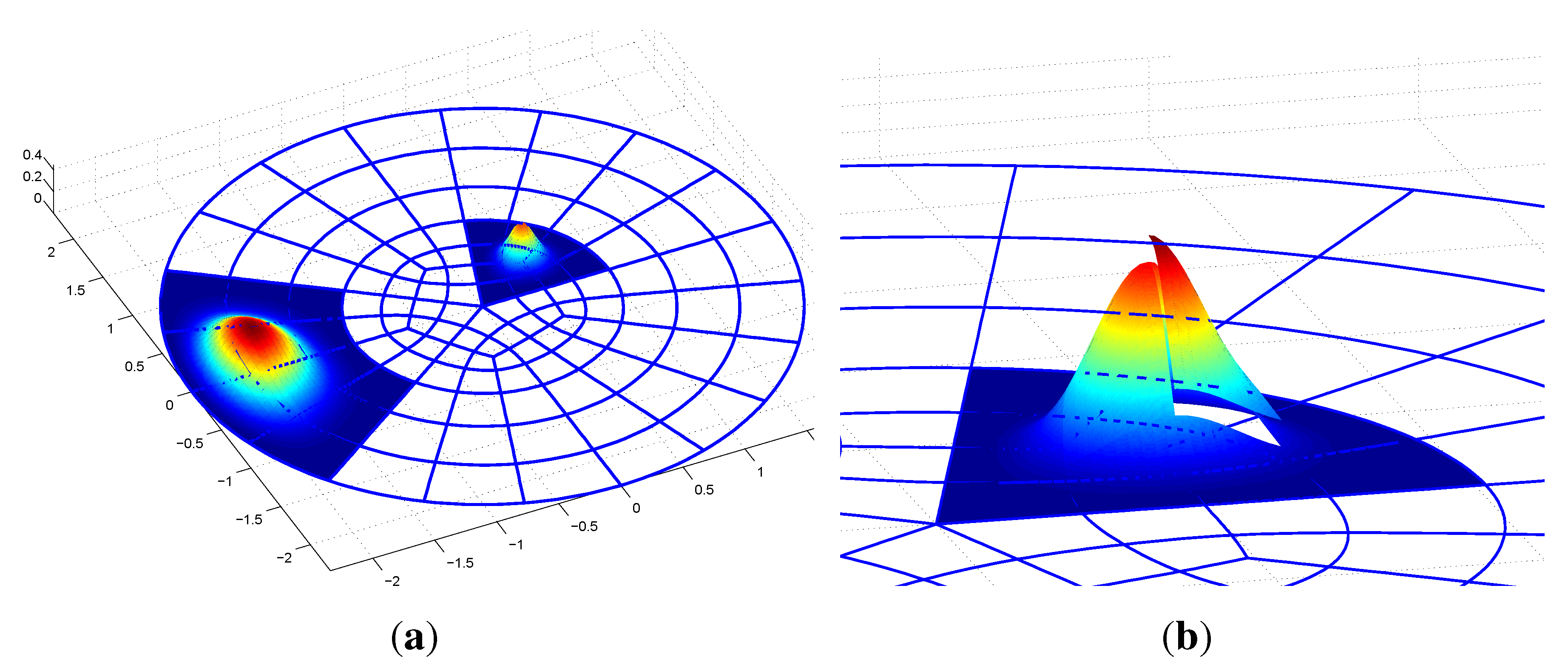
3.4. Polar Elements

4. Solving the Poisson Equation
5. Numerical Results and Comparison
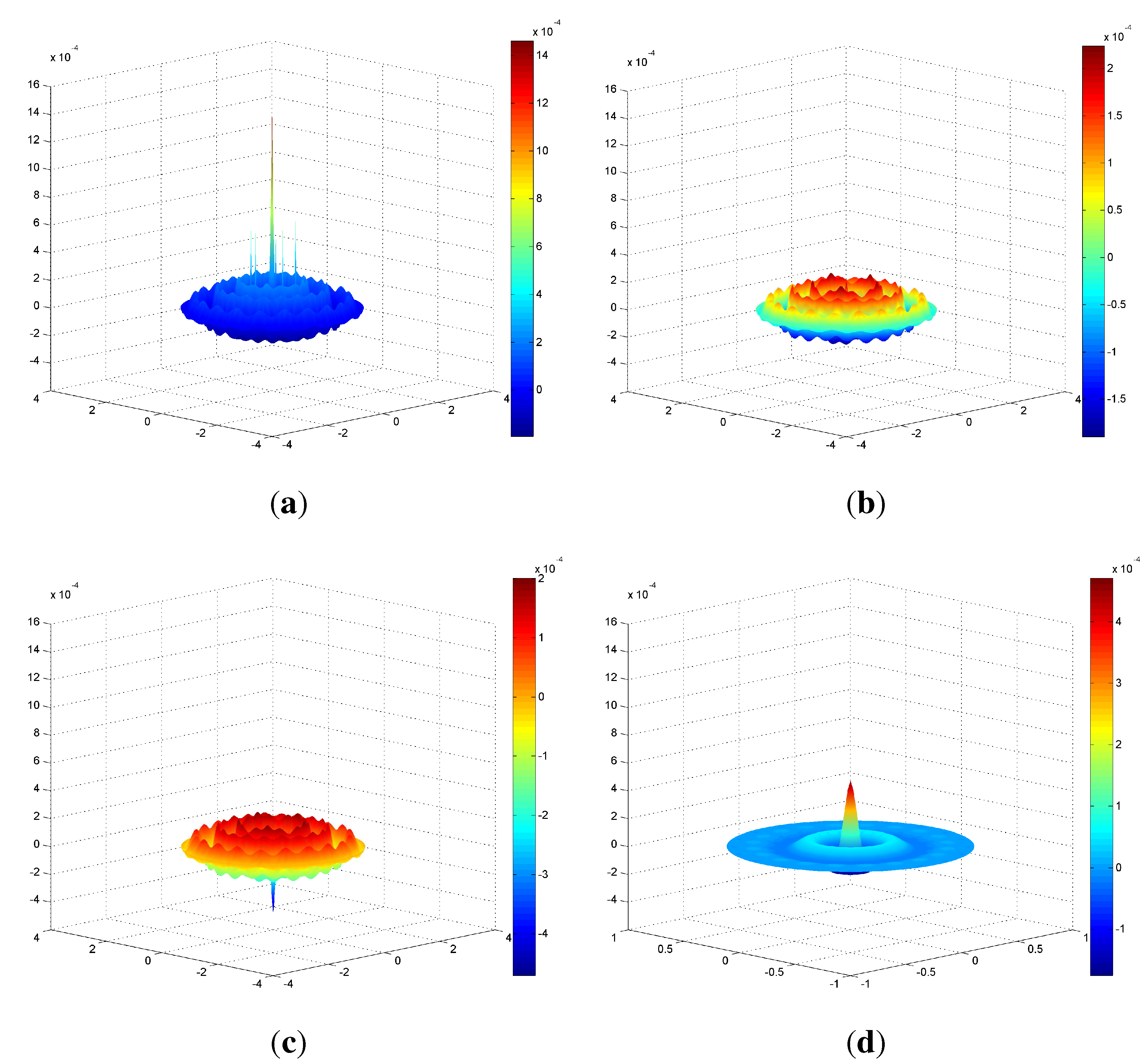
5.1. Correct Gauss Quadrature for Catmull–Clark Subdivision
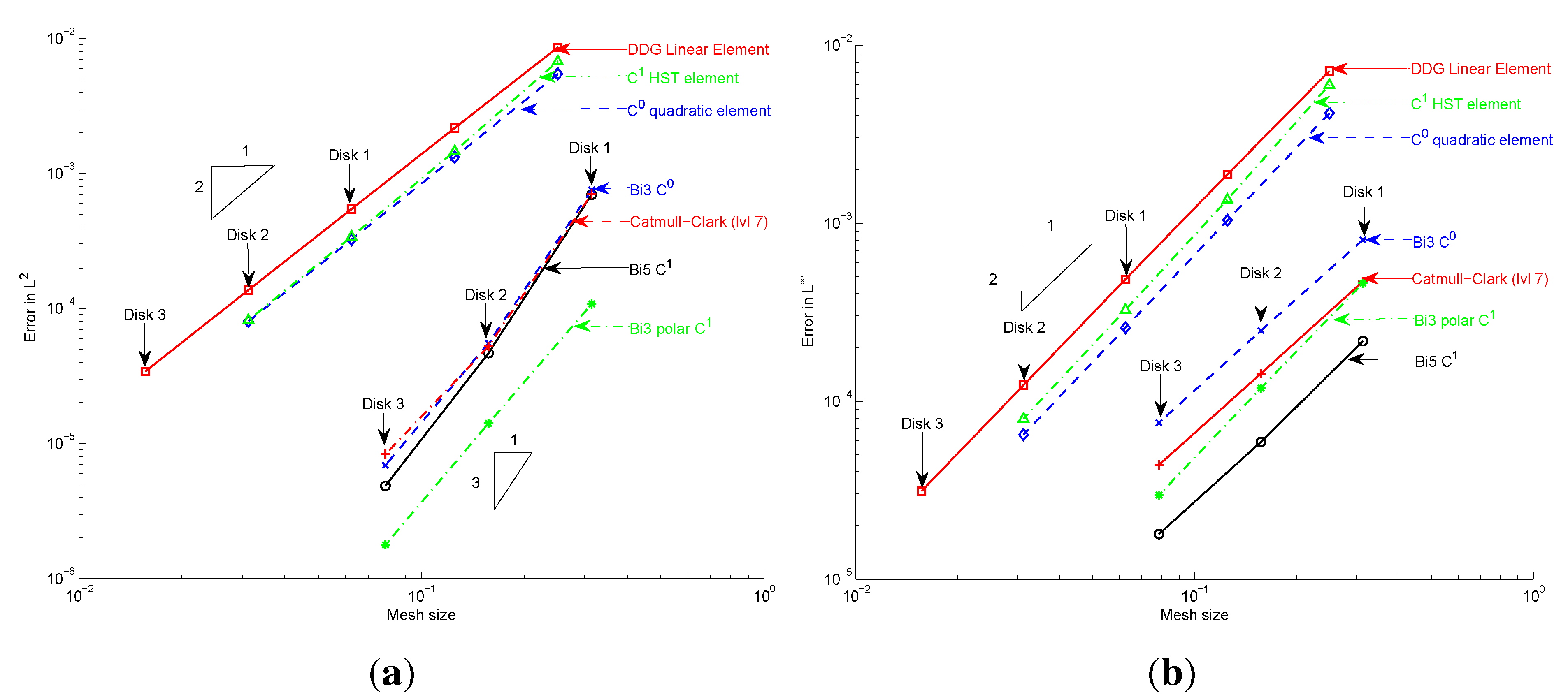
5.2. Convergence Rates
5.3. Complexity

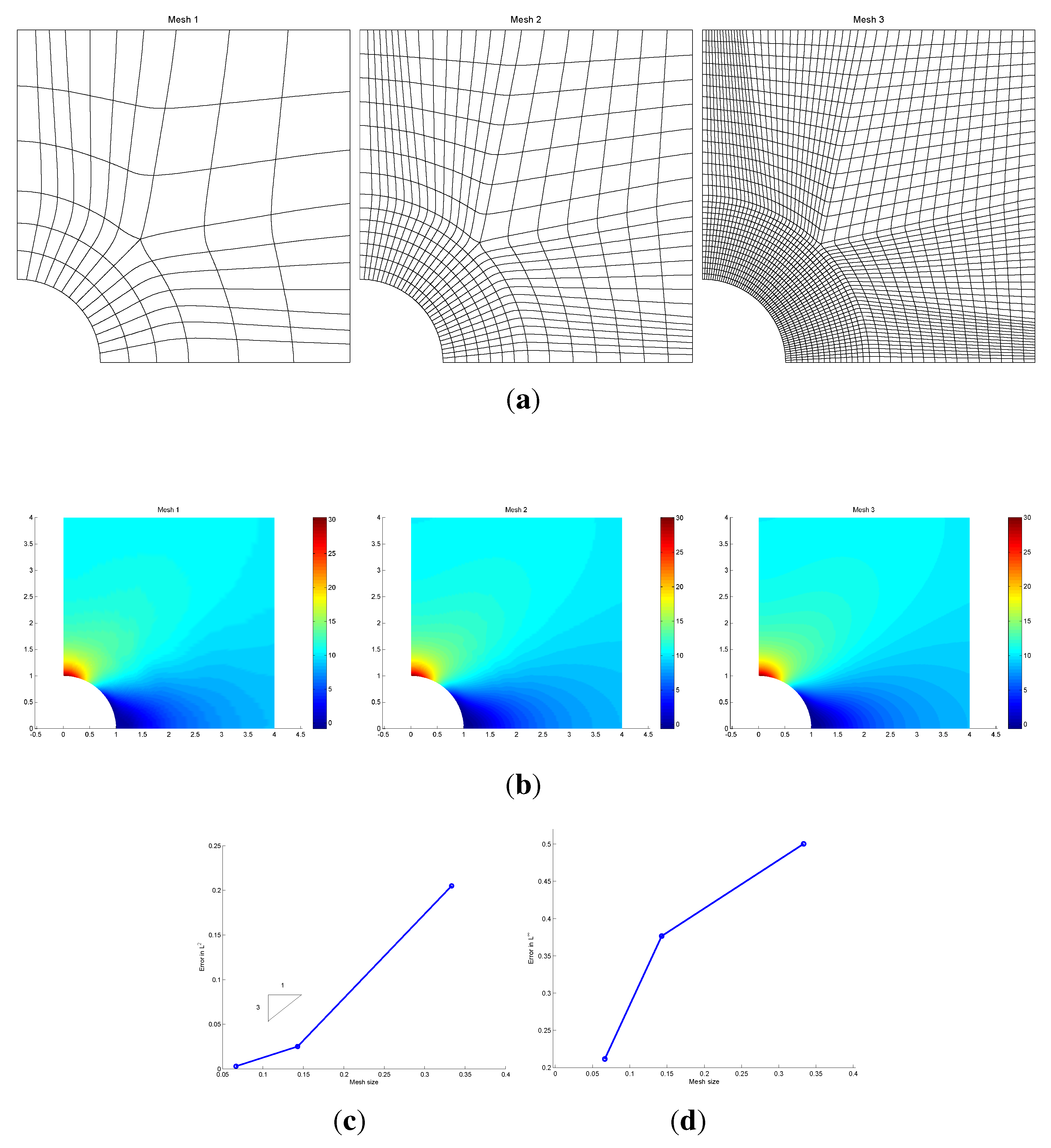
5.4. The bi-3/bi-5 Elements on the L-shape and on the Elastic-Plate-with-Hole
6. Conclusions

Acknowledgments
Author Contributions
- a qualitative comparison between classical finite elements, a DDG approach and four isogeometric constructions;
- an investigation of quadrature formulas for subdivision IgA finite elements;
- implementation of an IgA method for functions on complex domains that is based on constructions and yields convergence, also at irregular points; this improved convergence is confirmed for an L-shaped domain and for an elastic plate with a circular hole;
- implementation of an IgA method with singular parameterization at irregular points that yields convergence also at irregular points.
Conflicts of Interest
References
- Pinkall, U.; Polthier, K. Computing Discrete Minimal Surfaces and Their Conjugates. Exp. Math. 1993, 2, 15–36. [Google Scholar] [CrossRef]
- Bobenko, A.I.; Suris, Y.B. Discrete Differential Geometry: Integrable Structure; AMS Bookstore: Providence, RI 02904-2294 U.S.A, 2008; Volume 98. [Google Scholar]
- Kraft, R. Adaptive and linearly independent multilevel B-splines. In Surface Fitting and Multiresolution Methods; Vanderbilt University Press: Nashville, TN, USA, 1997; pp. 209–218. [Google Scholar]
- Sederberg, T.W.; Cardon, D.L.; Finnigan, G.T.; North, N.S.; Zheng, J.; Lyche, T. T-spline simplification and local refinement. ACM Trans. Graph. 2004, 23, 276–283. [Google Scholar] [CrossRef]
- Dokken, T.; Lyche, T.; Pettersen, K.F. Polynomial splines over locally refined box-partitions. Comput. Aided Geom. Des. 2013, 30, 331–356. [Google Scholar] [CrossRef]
- Giannelli, C.; Jüttler, B.; Speleers, H. THB–splines: The truncated basis for hierarchical splines. Comput. Aided Geom. Des. 2012, 29, 485–498. [Google Scholar] [CrossRef]
- Zienkiewicz, O. C. (2001) Displacement and equilibrium models in the finite element method by B. Fraeijs de Veubeke, Chapter 9, Pages 145–197, of Stress Analysis. Zienkiewicz, O. C., Holister, G. S., Eds.; John Wiley & Sons, 1965; In Int. J. Numer. Meth. Engng.; Volume 52, pp. 287–342. [Google Scholar] [CrossRef]
- Farin, G.E. Curves and Surfaces for CAGD: A Practical Guide, 5th ed.; The Morgan Kaufmann Series in Computer Graphics and Geometric Modeling; Morgan Kaufmann Publishers: Burlington, MA, USA, 2001; pp. xvii–497. [Google Scholar]
- Braess, D. Finite Elements: Theory, Fast Solvers, and Applications in Solid Mechanics; Cambridge University Press: New York, USA, 2007. [Google Scholar]
- Alfeld, P.; Schumaker, L.L. Smooth macro-elements based on Powell–Sabin triangle splits. Adv. Comput. Math. 2002, 16, 29–46. [Google Scholar] [CrossRef]
- Lai, M.J.; Schumaker, L.L. Spline Functions on Triangulations; Cambridge University Press: New York, USA, 2007; Volume 110. [Google Scholar]
- Speleers, H.; Manni, C.; Pelosi, F.; Sampoli, M.L. Isogeometric analysis with Powell–Sabin splines for advection–diffusion–reaction problems. Comput. Methods Appl. Mech. Eng. 2012, 221, 132–148. [Google Scholar] [CrossRef]
- Jaxon, N.; Qian, X. Isogeometric analysis on triangulations. Comput.-Aided Des. 2014, 46, 45–57. [Google Scholar] [CrossRef]
- Wardetzky, M.; Mathur, S.; Kälberer, F.; Grinspun, E. Discrete Laplace operators: no free lunch. In Proceedings of the Fifth Eurographics Symposium on Geometry Processing, Barcelona, Spain, 4–6 July 2007; pp. 33–37.
- Desbrun, M.; Meyer, M.; Schröder, P.; Barr, A.H. Implicit fairing of irregular meshes using diffusion and curvature flow. In Proceedings of the 26th Annual Conference on Computer Graphics and Interactive Techniques, Los Angeles, CA, USA, 8–13 August 1999; ACM Press/Addison-Wesley Publishing Co.: New York, NY, USA, 1999; pp. 317–324. [Google Scholar]
- Polthier, K. Computational aspects of discrete minimal surfaces. Glob. Theory Minimal Surf. 2005, 2, 65–111. [Google Scholar]
- Xu, G. Convergence of discrete Laplace-Beltrami operators over surfaces. Comput. Math. Appl. 2004, 48, 347–360. [Google Scholar] [CrossRef]
- Wardetzky, M. Convergence of the cotangent formula: An overview. In Discrete Differential Geometry; Birkhäuser: Basel, Switzerland, 2008; pp. 275–286. [Google Scholar]
- Crane, K.; de Goes, F.; Desbrun, M.; Schröder, P. Digital Geometry Processing with Discrete Exterior Calculus. In Proceedings of the SIGGRAPH ’13 Special Interest Group on Computer Graphics and Interactive Techniques Conference, Anaheim, CA, USA, 21–25 July 2013; ACM: New York, NY, USA, 2013. [Google Scholar]
- Grinspun, E.; Hirani, A.N.; Desbrun, M.; Schröder, P. Discrete Shells. In Proceedings of the Eurographics/SIGGRAPH Symposium on Computer Animation, San Diego, CA, USA, 26–27 July 2003; Breen, D., Lin, M., Eds.; Eurographics Association: San Diego, CA, USA, 2003; pp. 62–67. [Google Scholar]
- Pottmann, H.; Liu, Y.; Wallner, J.; Bobenko, A.; Wang, W. Geometry of multi-layer freeform structures for architecture. ACM Trans. Graph. 2007, 26. [Google Scholar] [CrossRef]
- Hirani, A.N. Discrete Exterior Calculus. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 2003. [Google Scholar]
- Grinspun, E.; Desbrun, M.; Polthier, K.; Schröder, P.; Stern, A. Discrete differential geometry: An applied introduction. In Proceedings of the ACM SIGGRAPH Course, Boston, MA, USA, 30 July–3 August 2006.
- Hughes, T.J.R.; Cottrell, J.A.; Bazilevs, Y. Isogeometric Analysis: CAD, Finite Elements, NURBS, Exact Geometry and Mesh Refinement. Comput. Methods Appl. Mech. Eng. 2005, 194, 4135–4195. [Google Scholar] [CrossRef]
- De Boor, C. A Practical Guide to Splines; Springer: New York, USA, 1978. [Google Scholar]
- Cirak, F.; Ortiz, M.; Schröder, P. Subdivision surfaces: A new paradigm for thin-shell finite-element analysis. Int. J. Numer. Methods Eng. 2000, 47, 2039–2072. [Google Scholar] [CrossRef]
- Cirak, F.; Scott, M.J.; Antonsson, E.K.; Ortiz, M.; Schröder, P. Integrated modeling, finite-element analysis, and engineering design for thin-shell structures using subdivision. Comput.-Aided Des. 2002, 34, 137–148. [Google Scholar] [CrossRef]
- Peters, J. Geometric Continuity. In Handbook of Computer Aided Geometric Design; Elsevier: Amsterdam, The Neitherlands, 2002; pp. 193–229. [Google Scholar]
- Karčiauskas, K.; Peters, J. Biquintic G2 surfaces. In Proceedings of the 14th IMA Conference on Mathematics of Surfaces, University of Birmingham, West Midlands, UK, 11–13 September 2013.
- Peters, J.; Reif, U. Subdivision Surfaces; Geometry and Computing; Springer-Verlag: New York, NY, USA, 2008; Volume 3, pp. i–204. [Google Scholar]
- Grinspun, E.; Krysl, P.; Schröder, P. CHARMS: A simple framework for adaptive simulation. ACM Trans. Graph. 2002, 21, 281–290. [Google Scholar] [CrossRef]
- Burkhart, D.; Hamann, B.; Umlauf, G. Iso-geometric Finite Element Analysis Based on Catmull-Clark : Subdivision Solids. Comput. Graph. Forum 2010, 29, 1575–1584. [Google Scholar] [CrossRef]
- Burkhart, D. Subdivision for Volumetric Finite Elements. Ph.D. Thesis, University of Kaiserslautern, Kaiserslautern, Germany, 2011. [Google Scholar]
- Wawrzinek, A.; Hildebrandt, K.; Polthier, K. Koiter’s Thin Shells on Catmull-Clark Limit Surfaces. In Proceedings of the Vision, Modeling, and Visualization Workshop 2011, Berlin, Germany, 4–6 October 2011; pp. 113–120.
- Dikici, E.; Snare, S.R.; Orderud, F. Isoparametric finite element analysis for Doo-Sabin subdivision models. In Proceedings of the 2012 Graphics Interace Conference, Toronto, ON, Canada, 28–30 May 2012; Canadian Information Processing Society: Toronto, ON, Canada, 2012; pp. 19–26. [Google Scholar]
- Vetter, R.; Stoop, N.; Jenni, T.; Wittel, F.K.; Herrmann, H.J. Subdivision shell elements with anisotropic growth. 2012; arXiv preprint arXiv:1208.4434. [Google Scholar]
- Barendrecht, P.J. IsoGeometric Analysis with Subdivision Surfaces; Eindhoven University of Technology: Eindhoven, The Netherlands, 2013. [Google Scholar]
- Karčiauskas, K.; Peters, J. Bi-5 Quad-Mesh Smoothing; Technical Report REP-2014-571; Department CISE, University of Florida: Gainesville, FL, USA, 2014. [Google Scholar]
- Myles, A.; Karčiauskas, K.; Peters, J. Pairs of bi-cubic surface constructions supporting polar connectivity. Comput. Aided Geom. Des. 2008, 25, 621–630. [Google Scholar] [CrossRef]
- Takacs, T.; Jüttler, B. H2 regularity properties of singular parameterizations in isogeometric analysis. Graph. Models 2012, 74, 361–372. [Google Scholar] [CrossRef] [PubMed]
- Halstead, M.; Kass, M.; DeRose, T. Efficient, Fair Interpolation Using Catmull-Clark Surfaces. In Proceedings of the 20th Annual Conference on Computer Graphics and Interactive Techniques, Anaheim, CA, USA, 2–6 August 1993; ACM: New York, NY, USA, 1993; pp. 35–44. [Google Scholar]
- Bazilevs, Y.; Beirao da Veiga, L.; Cottrell, J.; Hughes, T.; Sangalli, G. Isogeometric analysis: Approximation, stability and error estimates for h-refined meshes. Math. Models Methods Appl. Sci. 2006, 16, 1031–1090. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Nguyen, T.; Karčiauskas, K.; Peters, J. A Comparative Study of Several Classical, Discrete Differential and Isogeometric Methods for Solving Poisson’s Equation on the Disk. Axioms 2014, 3, 280-299. https://doi.org/10.3390/axioms3020280
Nguyen T, Karčiauskas K, Peters J. A Comparative Study of Several Classical, Discrete Differential and Isogeometric Methods for Solving Poisson’s Equation on the Disk. Axioms. 2014; 3(2):280-299. https://doi.org/10.3390/axioms3020280
Chicago/Turabian StyleNguyen, Thien, Keçstutis Karčiauskas, and Jörg Peters. 2014. "A Comparative Study of Several Classical, Discrete Differential and Isogeometric Methods for Solving Poisson’s Equation on the Disk" Axioms 3, no. 2: 280-299. https://doi.org/10.3390/axioms3020280
APA StyleNguyen, T., Karčiauskas, K., & Peters, J. (2014). A Comparative Study of Several Classical, Discrete Differential and Isogeometric Methods for Solving Poisson’s Equation on the Disk. Axioms, 3(2), 280-299. https://doi.org/10.3390/axioms3020280




