Extension of One-Dimensional Models for Hyperelastic String Structures under Coulomb Friction with Adhesion

Abstract

A stretching behavior of knitted and woven textiles is modeled. In our work, the yarns are modeled as one-dimensional hyperelastic strings with frictional contact. Capstan law known for Coulomb’s friction of yarns is extended to an additional adhesion due to gluing of filaments on the yarn surface or some chemical reaction. Two-step Newton’s method is applied for the solution of the large stretching with sliding evolution in the contact nodes. The approach is illustrated on a hysteresis of knitted textile and on the force-strain curve for a woven pattern and both compared with experimental effective curves.

1. Introduction

We model knitted and woven fabrics using a network of thin fibers in contact with each other. Let us recall the state of the art in models and numerical methods in application to textiles. Programs exist for a 3-dimensional contact modeling between yarns and integrating it into the simulation of textile structures. Examples are “Wisetex” of the university of Leuven, Belgium, developed in the group of Stepan Lomov and “TexGen” of the university of Nottingham, UK. They allow (see [1,2]) a detailed simulation of the interaction between yarns. In the works of Damien Durvielle (for example [3]) and also in [4], geometrically exact beam models and contact evolution are implemented. Such beams with many degrees of freedom are appropriated for wires very well, while the models discussed in our paper are mostly appropriated for knitted fabrics under large stretching deformations. In works of Philippe Boisse (for example [5,6]) and also in [7], similar to our paper, the textile shell-elements are replaced by a network of hyper-elastic springs. However, the focus of our paper will be put on the contact sliding in the knots of a knitted textile and an additional adhesive force between yarns, which prohibits an immediate sliding in the contact nodes due to the difference in tensional load and helps to keep a pre-stress in yarns. Furthermore, this adhesive force can decay, imitating the transversal deformation of yarns, or just its reduction due to some mechanical action on a textile. We will not mention all works in the simulation of textiles and move to our specific modeling.

We combine three different aspects in the manuscript: large elastic deformations utilizing a non-linear elastic energy, contact evolution based on the quasi-static Coulomb’s friction law, and regularization by an adhesion-term for lower-dimensional objects, ropes or trusses.

Since the 18th century, Coulomb’s friction law for ropes is known. It is called Euler-Eytelwein or Capstan equation and can be derived from simple geometric projections of the normal and tangential forces. It is widely used in the modeling of yarns, wires and ropes, e.g., [4,8,9]. In the two last references, the Euler-Eytelwein law was extended to a spiral rope on a cylinder via geometrically exact beam models.

The solvability of such evolution contact problems and the computation scheme for the Capstan’s law was investigated and presented in [10] and illustrated in [11,12] by numerical examples for woven and knitted textiles.

In this paper, we extend the frictional model and the full numerical procedure to an adhesion force, given by some ”gluing” of fine filaments on the yarns’ surfaces or due to some chemical adhesion. After some sliding caused by a mechanical action, the adhesion force may reduce. Also the transversal deformation of yarns can entail its reduction. We consider two models, one with a given constant adhesion force and a model with such a decaying adhesion.

In a resent work [13], a contact of stretched membranes and adhesive interaction was considered, which also combines the adhesive phenomenon with lower dimensional flexible structures (analogically to 1-dimensional ropes, 2-dimensional membranes may have large elastic deformations, but do not provide any bending resistance). However, our extension in the direction of the adhesion is a modification of the Capstan equation, developed for ropes especially.

Our Capstan models with added adhesion show better agreement with the hysteresis measurements than the standard Capstan model, discussed in [8,10,14].

The Newton-Raphson method is applied for the solution of the large stretching with sliding evolution in the contact nodes. The method is performed in two steps: the elastic stretching under a fixed position of the contact nodes and then a sliding step at the contact nodes to equilibrate the tension forces from the both sides of the node. Here, the adhesion force plays an additional regularization factor. Additionally, a so-called continuation method was implemented for robuster convergence.

The algorithm is implemented in C++ programs developed by the authors and illustrated on numerical examples with knitted fabrics and compared with real experiments.

2. Materials and Methods

We deal with a network of hyperelastic thin strings in frictional contact. The whole energy of the system is built by the elastic energy and the dissipational energy due to friction.

2.1. Description of Geometry

The domain $\Omega$ is a union of fibers $\Omega ={\cup }_{i=1}^N{F}_i$, each fiber is a rod that consists of a group of segments (or elements) $e_i$. Each fiber possesses certain material properties, which will be described below.

Each segment e is defined by two nodes $q_r$ and $q_{\ell }$, undeformed length parameter $L^0$, actual (deformed) length $l=|q_r-q_{\ell }|$, and the area of its cross-section A. We denote the common nodes between the different fibers as contact nodes and the union of contact points by $S_C$. When considering multiple segments, the notations $e_i$, $L_i^0$ and $l_i$ will be used.

2.2. Statement of the Problem

We consider hyperelastic incompressible material (some models can be found , e.g., in [15] or [16]). In the one-dimensional case the elasticity model is defined by elastic energy density function $W\left(u^{\prime }\right)$, where u is the local displacement vector and $u^{\prime }$ is the displacement gradient of the element. Since our fabric is represented by a network of fibers or elements, $e_i$, its total elastic energy $U_{\mathrm{total}}$ is

$$\begin{array}{c}{U}_{\mathrm{total}}=\sum _i{\int }_{{}_{e_i}}W\left(u^{\prime }\right)d{x}_1,\end{array}$$

(1)

The governing principle is that the sum of total elastic energy of the net $U_{\mathrm{total}}$ and the frictional forces work is minimized over the displacements, subject to constraints representing the stretching process. We thus come to the minimization problem

$$\begin{array}{c}{U}_{\mathrm{total}}+\sum _{n_c}{F}_{\mathrm{friction}}\left|{\left[u\right]}_{\mathrm{tangential}}\right|\to \underset{u}{min}\end{array}$$

(2)

where ${\left[u\right]}_{\mathrm{tangential}}$ is relative tangential displacement of the fibers at the contact interface, N is reaction force at the contact interface.

2.3. Elasticity Model

In this section, we deal with the first term of the energy functional of (2). The basis of the numerical scheme is Finite Element Method for trusses as described in [15]. Since only longitudinal tensional stress component is relevant, an equivalent Finite Element formulation can be derived for forces in the elements instead of stresses. Connection between the longitudinal tensional stress and tensional force is given by the equation

$$\begin{array}{c}f\left({\lambda }_1\right)={\int }_{S\left({\lambda }_1\right)}\sigma \left({\lambda }_1\right)ds,{\lambda }_1=l/L^0\end{array}$$

(3)

where $S\left(\epsilon \right)$ is the cross-sectional area of the fiber and $\epsilon$ is the longitudinal principal stretch of the element. From incompressibility condition it follows that $S\left({\lambda }_1\right)=S\left(1\right){\lambda }_1$ and assuming that tensional stress component is constant in elements we obtain

$$\begin{array}{c}f\left({\lambda }_1\right)={\displaystyle \frac{\sigma \left({\lambda }_1\right)}{{\lambda }_1}}S\left(1\right),\end{array}$$

(4)

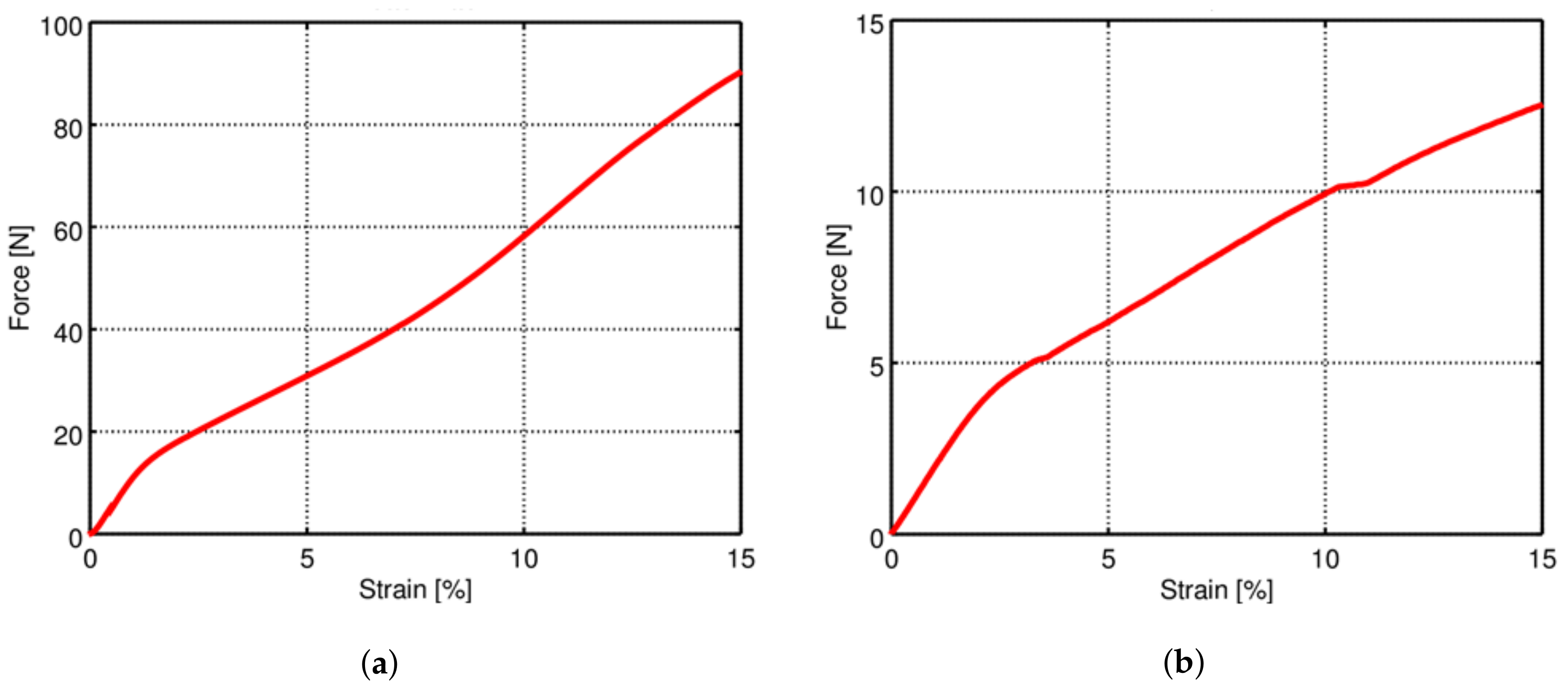
where $S\left(1\right)$ is cross-sectional area of undeformed element. Further, we assume that force curve is given from measurements and is a strictly monotonic function.

Following the scheme described in [15] (p. 313), we assume that truss elements’ displacement field is affine. For an element e with force-principal stretch curve $f\left({\lambda }_1\right)$, the total strain energy (1) reads

$$\begin{array}{c}{U}_e={\int }_0^{{\lambda }_1}f\left(x\right)L^{0}dx=L^0{\int }_0^{{\lambda }_1}f\left(x\right)dx.\end{array}$$

(5)

Each element has two nodes, one is denoted as “left” and other as “right”. Three spatial coordinates of left node in Global Coordinate System are denoted by $q_{\ell 1}$, $q_{\ell 2}$, $q_{\ell 3}$, analogously for coordinates of right node. Symbols “d” and “$-d$” will be used as variables for directions, i.e., if $d=r$, then $q_{dk}=q_{rk}$ and $q_{-dk}=q_{\ell k}$, k in $\{1,2,3\}$.

Then longitudinal principal stretch of the element can be represented as function of six variables $q_{\ell i}$, $q_{ri}$:

$$\begin{array}{c}{\lambda }_1={\displaystyle \frac{\sqrt{{(q_{\ell 1}-q_{r1})}^2+{(q_{\ell 2}-q_{r2})}^2+{(q_{\ell 3}-q_{r3})}^2}}{L^0}}.\end{array}$$

(6)

The derivatives of ${\lambda }_1\left(q\right)$ are required for linearization of the energy and read

$$\begin{array}{c}{\displaystyle \frac{\partial {\lambda }_1\left(q\left(e\right)\right)}{\partial q_{dk}}}={\displaystyle \frac{1}{L^0}}{\displaystyle \frac{q_{dk}-q_{-dk}}{\sqrt{{(q_{\ell 1}-q_{r1})}^2+{(q_{\ell 2}-q_{r2})}^2+{(q_{\ell 3}-q_{r3})}^2}}}.\end{array}$$

(7)

The derivatives of $U_e$ thus read

$$\begin{array}{c}{\displaystyle \frac{\partial U_e}{\partial q_{dk}}}=L^{0}f\left({\lambda }_1\right){\displaystyle \frac{\partial {\lambda }_1}{\partial q_{dk}}}.\end{array}$$

(8)

Linearization of $U_e$ is

$$\begin{array}{c}\delta U_e=\sum _{d,k}{\displaystyle \frac{f\left({\lambda }_1\right)(q_{dk}-q_{-dk})}{\sqrt{{(q_{\ell 1}-q_{r1})}^2+{(q_{\ell 2}-q_{r2})}^2+{(q_{\ell 3}-q_{r3})}^2}}}\delta q_{di}\end{array}$$

(9)

and equilibrium condition for the single element is

$$\begin{array}{c}\delta U_e-\sum _{d,k}{P}_{dk}\delta q_{dk}=0,\end{array}$$

(10)

where $P_{dk}$ are applied nodal forces.

Tangent stiffnesses K of the element, required to solve (10) with Newton-Raphson method are given by

$$\begin{array}{c}K=\left(\begin{array}{cc}Z& -Z\\ -Z& Z\end{array}\right),\end{array}$$

(11)

$$\begin{array}{c}Z={\displaystyle \frac{f}{l}}(I-c{c}^T)+{\displaystyle \frac{1}{l_0}}{\displaystyle \frac{df}{d\epsilon }}c{c}^T,\end{array}$$

(12)

$$\begin{array}{c}c={\displaystyle \frac{1}{l}}\left(\begin{array}{c}{q}_{\ell 1r1}\\ q_{\ell 2r2}\\ q_{\ell 3r3}\end{array}\right),\end{array}$$

(13)

where c is the direction vector of the element and $q_{d_1{k}_1{d}_2{k}_2}$ denote difference of corresponding variables: $q_{d_1{k}_1{d}_2{k}_2}=(q_{d_1{k}_1}-q_{d_2{k}_2})$. Together with (4), this is consistent with [15] (p. 320).

2.4. Friction Model

In this section, we deal with the second term of the energy functional of (2). On every element we define the tension force $T_e$ as:

$$T_e=f\left(\frac{l_e}{L_e^0}\right)$$

(14)

On each node n with neighboring elements $e_1$,$e_2$ we define

$$\begin{array}{cc}\hfill T_{\min }& =min(T_{e_1},T_{e_2})\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill T_{\max }& =max(T_{e_1},T_{e_2})\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill \left|\right[T\left]\right|& =T_{\max }-T_{\min }\hfill \end{array}$$

(17)

2.4.1. Capstan Equation

We consider the quasistatical contact problem with Coulomb friction.

Remark 1.

(on the quasistatical formulation of friction) The quasistatical contact problem with friction represents an incremental step of a discretization in time of a dynamical contact problem, see [17] (p. 29), therefore all the time-dependent terms may be dropped.

We include the frictional data into the total energy via a friction functional $j_t\left(u\right)={\int }_{S_C}\mu \left|{\sigma }_n\right|ds$, see [17]. The equilibrium problem thus reads:

$$\begin{array}{c}\mathrm{find}u\in \mathcal{K}:U\left(u\right)+j_t\left(u\right)\le U\left(v\right)+j_t\left(v\right),\forall v\in \mathcal{K},\end{array}$$

(18)

where u is a displacement vector, v is a test field, $\mathcal{K}$ is the set of admissible displacement fields, satisfying the non-penetration condition between the contacting elements.

For thin fibers, the friction model can be expressed in terms of tensional forces only. Consider a straight incompressible fiber clutched at certain point c with force N. Denote the difference of tension forces on the right and on the left of the point c as $\left[\mathbf{T}\right]$. Then we have

$$\begin{array}{c}\hfill \left|\left[\mathbf{T}\right]\right|\le \mu N,\begin{array}{c}\left|\left[\mathbf{T}\right]\right|<\mu N\Rightarrow \left[u_1\right]=0,\mathrm{a}\mathrm{stick}\mathrm{phase},\hfill \\ \left|\left[\mathbf{T}\right]\right|=\mu N\Rightarrow \exists \lambda >0\mathrm{such}\mathrm{that}\left[u_1\right]=-\lambda \left[\mathbf{T}\right],\mathrm{a}\mathrm{slip}\mathrm{phase}.\hfill \end{array}\end{array}$$

(19)

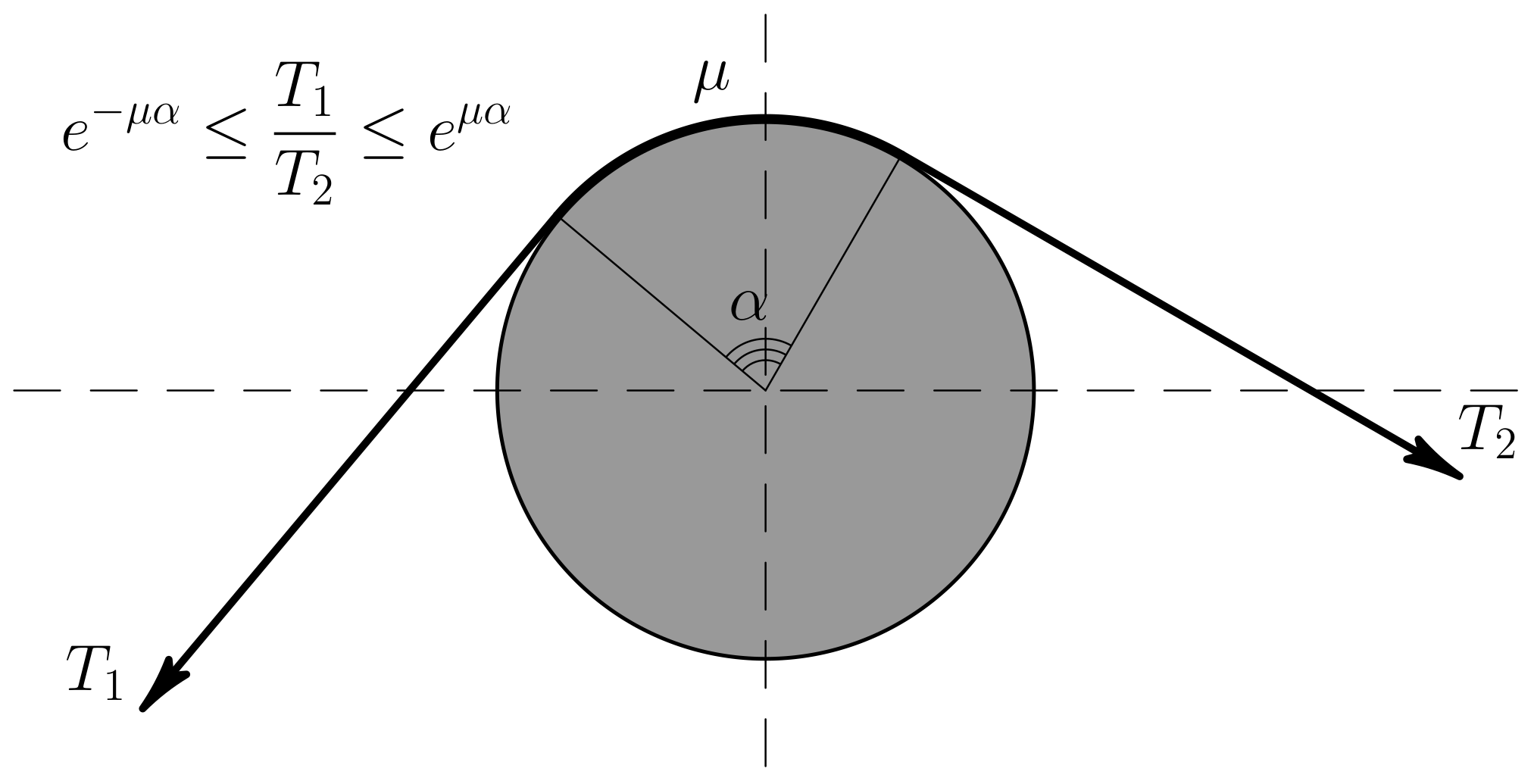
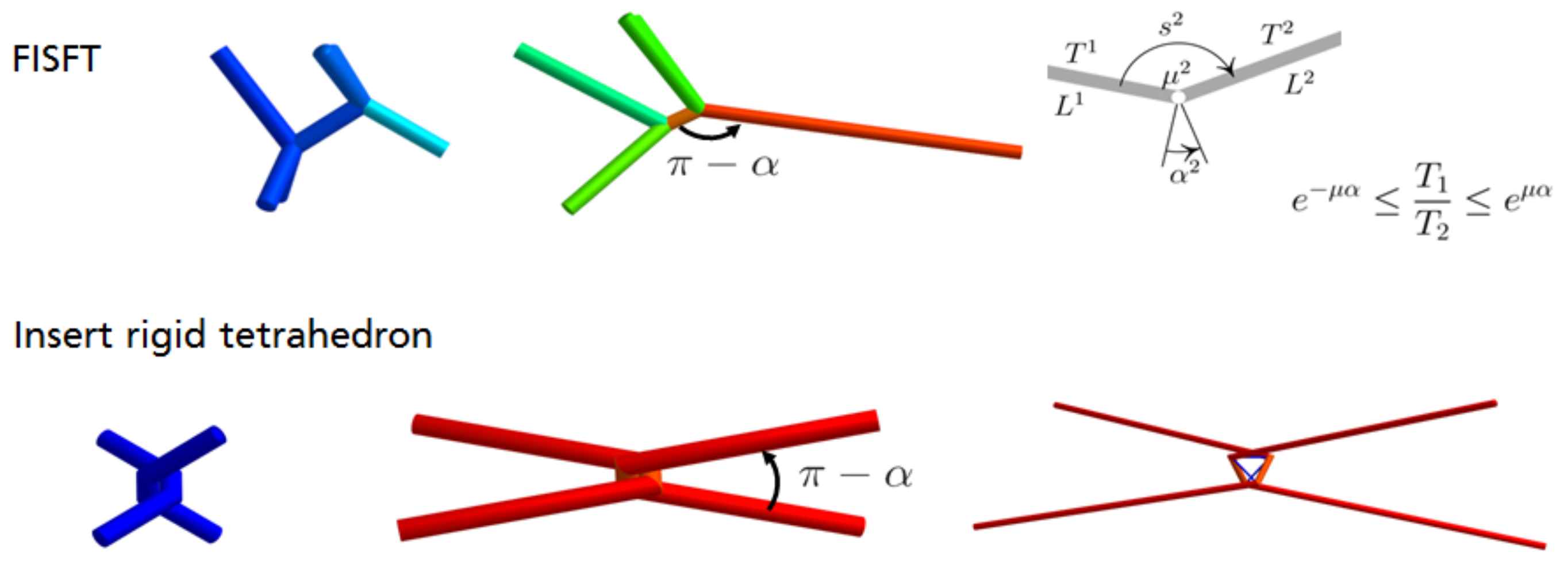
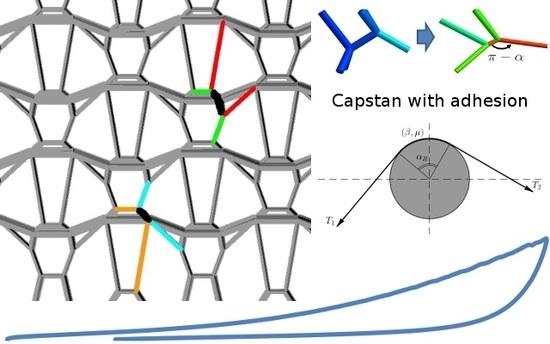
When the fiber is not straight, stick and slip conditions change their form. For the case of fiber in a contact with rigid cylindrical surface the friction stick or slip condition is given by the Euler-Eytelwein formula, also known as capstan equation or belt friction equation, see, e.g., [18]. It is illustrated in Figure 1. It has the following form:

$$\begin{array}{c}{e}^{-\mu \alpha }\le \left|{\displaystyle \frac{T_1}{T_2}}\right|\le e^{\mu \alpha },\begin{array}{c}{e}^{-\mu \alpha }<\left|{\displaystyle \frac{T_1}{T_2}}\right|<e^{\mu \alpha }\Rightarrow \left[u_1\right]=0,\mathrm{a}\mathrm{stick}\mathrm{phase},\hfill \\ e^{-\mu \alpha }=\left|{\displaystyle \frac{T_1}{T_2}}\right|\vee \left|{\displaystyle \frac{T_1}{T_2}}\right|=e^{\mu \alpha }\Rightarrow \exists \lambda >0\mathrm{s}.\mathrm{t}.\left[u_1\right]=-\lambda \left[\mathbf{T}\right],\mathrm{a}\mathrm{slip}\mathrm{phase},\hfill \end{array}\hfill \end{array}$$

(20)

where $\alpha$ defines the total angle, swept by the rope. We extrapolate this result for pairs of fibers in contact, where $\alpha$ is computed from angle between direction vectors of elements, adjacent to the contact node. The details will be provided further.

By the assumption on the geometry, the contact takes place only in nodes and never inside of elements. Any fiber is equilibrated iff (if and only if) for all pairs of the adjacent elements $e_1$ and $e_2$ of the fiber the friction stick condition from (20) is fulfilled:

$$\begin{array}{c}{e}^{-\mu \alpha }<\left|{\displaystyle \frac{T_1}{T_2}}\right|<e^{\mu \alpha },\end{array}$$

(21)

where $\mu$ is the friction coefficient between the fibers in contact and $\alpha =\pi -\gamma$. Here, $\gamma$ is the angle between the direction vectors of $e_1$ and $e_2$, starting from the contact point (see Figure 12 for an illustration in an example).

The slipping is modeled through redistribution of the material between the elements of the fiber, i.e., if the fiber is a sequence of elements $\{e_1,e_2,e_3,e_4,\dots ,e_N\}$ then their initial lengths $L_1^0,\dots ,L_N^0$ change to satisfy (21). This condition can be reformulated as an optimization problem.

Consider two adjacent elements $e_i$ and $e_{i+1}$. Let undeformed fiber length $\Delta L_i^0$ flow from element $e_i$ to element $e_{i+1}$. Then we observe that after this redistribution we have

$$\begin{array}{c}{l}_i^0=L_i^0-\Delta L_i^0+\Delta L_{i-1}^0,\end{array}$$

(22)

where $l_i^0$ denotes non-deformed length parameter after the redistribution. It is easy to see that the latter relation between $l_i^0$ and $L_i^0$ automatically ensures that the material conservation equation

$$\begin{array}{c}\sum _i{l}_i^0=\sum _i{L}_i^0\end{array}$$

(23)

holds.

Recall that the tension force in each element of the fiber is given by $f(l/L^0)$. The function $f\left(x\right)$ is assumed to satisfy following natural conditions: $f\left(1\right)=0$, $f\left(x\right)$ is strictly monotonic. Consider a function

$$J(\Delta L_1^0,\dots ,\Delta L_{N-1}^0)=\sum _{j=1}^{N-1}max{\left({\left(f\left(l_{j+1}\right)-e^{{\mu }_{j,j+1}{\alpha }_{j,j+1}}f\left(l_j\right)\right)}_{+},{\left(f\left(l_j\right)-e^{{\mu }_{j,j+1}{\alpha }_{j,j+1}}f\left(l_{j+1}\right)\right)}_{+}\right)}^2,$$

(24)

where ${(·)}_{+}$ means the positive part (zero, if the expression is negative). J is always non-negative. One can easily observe that point $(\Delta L_1^0,\dots ,\Delta L_{N-1}^0)$ satisfying

$$\begin{array}{c}{l}_1/l_1^0=l_2/l_2^0=\dots =l_N/l_N^0\end{array}$$

(25)

is a minimizer of J, and we have $J(\Delta L_1^0,\dots ,\Delta L_{N-1}^0)=0$, i. e. the minimum is attainable. However, this minimizer is in general not unique and not the desired one (one can observe that it corresponds to ${\mu }_{j,j+1}=0$).

If function f is smooth, $J\in C^1(\Delta L_1^0,\dots ,\Delta L_{N-1}^0)$. A problem

$$\begin{array}{c}J(\Delta L_1^0,\dots ,\Delta L_{N-1}^0)\to min\end{array}$$

(26)

is thus suitable for numerical treatment by gradient methods.

The gradient of J can be computed explicitly. Introduce notations

$$\begin{array}{c}{f}_j=f(l_j/l_j^0),J_j=max{\left({\left(f_{j+1}-e^{{\mu }_{j,j+1}{\alpha }_{j,j+1}}{f}_j\right)}_{+},{\left(f_j-e^{{\mu }_{j,j+1}{\alpha }_{j,j+1}}{f}_{j+1}\right)}_{+}\right)}^2.\end{array}$$

(27)

$J_j$ depends only on $\Delta L_{j-1}^0$, $\Delta L_j^0$ and $\Delta L_{j+1}^0$. We have

$$\begin{array}{c}\left(\begin{array}{c}{\displaystyle \frac{\partial J_j}{\partial \Delta L_{j-1}^0}}\\ {\displaystyle \frac{\partial J_j}{\partial \Delta L_j^0}}\\ {\displaystyle \frac{\partial J_j}{\partial \Delta L_{j+1}^0}}\end{array}\right)=2{\left(f_{j+1}-{\zeta }_j{f}_j\right)}_{+}\left(\begin{array}{c}{\zeta }_j{\gamma }_j\\ -{\gamma }_{j+1}-{\zeta }_j{\gamma }_j\\ {\gamma }_{j+1}\end{array}\right)+2{\left(f_j-{\zeta }_j{f}_{j+1}\right)}_{+}\left(\begin{array}{c}-{\gamma }_j\\ {\gamma }_j+{\zeta }_j{\gamma }_j+1\\ -{\zeta }_i{\gamma }_{j+1}\end{array}\right),\end{array}$$

(28)

$$\begin{array}{c}\mathrm{where}{\zeta }_j=e^{{\mu }_{j,j+1}{\alpha }_{j,j+1}},{\gamma }_i=f_i^{\prime }{\displaystyle \frac{l_i}{{\left(l_i^0\right)}^2}},\end{array}$$

(29)

for $2\le j\le N-2$. Cases $j=1$ and $j=N-1$ can be easily derived from the latter equation by omitting certain terms. The gradient of J is constructed from gradients of $J_j$ in obvious way, since $J=J_1+\dots +J_{N-1}$.

2.4.2. The Adhesive Friction Model

Consider two bodies in frictional contact with contact interface measure A and the total reaction force between the bodies N.

The adhesive term is a kind of Tresca friction, which is given by a known traction, a material characteristics, and should be multiplied by the contact measure. In our case, the contact area is one-dimensional manifold, A and the distributed force or traction is in $[N/m]$. However, the adhesive experiments with yarns are for specific yarn thicknesses and results are measured in Newton. Thus, the adhesion coefficient $\beta$ is chosen to be in Newton, with the adhesive force in a node being $\beta \alpha$. 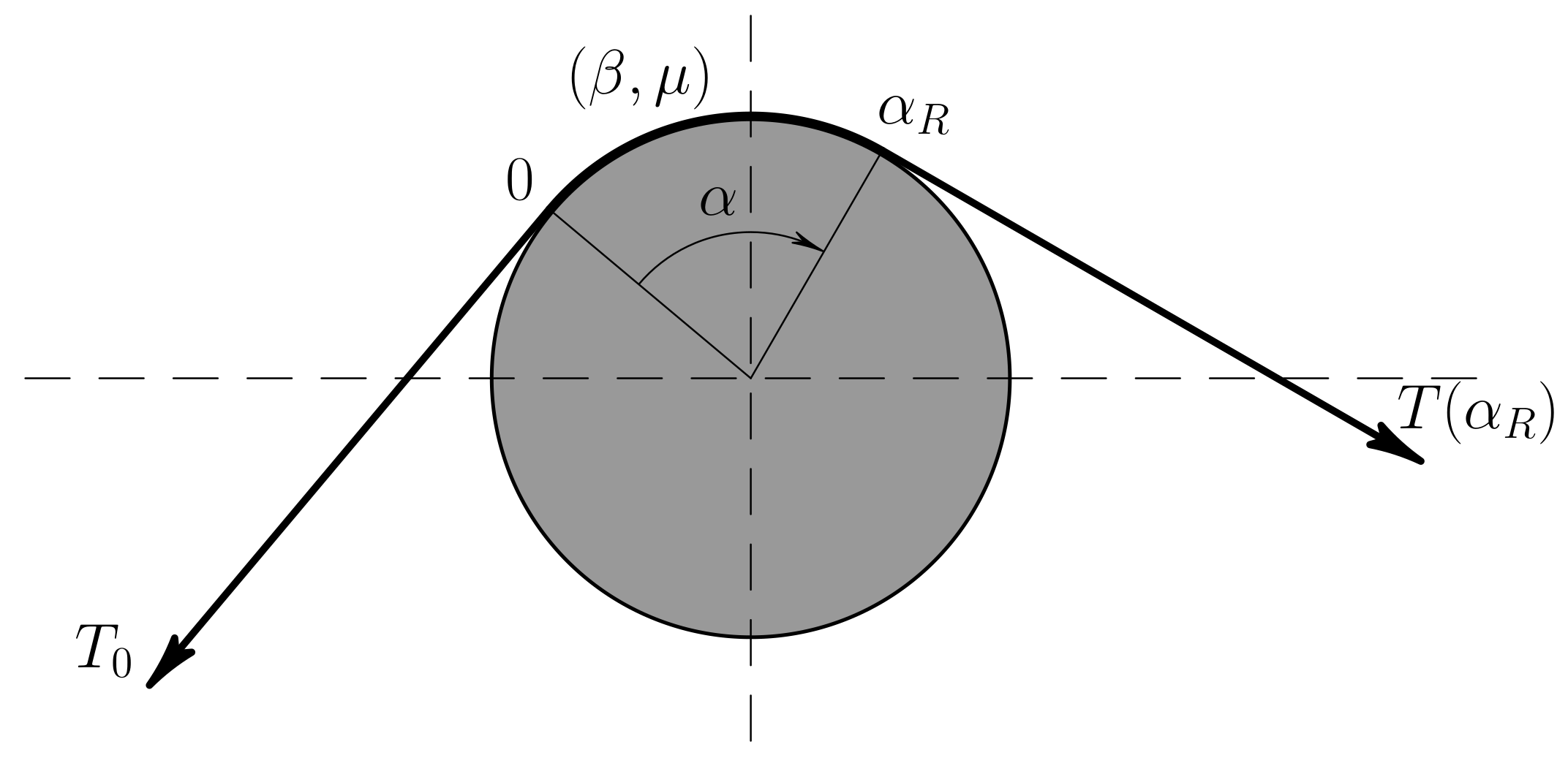Here, the angle $\alpha$ is defined shown in Figure 2.

Consider the following friction law:

$$\begin{array}{c}{F}_{\mathrm{friction}}\le max(\beta \alpha ,\mu N).\end{array}$$

(30)

This is standard Coulomb friction law augmented with adhesive friction. Adhesion arises from interaction of yarns with each other after the relaxation due to interweaving of their filaments.

Consider a cylinder and a rope as shown in Figure 2. Assume that:

• tension force at the left end of the rope is known and equals $T_0$,
• the system is in critical statical condition,
• the friction force is such that the tension force is a monotonically increasing function of $\alpha$.

The problem is to determine the critical tension force at the right end of the rope, i. e. a value, such that for greater force values at the right end the sliding occurs and for lower values the system is in equilibrium.

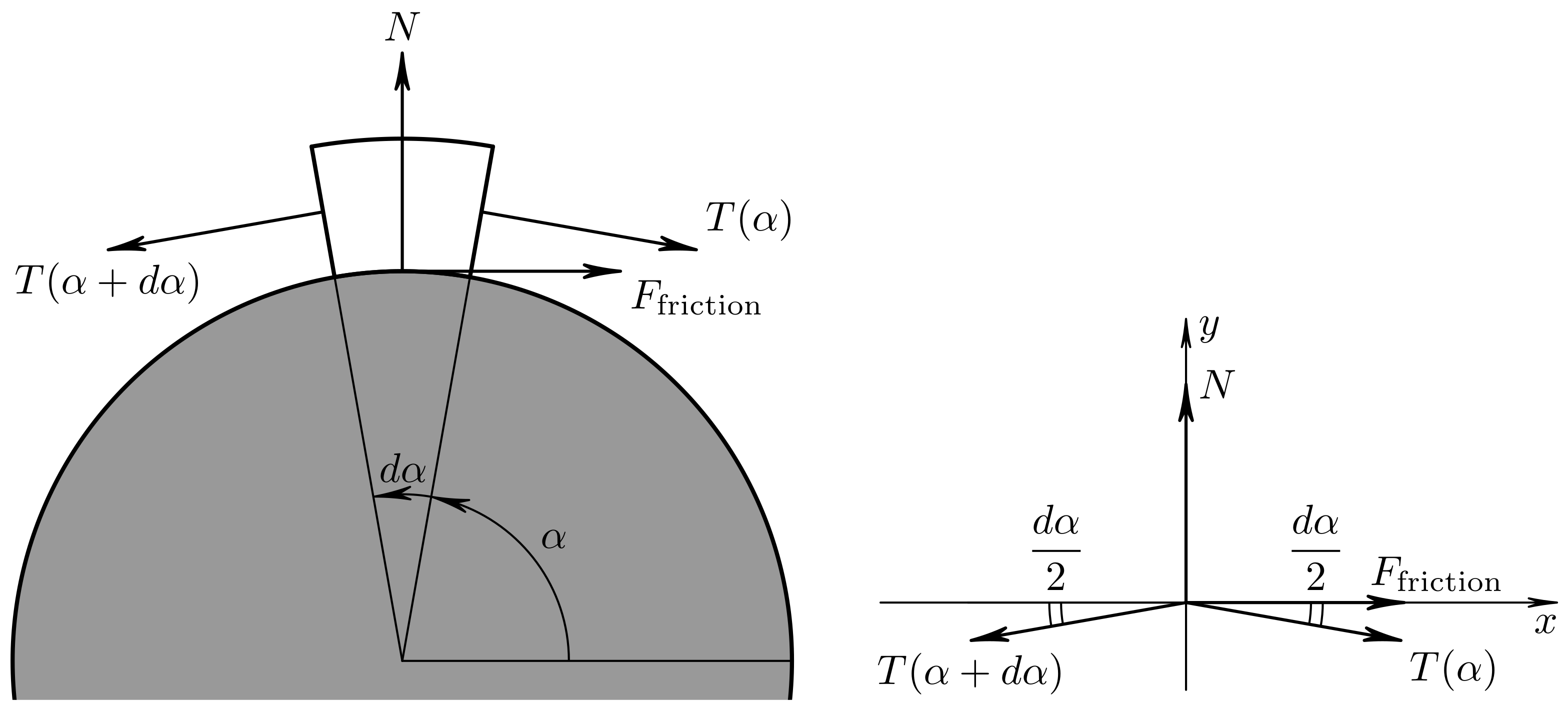
To do this consider equilibrium of a small element of the rope on the cylinder. Let the tension force T be a function of $\alpha$. The total force acting on the element is depicted in Figure 3. Projecting on the axes x and y we obtain the differentials

$$\begin{array}{c}\left\{\begin{array}{ccc}\hfill d{F}_{\mathrm{friction}}& =& \left(T\right(\alpha +d\alpha )-T(\alpha \left)\right)cos(d\alpha /2),\hfill \\ \hfill dN& =& \left(T\right(\alpha +d\alpha )+T(\alpha \left)\right)sin(d\alpha /2),\hfill \end{array}\right.\end{array}$$

(31)

substituting $F_{\mathrm{friction}}$ from (30) for the critical case yields

$$\begin{array}{c}\hfill \left\{\begin{array}{ccc}\hfill max(\beta d\alpha ,\mu dN)& =& \left(T\right(\alpha +d\alpha )-T(\alpha \left)\right)cos(d\alpha /2),\hfill \\ \hfill dN& =& \left(T\right(\alpha +d\alpha )+T(\alpha \left)\right)sin(d\alpha /2).\hfill \end{array}\right.\end{array}$$

(32)

Substitute N from the second equation into the first and divide both sides over $d\alpha$:

$$\begin{array}{c}\hfill max\left(\beta ,\mu {\displaystyle \frac{T(\alpha +d\alpha )+T\left(\alpha \right)}{2}}{\displaystyle \frac{sin(d\alpha /2)}{d\alpha /2}}\right)={\displaystyle \frac{T(\alpha +d\alpha )-T\left(\alpha \right)}{d\alpha }}cos(d\alpha /2).\end{array}$$

(33)

Passage to the limit $d\alpha \to 0$ yields the Cauchy problem for the tensional force in the rope:

$$\begin{array}{c}\left\{\begin{array}{cc}\hfill \dot{T}\left(\alpha \right)& =max(\mu T,\beta ),\hfill \\ \hfill T\left(0\right)& =T_0.\hfill \end{array}\right.\end{array}$$

(34)

The solution to it is

$$\begin{array}{c}\begin{array}{c}\hfill \mathrm{if}{T}_0\le {\displaystyle \frac{\beta }{\mu }},\mathrm{then}T\left(\alpha \right)=\left\{\begin{array}{cc}{T}_0+\alpha \beta \hfill & \mathrm{for}0\le \alpha \le {\alpha }^{\star },\hfill \\ {\displaystyle \frac{\beta }{\mu }}{e}^{\mu (\alpha -{\alpha }^{\star })}\hfill & \mathrm{for}{\alpha }^{\star }<\alpha \le {\alpha }_R,\hfill \end{array}\right.\\ \mathrm{if}{T}_0>{\displaystyle \frac{\beta }{\mu }},\mathrm{then}T\left(\alpha \right)=T_0{e}^{\alpha \mu },0\le \alpha \le {\alpha }_R,\hfill \\ \mathrm{where}{\alpha }^{\star }={\displaystyle \frac{1}{\mu }}-{\displaystyle \frac{T_1}{\beta }}.\end{array}\hfill \end{array}$$

(35)

Further, consider a cylinder and a rope with tension force values given at both ends and ${\alpha }_R$ as shown in Figure 2. The problem is to determine whether the system is in equilibrium (stick) or the rope slides on the cylinder (slip). We approach this problem in the following way:

• compute $T_{min}=min(T_1,T_2)$ and $T_{max}=max(T_1,T_2)$,
• solve the problem (34) with $T_0=T_{min}$ and compute $T\left({\alpha }_R\right)$,
• the state of the system (stick/slip) is determined from comparison of $T\left({\alpha }_R\right)$ and $T_{max}$.

This approach yields the following rule:

$$\begin{array}{cc}\mathrm{if}{T}_{max}\le {\displaystyle \frac{\beta }{\mu }}& \mathrm{then}\mathrm{the}\mathrm{system}\mathrm{is}\mathrm{in}\mathrm{equilibrium}\mathrm{iff}{T}_{max}-T_{min}\le {\alpha }_R\beta ,\hfill \\ \mathrm{if}{T}_{min}\ge {\displaystyle \frac{\beta }{\mu }}& \mathrm{then}\mathrm{the}\mathrm{system}\mathrm{is}\mathrm{in}\mathrm{equilibrium}\mathrm{iff}{T}_{max}\le e^{{\alpha }_R\mu }{T}_{min},\hfill \\ & \mathrm{else}\mathrm{the}\mathrm{system}\mathrm{is}\mathrm{in}\mathrm{equilibrium}\mathrm{iff}{T}_{max}\le {\displaystyle \frac{\beta }{\mu }}{e}^{\left({\alpha }_R\mu -1+\frac{\mu }{\beta }{T}_{min}\right)}.\hfill \end{array}$$

(36)

The conditions are checked in the numerical scheme. If they are not fulfilled, the sliding process takes place and the rope slides in the direction of greater force.

2.4.3. General Case

A more general case of (30) can be considered:

$$\begin{array}{c}{F}_{\mathrm{friction}}\le G(\alpha ,N),\end{array}$$

(37)

where G is certain non-negative function. It can be parametrized by additional parameters, for example in (30) we had

$$\begin{array}{c}G(\alpha ,N)=G_{\mathrm{A}}(\alpha ,N,\beta ,\mu )=max(\beta \alpha ,\mu N).\end{array}$$

(38)

For a cylinder and a rope we make the same assumptions as before and arrive to the Cauchy problem for the tensional force in the rope:

$$\begin{array}{c}\left\{\begin{array}{cc}\hfill \dot{T}\left(\alpha \right)& =g\left(T\right),\hfill \\ \hfill T\left(0\right)& =T_0,\hfill \end{array}\right.\end{array}$$

(39)

where $g\left(0\right)\ge 0$, $g\left(T\right)>0$ for $T>0$. Under these assumptions, problem (39) has a unique monotonically increasing solution and can be solved numerically.

Further, consider a cylinder and a rope with tension force values given at both ends and ${\alpha }_R$ as shown in Figure 2 but now with (30). Then to determine whether the system is in equilibrium:

• compute $T_{min}=min(T_1,T_2)$ and $T_{max}=max(T_1,T_2)$,
• solve the problem (39) with $T_0=T_{min}$ and compute $T\left({\alpha }_R\right)$,
• the state of the system (stick/slip) is determined from comparison of $T\left({\alpha }_R\right)$ and $T_{max}$.

2.4.4. The decaying adhesion friction model

This model is defined by

$$\begin{array}{c}G(\alpha ,N)=G_{\mathrm{DA}}(\alpha ,N,\beta ,\mu ,s_d,w_d)=max\left(min\left(1,{\displaystyle \frac{s_d-N/\alpha }{s_d-w_d}}\right)\beta \alpha ,\mu N\right),\end{array}$$

(40)

where the decay parameter $s_d$ and $w_d$ are the material parameters: $s_d$ can be seen as a lower bound for the Tresca friction (when adhesion disappears) and $w_d$ as an upper bound for Tresca adhesive friction.

If $\mu (s_d-w_d)\ge \beta \alpha$, then the model reduces to the adhesive model described above.

The following Cauchy problem is obtained for a cylinder and a rope:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill \dot{T}\left(\alpha \right)& =max\left(\beta min\left(1,{\displaystyle \frac{s_d-T}{s_d-w_d}}\right),\mu T\right),\hfill \\ \hfill T\left(0\right)& =T_0.\hfill \end{array}\right.\end{array}$$

(41)

The right-hand side is of Caratheodory type and positive if $\mu$, $\beta$, $s_d$ and $s_d-w_d$ are positive. The whole problem is thus well-posed.

Observe first that if $\mu w_d\ge \beta$, then (41) is equivalent to (34). Assume that $\mu w_d<\beta$. The solution of (41) is given by

$$\begin{array}{c}\begin{array}{cc}\mathrm{if}{T}_0\le w_d,\hfill & T\left(\alpha \right)=T_1^d\left(\alpha \right)=\left\{\begin{array}{cc}{T}_0+\alpha \beta \hfill & \mathrm{for}0\le \alpha \le {\alpha }_{d1}^{\star },\hfill \\ w_d{e}^{-\frac{(\alpha -{\alpha }_{d1}^{\star })\beta }{s_d-w_d}}+s_d\left(1-e^{-\frac{(\alpha -{\alpha }_{d1}^{\star })\beta }{s_d-w_d}}\right)\hfill & \mathrm{for}{\alpha }_{d1}^{\star }\le \alpha \le {\alpha }_{d1}^{\star \star },\hfill \\ T^{\star }{e}^{\mu (\alpha -{\alpha }_{d1}^{\star \star })}\hfill & \mathrm{for}{\alpha }_{d1}^{\star \star }<\alpha \le {\alpha }_R,\hfill \end{array}\right.\hfill \\ \mathrm{if}{w}_d<T_0\le T^{\star },\hfill & T\left(\alpha \right)=T_2^d\left(\alpha \right)=\left\{\begin{array}{cc}{T}_0{e}^{-\frac{\alpha \beta }{s_d-w_d}}+s_d\left(1-e^{-\frac{\alpha \beta }{s_d-w_d}}\right)\hfill & \mathrm{for}0\le \alpha \le {\alpha }_{d2}^{\star \star },\hfill \\ T^{\star }{e}^{\mu (\alpha -{\alpha }_{d2}^{\star \star })}\hfill & \mathrm{for}{\alpha }_{d2}^{\star \star }<\alpha \le {\alpha }_R,\hfill \end{array}\right.\hfill \\ \mathrm{if}{T}_0>T^{\star },\hfill & T\left(\alpha \right)=T_3^d\left(\alpha \right)=T_0{e}^{\alpha \mu },0\le \alpha \le {\alpha }_R,\hfill \end{array}\end{array}$$

(42)

$$\begin{array}{c}\mathrm{where}{\alpha }_{d1}^{\star }={\displaystyle \frac{w-T_0}{\beta }},{\alpha }_{d1}^{\star \star }={\alpha }_{d1}^{\star }+{\displaystyle \frac{s_d-w_d}{\beta }}ln\left({\displaystyle \frac{\mu (s_d-w_d)+\beta }{\mu s_d}}\right),\end{array}$$

(43)

$$\begin{array}{c}{\alpha }_{d2}^{\star \star }={\displaystyle \frac{s_d-w_d}{\beta }}ln\left({\displaystyle \frac{(s_d-T_0)(\mu (s_d-w_d)+\beta )}{\mu (s_d-w_d)s_d}}\right),\mathrm{and}{T}^{\star }={\displaystyle \frac{\beta s_d}{\mu (s_d-w_d)+\beta }}.\end{array}$$

(44)

Finally, the state of the system with given angle ${\alpha }_R$ and forces at the ends $T_1$ and $T_2$ is defined from the following rule:

$$\begin{array}{c}\begin{array}{cc}\mathrm{if}{T}_{min}\le w_d,\hfill & \mathrm{then}\mathrm{equilibrium}\mathrm{iff}{T}_{max}\le T_1^d\left({\alpha }_R\right),\hfill \\ \mathrm{if}{w}_d<T_{min}\le T^{\star },\hfill & \mathrm{then}\mathrm{equilibrium}\mathrm{iff}{T}_{max}\le T_2^d\left({\alpha }_R\right),\hfill \\ \mathrm{if}{T}^{\star }<T_{min},\hfill & \mathrm{then}\mathrm{equilibrium}\mathrm{iff}{T}_{max}\le T_3^d\left({\alpha }_R\right).\hfill \end{array}\end{array}$$

(45)

2.5. Finite Element Formulation

Summing up (10) over all elements will result to system of equations for nodal displacements (and in coupled case also for material redistribution parameters)

$$\begin{array}{c}\sum _{e\in E\left(n\right)}{\overline{T}}_e=P_n,\forall n\in N_{\mathrm{free}}\end{array}$$

(46)

where $E\left(n\right)$ denotes the set of elements incoming in node n, ${\overline{T}}_e$ is force vector of element e, $P_n$ is prescribed force in node n, and $N_{\mathrm{free}}$ is the set of all free nodes, i.e., nodes, where no constraints for coordinates are prescribed. For some nodes $n\in N_{\mathrm{Dirichlet}}$ Dirichlet values are given, the displacements of these nodes are thus given:

$$\begin{array}{c}{u}_{n_d}=D_{n_d},\forall n_d\in N_{\mathrm{Dirichlet}}.\end{array}$$

(47)

Let $N_{\mathrm{friction}\mathrm{nodes}}$ denote nodes where at least two fibers touch each other (i.e., those nodes where pairs of elements, which can exchange the material directly, touch). Further, let ${\mu }_n$, ${\beta }_n$, ${\alpha }_n$ be friction parameter, adhesion parameters and angle at such a node. $T_{max}$ and $T_{min}$ are refined as in (15).

The friction condition leads to inequality constraints for material redistribution parameters:

• Coulomb Friction:

  $$\begin{array}{c}{\displaystyle \frac{T_{max}}{T_{min}}}\le e^{{\mu }_n{\alpha }_n}\forall n\in N_{\mathrm{friction}\mathrm{nodes}}\end{array}$$

  (48)
• Coulomb Friction with adhesion:

  $$\begin{array}{c}\hfill \begin{array}{c}\hfill \left(T_{max}\le {\displaystyle \frac{{\beta }_n}{{\mu }_n}}\wedge T_{max}-T_{min}\le {\alpha }_n{\beta }_n\right)\vee \left(T_{min}\ge {\displaystyle \frac{{\beta }_n}{{\mu }_n}}\wedge T_{max}\le e^{{\alpha }_n{\mu }_n}{T}_{min}\right)\\ \hfill \vee \left(T_{min}<{\displaystyle \frac{{\beta }_n}{{\mu }_n}}<T_{max}\le {\displaystyle \frac{{\beta }_n}{{\mu }_n}}{e}^{\left({\alpha }_n{\mu }_n-1+\frac{{\mu }_n}{{\beta }_n}{T}_{min}\right)}\right)\forall n\in N_{\mathrm{friction}\mathrm{nodes}}\end{array}\end{array}$$

  (49)
• Coulomb Friction with decaying adhesion:

Further, define $w_n$ and $T^{\star }$ as in Section 2.4.4.

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \left(T_{min}\le w_n\wedge T_{max}\le T_1^d\left({\alpha }_n\right)\right)\vee \left(w_n<T_{min}\le T^{\star }\wedge T_{max}\le T_2^d\left({\alpha }_n\right)\right)\\ \hfill \vee \left(T^{\star }<T_{min}\wedge T_{max}\le T_3^d\left({\alpha }_R\right)\right)\forall n\in N_{\mathrm{friction}\mathrm{nodes}}\end{array}\end{array}$$

(50)

2.6. Numerical Algorithm

The problem (46)–(48) inherits all properties of the same problem without friction. One can face strong non-linearities, high condition numbers (how much the output value of the function can change for a small change in the input argument), instabilities of the structure itself, and snap-throughs. Even more, when an element e is relaxed, then its tangential stiffness matrix is degenerate. This is explained by the behavior of the energy (5) at point ${\lambda }_1=1$: for nodal displacement vectors, perpendicular to element’s current axis, the functional behaves the same way as function $f\left(x\right)=x^4$ at point $x=0$. Taylor expansion of this function up to the fourth order term is zero, delivering problems to numerical methods of optimization or non-linear equations solution, which use at most second-order information. Either higher order methods or regularization is thus required together with robust Newton-Raphson or Gradient method to solve (46)–(48), where friction constraints complicate the matters even further.

2.6.1. Continuation Method

We apply the standard Continuation technique [19,20,21] to deal with the issues mentioned. Consider a family of parametrized problems $\mathcal{P}(p_{\mathrm{VF}},p_{\mathrm{Dd}})$, $0\le p_{\mathrm{VF}},p_{\mathrm{Dd}}\le 1$, defined as

$$\begin{array}{c}\hfill \sum _{e\in E\left(n\right)}{\overline{f}}_e=p_{\mathrm{VF}}{P}_n,\forall n\in N_{\mathrm{free}},\end{array}$$

(51)

$$\begin{array}{c}\hfill u_{n_d}=p_{\mathrm{Dd}}{D}_{n_d},\forall n_d\in N_{\mathrm{Dirichlet}},\end{array}$$

(52)

$$\begin{array}{c}\hfill u_{n_i}=u_{n_j},\mathrm{for}\mathrm{all}\mathrm{pairs}\mathrm{of}\mathrm{corresponding}\mathrm{nodes}(n_i,n_j),\end{array}$$

(53)

$$\begin{array}{c}\hfill {\displaystyle \frac{T_{max}}{T_{min}}}\le e^{{\mu }_n{\alpha }_n},\forall n\in N_{\mathrm{friction}\mathrm{nodes}},\end{array}$$

(54)

Equation (54) has to be replaced by (49) or (50) for the two adhesion cases.

The problem $\mathcal{P}(0,0)$ corresponds to the structure without any outer forces, while $\mathcal{P}(1,1)$ is equivalent to (46)–(48), the equations with applied outer forces and boundary nodal displacements (Dirichlet values) that have to be solved. We assume that for some values $p_{\mathrm{VF}}^0$ and $p_{\mathrm{Dd}}^0$ the solution to $\mathcal{P}(p_{\mathrm{VF}}^0,p_{\mathrm{Dd}}^0)$ is known. Then we approach to the solution of $\mathcal{P}(1,1)$, consequently solving $\mathcal{P}(p_{\mathrm{VF}}^i,p_{\mathrm{Dd}}^i)$ for $1\le i\le K$, where $p_{\mathrm{VF}}^K=p_{\mathrm{Dd}}^K=1$ and points $(p_{\mathrm{VF}}^i,p_{\mathrm{Dd}}^i)$ and $(p_{\mathrm{VF}}^{i+1},p_{\mathrm{Dd}}^{i+1})$ are close in some sense (K is the number of necessary iterations). The benefit of such method is that to numerically solve problem $\mathcal{P}(p_{\mathrm{VF}}^{i+1},p_{\mathrm{Dd}}^{i+1})$ one can use the solution of $\mathcal{P}(p_{\mathrm{VF}}^i,p_{\mathrm{Dd}}^i)$ as the initial guess, thus ensuring the convergence of each single step and then the whole algorithm.

If at some step i numerical methods fail, we try to reduce the step size. We achieve this by introduction of additional step between i and $i+1$.

2.6.2. Step of Continuation Method

Assume that the solution $u(p_{\mathrm{VF}}^i,p_{\mathrm{Dd}}^i)$ of the problem $\mathcal{P}(p_{\mathrm{VF}}^0,p_{\mathrm{Dd}}^i)$ is available. Show how one computes $u(p_{\mathrm{VF}}^{i+1},p_{\mathrm{Dd}}^{i+1})$. For the sake of simplicity we consider decoupled case here, i.e., when problems (51)–(53) and (54) are solved separately.

• Set initial guess to $u(p_{\mathrm{VF}}^i,p_{\mathrm{Dd}}^i)$.
• Update Dirichlet displacements and Volume Force values.
• Solve decoupled displacements-flow problem:

  (a)

  If error norm is acceptable, go to 4.

  (b)

  Obtain nodal displacements from (51)–(53) with material flow variables fixed. It can be solved numerically as a system of non-linear equations.

  (c)

  Obtain flow variables from (54) with nodal displacements fixed. It can be solved numerically as an optimization problem.

  (d)

  After solution of (54) the error norm of (51)–(53) can increase. If it violates predefined criteria of the error to be small, go to 3b.

• At this point the problem $\mathcal{P}(p_{\mathrm{VF}}^{i+1},p_{\mathrm{Dd}}^{i+1})$ is solved. Proceed to the next step.

The process is visualized in Figure 4.

3. Results

3.1. The Model Verification and Comparison to Measured Data

The described adhesive friction model is implemented for one-dimensional non-linear trusses element.

3.1.1. Knitted Fabric

First, we considered a knitted fabric which is reinforced by a strongly elastic inlay yarn as shown in Figure 5. The fabric was taken from a medical application and represents a pattern of a compressible stocking.

The described above algorithm was applied to the horizontal tension of the structure.

Figure 6a,b demonstrate the sensitivity of computed macroscopic behavior of the knitted fabric on the variation of friction and adhesion parameters between the knitting and inlay yarns, $ikmu$ and $ikbeta$, respectively (letters ”i” and ”k” stay for inlay and knit).

In Figure 6a, the friction coefficient between inlay and knit yarn, $ikmu$, was varied in the measured range, $[0.3333,0.4666]$. Our computations show, that the error in measurements of the friction coefficient does not influence the macroscopic fabric behavior significantly. The experiments were performed under the adhesive force between the inlay and knit equal to the adhesive force between two knitting yarns in contact, $ikbeta=kkbeta=0.015$ N and the friction coefficient between two knitting yarns, $kkmu=0.3999$.

In Figure 6b, we varied the adhesion parameter between the inlay and knitting yarn in the measured range. The parameters $kkbeta$, $kkmu$ were taken as in the first example, $ikmu=0.3999$. The knitting yarns were pre-stressed by $2cN$ in both experiments. This example demonstrates that the introduced adhesion makes a difference in the stretching material response after stretch by factor 2. The considered fabric can be applied in the range 50–150% of the stretch, therefore the adhesion force may be significant.

The results available in Figure 7 and Figure 8 show the comparison of our numerical simulation with measurements. The experimental force-strain curves of yarns were provided by BSN medical, producer of the compressible stockings, and were performed at the ITA, a textile institute in Aachen, Germany. The data was obtained as a list of force-strain measured value and approximated by splines via Matlab scripts. The measured data are plotted in black (and called ”target” in figures), while colored curves correspond to computed results for a variation of values of friction and adhesion coefficients between the knitting and inlay yarns. In [10], the Capstan model without adhesion was implemented and compared with the same measurements. The results and comparison presented in this manuscript show a better suitability of the adhesion model.

We remark here that we considered large stretch deformations in this example and the size of contact knots becomes very thin compared to the distance between them and they can be considered as point-contacts. The reduced cross-section of the yarns due to the transverse deformation can be captured by the decaying adhesive force.

3.1.2. Woven Fabric

In this section, we consider a safety belt with prescribed pattern shown in Figure 9.

The force-strain curves of elongation and shutting yarns were provided by experiments in Figure 10a,b. The local simulation on the fiber structure shows some local fording pattern due to the weaving kind, providing some instability on shear loading in the structure, Figure 11a,b shows simulation of the belt stretching.

Since the yarns are cylinders in a three-dimensional network and on the nodes they change the slope to the outer-plane direction, which influence their effective stretching response, we modified the point-contact to introducing some rigid tetrahedron between the yarns as a gap-holder, see Figure 12. It is easy to see, that the angles form the Euler-Eytelwein or Capstan model preserves with such a gap-holder. In Figure 13a, the red curve is the experimental one, called ”target”. Other curves are simulated for different gap-holders or distance factors. The curves show that for different stretching-regions, different gap-factors are appropriate. Of course the yarns become thinner during the stretching and this fact should be accounted for in replacing the 3-dimensional evolution contact models by one-dimensional string in contact. Figure 13b shows an adopted gap-factor.

4. Discussion

An important issue is that the developed model is appropriated for large stretch deformations, when the size of contact knots becomes very thin compared to the distance between them and they can be considered as point-contacts. The results indicate that the reduced cross-section of the yarns due to the transverse deformation can be captured by the decaying adhesive force.

In the case of thick yarns and dense structure, the model should either be replaced by a two-scale model, resolving the contact knots in all 3-dimensional details, as in works of S. Lomov, or extended to the bending of yarns at the contact points, as in works of Damien Durville [4,22,23,24,25] and a simplification in a form of a changing gap-factor can be introduced, imitating the yarn thickness reduction on the contact nodes during the stretching, as in the last example.

The last remark is that the presented model is suitable for multifilaments rather than for monofils, since it ignores bending and shear stresses and deformations in yarns and is appropriated for yarns working mostly on tension and providing a very lower shear and bending resistance. The approach is based on the computation in terms of forces and not in terms of stresses, which avoids some cross-sectional effects.

5. Conclusions

The numerical approach for simulation of textile behavior by 1D models of hyper-elastic yarns in frictional contact has been shown. The model and approach presented in [10] were extended to Capstan law with constant and decaying adhesion. This is the main result of the paper. The truss finite elements and the two-step Newton approach with continuation were adopted for the numerical solution of the problem. Each iteration contains two steps, the elastic stretching under the fixed contact configuration and the pure contact sliding under the frozen elastic deformation. The method is presented in a flow chart and described in a sequence of necessary steps. The suggested model and numerical approach are illustrated on two real industrial applications, tension of a knitted and a woven fabric. Both simulations are compared with experimental curves. The sensitivity with respect to frictional and adhesion parameters is presented and the model coincides very well with experimental results, especially describing hysteresis well.