Anisotropic Hardening Behaviour and Springback of Advanced High-Strength Steels
Abstract
:1. Introduction
2. Constitutive Equations
2.1. Elasticity
2.2. Yield Criterion
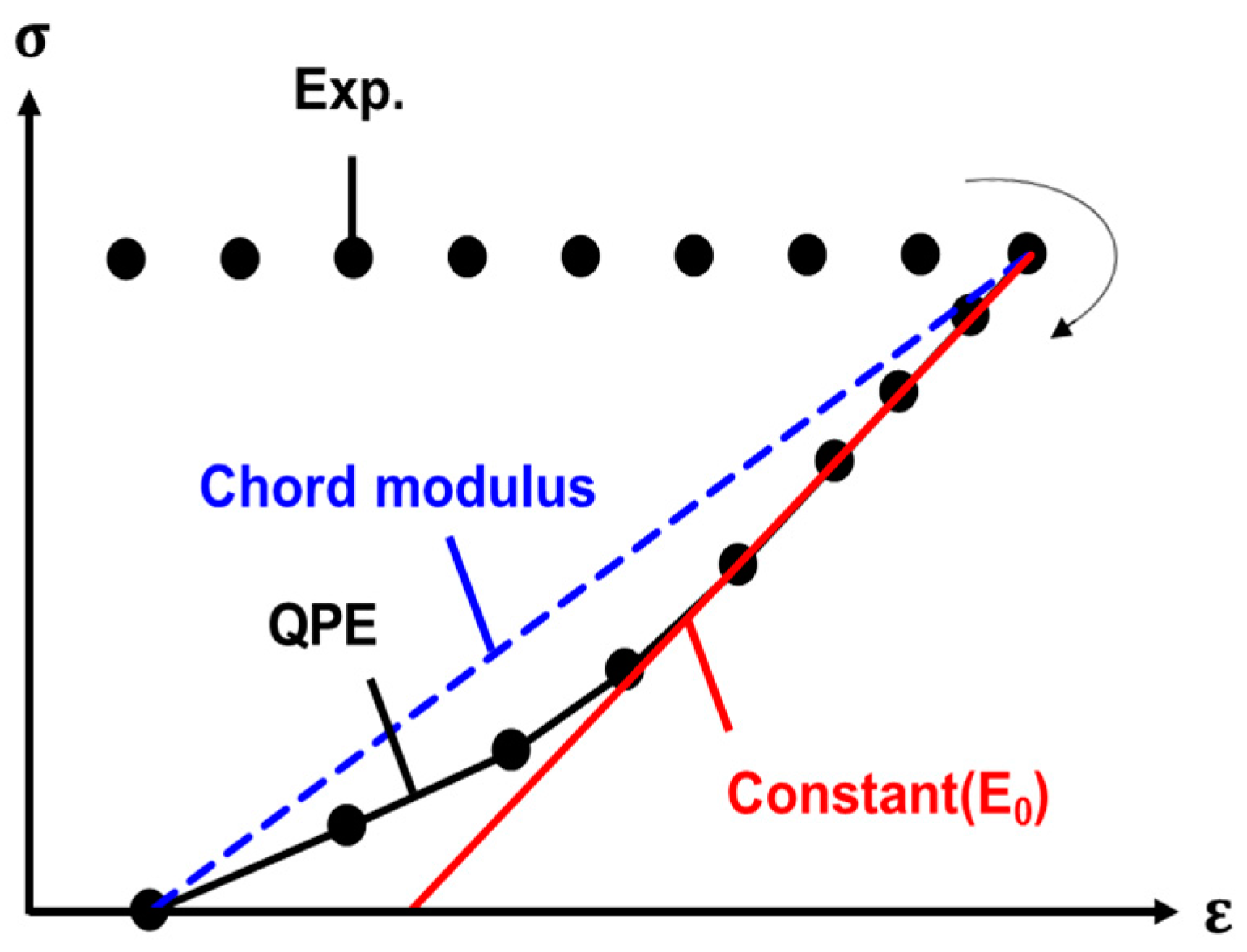
2.3. Hardening Law
3. Experiments
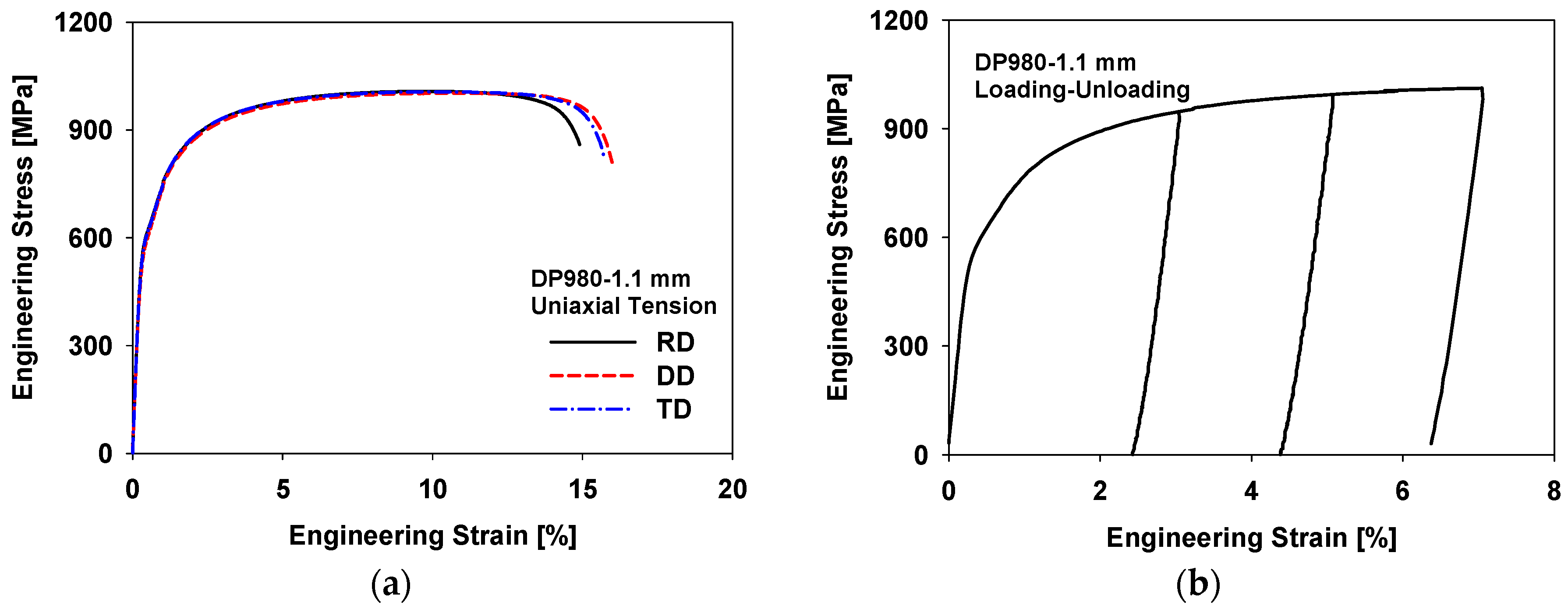
3.1. Uniaxial Tensile and Loading–Unloading Tests
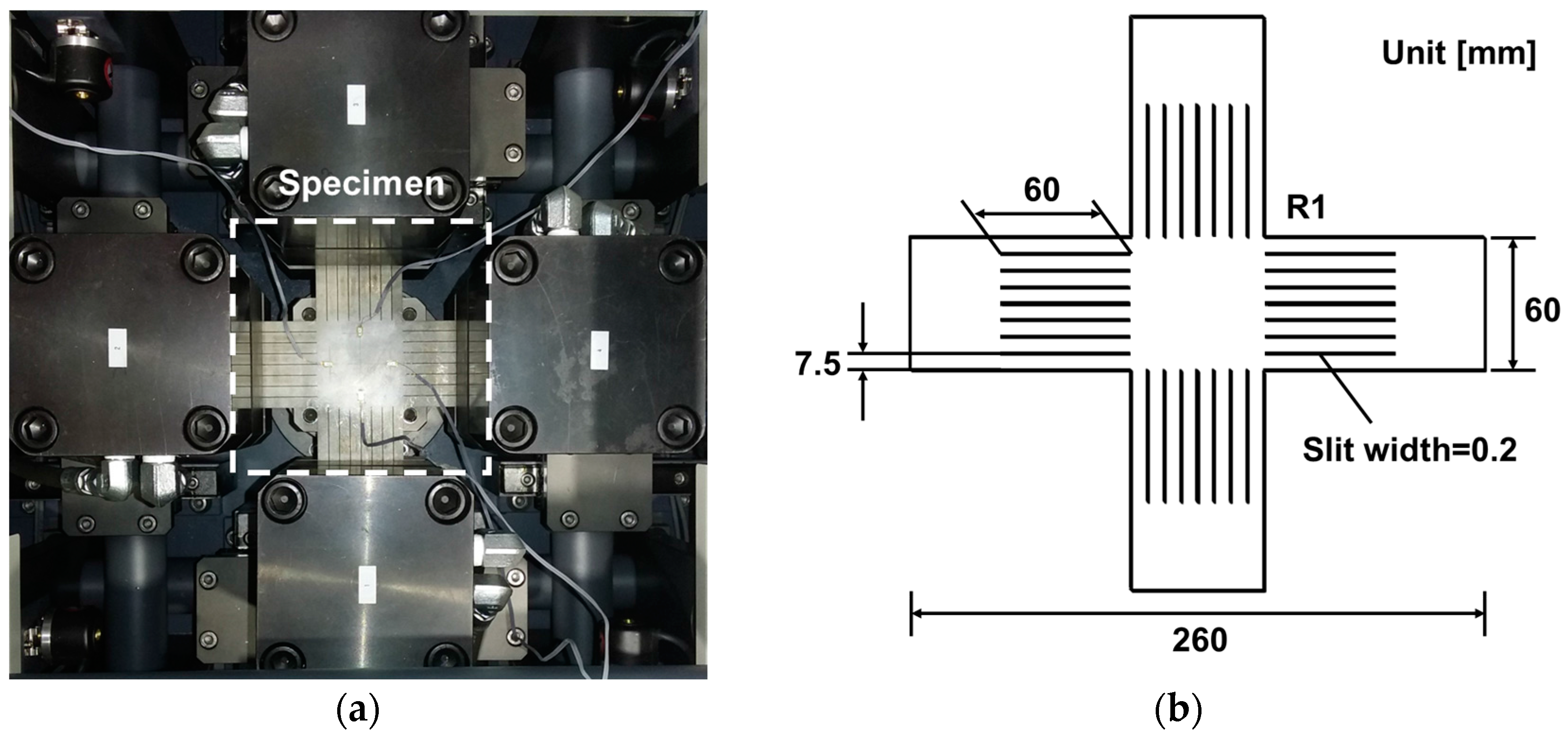
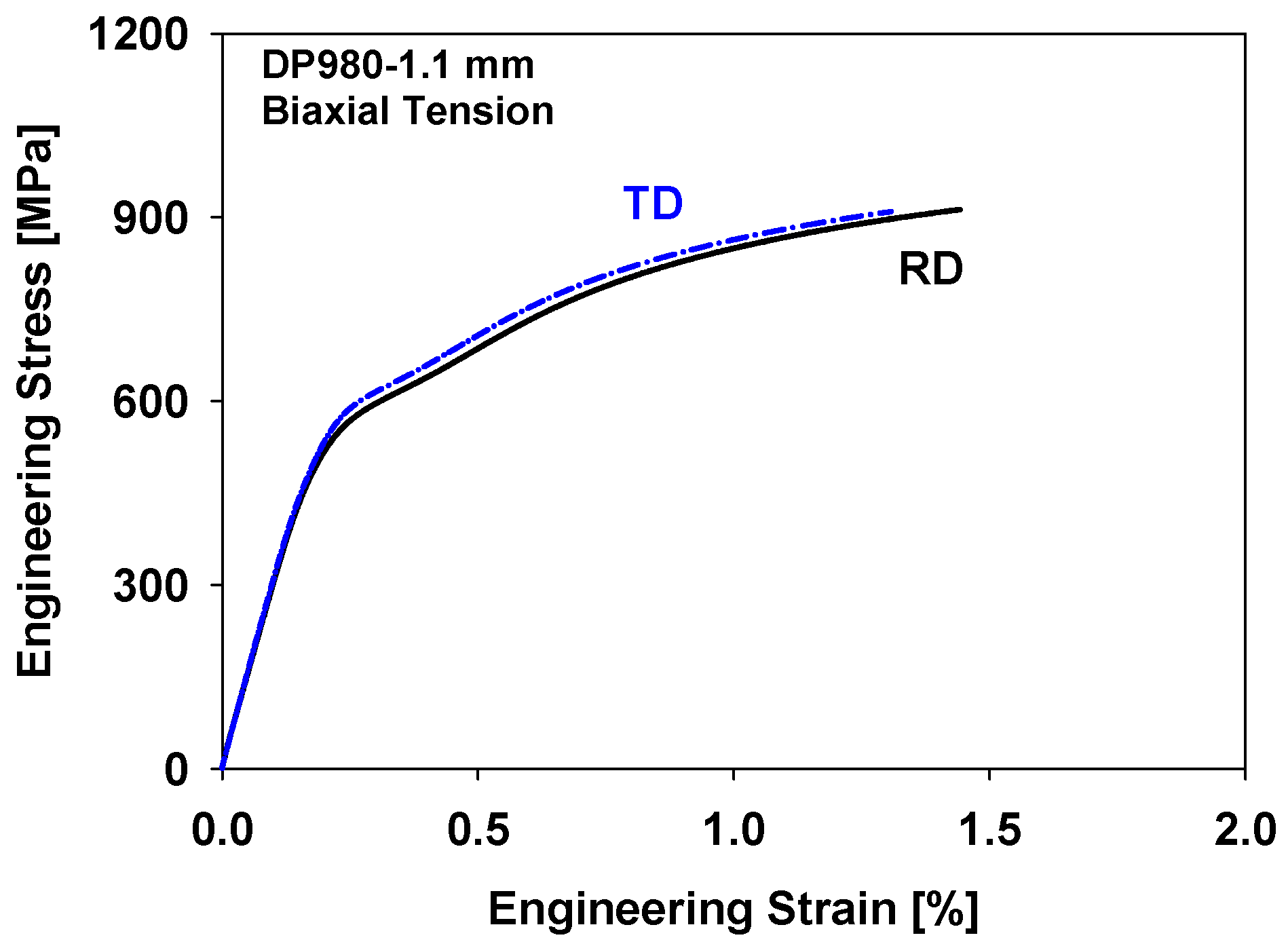
3.2. Biaxial Tensile Test
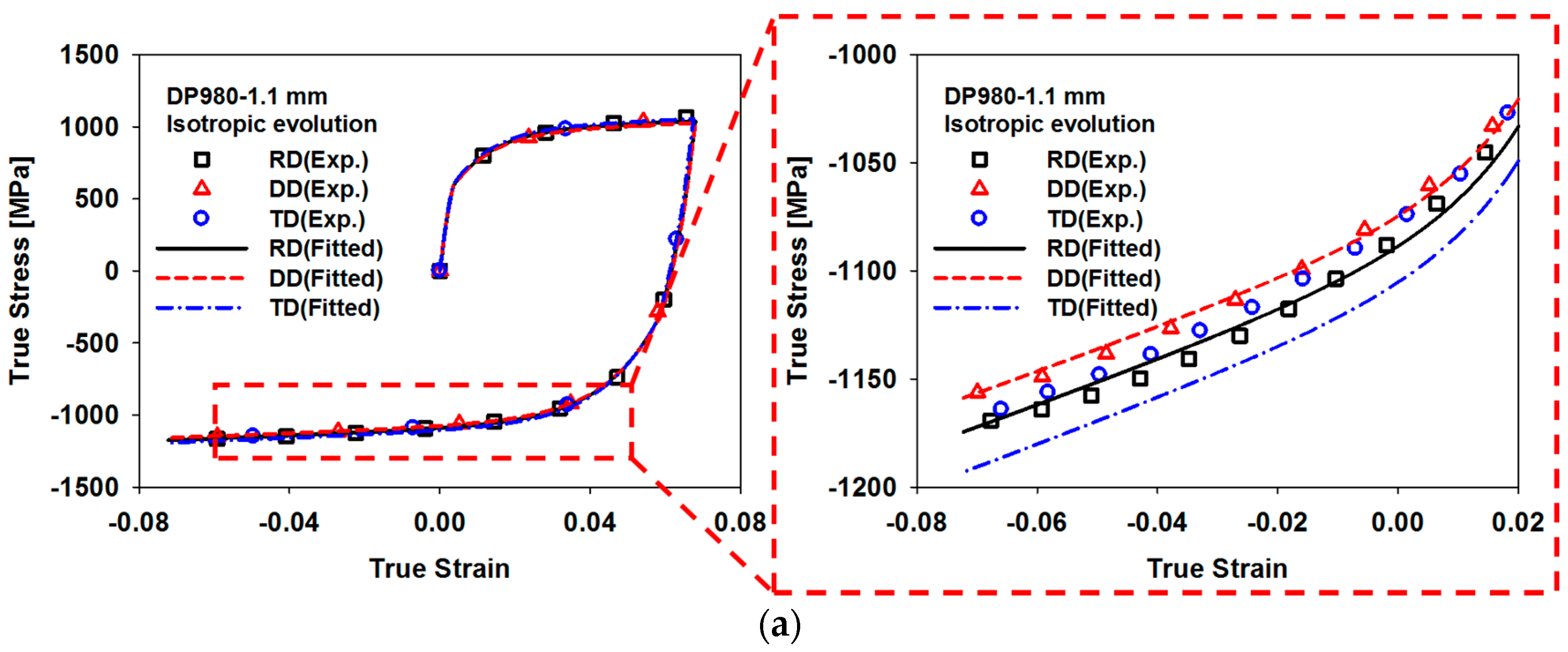
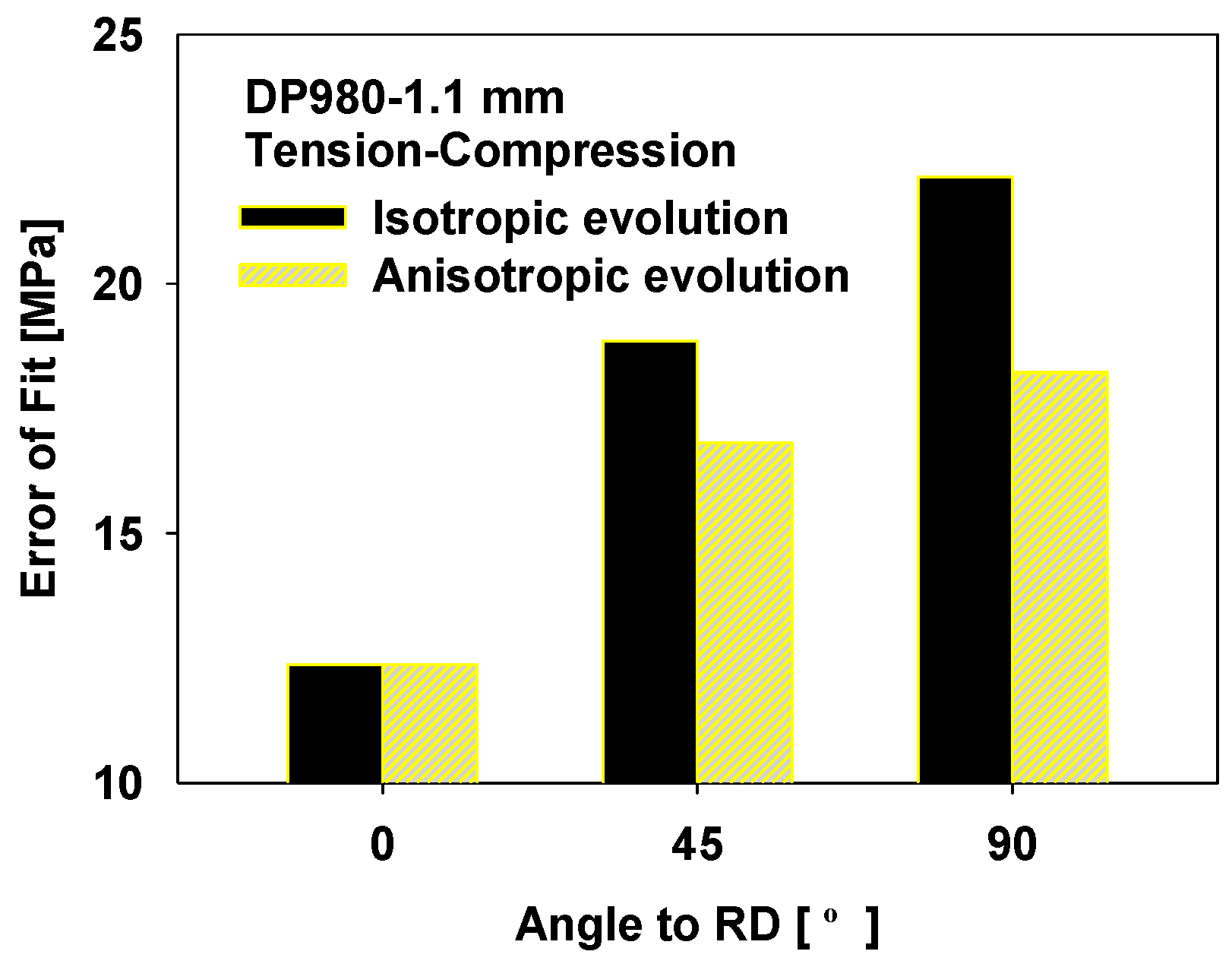
3.3. Tension-Compression Test
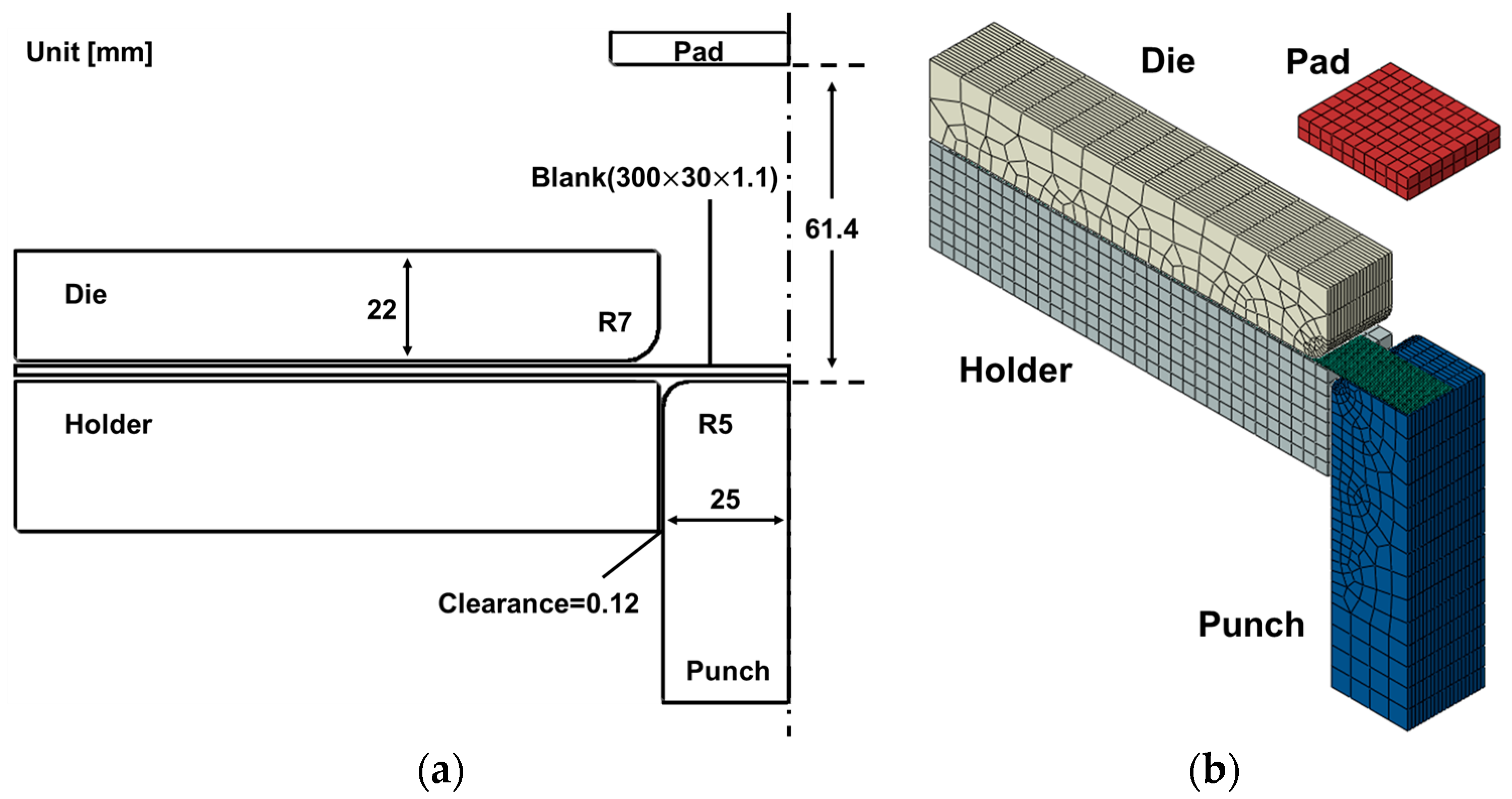
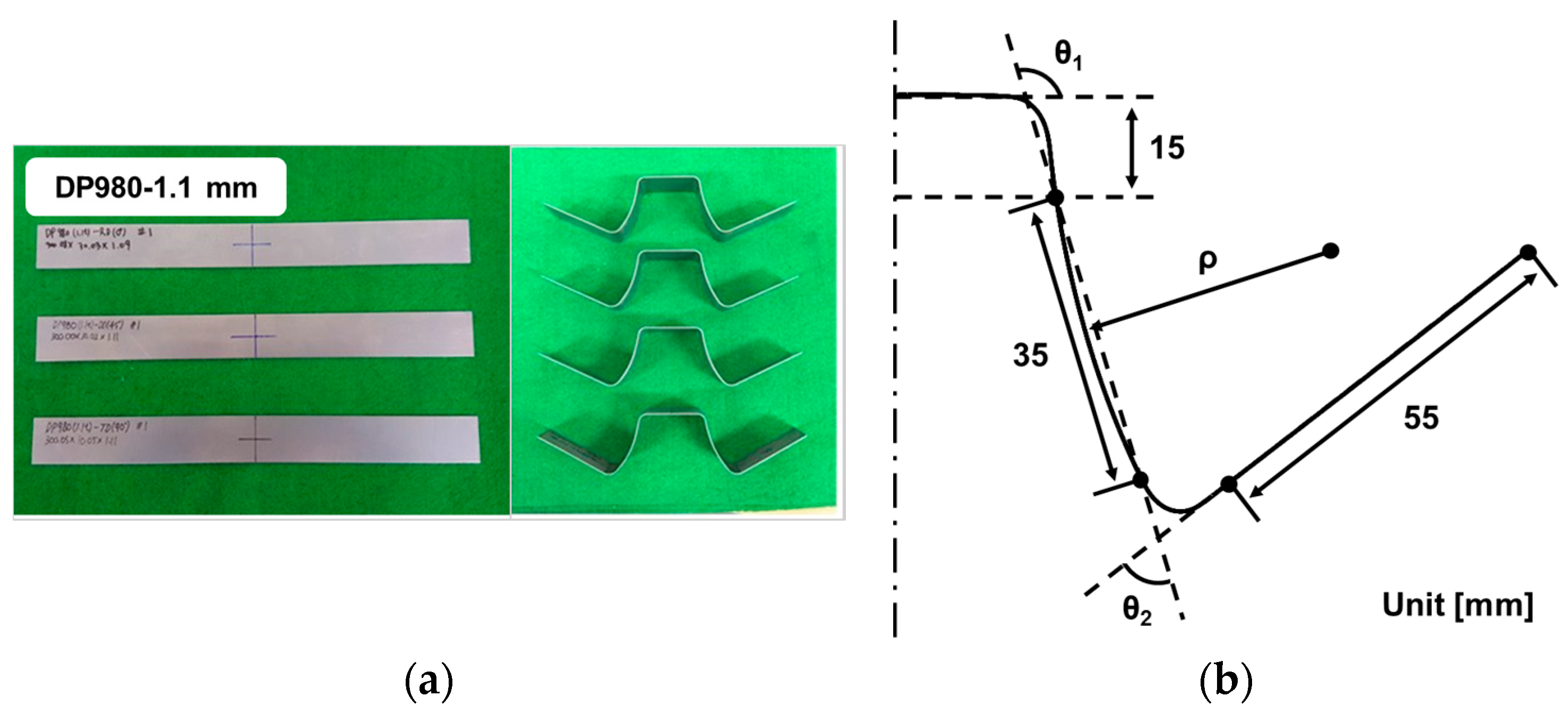
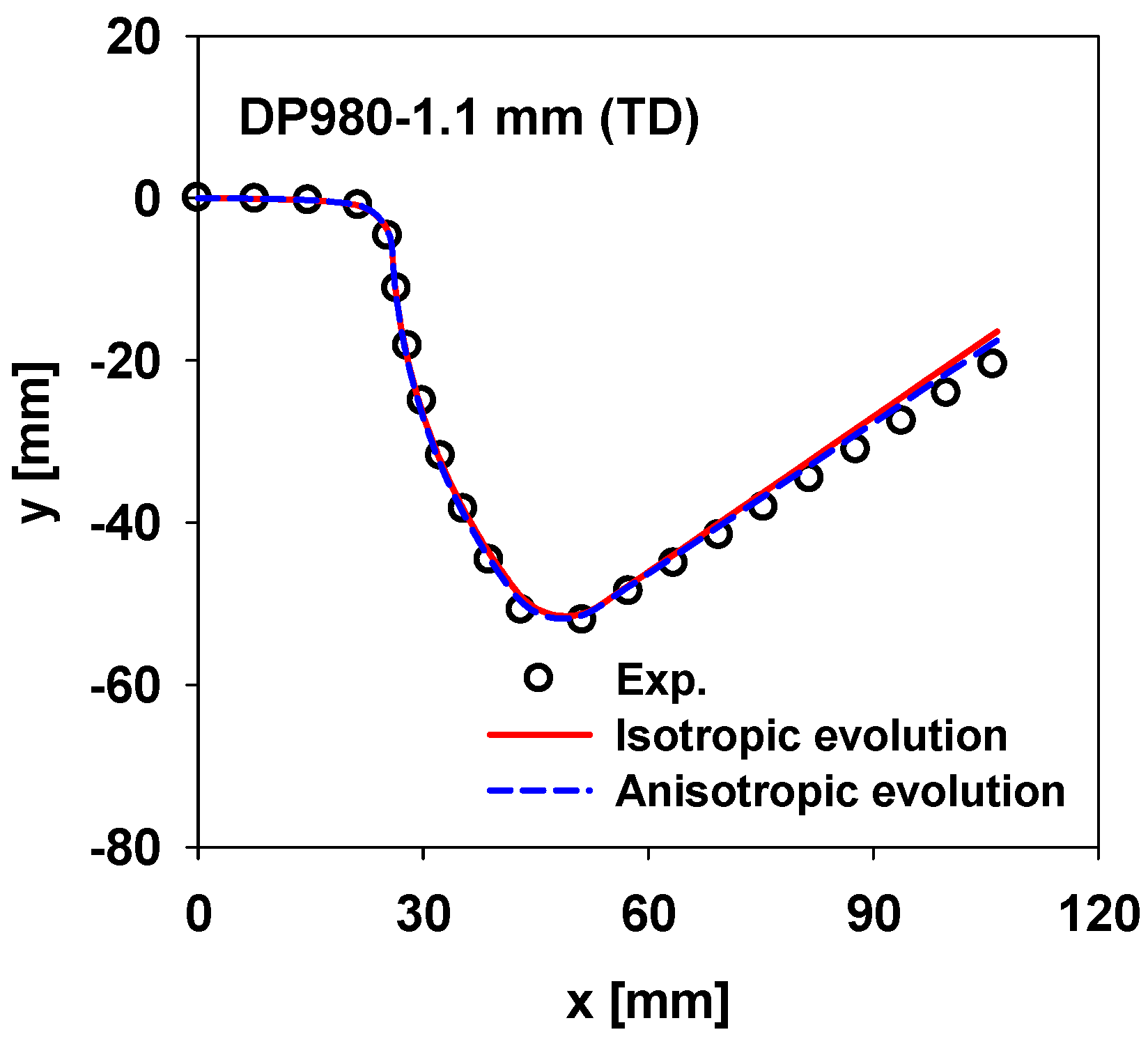
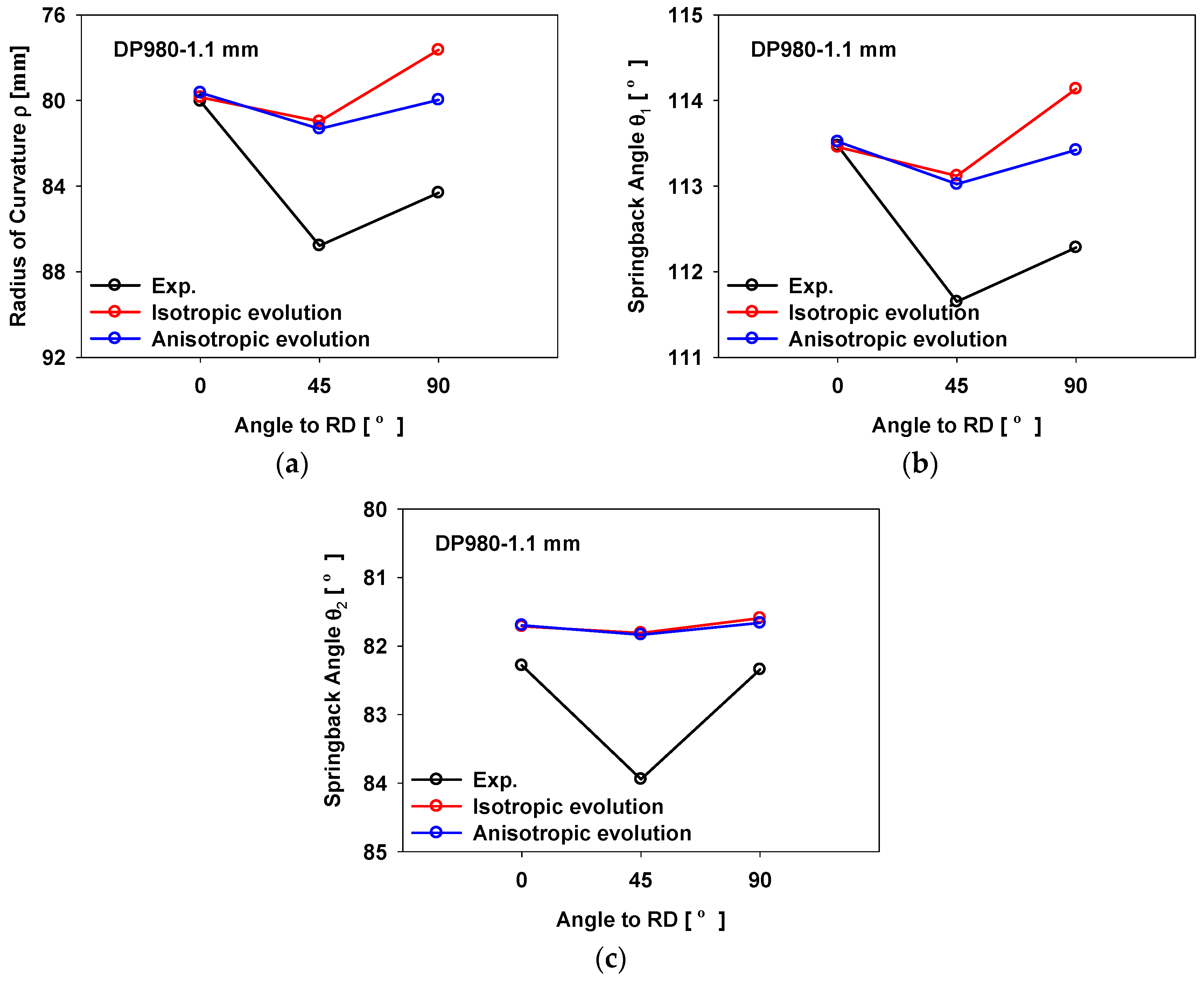
4. Application
5. Conclusions
- The dual-phase steel studied in this work exhibited a change in the anisotropic properties during deformation.
- The hardening model with the anisotropic evolution successfully captured the evolution of the angular variation of anisotropic properties.
- Using the hardening model with anisotropic evolution, it was possible to accurately predict the springback in different directions.
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
References
- Keeler, S.; Kimchi, M. Advanced High-Strength Steels Application Guidelines Version 5.0; WorldAutoSteel: Middletown, OH, USA, 2014. [Google Scholar]
- Cheah, L.W. Cars on a Diet: The Material and Energy Impacts of Passenger Vehicle Weight Reduction in the U.S. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, September 2010. [Google Scholar]
- Amigo, F.J.; Camacho, A.M. Reduction of induced central damage in cold extrusion of dual-phase steel DP980 using double-pass dies. Metals 2017, 7, 335. [Google Scholar] [CrossRef]
- Xue, X.; Pereira, A.B.; Amorim, J.; Liao, J. Effects of pulsed Nd: YAG laser welding parameters on penetration and microstructure characterization of a DP1000 steel butt joint. Metals 2017, 7, 292. [Google Scholar] [CrossRef]
- Evin, E.; Tomas, M. The influence of laser welding on the mechanical properties of dual phase and TRIP steels. Metals 2017, 7, 239. [Google Scholar] [CrossRef]
- Moeini, G.; Ramazani, A.; Myslicki, S.; Sundararaghavan, V.; Konke, C. Low cycle fatigue behaviour of DP steels: Micromechanical modelling vs. validation. Metals 2017, 7, 265. [Google Scholar] [CrossRef]
- Emre, H.E.; Kacar, R. Resistance spot weldability of galvanize coated and uncoated TRIP steels. Metals 2016, 6, 299. [Google Scholar] [CrossRef]
- Hassan, H.U.; Traphoner, H.; Guner, A.; Tekkaya, A.E. Accurate springback prediction in deep drawing using pre-strain based multiple cyclic stress-strain curves in finite element simulation. Int. J. Mech. Sci. 2016, 110, 229–241. [Google Scholar] [CrossRef]
- Lee, H.S.; Kim, J.H.; Kang, G.S.; Ko, D.C.; Kim, B.M. Development of seat side frame by sheet forming of DP980 with die compensation. Int. J. Precis. Eng. Manuf. 2017, 18, 115–120. [Google Scholar] [CrossRef]
- Abvabi, A.; Rolfe, B.; Hodgson, P.D.; Weiss, M. The influence of residual stress on a roll forming process. Int. J. Mech. Sci. 2015, 101–102, 124–136. [Google Scholar] [CrossRef]
- Liu, X.; Cao, J.; Chai, X.; Liu, J.; Zhao, R.; Kong, N. Investigation of forming parameters on springback for ultra high strength steel considering Young’s modulus variation in cold roll forming. J. Manuf. Process. 2017, 29, 289–297. [Google Scholar] [CrossRef]
- Lee, J.; Lee, J.Y.; Barlat, F.; Wagoner, R.H.; Chung, K.; Lee, M.G. Extension of quasi-plastic-elastic approach to incorporate complex plastic flow behaviour–application to springback of advanced high-strength steels. Int. J. Plast. 2013, 45, 140–159. [Google Scholar] [CrossRef]
- Chen, Z.; Bong, H.J.; Li, D.; Wagoner, R.H. The elastic-plastic transition of metals. Int. J. Plast. 2016, 83, 178–201. [Google Scholar] [CrossRef]
- Torkabadi, A.; Perdahcioglu, E.S.; Meinders, V.T.; Boogaard, V.D. On the nonlinear anelastic behaviour of AHSS. Int. J. Solids Struct. 2017, in press. [Google Scholar] [CrossRef]
- Lee, J.Y.; Lee, M.G.; Barlat, F.; Bae, G. Piecewise linear approximation of nonlinear unloading-reloading behaviours using a multi-surface approach. Int. J. Plast. 2017, 93, 112–136. [Google Scholar] [CrossRef]
- Lems, W. The change of Young’s modulus of copper and silver after deformation at low temperature and its recovery. Physica 1962, 28, 445–452. [Google Scholar] [CrossRef]
- Morestin, F.; Boivin, M. On the necessity of taking into account the variation in the Young modulus with plastic strain in elastic-plastic software. Nucl. Eng. Des. 1996, 162, 107–116. [Google Scholar] [CrossRef]
- Yoshida, F.; Uemori, T.; Fujiwara, K. Elastic-plastic behaviour of steel sheets under in-plane cyclic tension-compression at large strain. Int. J. Plast. 2002, 18, 633–659. [Google Scholar] [CrossRef]
- Sun, L.; Wagoner, R.H. Complex unloading behaviour: Nature of the deformation and its consistent constitutive representation. Int. J. Plast. 2011, 27, 1126–1144. [Google Scholar] [CrossRef]
- Cardoso, R.P.R.; Yoon, J.W. Stress integration method for a nonlinear kinematic/isotropic hardening model and its characterization based on polycrystal plasticity. Int. J. Plast. 2009, 25, 1684–1710. [Google Scholar] [CrossRef]
- Cao, J.; Lee, W.; Cheng, H.S.; Seniw, M.; Wang, H.P.; Chung, K. Experimental and numerical investigation of combined isotropic-kinematic hardening behaviour of sheet metals. Int. J. Plast. 2009, 25, 942–972. [Google Scholar] [CrossRef]
- Sumikawa, S.; Ishiwatari, A.; Hiramoto, J.; Urabe, T. Improvement of springback prediction accuracy using material model considering elastoplastic anisotropy and Bauschinger effect. J. Mater. Proc. Technol. 2016, 230, 1–7. [Google Scholar] [CrossRef]
- Barlat, F.; Brem, J.C.; Yoon, J.W.; Chung, K.; Dick, R.E.; Lege, D.J.; Pourboghrat, F.; Choi, S.H.; Chu, E. Plane stress yield function for aluminum alloy sheets-part 1: Theory. Int. J. Plast. 2003, 19, 1297–1319. [Google Scholar] [CrossRef]
- Frederick, C.O.; Armstrong, P.J. A mathematical representation of the multiaxial Bauschinger effect. Mater. High Temp. 1966, 24, 1–26. [Google Scholar] [CrossRef]
- Chung, K.; Lee, M.G.; Kim, D.; Kim, C.; Wenner, M.L.; Barlat, F. Spring-back evaluation of automotive sheets based on isotropic-kinematic hardening laws and non-quadratic anisotropic yield functions part 1: Theory and formulation. Int. J. Plast. 2005, 21, 861–882. [Google Scholar]
- Lee, M.G.; Kim, D.; Chung, K.; Youn, J.R.; Kang, T.J. Combined isotropic-kinematic hardening laws with anisotropic back-stress evolution for orthotropic fiber-reinforced composites. Polym. Polym. Compos. 2004, 12, 225–234. [Google Scholar]
- Barlat, F.; Gracio, J.J.; Lee, M.G.; Rauch, E.F.; Vincze, G. An alternative to kinematic hardening in classical plasticity. Int. J. Plast. 2011, 27, 1309–1327. [Google Scholar] [CrossRef]
- Lee, J.Y.; Lee, J.W.; Lee, M.G.; Barlat, F. An application of homogeneous anisotropic hardening to springback prediction in pre-strained U-draw/bending. Int. J. Solids Struct. 2012, 49, 3562–3572. [Google Scholar] [CrossRef]
- Lee, J.Y.; Barlat, F.; Lee, M.G. Constitutive and friction modeling for accurate springback analysis of advanced high strength steel sheets. Int. J. Plast. 2015, 71, 113–135. [Google Scholar] [CrossRef]
- Choi, J.; Lee, J.; Lee, M.G.; Barlat, F. Advanced constitutive modeling of AHSS sheets for application to springback prediction after U-draw double stamping process. J. Phys. 2016, 734. [Google Scholar] [CrossRef]
- Speich, G.R.; Demarest, V.A.; Miller, R.L. Formation of austenite during intercritical annealing of dual-phase steels. Metall. Mater. Trans. A 1981, 12, 1419–1428. [Google Scholar] [CrossRef]
- Shames, I.H. Introduction to Solid Mechanics, 2nd ed.; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1989. [Google Scholar]
- Voce, E. A practical strain hardening function. Metallurgica 1955, 51, 219–226. [Google Scholar]
- Krahmer, D.M.; Polvorosa, R.; López de Lacalle, L.; Alonso-Pinillos, U.; Riu, F. Alternatives for Specimen Manufacturing in Tensile Testing of Steel Plates. Exp. Tech. 2016, 40, 1555–1565. [Google Scholar] [CrossRef]
- Hanabusa, Y.; Takizawa, H.; Kuwabara, T. Numerical verification of a biaxial tensile test method using a cruciform specimen. J. Mater. Proc. Technol. 2013, 213, 961–970. [Google Scholar] [CrossRef]
- Lee, M.G.; Kim, J.H.; Kim, D.; Seo, O.S.; Nguyen, N.T.; Kim, H.Y. Anisotropic Hardening of Sheet Metals at Elevated Temperature: Tension-Compressions Test Development and Validation. Exp. Mech. 2013, 53, 1039–1055. [Google Scholar] [CrossRef]
- Nelder, J.A.; Mead, R. A simplex method for function minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Del Pozo, D.; López de Lacalle, L.N.; López, J.M.; Hernández, A. Prediction of press/die deformation for an accurate manufacturing of drawing dies. Int. J. Adv. Manuf. Technol. 2008, 37, 649–656. [Google Scholar] [CrossRef]
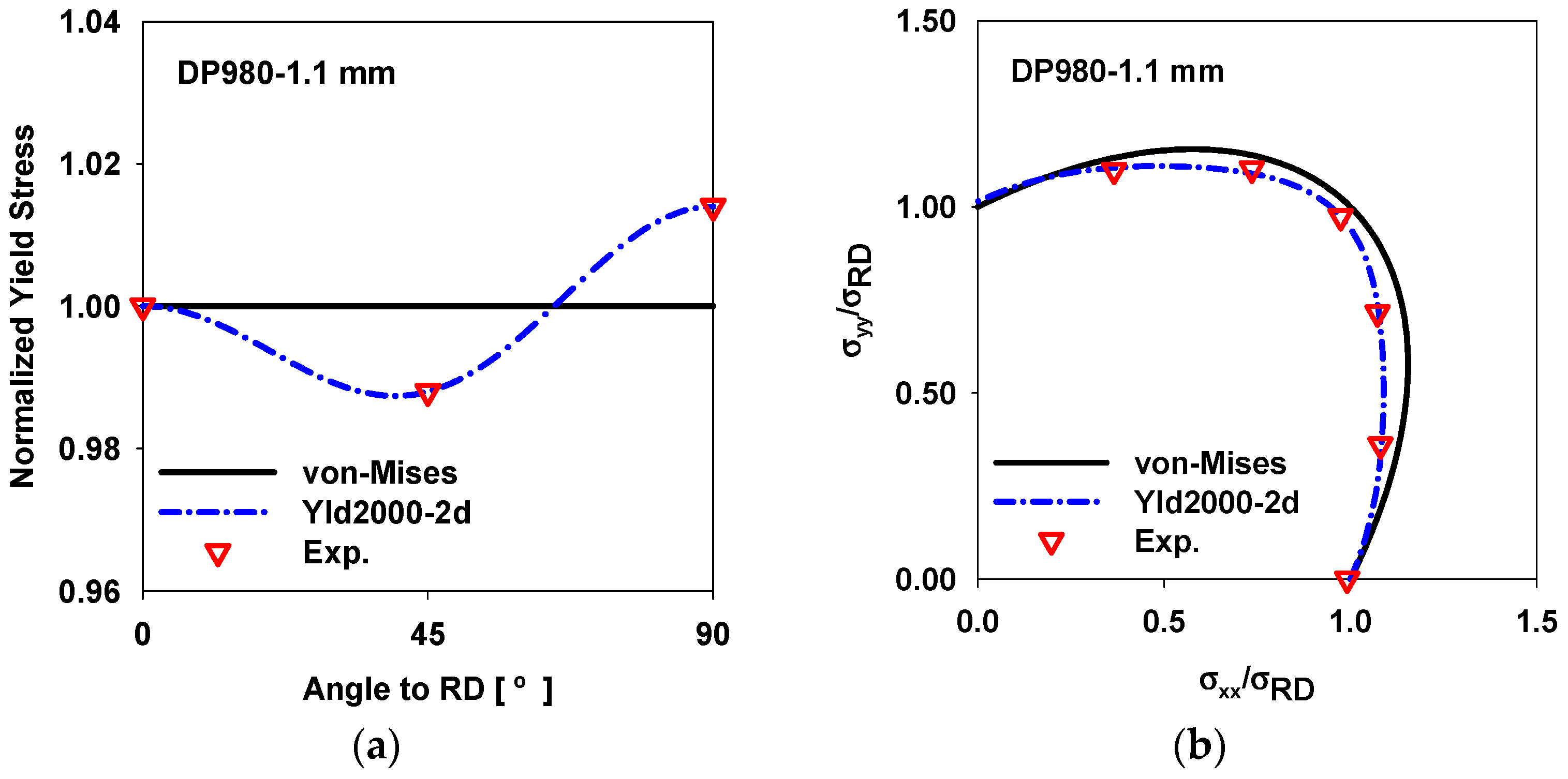
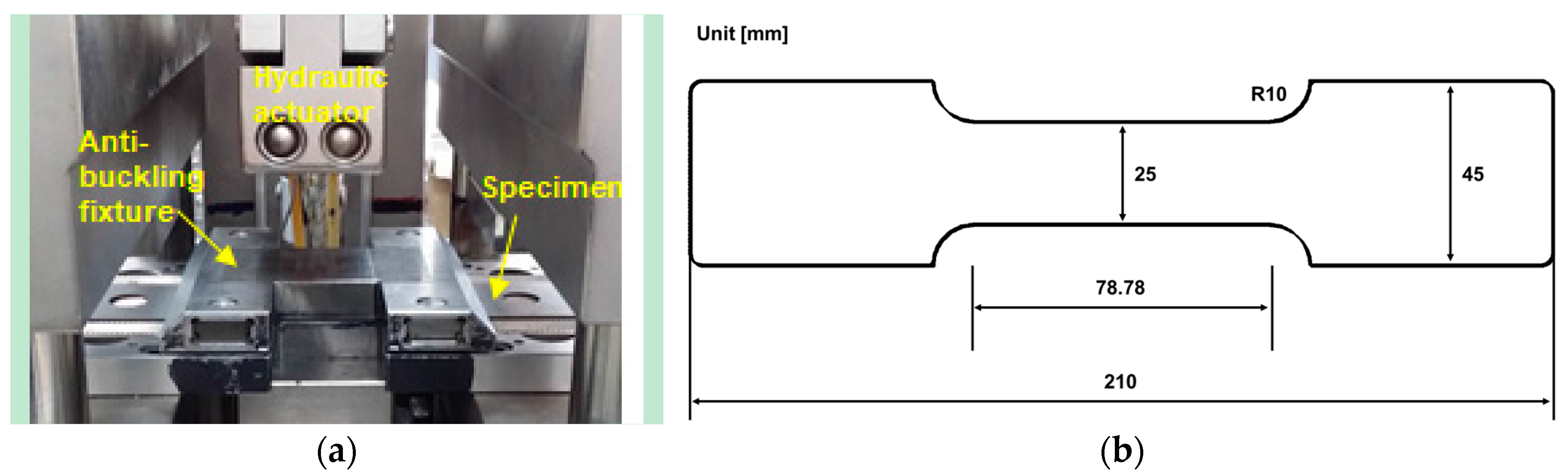
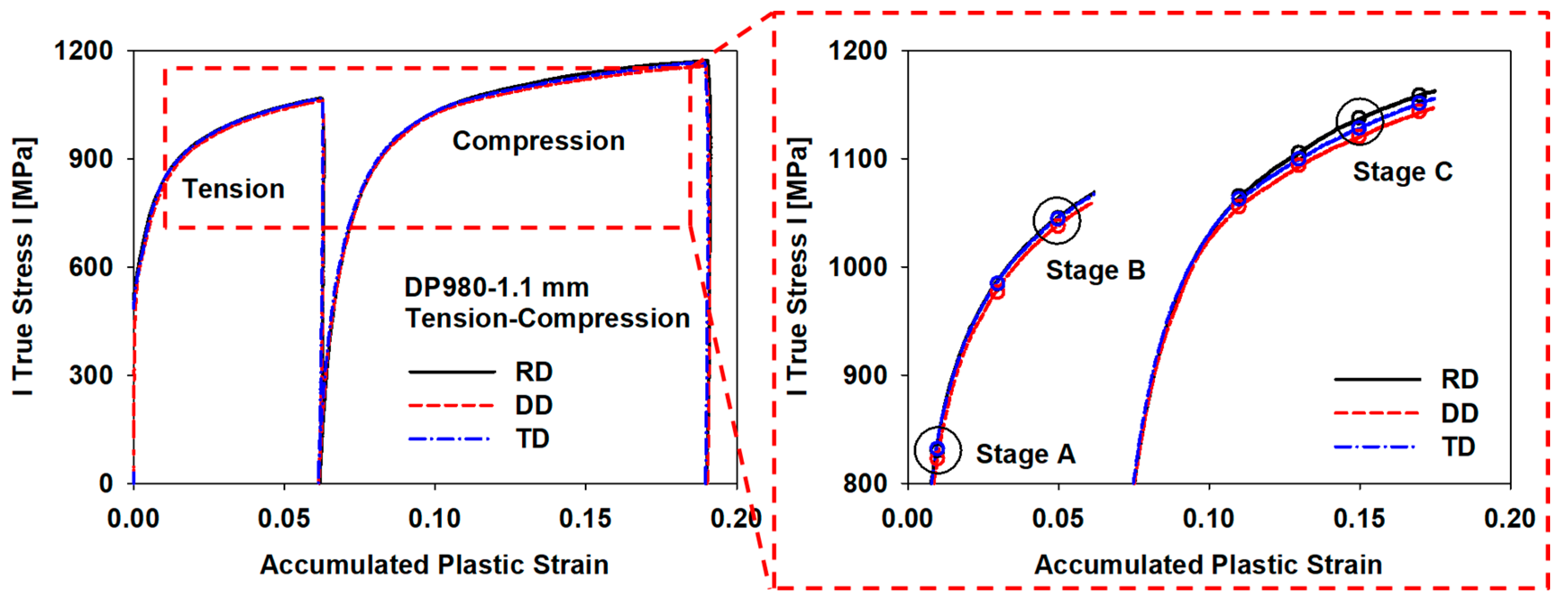

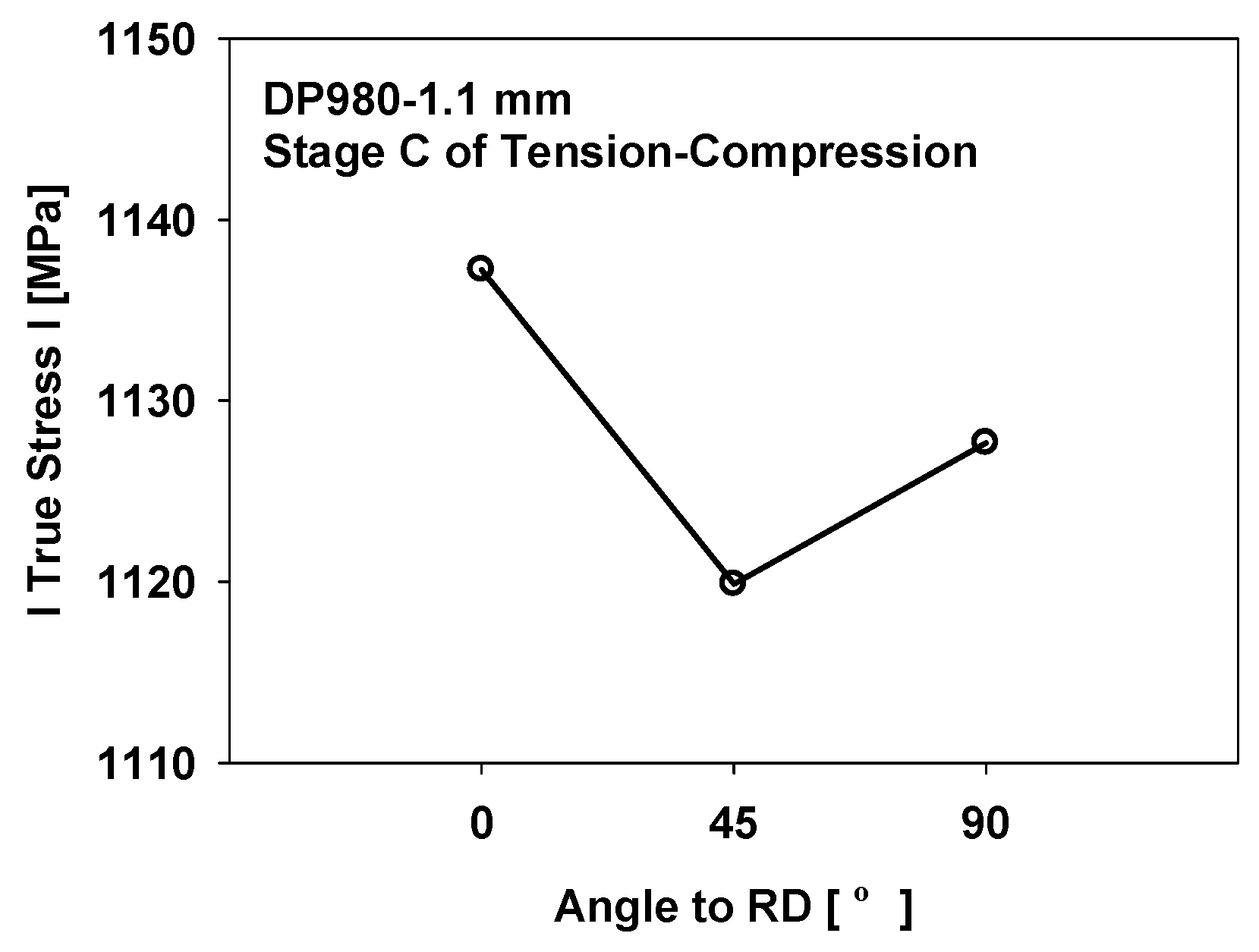


| Direction | Young’s Modulus [GPa] | Yield Strength [MPa] | r-Value | Tensile Strength [MPa] | Elonagtion [%] |
|---|---|---|---|---|---|
| RD | 202.2 | 618.1 | 0.757 | 1014.1 | 15.6 |
| DD | 206.1 | 610.7 | 0.851 | 1015.6 | 16.4 |
| TD | 208.8 | 626.7 | 0.856 | 1021.9 | 14.0 |
| [GPa] | [GPa] | [MPa] | |
|---|---|---|---|
| 205.8 | 105.7 | 345 | 300 |
| Elastic Modulus [GPa] | Yield Strength [MPa] | |
|---|---|---|
| 297.0 | 601.9 | 0.915 |
| 6 | 0.978 | 0.978 | 1.049 | 1.008 | 1.026 | 1.044 | 0.998 | 1.023 |
| Hardening Model with Isotropic Evolution | ||||||||
| [MPa] | [MPa] | [MPa] | [MPa] | |||||
| 583.9 | 409.7 | 3.861 | 17,896 | 26,144 | 9.537 | 34.74 | 80.27 | 6.551 |
| Hardening Model with Anisotropic Evolution | ||||||||
| [MPa] | [MPa] | [MPa] | [MPa] | |||||
| 583.9 | 409.7 | 3.861 | 17,896 | 26,144 | 9.537 | 34.74 | 80.27 | 6.551 |
| 0.948 | 0.975 | 1.014 | 0.940 | |||||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jung, J.; Jun, S.; Lee, H.-S.; Kim, B.-M.; Lee, M.-G.; Kim, J.H. Anisotropic Hardening Behaviour and Springback of Advanced High-Strength Steels. Metals 2017, 7, 480. https://doi.org/10.3390/met7110480
Jung J, Jun S, Lee H-S, Kim B-M, Lee M-G, Kim JH. Anisotropic Hardening Behaviour and Springback of Advanced High-Strength Steels. Metals. 2017; 7(11):480. https://doi.org/10.3390/met7110480
Chicago/Turabian StyleJung, Jaebong, Sungwook Jun, Hyun-Seok Lee, Byung-Min Kim, Myoung-Gyu Lee, and Ji Hoon Kim. 2017. "Anisotropic Hardening Behaviour and Springback of Advanced High-Strength Steels" Metals 7, no. 11: 480. https://doi.org/10.3390/met7110480





