Softening Characterization of 300M High-Strength Steel during Post-Dynamic Recrystallization
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Isothermal Interrupted Compression
2.3. Hardness Tests
3. Results and Discussion
3.1. Microstructures during Post-Dynamic Recrystallization
3.2. Microhardness and Young’s Modulus
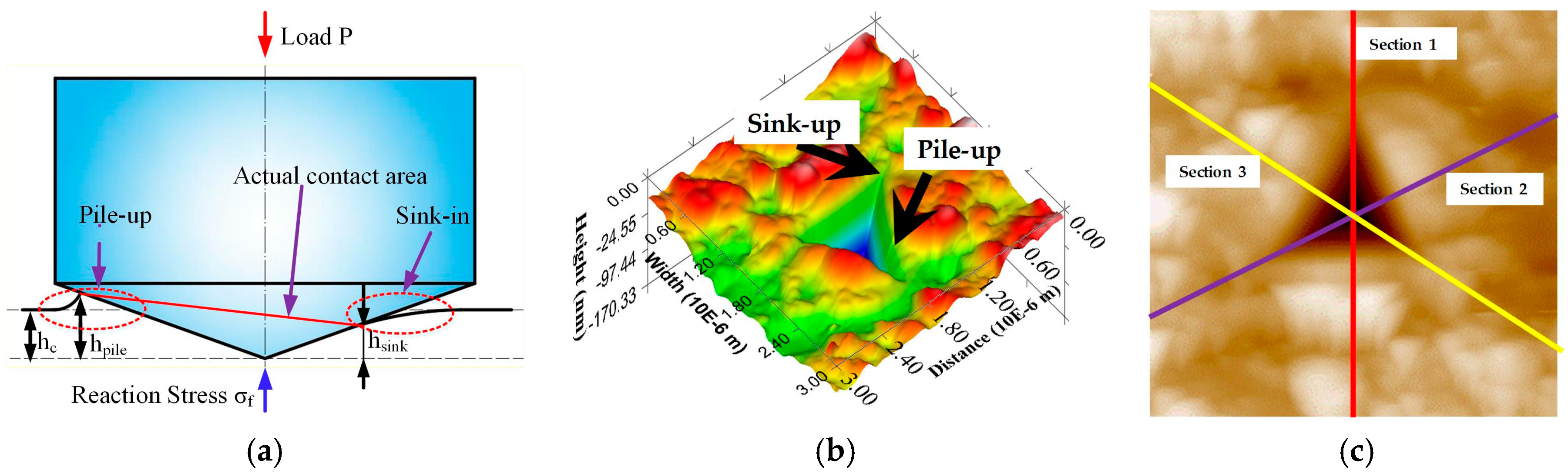
3.3. SPM Images of Indentation Morphology
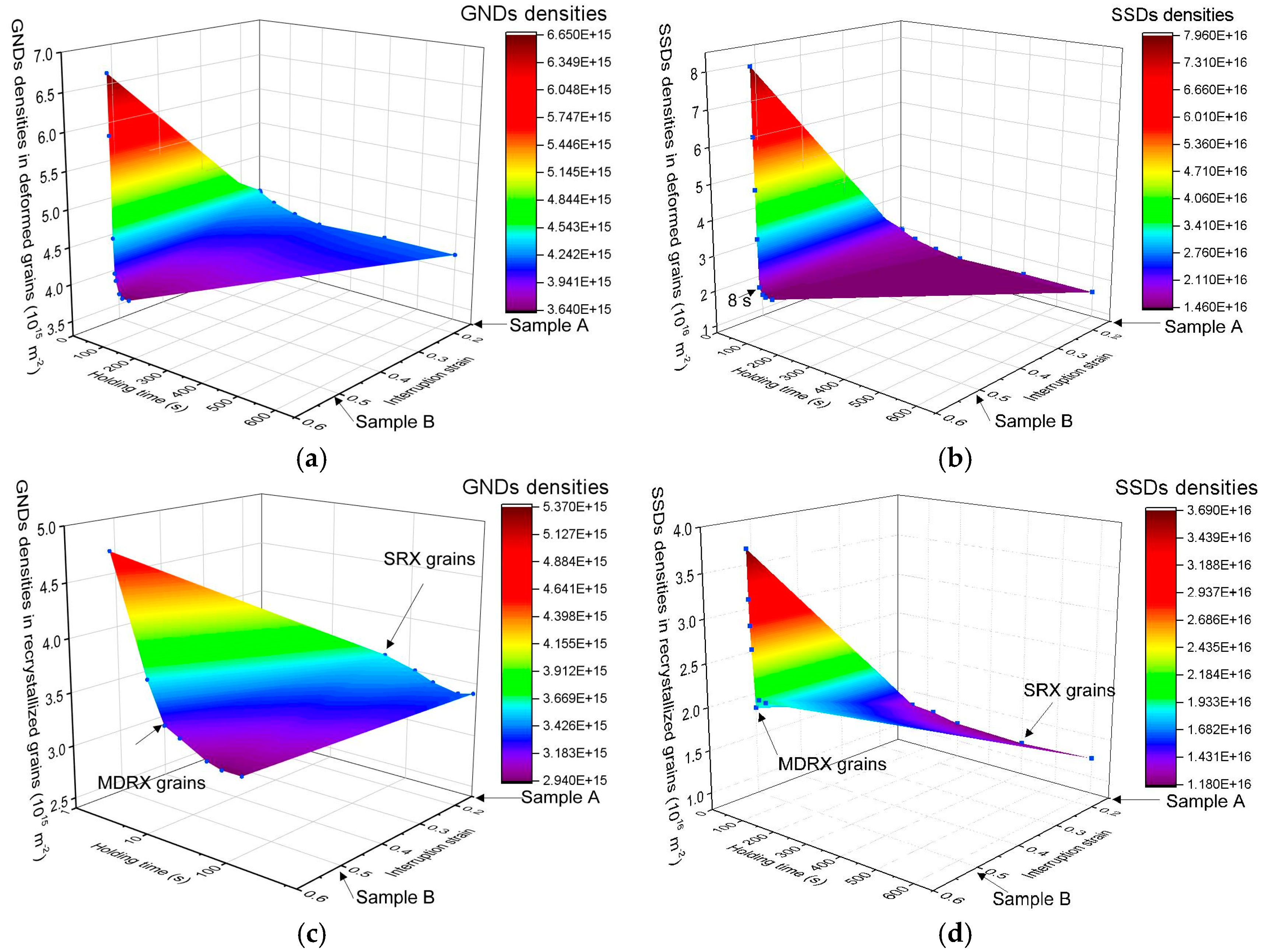
3.4. Densities of SSDs and GNDs
4. Conclusions
- The SRX occurred alone in samples without initial DRX grains, after an incubation time around 50 s. In contrast, MDRX grain initially appeared within 1 s and completed at about 8 s in samples with a high initial volume fraction of DRX grains.
- The microhardness, indentation hardness, and Young’s modulus at deformed grains and recrystallized grains decreased gradually with the increase of MDRX and SRX volume fractions. The dependencies of the integrated softening effects on volume fractions of MDRX and SRX were observed. Sink-in and pile-up phenomena were enhanced by the SRX and MDRX processes, respectively.
- SSDs and GNDs densities decreased in relation to an increase in volume fraction of MDRX and SRX grains.
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Luo, J.; Li, M.Q.; Liu, Y.G.; Sun, H.M. The deformation behavior in isothermal compression of 300M ultrahigh-strength steel. Mater. Sci. Eng. A 2012, 534, 314–322. [Google Scholar] [CrossRef]
- Sun, H.M.; Li, M.Q.; Liu, Y.G. Development of processing map coupling grain size for the isothermal compression of 300 M steel. Mater. Sci. Eng. A 2014, 595, 77–85. [Google Scholar] [CrossRef]
- Doherty, R.D.; Hughes, D.A.; Humphreys, F.J.; Jonas, J.J.; Jensen, D.J.; Kassner, M.E.; King, W.E.; McNelley, T.R.; McQueen, H.J.; Rollett, A.D. Current issues in recrystallization: A review. Mater. Sci. Eng. A 1997, 238, 219–274. [Google Scholar] [CrossRef]
- Humphreys, F.J.; Hatherly, M. Recrystallization and Related Annealing Phenomena; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Huang, K.; Marthinsen, K.; Zhao, Q.; Logé, R.E. The double-edge effect of second-phase particles on the recrystallization behaviour and associated mechanical properties of metallic materials. Prog. Mater. Sci. 2018, 92, 284–359. [Google Scholar] [CrossRef]
- Beladi, H.; Cizek, P.; Hodgson, P.D. The mechanism of metadynamic softening in austenite after complete dynamic recrystallization. Scr. Mater. 2010, 62, 191–194. [Google Scholar] [CrossRef]
- Dehghan-Manshadi, A.; Barnett, M.R.; Hodgson, P.D. Recrystallization in AISI 304 austenitic stainless steel during and after hot deformation. Mater. Sci. Eng. A 2008, 485, 664–672. [Google Scholar] [CrossRef]
- Takayama, A.; Yang, X.; Miura, H.; Sakai, T. Continuous static recrystallization in ultrafine-grained copper processed by multi-directional forging. Mater. Sci. Eng. A 2008, 478, 221–228. [Google Scholar] [CrossRef]
- Tang, X.; Wang, B.; Ji, H.; Fu, X.; Xiao, W. Behavior and modeling of microstructure evolution during metadynamic recrystallization of a Ni-based superalloy. Mater. Sci. Eng. A 2016, 675, 192–203. [Google Scholar] [CrossRef]
- Cao, Y.; Di, H. Grain boundary character distribution during the post-deformation recrystallization of Incoloy 800H at elevated temperature. Mater. Lett. 2016, 163, 24–27. [Google Scholar] [CrossRef]
- Sakai, T.; Belyakov, A.; Kaibyshev, R.; Miura, H.; Jonas, J.J. Dynamic and post-dynamic recrystallization under hot, cold and severe plastic deformation conditions. Prog. Mater. Sci. 2014, 60, 130–207. [Google Scholar] [CrossRef]
- Djaic, R.A.P.; Jonas, J.J. Static recrystallization of austenite between intervals of hot working. J. Iron Steel Inst. 1972, 210, 256–261. [Google Scholar]
- Beladi, H.; Cizek, P.; Hodgson, P.D. New insight into the mechanism of metadynamic softening in austenite. Acta Mater. 2011, 59, 1482–1492. [Google Scholar] [CrossRef]
- Huang, K. Towards the Modelling of Recrystallization Phenomena in Multi-Pass Conditions: Application to 304L Steel. Ph.D. Dissertation, Ecole Nationale Superieure des Mines de, Paris, France, 2011. [Google Scholar]
- Zeng, R.; Huang, L.; Zhang, X.; Li, J.J.; Hu, J. Influence of strain induced grain boundary migration on grain growth of 300M during static and meta-dynamic recrystallization. Procedia Eng. 2017, 207, 460–465. [Google Scholar] [CrossRef]
- Zouari, M.; Logé, R.E.; Bozzolo, N. In Situ Characterization of Inconel 718 Post-Dynamic Recrystallization within a Scanning Electron Microscope. Metals 2017, 7, 476. [Google Scholar] [CrossRef]
- Huang, C.Q.; Deng, J.; Wang, S.X.; Liu, L. An investigation on the softening mechanism of 5754 aluminum alloy during multistage hot deformation. Metals 2017, 7, 107. [Google Scholar] [CrossRef]
- Ashby, M.F. The deformation of plastically non-homogeneous materials. Philos. Mag. 1970, 21, 399–424. [Google Scholar] [CrossRef]
- Chen, H.; Li, F.; Li, J.; Ma, X.; Li, J.; Wang, Q. Hardening and softening analysis of pure titanium based on the dislocation density during torsion deformation. Mater. Sci. Eng. A 2016, 671, 17–31. [Google Scholar] [CrossRef]
- Wang, C.; Li, F.; Wei, L.; Yang, Y.; Dong, J. Experimental microindentation of pure copper subjected to severe plastic deformation by combined tension–torsion. Mater. Sci. Eng. A 2013, 571, 95–102. [Google Scholar] [CrossRef]
- Zhang, M.; Li, F.; Chen, B.; Wang, S. Investigation of micro-indentation characteristics of P/M nickel-base superalloy FGH96 using dislocation-power theory. Mater. Sci. Eng. A 2012, 535, 170–181. [Google Scholar] [CrossRef]
- Nix, W.D.; Gao, H. Indentation size effects in crystalline materials: A law for strain gradient plasticity. J. Mech. Phys. Solids 1998, 46, 411–425. [Google Scholar] [CrossRef]
- Pharr, G.M.; Oliver, W.C. Measurement of thin film mechanical properties using nanoindentation. MRS Bull. 1992, 17, 28–33. [Google Scholar] [CrossRef]
- Taylor, G.I. The mechanism of plastic deformation of crystals. Part I. Theoretical. Proc. R. Soc. Lond. Ser. A 1934, 145, 362–387. [Google Scholar] [CrossRef]
- Lei, Z.; Gao, P.; Li, H.; Fan, X.; Cai, Y.; Zhan, M. Microstructure characterization and nano & micro hardness of tri-modal microstructure of titanium alloy under different hot working conditions. Mater. Charact. 2017, 134, 236–245. [Google Scholar]
- Carter, C.S. The effect of silicon on the stress corrosion resistance of low alloy high strength steels. Corrosion 1969, 25, 423–431. [Google Scholar] [CrossRef]
- Davis, J.R. ASM Specialty Handbook: Cast Irons; ASM International: Geauga County, OH, USA, 1996. [Google Scholar]
- Zhang, L.; Ohmura, T.; Tsuzaki, K. Nanoindentation in Materials Science, Chapter 5. In Application of Nanoindentation Technique in Martensitic Structures; InTech: Vienna, Austria, 2012. [Google Scholar]
- Levitas, V.I.; Javanbakht, M. Interaction between phase transformations and dislocations at the nanoscale. Part 1. General phase field approach. J. Mech. Phys. Solids 2015, 82, 287–319. [Google Scholar] [CrossRef]
- Du, C.; Hoefnagels, J.P.M.; Kölling, S.; Geers, M.G.D.; Sietsma, J.; Petrov, R.; Bliznuk, V.; Koenraad, P.M.; Schryvers, D.; Amin-Ahmadi, B. Martensite crystallography and chemistry in dual phase and fully martensitic steels. Mater. Charact. 2018, 139, 411–420. [Google Scholar] [CrossRef]
- Ramazani, A.; Mukherjee, K.; Schwedt, A.; Goravanchi, P.; Prahl, U.; Bleck, W. Quantification of the effect of transformation-induced geometrically necessary dislocations on the flow-curve modelling of dual-phase steels. Int. J. Plast. 2013, 43, 128–152. [Google Scholar] [CrossRef]
- Hossain, R.; Pahlevani, F.; Quadir, M.Z.; Sahajwalla, V. Stability of retained austenite in high carbon steel under compressive stress: An investigation from macro to nano scale. Sci. Rep. 2016, 6, 34958. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Li, F.; Xue, F.; Cai, J.; Chen, B. Micromechanical behavior study of forged 7050 aluminum alloy by microindentation. Mater. Des. 2012, 37, 491–499. [Google Scholar] [CrossRef]
- Hardiman, M.; Vaughan, T.J.; McCarthy, C.T. A review of key developments and pertinent issues in nanoindentation testing of fibre reinforced plastic microstructures. Compos. Struct. 2017, 180, 782–798. [Google Scholar] [CrossRef]
- Sneddon, I.N. The relation between load and penetration in the axisymmetric Boussinesq problem for a punch of arbitrary profile. Int. J. Eng. Sci. 1965, 3, 47–57. [Google Scholar] [CrossRef]
- Swadener, J.G.; George, E.P.; Pharr, G.M. The correlation of the indentation size effect measured with indenters of various shapes. J. Mech. Phys. Solids 2002, 50, 681–694. [Google Scholar] [CrossRef]
- Bolshakov, A.; Pharr, G.M. Influences of pileup on the measurement of mechanical properties by load and depth sensing indentation techniques. J. Mater. Res. 1998, 13, 1049–1058. [Google Scholar] [CrossRef]
- He, B.B.; Liang, Z.Y.; Huang, M.X. Nanoindentation investigation on the initiation of yield point phenomenon in a medium Mn steel. Scr. Mater. 2018, 150, 134–138. [Google Scholar] [CrossRef]
- Sankaran, K.K.; Mishra, R.S. Ultrahigh Strength Steels. In Metallurgy and Design of Alloys with Hierarchical Microstructures; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]











| Composition | C | Si | Mn | Cr | Mo | Ni | Cu | P | Fe | V |
|---|---|---|---|---|---|---|---|---|---|---|
| Content | 0.39 | 1.60 | 0.70 | 0.89 | 0.40 | 1.80 | 0.06 | 0.01 | 94.08 | 0.07 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, R.; Huang, L.; Su, H.; Ma, H.; Ma, Y.; Li, J. Softening Characterization of 300M High-Strength Steel during Post-Dynamic Recrystallization. Metals 2018, 8, 340. https://doi.org/10.3390/met8050340
Zeng R, Huang L, Su H, Ma H, Ma Y, Li J. Softening Characterization of 300M High-Strength Steel during Post-Dynamic Recrystallization. Metals. 2018; 8(5):340. https://doi.org/10.3390/met8050340
Chicago/Turabian StyleZeng, Rong, Liang Huang, Hongliang Su, Huijuan Ma, Yangfei Ma, and Jianjun Li. 2018. "Softening Characterization of 300M High-Strength Steel during Post-Dynamic Recrystallization" Metals 8, no. 5: 340. https://doi.org/10.3390/met8050340
APA StyleZeng, R., Huang, L., Su, H., Ma, H., Ma, Y., & Li, J. (2018). Softening Characterization of 300M High-Strength Steel during Post-Dynamic Recrystallization. Metals, 8(5), 340. https://doi.org/10.3390/met8050340






