Accurate Prediction of the Weld Bead Characteristic in Laser Keyhole Welding Based on the Stochastic Kriging Model
Abstract
:1. Introduction
2. Laser Keyhole Welding Procedure
2.1. Problem Definition
2.2. Materials
2.3. Laser Keyhole Welding Process
3. The Proposed Approach
3.1. General Framework
3.2. Theory of Stochastic Kriging
4. Result and Discussion
4.1. Design of Experiment
4.2. Data Processing
4.2.1. Weld Bead Scanning
4.2.2. Image Processing and Feature Extracting
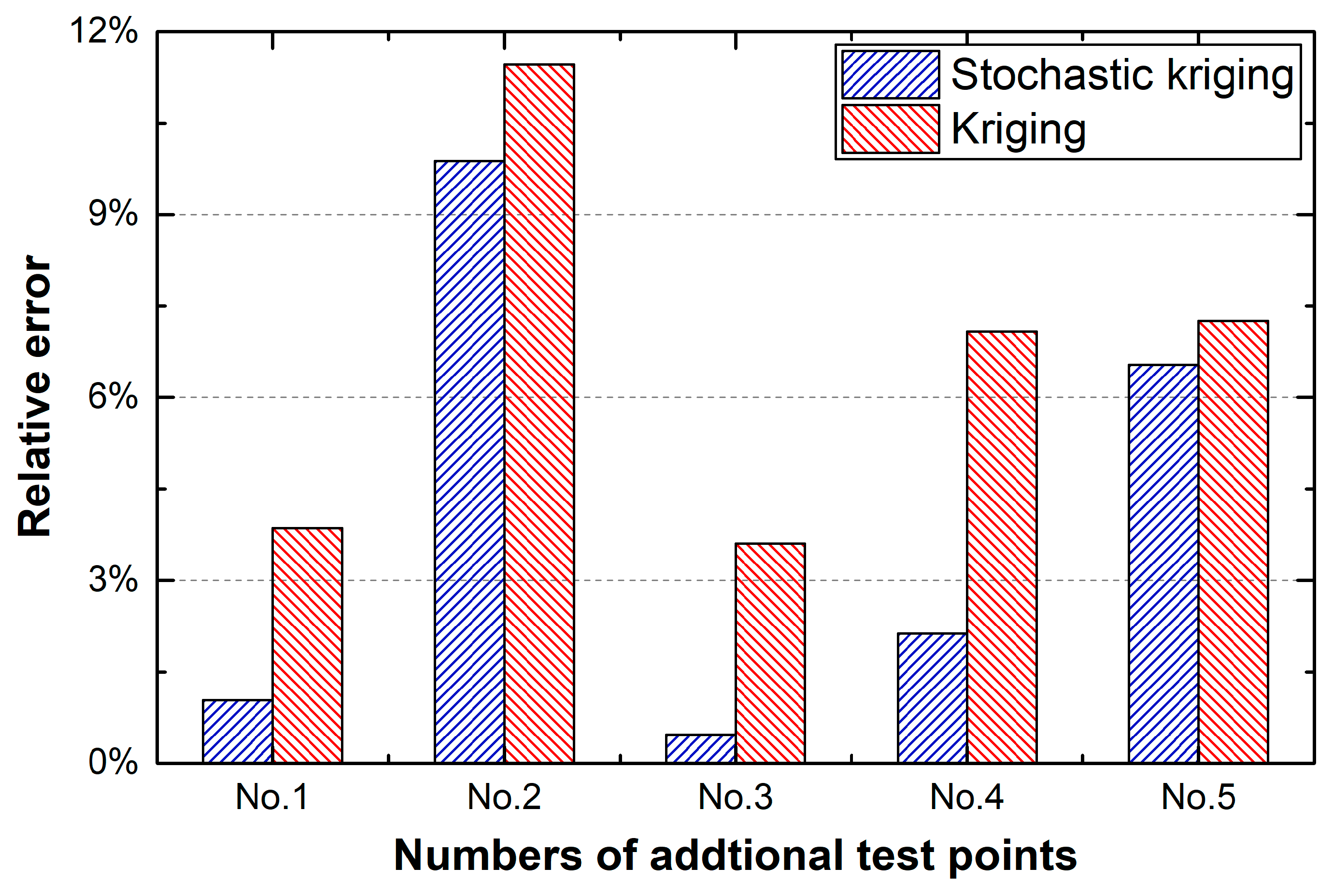
4.3. Prediction Performance of the Stochastic Kriging Model
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| DOE | Design of experiment |
| FP | Focal position |
| LKW | Laser keyhole welding |
| LP | Laser power |
| OLHS | Optimal Latin hypercube sampling |
| SKM | Stochastic kriging model |
| WPP | Welding process parameters |
| WS | Welding speed |
| WW | Weld width |
References
- Yuce, C.; Tutar, M.; Karpat, F.; Yavuz, N. The optimization of process parameters and microstructural characterization of fiber laser welded dissimilar HSLA and MART steel joints. Metals 2016, 6, 245. [Google Scholar] [CrossRef]
- Cao, L.; Shao, X.; Jiang, P.; Zhou, Q.; Rong, Y.; Geng, S.; Mi, G. Effects of welding speed on microstructure and mechanical property of fiber laser welded dissimilar butt joints between AISI316L and EH36. Metals 2017, 7, 270. [Google Scholar] [CrossRef]
- Murugan, N.; Gunaraj, V. Prediction and control of weld bead geometry and shape relationships in submerged arc welding of pipes. J. Mater. Process. Technol. 2005, 168, 478–487. [Google Scholar] [CrossRef]
- Ridha Mohammed, G.; Ishak, M.; Ahmad, S.N.A.S.; Abdulhadi, H.A. Fiber laser welding of dissimilar 2205/304 stainless steel plates. Metals 2017, 7, 546. [Google Scholar] [CrossRef]
- Loginova, I.; Khalil, A.; Pozdniakov, A.; Solonin, A.; Zolotorevskiy, V. Effect of pulse laser welding parameters and filler metal on microstructure and mechanical properties of Al-4.7 Mg-0.32 Mn-0.21 Sc-0.1 Zr Alloy. Metals 2017, 7, 564. [Google Scholar] [CrossRef]
- Kim, I.; Son, J.; Kim, I.; Kim, J.; Kim, O. A study on relationship between process variables and bead penetration for robotic CO2 arc welding. J. Mater. Process. Technol. 2003, 136, 139–145. [Google Scholar] [CrossRef]
- Fukuda, S.; Morita, H.; Yamauchi, Y.; Nagasawa, I.; Tsuji, S. Expert system for determining welding condition for a pressure vessel. ISIJ Int. 1990, 30, 150–154. [Google Scholar] [CrossRef]
- Gunaraj, V.; Murugan, N. Application of response surface methodology for predicting weld bead quality in submerged arc welding of pipes. J. Mater. Process. Technol. 1999, 88, 266–275. [Google Scholar] [CrossRef]
- Nagesh, D.; Datta, G. Prediction of weld bead geometry and penetration in shielded metal-arc welding using artificial neural networks. J. Mater. Process. Technol. 2002, 123, 303–312. [Google Scholar] [CrossRef]
- Srivastava, S.; Garg, R. Process parameter optimization of gas metal arc welding on IS: 2062 mild steel using response surface methodology. J. Manuf. Process. 2017, 25, 296–305. [Google Scholar] [CrossRef]
- Pal, S.; Pal, S.K.; Samantaray, A.K. Radial basis function neural network model based prediction of weld plate distortion due to pulsed metal inert gas welding. Sci. Technol. Weld. Join. 2007, 12, 725–731. [Google Scholar] [CrossRef]
- Jiang, P.; Wang, C.; Zhou, Q.; Shao, X.; Shu, L.; Li, X. Optimization of laser welding process parameters of stainless steel 316L using FEM, Kriging and NSGA-II. Adv. Eng. Softw. 2016, 99, 147–160. [Google Scholar] [CrossRef]
- Ankenman, B.; Nelson, B.L.; Staum, J. Stochastic kriging for simulation metamodeling. Oper. Res. 2010, 58, 371–382. [Google Scholar] [CrossRef]
- Chen, X.; Ankenman, B.E.; Nelson, B.L. The effects of common random numbers on stochastic kriging metamodels. ACM Trans. Model. Comput. Simul. (TOMACS) 2012, 22, 7. [Google Scholar] [CrossRef]
- Xie, W.; Nelson, B.; Staum, J. The influence of correlation functions on stochastic kriging metamodels. In Proceedings of the 2010 Winter Simulation Conference, Baltimore, MD, USA, 5–8 December 2010; pp. 1067–1078. [Google Scholar]
- Kamiński, B. A method for the updating of stochastic kriging metamodels. Eur. J. Oper. Res. 2015, 247, 859–866. [Google Scholar] [CrossRef]
- Liu, M.; Staum, J. Stochastic kriging for efficient nested simulation of expected shortfall. J. Risk 2010, 12, 3. [Google Scholar] [CrossRef]
- El-Batahgy, A.-M. Effect of laser welding parameters on fusion zone shape and solidification structure of austenitic stainless steels. Mater. Lett. 1997, 32, 155–163. [Google Scholar] [CrossRef]
- Cicală, E.; Duffet, G.; Andrzejewski, H.; Grevey, D.; Ignat, S. Hot cracking in Al–Mg–Si alloy laser welding-operating parameters and their effects. Mater. Sci. Eng. A 2005, 395, 1–9. [Google Scholar] [CrossRef]
- Cao, L.; Yang, Y.; Jiang, P.; Zhou, Q.; Mi, G.; Gao, Z.; Rong, Y.; Wang, C. Optimization of processing parameters of AISI 316L laser welding influenced by external magnetic field combining RBFNN and GA. Results Phys. 2017, 7, 1329–1338. [Google Scholar] [CrossRef]
- Zhou, Q.; Rong, Y.; Shao, X.; Jiang, P.; Gao, Z.; Cao, L. Optimization of laser brazing onto galvanized steel based on ensemble of metamodels. J. Intell. Manuf. 2016, 1–15. [Google Scholar] [CrossRef]
- Jiang, P.; Cao, L.; Zhou, Q.; Gao, Z.; Rong, Y.; Shao, X. Optimization of welding process parameters by combining Kriging surrogate with particle swarm optimization algorithm. Int. J. Adv. Manuf. Technol. 2016, 86, 2473–2483. [Google Scholar] [CrossRef]
- Michalska, J.; Sozańska, M. Qualitative and quantitative analysis of σ and χ phases in 2205 duplex stainless steel. Mater. Charact. 2006, 56, 355–362. [Google Scholar] [CrossRef]
- Lophaven, S.; Nielsen, H.; Søndergaard, J. DACE-A MATLAB Kriging Toolbox—Version 2.0.(2002); Technical University of Denmark: Lyngby, Denmark, 2002. [Google Scholar]
- Seberry, J. Orthogonal designs. In Orthogonal Designs: Hadamard Matrices, Quadratic Forms and Algebras; Springer: Cham, Switzerland, 2017; pp. 1–5. [Google Scholar]
- Montgomery, D.C.; Runger, G.C.; Hubele, N.F. Engineering Statistics; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Park, J.-S. Optimal Latin-hypercube designs for computer experiments. J. Stat. Plan. Inference 1994, 39, 95–111. [Google Scholar] [CrossRef]
- Refaeilzadeh, P.; Tang, L.; Liu, H. Cross-validation. In Encyclopedia of Database Systems; Springer: Cham, Switzerland, 2009; pp. 532–538. [Google Scholar]




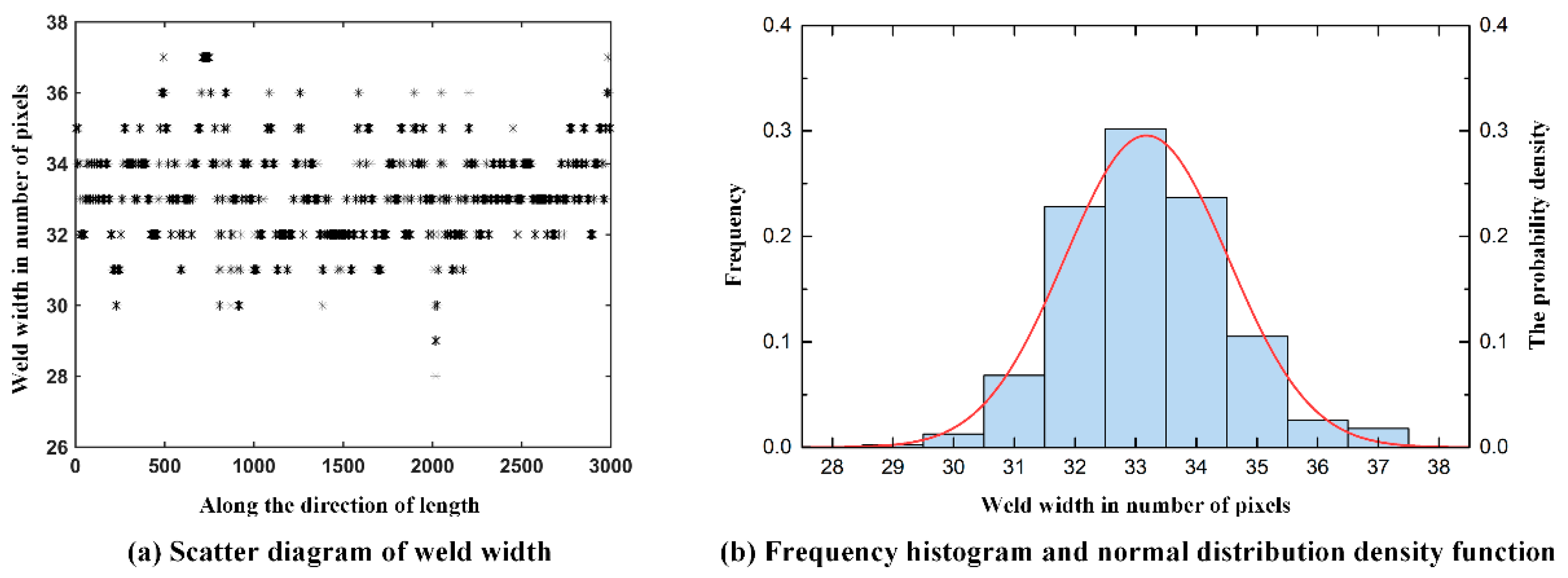
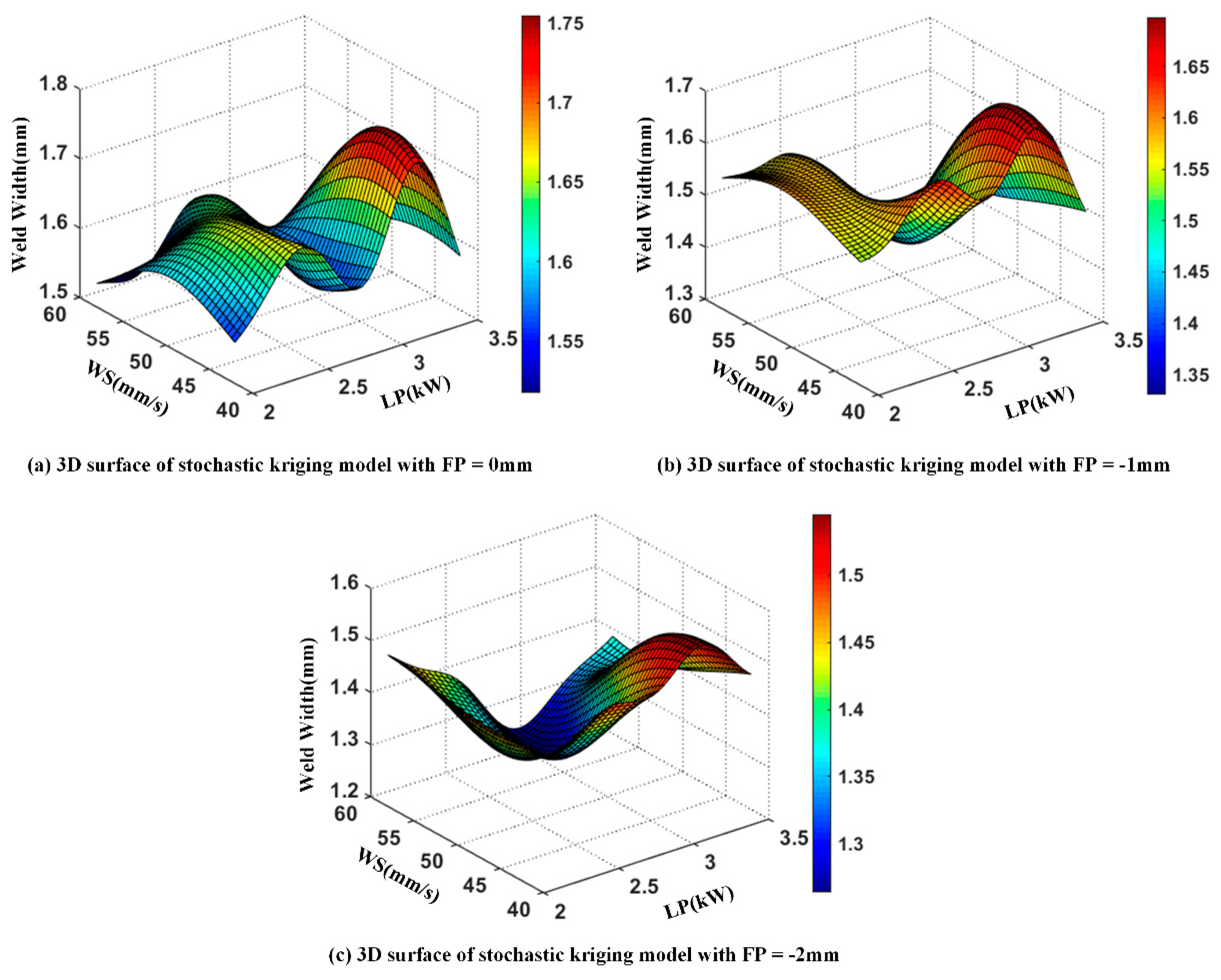


| Chemical Elements | C | Cr | Ni | Mo | Mn | Si | P | S | N |
|---|---|---|---|---|---|---|---|---|---|
| Composition (%) | 0.025 | 22.73 | 5.53 | 3.03 | 1.89 | 0.34 | 0.028 | 0.002 | 0.170 |
| No. | FP (mm) | LP (kW) | WS (mm/s) | Weld Width (mm) | Variance (10−6) |
|---|---|---|---|---|---|
| 1 | −2 | 2.2 | 44 | 1.40 | 1.09 |
| 2 | −2 | 2.3 | 51 | 1.35 | 2.1 |
| 3 | −2 | 3.3 | 55 | 1.37 | 1.33 |
| 4 | −2 | 2.8 | 43 | 1.46 | 1.49 |
| 5 | −2 | 2.9 | 49 | 1.37 | 1.50 |
| 6 | −2 | 2.7 | 56 | 1.29 | 0.89 |
| 7 | −1 | 2.0 | 50 | 1.59 | 1.06 |
| 8 | −1 | 2.1 | 46 | 1.56 | 3.54 |
| 9 | −1 | 2.1 | 57 | 1.56 | 1.29 |
| 10 | −1 | 2.5 | 53 | 1.55 | 6.27 |
| 11 | −1 | 2.6 | 48 | 1.50 | 4.82 |
| 12 | −1 | 2.6 | 42 | 1.63 | 2.38 |
| 13 | −1 | 3.0 | 58 | 1.33 | 3.44 |
| 14 | −1 | 3.1 | 42 | 1.67 | 3.20 |
| 15 | −1 | 3.1 | 52 | 1.52 | 2.35 |
| 16 | −1 | 3.3 | 47 | 1.64 | 2.56 |
| 17 | −1 | 3.4 | 47 | 1.55 | 2.32 |
| 18 | −1 | 3.5 | 56 | 1.41 | 2.68 |
| 19 | 0 | 2.3 | 51 | 1.64 | 0.98 |
| 20 | 0 | 2.4 | 45 | 1.66 | 5.16 |
| 21 | 0 | 2.4 | 58 | 1.55 | 2.29 |
| 22 | 0 | 2.8 | 54 | 1.60 | 3.08 |
| 23 | 0 | 2.9 | 49 | 1.57 | 6.77 |
| 24 | 0 | 3.2 | 44 | 1.75 | 3.11 |
| 25 | 0 | 3.4 | 53 | 1.61 | 3.62 |
| No. | Weld Appearance | Image Processing |
|---|---|---|
| 1 |  |  |
| 2 |  |  |
| 3 |  |  |
| 4 |  |  |
| 5 |  |  |
| No. | FP (mm) | LP (kW) | WS (mm/s) | Weld Width (mm) | Variance (10−6) |
|---|---|---|---|---|---|
| 1 | −2 | 3.2 | 58 | 1.32 | 1.22 |
| 2 | −2 | 3.3 | 42 | 1.69 | 1.71 |
| 3 | −1 | 2.7 | 53 | 1.45 | 4.55 |
| 4 | −1 | 3.0 | 51 | 1.46 | 2.39 |
| 5 | 0 | 2.5 | 55 | 1.74 | 3.29 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruan, X.; Zhou, Q.; Shu, L.; Hu, J.; Cao, L. Accurate Prediction of the Weld Bead Characteristic in Laser Keyhole Welding Based on the Stochastic Kriging Model. Metals 2018, 8, 486. https://doi.org/10.3390/met8070486
Ruan X, Zhou Q, Shu L, Hu J, Cao L. Accurate Prediction of the Weld Bead Characteristic in Laser Keyhole Welding Based on the Stochastic Kriging Model. Metals. 2018; 8(7):486. https://doi.org/10.3390/met8070486
Chicago/Turabian StyleRuan, Xiongfeng, Qi Zhou, Leshi Shu, Jiexiang Hu, and Longchao Cao. 2018. "Accurate Prediction of the Weld Bead Characteristic in Laser Keyhole Welding Based on the Stochastic Kriging Model" Metals 8, no. 7: 486. https://doi.org/10.3390/met8070486
APA StyleRuan, X., Zhou, Q., Shu, L., Hu, J., & Cao, L. (2018). Accurate Prediction of the Weld Bead Characteristic in Laser Keyhole Welding Based on the Stochastic Kriging Model. Metals, 8(7), 486. https://doi.org/10.3390/met8070486






