Validity of Galerkin Method at Beam’s Nonlinear Vibrations of the Single Mode with the Initial Curvature
Abstract
:1. Introduction
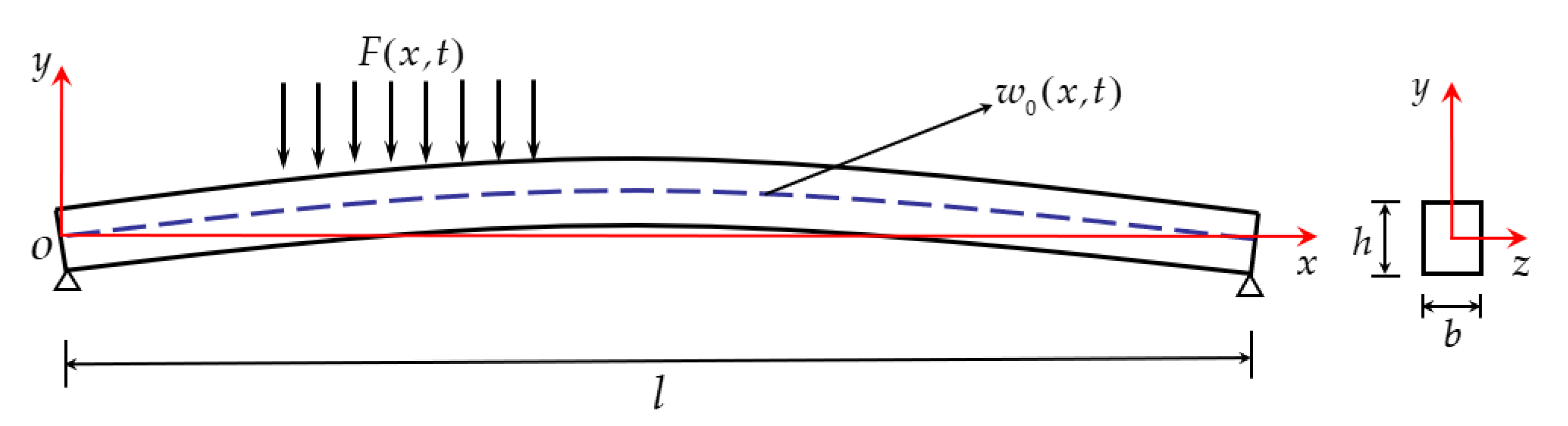
2. Mathematical Model
2.1. Equations of Motion
2.2. Galerkin Discretization
3. Methods Obtained Solutions
3.1. Multiple Scales Method
3.2. Finite Element Method
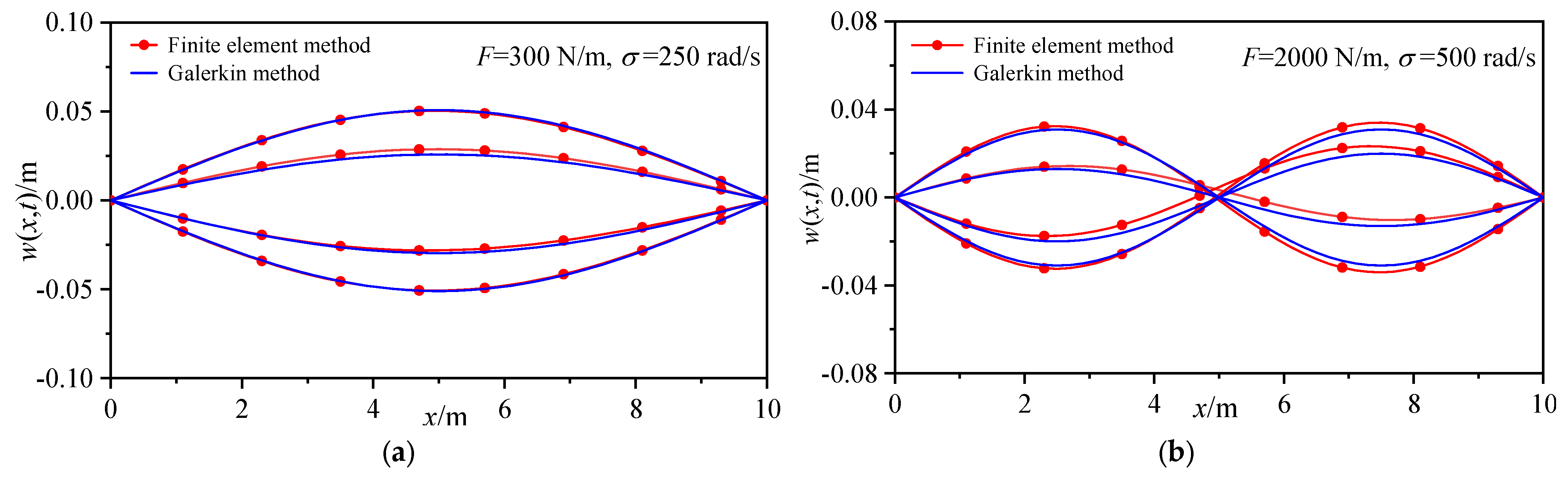
4. Results and Discussion
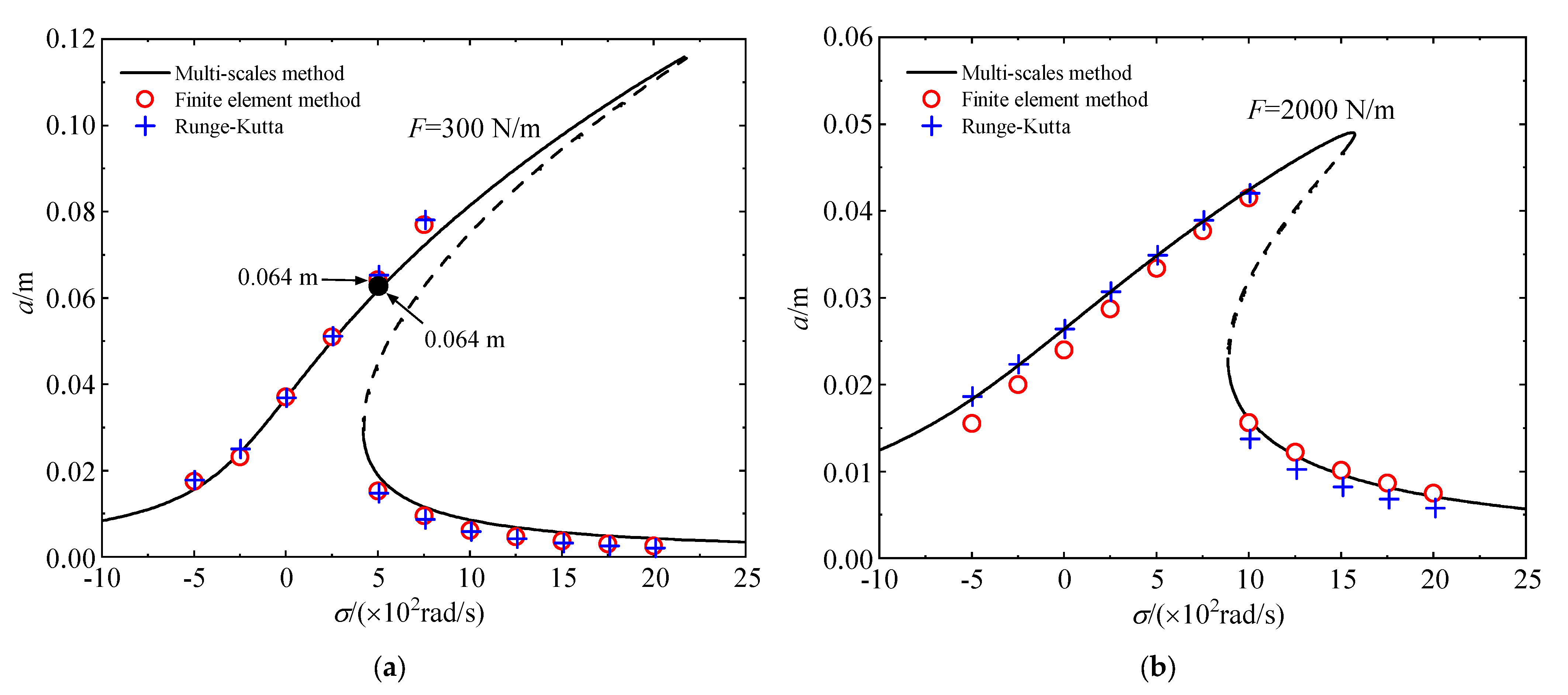
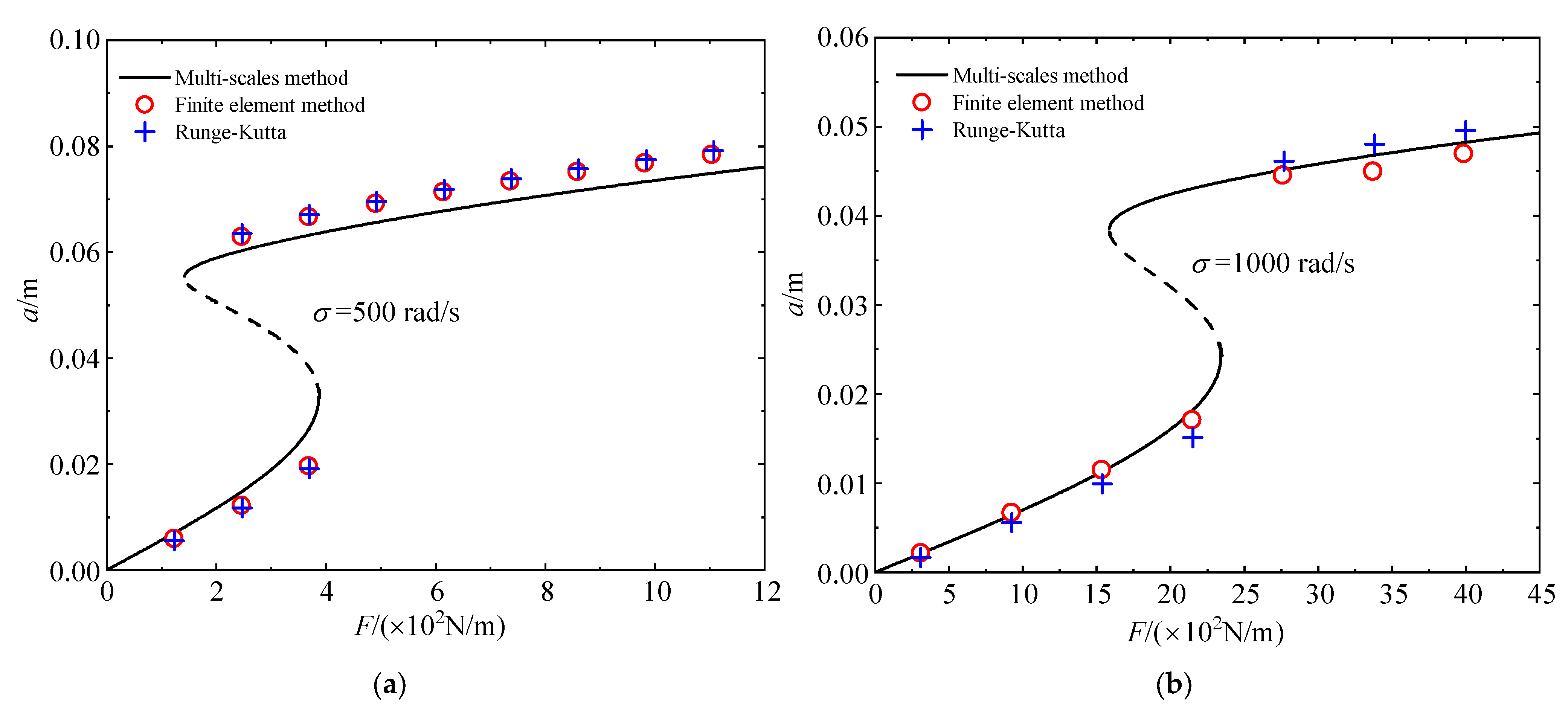
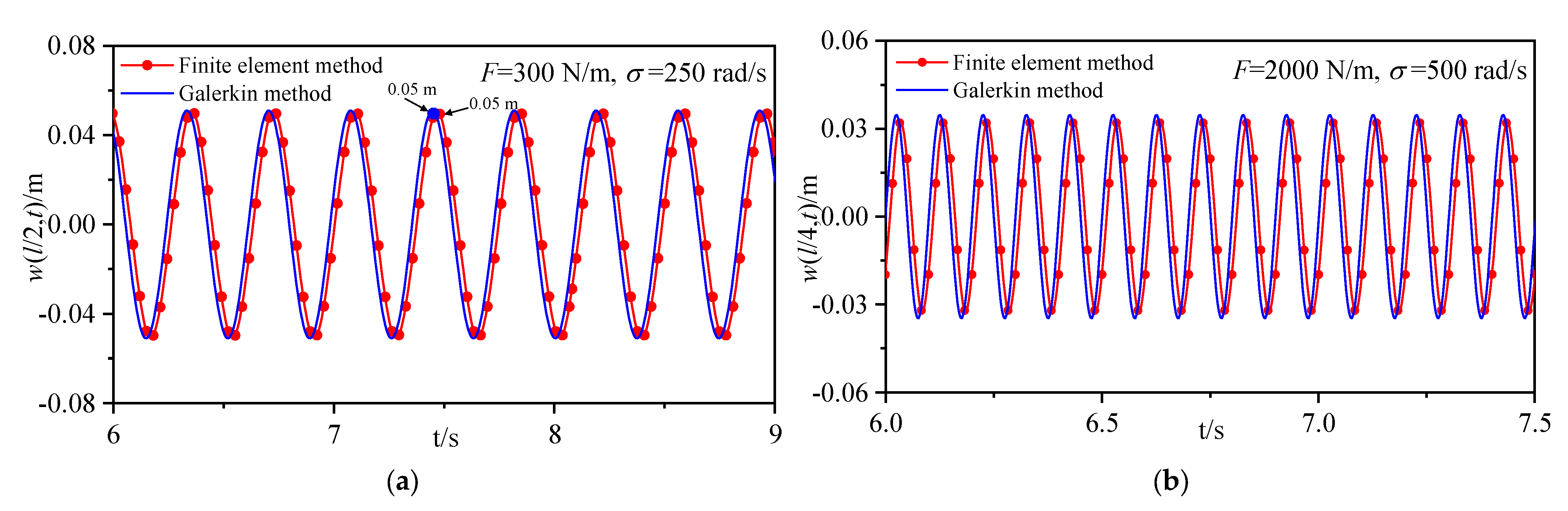
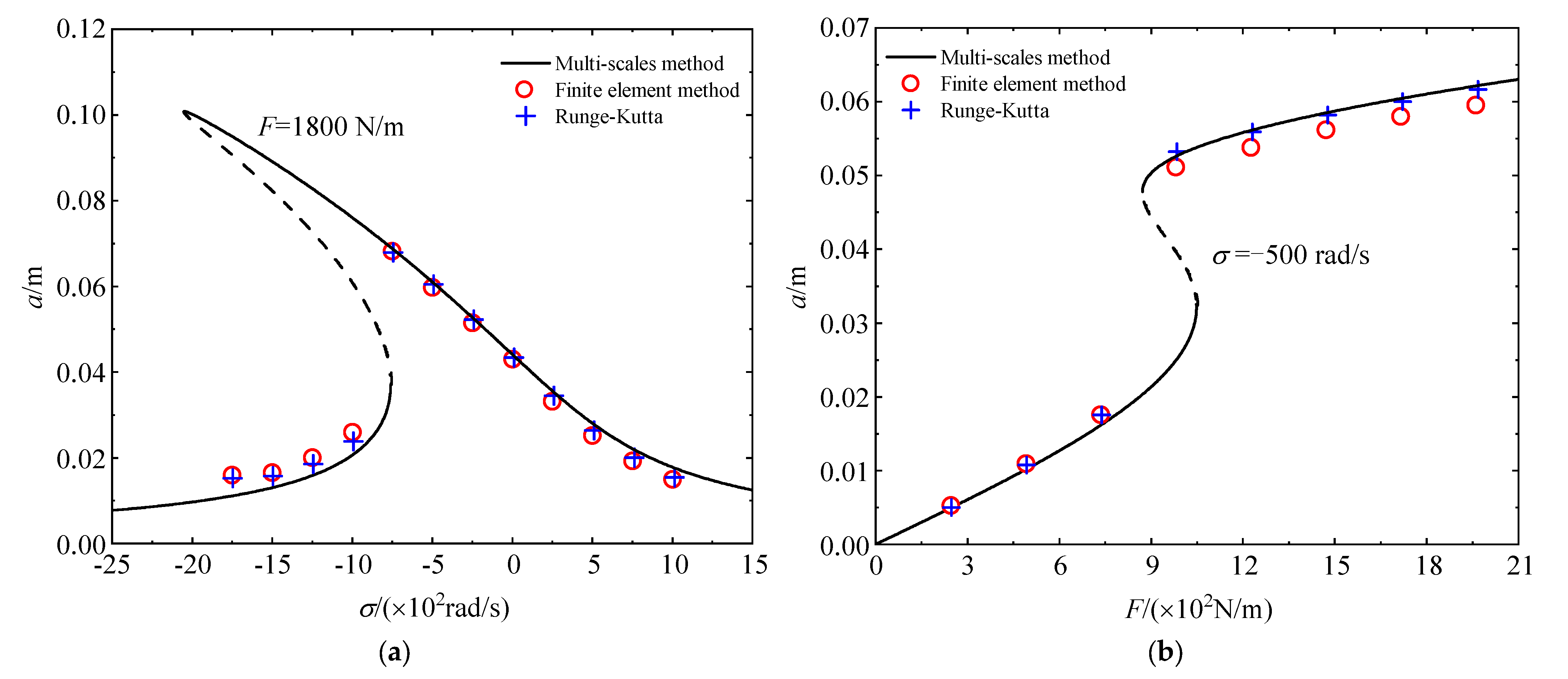
4.1. The First− and Second−Order Modal Primary Resonances without Initial Curvatures
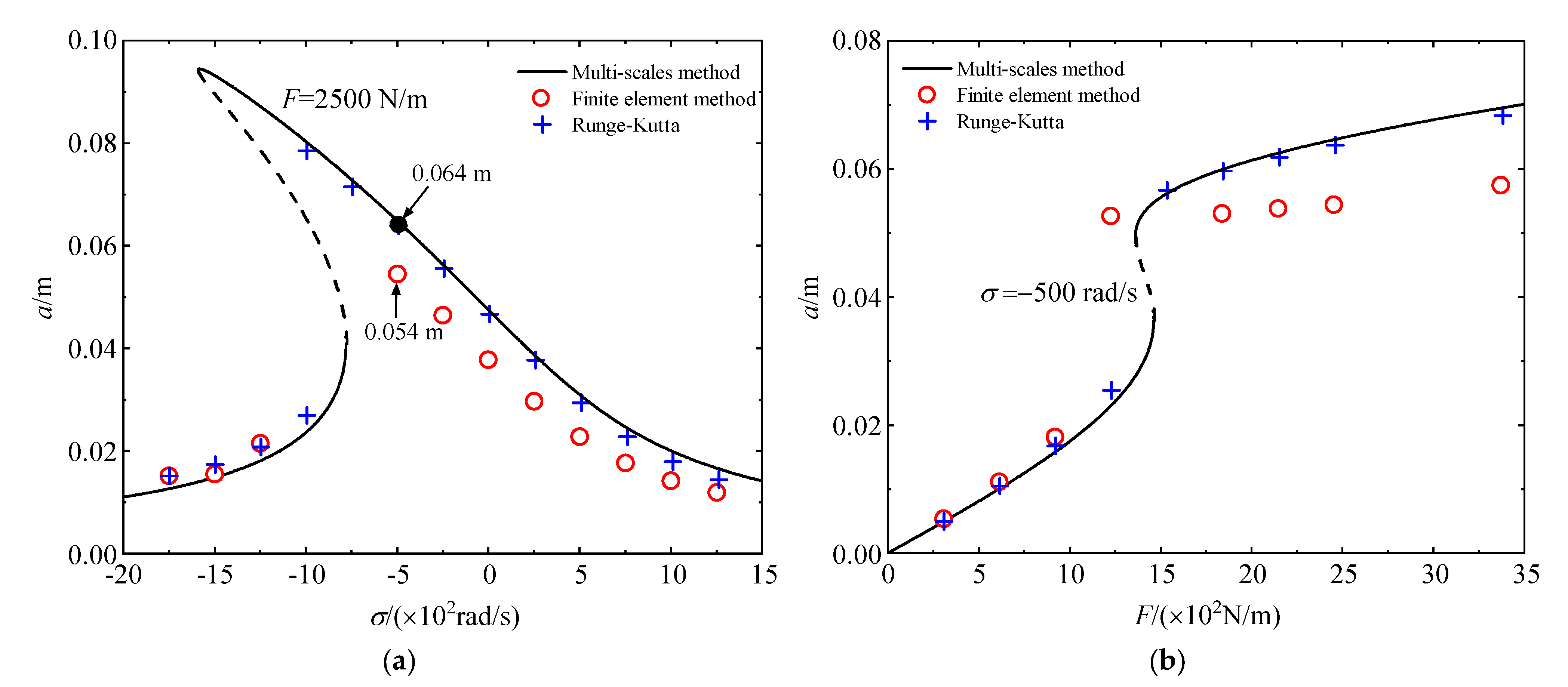
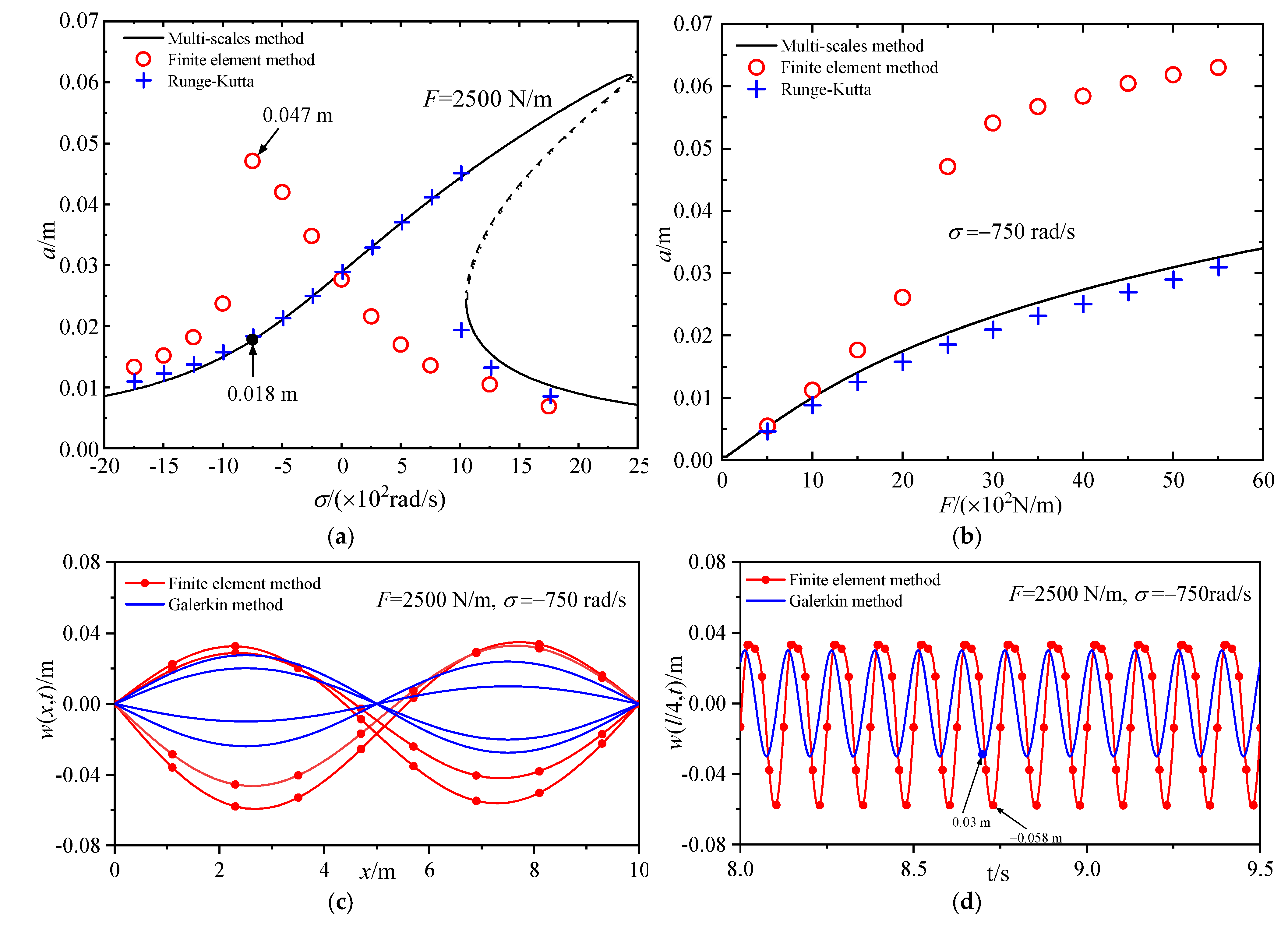
4.2. The First– and Second-order Modal Primary Resonances of Beams with the Initial Curvature
5. Conclusions
- (1)
- If a beam does not have initial curvature, the amplitude–frequency response curves and the load–amplitude response curves calculated by the two methods are consistent. Therefore, one can use the Galerkin method to obtain the dynamic behaviors of straight beams accurately.
- (2)
- The initial curvature brings out a quadratic nonlinear term, and it has a softening effect on the amplitude–frequency response curve.
- (3)
- The mechanical behaviors of beams may change from hardening nonlinear behavior to softening nonlinear behavior with the increase in the initial curvature.
- (4)
- The square nonlinear terms drift the vibration’s center of the beams with the initial curvatures.
- (5)
- The Galerkin method may lead to a quantitative mistake at the single–mode discretization because the method underestimates the softening effect of the initial curvature.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rega, G.; Lacarbonara, W.; Nayfeh, A.H. Reduction methods for nonlinear vibrations of spatially continuous systems with initial curvature. In Proceedings of the IUTAM Symposium on Recent Developments in Nonlinear Oscillations of Mechanical Systems, Hanoi, Vietnam, 2–5 March 1999; pp. 235–246. [Google Scholar]
- Kreider, W.; Nayfeh, A.H. Experimental investigation of single-mode responses in a fixed-fixed buckled beam. Nonlinear Dyn. 1998, 15, 155–177. [Google Scholar] [CrossRef]
- Tien, W.M.; Namachchivaya, N.S.; Bajaj, A.K. Non-linear dynamics of a shallow arch under periodic excitation–I. 1: 2 internal resonance. Int. J. Non-Linear Mech. 1994, 29, 349–366. [Google Scholar] [CrossRef]
- Huang, K.; Zhang, S.; Li, J.; Li, Z. Nonlocal nonlinear model of Bernoulli-Euler nanobeam with small initial curvature and its application to single-walled carbon nanotubes. Microsyst. Technol. 2019, 25, 4303–4310. [Google Scholar] [CrossRef]
- Qiao, W.; Guo, T.; Kang, H.; Zhao, Y. Softening–hardening transition in nonlinear structures with an initial curvature: A refined asymptotic analysis. Nonlinear Dyn. 2022, 107, 357–374. [Google Scholar] [CrossRef]
- Han, S.M.; Benaroya, H.; Wei, T. Dynamics of transversely vibrating beams using four engineering theories. J. Sound Vib. 1999, 225, 935–988. [Google Scholar] [CrossRef]
- Barari, A.; Kaliji, H.D.; Ghadimi, M.; Domairry, G. Non-linear vibration of Euler-Bernoulli beams. Lat. Am. J. Solids Struct. 2011, 8, 139–148. [Google Scholar] [CrossRef]
- Eltaher, M.A.; Khater, M.E.; Emam, S.A. A review on nonlocal elastic models for bending, buckling, vibrations, and wave propagation of nanoscale beams. Appl. Math. Model. 2016, 40, 4109–4128. [Google Scholar] [CrossRef]
- Younesian, D.; Hosseinkhani, A.; Askari, H.; Esmailzadeh, E. Elastic and viscoelastic foundations: A review on linear and nonlinear vibration modeling and Applications. Nonlinear Dyn. 2019, 97, 853–895. [Google Scholar] [CrossRef]
- Huang, K.; Feng, Q.; Qu, B. Bending aeroelastic instability of the structure of suspended cable-stayed beam. Nonlinear Dyn. 2017, 87, 2765–2778. [Google Scholar] [CrossRef]
- Huang, K.; Feng, Q.; Yin, Y. Nonlinear vibration of the coupled structure of suspended-cable-stayed beam–1:2 internal resonance. Acta Mech. Solida Sin. 2014, 27, 467–476. [Google Scholar] [CrossRef]
- Yao, J.; Huang, K.; Li, T. Vortex-Induced Nonlinear Bending Vibrations of Suspension Bridges with Static Wind Loads. Buildings 2023, 13, 2017. [Google Scholar] [CrossRef]
- Ansari, M.; Esmailzadeh, E.; Younesian, D. Internal-external resonance of beams on non-linear viscoelastic foundation traversed by moving load. Nonlinear Dyn. 2010, 61, 163–182. [Google Scholar] [CrossRef]
- Nayfeh, A.H. Reduced-order models of weakly nonlinear spatially continuous systems. Nonlinear Dyn. 1998, 16, 105–125. [Google Scholar] [CrossRef]
- Nayfeh, A.H. Introduction to Perturbation Techniques; Wiley-Interscience: New York, NY, USA, 1981. [Google Scholar]
- Ding, H.; Chen, L.-Q.; Yang, S.-P. Convergence of Galerkin truncation for dynamic response of finite beams on nonlinear foundations under a moving load. J. Sound Vib. 2012, 331, 2426–2442. [Google Scholar] [CrossRef]
- Chen, H.-Y.; Ding, H.; Li, S.-H.; Chen, L.-Q. The Scheme to Determine the Convergence Term of the Galerkin Method for Dynamic Analysis of Sandwich Plates on Nonlinear Foundations. Acta Mech. Solida Sin. 2021, 34, 1–11. [Google Scholar] [CrossRef]
- Chen, H.-Y.; Ding, H.; Li, S.-H.; Chen, L.-Q. Convergent term of the Galerkin truncation for dynamic response of sandwich beams on nonlinear foundations. J. Sound Vib. 2020, 483, 115514. [Google Scholar] [CrossRef]
- Lacarbonara, W. Direct treatment and discretizations of non-linear spatially continuous systems. J. Sound Vib. 1999, 221, 849–866. [Google Scholar] [CrossRef]
- Lacarbonara, W.; Nayfeh, A.H.; Kreider, W. Experimental validation of reduction methods for weakly nonlinear distributed-parameter systems: Analysis of a buckled beam. Nonlinear Dyn. 1998, 17, 95–117. [Google Scholar] [CrossRef]
- Rega, G.; Lacarbonara, W.; Nayfeh, A.H.; Chin, C.M. Multiple resonances in suspended cables: Direct versus reduced-order models. Int. J. Non-Linear Mech. 1999, 34, 901–924. [Google Scholar] [CrossRef]
- Pai, P.F.; Nayfeh, A.H. Fully nonlinear model of cables. AIAA J. 1992, 30, 2993–2996. [Google Scholar] [CrossRef]
- Arafat, H.N.; Nayfeh, A.H. Non-linear responses of suspended cables to primary resonance excitations. J. Sound Vib. 2003, 266, 325–354. [Google Scholar] [CrossRef]
- Pakdemirli, M.; Nayfeh, S.A.; Nayfeh, A.H. Analysis of one-to-one autoparametric resonances in cables–discretization vs. direct treatment. Nonlinear Dyn. 1995, 8, 65–83. [Google Scholar] [CrossRef]
- Rega, G. Nonlinear vibrations of suspended cable—Part II: Deterministic phenomena. Appl. Mech. Rev. 2004, 57, 479–514. [Google Scholar] [CrossRef]
- Nayfeh, A.H.; Nayfeh, J.F.; Mook, D.T. On methods for continuous systems with quadratic and cubic nonlinearities. Nonlinear Dyn. 1992, 3, 145–162. [Google Scholar] [CrossRef]
- Nayfeh, A.H.; Lacarbonara, W. On the discretization of distributed-parameter systems with quadratic and cubic nonlinearities. Nonlinear Dyn. 1997, 13, 203–220. [Google Scholar] [CrossRef]
- Ding, H.; Chen, L.-Q. Nonlinear vibration of a slightly curved beam with quasi-zero-stiffness isolators. Nonlinear Dyn. 2019, 95, 2367–2382. [Google Scholar] [CrossRef]
- Guo, T.D.; Rega, G. Direct and discretized perturbations revisited: A new error source interpretation, with application to moving boundary problem. Eur. J. Mech. A Solids 2020, 81, 103936. [Google Scholar] [CrossRef]
- Wang, S.; Wan, X.; Guo, M.; Qiao, H.; Zhang, N.; Ye, Q. Nonlinear Dynamic Analysis of the Wind–Train–Bridge System of a Long-Span Railway Suspension Truss Bridge. Buildings 2023, 13, 277. [Google Scholar] [CrossRef]
- Salenko, S.; Obukhovskiy, A.; Gosteev, Y.; Yashnov, A.; Lebedev, A. Strength, flexural rigidity and aerodynamic stability of fiberglass spans in pedestrian suspension bridge. Transp. Res. Procedia 2021, 54, 758–767. [Google Scholar] [CrossRef]
- Guan, Q.; Liu, L.; Gao, H.; Wang, Y.; Li, J. Research on Soft Flutter of 420m-Span Pedestrian Suspension Bridge and Its Aerodynamic Measures. Buildings 2022, 12, 1173. [Google Scholar] [CrossRef]
- Qi, D.; Chen, X.; Zhu, Y.; Zhang, Q. A new type of wind-resistance cable net for narrow suspension bridges and wind-resistance cable element for its calculation. Structures 2021, 33, 4243–4255. [Google Scholar] [CrossRef]
- Rodrigues, C.; Simões, F.M.F.; Pinto da Costa, A.; Froio, D.; Rizzi, E. Finite element dynamic analysis of beams on nonlinear elastic foundations under a moving oscillator. Eur. J. Mech. A Solids 2018, 68, 9–24. [Google Scholar] [CrossRef]
- Abdelrahman, A.A.; Nabawy, A.E.; Abdelhaleem, A.M.; Alieldin, S.S.; Eltaher, M.A. Nonlinear dynamics of viscoelastic flexible structural systems by finite element method. Eng. Comput. 2020, 38, 169–190. [Google Scholar] [CrossRef]
- Zhang, Y.; Teng, J.; Huang, J.; Zhou, K.; Huang, L. Free and Forced Vibration Analyses of Functionally Graded Graphene-Nanoplatelet-Reinforced Beams Based on the Finite Element Method. Materials 2022, 15, 6135. [Google Scholar] [CrossRef] [PubMed]
- Thompson, M.K.; Thompson, J.M. ANSYS Mechanical APDL for Finite Element Analysis; Elsevier Inc.: New York, NY, USA, 2017. [Google Scholar]
- Alawadhi, E.M. Finite Element Simulations Using ANSYS; CRC Press: Panama City, FL, USA, 2009. [Google Scholar]
- Lee, Y.Y.; Su, R.K.L.; Hui, C.K. The effect of the modal energy transfer on the sound radiation and vibration of a curved panel: Theory and experiment. J. Sound Vib. 2009, 324, 1003–1015. [Google Scholar] [CrossRef]
- Nayfeh, A.H.; Mook, D.T. Nonlinear Oscillations; John Wiley & Sons: New York, NY, USA, 2008. [Google Scholar]
- Bathe, K.J. Finite Element Procedures; Prentice Hall Inc.: Upper Saddle River, NJ, USA, 1996. [Google Scholar]



| 78 | 10 | 0.1 | 0.1 | 200 | 0.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Huang, K.; Xu, W. Validity of Galerkin Method at Beam’s Nonlinear Vibrations of the Single Mode with the Initial Curvature. Buildings 2023, 13, 2645. https://doi.org/10.3390/buildings13102645
Zhang Y, Huang K, Xu W. Validity of Galerkin Method at Beam’s Nonlinear Vibrations of the Single Mode with the Initial Curvature. Buildings. 2023; 13(10):2645. https://doi.org/10.3390/buildings13102645
Chicago/Turabian StyleZhang, Yunbo, Kun Huang, and Wei Xu. 2023. "Validity of Galerkin Method at Beam’s Nonlinear Vibrations of the Single Mode with the Initial Curvature" Buildings 13, no. 10: 2645. https://doi.org/10.3390/buildings13102645




