A Spectral Method Algorithm for Modeling the Dispersion of Non-Axisymmetric Modes in Fluid-Filled Elastic Tubes
Abstract
:1. Introduction
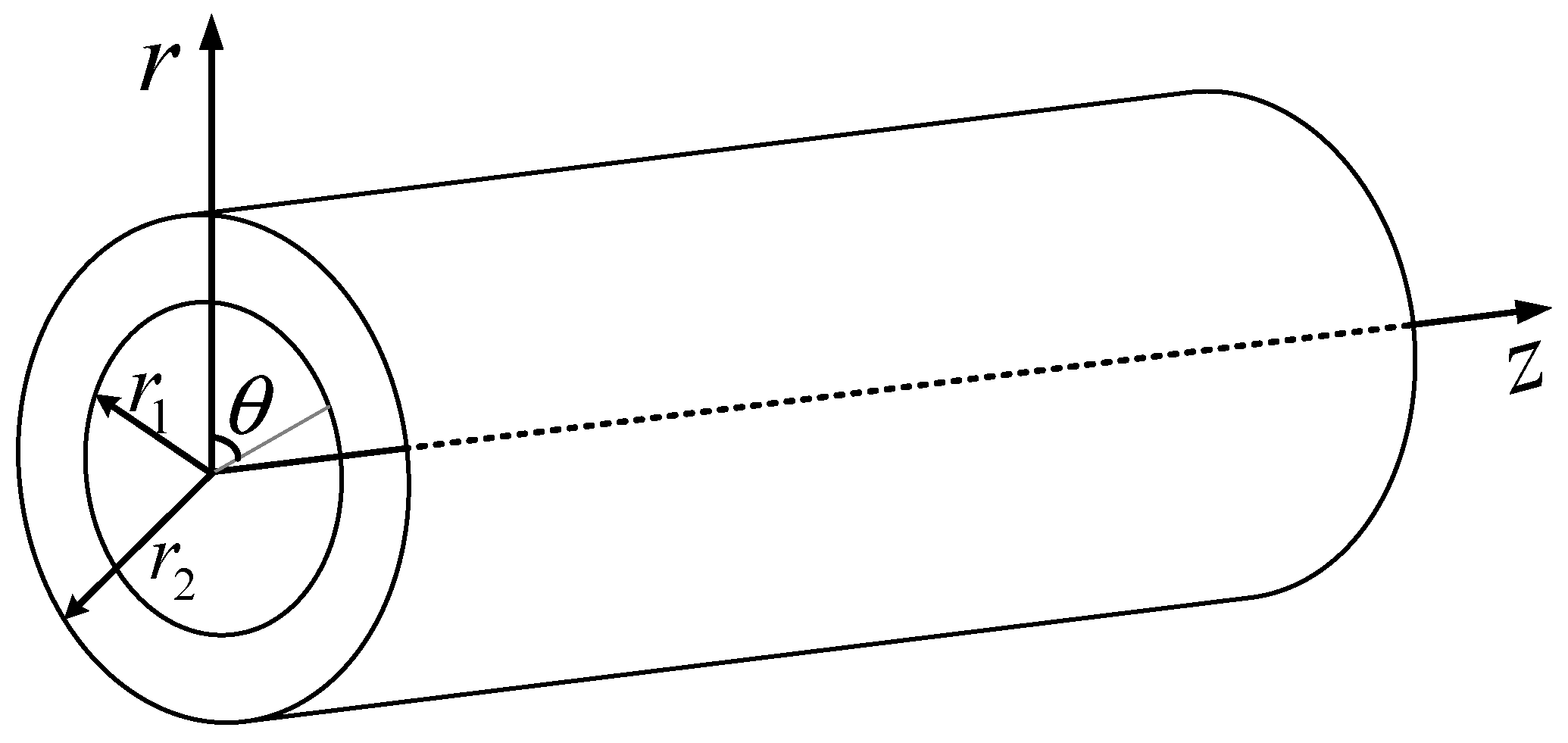
2. Theory
2.1. Wave Equations
2.2. Boundary Conditions
2.2.1. Physical Quantities in the Tube Wall
2.2.2. Physical Quantities in the Fluid
3. The Spectral Method Algorithm for a Fluid-Filled Elastic Tube
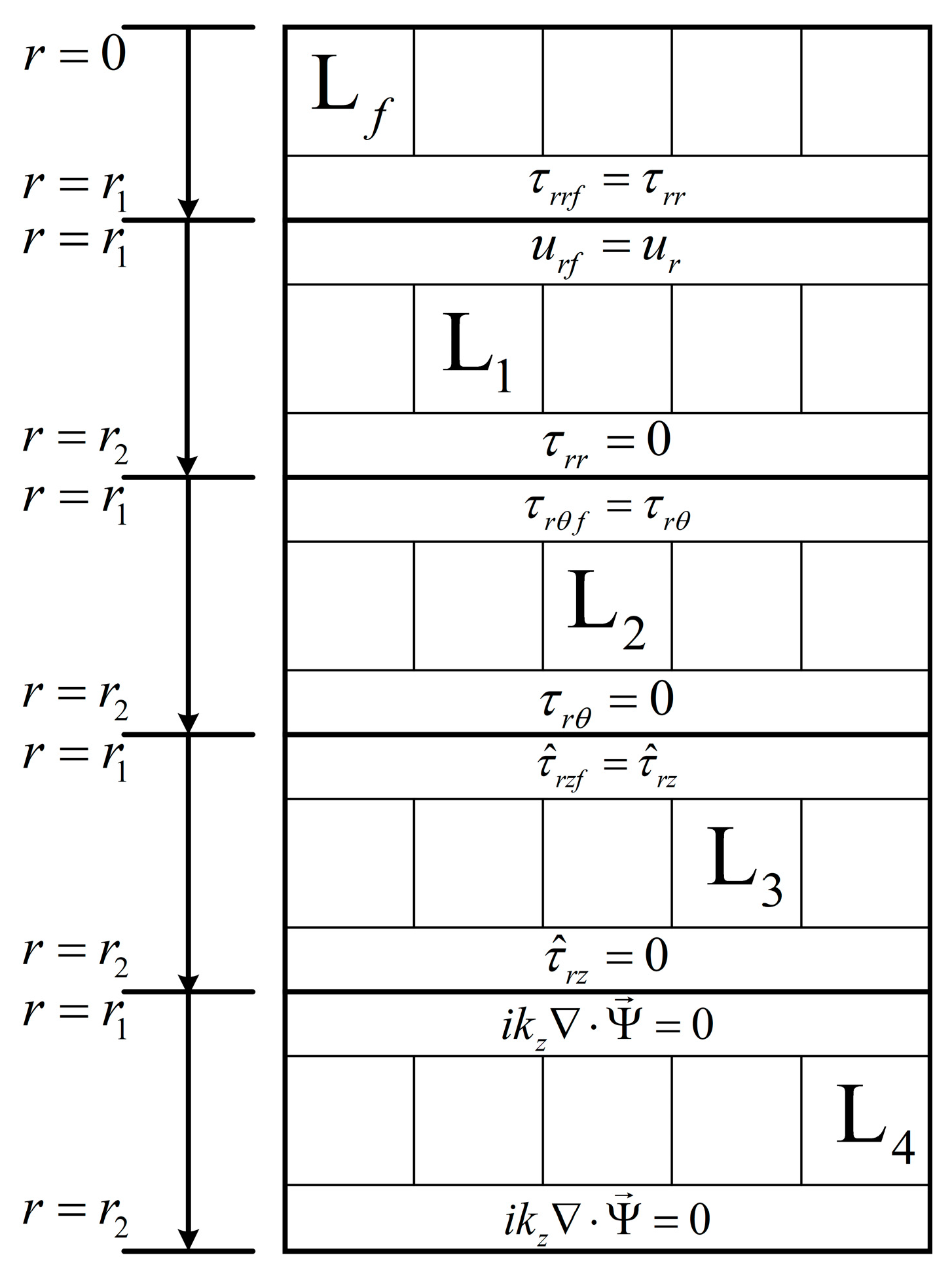
3.1. The Spectral Method Theory
3.2. The Spectral Method Algorithm
4. Discussion
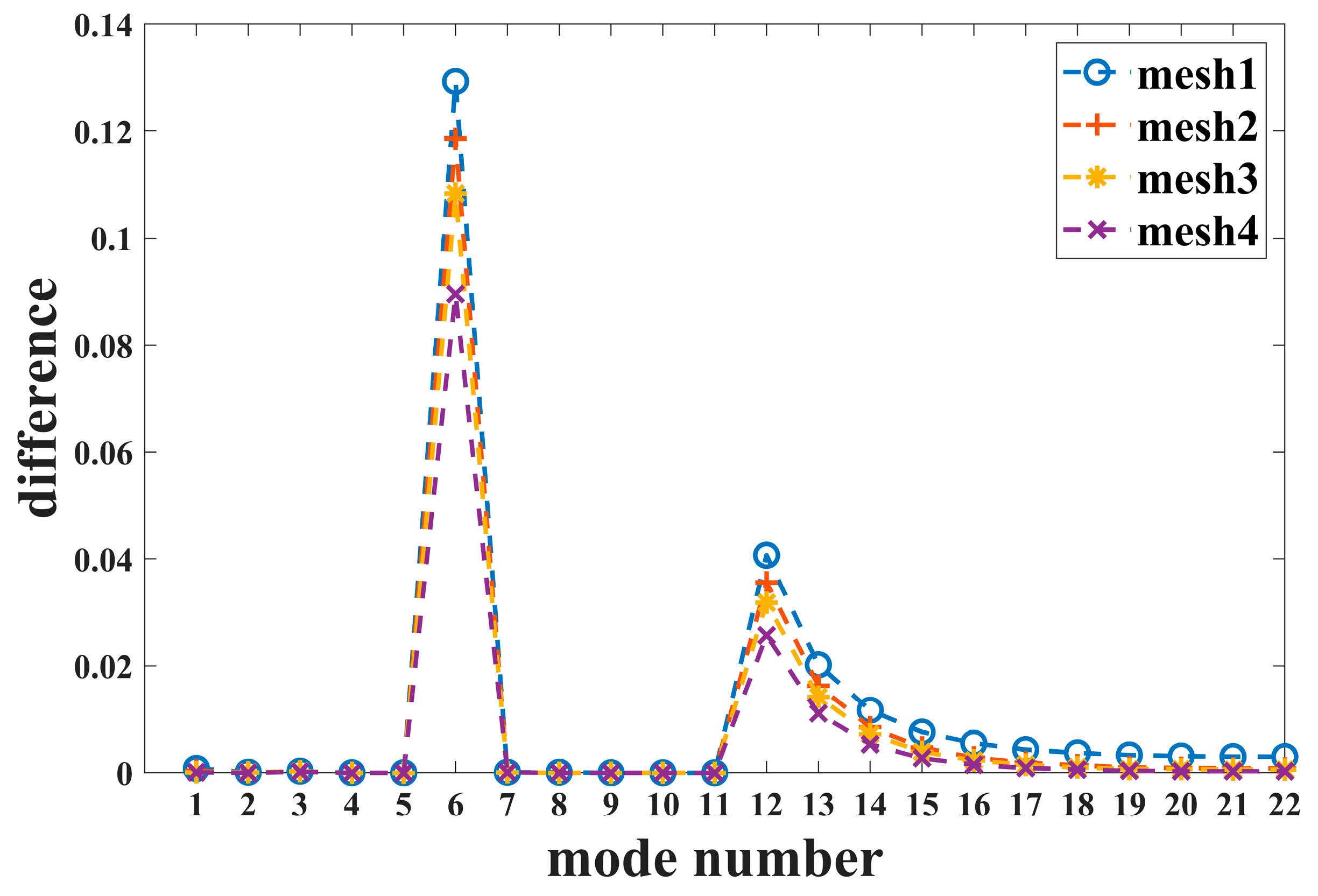
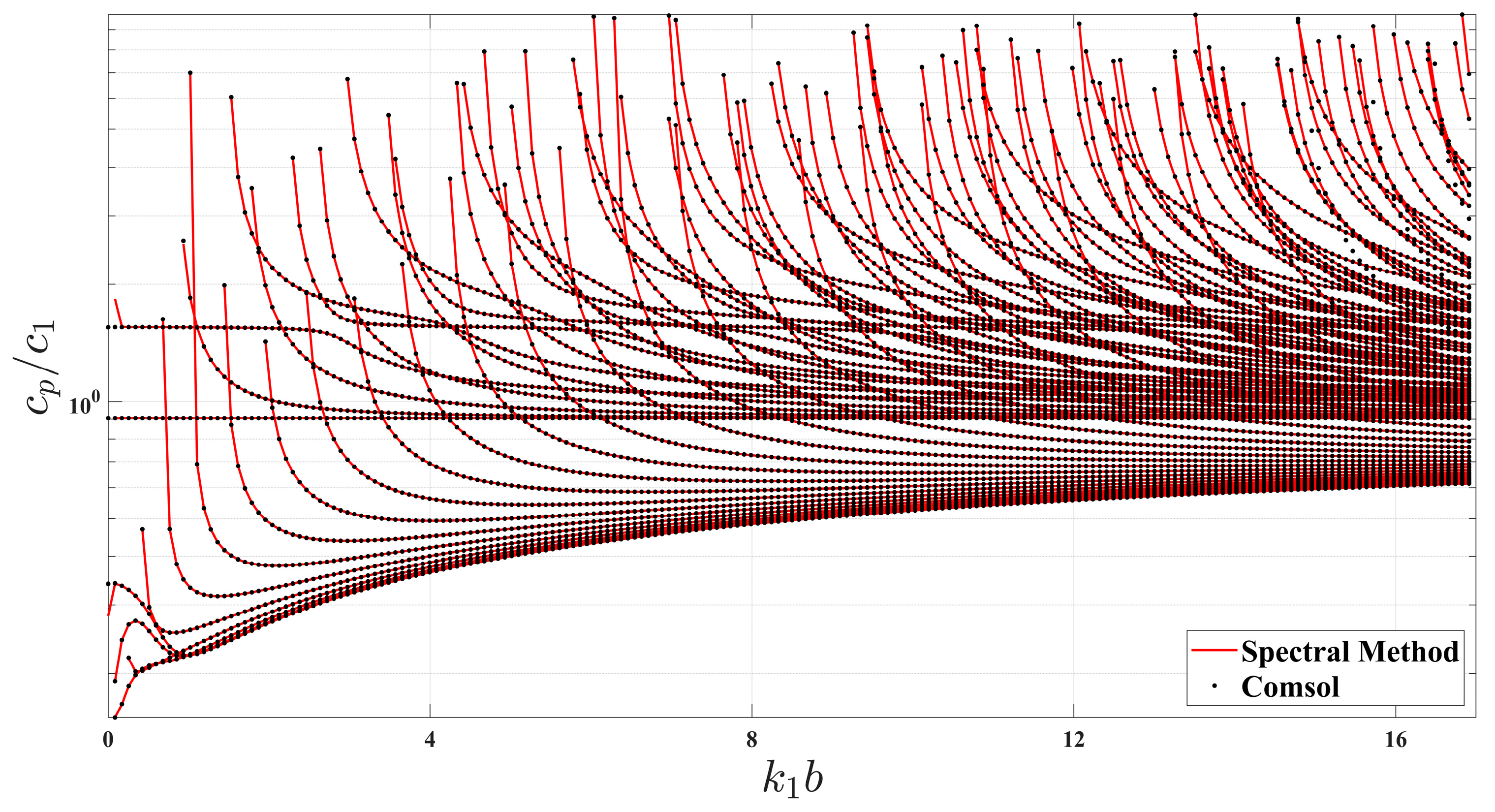
4.1. Comparison between the Spectral Method Algorithm and the COMSOL Simulation
4.2. Differences between the Results from the Spectral Method Algorithm and Baik [26]
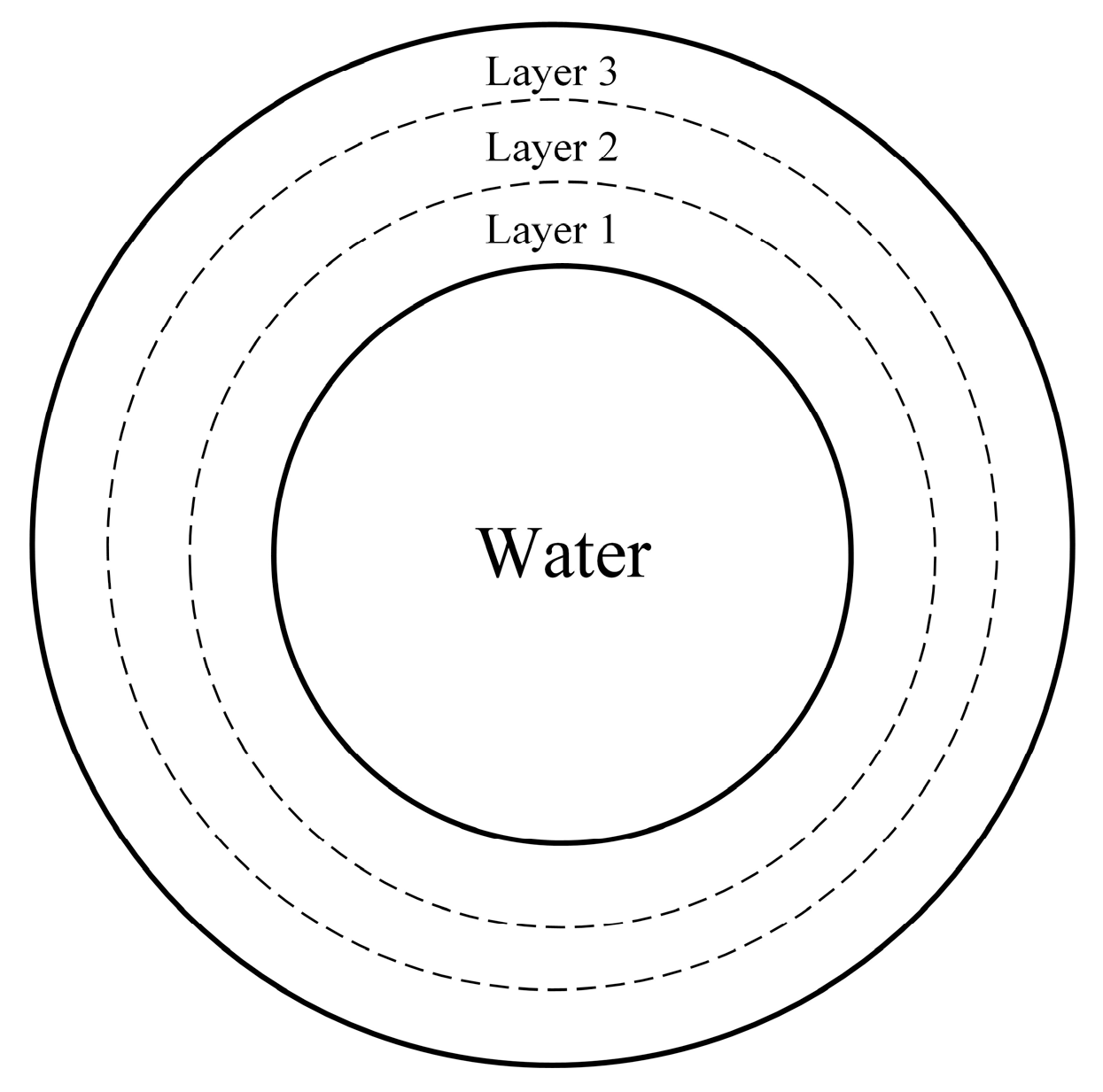
4.3. A Water-Filled Elastic Multi-Layer Tube Model
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| If | Basis Set Is |
|---|---|
| is periodic | Fourier series |
| Fourier cosine | |
| Fourier sine | |
| is non-periodic | Chebyshev polys, Legendre polys. |
References
- Jacobi, W.J. Propagation of Sound Waves along Liquid Cylinders. J. Acoust. Soc. Am. 1949, 21, 120–127. [Google Scholar] [CrossRef]
- Lin, T.C.; Morgan, G.W. Wave Propagation through Fluid Contained in a Cylindrical, Elastic Shell. J. Acoust. Soc. Am. 1956, 28, 1165–1176. [Google Scholar] [CrossRef]
- Gazis, D.C. Three-dimensional Investigation of the Propagation of Waves in Hollow Circular Cylinders. I. Analytical Foundation. J. Acoust. Soc. Am. 1959, 31, 568–573. [Google Scholar] [CrossRef]
- Gazis, D.C. Three-dimensional Investigation of the Propagation of Waves in Hollow Circular Cylinders. II. Numerical Results. J. Acoust. Soc. Am. 1959, 31, 573–578. [Google Scholar] [CrossRef]
- Pochhammer, L. On the Propagation Velocities of Small Oscillations in an Unlimited Isotropic Circular Cylinder. J. Reine Angew. Math 1876, 81, 324. [Google Scholar]
- Chree, C. Longitudinal Vibrations of a Circular Bar. Quart. J. Pure Appl. Math 1886, 21, 287–298. [Google Scholar]
- Del Grosso, V.A. Analysis of Multimode Acoustic Propagation in Liquid Cylinders with Realistic Boundary Conditions–Application to Sound Speed and Absorption Measurements. Acta Acust. United Acust. 1971, 24, 299–311. [Google Scholar]
- Kumar, R. Dispersion of Axially Symmetric Waves in Empty and Fluid-Filled Cylindrical Shells. Acta Acust. United Acust. 1972, 27, 317–329. [Google Scholar]
- Lafleur, L.D.; Shields, F.D. Low-frequency Propagation Modes in a Liquid-filled Elastic Tube Waveguide. J. Acoust. Soc. Am. 1995, 97, 1435–1445. [Google Scholar] [CrossRef]
- Sinha, B.K.; Plona, T.J.; Kostek, S.; Chang, S.-K. Axisymmetric Wave Propagation in Fluid-loaded Cylindrical Shells. I: Theory. J. Acoust. Soc. Am. 1992, 92, 1132–1143. [Google Scholar] [CrossRef]
- Sinha, B.K.; Asvadurov, S. Dispersion and Radial Depth of Investigation of Borehole Modes. Geophys. Prospect. 2004, 52, 271–286. [Google Scholar] [CrossRef]
- Easwaran, V.; Munjal, M.L. A Note on the Effect of Wall Compliance on Lowest-order Mode Propagation in Fluid-filled/Submerged Impedance Tubes. J. Acoust. Soc. Am. 1995, 97, 3494–3501. [Google Scholar] [CrossRef]
- Greenspon, J.E.; Singer, E.G. Propagation in Fluids inside Thick Viscoelastic Cylinders. J. Acoust. Soc. Am. 1995, 97, 3502–3509. [Google Scholar] [CrossRef]
- Berliner, M.J.; Solecki, R. Wave Propagation in Fluid-loaded, Transversely Isotropic Cylinders. Part I. Analytical Formulation. J. Acoust. Soc. Am. 1996, 99, 1841–1847. [Google Scholar] [CrossRef]
- Berliner, M.J.; Solecki, R. Wave Propagation in Fluid-loaded, Transversely Isotropic Cylinders. Part II. Numerical Results. J. Acoust. Soc. Am. 1996, 99, 1848–1853. [Google Scholar] [CrossRef]
- Baik, K.; Jiang, J.; Leighton, T.G. Acoustic Attenuation, Phase and Group Velocities in Liquid-Filled Pipes: Theory, Experiment, and Examples of Water and Mercury. J. Acoust. Soc. Am. 2010, 128, 2610–2624. [Google Scholar] [CrossRef]
- Thomson, W.T. Transmission of Elastic Waves through a Stratified Solid Medium. J. Appl. Phys. 1950, 21, 89–93. [Google Scholar] [CrossRef]
- Haskell, N.A. The Dispersion of Surface Waves on Multilayered Media. Bull. Seismol. Soc. Am. 1953, 43, 17–34. [Google Scholar] [CrossRef]
- Knopoff, L. A Matrix Method for Elastic Wave Problems. Bull. Seismol. Soc. Am. 1964, 54, 431–438. [Google Scholar] [CrossRef]
- Dunkin, J.W. Computation of Modal Solutions in Layered, Elastic Media at High Frequencies. Bull. Seismol. Soc. Am. 1965, 55, 335–358. [Google Scholar] [CrossRef]
- Kreiss, H.-O.; Oliger, J. Comparison of Accurate Methods for the Integration of Hyperbolic Equations. Tellus 1972, 24, 199–215. [Google Scholar] [CrossRef]
- Orszag, S.A. Comparison of Pseudospectral and Spectral Approximation. Stud. Appl. Math. 1972, 51, 253–259. [Google Scholar] [CrossRef]
- Adamou, A.T.I.; Craster, R.V. Spectral Methods for Modelling Guided Waves in Elastic Media. J. Acoust. Soc. Am. 2004, 116, 1524–1535. [Google Scholar] [CrossRef]
- Karpfinger, F.; Gurevich, B.; Bakulin, A. Modeling of Wave Dispersion along Cylindrical Structures Using the Spectral Method. J. Acoust. Soc. Am. 2008, 124, 859–865. [Google Scholar] [CrossRef]
- Karpfinger, F.; Valero, H.-P.; Gurevich, B.; Bakulin, A.; Sinha, B. Spectral-Method Algorithm for Modeling Dispersion of Acoustic Modes in Elastic Cylindrical Structures. Geophysics 2010, 75, H19–H27. [Google Scholar] [CrossRef]
- Baik, K.; Jiang, J.; Leighton, T.G. Acoustic Attenuation, Phase and Group Velocities in Liquid-Filled Pipes III: Nonaxisymmetric Propagation and Circumferential Modes in Lossless Conditions. J. Acoust. Soc. Am. 2013, 133, 1225–1236. [Google Scholar] [CrossRef] [PubMed]
- Rose, J.L. Ultrasonic Guided Waves in Solid Media; Cambridge University Press: Cambridge, UK, 2014; ISBN 978-1-107-04895-9. [Google Scholar]
- Boyd, J.P. Chebyshev and Fourier Spectral Methods; Courier Corporation: Chelmsford, MA, USA, 2001; ISBN 0-486-41183-4. [Google Scholar]
- Weideman, J.A.; Reddy, S.C. A MATLAB Differentiation Matrix Suite. ACM Trans. Math. Softw. 2000, 26, 465–519. [Google Scholar] [CrossRef]
- Gottlieb, D.; Orszag, S.A. Numerical Analysis of Spectral Methods: Theory and Applications; Regional Conference Series in Applied Mathematics; SIAM: Philadelphia, PA, USA, 1977. [Google Scholar]


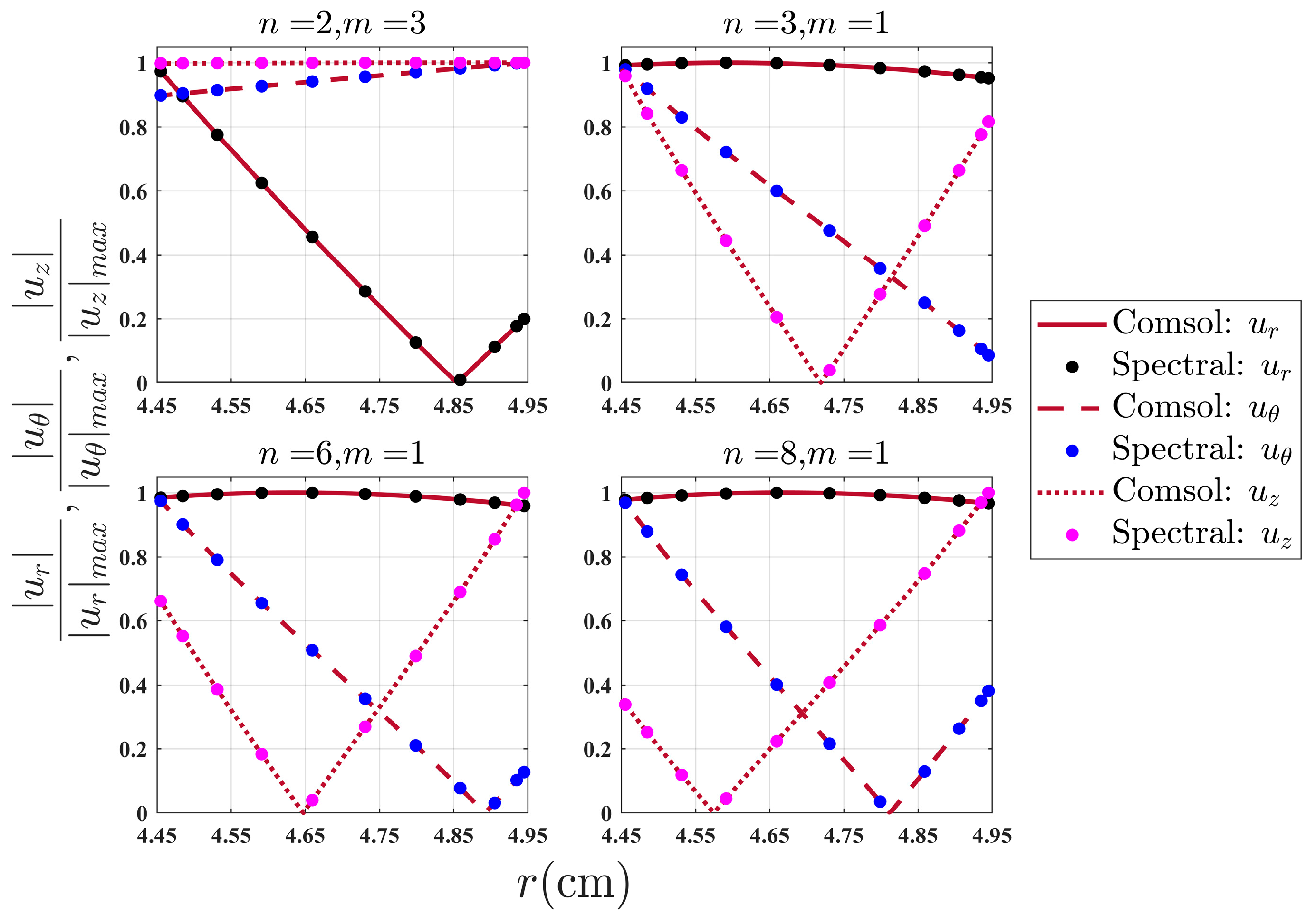


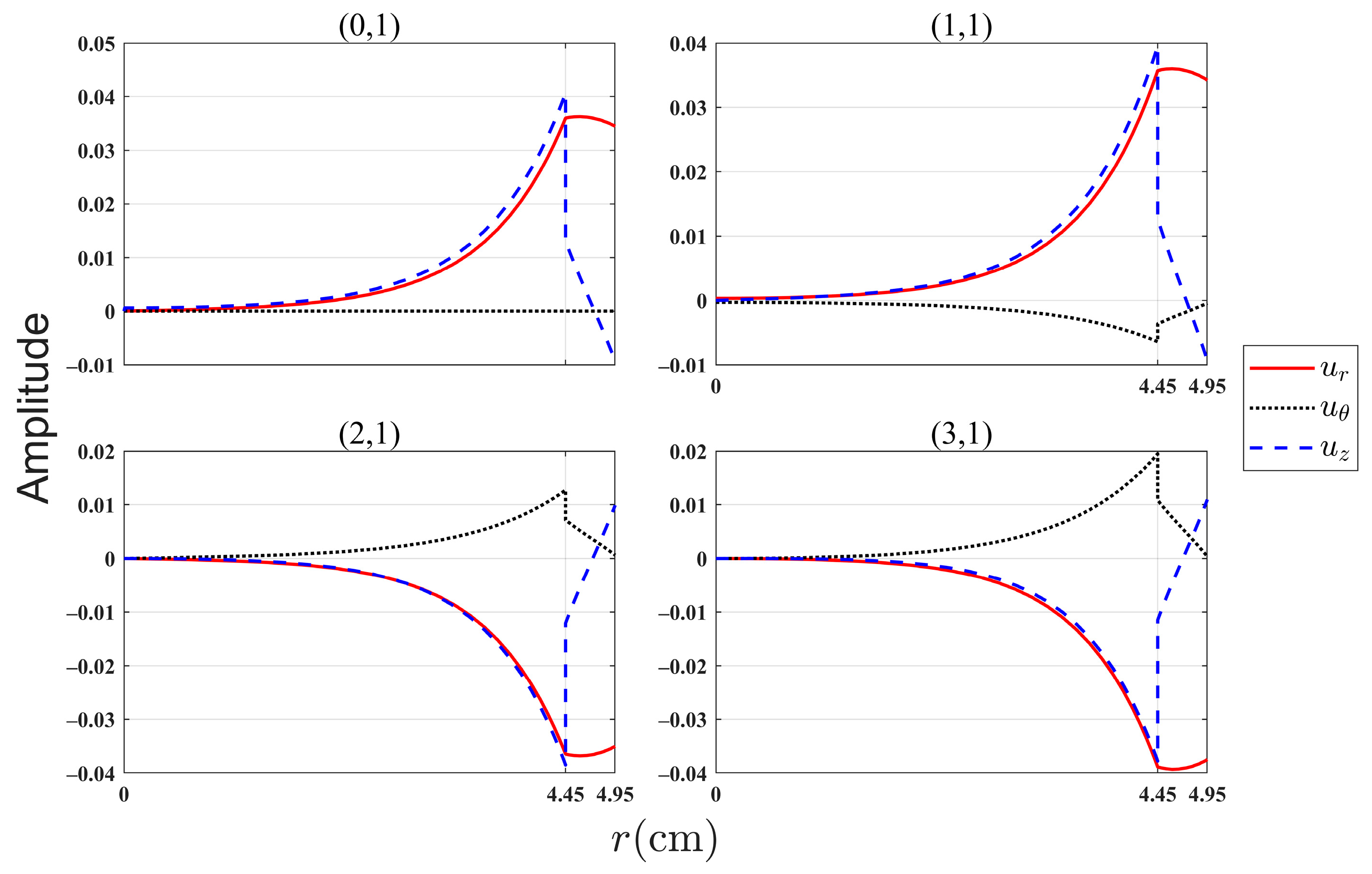
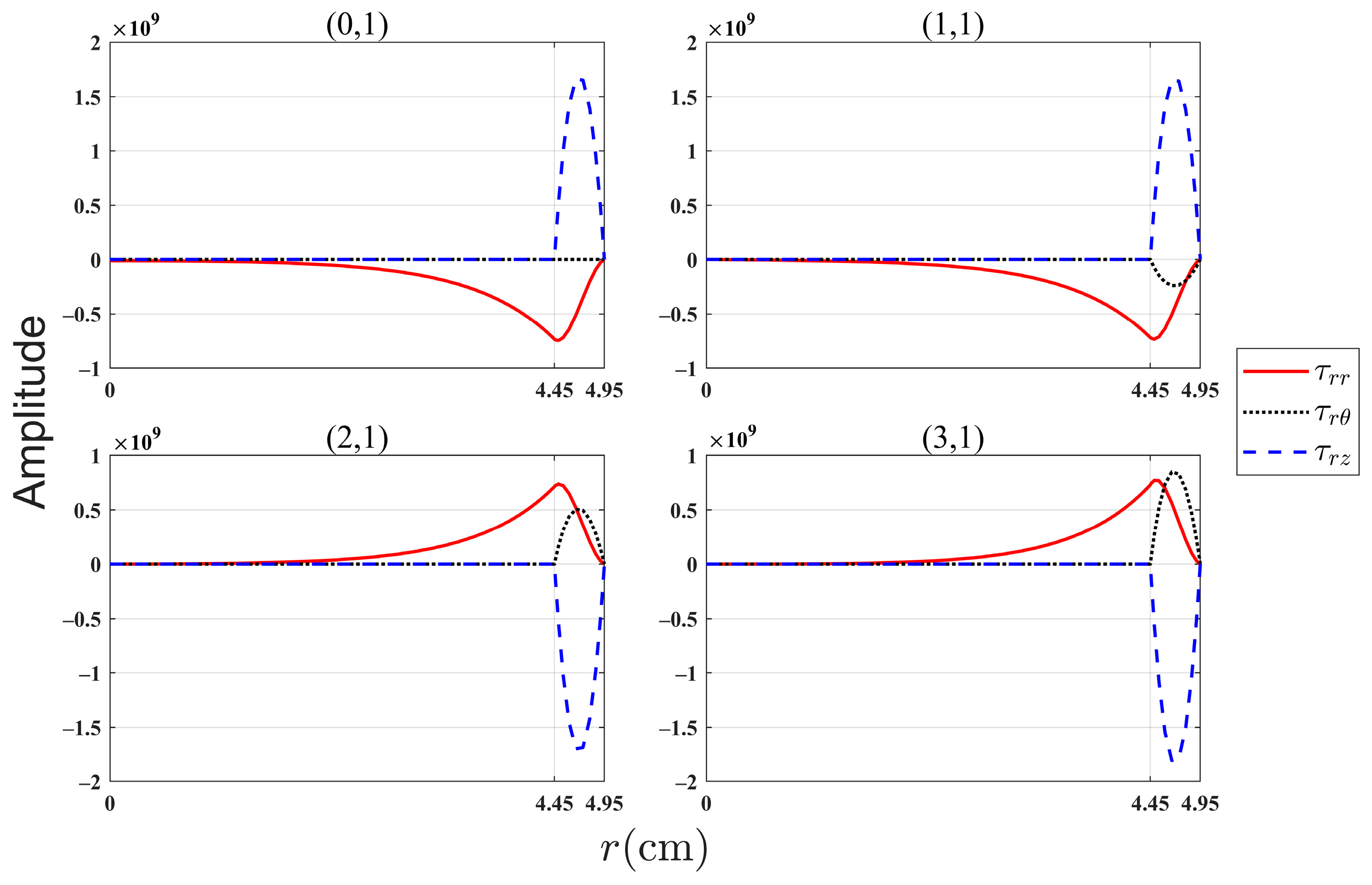

| (cm) | (cm) | (m/s) | (m/s) | (m/s) | (kg/m3) | (kg/m3) |
|---|---|---|---|---|---|---|
| 4.445 | 0.5 | 2690 | 1340 | 1479 | 1190 | 1000 |
| Mesh | Mesh 1 | Mesh 2 | Mesh 3 | Mesh 4 | Mesh 5 |
|---|---|---|---|---|---|
| Element Number | 2214 | 3146 | 4644 | 8698 | 27,842 |
| Calculation Methods | Calculation Time |
|---|---|
| COMSOL Multiphysics | Approximately 10 h |
| The spectral method algorithm | A few tens of seconds |
| COMSOL Multiphysics | 4.3629 | 21.9621 | 30.1711 | 35.6921 | 37.5116 | 84.0532 |
| 107.1383 | 121.4523 | 130.5509 | 136.0542 | 138.9479 | 139.8424 | |
| Spectral Method | 4.3678 | 21.9621 | 30.1706 | 35.6932 | 37.5116 | 84.0534 |
| 107.1380 | 121.4523 | 130.5509 | 136.0542 | 138.9479 | 139.8424 | |
| Error | 1.12 × 10−3 | 0 | 1.66 × 10−5 | 3.08 × 10−5 | 0 | 2.38 × 10−6 |
| 2.80 × 10−6 | 0 | 0 | 0 | 0 | 0 | |
| Circumferential Order | Spectral Method Results | Results from Baik [26] |
|---|---|---|
| Dimension | (cm) | (cm) | (cm) | (cm) |
| 50 | 5 | 5 | 5 | |
| PVC | (m/s) | (m/s) | (kg/m3) | |
| 2388 | 1060 | 1380 | ||
| Iron | (m/s) | (m/s) | (kg/m3) | |
| 5893 | 3230 | 7800 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Z.; Li, Q.; Tang, R.; Shang, D. A Spectral Method Algorithm for Modeling the Dispersion of Non-Axisymmetric Modes in Fluid-Filled Elastic Tubes. Appl. Sci. 2023, 13, 12415. https://doi.org/10.3390/app132212415
Gao Z, Li Q, Tang R, Shang D. A Spectral Method Algorithm for Modeling the Dispersion of Non-Axisymmetric Modes in Fluid-Filled Elastic Tubes. Applied Sciences. 2023; 13(22):12415. https://doi.org/10.3390/app132212415
Chicago/Turabian StyleGao, Zirong, Qi Li, Rui Tang, and Dajing Shang. 2023. "A Spectral Method Algorithm for Modeling the Dispersion of Non-Axisymmetric Modes in Fluid-Filled Elastic Tubes" Applied Sciences 13, no. 22: 12415. https://doi.org/10.3390/app132212415





