Analytical and Experimental Investigation of the Rotary Inertia Effects of Unequal End Masses on Transverse Vibration of Beams
Abstract
:1. Introduction
2. The Equations of Motion and Boundary Conditions
3. Frequency Equation
4. Results
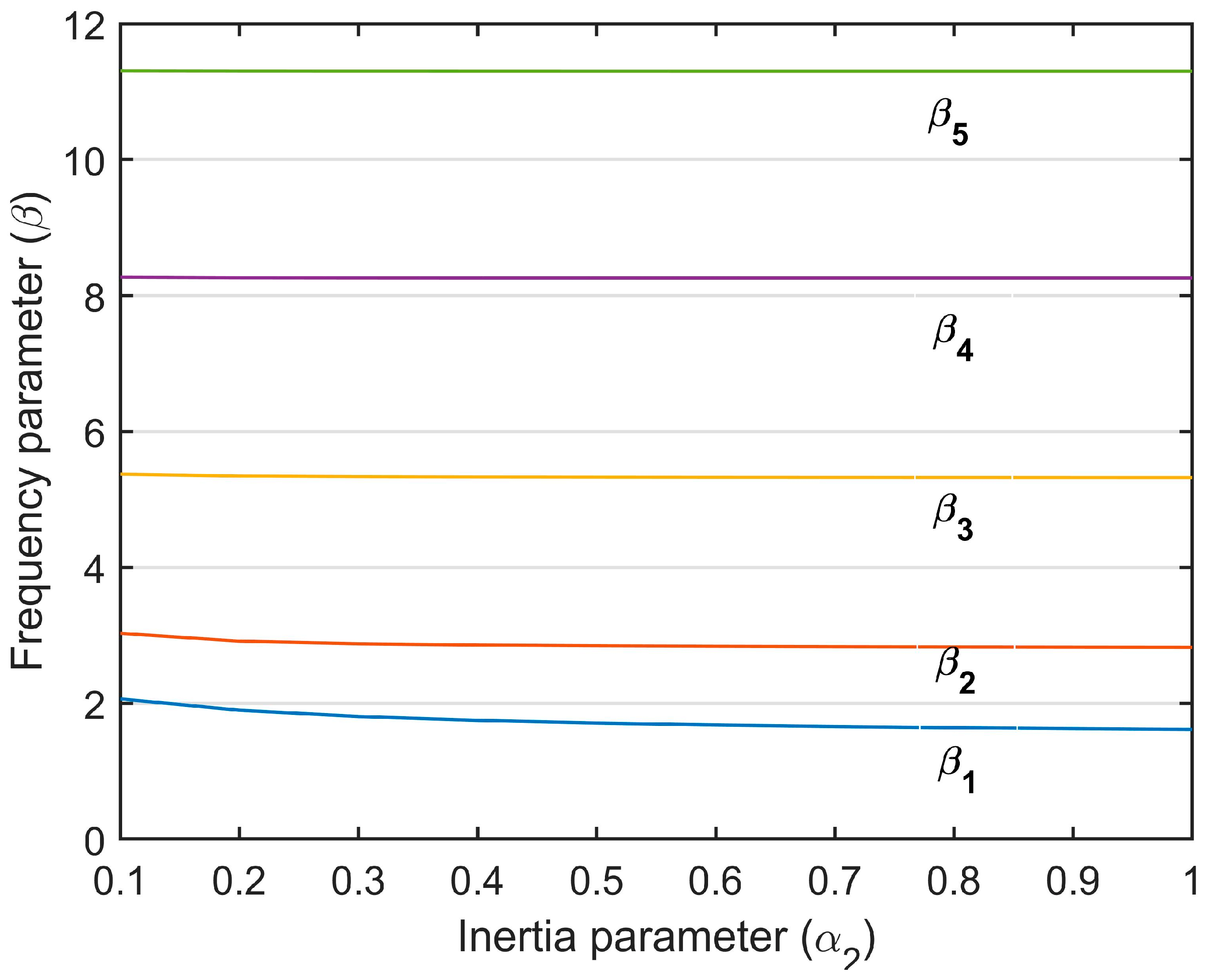
4.1. Natural Frequencies
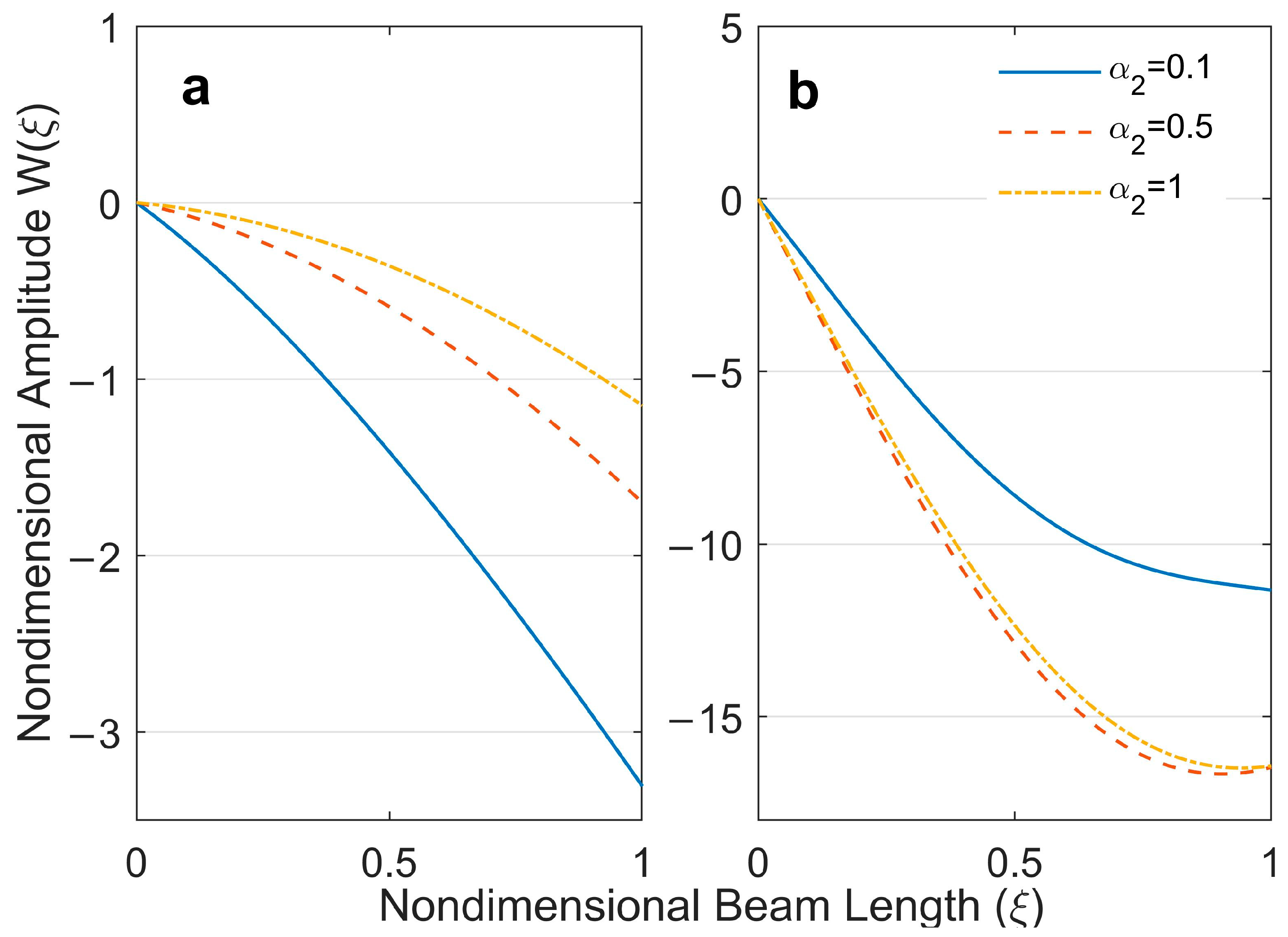
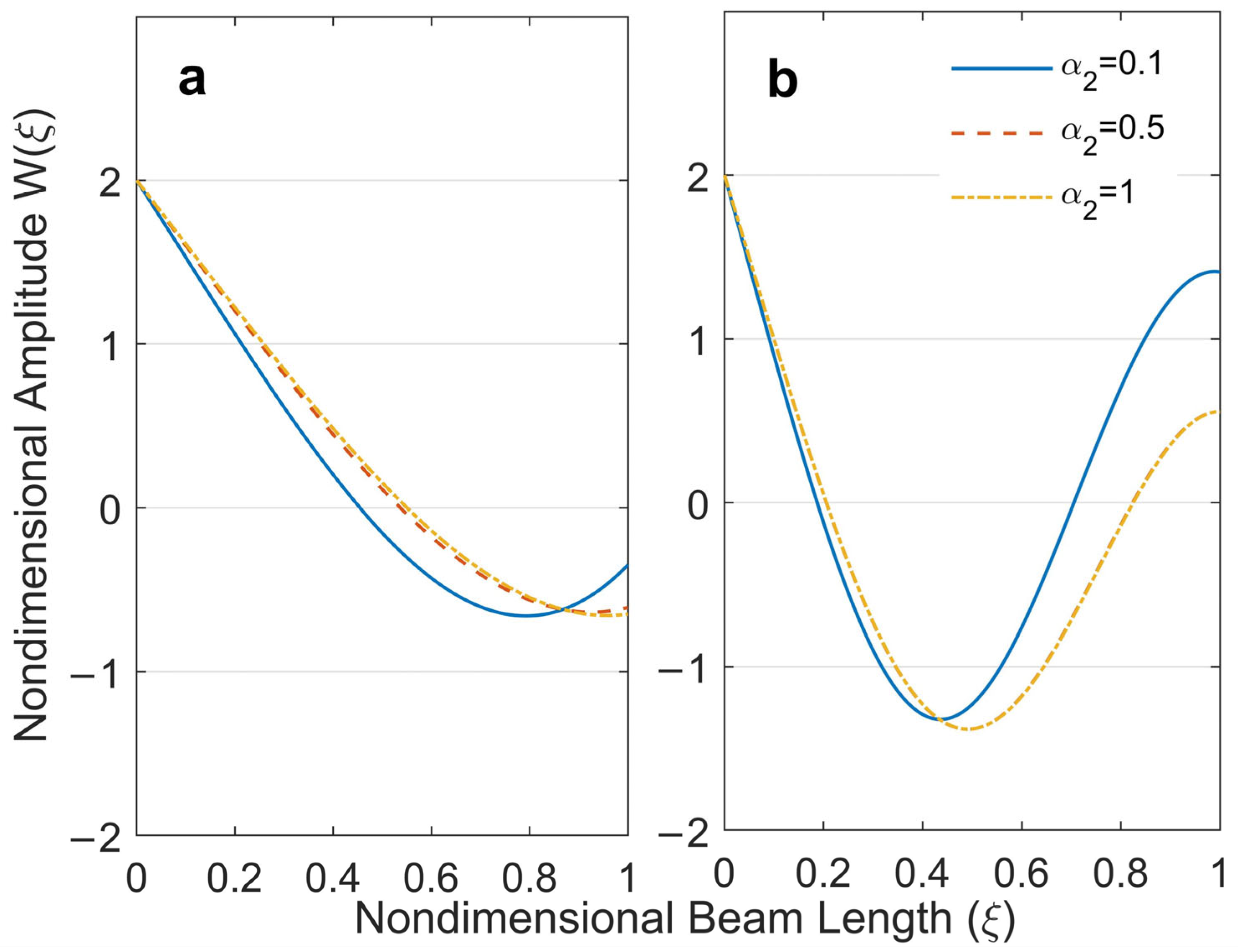
4.2. Modal Shape Functions
5. Experimental Verification
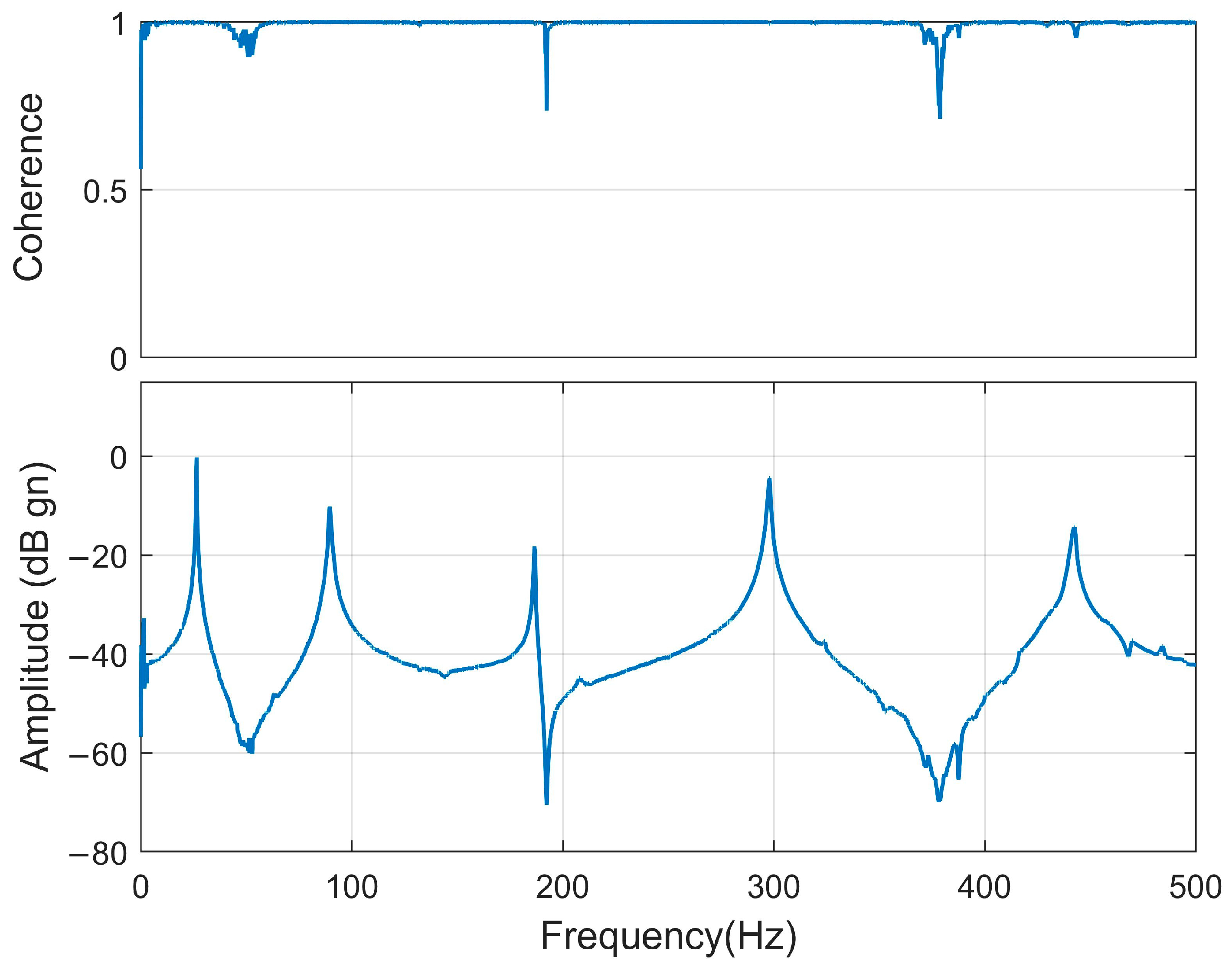
5.1. Experimental Setup
5.2. Experimental Results and Comparison with Analytical Results
6. Conclusions
- The natural frequencies and mode shapes of the free–free beam with unequal end masses were obtained by including the rotary inertia of the end masses.
- The first five nondimensional frequency parameters were obtained and presented in a table for different values of .
- The first and second mode shapes of the free–free beam with unequal end masses were obtained for different values of .
- It was concluded that the increase in the rotational inertia of the end mass was more effective at low frequencies and mode shapes of the structure.
- The increase in the distance between the gravity center of the end mass and the beam connection point decreases the beam’s natural frequencies.
- Experimental testing was performed to verify the frequency equation. The results obtained were in good agreement with analytical results. Due to undesirable interference effects in the experimental study, the difference between the experimental results and the analytical results could be accepted by up to 15%. In our study, the highest difference was 1.86%. This showed that the frequency equation obtained analytically represented the real operating conditions as well as possible.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
Appendix C
References
- Meirovitch, L. Analytical Methods in Vibrations; Macmillian Company: New York, NY, USA, 1967. [Google Scholar]
- Blevins, R.D. Formulas for Natural Frequency and Mode Shape; Van Nostrand Reinhold: New York, NY, USA, 1979. [Google Scholar]
- Pilkey, W. Formulas for Stress, Strain, and Structural Matrices; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Karnovsky, I.; Lebed, O.; Karnovskii, I. Free Vibrations of Beams and Frames; McGraw-Hill Professional Publishing: New York, NY, USA, 2004. [Google Scholar]
- Wang, C.; Wang, C. Structural Vibration: Exact Solutions for Strings, Membranes, Beams, and Plates; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Rao, S.S. Mechanical Vibrations, 6th ed.; Prentice Hall: Hoboken, NJ, USA, 2018. [Google Scholar]
- Srinath, L.S.; Das, Y.C. Vibrations of Beams Carrying Mass. J. Appl. Mech. Trans. ASME 1964, 34, 784–785. [Google Scholar] [CrossRef]
- Lau, J.H. Fundamental Frequency of a Constrained Beam. J. Sound Vib. 1981, 78, 154–157. [Google Scholar] [CrossRef]
- Gürgöze, M. A Note on the Vibrations of Restrained Beams and Rods with Point Masses. J. Sound Vib. 1984, 96, 461–468. [Google Scholar] [CrossRef]
- Laura, P.A.A.; Cortinez, V.H. Optimization of Eigenvalues in the Case of Vibrating Beams with Point Masses. J. Sound Vib. 1986, 108, 346–347. [Google Scholar] [CrossRef]
- Oguamanam, D.C.D. Free Vibration of Beams with Finite Mass Rigid Tip Load and Flexural-Torsional Coupling. Int. J. Mech. Sci. 2003, 45, 963–979. [Google Scholar] [CrossRef]
- Wu, J.S.; Hsu, T.F. Free Vibration Analyses of Simply Supported Beams Carrying Multiple Point Masses and Spring-Mass Systems with Mass of Each Helical Spring Considered. Int. J. Mech. Sci. 2007, 49, 834–852. [Google Scholar] [CrossRef]
- Jafarzadeh Jazi, A.; Shahriari, B.; Torabi, K. Exact Closed Form Solution for the Analysis of the Transverse Vibration Mode of a Nano-Timoshenko Beam with Multiple Concentrated Masses. Int. J. Mech. Sci. 2017, 131–132, 728–743. [Google Scholar] [CrossRef]
- Mahmoud, M.A. Natural Frequency of Axially Functionally Graded, Tapered Cantilever Beams with Tip Masses. Eng. Struct. 2019, 187, 34–42. [Google Scholar] [CrossRef]
- Dal, H.; Baklaci, M. Design, Fabrication and Vibration Analysis of a Lightweight Head Expander for a High Frequency Electrodynamic Shaker. Mater. Test. 2019, 61, 965–972. [Google Scholar] [CrossRef]
- Boyce, W.E.; Handelman, G.H. Vibrations of Rotating Beams with Tip Mass. Zeitschrift Angew. Math. Phys. ZAMP 1961, 12, 369–392. [Google Scholar] [CrossRef]
- Craig, R.R. Rotating Beam with Tip Mass Analyzed by a Variational Method. J. Acoust. Soc. Am. 1963, 35, 990–993. [Google Scholar] [CrossRef]
- Öz, H.R.; Özkaya, E. Natural Frequencies of Beam-Mass Systems in Transverse Motion for Different End Conditions. Math. Comput. Appl. 2005, 10, 369–376. [Google Scholar] [CrossRef] [Green Version]
- Hong, J.; Dodson, J.; Laflamme, S.; Downey, A. Transverse Vibration of Clamped-Pinned-Free Beam with Mass at Free End. Appl. Sci. 2 2019, 9, 2996. [Google Scholar] [CrossRef] [Green Version]
- Langer, P.; Jelich, C.; Guist, C.; Peplow, A.; Marburg, S. Simplification of Complex Structural Dynamic Models: A Case Study Related to a Cantilever Beam and a Large Mass Attachment. Appl. Sci. 2021, 11, 5428. [Google Scholar] [CrossRef]
- Du, X.; Zhang, J.; Guo, X.; Li, L.; Zhang, D. Dynamics Analysis of Rotating Cantilever Beams with Free End Mass. Appl. Sci. 2022, 12, 7553. [Google Scholar] [CrossRef]
- Beal, T.R. Dynamic Stability of a Flexible Missile under Constant and Pulsating Thrusts. AIAA J. 1965, 3, 486–494. [Google Scholar] [CrossRef]
- Kavianipour, O.; Khoshnood, A.M.; Irani, S.; Roshanian, J. Reduction of the Actuator Oscillations in a Free-Free Jointed Bipartite Beam Model under a Follower Force. Aerosp. Sci. Technol. 2012, 22, 45–57. [Google Scholar] [CrossRef]
- Park, Y.P.; Mote, C.D. The Maximum Controlled Follower Force on a Free-Free Beam Carrying a Concentrated Mass. J. Sound Vib. 1985, 98, 247–256. [Google Scholar] [CrossRef]
- Kirk, C.L.; Wiedemann, S.M. Natural Frequencies and Mode Shapes of a Free-Free Beam with Large End Masses. J. Sound Vib. 2002, 254, 939–949. [Google Scholar] [CrossRef]
- Yoon, S.J.; Kim, J.H. A Concentrated Mass on the Spinning Unconstrained Beam Subjected to a Thrust. J. Sound Vib. 2002, 254, 621–634. [Google Scholar] [CrossRef]
- Haener, J. Formulas for the Frequencies Including Higher Frequencies of Uniform Cantilever and Free-Free Beams With Additional Masses at the Ends. J. Appl. Mech. 1958, 25, 412. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D.J. On the Fundamental Transverse Vibration Frequency of a Free-Free Thin Beam with Identical End Masses. J. Vib. Acoust. Trans. ASME 2007, 129, 656–662. [Google Scholar] [CrossRef]
- Shi, W.; Li, X.F.; Lee, K.Y. Transverse Vibration of Free-Free Beams Carrying Two Unequal End Masses. Int. J. Mech. Sci. 2015, 90, 251–257. [Google Scholar] [CrossRef]
- Shi, W.; Shen, Z.B.; Peng, X.L.; Li, X.F. Frequency Equation and Resonant Frequencies of Free–Free Timoshenko Beams with Unequal End Masses. Int. J. Mech. Sci. 2016, 115–116, 406–415. [Google Scholar] [CrossRef]
- Khalili, S.M.R.; Damanpack, A.R.; Nemati, N.; Malekzadeh, K. Free Vibration Analysis of Sandwich Beam Carrying Sprung Masses. Int. J. Mech. Sci. 2010, 52, 1620–1633. [Google Scholar] [CrossRef]
- Banerjee, J.R. Free Vibration of Beams Carrying Spring-Mass Systems—A Dynamic Stiffness Approach. Comput. Struct. 2012, 104–105, 21–26. [Google Scholar] [CrossRef]
- Wang, D. Frequency Sensitivity Analysis for Beams Carrying Lumped Masses with Translational and Rotary Inertias (IJMS-11890). Int. J. Mech. Sci. 2012, 65, 192–202. [Google Scholar] [CrossRef]
- Kalsoom, A.; Shankar, A.N.; Kakaravada, I.; Jindal, P.; Lakshmi, V.V.K.; Rajeshkumar, S. Investigation of Dynamic Properties of a Three-Dimensional Printed Thermoplastic Composite Beam Containing Controllable Core under Non-Uniform Magnetic Fields. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2021, 236, 404–412. [Google Scholar] [CrossRef]
- Mahmoud, M.A. Free Vibrations of Tapered and Stepped, Axially Functionally Graded Beams with Any Number of Attached Masses. Eng. Struct. 2022, 267, 114696. [Google Scholar] [CrossRef]
- Timoshenko, S.; Young, D. Vibration Problems in Engineering; Wiley: New York, NY, USA, 1974. [Google Scholar]
- To, C.W.S. Vibration of a Cantilever Beam with a Base Excitation and Tip Mass. J. Sound Vib. 1982, 83, 445–460. [Google Scholar] [CrossRef]
- Harris, C.M.; Piersol, A.G. Harris’ Shock and Vibration Handbook, 5th ed.; McGraw-Hill Professional: New York, NY, USA, 2002; p. 1568. [Google Scholar]


| Nondimensional Frequency Parameters | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | Present study | 4.7300 | 7.8532 | 10.9956 | 14.1372 | 17.2788 |
| Reference [6] | 4.730041 | 7.853205 | 10.995608 | 14.137165 | -- | ||||
| 0 | 0 | Present study | 1.8751 | 4.6941 | 7.8548 | 10.9955 | 14.1372 | ||
| Reference [6] | 1.875104 | 4.694091 | 7.854757 | 10.995541 | -- | ||||
| 0 | 0 | Present study | 3.1416 | 6.2832 | 9.4248 | 12.5664 | 15.7080 | ||
| Reference [6] | 3.141592 | 6.283185 | 9.424777 | 12.566370 | -- | ||||
| Present study | 4.7300 | 7.8532 | 10.9956 | 14.1372 | 17.2788 | ||||
| Reference [6] | 4.730041 | 7.853205 | 10.995608 | 14.137165 | -- | ||||
| 0 | 0 | 0 | Present study | 3.9266 | 7.0686 | 10.2102 | 13.3518 | 16.4934 | |
| Reference [6] | 3.926602 | 7.068583 | 10.210176 | 13.351768 | -- | ||||
| 0 | Present study | 3.9266 | 7.0686 | 10.2102 | 13.3518 | 16.4934 | |||
| Reference [6] | 3.926602 | 7.068583 | 10.210176 | 13.351768 | -- | ||||
| Nondimensional Frequency Parameters | ||||||||
|---|---|---|---|---|---|---|---|---|
| 0.5 | 0.1 | 0.5 | 0.01 | 2.3587 | 3.9918 | 5.8927 | 8.4328 | 11.3698 |
| 0.1 | 2.0652 | 3.0312 | 5.3734 | 8.2727 | 11.3075 | |||
| 1 | 1.6155 | 2.8248 | 5.3220 | 8.2578 | 11.3016 | |||
| 0.5 | 1 | 0.5 | 0.01 | 1.8035 | 3.9030 | 5.8626 | 8.4196 | 11.3640 |
| 0.1 | 1.6155 | 2.8248 | 5.3220 | 8.2578 | 11.3016 | |||
| 1 | 1.1863 | 2.4757 | 5.2674 | 8.2428 | 11.2956 | |||
| 0.5 | 0.1 | 1 | 0.01 | 2.3046 | 3.9818 | 5.8622 | 8.3642 | 11.3060 |
| 0.1 | 2.0594 | 2.9811 | 5.2816 | 8.1918 | 11.2410 | |||
| 1 | 1.5960 | 2.7360 | 5.2241 | 8.1759 | 11.2348 | |||
| 0.5 | 1 | 1 | 0.01 | 1.7069 | 3.8892 | 5.8327 | 8.3506 | 11.3001 |
| 0.1 | 1.5689 | 2.7814 | 5.2273 | 8.1763 | 11.2349 | |||
| 1 | 1.1859 | 2.3570 | 5.1659 | 8.1603 | 11.2286 | |||
| Properties | Beam | Tip Mass (M1) | Tip Mass (M2) |
|---|---|---|---|
| Modulus of elasticity, E (GPa) | 210 | 210 | 210 |
| Density, ρ (kg/m3) | 7800 | 7800 | 7800 |
| Length, L or LM, (mm) | 323.5 | 25.555 | 15.35 |
| Width, w (mm) | 30 | 30 | 30 |
| Thickness, tb or tM, (mm) | 1.185 | 21.185 | 21.185 |
| Mass, Mb or Mtip, (gr) | 87.520 | 126.660 | 76.090 |
| Distances, d, (mm) | - | 12.777 | 7.675 |
| Rotary inertia (according to the attachment point), Jz, (kg.m2) | - | 32.30 × 10−6 | 8.822 × 10−6 |
| Natural Frequencies | Analytical (Hz) | Experimental (Hz) | Error (%) |
|---|---|---|---|
| 1st | 30.086 | 29.68 | 1.35 |
| 2nd | 100.012 | 98.15 | 1.86 |
| 3rd | 191.337 | 188.6 | 1.43 |
| 4th | 293.348 | 298 | −1.59 |
| 5th | 437.994 | 442 | −0.91 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bilge, H.; Morgül, Ö.K. Analytical and Experimental Investigation of the Rotary Inertia Effects of Unequal End Masses on Transverse Vibration of Beams. Appl. Sci. 2023, 13, 2518. https://doi.org/10.3390/app13042518
Bilge H, Morgül ÖK. Analytical and Experimental Investigation of the Rotary Inertia Effects of Unequal End Masses on Transverse Vibration of Beams. Applied Sciences. 2023; 13(4):2518. https://doi.org/10.3390/app13042518
Chicago/Turabian StyleBilge, Habibullah, and Ömer Kadir Morgül. 2023. "Analytical and Experimental Investigation of the Rotary Inertia Effects of Unequal End Masses on Transverse Vibration of Beams" Applied Sciences 13, no. 4: 2518. https://doi.org/10.3390/app13042518





