Enhancing Heat Transfer Efficiency in Permanent Magnet Machines through Innovative Thermal Design of Stator Windings
Abstract
Featured Application
Abstract
1. Introduction
2. Modelling Description
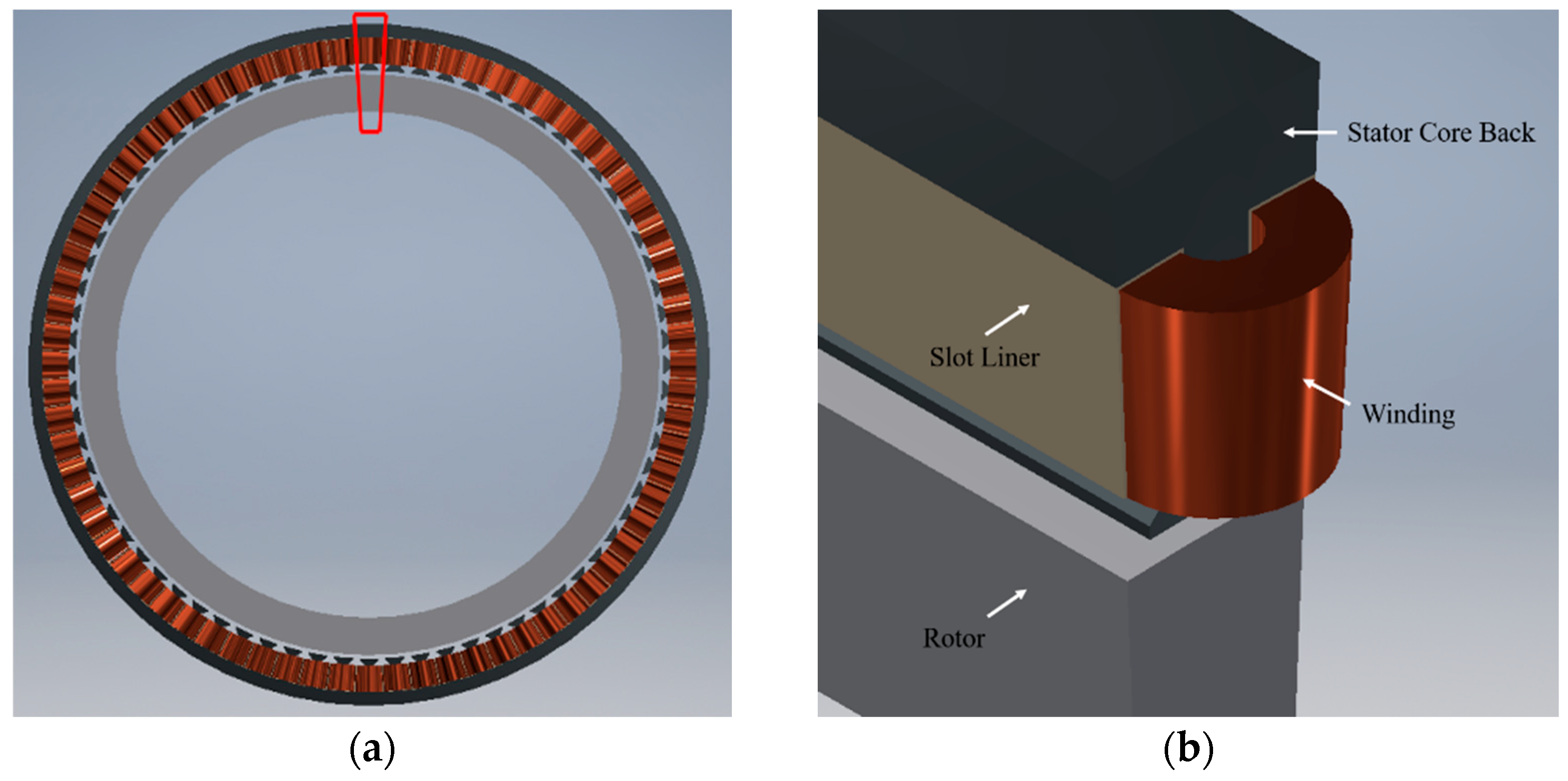
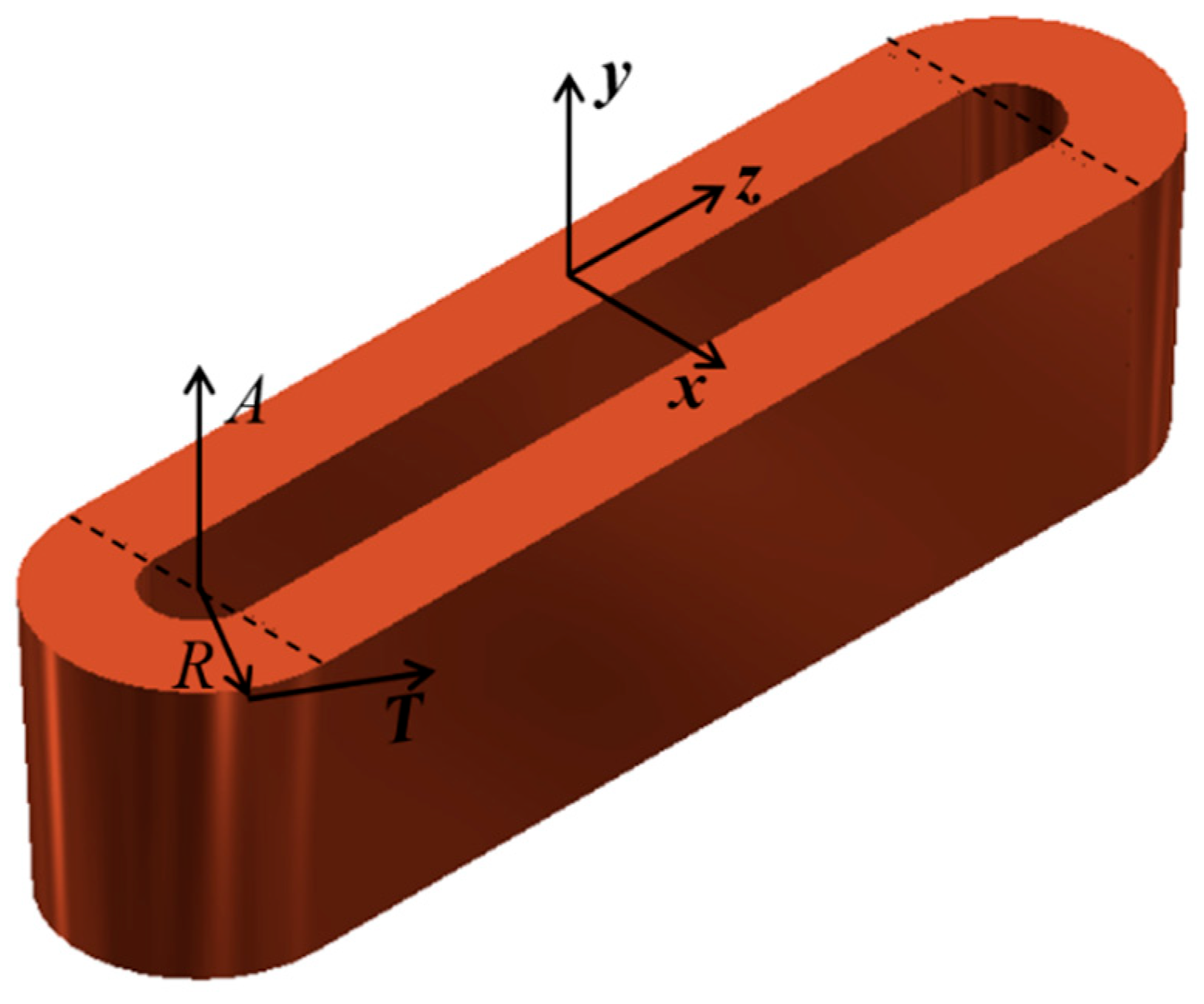
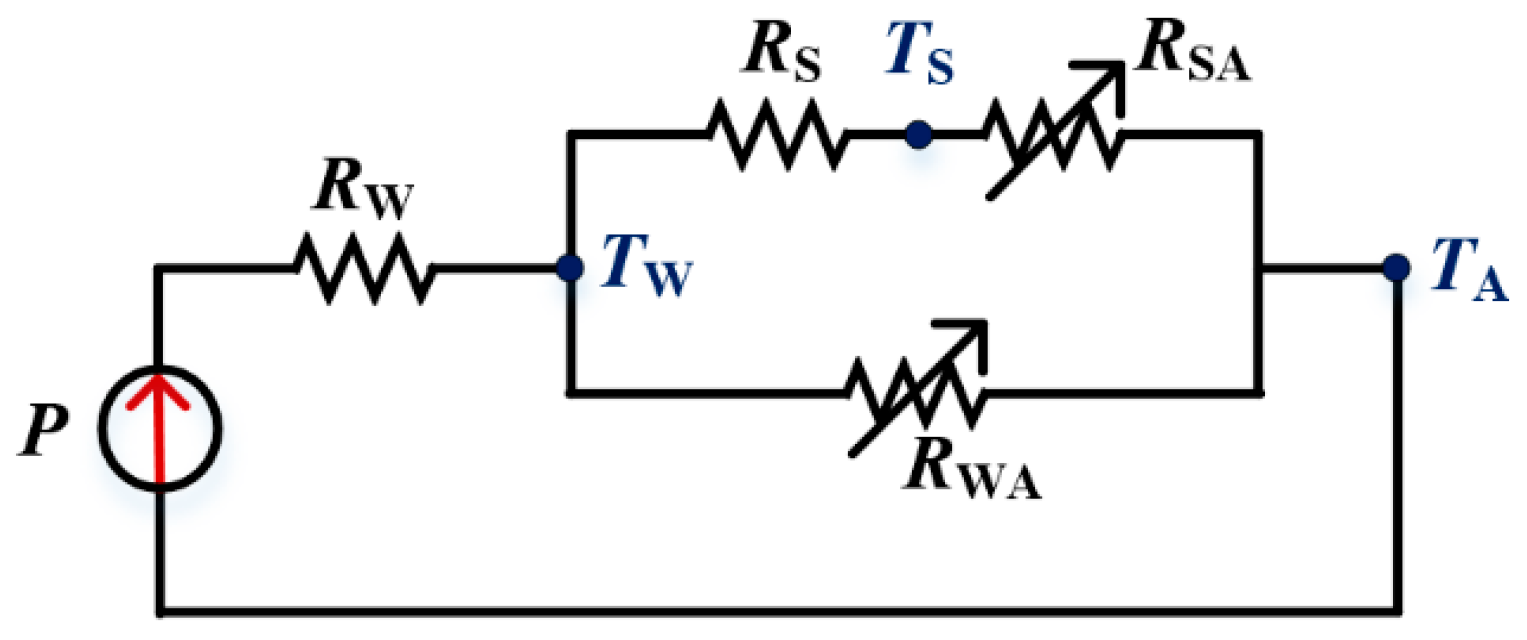
2.1. Approximation of Stator Windings
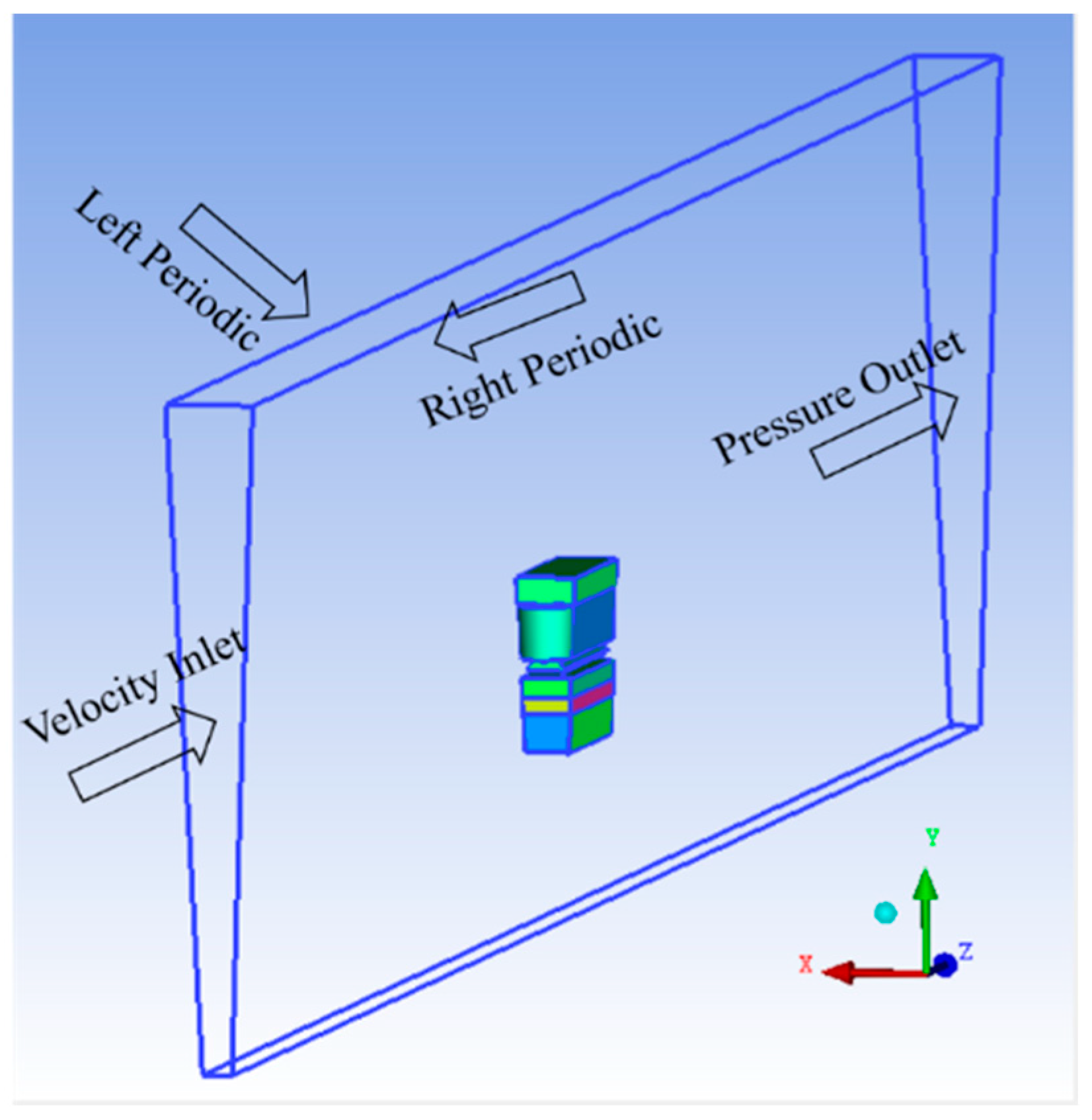
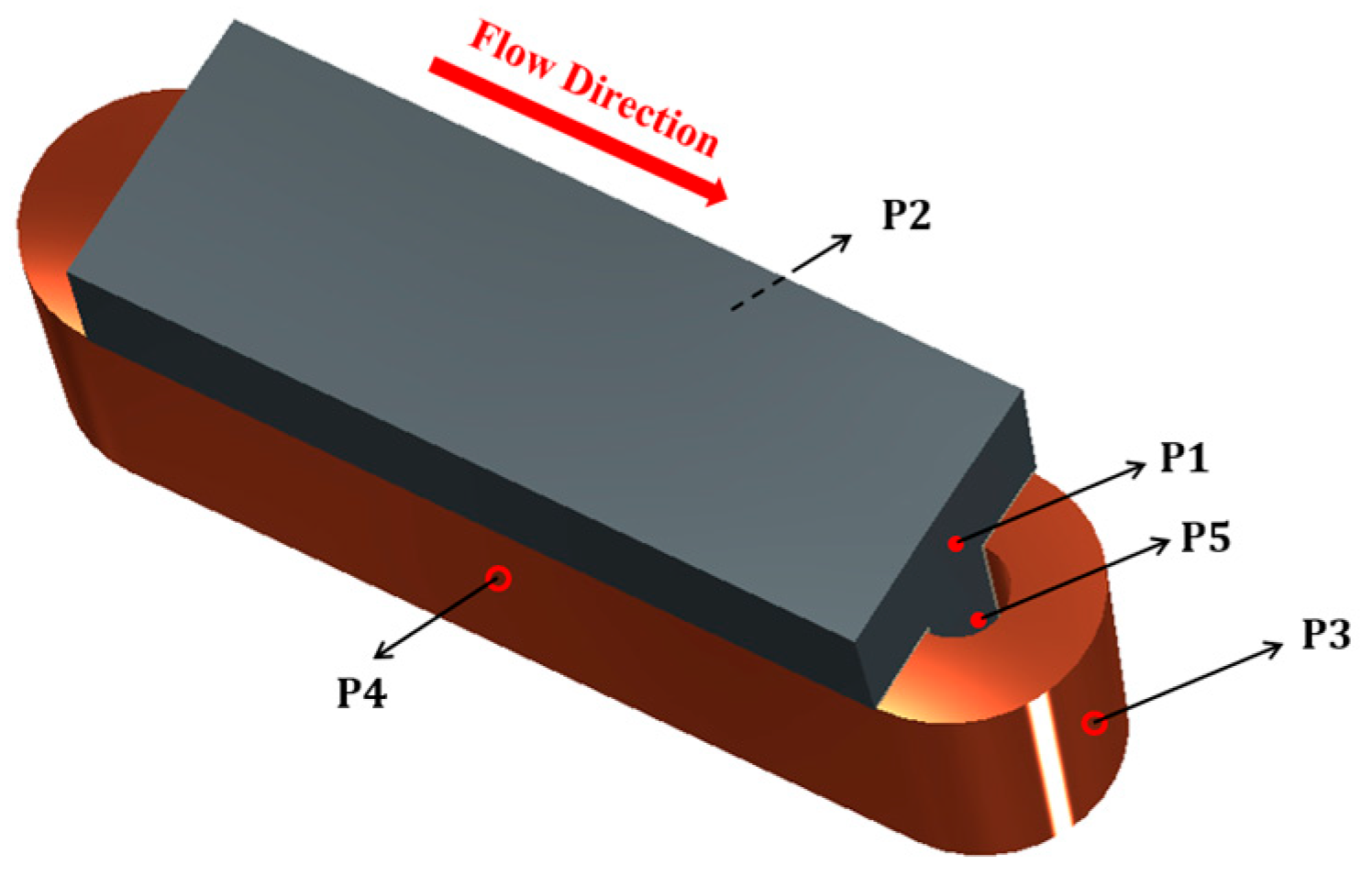
2.2. Description of CFD Simulations
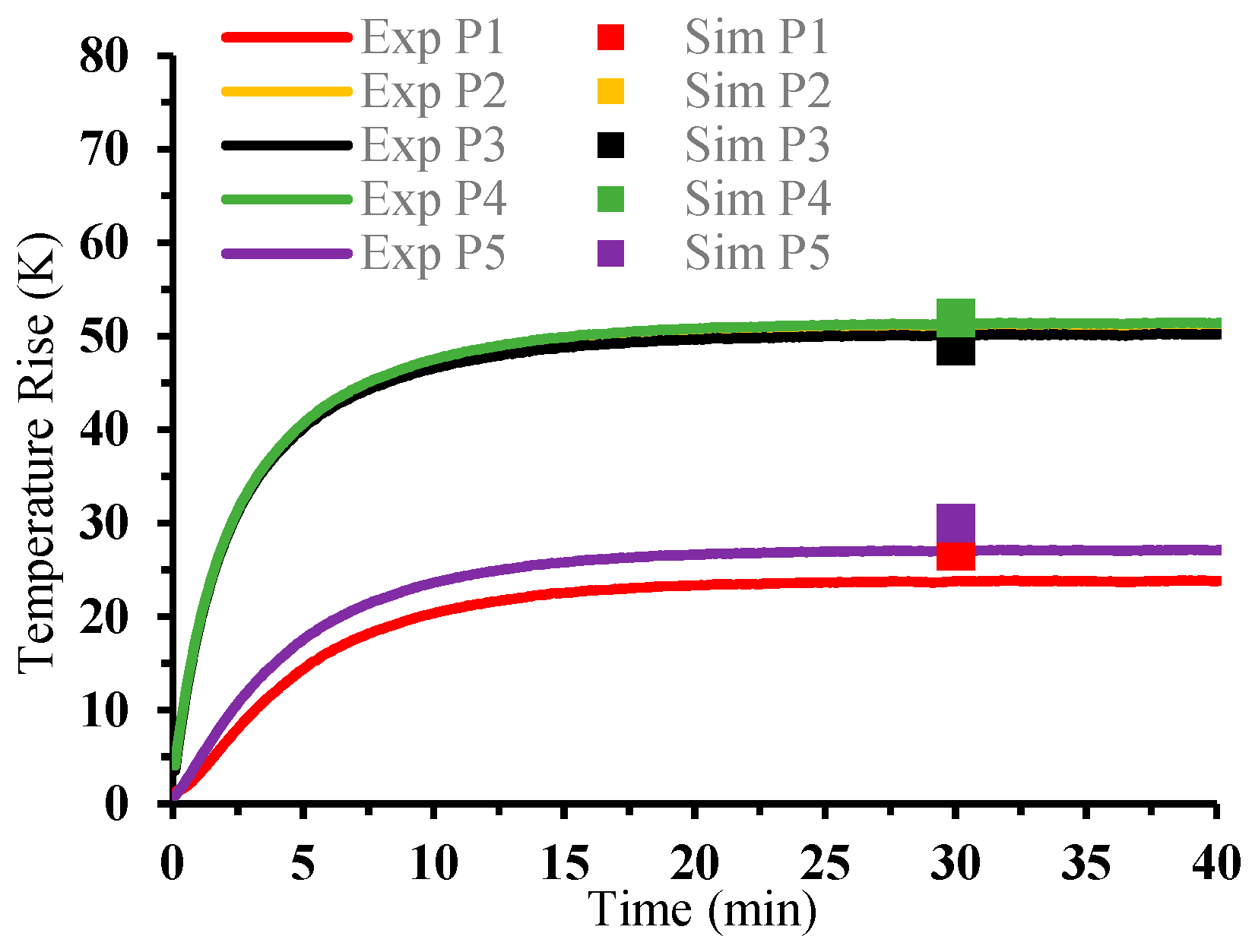
3. Wind Tunnel Validation for CFD Simulations
4. Thermal Design Investigations with the Validated CFD Model
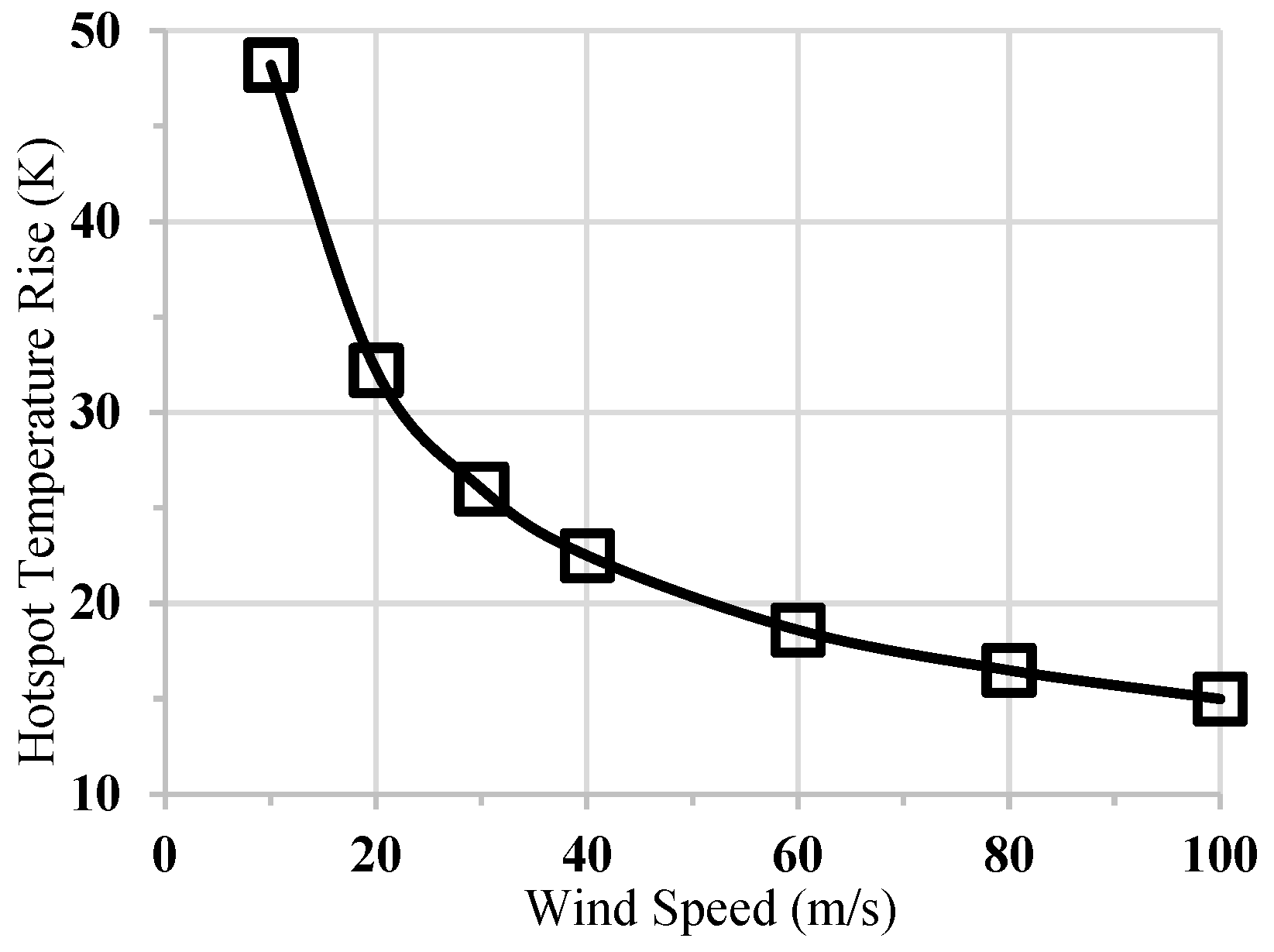
4.1. Effects of Airflow Velocity
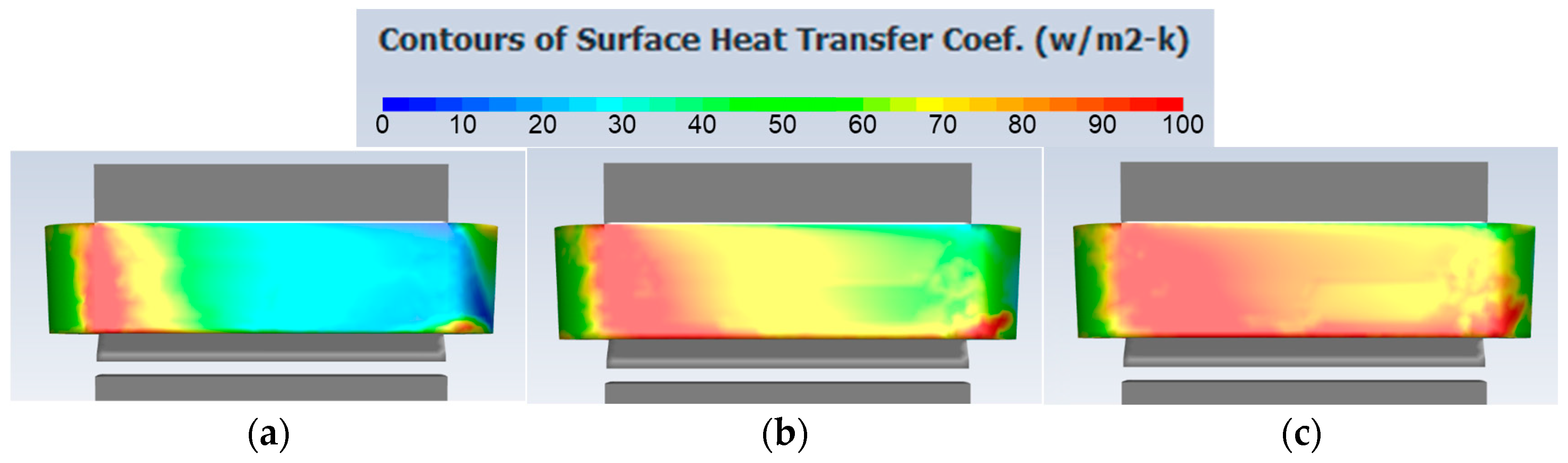
4.2. Effects of Turbulence Intensity
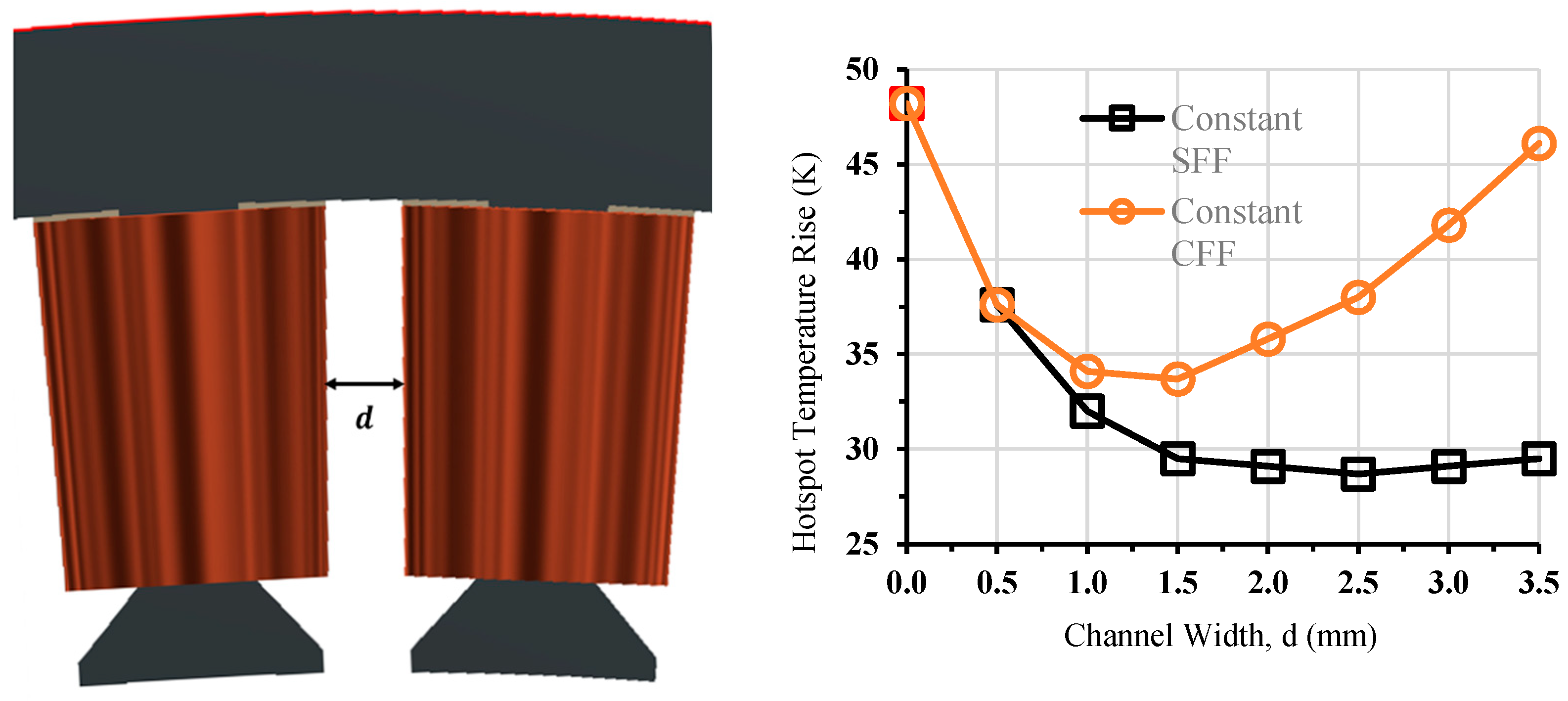
4.3. Effects of Spacing between Windings
- Concept 1: Keeping the SFF constant while augmenting the CFF. This adjustment maintains the copper cross-sectional area as the inter-coil channel expands, enhancing the thermal conductivity of the coil without altering the coil’s loss for a given MMF.
- Concept 2: Preserving the CFF constant and diminishing the SFF, achievable through reducing the wire diameter. This maintains the thermal conductivity of the winding constant while increasing the loss density in the copper for a constant MMF.
4.4. Overall Improvement Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Larsson, J.; Elofsson, A.; Sterner, T.; Åkerman, J. International and national climate policies for aviation: A review. Clim. Policy 2019, 19, 787–799. [Google Scholar] [CrossRef]
- Greitzer, E.M.; Bonnefoy, P.; De la Rosa Blanco, E.; Dorbian, C.; Drela, M.; Hall, D.; Hansman, R.; Hileman, J.; Liebeck, R.; Lovegren, J. N+ 3 Aircraft Concept Designs and Trade Studies, Final Report; Nasa cr-2010-216794/vol2; NASA Glenn Research Center: Cleveland, OH, USA, 2010. [Google Scholar]
- Mecrow, B.C.; Bennett, J.W.; Jack, A.G.; Atkinson, D.J.; Freeman, A.J. Drive topologies for solar-powered aircraft. IEEE Trans. Ind. Electron. 2009, 57, 457–464. [Google Scholar] [CrossRef]
- Jordan, S.; Baker, N.J. Design and build of a mass critical, air-cooled transverse flux machine for aerospace. In Proceedings of the 2016 XXII International Conference on Electrical Machines (ICEM), Lausanne, Switzerland, 4–7 September 2016; pp. 1453–1458. [Google Scholar]
- Simpson, N.; Wrobel, R.; Mellor, P.H. Estimation of equivalent thermal parameters of impregnated electrical windings. IEEE Trans. Ind. Appl. 2013, 49, 2505–2515. [Google Scholar] [CrossRef]
- Yang, Y.; Bilgin, B.; Kasprzak, M.; Nalakath, S.; Sadek, H.; Preindl, M.; Cotton, J.; Schofield, N.; Emadi, A. Thermal management of electric machines. IET Electr. Syst. Transp. 2017, 7, 104–116. [Google Scholar] [CrossRef]
- Nishanth, F.; Johnson, M.; Severson, E.L. A review of thermal analysis and management of power dense electric machines. In Proceedings of the 2021 IEEE International Electric Machines & Drives Conference (IEMDC), Hartford, CT, USA, 17–20 May 2021; pp. 1–8. [Google Scholar]
- Boglietti, A.; Cavagnino, A.; Staton, D.; Shanel, M.; Mueller, M.; Mejuto, C. Evolution and modern approaches for thermal analysis of electrical machines. IEEE Trans. Ind. Electron. 2009, 56, 871–882. [Google Scholar] [CrossRef]
- Gerada, D.; Mebarki, A.; Mokhadkar, R.; Brown, N.; Gerada, C. Design issues of high-speed permanent magnet machines for high-temperature applications. In Proceedings of the 2009 IEEE International Electric Machines and Drives Conference, Miami, FL, USA, 3–6 May 2009; pp. 1036–1042. [Google Scholar]
- Wang, X.; Li, B.; Gerada, D.; Huang, K.; Stone, I.; Worrall, S.; Yan, Y. A critical review on thermal management technologies for motors in electric cars. Appl. Therm. Eng. 2022, 201, 117758. [Google Scholar] [CrossRef]
- Estenlund, S. Air Cooling of an Emsm Field Winding. Licentiate Thesis, Lund University, Lund, Sweden, 2018. [Google Scholar]
- Cheng, L.; Zhu, H.; Jiang, R.; Fu, Z.; Xu, W. The effect of turbulence intensity on full coverage film cooling for a turbine guide vane. In Proceedings of the 2018 Joint Propulsion Conference, Cincinnati, OH, USA, 9–11 July 2018; p. 4523. [Google Scholar]
- Wright, L.M.; McClain, S.T.; Clemenson, M.D. Effect of freestream turbulence intensity on film cooling jet structure and surface effectiveness using PIV and PSP. J. Turbomach. 2011, 133, 041023. [Google Scholar] [CrossRef]
- Bogard, D.G.; Thole, K.A. Gas turbine film cooling. J. Propuls. Power 2006, 22, 249–270. [Google Scholar] [CrossRef]
- Fouladi, F.; Henshaw, P.; Ting, D.S.-K.; Ray, S. Wind turbulence impact on solar energy harvesting. Heat Transf. Eng. 2020, 41, 407–417. [Google Scholar] [CrossRef]
- Iakovidis, F.; Ting, D.S.-K. Effect of Free Stream Turbulence on Air Cooling of a Surrogate PV Panel. Proceedings the of ASME 2014 International Mechanical Engineering Congress and Exposition, Montreal, QC, Canada, 14–20 November 2014; Volume 46521, p. V06BT07A001. [Google Scholar]
- Zhao, C.-J.; Han, J.-W.; Yang, X.-T.; Qian, J.-P.; Fan, B.-L. A review of computational fluid dynamics for forced-air cooling process. Appl. Energy 2016, 168, 314–331. [Google Scholar] [CrossRef]
- Banjac, M.J. Application of Computational Fluid Dynamics in cooling systems design for special purpose objects. FME Trans. 2014, 42, 26–33. [Google Scholar] [CrossRef]
- Shen, X.; Mecrow, B.; Deng, X.; Donaghy-Spargo, C.; Whalley, R.; Chakraborty, N. Direct Air Cooling of High-Power Permanent Magnet Machines. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; pp. 5637–5644. [Google Scholar]
- Economou, J.T.; Tsourdos, A.; Wang, S. Design of a Distributed Hybrid Electric Propulsion System for a Light Aircraft based on genetic algorithm. In Proceedings of the AIAA Propulsion and Energy 2019 Forum, Indianapolis, IN, USA, 19–22 August 2019; p. 4305. [Google Scholar]
- Kondjoyan, A.; Daudin, J. Effects of free stream turbulence intensity on heat and mass transfers at the surface of a circular cylinder and an elliptical cylinder, axis ratio 4. Int. J. Heat Mass Transf. 1995, 38, 1735–1749. [Google Scholar] [CrossRef]
- Kondjoyan, A.; Péneau, F.; Boisson, H.-C. Effect of high free stream turbulence on heat transfer between plates and air flows: A review of existing experimental results. Int. J. Therm. Sci. 2002, 41, 1–16. [Google Scholar] [CrossRef]
- Shen, X.; Avital, E.; Zhao, Q.; Gao, J.; Li, X.; Paul, G.; Korakianitis, T. Surface curvature effects on the tonal noise performance of a low Reynolds number aerofoil. Appl. Acoust. 2017, 125, 34–40. [Google Scholar] [CrossRef]
- Heffron, A.P.; Williams, J.J.; Avital, E. Numerical and Experimental Study of Microvortex Generators. J. Aircr. 2018, 55, 2256–2266. [Google Scholar] [CrossRef]
- Shen, X.; Avital, E.; Paul, G.; Rezaienia, M.A.; Wen, P.; Korakianitis, T. Experimental study of surface curvature effects on aerodynamic performance of a low Reynolds number airfoil for use in small wind turbines. J. Renew. Sustain. Energy 2016, 8, 053303. [Google Scholar] [CrossRef]






| Rated Power | Number of Stator Teeth | Slot Fill Factor | Stator Length | Stator OD | Rotor ID | Stator Slot Area | Winding Length |
|---|---|---|---|---|---|---|---|
| 250 kW | 72 | 43.4% | 50 mm | 404.4 mm | 300 mm | 193 mm2 | 63.4 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, X.; Deng, X.; Mecrow, B.; Wrobel, R.; Whalley, R. Enhancing Heat Transfer Efficiency in Permanent Magnet Machines through Innovative Thermal Design of Stator Windings. Appl. Sci. 2024, 14, 2658. https://doi.org/10.3390/app14062658
Shen X, Deng X, Mecrow B, Wrobel R, Whalley R. Enhancing Heat Transfer Efficiency in Permanent Magnet Machines through Innovative Thermal Design of Stator Windings. Applied Sciences. 2024; 14(6):2658. https://doi.org/10.3390/app14062658
Chicago/Turabian StyleShen, Xiang, Xu Deng, Barrie Mecrow, Rafal Wrobel, and Richard Whalley. 2024. "Enhancing Heat Transfer Efficiency in Permanent Magnet Machines through Innovative Thermal Design of Stator Windings" Applied Sciences 14, no. 6: 2658. https://doi.org/10.3390/app14062658
APA StyleShen, X., Deng, X., Mecrow, B., Wrobel, R., & Whalley, R. (2024). Enhancing Heat Transfer Efficiency in Permanent Magnet Machines through Innovative Thermal Design of Stator Windings. Applied Sciences, 14(6), 2658. https://doi.org/10.3390/app14062658







