Active Tunable Elastic Metasurface for Abnormal Flexural Wave Transmission
Abstract
:1. Introduction
2. Mechanisms of Actively Tunable Elastic Metasurface
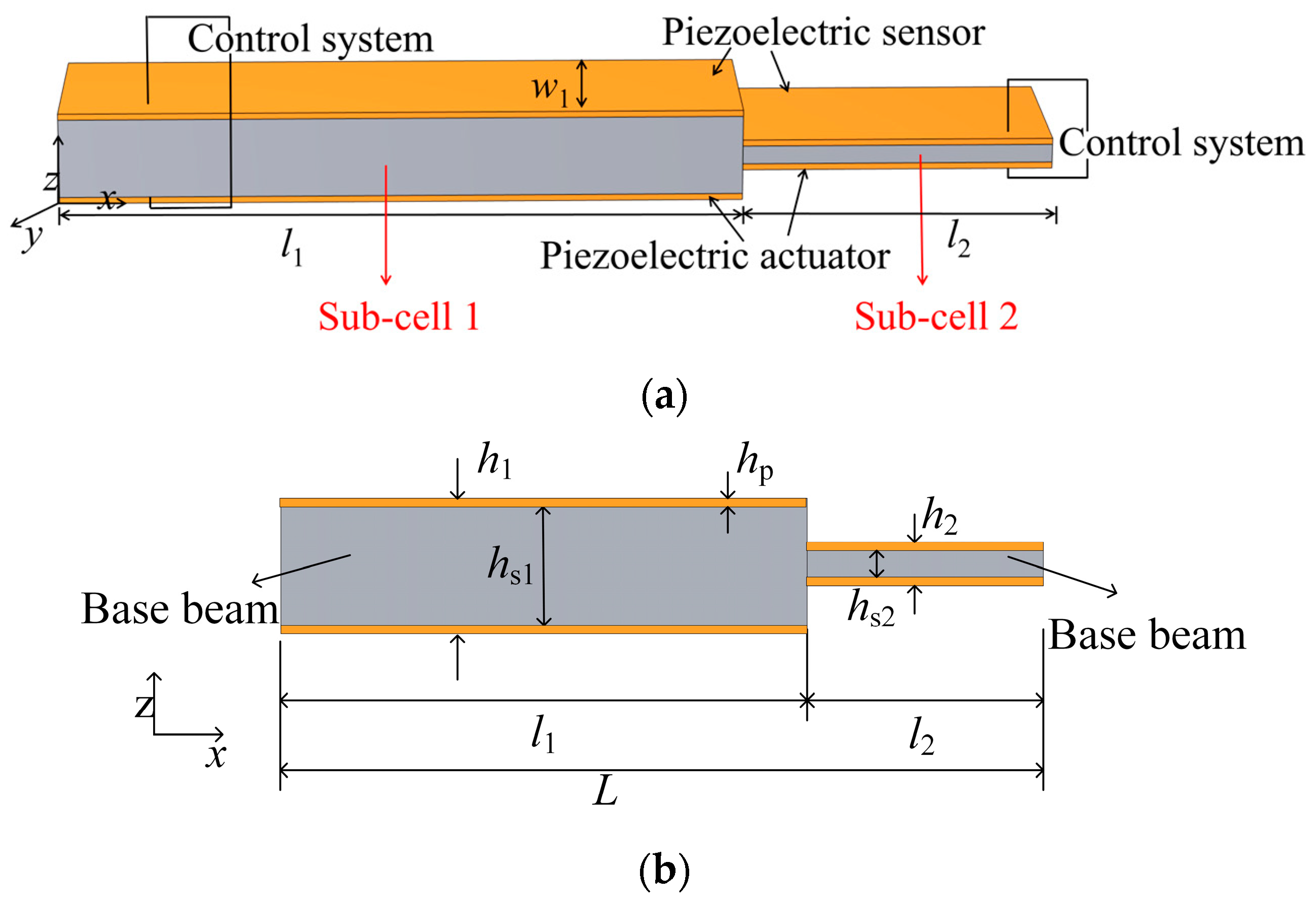
2.1. Description of Adaptive Unit Cells
2.2. Derivations of the Governing Equation
2.3. Generalized Snell’s Law
2.4. Focusing Principle
2.5. Theoretical Formulations of the Transmission Matrix Method
3. Numerical Results and Discussion
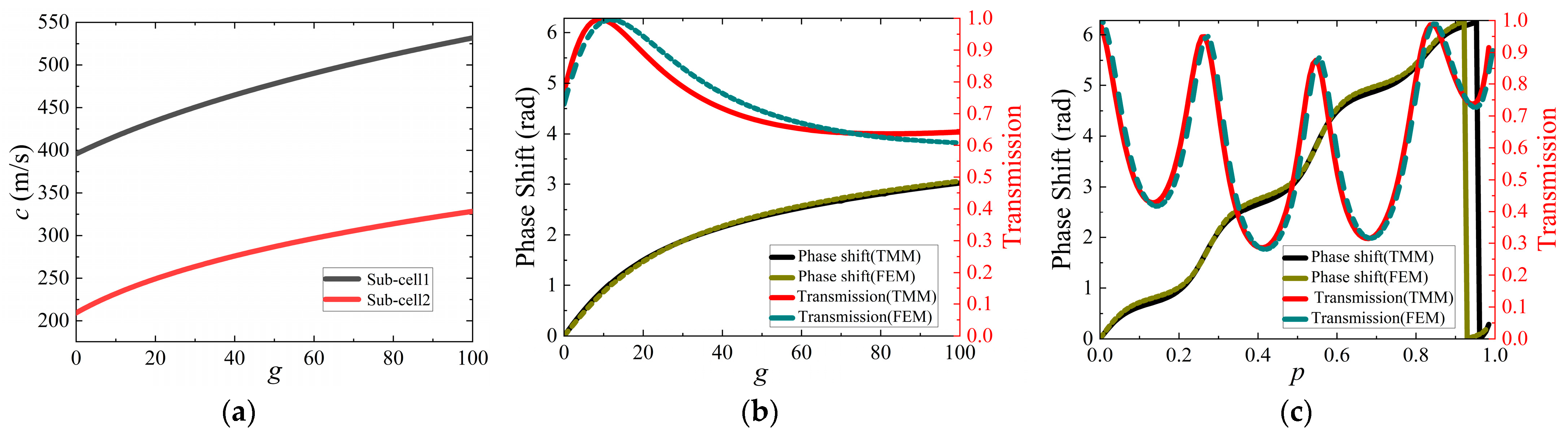
3.1. The Validation of Transmittance and Phase Shift
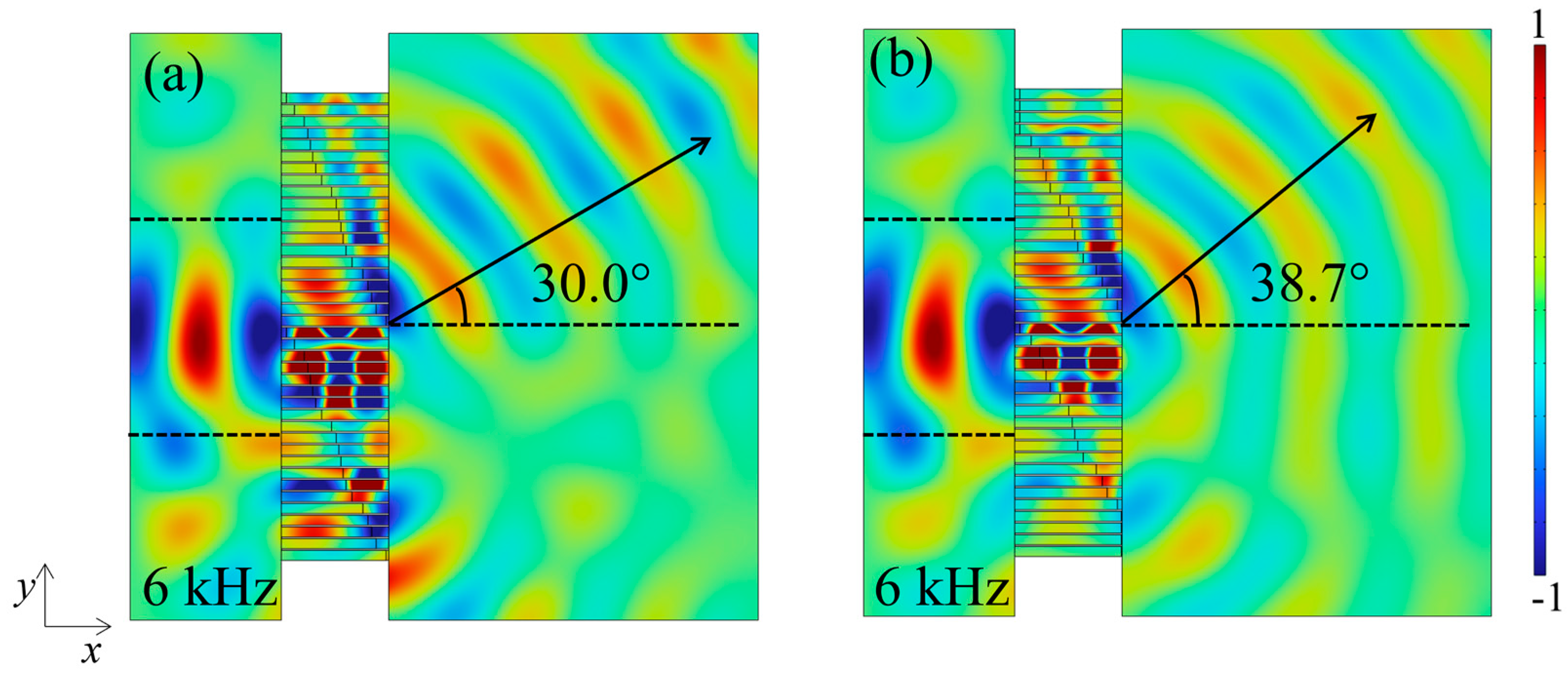
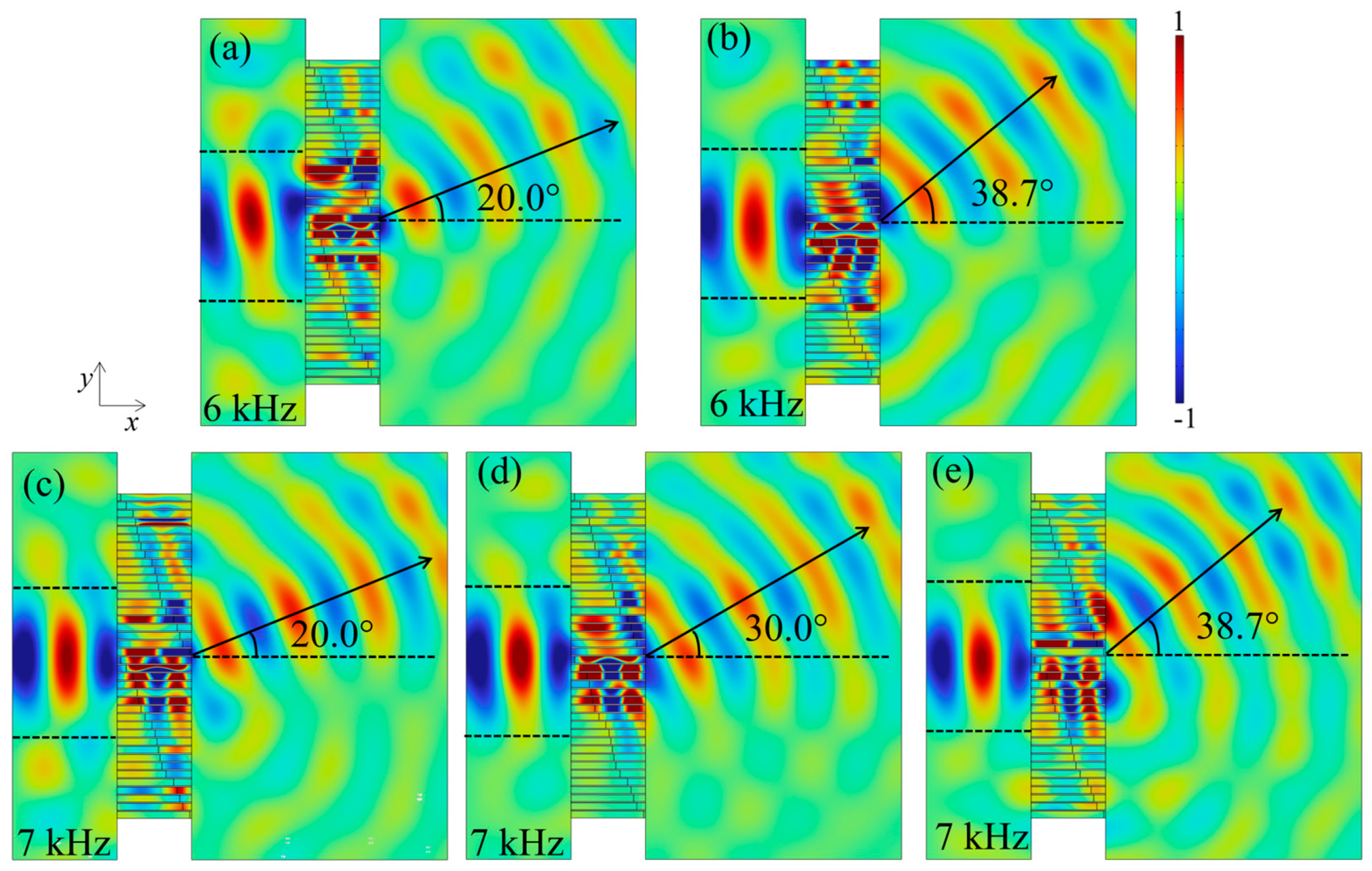
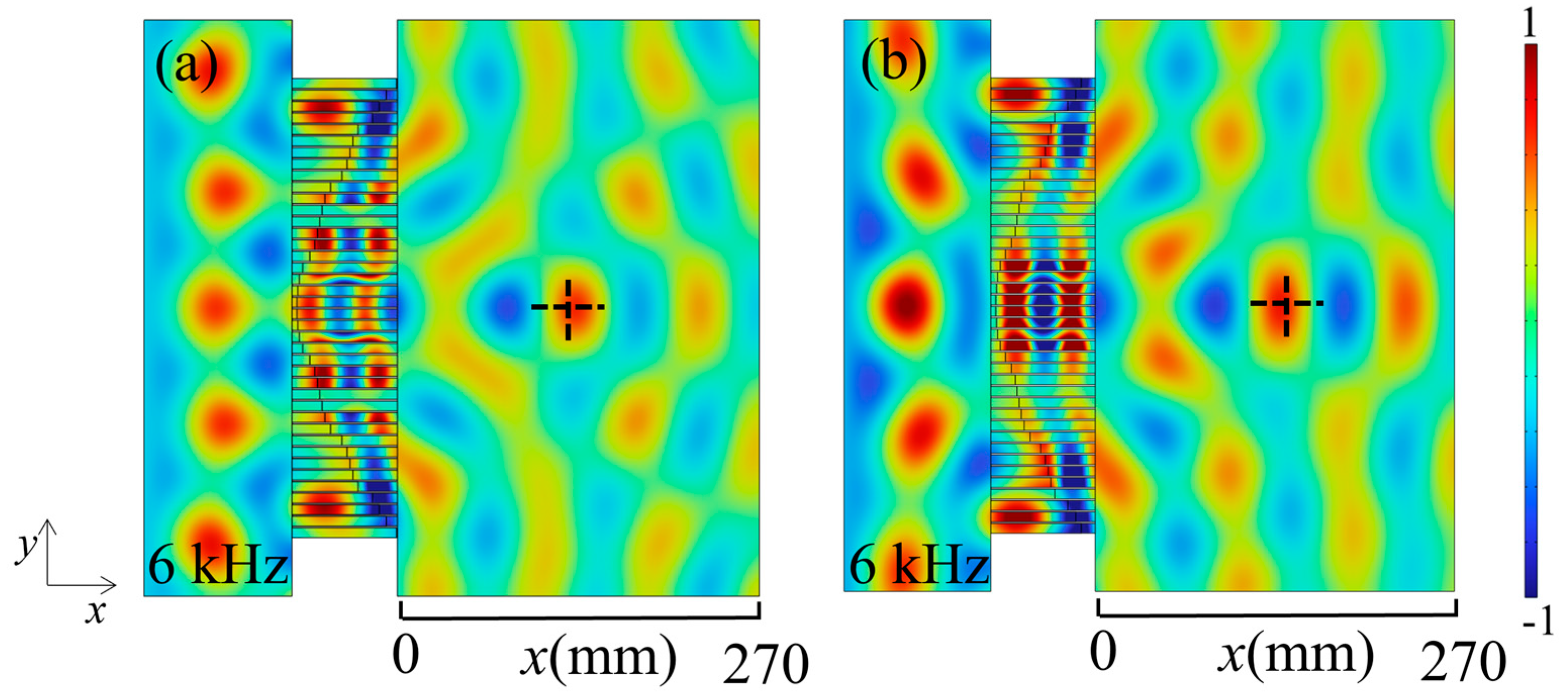
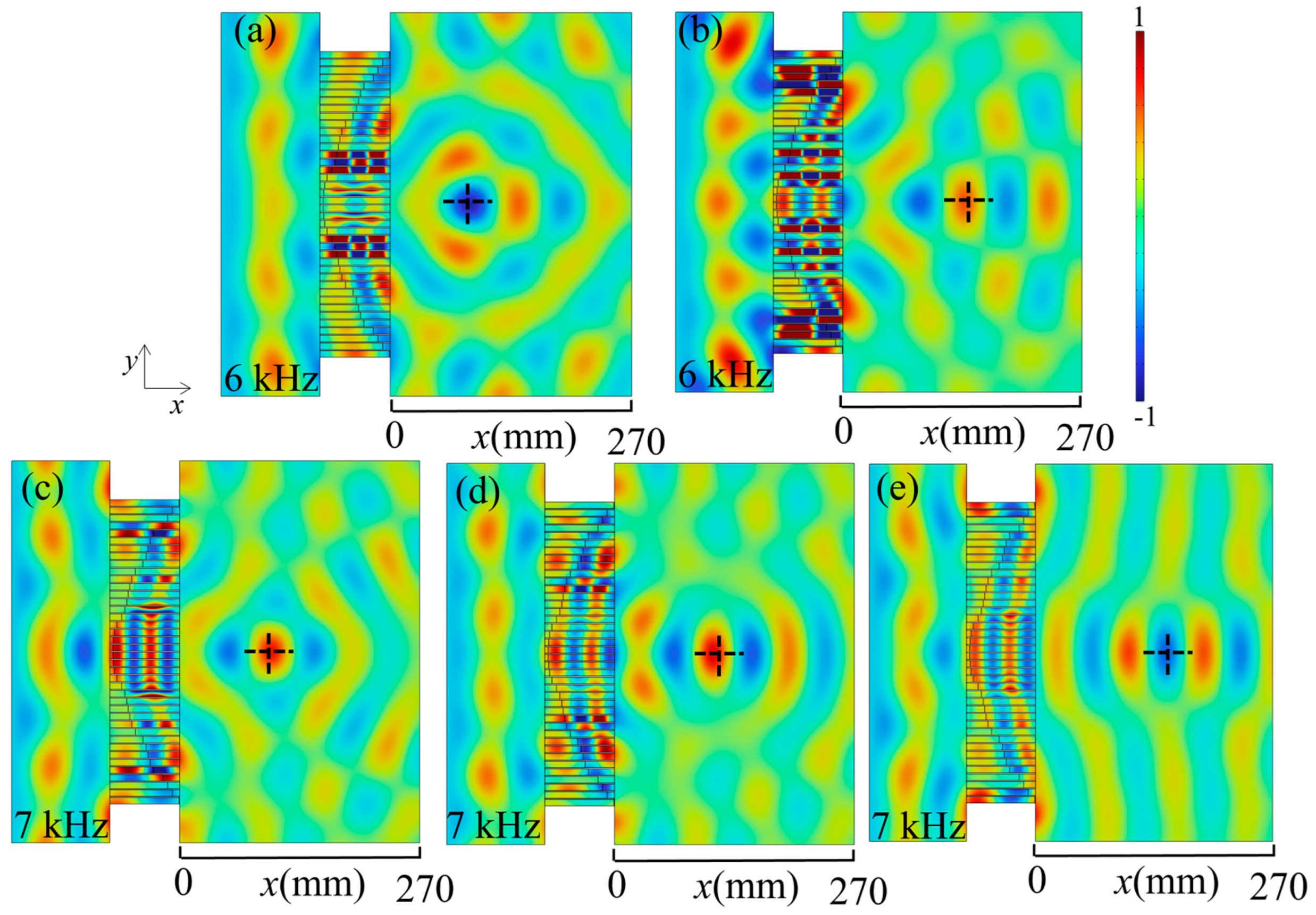
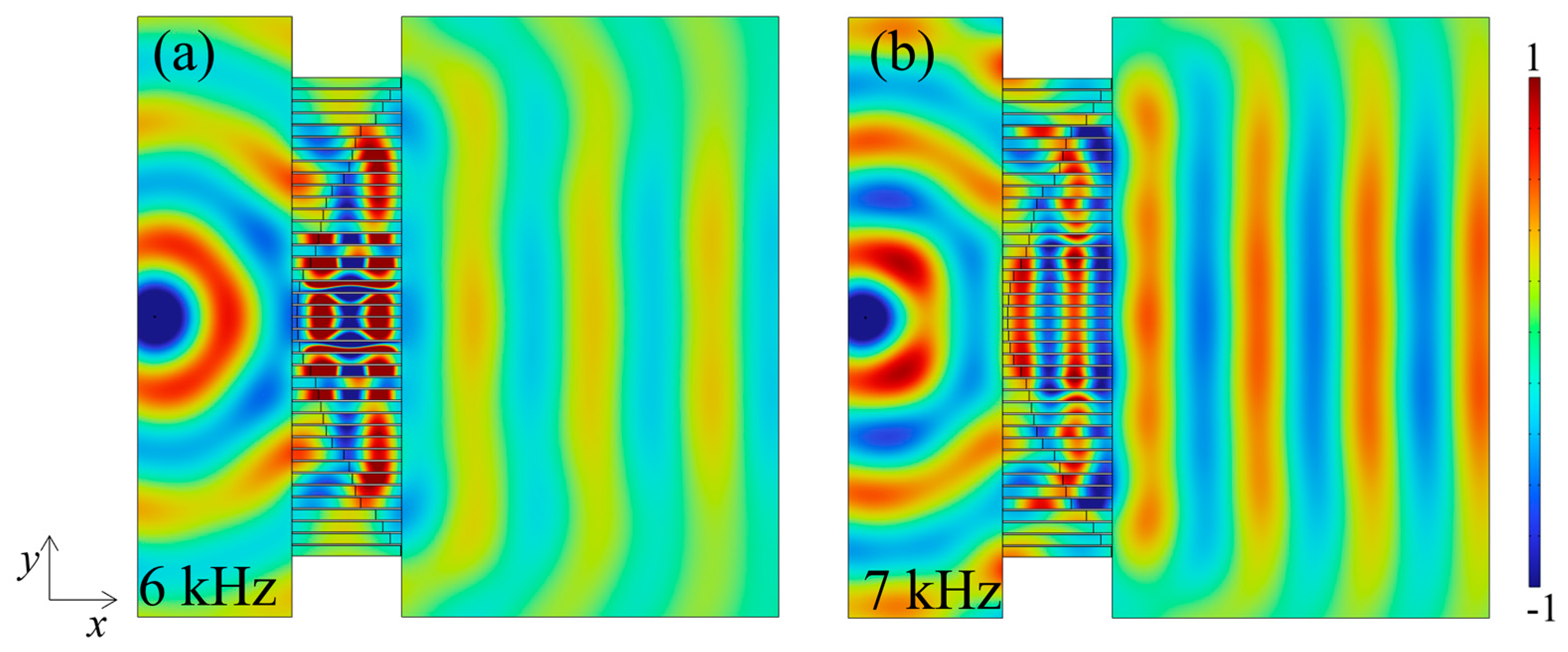
3.2. Results of Abnormal Transmittance
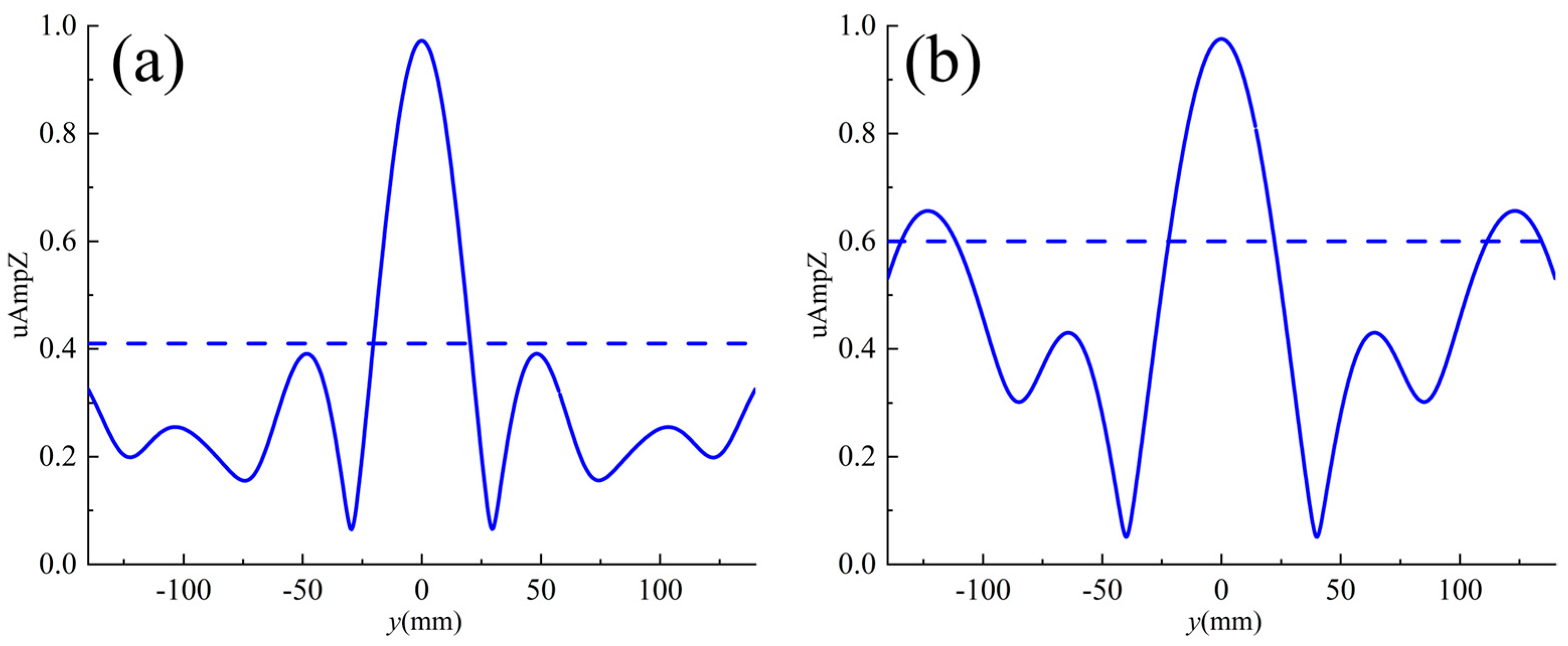
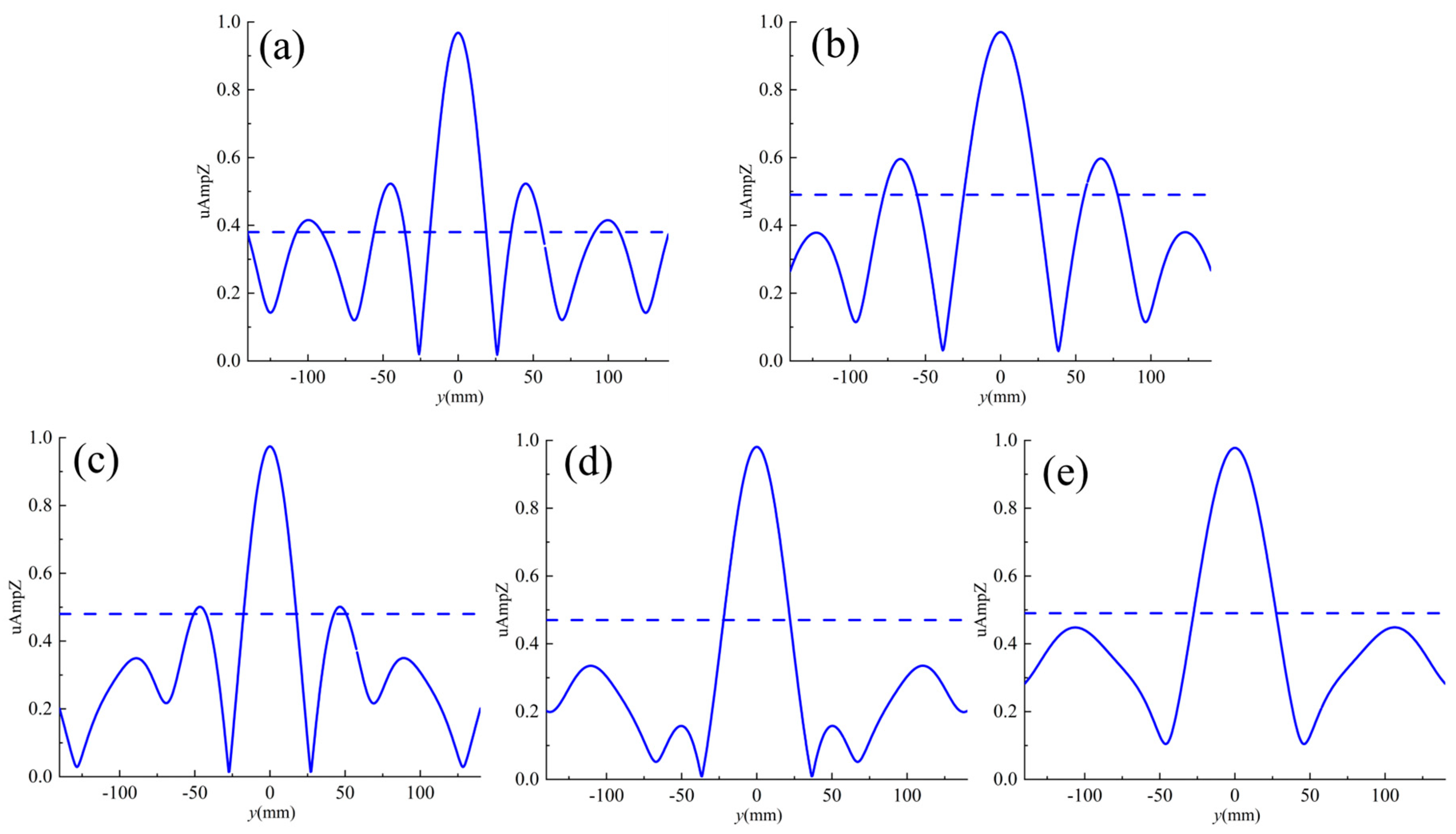
3.3. Realization of Focus Functionality
3.4. Transforming Guided Wave
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Ri | The p of the Adaptive Unit Cell at 6 kHz | |||||
|---|---|---|---|---|---|---|
| Abnormal Transmittance | Focusing | |||||
| θt = 30° | θt = 38.7° | x0 = 100 mm | x0 = 120 mm | |||
| 1 | 0.047 | 0.047 | 0.047 | 0.047 | ||
| 2 | 0.122 | 0.153 | 0.055 | 0.055 | ||
| 3 | 0.213 | 0.233 | 0.069 | 0.064 | ||
| 4 | 0.247 | 0.265 | 0.102 | 0.091 | ||
| 5 | 0.27 | 0.292 | 0.169 | 0.141 | ||
| 6 | 0.292 | 0.33 | 0.216 | 0.197 | ||
| 7 | 0.32 | 0.423 | 0.242 | 0.234 | ||
| 8 | 0.375 | 0.503 | 0.263 | 0.25 | ||
| 9 | 0.467 | 0.536 | 0.285 | 0.27 | ||
| 10 | 0.511 | 0.559 | 0.313 | 0.291 | ||
| 11 | 0.536 | 0.588 | 0.366 | 0.319 | ||
| 12 | 0.555 | 0.638 | 0.473 | 0.375 | ||
| 13 | 0.575 | 0.759 | 0.522 | 0.477 | ||
| 14 | 0.602 | 0.816 | 0.55 | 0.52 | ||
| 15 | 0.658 | 0.861 | 0.578 | 0.548 | ||
| 16 | 0.759 | 0.956 | 0.627 | 0.573 | ||
| 17 | 0.806 | 0.994 | 0.764 | 0.613 | ||
| 18 | 0.841 | 0.994 | 0.828 | 0.736 | ||
| 19 | 0.883 | 0.994 | 0.895 | 0.813 | ||
| 20 | 0.975 | 0.994 | 0.992 | 0.866 | ||
| 21 | 0.047 | 0.047 | ||||
| 22 | 0.122 | 0.047 | ||||
| 23 | 0.213 | 0.047 | ||||
| 24 | 0.247 | 0.047 | ||||
| 25 | 0.27 | 0.153 | ||||
| 26 | 0.292 | 0.233 | ||||
| 27 | 0.32 | 0.265 | ||||
| 28 | 0.375 | 0.292 | ||||
| 29 | 0.467 | 0.33 | ||||
| 30 | 0.511 | 0.423 | ||||
| 31 | 0.536 | 0.503 | ||||
| 32 | 0.555 | 0.536 | ||||
| 33 | 0.575 | 0.559 | ||||
| 34 | 0.602 | 0.588 | ||||
| 35 | 0.658 | 0.638 | ||||
| 36 | 0.759 | 0.759 | ||||
| 37 | 0.806 | 0.816 | ||||
| 38 | 0.841 | 0.861 | ||||
| 39 | 0.883 | 0.956 | ||||
| 40 | 0.975 | 0.994 | ||||
| Ri | The g of the Adaptive Unit Cell | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 6 kHz | 7 kHz | |||||||||
| θt = 20° | θt = 38.7° | θt = 20° | θt = 30° | θt = 38.7° | ||||||
| Sub-Cell1 | Sub-Cell2 | Sub-Cell1 | Sub-Cell2 | Sub-Cell1 | Sub-Cell2 | Sub-Cell1 | Sub-Cell2 | Sub-Cell1 | Sub-Cell2 | |
| 1 | 100 | 16.805 | 0 | 2.999 | 100 | 7.749 | 100 | 8.731 | 100 | 9.572 |
| 2 | 100 | 14.507 | 0 | 5.8 | 100 | 5.342 | 100 | 3.81 | 100 | 8.58 |
| 3 | 100 | 10.645 | 0 | 2.069 | 100 | 1.786 | 100 | 13.6 | 100 | 6.251 |
| 4 | 100 | 11.585 | 0 | 0.705 | 100 | 1.867 | 100 | 4.515 | 100 | 8.263 |
| 5 | 100 | 13.758 | 0 | 2.363 | 100 | 2.75 | 100 | 6.301 | 0.6 | 0 |
| 6 | 100 | 16.46 | 0 | 4.478 | 100 | 3.865 | 100 | 8.533 | 16.84 | 0 |
| 7 | 100 | 18.877 | 0 | 6.772 | 100 | 4.602 | 100 | 10.546 | 53.001 | 0 |
| 8 | 100 | 18.225 | 0 | 7.986 | 100 | 3.091 | 100 | 10.038 | 54.47 | 0 |
| 9 | 100 | 12.318 | 0 | 6.826 | 0 | 9.636 | 100 | 5.223 | 22.518 | 0 |
| 10 | 100 | 12.594 | 0 | 9.37 | 0 | 10.811 | 100 | 5.484 | 32.928 | 0 |
| 11 | 100 | 16.023 | 0 | 14.891 | 0 | 14.472 | 100 | 8.344 | 60.358 | 0 |
| 12 | 100 | 21.612 | 0 | 23.931 | 0 | 20.047 | 100 | 13.037 | 100 | 0.456 |
| 13 | 100 | 28.629 | 100 | 8.643 | 0 | 27.227 | 100 | 19.006 | 100 | 4.62 |
| 14 | 100 | 36.432 | 100 | 13.586 | 0 | 36.009 | 100 | 25.756 | 100 | 1.162 |
| 15 | 100 | 37.548 | 100 | 15.148 | 0 | 42.483 | 100 | 26.901 | 100 | 10.512 |
| 16 | 100 | 21.838 | 9.43 | 100 | 0 | 40.168 | 100 | 13.775 | 100 | 1.579 |
| 17 | 100 | 23.974 | 27.056 | 100 | 0 | 59.865 | 100 | 15.926 | 100 | 3.479 |
| 18 | 100 | 36.205 | 51.797 | 100 | 1.533 | 100 | 100 | 27.188 | 100 | 12.509 |
| 19 | 100 | 55.872 | 82.227 | 100 | 8.473 | 100 | 100 | 46.716 | 100 | 30.409 |
| 20 | 100 | 0 | 0 | 0 | 12.369 | 100 | 100 | 0 | 100 | 0 |
| 21 | 100 | 16.805 | 0 | 0 | 100 | 7.749 | 100 | 8.731 | 100 | 4.123 |
| 22 | 100 | 14.507 | 0 | 0.884 | 100 | 5.342 | 100 | 3.81 | 100 | 2.966 |
| 23 | 100 | 10.645 | 0 | 0.035 | 100 | 1.786 | 100 | 13.6 | 100 | 0.695 |
| 24 | 100 | 11.585 | 0 | 1.857 | 100 | 1.867 | 100 | 4.515 | 100 | 1.945 |
| 25 | 100 | 13.758 | 0 | 4.743 | 100 | 2.75 | 100 | 6.301 | 100 | 4.264 |
| 26 | 100 | 16.46 | 0 | 8.502 | 100 | 3.865 | 100 | 8.533 | 100 | 7.227 |
| 27 | 100 | 18.877 | 0 | 12.894 | 100 | 4.602 | 100 | 10.546 | 100 | 10.274 |
| 28 | 100 | 18.225 | 0 | 16.395 | 100 | 3.091 | 100 | 10.038 | 100 | 11.102 |
| 29 | 100 | 12.318 | 0 | 17.327 | 0 | 9.636 | 100 | 5.223 | 100 | 7.587 |
| 30 | 100 | 12.594 | 0 | 24.902 | 0 | 10.811 | 100 | 5.484 | 100 | 9.73 |
| 31 | 100 | 16.023 | 0 | 39.7 | 0 | 14.472 | 100 | 8.344 | 100 | 15.647 |
| 32 | 100 | 21.612 | 0 | 65.535 | 0 | 20.047 | 100 | 13.037 | 100 | 25.399 |
| 33 | 100 | 28.629 | 100 | 27.918 | 0 | 27.227 | 100 | 19.006 | 100 | 39.729 |
| 34 | 100 | 36.432 | 100 | 44.143 | 0 | 36.009 | 100 | 25.756 | 100 | 60.514 |
| 35 | 100 | 37.548 | 100 | 60.131 | 0 | 42.483 | 100 | 26.901 | 100 | 82.342 |
| 36 | 100 | 21.838 | 100 | 64.353 | 0 | 40.168 | 100 | 13.775 | 21.271 | 100 |
| 37 | 100 | 23.974 | 63.58 | 0 | 0 | 59.865 | 100 | 15.926 | 100 | 59.331 |
| 38 | 100 | 36.205 | 4.688 | 0 | 1.533 | 100 | 100 | 27.188 | 100 | 35.139 |
| 39 | 100 | 55.872 | 24.714 | 0 | 8.473 | 100 | 100 | 46.716 | 100 | 8.848 |
| 40 | 100 | 0 | 1.95 | 0 | 12.369 | 100 | 100 | 0 | 80.731 | 0 |
| Ri | The g of the Rith Adaptive Unit Cell | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 6 kHz | 7 kHz | |||||||||
| x0 = 80 mm | x0 = 120 mm | x0 = 80 mm | x0 = 100 mm | x0 = 120 mm | ||||||
| Sub-Cell1 | Sub-Cell2 | Sub-Cell1 | Sub-Cell2 | Sub-Cell1 | Sub-Cell2 | Sub-Cell1 | Sub-Cell2 | Sub-Cell1 | Sub-Cell1 | |
| 1 | 0 | 1.435 | 0 | 3.533 | 0 | 1.73 | 0 | 1.93 | 0 | 3.534 |
| 2 | 0 | 1.497 | 0 | 3.527 | 0 | 1.816 | 0 | 1.958 | 0 | 3.529 |
| 3 | 0 | 1.674 | 0 | 3.508 | 0 | 1.962 | 0 | 2.077 | 0 | 3.509 |
| 4 | 0 | 1.485 | 0 | 2.984 | 0 | 1.746 | 0 | 1.736 | 0 | 2.985 |
| 5 | 0 | 0.192 | 0 | 1.254 | 0 | 0.525 | 0 | 0.167 | 0 | 1.25 |
| 6 | 0 | 0.06 | 0 | 0.559 | 0 | 0.311 | 0 | 0.065 | 0 | 0.56 |
| 7 | 0 | 1.038 | 0 | 0.97 | 0 | 1.127 | 0 | 0.662 | 0 | 0.971 |
| 8 | 0 | 2.752 | 0 | 3.002 | 0 | 5.623 | 0 | 2.328 | 0 | 1.946 |
| 9 | 0 | 1.599 | 0 | 3.283 | 0 | 4.663 | 0 | 4.612 | 0 | 3.285 |
| 10 | 0 | 4.53 | 0 | 4.819 | 0 | 3.176 | 0 | 7.419 | 0 | 4.82 |
| 11 | 0 | 6.835 | 0 | 5.322 | 0 | 4.997 | 0 | 9.412 | 0 | 5.324 |
| 12 | 0 | 5.714 | 0 | 3.5 | 0 | 3.515 | 0 | 7.637 | 0 | 2.414 |
| 13 | 0 | 10.698 | 2.94 | 0 | 0 | 7.347 | 0 | 12.01 | 2.947 | 0 |
| 14 | 0 | 21.957 | 18.275 | 0 | 0 | 16.2 | 0 | 22.068 | 18.285 | 0 |
| 15 | 0 | 42.822 | 39.794 | 0 | 0 | 32.079 | 0 | 39.881 | 39.808 | 0 |
| 16 | 0 | 83.017 | 51.791 | 0 | 0 | 60.175 | 0 | 71.127 | 51.808 | 0 |
| 17 | 10.033 | 100 | 16.464 | 0 | 1.457 | 100 | 83.942 | 0 | 16.474 | 0 |
| 18 | 34.214 | 100 | 19.949 | 0 | 21.692 | 100 | 89.628 | 0 | 19.959 | 0 |
| 19 | 66.646 | 100 | 22.789 | 0 | 48.817 | 100 | 93.326 | 0 | 22.8 | 0 |
| 20 | 98.763 | 100 | 17.278 | 0 | 76.565 | 100 | 74.579 | 0 | 17.288 | 0 |
References
- Yi, K.; Collet, M.; Ichchou, M.; Li, L. Flexural waves focusing through shunted piezoelectric patches. Smart Mater. Struct. 2016, 25, 075007. [Google Scholar] [CrossRef]
- Cao, L.; Yang, Z.; Xu, Y.; Fan, S.-W.; Zhu, Y.; Chen, Z.; Li, Y.; Assouar, B. Flexural wave absorption by lossy gradient elastic metasurface. J. Mech. Phys. Solids 2020, 143, 104052. [Google Scholar] [CrossRef]
- Shen, Y.; Xu, Y.; Liu, F.; Yang, Z. Metasurface-guided flexural waves and their manipulations. Int. J. Mech. Sci. 2023, 257, 108538. [Google Scholar] [CrossRef]
- Chen, A.-L.; Wang, Y.-S.; Wang, Y.-F.; Zhou, H.-T.; Yuan, S.-M. Design of Acoustic/Elastic Phase Gradient Metasurfaces: Principles, Functional Elements, Tunability, and Coding. Appl. Mech. Rev. 2022, 74, 020801. [Google Scholar] [CrossRef]
- Wang, W.; Iglesias, J.; Jin, Y.; Djafari-Rouhani, B.; Khelif, A. Experimental realization of a pillared metasurface for flexural wave focusing. APL Mater. 2021, 9, 051125. [Google Scholar] [CrossRef]
- Feng, L.; Liu, X.-P.; Lu, M.-H.; Chen, Y.-B.; Chen, Y.-F.; Mao, Y.-W.; Zi, J.; Zhu, Y.-Y.; Zhu, S.-N.; Ming, N.-B. Acoustic Backward-Wave Negative Refractions in the Second Band of a Sonic Crystal. Phys. Rev. Lett. 2006, 96, 014301. [Google Scholar] [CrossRef]
- Lu, Y.; Srivastava, A. Level Repulsion and Band Sorting in Phononic Crystals. J. Mech. Phys. Solids 2017, 111, 100–112. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, X.; Mao, Y.; Zhu, Y.Y.; Yang, Z.; Chan, C.T.; Sheng, P. Locally Resonant Sonic Materials. Science 2000, 289, 1734–1736. [Google Scholar] [CrossRef] [PubMed]
- Oh, J.H.; Kwon, Y.E.; Lee, H.J.; Kim, Y.Y. Elastic metamaterials for independent realization of negativity in density and stiffness. Sci. Rep. 2016, 6, 23630. [Google Scholar] [CrossRef] [PubMed]
- Reynolds, M.; Daley, S. An active viscoelastic metamaterial for isolation applications. Smart Mater. Struct. 2014, 23, 045030. [Google Scholar] [CrossRef]
- Sun, S.; He, Q.; Xiao, S.; Xu, Q.; Li, X.; Zhou, L. Gradient-index meta-surfaces as a bridge linking propagating waves and surface waves. Nat. Mater. 2012, 11, 426–431. [Google Scholar] [CrossRef]
- Yu, N.; Capasso, F. Flat optics with designer metasurfaces. Nat. Mater. 2014, 13, 139–150. [Google Scholar] [CrossRef]
- Zhang, J.; Kosugi, Y.; Otomo, A.; Nakano, Y.; Tanemura, T. Active metasurface modulator with electro-optic polymer using bimodal plasmonic resonance. Opt. Express 2017, 25, 30304–30311. [Google Scholar] [CrossRef]
- Qi, S.; Li, Y.; Assouar, B. Acoustic Focusing and Energy Confinement Based on Multilateral Metasurfaces. Phys. Rev. Appl. 2017, 7, 054006. [Google Scholar] [CrossRef]
- Xie, B.; Tang, K.; Cheng, H.; Liu, Z.; Chen, S.; Tian, J. Coding Acoustic Metasurfaces. Adv. Mater. 2017, 29, 1603507. [Google Scholar] [CrossRef] [PubMed]
- Liang, Z.; Li, J. Extreme Acoustic Metamaterial by Coiling Up Space. Phys. Rev. Lett. 2012, 108, 114301. [Google Scholar] [CrossRef] [PubMed]
- Fan, S.-W.; Zhao, S.-D.; Cao, L.; Zhu, Y.; Chen, A.-L.; Wang, Y.-F.; Donda, K.; Wang, Y.-S.; Assouar, B. Reconfigurable curved metasurface for acoustic cloaking and illusion. Phys. Rev. B 2020, 101, 024104. [Google Scholar] [CrossRef]
- Li, Y.; Liang, B.; Gu, Z.-M.; Zou, X.-Y.; Cheng, J.-C. Reflected wavefront manipulation based on ultrathin planar acoustic metasurfaces. Sci. Rep. 2013, 3, 2546. [Google Scholar] [CrossRef] [PubMed]
- Schwan, L.; Umnova, O.; Boutin, C. Sound absorption and reflection from a resonant metasurface: Homogenisation model with experimental validation. Wave Motion 2017, 72, 154–172. [Google Scholar] [CrossRef]
- Shen, Y.; Xu, Y.; Liu, F.; Wang, F.; Yang, Z. 3D-printed meta-slab for focusing flexural waves in broadband. Extrem. Mech. Lett. 2021, 48, 101410. [Google Scholar] [CrossRef]
- Zhu, H.; Semperlotti, F. Anomalous Refraction of Acoustic Guided Waves in Solids with Geometrically Tapered Metasurfaces. Phys. Rev. Lett. 2016, 117, 034302. [Google Scholar] [CrossRef]
- Zeng, L.; Zhang, J.; Liu, Y.; Zhao, Y.; Hu, N. Asymmetric transmission of elastic shear vertical waves in solids. Ultrasonics 2019, 96, 34–39. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.; Li, M.; Liu, H.; Li, B. Broadband manipulation of flexural waves based on phase-modulated elastic metasurfaces. Eng. Struct. 2023, 275, 115209. [Google Scholar] [CrossRef]
- Kim, M.S.; Lee, W.R.; Kim, Y.Y.; Oh, J.H. Transmodal elastic metasurface for broad angle total mode conversion. Appl. Phys. Lett. 2018, 112, 241905. [Google Scholar] [CrossRef]
- Tian, Z.; Yu, L. Elastic Phased Diffraction Gratings for Manipulation of Ultrasonic Guided Waves in Solids. Phys. Rev. Appl. 2019, 11, 024052. [Google Scholar] [CrossRef]
- Lee, H.; Lee, J.K.; Seung, H.M.; Kim, Y.Y. Mass-stiffness substructuring of an elastic metasurface for full transmission beam steering. J. Mech. Phys. Solids 2018, 112, 577–593. [Google Scholar] [CrossRef]
- Xu, Y.; Zhou, X.; Wang, W.; Wang, L.; Peng, F.; Li, B. On natural frequencies of non-uniform beams modulated by finite periodic cells. Phys. Lett. A 2016, 380, 3278–3283. [Google Scholar] [CrossRef]
- Cao, L.; Yang, Z.; Xu, Y. Steering elastic SH waves in an anomalous way by metasurface. J. Sound Vib. 2018, 418, 1–14. [Google Scholar] [CrossRef]
- Xu, Y.; Cao, L.; Peng, P.; Zhou, X.; Assouar, B.; Yang, Z. Beam splitting of flexural waves with a coding meta-slab. Appl. Phys. Express 2019, 12, 097002. [Google Scholar] [CrossRef]
- Zhu, H.; Walsh, T.F.; Semperlotti, F. Total-internal-reflection elastic metasurfaces: Design and application to structural vibration isolation. Appl. Phys. Lett. 2018, 113, 221903. [Google Scholar] [CrossRef]
- Liu, Y.; Liang, Z.; Liu, F.; Diba, O.; Lamb, A.; Li, J. Source Illusion Devices for Flexural Lamb Waves Using Elastic Metasurfaces. Phys. Rev. Lett. 2017, 119, 034301. [Google Scholar] [CrossRef]
- Cao, L.; Yang, Z.; Xu, Y.; Fan, S.-W.; Zhu, Y.; Chen, Z.; Vincent, B.; Assouar, B. Disordered Elastic Metasurfaces. Phys. Rev. Appl. 2020, 13, 014054. [Google Scholar] [CrossRef]
- Su, X.; Lu, Z.; Norris, A.N. Elastic metasurfaces for splitting SV- and P-waves in elastic solids. J. Appl. Phys. 2018, 123, 091701. [Google Scholar] [CrossRef]
- Lin, Z.; Xu, W.; Xuan, C.; Qi, W.; Wang, W. Modular elastic metasurfaces with mass oscillators for transmitted flexural wave manipulation. J. Phys. D Appl. Phys. 2021, 54, 255303. [Google Scholar] [CrossRef]
- Xu, W.; Zhang, M.; Lin, Z.; Liu, C.; Qi, W.; Wang, W. Anomalous refraction manipulation of Lamb waves using single-groove metasurfaces. Phys. Scr. 2019, 94, 105807. [Google Scholar] [CrossRef]
- Zhou, W.; Wang, S.; Wu, Q.; Xu, X.; Huang, X.; Huang, G.; Liu, Y.; Fan, Z. An inverse design paradigm of multi-functional elastic metasurface via data-driven machine learning. Mater. Des. 2023, 226, 111560. [Google Scholar] [CrossRef]
- Yuan, S.-M.; Chen, A.-L.; Du, X.-Y.; Zhang, H.-W.; Assouar, B.; Wang, Y.-S. Reconfigurable flexural waves manipulation by broadband elastic metasurface. Mech. Syst. Signal Process. 2022, 179, 109371. [Google Scholar] [CrossRef]
- Li, S.; Xu, J.; Tang, J. Tunable modulation of refracted lamb wave front facilitated by adaptive elastic metasurfaces. Appl. Phys. Lett. 2018, 112, 021903. [Google Scholar] [CrossRef]
- Shao, S.; Xia, R.; Li, Z. Tunable piezoelectric metasurface for manipulating multi-mode guided waves in plate. Eng. Struct. 2022, 270, 114917. [Google Scholar] [CrossRef]
- Ren, T.; Liu, C.; Li, F.; Zhang, C. Active tuning of the vibration band gap characteristics of periodic laminated composite metamaterial beams. J. Intell. Mater. Syst. Struct. 2020, 31, 843–859. [Google Scholar] [CrossRef]
- Liu, F.; Shi, P.; Chen, Z.; Shen, Y.; Xu, Y.; Yang, Z. Tunable reflection and broadband absorption of flexural waves by adaptive elastic metasurface with piezoelectric shunting circuits. Smart Mater. Struct. 2023, 32, 055018. [Google Scholar] [CrossRef]
- Yaw, Z.; Zhou, W.; Chen, Z.; Lim, C. Stiffness tuning of a functional-switchable active coding elastic metasurface. Int. J. Mech. Sci. 2021, 207, 106654. [Google Scholar] [CrossRef]
- Li, B.; Hu, Y.; Chen, J.; Su, G.; Liu, Y.; Zhao, M.; Li, Z. Efficient Asymmetric Transmission of Elastic Waves in Thin Plates with Lossless Metasurfaces. Phys. Rev. Appl. 2020, 14, 054029. [Google Scholar] [CrossRef]
- Xu, Y.; Cao, L.; Yang, Z. Deflecting incident flexural waves by nonresonant single-phase meta-slab with subunits of graded thicknesses. J. Sound Vib. 2019, 454, 51–62. [Google Scholar] [CrossRef]
- Qiu, H.; Chen, M.; Huan, Q.; Li, F. Steering and focusing of fundamental shear horizontal guided waves in plates by using multiple-strip metasurfaces. Europhys. Lett. 2019, 127, 46004. [Google Scholar] [CrossRef]
- Lin, Z.; Tol, S. Electroelastic metasurface with resonant piezoelectric shunts for tunable wavefront control. J. Phys. D Appl. Phys. 2023, 56, 164001. [Google Scholar] [CrossRef]
- Chen, Y.; Li, X.; Nassar, H.; Hu, G.-K.; Huang, G. A programmable metasurface for real time control of broadband elastic rays. Smart Mater. Struct. 2018, 27, 115011. [Google Scholar] [CrossRef]
- Wang, G.; Chen, S.; Wen, J. Low-frequency locally resonant band gaps induced by arrays of resonant shunts with Antoniou’s circuit: Experimental investigation on beams. Smart Mater. Struct. 2010, 20, 015026. [Google Scholar] [CrossRef]
- Zhang, H.; Wen, J.-H.; Chen, S.-B.; Wang, G.; Wen, X.-S. Flexural wave band-gaps in phononic metamaterial beam with hybrid shunting circuits. Chin. Phys. B 2015, 24, 036201. [Google Scholar] [CrossRef]
- Li, F.; Zhang, C.; Liu, C. Active tuning of vibration and wave propagation in elastic beams with periodically placed piezoelectric actuator/sensor pairs. J. Sound Vib. 2017, 393, 14–29. [Google Scholar] [CrossRef]
- Xu, Y.; Yang, Z.; Cao, L. Deflecting Rayleigh surface acoustic waves by a meta-ridge with a gradient phase shift. J. Phys. D Appl. Phys. 2018, 51, 175106. [Google Scholar] [CrossRef]

| h0 | h1 | h2 | hs1 | hs2 | hp | L | w1 |
|---|---|---|---|---|---|---|---|
| 3 mm | 3 mm | 1 mm | 2.6 mm | 0.6 mm | 0.2 mm | 64 mm | 5 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, B.; Li, J.; Lin, W.; Ma, Q. Active Tunable Elastic Metasurface for Abnormal Flexural Wave Transmission. Appl. Sci. 2024, 14, 2717. https://doi.org/10.3390/app14072717
Lin B, Li J, Lin W, Ma Q. Active Tunable Elastic Metasurface for Abnormal Flexural Wave Transmission. Applied Sciences. 2024; 14(7):2717. https://doi.org/10.3390/app14072717
Chicago/Turabian StyleLin, Bizun, Jingru Li, Wei Lin, and Qingfen Ma. 2024. "Active Tunable Elastic Metasurface for Abnormal Flexural Wave Transmission" Applied Sciences 14, no. 7: 2717. https://doi.org/10.3390/app14072717




