1. Introduction
In the last decade, event-triggered control attracts more and more attention due to the advantages of reducing the number of control task executions and the cost of communication resources. In this control strategy, the control task execution is decided by an event instead of a certain fixed period of time. The latter is known as periodic sampling or time-triggered control [
1]. The event is generated by the designed event condition, which is a state-related criterion. Therefore, event-triggered control can make the control tasks executed when necessary as the way a human performs [
2]. In [
3,
4,
5], the authors studied the state-feedback event-triggered control from an input-to-state stable point of view and proposed several types of event conditions to guarantee the asymptotic stability of the closed-loop systems. It is noted that the aforementioned works assumed that all the states are available to the controller, but this assumption is excessive and inappropriate in some situations. Therefore, [
6,
7] studied the dynamic output feedback event-triggered control for certain and uncertain linear systems. Furthermore, the quantization effect on the dynamic output-feedback event-triggered control was considered in [
8]. Ref. [
9] applied a cyclic small-gain approach to analyze the event-triggered control systems with partial states and output feedback. The centralized or decentralized event-triggered control in networks was studied in [
10,
11,
12]. The latest survey on event-triggered control can be found in [
13,
14]. To further improve the sampling performance, such as enlarging the average inter-event time or equivalently decreasing the sampling numbers within a fixed time interval, a novel integral-based event-triggered control scheme was recently proposed in [
15,
16]. Literally, the integral-based event-triggered control utilizes the integrals of the measurement signals to construct the event conditions. By this means, this control scheme can allow the Lyapunov function to be non-decrescent between two consecutive triggering instants. Consequently, the integral-based event-triggered control can be proved to yield better sampling performance than the scheme in [
3].
Additionally, actuator saturation is a ubiquitous phenomenon in practical control systems due to the limitation of the facilities. It has been observed that the actuator saturation has a remarkable effect on the performance of the control systems (see [
17] and the references therein). There are few literatures studied event-triggered control with saturated inputs. In [
18] and its follow-up work [
19], the authors studied event-triggered output feedback control for linear systems with actuator saturation, where the practical stability is guaranteed. Then, they applied the anti-windup approach to improve the performance of the systems. For a discrete-time linear plant, the event-triggered control subject to actuator saturation was studied in [
20]. Recently, Ref. [
21] studied the event-triggered asymptotic stabilization of a continuous-time plant with saturated inputs in both static state feedback and dynamic output feedback configurations. A kind of centralized relative event condition is employed in [
21], which is also applied in [
3,
22].
In this paper, we study the event-triggered asymptotic stabilization of a continuous-time linear plant with output feedbacks and saturated inputs. The contributions of this paper are described as follows. First, the decentralized event-triggered control with actuator saturation and output feedback is considered. In some situations, such as implementations over Wireless Sensor Actuator Networks, the sensors and actuators are grouped physically into several nodes and each of them has no access to the measurements of the others (see, e.g., [
23,
24,
25]). As a result, the event condition of each node can only utilize its own measurement, and, hence, the event-triggered control in this paper is executed in a decentralized manner. Second, a type of Zeno-free integral-based event condition is proposed to ensure the asymptotic stability. By enforcing the decentralized event conditions to not be triggered until some fixed intervals, the positive lower bound of inter-event time is guaranteed. Then, beyond these intervals, the integral-based event conditions are used to improve the sampling performance. Compared to [
25], a different mathematical technique (which is based on the Cauchy–Schwarz inequality) is employed to design these intervals analytically from the integral-based event conditions. To the best of our knowledge, the existing contributions on integral-based event-triggered control (see, e.g., [
15,
16,
26]) did not involve the decentralised output feedback configuration and/or the saturated input signals.
The remainder of this paper is organised as follows. After the necessary notation is introduced in
Section 3, a decentralized integral-based event-triggered output feedback saturated control system is formulated in
Section 2. The main results of this paper are included in
Section 4. Two numerical examples are provided to illustrate the efficiency and the feasibility of the proposed results in
Section 5. Finally, the conclusions of this paper are drawn in
Section 6.
2. Preliminaries
The set of real numbers is denoted by . The set of nonnegative integers is denoted by . The transpose of a matrix is denoted by . represents the absolute value of a scalar s. The Euclidian norm of a vector is denoted by , and let denote its infinity norm, i.e., . represents the trace of a matrix A and its induced two-norm is denoted by , where denotes all of the eigenvalues of . An asterisk in the matrix is used to present a symmetry block. For a symmetric matrix , () denotes that it is positive (semi-)definite, and, similarly, () means that it is a negative (semi-)definite matrix. Let represent the identity (zero) matrix, and, for brevity, we sometimes omit the subscript of if there is no confusion from the contexts. The saturation function for a scalar s with upper bound c, , is defined as , where denotes the sign function. In addition, the vector saturation function is defined as with . For a group of points, , the convex hull of these points is defined as .
To deal with the saturation property, we introduce some lemmas for later use. Define
as the set of
m-demision diagonal matrices whose diagonal elements are either 1 or 0. Obviously, there are
elements in
. Label all elements in
as
and denote
. For a positive definite matrix
, define an ellipsoid
by
For a given matrix
, denote the
j-th row of
H as
. Then, we define
With these definitions, we introduce the following lemmas.
Lemma 1. [
27]
For a given with and , suppose . Then, Lemma 2. [
28]
For a given and , ifwhere denotes the row of H, then . 3. Problem Formulation
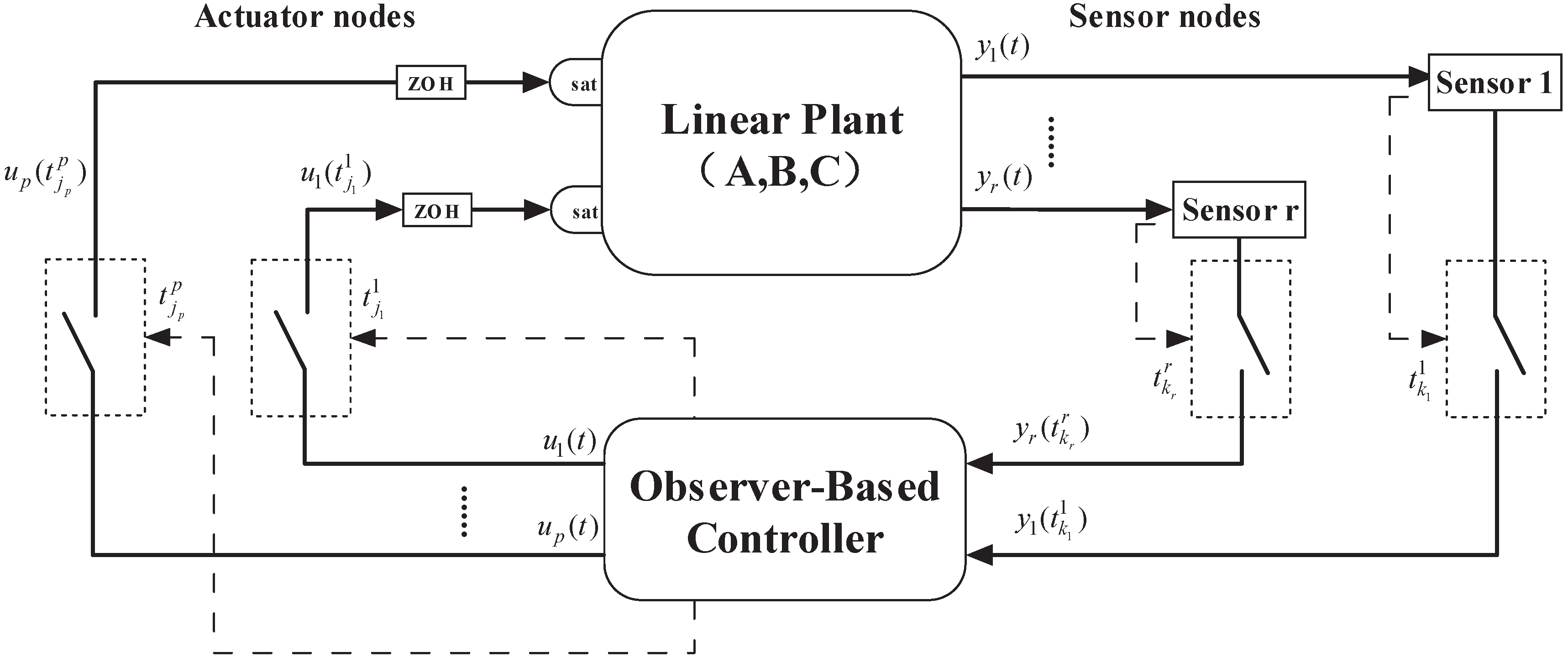
For clarity, the decentralized event-triggered output feedback saturated control system is illustrated in
Figure 1 at first, and the specific details will be given later.
Consider the following linear time-invariant plant with saturated input
where
,
, and
are, respectively, the state vector, the control input, and the output.
are constant matrices of appropriate dimensions.
is supposed to be controllable, and
is supposed to be observable. For briefness, we assume that in the following analysis, the upper bound for the saturation function is
and the subscript
c is dropped. As shown in
Figure 1, both control signal
and output
are implemented in a decentralized manner. Hence, they are, respectively, partitioned into
p actuator nodes and
r sensor nodes, i.e.,
and
, where
and
.
(
) denotes the dimension of the
sth (
lth) actuator (sensor) node and satisfies
(
). To identify the nodes, we introduce the matrices
and
defined as
Thus, and . Because of the communication constraints, either between sensors and observer, or between observer and actuators, the information cannot be transmitted continuously.
Denote
as the latest sampled value at the
sensor node, which is available for the observer-based controller to calculate the control signal.
is the latest sampled actuator signal applied to the system. The triggering instants
are decided by the designed event condition. It is worth noting that different sensor nodes and different actuator nodes are sampled asynchronously. Thus, at time
t, the latest available output
is
and the input
is
Moreover, it is supposed that the first triggering instants of all the nodes are the initial instant, i.e., , for and .
Therefore, the observer-based controller can be described as
where
is the state of observer. The matrices
K and
L are gain matrices to be designed. Denote the observer error by
. Then, its dynamic becomes
Define the sampling error as
, where
and
. Then, we introduce the following decentralized integral-based event condition for each sensor/actuator node:
where
and
are positive constants to be designed.
Remark 1. In Ref. [15], the centralised state feedback was considered, and it was proved that the positive minimum inter-event time can be ensured automatically by the integral part of the event condition (4). According to [22,24], however, it is difficult to avoid Zeno behaviors in both the decentralised and the output feedback configurations. Hence, we introduce the positive constants and to guarantee the positive minimum inter-event time. For example, the minimum inter-event time of cannot obviously be less than . From Label (
1) and Label (
3), the closed-loop system becomes
Therefore, the main interest of this paper is to design the gain matrices K, L and the decentralized integral-based event condition (4) such that the closed-loop system (5) is asymptotically stable. To this end, we first assume the gain matrices to be given and provide results for designing the event condition. Then, we consider the co-design problem of the gain matrices and the event condition.
4. Theoretical Results
In this section, we provide the main results of this paper. First, we propose a method based on linear matrix inequality (LMI) to design the event condition (4) in the case that the gain matrices are supposed to be given. Then, we will study the synthesis of the gain matrices. Let the argument variable be
. Motivated by [
21], we initially use Lemma 1 to deal with the saturation nonlinearity, which shows that if
for a matrix
, then
Now, consider the state
in the set
. At this moment, the closed-loop system (5) is translated into the following form:
Then, we study the stability of this differential inclusion. Let
with
being
n-dimension positive definite matrices. The derivative of
V along the trajectories of Label (6) is
with
. From the fact
for any
,
According to Label (7), a sufficient condition for
is
where
and
. Due to the fact that, for any
if the following matrix inequality holds for some positive scalar
,
then
.
By a Schur complement, Label (9) is equivalent to
where
,
and
. Hence, at this moment,
. If the event condition (4) ensures
with
, then
. As a result, if the ellipsoid
satisfies
then the set
is an invariant set of the closed-loop system (5). Consequently,
holds for all
. This means that the closed-loop system is stable. From Lemma 2, a sufficient condition for Label (11) is
where
is the
row of
and
is the
row of
. Then, we propose the following theorem to obtain the asymptotic stability.
Theorem 1. Consider the closed-loop system (5). Suppose that there exist a group of solutions , , to the LMIs (10) and (12) for some . If the parameters in event condition (4) satisfy the following conditions:- 1.
- 2.
and,
where , and the matrices are Then, for any initial state in the ellipsoid , the corresponding closed-loop system (5) is asymptotically stable.
Proof of Theorem 1. If it is shown that the parameters in the theorem can guarantee
for
, then the stability can be proved directly according to the preceding analysis. To this end, we first consider the derivative of
. From Label (6),
which leads to
Similarly, one has
where
,
,
, and
.
Denote by the overall triggering instants. By definitions, there may exist more than one node being triggered for some . In addition, since there is no Zeno phenomenon, .
Initially, by contradiction, we prove the inequality
for
. If
, the conclusion holds obviously. In the case
, assume the positive instant
(it allows being infinity) as the first time when
. Such a
exists because of
. If
, the inequality holds. If
,
for
, and, at this point, it can be proved that for
,
To illustrate Label (15), for example, we consider .
First, in the case
, Label (14a) implies that
where the last inequality employs the Cauchy–Schwarz inequality and the fact that
. By integrating Label (16), one has
Since
for
, Label (17) leads to
Due to item 2 and the fact , for .
In the case
, Label (15) can be obtained by the integral part of the event condition (4). In fact,
The similar analysis can be applied to other and by using Label (14a) and Label (14b). Hence, Label (15) holds for .
Thus, according to the item 1 in the theorem, for
,
Namely, , which contradicts the definition of . Therefore, for .
Next, we consider the interval . At this point, assume that Label (15) and hold for . Define as the first time when . If the event conditions in all of the nodes are triggered at , then as well as , and, hence, is proved to obviously exist. If there are some nodes where the event conditions are not triggered at , for example , one has . As a result, implies the existence of .
For , if , then . By analyzing the case of or , one has , . This means that Label (15) holds for . If , there must exist such that . Then, one can prove Label (15) for via the parallel process for the case of , where is replaced by . As a result, can be proved for by the contradiction with .
Then, by induction, one has
for
. Thereby, the stability can be proved. Moreover, the stability implies the uniform continuity of
. The limit of the monotone decreasing function
exists, since the function is lower bounded by
. Then, from Barbalat’s Lemma (see [
29] for more details),
converges to zero. Therefore, the closed-loop system is asymptotically stable and the proof is completed. ☐
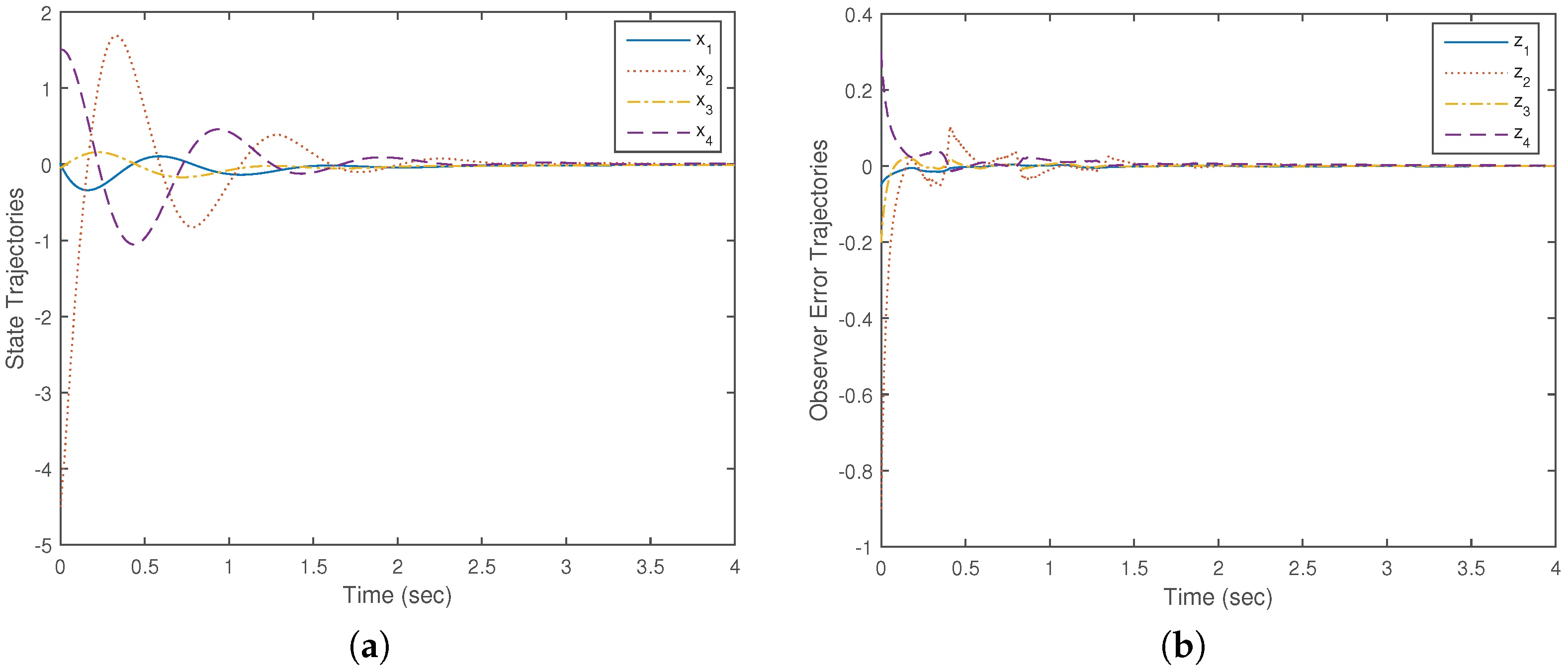
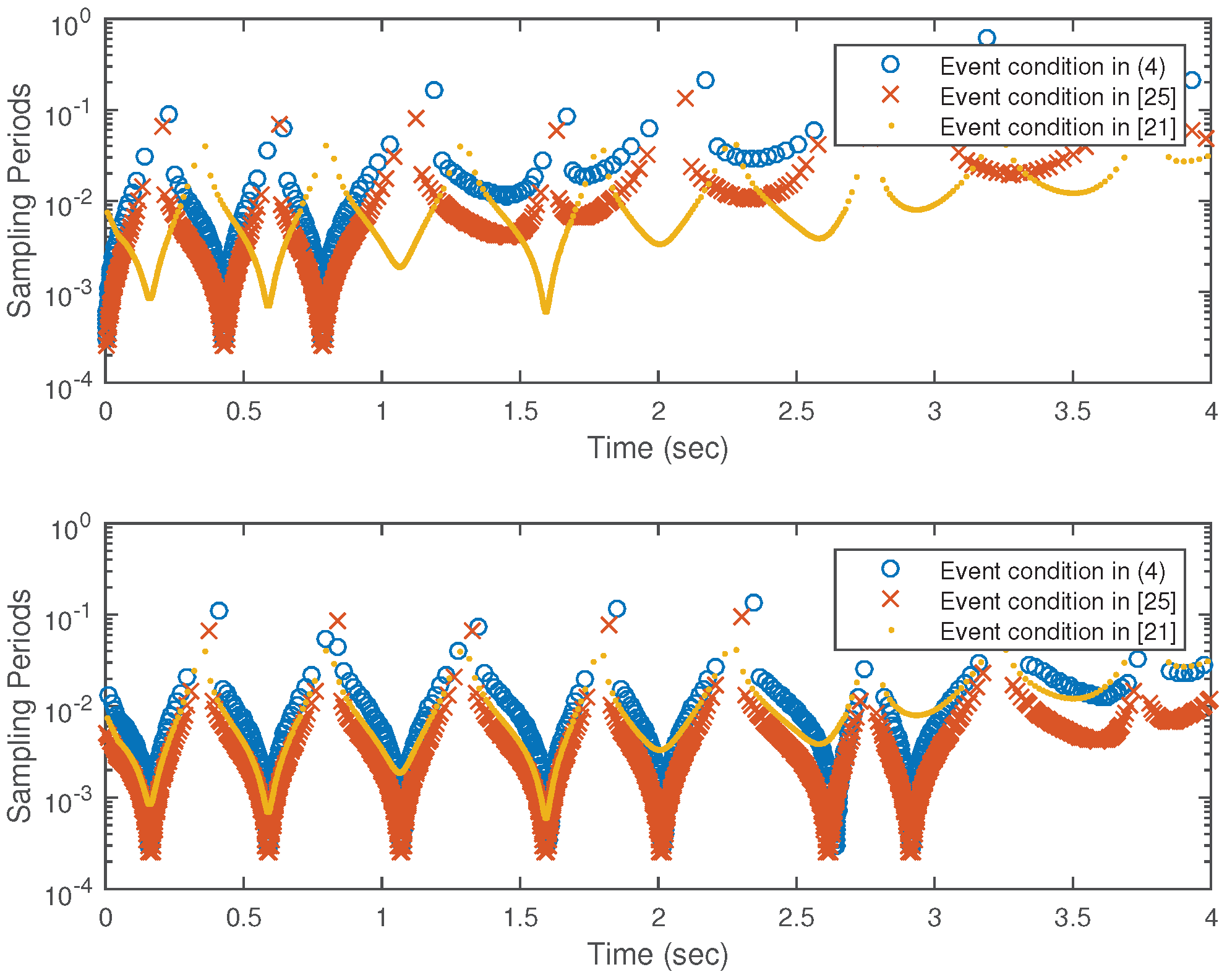
Remark 2. The proof of Theorem 1 implies that, to guarantee the stability, one can also adopt a time-triggered control where the sampling period of sensor and actuator nodes are and , respectively. Hence, for stability, the event conditions are not necessary. However, the time-triggered control is not preferable to save communication resources. As shown in the Simulation section, by introducing event-triggered control, quite a larger average inter-event time can be obtained.
For given
K,
L and
, the ellipsoid
describes the admissible region for initial states such that the closed-loop system is asymptotically stable. Thereby, one may expect to find the largest one among them. To define the “largest”, a measure that can reflect the geometrical size of
is required. Generally, the measure is often considered as volume. However, Ref. [
30] pointed out that the volume optimization can lead ellipsoids to be “flat” in some directions. On the contrary, the trace optimization yields the ellipsoids that tend to be homogeneous in all directions. Referring to [
18,
30], we consider the following optimization problem to find the largest ellipsoid for given
K,
L,
and some
:
where the optimization variables are
. However, the optimization problem (18) is nonlinear subject to
and
. Hence, to transfer the above problem into a linear form, we propose the following theorem, where the LMI optimization problem can be solved by the standard LMI toolbox in MATLAB (8.4.0.150421, The MathWorks, Natick, Massachusetts, United States, 2014).
Theorem 2. The solutions to Label (18) can be obtained from the following LMI optimization problem:where , and . The LMI variables are positive definite matrices ,, and matrices , . and are the row of and , respectively. Moreover, the solutions to Label (18) are . Proof of Theorem 2. Using the Schur complement, Label (20) is equivalent to
Pre- and post-multiplying both sides of the above inequality by
, it is transformed to
By denoting , , and , Label (21) is the same as Label (10) obviously. By a similar process, it is proved that Label (20) is equivalent to Label (12) with and . Therefore, the proof is completed. ☐
For given gain matrices K and L, if the LMIs (10) and (12) are feasible, one can design the parameters in event condition (4) according to Theorem 1 and give the largest ellipsoid by solving the LMI optimization problem in Theorem 2. Hence, in the following, we focus attention on how to find such gain matrices, i.e., a controller synthesis jointly with the parameters in the event condition.
Theorem 3. For the closed-loop system (5), if there exist positive definite matrices , , matrices , , and , and a positive scalar such that the following LMIs hold for some :where and . and are, respectively, the row of and . Then, are the solutions to the LMIs (10) and (12) with and . Proof of Theorem 3. Due to the Schur complement and the fact that
, Label (22) yields
Pre- and post-multiplying both sides of Label (24) by
and substituting
and
into Label (24), one has that Label (24) is equivalent to
where
, and
. By denoting
,
and
, Label (25) is the same as Label (10). This shows that Label (22) is a sufficient condition for Label (10). Similarly, by pre- and post-multiplying both sides of Label (23) by
, Label (23) is equivalent to Label (12). Therefore, the proof is completed. ☐
Remark 3. In Label (10), scalars are two free parameters for improving the feasibility of the LMI. To make the LMI feasible, properly large and are expected. On the one hand, has a counter effect on the feasibility. In fact, as shown in the last column, for a fixed , is expected to be large enough, which, however, may yield a large . On the other hand, for a large , as shown in the forth column, a large is expected as well. To eliminate the effect of large , as shown in , is required to be small enough, which can always be satisfied. Therefore, to make Label (10) feasible, large and are expected, although too large and lead to be very small. Since a small would make the event condition more easy to be triggered, small are expected to improve the sampling performance. To balance the feasibility of LMIs and the sampling performance, one may follow a two-step procedure for choosing the proper free parameters. First, one should select large enough such that the LMIs are feasible. Second, to obtain a large , one should gradually decrease the values of the free parameters until the obtained is satisfactory or the LMIs are not feasible. The above analysis is also applicable to the LMIs in Theorems 2 and 3.
Remark 4. In Ref. [25], the decentralised relative event condition is employed, i.e.,Similar to the analysis in [15] (Theorem 2), the integral-based event condition (4) is better than the relative one to some degree. For example, we consider the node . For the same triggering input , the next triggering instant decided by the relative event condition cannot be larger than that decided by Label (4). In fact, when determined by the relative event condition is , the statement is obvious. In addition, when , from the relative event condition, one has that for all . Clearly, the inequality also holds if one integrates on both sides. Thus, the input signal at that is decided by the relative event condition would not satisfy the integral-based event condition (4), and the statement is valid.