Analysis of Nonlinear Vibration in Permanent Magnet Synchronous Motors under Unbalanced Magnetic Pull
Abstract
:1. Introduction
2. Analysis of the Radial Air-Gap Flux Density in a Permanent Magnet Synchronous Motor (PMSM)
2.1. Radial Air-Gap Flux Density without Eccentricity
2.2. Correction Factor of Relative Permeance
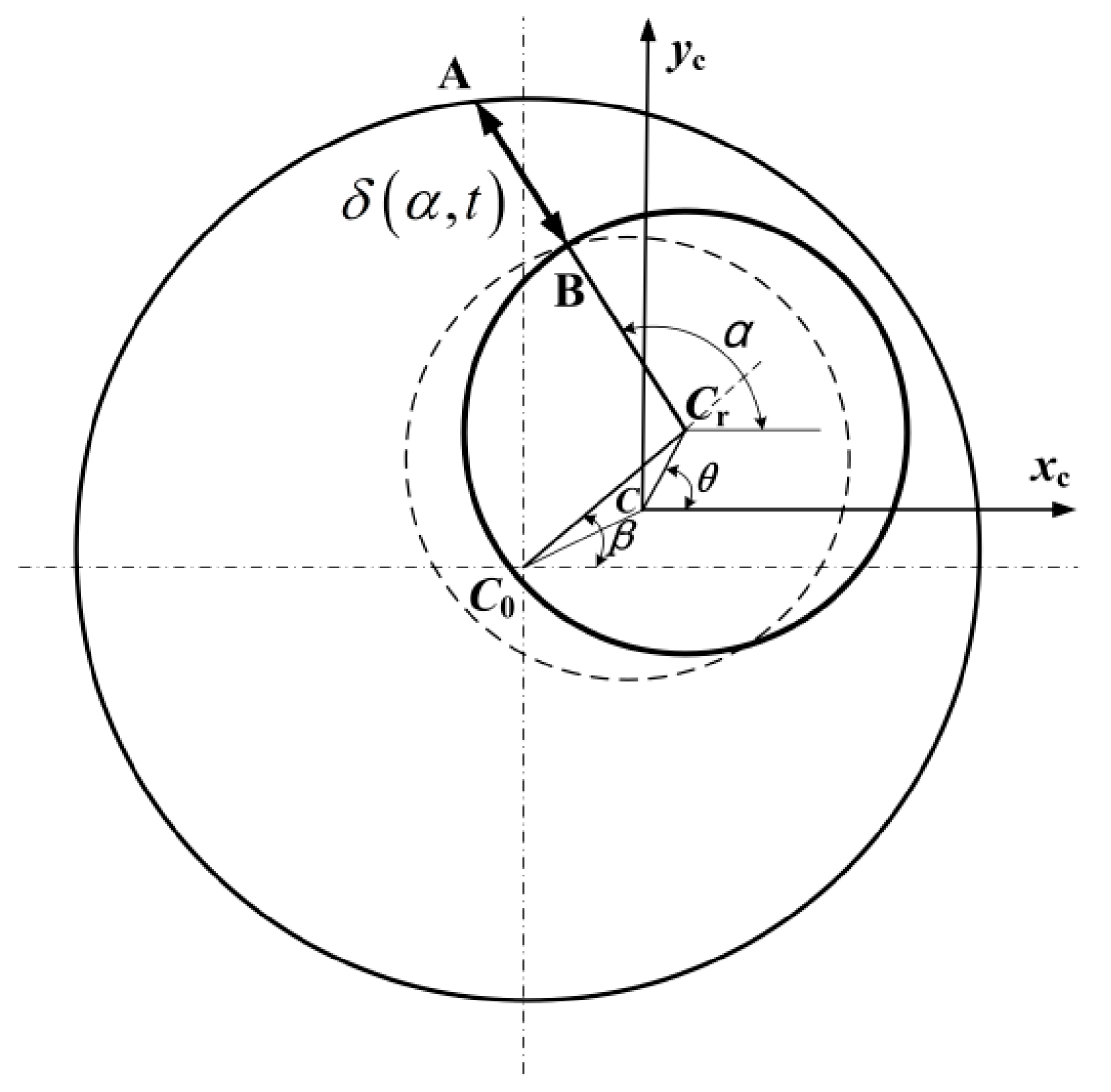
2.3. Radial Air-Gap Flux Density with Eccentricity
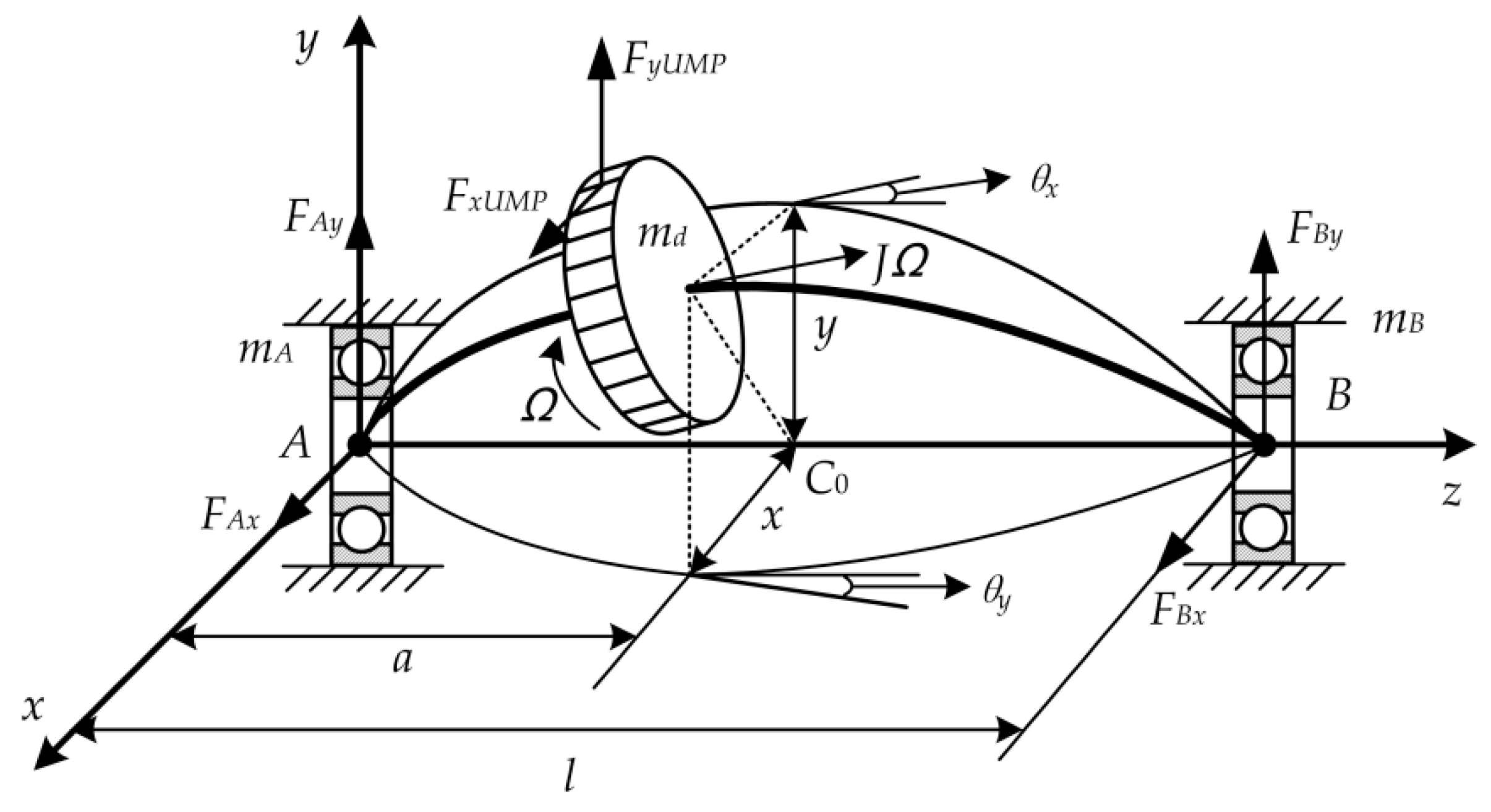
3. Dynamic Model of a Rotor Bearing System
3.1. Unbalanced Magnetic Pull (UMP) Model of Rotor
3.2. Ball-Bearing Forces
3.3. Equations of Motion
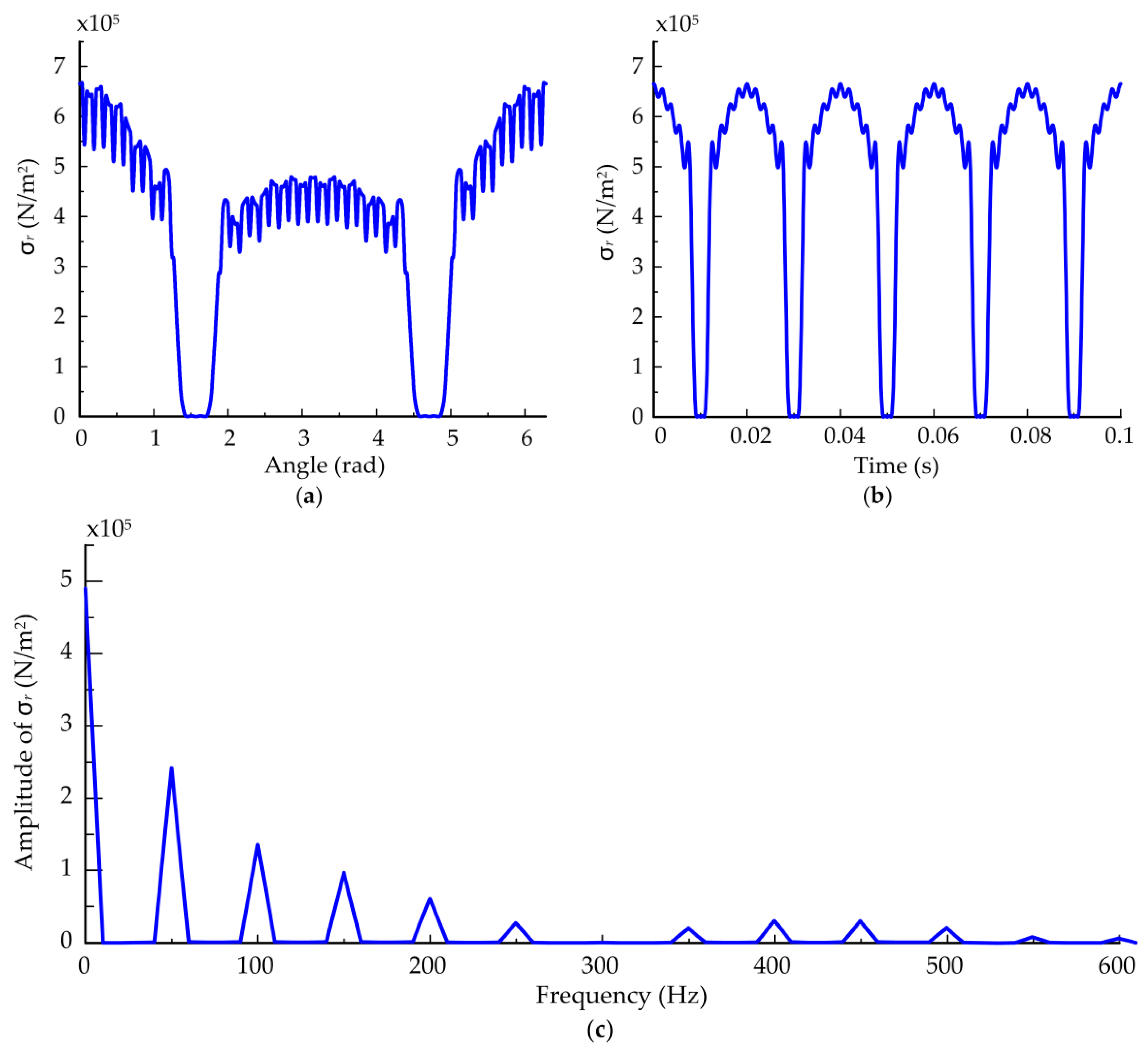
4. Simulation Results and Analysis
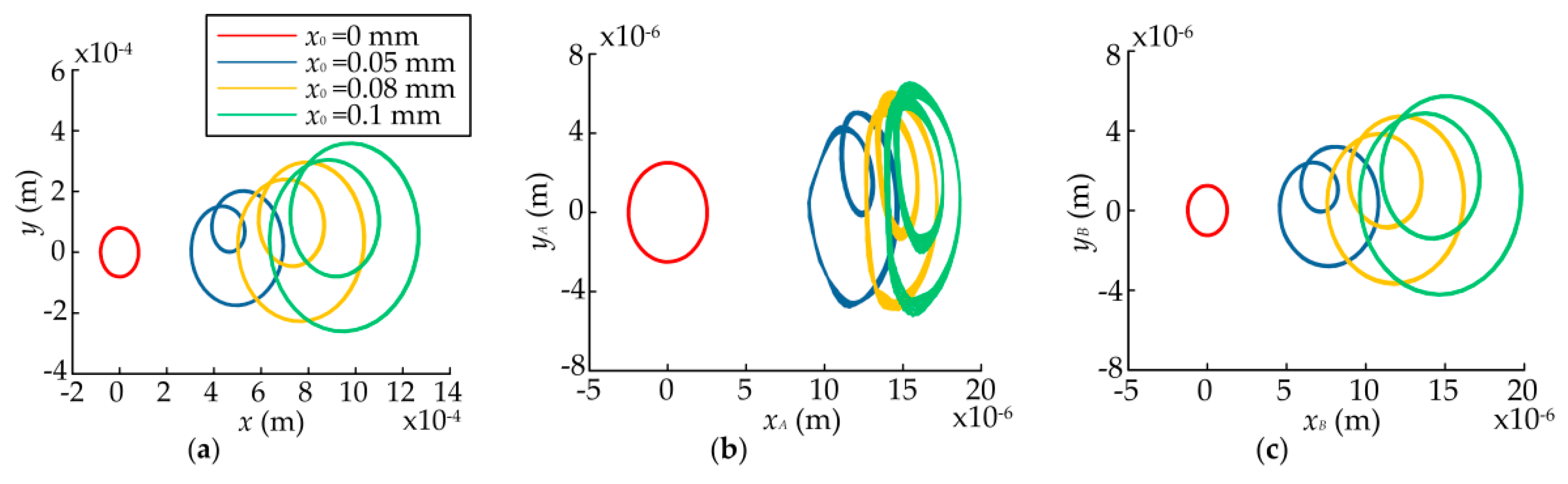
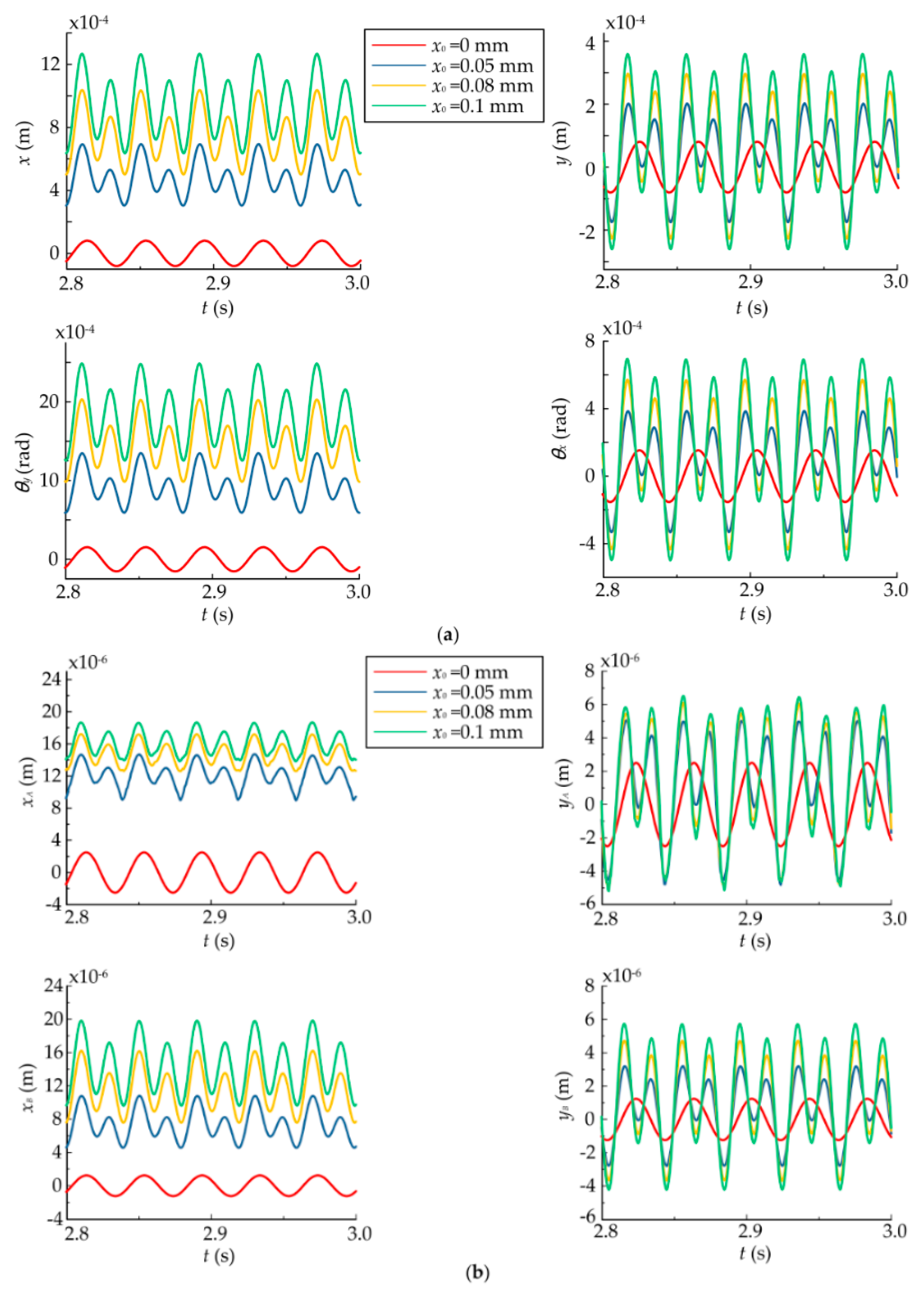
4.1. Effects of Static Displacement Eccentricity
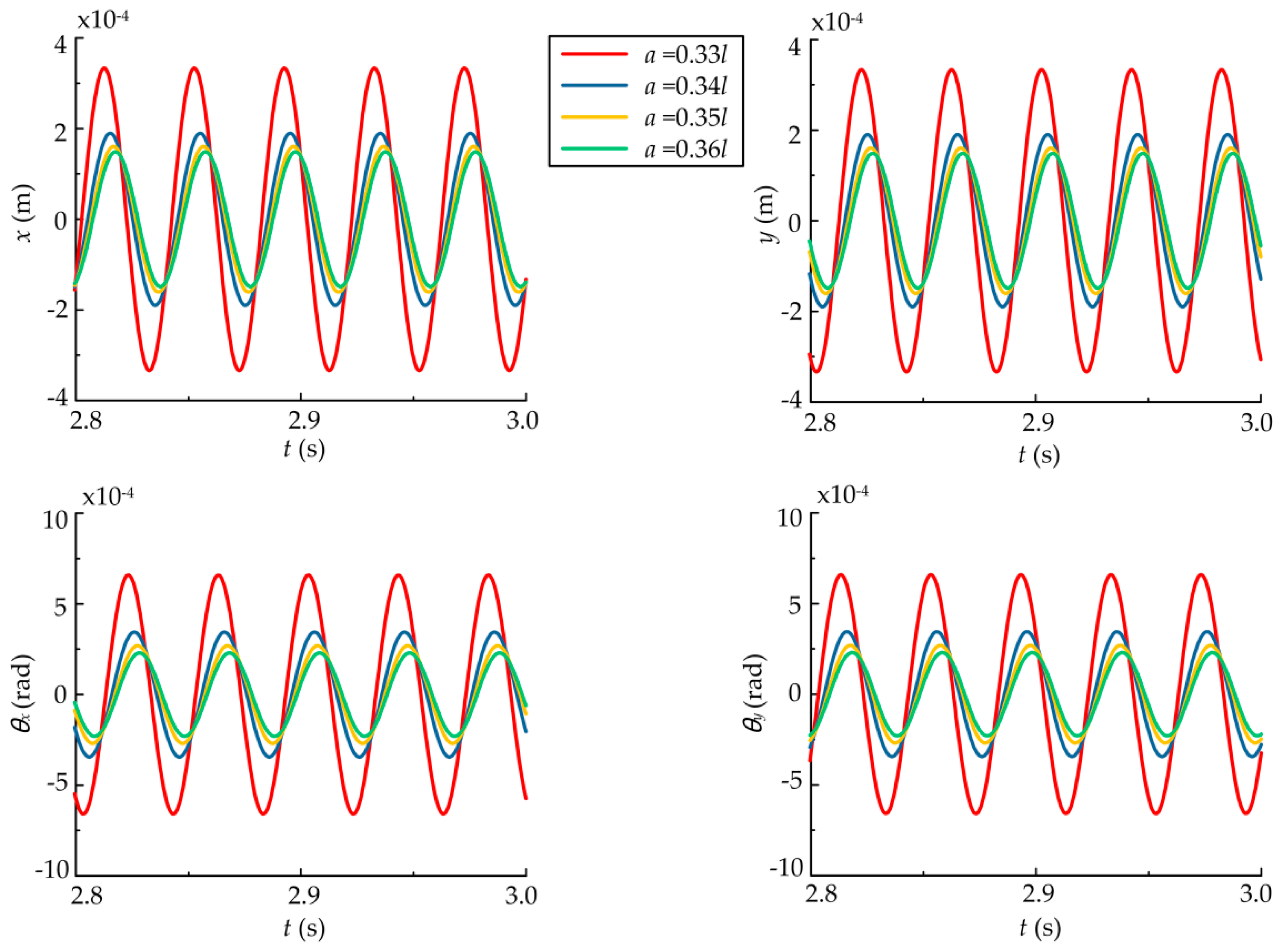
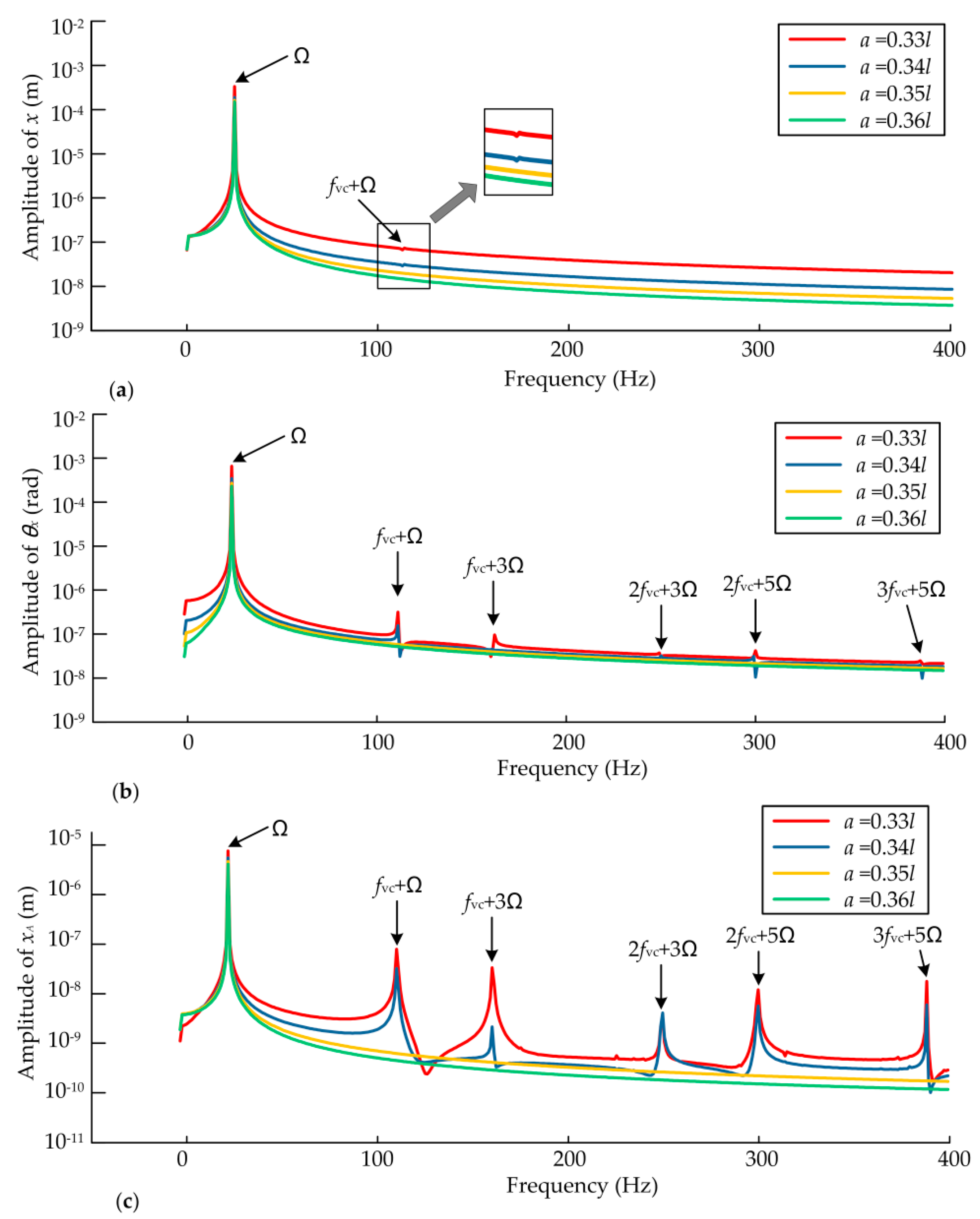
4.2. Effects of Rotor Offset
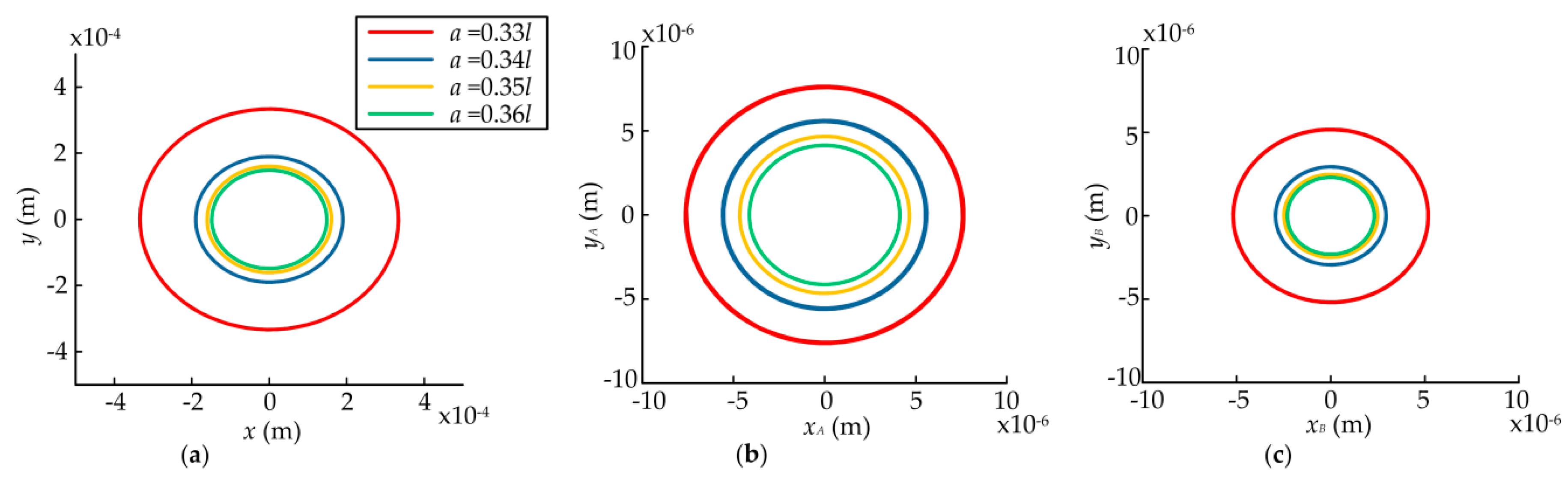
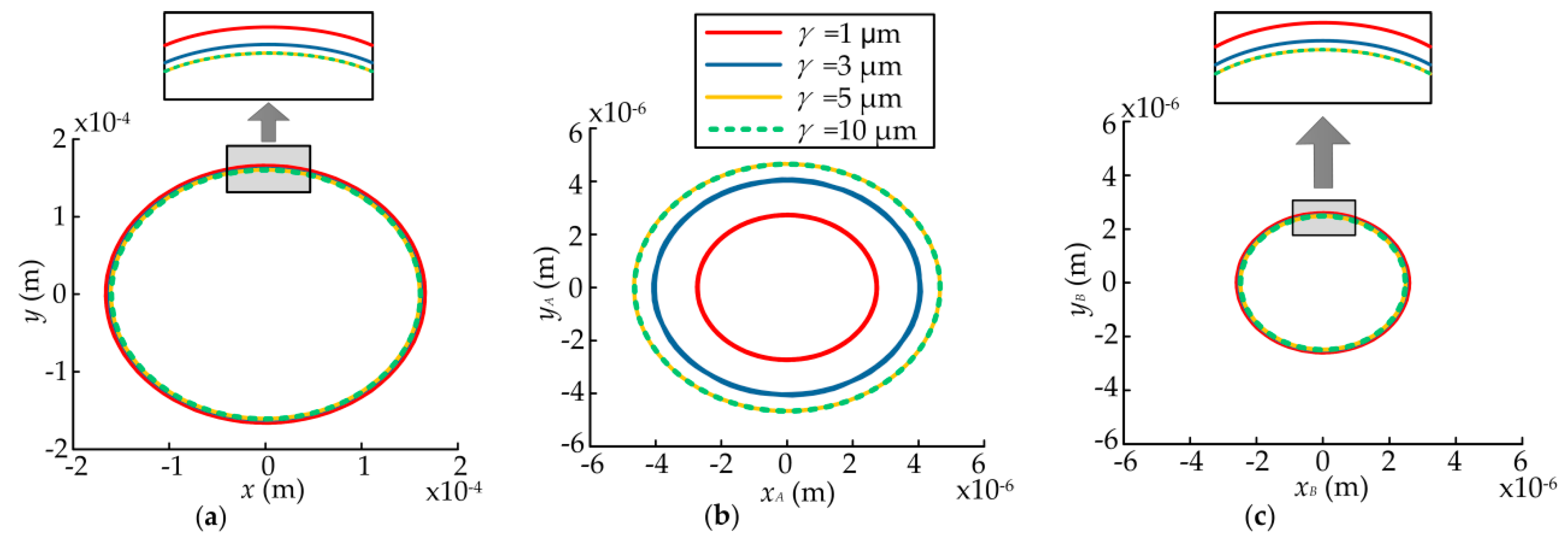
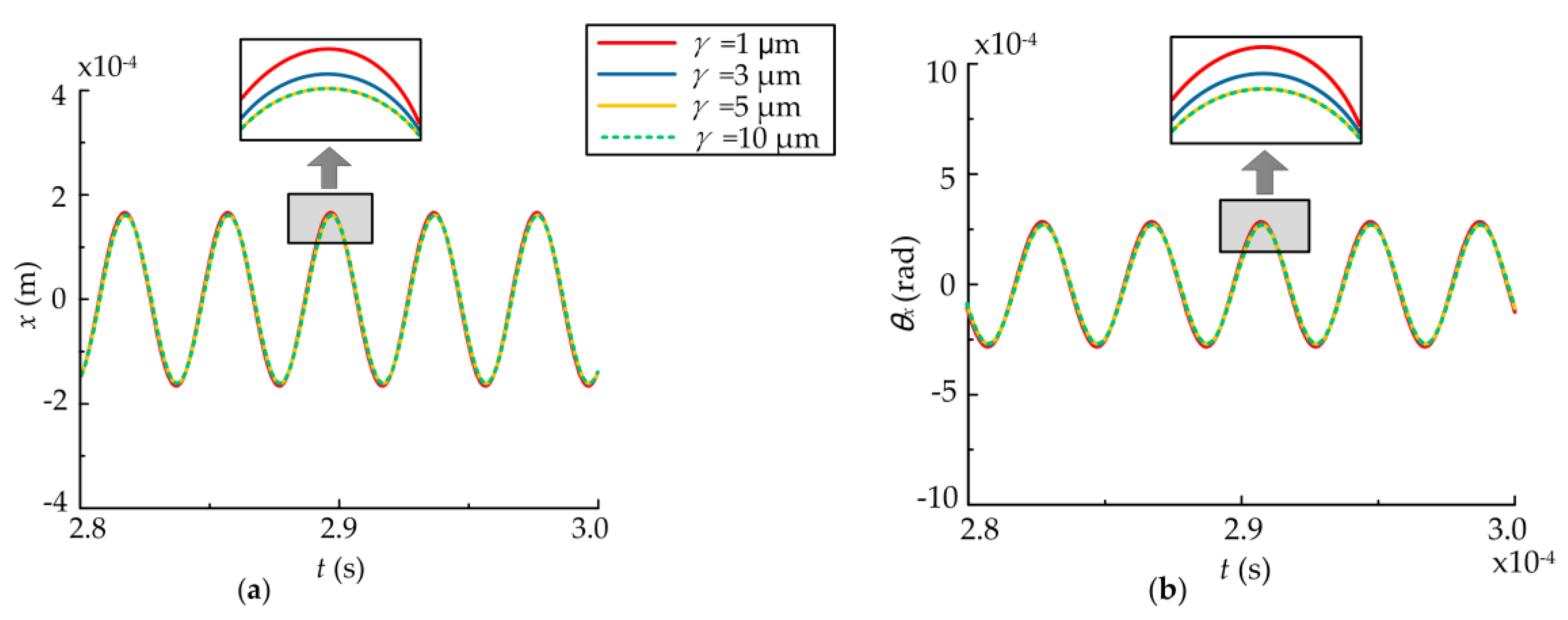
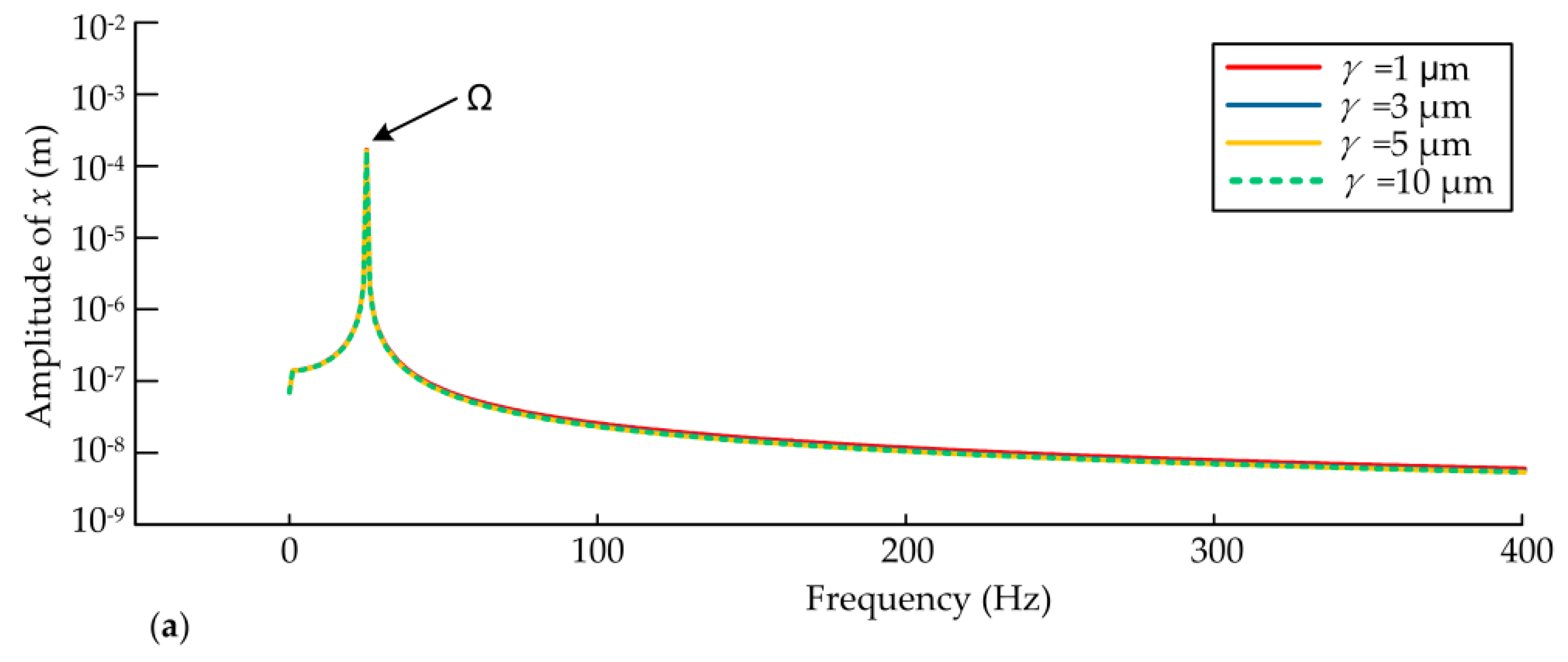
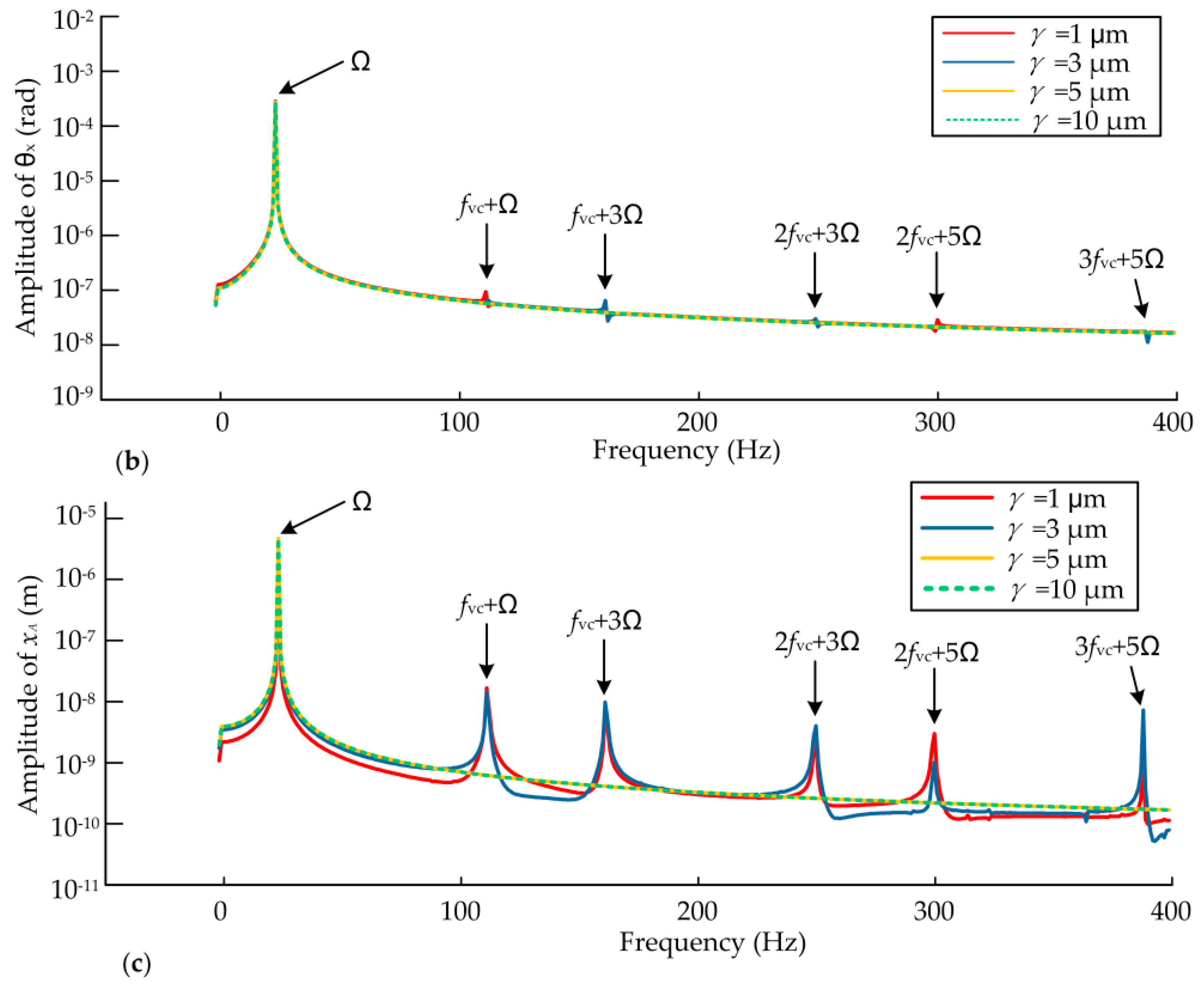
4.3. Effects of the Radial Clearance of Bearings
5. Conclusions
- The static displacement eccentricity has a great effect on the system and the orbits of the rotor and bearings are center circles when the static displacement eccentricity is zero, while they become irregular and lager when the eccentricity exists. The bearing closer to the rotor can be affected more easily when the rotor is not in the middle of the shaft. The dynamic responses increase nonlinearly with the eccentricity and rotor offset due to the effects of UMP and bearing forces. When the radial clearance increases within a certain range, the dynamic responses of the rotor and the bearing farther away from the rotor decrease, while the dynamic responses of the bearing closer to the rotor increase. When the radial clearance reaches a certain value, the dynamic responses of the system will no longer be changed since the effects of the bearings disappear.
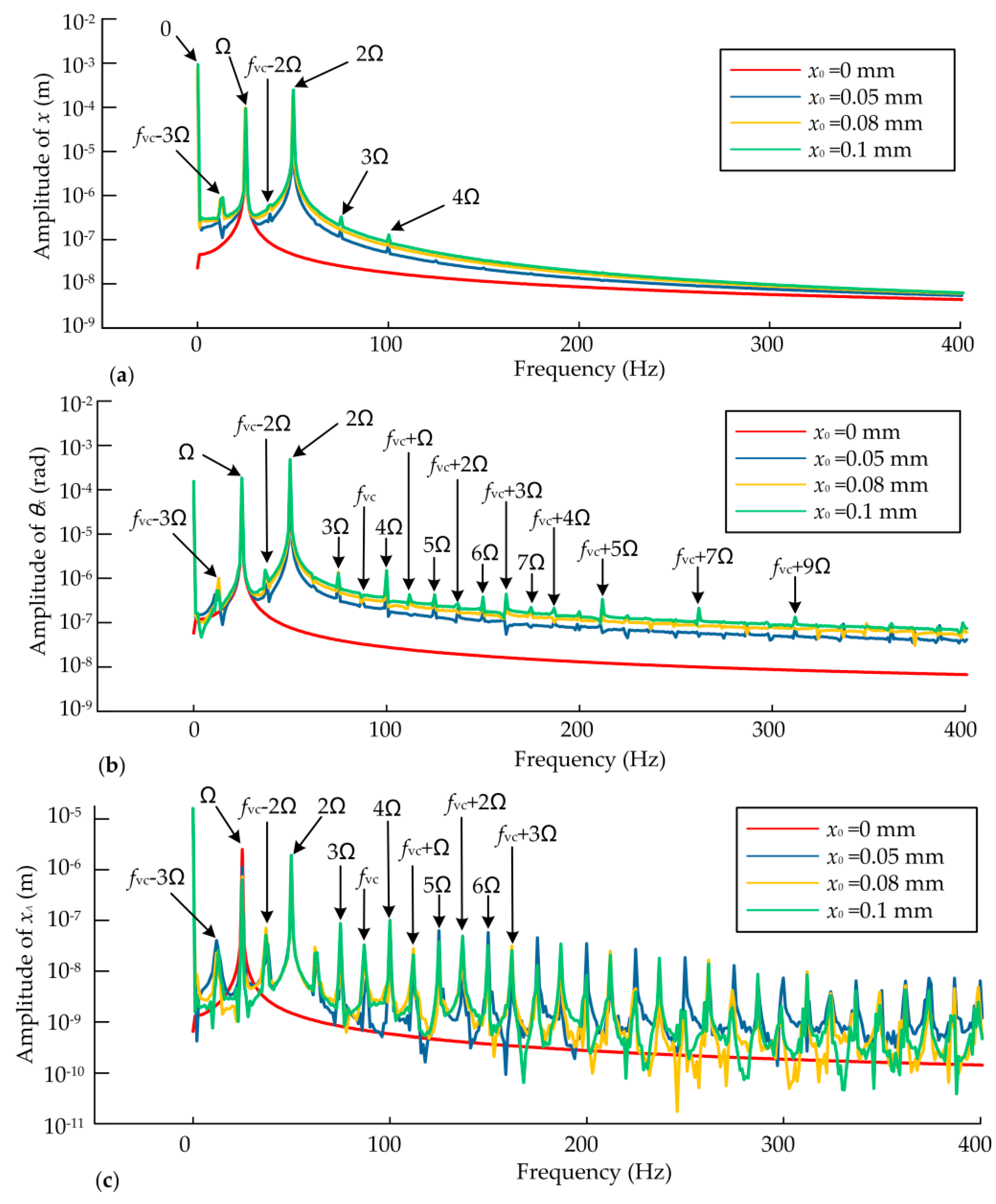
- The bearings have an effect on the system and the coupling effects of the bearing forces, unbalanced mass force and UMP are discovered in this study. The coupling effects exist when the bearing forces are formed, while the coupling effects disappear when the bearing forces are not formed. The dynamic angle responses are affected more obviously by the coupling effects than the displacement responses in the frequency domain.
- The main frequencies of dynamic responses are the rotating frequency and the double rotating frequency when the static displacement eccentricity exists and the frequency components of the bearing are more complex, while the main frequency is the rotating frequency when the static eccentricity is zero. Moreover, high integer multiples of rotating frequency can be found with the increase of static displacement eccentricity. The combination of VC frequency and odd multiples of rotating frequency can be observed more obviously than other combined frequencies due to the coupling effects, and the coupling effects on the bearings are greater.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Mehrjou, M.R.; Mariun, N.; Misron, N.; Radzi, M.A.M.; Musa, S. Broken Rotor Bar Detection in LS-PMSM Based on Startup Current Analysis Using Wavelet Entropy Features. Appl. Sci. 2017, 7, 845. [Google Scholar] [CrossRef]
- Yang, H.; Chen, Y. Influence of Radial Force Harmonics with Low Mode Number on Electromagnetic Vibration of PMSM. IEEE Trans. Energy Convers. 2014, 29, 38–45. [Google Scholar] [CrossRef]
- Kuo, C.; Liu, C.; Chang, H.; Lin, K. Implementation of a Motor Diagnosis System for Rotor Failure Using Genetic Algorithm and Fuzzy Classification. Appl. Sci. 2017, 7, 31. [Google Scholar] [CrossRef]
- Pennacchi, P.; Frosini, L. Dynamical Behaviour of a Three-phase Generator due to Unbalanced Magnetic Pull. IEE Proc. Electr. Power Appl. 2005, 152, 1389–1400. [Google Scholar] [CrossRef] [Green Version]
- Gustavsson, R.K.; Aidanpaa, J. The Influence of Nonlinear Magnetic Pull on Hydropower Generator Rotors. J. Sound Vib. 2006, 297, 551–562. [Google Scholar] [CrossRef]
- Zhu, Z.Q.; Ishak, D.; Howe, D.; Chen, J. Unbalanced Magnetic Forces in Permanent-Magnet Brushless Machines with Diametrically Asymmetric Phase Windings. IEEE Trans. Ind. Appl. 2007, 43, 1544–1553. [Google Scholar] [CrossRef]
- Calleecharan, Y.; Aidanpaa, J.O. Stability Analysis of an Hydropower Generator Subjected to Unbalanced Magnetic Pull. IET Sci. Meas. Technol. 2011, 5, 231–243. [Google Scholar] [CrossRef]
- Ebrahimi, B.M.; Roshtkhari, M.J.; Faiz, J.; Khatami, S.V. Advanced Eccentricity Fault Recognition in Permanent Magnet Synchronous Motors Using Stator Current Signature Analysis. IEEE Trans. Ind. Electron. 2014, 61, 2041–2052. [Google Scholar] [CrossRef]
- Behrend, A.B. On the Mechanical Forces in Dynamos Caused by Magnetic Attraction. Trans. Am. Inst. Electr. Eng. 1900, 17, 613–633. [Google Scholar] [CrossRef]
- Covo, C. Unbalanced Magnetic Pull in Induction Motors with Eccentric Rotors. Trans. Am. Inst. Electr. Eng. 1954, 73, 1421–1425. [Google Scholar] [CrossRef]
- Funke, H.; Maciosehek, G. Influence of Unbalanced Magnetic Pull on the Running of Synchronous Machine. Electric 1965, 19, 233–238. [Google Scholar]
- Belmans, R.; Vandenput, A.; Geysen, W. Calculation of the Flux Density and the Unbalanced Pull in Two Pole Induction Machines. Arch. Elektrotech. 1987, 70, 151–161. [Google Scholar] [CrossRef]
- Guo, D.; Chu, F.; Chen, D. The Unbalanced Magnetic Pull and its Effects on Vibration in a Three-Phase Generator with Eccentric Rotor. J. Sound Vib. 2002, 254, 297–312. [Google Scholar] [CrossRef]
- Pennacchi, P. Computational Model for Calculating the Dynamical Behaviour of Generators Caused by Unbalanced Magnetic Pull and Experimental Validation. J. Sound Vib. 2008, 312, 332–353. [Google Scholar] [CrossRef] [Green Version]
- Pennacchi, P. Nonlinear Effects Due to Electromechanical Interaction in Generators with Smooth Poles. Nonlinear Dyn. 2009, 57, 607–622. [Google Scholar] [CrossRef]
- Im, H.; Hong, H.Y.; Chung, J. Dynamic Analysis of a BLDC Motor with Mechanical and Electromagnetic Interaction Due to Air Gap Variation. J. Sound Vib. 2011, 330, 1680–1691. [Google Scholar] [CrossRef]
- Wu, B.; Sun, W.; Li, Z.; Li, Z. Circular Whirling and Stability Due to Unbalanced Magnetic Pull and Eccentric Force. J. Sound Vib. 2011, 330, 4949–4954. [Google Scholar] [CrossRef]
- Chen, X.; Yuan, S.; Peng, Z. Nonlinear Vibration for PMSM Used in HEV Considering Mechanical and Magnetic Coupling Effects. Nonlinear Dyn. 2015, 80, 541–552. [Google Scholar] [CrossRef]
- Lundström, N.L.P.; Aidanpaa, J. Dynamic Consequences of Electromagnetic Pull Due to Deviations in Generator Shape. J. Sound Vib. 2007, 301, 207–225. [Google Scholar] [CrossRef]
- Xiang, C.; Liu, F.; Liu, H.; Han, L.; Zhang, X. Nonlinear Dynamic Behaviors of Permanent Magnet Synchronous Motors in Electric Vehicles Caused by Unbalanced Magnetic Pull. J. Sound Vib. 2016, 371, 277–294. [Google Scholar] [CrossRef]
- Zhang, L.; Ma, Z.; Song, B. Dynamic Characteristics of a Rub-Impact Rotor-Bearing System for Hydraulic Generating Set Under Unbalanced Magnetic Pull. Arch. Appl. Mech. 2013, 83, 817–830. [Google Scholar] [CrossRef]
- Gan, C.; Wang, Y.; Yang, S.; Cao, Y. Nonparametric Modeling and Vibration Analysis of Uncertain Jeffcott Rotor with Disc Offset. Int. J. Mech. Sci. 2014, 78, 126–134. [Google Scholar] [CrossRef]
- Xu, X.; Han, Q.; Chu, F. A Four Degrees-Of-Freedom Model for a Misaligned Electrical Rotor. J. Sound Vib. 2015, 358, 356–374. [Google Scholar] [CrossRef]
- Zhu, Z.Q.; Howe, D. Instantaneous Magnetic Field Distribution in Brushless Permanent Magnet DC Motors. I. Open-Circuit Field. IEEE Trans. Magn. 1993, 29, 124–135. [Google Scholar] [CrossRef]
- Zhu, Z.Q.; Howe, D. Instantaneous Magnetic Field Distribution in Brushless Permanent Magnet DC Motors. II. Armature-Reaction Field. IEEE Trans. Magn. 1993, 29, 136–142. [Google Scholar] [CrossRef]
- Zhu, Z.Q.; Howe, D. Instantaneous Magnetic Field Distribution in Brushless Permanent Magnet DC Motors. III. Effect of Stator Slotting. IEEE Trans. Magn. 1993, 29, 143–151. [Google Scholar] [CrossRef]
- Zhu, Z.Q.; Howe, D. Instantaneous Magnetic Field Distribution in Permanent Magnet Brushless DC Motors. IV. Magnetic Field on Load. IEEE Trans. Magn. 1993, 29, 152–158. [Google Scholar] [CrossRef]
- Ma, C.; Zuo, S. Black-Box Method of Identification and Diagnosis of Abnormal Noise Sources of Permanent Magnet Synchronous Machines for Electric Vehicles. IEEE Trans. Ind. Electron. 2014, 61, 5538–5549. [Google Scholar] [CrossRef]
- Sahraoui, M.; Ghoggal, A.; Zouzou, S.E.; Benbouzid, M.E. Dynamic Eccentricity in Squirrel Cage Induction Motors-Simulation and Analytical Study of its Spectral Signatures on Stator Currents. Simul. Model. Pract. Theory 2008, 16, 1503–1513. [Google Scholar] [CrossRef]
- Dorrell, D.G. Sources and Characteristics of Unbalanced Magnetic Pull in Three-Phase Cage Induction Motors with Axial-Varying Rotor Eccentricity. IEEE Trans. Ind. Appl. 2011, 47, 12–24. [Google Scholar] [CrossRef]
- Hou, L.; Chen, Y.; Cao, Q.; Zhang, Z. Turning Maneuver Caused Response in an Aircraft Rotor-Ball Bearing System. Nonlinear Dyn. 2015, 79, 229–240. [Google Scholar] [CrossRef]
- Genta, G. Dynamics of Rotating Systems; Springer: New York, NY, USA, 2005. [Google Scholar]
- Zhang, Z.; Chen, Y.; Cao, Q. Bifurcations and Hysteresis of Varying Compliance Vibrations in the Primary Parametric Resonance for a Ball Bearing. J. Sound Vib. 2015, 350, 171–184. [Google Scholar] [CrossRef]
- Tiwari, M.; Gupta, K.; Prakash, O. Effect of Radial Internal Clearance of a Ball, Bearing On the Dynamics of a Balanced Horizontal Rotor. J. Sound Vib. 2000, 238, 723–756. [Google Scholar] [CrossRef]
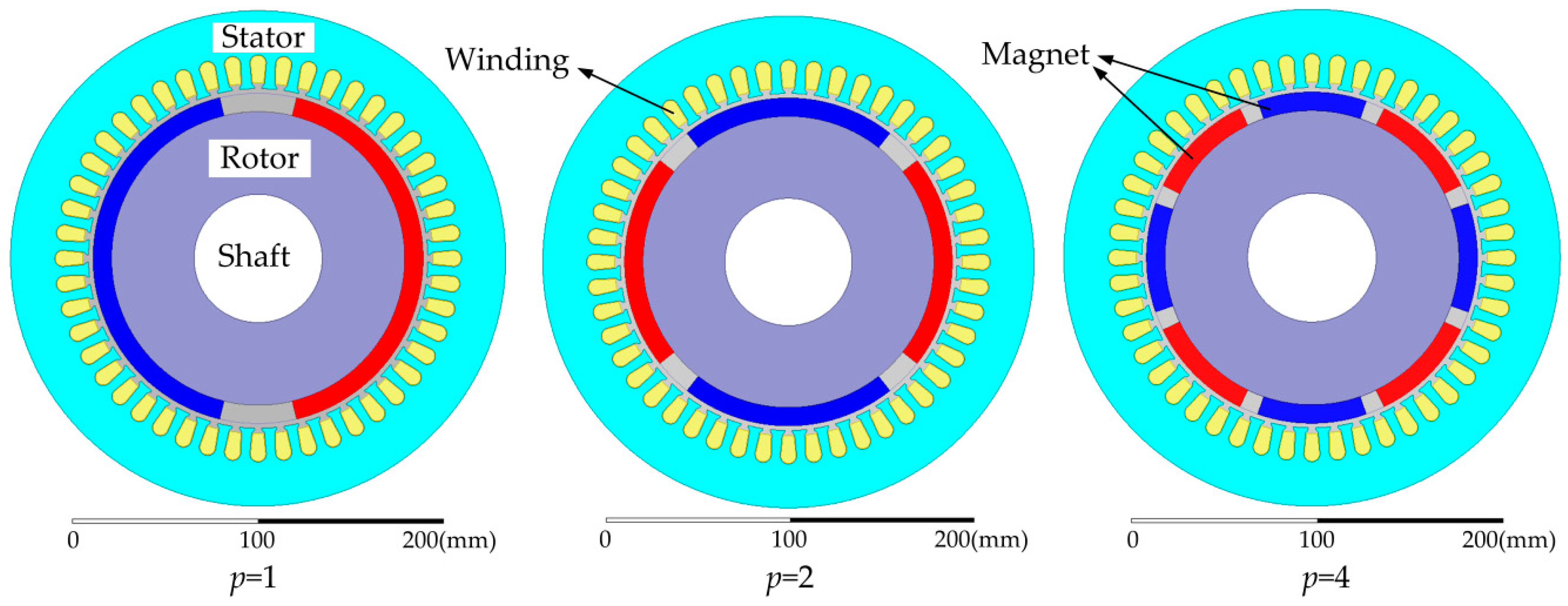

| Parameter | Value |
|---|---|
| Outer radius of the rotor core (Rr) | 80 mm |
| Inner radius of the stator core (Rs) | 92.5 mm |
| Pole-arc/pole-pitch ratio (αp) | 0.85 |
| Slot-opening (b0) | 4 mm |
| Vacuum permeability () | 4π × 10−7 H/m |
| Current amplitude (I) | 10 A |
| Slot number (Z) | 48 |
| Magnet thickness (hm) | 10 mm |
| Magnet remanence (Br) | 1.25 T |
| Relative recoil permeability () | 1.05 |
| Rotor rotational speed (n) | 1500 r/min |
| Length of the stator core | 165 mm |
| Outer radius of the stator core | 135 mm |
| Steel type of the stator core | DW315_50 |
| Slot type of the stator core | No. 2 |
| Number of winding layers | 1 |
| Winding type | Whole-Coiled |
| Number of parallel branches of stator winding | 1 |
| Conductors per slot | 50 |
| Inner radius of the rotor core | 35 mm |
| Steel type of the rotor core | DW315_50 |
| Length of the rotor core | 165 mm |
| Stacking factor of the rotor core | 0.95 |
| mA, mB, mass of the bearings | md, mass of the rotor |
| a, distance between the rotor and the left bearing | l, length of the shaft |
| (x, y), position of rotor in coordinate system | (θx, θy), rotational angles of rotor |
| (xA, yA), position of left bearing in coordinate system | e0, mass eccentricity of the rotor |
| (xB, yB), position of right bearing in coordinate system | Ω, rotating speed of the rotor |
| Jd, moment of inertia of rotor | Jp, polar moment of inertia of rotor |
| E, Young’s modulus of the shaft | I, moment of inertia of shaft |
| c, damping of rotor | cb, damping of bearings |
| Parameter | Value |
|---|---|
| Outer race radius (Ro) | 63.9 mm |
| Inner race radius (Ri) | 40.1 mm |
| Number of balls (Nb) | 9 |
| Radial clearance (γ) | 10 μm |
| Hertzian contact stiffness (Cb) | 1.334 × 1010 N/m3/2 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, A.; Bai, Y.; Yang, B.; Li, H. Analysis of Nonlinear Vibration in Permanent Magnet Synchronous Motors under Unbalanced Magnetic Pull. Appl. Sci. 2018, 8, 113. https://doi.org/10.3390/app8010113
Zhang A, Bai Y, Yang B, Li H. Analysis of Nonlinear Vibration in Permanent Magnet Synchronous Motors under Unbalanced Magnetic Pull. Applied Sciences. 2018; 8(1):113. https://doi.org/10.3390/app8010113
Chicago/Turabian StyleZhang, Ao, Yan Bai, Bo Yang, and He Li. 2018. "Analysis of Nonlinear Vibration in Permanent Magnet Synchronous Motors under Unbalanced Magnetic Pull" Applied Sciences 8, no. 1: 113. https://doi.org/10.3390/app8010113
APA StyleZhang, A., Bai, Y., Yang, B., & Li, H. (2018). Analysis of Nonlinear Vibration in Permanent Magnet Synchronous Motors under Unbalanced Magnetic Pull. Applied Sciences, 8(1), 113. https://doi.org/10.3390/app8010113





