Measurement of High Numerical Aperture Cylindrical Surface with Iterative Stitching Algorithm
Abstract
:Featured Application
Abstract
1. Introduction
2. Principles
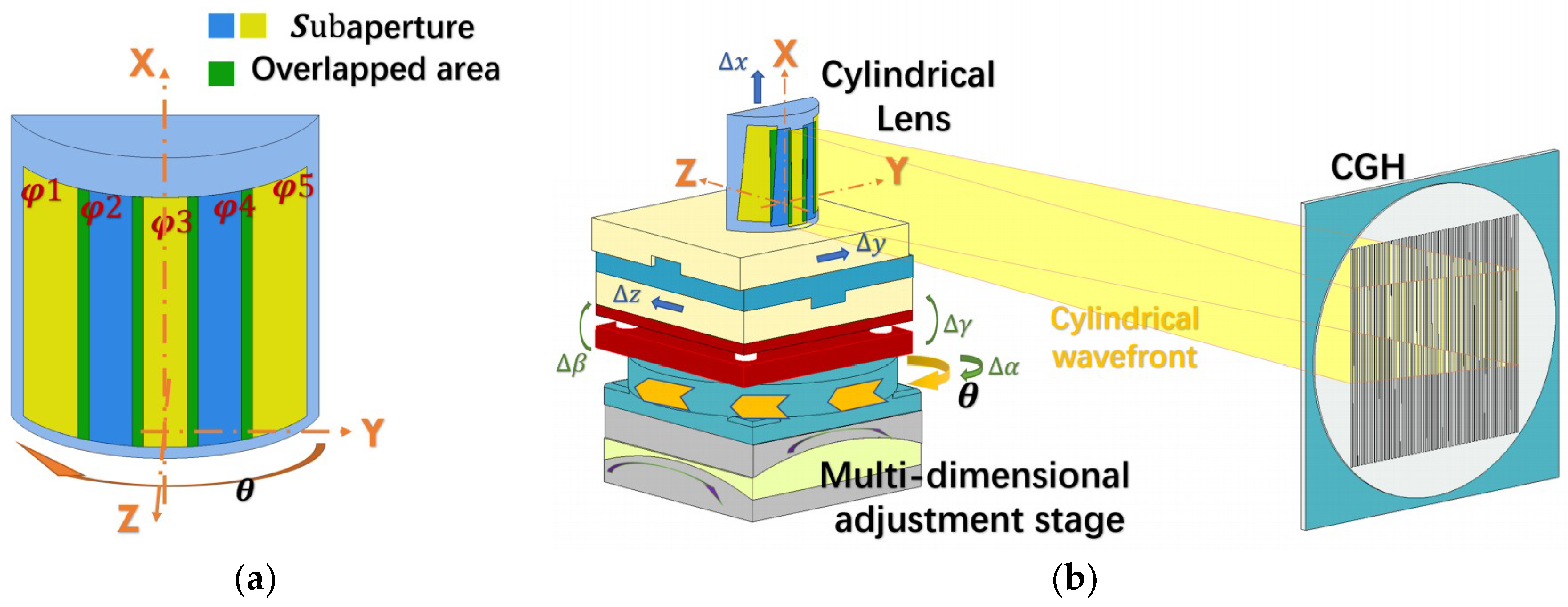
2.1. Experimental Setup and Error Analysis
2.2. Stitching Algorithm for the Cylindrical Lens
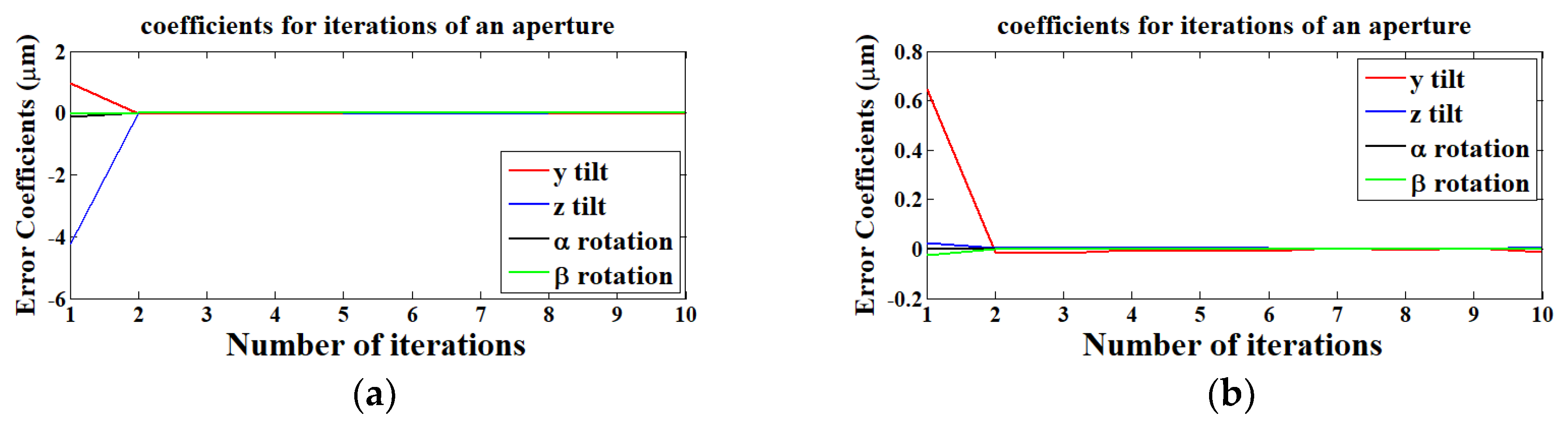
2.3. Iterative Algorithm for the Cylindrical Sub-Aperture
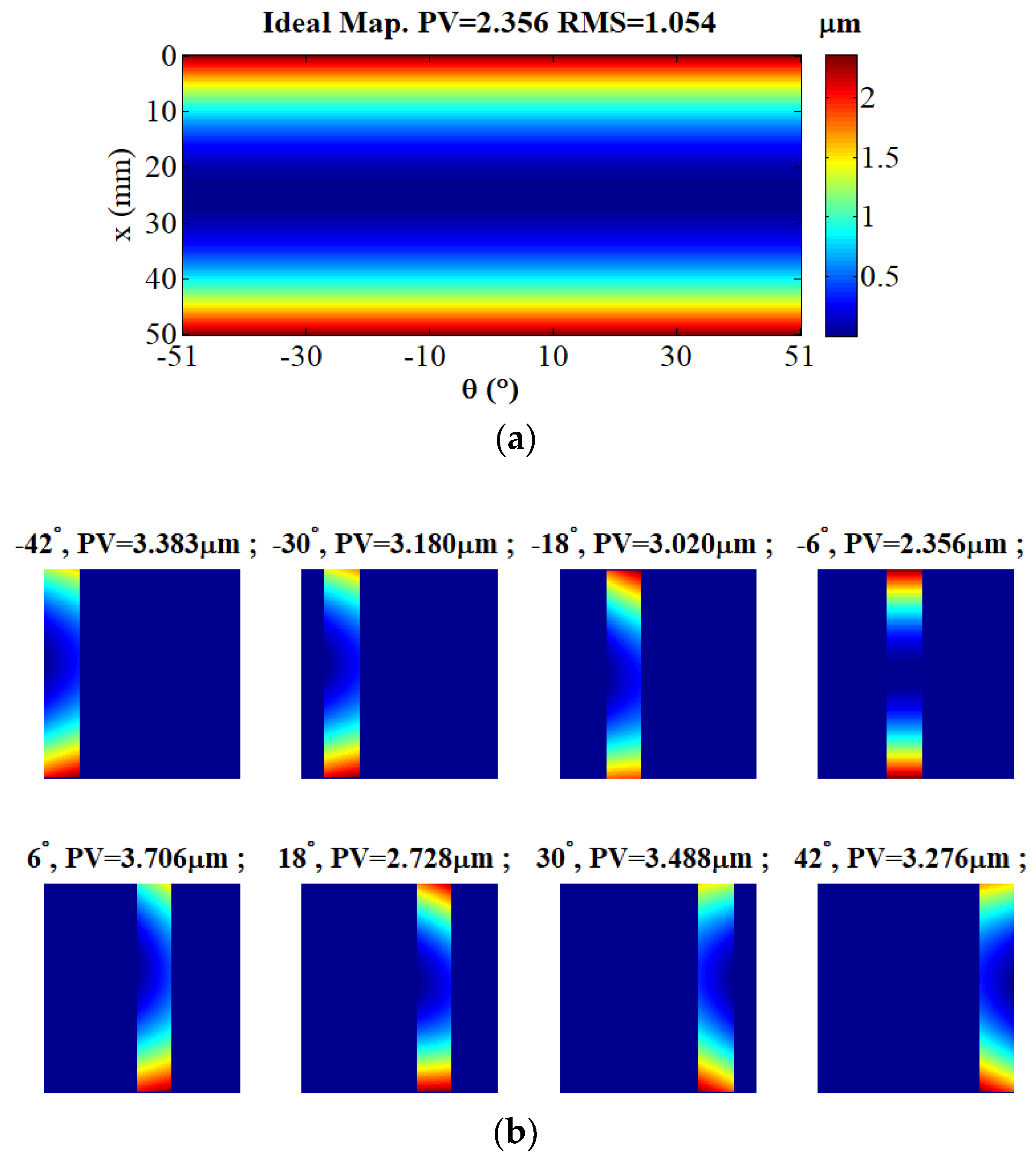
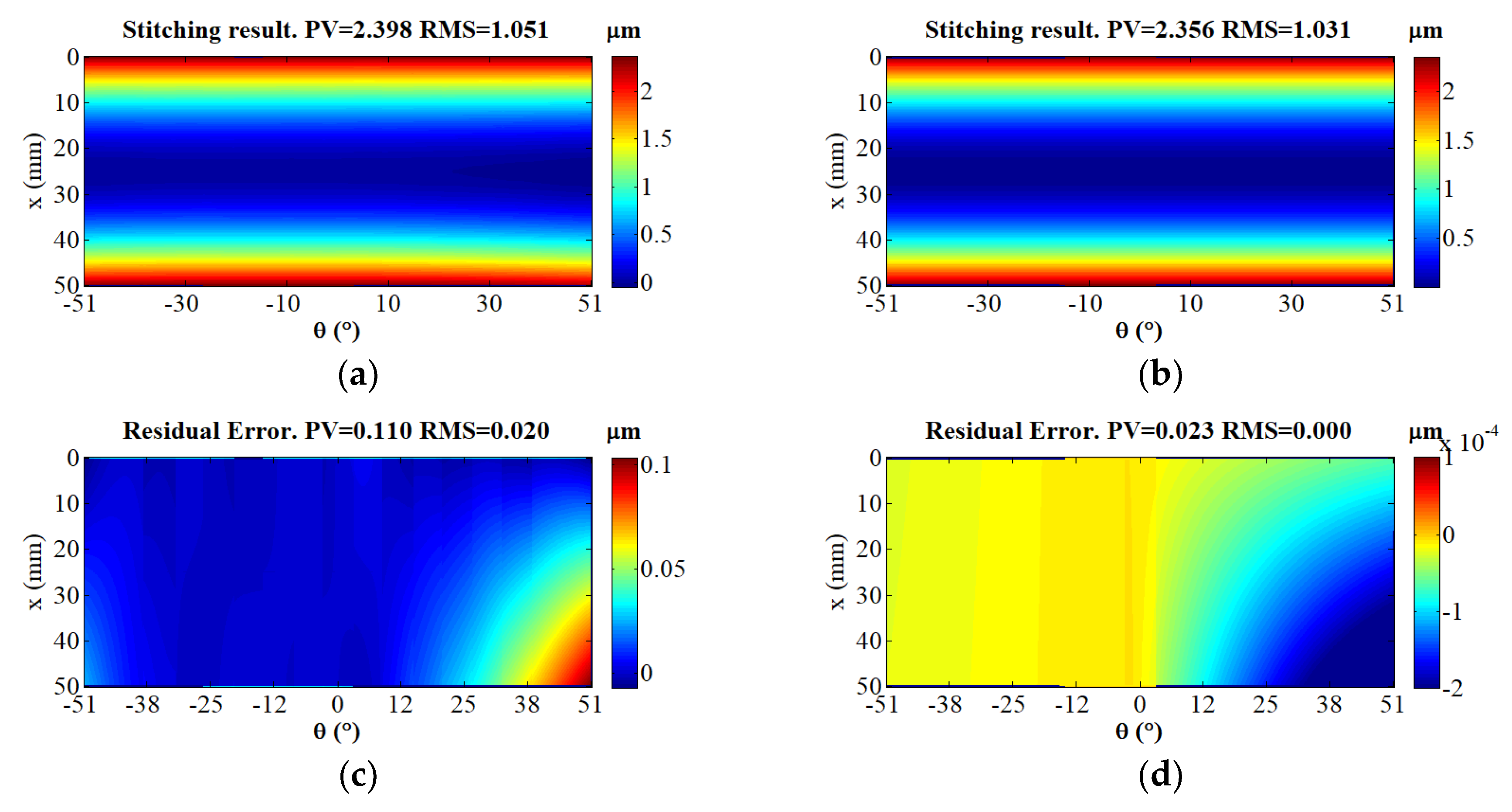
3. Simulation
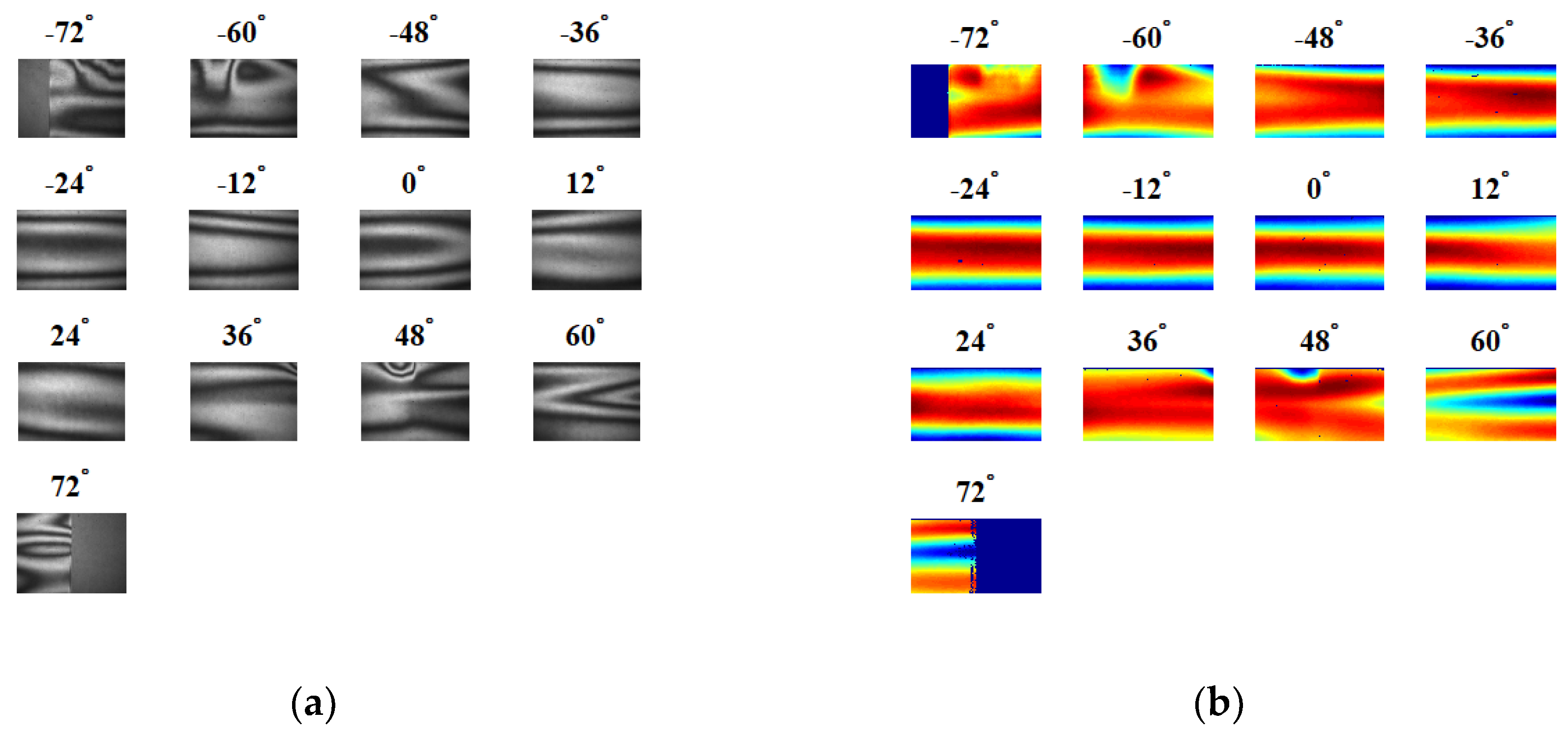
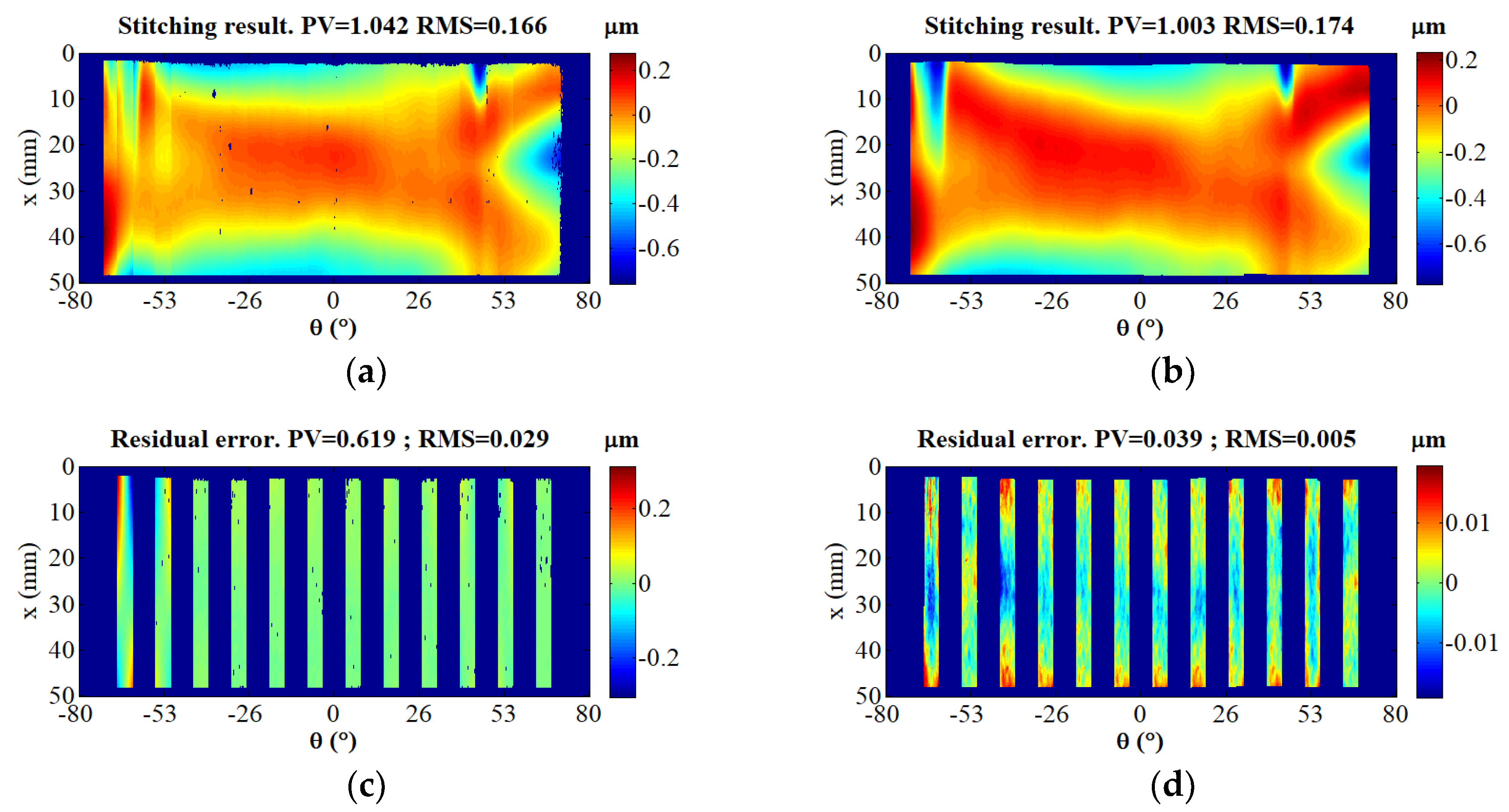
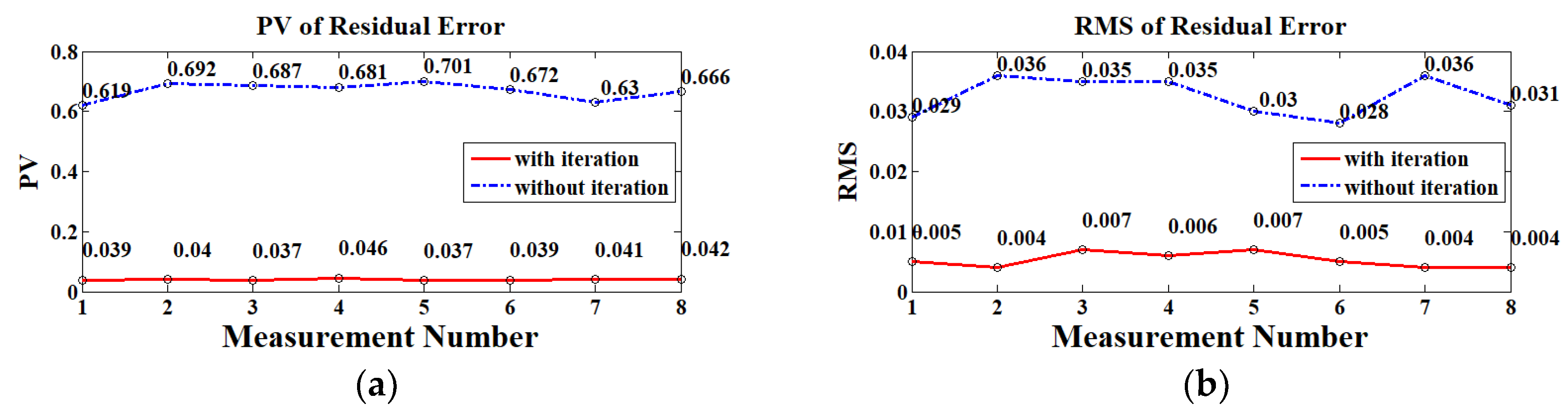
4. Experimental Demonstration
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Fang, F.; Zhang, X.; Hu, X. Cylindrical coordinate machining of optical freeform surfaces. Opt. Express 2008, 16, 7323–7329. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Zeng, Z.; Liu, X.; Fang, F. Compensation strategy for machining optical freeform surfaces by the combined on- and off-machine measurement. Opt. Express. 2015, 23, 24800–24810. [Google Scholar] [CrossRef] [PubMed]
- Ramaswami, H.; Kanagaraj, S.; Anand, S. An inspection advisor for form error in cylindrical features. Int. J. Adv. Manuf. Technol. 2009, 40, 128–143. [Google Scholar] [CrossRef]
- Chen, M.; Cheng, W.; Wang, C.W.W. Multi aperture overlap scanning technique for large-aperture test. Proc. SPIE 1991, 1553, 626–635. [Google Scholar] [CrossRef]
- Otsubo, M.; Okada, K.; Tsujiuchi, J. Measurement of large plane surface shapes by connecting small aperture interferograms. Opt. Eng. 1994, 33, 608–613. [Google Scholar] [CrossRef]
- Peng, J.; Chen, D.; Guo, H.; Zhong, J.; Yu, Y. Variable optical null based on yawing CGH for measuring steep acylindrical surface. Opt. Express 2018, 16, 20306–20318. [Google Scholar] [CrossRef] [PubMed]
- Wen, Y.; Cheng, H.; Tam, H.Y.; Zhou, D. Modified stitching algorithm for annular subaperture stitching interferometry for aspheric surface. Appl. Opt. 2013, 52, 5686–5694. [Google Scholar] [CrossRef] [PubMed]
- Tricard, M.; Kulawiec, A.; Bauer, M. Subaperture stitching interferometry of high-departure aspheres by incorporating a variable optical null. CIRP Ann. Manuf. Technol. 2010, 59, 547–550. [Google Scholar] [CrossRef]
- Hagino, T.; Yokoyama, Y.; Kuriyama, Y.; Haitjema, H. Sphericity measurement using stitching interferometry. Key Eng. Mater. 2012, 523, 883–888. [Google Scholar] [CrossRef]
- Fan, Y.; Struik, K.; Mulders, P.; Velzel, C. Stitching interferometry for the measurement of aspheric surfaces. CIRP Ann. Manuf. Technol. 1997, 46, 459–462. [Google Scholar] [CrossRef]
- Peng, J.; Wang, Q.; Peng, X.; Yu, Y. Stitching interferometry of high numerical aperture cylindrical optics without using a fringe-nulling routine. J. Opt. Soc. Am. A 2015, 32, 1964–1972. [Google Scholar] [CrossRef] [PubMed]
- Peng, J.; Xu, H.; Yu, Y. Stitching interferometry for cylindrical optics with large angular aperture. Meas. Sci. Technol. 2015, 26, 025204. [Google Scholar] [CrossRef]
- Mac Govern, A.J.; Wyant, J.C. Computer Generated Holograms for Testing Optical Elements. Appl. Opt. 1971, 10, 619–624. [Google Scholar] [CrossRef] [PubMed]
- Asfour, J.M.; Poleshchuk, A.G. Asphere testing with a Fizeau interferometer based on a combined computer-generated hologram. J. Opt. Soc. Am. A 2006, 23, 172–178. [Google Scholar] [CrossRef]
- Peng, J.; Yu, Y.; Chen, D. Stitching interferometry of full cylinder by use of the first-order approximation of cylindrical coordinate transformation. Opt. Express 2017, 25. [Google Scholar] [CrossRef] [PubMed]
- Guo, H.; Chen, M. Multiview connection technique for 360-deg 3D measurement. Opt. Eng. 2003, 42, 900–905. [Google Scholar] [CrossRef]
- Valyukh, S.; Osterman, J.; Valyukh, I.; Skarp, K. Characterization of flexible reflective liquid crystal cells. J. SID 2005, 13, 501–506. [Google Scholar] [CrossRef]
- Valyukh, S.; Valyukh, I.; Skarp, K. Spectrophotometric determination of reflective liquid crystal cell parameters. J. Appl. Phys. 2006, 99, 053102. [Google Scholar] [CrossRef]
- Valyukh, S.; Sorokin, S.; Chigrinov, V. Inline quality control of liquid crystal cells. IEEE/OSA J. Disp. Technol. 2015, 11, 1042–1047. [Google Scholar] [CrossRef]



| Error | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Δz (µm) | 1.2 | 0.6 | 2.3 | 0 | −1.9 | −2.1 | 1.1 | 1 |
| Δy (µm) | 0.8 | 1.4 | 1.5 | 0 | 2.6 | 1.4 | −0.5 | −0.3 |
| Δγ (″) | −3.1 | −3.7 | −6.4 | 0 | −5.6 | −6.6 | −2.9 | −1.7 |
| Δβ (″) | −3.5 | −2.3 | 3.7 | 0 | −7.0 | −3.9 | −6.4 | −5.6 |
| Δx (µm) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Δα (″) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| Δz (µm) | 1.2137 | −0.5741 | 0.8844 | 0.7786 | 0.7942 | 0.7232 | 0.5038 | 0.4332 |
| Δy (µm) | −4.4061 | 2.7769 | −0.1865 | 0.0128 | 0.0205 | 0.0574 | 0.1129 | 0.0850 |
| Δγ (″) | −14 | −16 | −0.7 | −0.5 | −0.27 | 0 | 0.2 | 0.3 |
| Δβ (″) | −3.51 | −2.27 | 3.71 | 0 | −7.01 | −3.92 | −6.39 | −5.57 |
| 9 | 10 | 11 | 12 | 13 | ||||
| Δz (µm) | 0 | 0.4166 | −0.6006 | 0.5141 | 0.5827 | |||
| Δy (µm) | 0 | 0.1540 | −0.5952 | 0.3576 | 0.3520 | |||
| Δγ (″) | 0 | −1.6 | −4.4 | −0.3 | −0.3 | |||
| Δβ (″) | 0 | −4.1 | 4.6 | −0.8 | −0.9 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, D.; Peng, J.; Valyukh, S.; Asundi, A.; Yu, Y. Measurement of High Numerical Aperture Cylindrical Surface with Iterative Stitching Algorithm. Appl. Sci. 2018, 8, 2092. https://doi.org/10.3390/app8112092
Chen D, Peng J, Valyukh S, Asundi A, Yu Y. Measurement of High Numerical Aperture Cylindrical Surface with Iterative Stitching Algorithm. Applied Sciences. 2018; 8(11):2092. https://doi.org/10.3390/app8112092
Chicago/Turabian StyleChen, Dingfu, Junzheng Peng, Sergiy Valyukh, Anand Asundi, and Yingjie Yu. 2018. "Measurement of High Numerical Aperture Cylindrical Surface with Iterative Stitching Algorithm" Applied Sciences 8, no. 11: 2092. https://doi.org/10.3390/app8112092
APA StyleChen, D., Peng, J., Valyukh, S., Asundi, A., & Yu, Y. (2018). Measurement of High Numerical Aperture Cylindrical Surface with Iterative Stitching Algorithm. Applied Sciences, 8(11), 2092. https://doi.org/10.3390/app8112092




