A Damage Model for Concrete under Fatigue Loading
Abstract
:1. Introduction
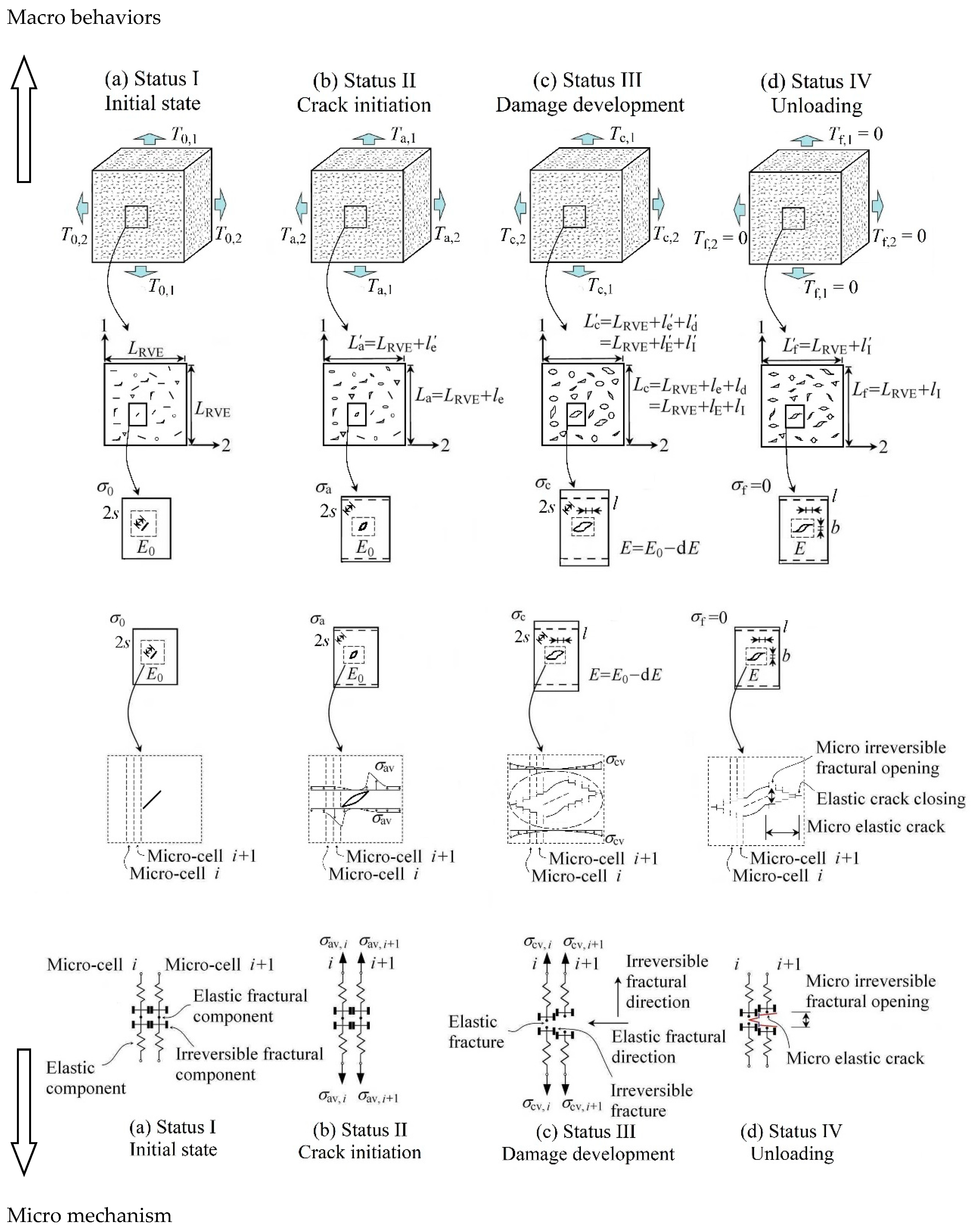
2. Microcrack Mechanism in Concrete under Multi-Axial Loading
2.1. The Definition of the Mode-II Microcracks
2.2. The Causes for the Mode-II Microcracks under Multi-Axial Loading
2.3. Influence of the Mode-II Microcracks on the Irreversible Strains in Concrete
2.4. Irreversible Strains in Concrete under Multi-Axial Loading
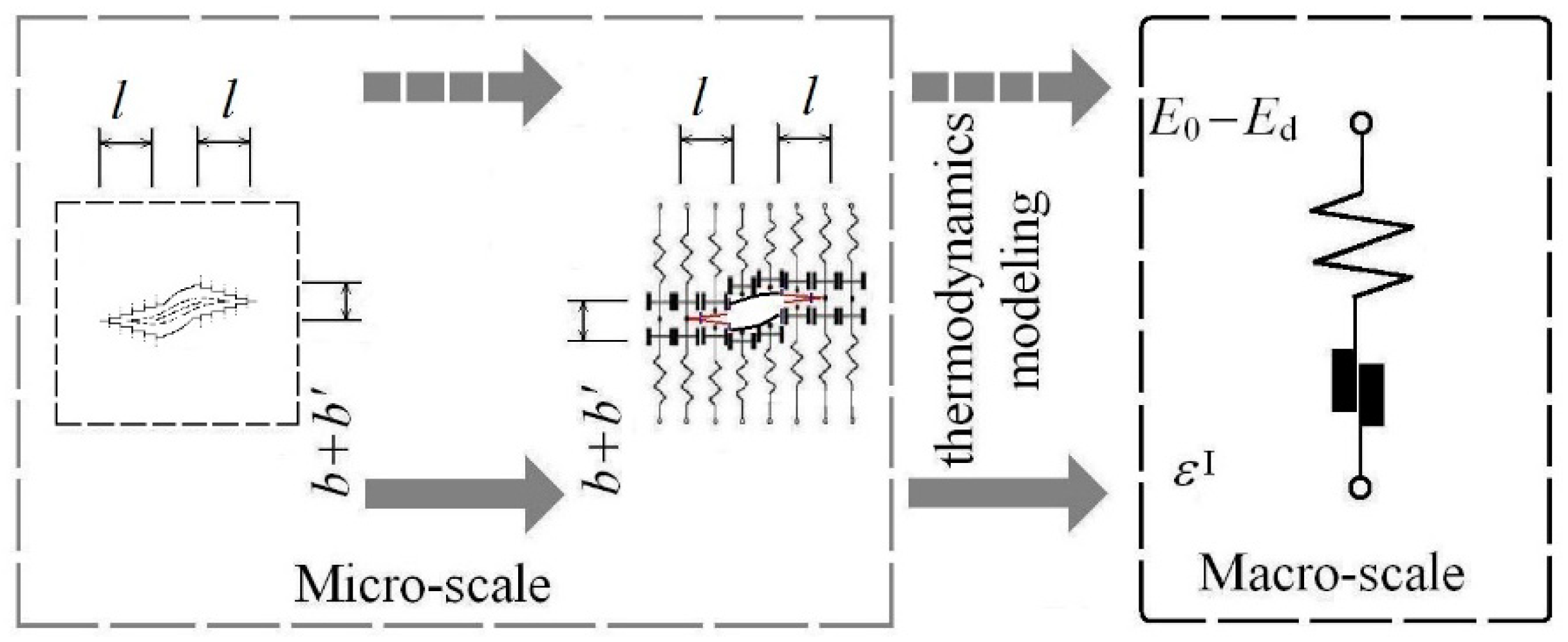
3. Thermodynamics Based Continuum Damage Mechanics Model
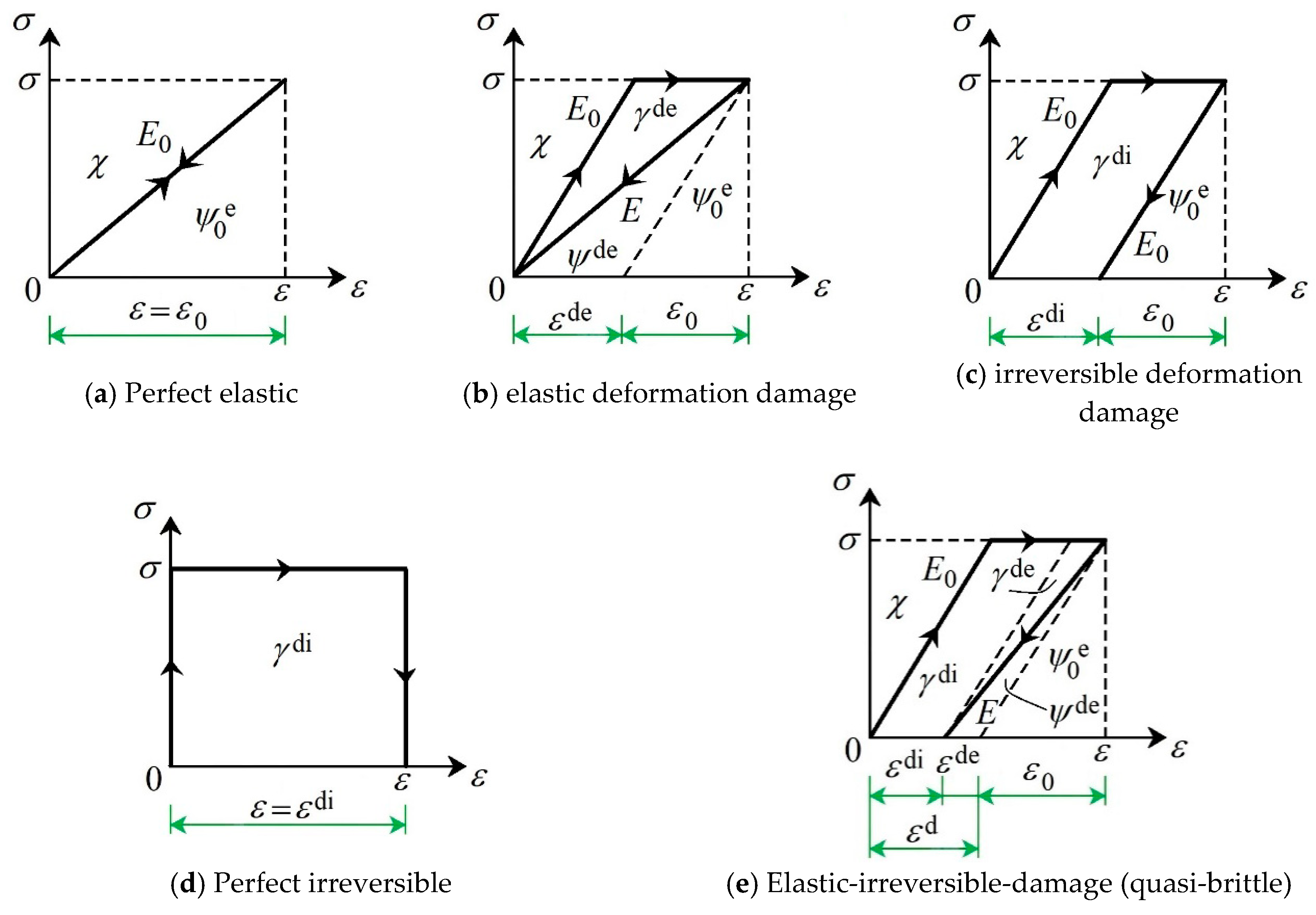
3.1. Thermodynamics Interpretation
3.1.1. Interpretation in First and Second Loading Cycle
3.1.2. Interpretation in nth Loading Cycle
3.1.3. Damage Variable Definition and Its Thermodynamics Interpretation
3.2. Continuum Damage Mechanics Model
4. Verification and Discussions
4.1. Solution Procedure of CDM Model for Concrete under Fatigue Loading
4.2. Behaviors of Concrete under Fatigue Compression with Constant Amplitude
4.3. Behaviors of Concrete under Fatigue Compression with Various Stress Levels
4.4. Behaviors of Concrete under Biaxial Fatigue Compression
4.5. Post-Fatigue Constitutive Behaviors of Concrete under Monotonic Loading
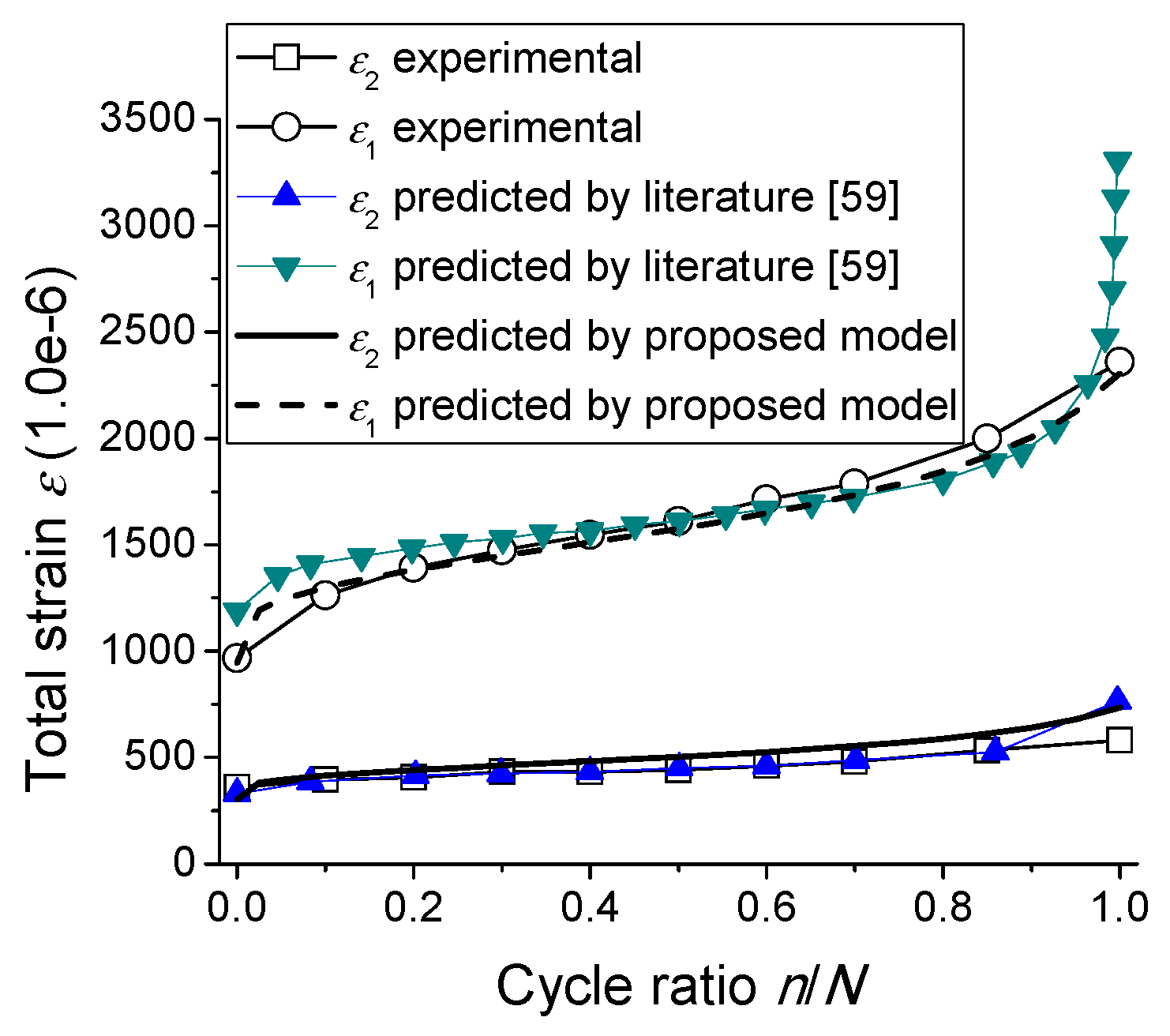
4.6. Comparison among Proposed Model and Other Models
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Damage Variable Definition Based on Thermodynamics
References
- Susmel, L. A unifying methodology to design un-notched plain and short-fibre/particle reinforced concretes against fatigue. Int. J. Fatigue 2014, 61, 226–243. [Google Scholar] [CrossRef]
- Chen, Y.; Ni, J.; Zheng, P.; Azzam, R.; Zhou, Y.; Shao, W. Experimental research on the behaviour of high frequency fatigue in concrete. Eng. Fail. Anal. 2011, 18, 1848–1857. [Google Scholar] [CrossRef]
- Guo, L.P.; Carpinteri, A.; Spagnoli, A.; Wei, S. Effects of mechanical properties of concrete constituents including active mineral admixtures on fatigue behaviours of high performance concrete. Fatigue Fract. Eng. Mater. Struct. 2010, 33, 66–75. [Google Scholar]
- Kim, J.K.; Kim, Y.Y. Experimental study of the fatigue behavior of high strength concrete. Cem. Concr. Res. 1996, 26, 1513–1523. [Google Scholar] [CrossRef]
- Nor, N.M.; Ibrahim, A.; Bunnori, N.M.; Saman, H.M.; Saliah, S.N.M.; Shahidan, S. Diagnostic of fatigue damage severity on reinforced concrete beam using acoustic emission technique. Eng. Fail. Anal. 2014, 41, 1–9. [Google Scholar] [CrossRef]
- Bazant, Z.P.; Hubler, M.H. Theory of cyclic creep of concrete based on Paris law for fatigue growth of subcritical microcracks. J. Mech. Phys. Solids 2014, 63, 187–200. [Google Scholar] [CrossRef]
- Saucedo, L.; Yu, R.C.; Medeiros, A.; Zhang, X.X.; Ruiz, G. A probabilistic fatigue model based on the initial distribution to consider frequency effect in plain and fibre reinforced concrete. Int. J. Fatigue 2013, 48, 308–318. [Google Scholar] [CrossRef]
- Bazant, Z.P.; Panula, L. Practical prediction of time-dependent deformations of concrete. Part VI: Cyclic creep, nonlinearity and statistical scatter. Mater. Struct. 1979, 12, 175–183. [Google Scholar]
- Breitenbucher, R.; Ibuk, H. Experimentally based investigations on the degradation process of concrete under cyclic load. Mater. Struct. 2006, 39, 717–724. [Google Scholar] [CrossRef]
- Neville, A.M.; Hirst, G.A. Mechanism of cyclic creep of concrete. In Douglas McHenry International Symposium on Concrete and Concrete Structures; ACISP-55; Special Publication: London, UK, 1978; pp. 83–101. [Google Scholar]
- Garrett, G.G.; Jennings, H.M.; Tait, R.B. The fatigue hardening behavior of cement-based materials. J. Mater. Sci. 1979, 14, 296–306. [Google Scholar] [CrossRef]
- Le, J.L.; Bazant, Z.P. Unified nano-mechanics based probabilistic theory of quasibrittle and brittle structures: II. Fatigue crack growth, lifetime and scaling. J. Mech. Phys. Solids 2011, 59, 1322–1337. [Google Scholar] [CrossRef]
- Slate, F.O.; Olsefski, S. X-Rays for Study of Internal Structure and Microcracking of Concrete. J. Am. Concr. Inst. 1963, 60, 575–588. [Google Scholar]
- Abu Al-Rub, R.K.; Voyiadjis, G.Z. On the coupling of anisotropic damage and plasticity models for ductile Materials. Int. J. Solids Struct. 2003, 40, 2611–2643. [Google Scholar] [CrossRef]
- Paskin, A.; Massoumzadeh, B.; Shukla, K.; Sieradzki, K.; Dienes, G.J. Effect of atomic crack tip geometry on local stresses. Acta Met. 1985, 33, 1987–1996. [Google Scholar] [CrossRef]
- Dienes, G.J.; Paskin, A. Molecular dynamic simulations of crack propagation. J. Phys. Chem. Solids 1987, 48, 1015–1033. [Google Scholar] [CrossRef]
- Gumbsch, P. An atomistic study of brittle fracture: Toward explicit failure criteria from atomistic modeling. J. Mater. Res. 1995, 10, 2897–2907. [Google Scholar] [CrossRef]
- Gumbsch, P.; Beltz, G.E. On the continuum versus atomistic descriptions of dislocation nucleation and cleavage in nickel. Model. Simul. Mater. Sci. Eng. 1995, 3, 597–613. [Google Scholar] [CrossRef]
- Zhou, Z.L.; Gu, J.L.; Chen, N.P.; Li, D.C.; Liu, H.Q. Comparison of finite element calculation and experimental study of elastic-plastic deformation at crack tip. Acta Mech. Sin. 1995, 27, 51–57. [Google Scholar]
- Fischer, L.L.; Beltz, G.E. The effect of crack blunting on the competition between dislocation nucleation and Cleavage. J. Mech. Phys. Solids 2001, 49, 635–654. [Google Scholar] [CrossRef]
- Hajlaoui, K.; Yavari, A.R.; Doisneau, B.; LeMoulec, A.; Vaughan, G.; Greer, A.L.; Inoue, A.; Zhang, W.; Kvick, Å. Shear delocalization and crack blunting of a metallic glass containing nanoparticles: In situ deformation in TEM analysis. Scr. Mater. 2006, 54, 1829–1834. [Google Scholar] [CrossRef]
- Yu, Z.; Shan, Z.; Ouyang, Z.; Guo, F. A simple damage model for concrete considering irreversible mode-II microcracks. Fatigue Fract. Eng. Mater. Struct. 2016, 39, 1419–1432. [Google Scholar] [CrossRef]
- Yu, Z.W.; Tan, S.; Shan, Z.; Tian, X.Q. X-ray computed tomography quantification of damage in concrete under compression considering irreversible mode-II microcracks. Fatigue Fract. Eng. Mater. Struct. 2017, 40, 1960–1972. [Google Scholar] [CrossRef]
- Suresh, S.; Tschegg, E.K.; Brockenbrough, J.R. Fatigue Crack growth in cementitious composites under cyclic compressive loads. Cem. Concr. Res. 1989, 19, 827–833. [Google Scholar] [CrossRef]
- Eliáš, J.; Le, J.L. Modeling of mode-I fatigue crack growth in quasi brittle structures under cyclic compression. Eng. Fract. Mech. 2012, 96, 26–36. [Google Scholar]
- Bazant, Z.P.; Xiang, Y. Size effect in compression fracture: Splitting crack band propagation. J. Eng. Mech. 1997, 123, 207–213. [Google Scholar] [CrossRef]
- Fairhurst, C.; Comet, F. Rock fracture and fragmentation. In Rock Mechanics: From Research to Application. Proceedings of the U.S. Symposium on Rock Mechanics; Einstein, H.H., Ed.; MIT Press: Cambridge, MA, USA, 1981; pp. 21–46. [Google Scholar]
- Sammis, C.G.; Ashby, M.F. The failure of brittle porous solids under compressive stress state. Acta Metall. 1986, 34, 511–526. [Google Scholar] [CrossRef]
- Horii, H.; Nemat-Nasser, S. Compression induced nonplanar crack extension with application to splitting, exfoliation and rock burst. J. Geophys. Res. 1982, 87, 6805–6822. [Google Scholar]
- Kachanov, M. A micro crack model of rock in elasticity—Part I. Frictional sliding on micro cracks. Mech. Mater. 1982, 1, 19–27. [Google Scholar] [CrossRef]
- Nemat-Nasser, S.; Obata, M. A microcrack model of dilatancy in brittle materials. J. Appl. Mech. 1988, 55, 24–35. [Google Scholar] [CrossRef]
- Budiansky, B.; O’Connell, R.J. Elastic moduli of a cracked solid. Int. J. Solids Strcut. 1976, 12, 81–97. [Google Scholar] [CrossRef]
- Ning, J.; Ren, H.; Fang, M. Reseasrch on the process of micro-crack damage evolution and coalescence in brittle materials. Eng. Fail. Anal. 2014, 41, 65–72. [Google Scholar]
- Hu, G.; Liu, J.; Graham-Brady, L.; Ramesh, K.T. A 3D mechanistic model for brittle materials containing evolving flaw distributions under dynamic multiaxial loading. J. Mech. Phys. Solids 2015, 78, 269–297. [Google Scholar] [CrossRef]
- Burr, A.; Hild, F.; Leckie, F.A. Micro-mechanics and continuum damage mechanics. Arch. Appl. Mech. 1995, 65, 437–456. [Google Scholar] [CrossRef]
- Mazars, J.; Pijaudier-Cabot, G. Continuum damage theory—Application to concrete. J. Eng. Mech. 1989, 115, 345–365. [Google Scholar] [CrossRef]
- Halm, D.; Dragon, A. An anisotropic model of damage and frictional sliding for brittle materials. Eur. J. Mech. A Solids 1998, 17, 439–460. [Google Scholar] [CrossRef]
- Dragon, A.; Halm, D.; Desoyer, T. Anisotropic damage in quasi-brittle solids: Modelling, computational issues and applications. Comput. Methods Appl. Mech. Eng. 2000, 183, 331–352. [Google Scholar] [CrossRef]
- Le, J.L.; Bazant, Z.P.; Bazant, M.Z. Unified nano-mechanics based probabilistic theory of quasibrittle and brittle structures: I. Strength, static crack growth, lifetime and scaling. J. Mech. Phys. Solids 2011, 59, 1291–1321. [Google Scholar] [CrossRef]
- Feng, X.Q.; Gross, D. Three-dimensional micromechanical model for quasi-brittle solids with residual strains under tension. Int. J. Damage Mech. 2000, 9, 79–110. [Google Scholar] [CrossRef]
- Xiao, J.Z.; Li, H.; Yang, Z.J. Fatigue behavior of recycled aggregate concrete under compression and bending cyclic loadings. Constr. Build. Mater. 2013, 38, 681–688. [Google Scholar] [CrossRef]
- Pandolfi, A.; Taliercio, A. Bounding surface models applied to fatigue of plain concrete. J. Eng. Mech. 1998, 5, 556–564. [Google Scholar] [CrossRef]
- Papa, E.; Taliercio, A. Anisotropic damage model for the multiaxial static and fatigue behavior for plain concrete. Eng. Fract. Mech. 1996, 55, 163–179. [Google Scholar] [CrossRef]
- Alliche, A. Damage model for fatigue loading of concrete. Int. J. Fatigue 2004, 26, 915–921. [Google Scholar] [CrossRef]
- Mai, S.H.; Le-Corre, F.; Forêt, G.; Nedjar, B. A continuum damage modeling of quasi-static fatigue strength of plain concrete. Int. J. Fatigue 2012, 37, 79–85. [Google Scholar] [CrossRef] [Green Version]
- Lemaitre, J.; Lippmann, H. A Course on Damage Mechanics; Springer: Berlin, Germany, 1996. [Google Scholar]
- Richard, B.; Ragueneau, F.; Cremona, C.; Adelaide, L. Isotropic continuum damage mechanics for concrete under cyclic loading: Stiffness recovery, inelastic strains and frictional sliding. Eng. Fract. Mech. 2010, 77, 1203–1223. [Google Scholar] [CrossRef]
- Lu, P.Y.; Li, Q.B.; Song, Y.P. Damage constitutive of concrete under uniaxial alternate tension- compression fatigue loading based on double bounding surfaces. Int. J. Solids Struct. 2004, 41, 3151–3166. [Google Scholar] [CrossRef]
- Najar, J. Brittle residual strain and continuum damage at variable uniaxial loading. Int. J. Damage Mech. 1994, 3, 260–276. [Google Scholar] [CrossRef]
- Shan, Z.; Yu, Z.W. A fiber bundle-plastic chain model for quasi-brittle materials under uniaxial loading. J. Stat. Mech. Theory Exp. 2015, 2015, P11010. [Google Scholar] [CrossRef]
- Yazdani, S.; Schreyer, H.L. Combined plasticity and damage mechanics model for plain concrete. J. Eng. Mech. 1990, 116, 1435–1450. [Google Scholar] [CrossRef]
- Voyiadjis, G.Z.; Park, T. The kinematics of damage for finite-strain elasto-plastic solids. Int. J. Eng. Sci. 1999, 37, 803–830. [Google Scholar] [CrossRef]
- Li, J.; Wu, J.Y.; Chen, J.B. Stochastic Damage Mechanics of Concrete Structure; Science Press: Beijing, China, 2017. (In Chinese) [Google Scholar]
- Yu, Z.W.; Song, L.; Xie, Y.; Shan, Z. Experimental study on performance of CRTS III slab ballastless track system under service condition. In Third Report: Numerical Simulation on Fatigue Performance of CRTS III Slab Ballastless Track Structure Under High Speed Train Load; China State Railway Group Co., Ltd.: Beijing, China, 2015. (In Chinese) [Google Scholar]
- Sima, J.F.; Roca, P.; Molins, C. Cyclic constitutive model for concrete. Eng. Struct. 2008, 30, 695–706. [Google Scholar] [CrossRef] [Green Version]
- Research Group on Concrete Fatigue Behaviors. Reliability Evaluation Method of Concrete Bending Members under Fatigue Loading; China Architecture & Building Press: Beijing, China, 1994. (In Chinese) [Google Scholar]
- Thomas, C.; Setien, J.; Polanco, J.A.; Lompillo, I.; Cimentada, A. Fatigue limit of recycled aggregate concrete. Constr. Build. Mater. 2014, 52, 146–154. [Google Scholar] [CrossRef] [Green Version]
- Lu, P.; Song, Y.; Li, Q. Behavior of concrete under compressive fatigue loading with constant lateral stress. Eng. Mech. 2004, 21, 173–177. [Google Scholar]
- The National Standard of the People’s Republic of China: Code for Design of Concrete Structures (GB50011-2010); China Building Industry Press: Beijing, China, 2010. (In Chinese)
- Liang, J.S.; Ren, X.D.; Li, J. A competitive mechanism driven damage-plasticity model for fatigue behavior of concrete. Int. J. Damage Mech. 2016, 25, 377–399. [Google Scholar] [CrossRef]
- Xiao, J. Theoretical and Experimental Investigation on Fatigue Properties of Rock under Cyclic Loading. Master’s Thesis, Central South University, Changsha, China, 2009. (In Chinese). [Google Scholar]
- Marigo, J. Modelling of brittle and fatigue damage for elastic material by growth of microvoids. Eng. Fract. Mech. 1985, 21, 861–874. [Google Scholar] [CrossRef]








© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shan, Z.; Yu, Z.; Li, X.; Lv, X.; Liao, Z. A Damage Model for Concrete under Fatigue Loading. Appl. Sci. 2019, 9, 2768. https://doi.org/10.3390/app9132768
Shan Z, Yu Z, Li X, Lv X, Liao Z. A Damage Model for Concrete under Fatigue Loading. Applied Sciences. 2019; 9(13):2768. https://doi.org/10.3390/app9132768
Chicago/Turabian StyleShan, Zhi, Zhiwu Yu, Xiao Li, Xiaoyong Lv, and Zhenyu Liao. 2019. "A Damage Model for Concrete under Fatigue Loading" Applied Sciences 9, no. 13: 2768. https://doi.org/10.3390/app9132768




