Complex Dispersion Relation Recovery from 2D Periodic Resonant Systems of Finite Size
Abstract
:1. Introduction
2. Methods
2.1. SLatCoW
2.2. Spatial Sampling Criteria for Dispersion Relation Recovery
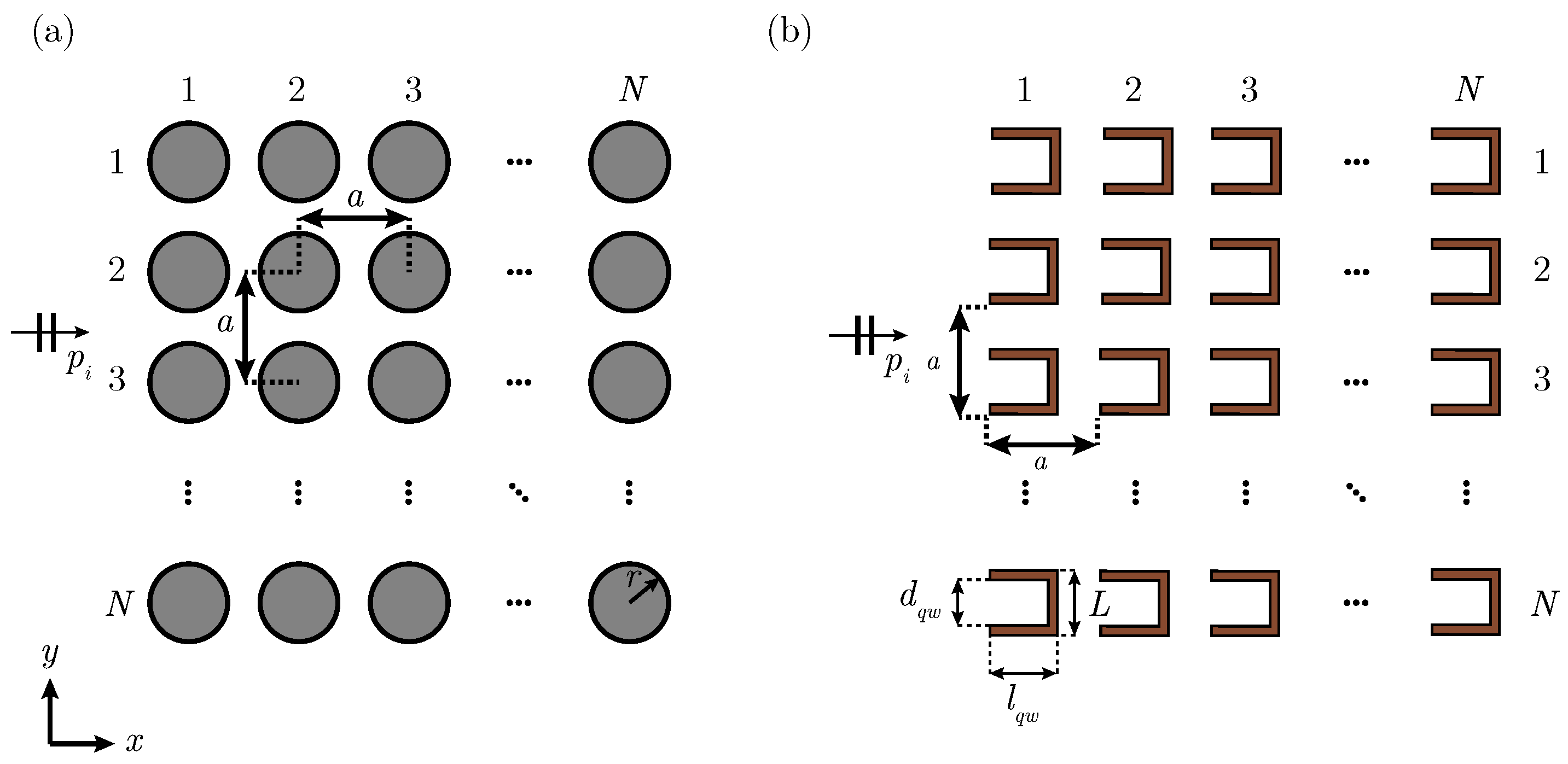
3. Numerical Set-Up
4. Results
4.1. Complex Dispersion Relation. SLaTCoW vs. EPWE
4.2. Complex Dispersion Relation of a 2D Periodic Resonant System
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Liu, Z.; Zhang, X.; Mao, Y.; Zhu, Y.; Yang, Z.; Chan, C.; Sheng, P. Locally resonant sonic materials. Science 2000, 289, 1734–1736. [Google Scholar] [CrossRef] [PubMed]
- Fang, N.; Xi, D.; Xu, J.; Ambati, M.; Srituravanich, W.; Sun, C.; Zhang, X. Ultrasonic metamaterials with negative modulus. Nat. Mater. 2006, 5, 452–456. [Google Scholar] [CrossRef] [PubMed]
- Bradley, C.E. Acoustic Bloch Wave Propagation in a Periodic Waveguide; Technical Report of Applied Research Laboratories, Report No. ARL-TR-91-19; The University of Texas at Austin: Austin, TX, USA, 1991. [Google Scholar]
- Sugimoto, N.; Horioka, T. Dispersion characteristics of sound waves in a tunnel with an array of helmholtz resonators. J. Acoust. Soc. Am. 1995, 97, 1446. [Google Scholar] [CrossRef]
- Theocharis, G.; Richoux, O.; García, V.R.; Merkel, A.; Tournat, V. Limits of slow sound propagation and transparency in lossy, locally resonant periodic structures. New J. Phys. 2014, 16, 093017. [Google Scholar] [CrossRef] [Green Version]
- Groby, J.-P.; Huand, W.; Lardeau, A.; Aurégan, Y. The use of slow sound to design simple sound absorbing materials. J. Appl. Phys. 2015, 117, 124903. [Google Scholar] [CrossRef]
- Romero-García, V.; Picó, R.; Cebrecos, A.; Staliunas, K.; Sánchez-Morcillo, V.J. Angular Band Gaps in Sonic Crystals: Evanescent Waves and Spatial Complex Dispersion Relation. J. Vib. Acoust. 2013, 135, 041012. [Google Scholar] [CrossRef] [Green Version]
- Philippe, F.D.; Roux, P.; Cassereau, D. Iterative high-resolution wavenumber inversion applied to broadband acoustic data. IEEE Trans. Ultrason. Ferroelectr. Frequency Control 2008, 55, 2306–2311. [Google Scholar] [CrossRef]
- Laude, V.; Achaoui, Y.; Benchabane, S.; Khelif, A. Evanescent Bloch waves and the complex band structure of phononic crystals. Phys. Rev. B 2009, 80, 092301. [Google Scholar] [CrossRef]
- Romero-García, V.; Sánchez-Pérez, J.V.; García-Raffi, L.M. Evanescent modes in sonic crystals: Complex dispersion relation and supercell approximation. J. Appl. Phys. 2010, 108, 044907. [Google Scholar] [CrossRef] [Green Version]
- Geslain, A.; Raetz, S.; Hirwia, M.; Ghamen, M.A.; Wallen, S.P.; Khanolkar, A.; Boechler, N.; Laurent, J.; Prada, C.; Duclos, A.; et al. Spatial Laplace transform for complex wavenumber recovery and its application to the analysis of attenuation in acoustic systems. J. Appl. Phys. 2016, 120, 135107. [Google Scholar] [CrossRef] [Green Version]
- Schwan, L.; Geslain, A.; Romero-García, V.; Groby, J.-P. Complex dispersion relation of surface acoustic waves at a lossy metasurface. Appl. Phys. Lett. 2017, 110, 051902. [Google Scholar] [CrossRef]
- Botten, L.; Nicorovici, N.; McPhedran, R.; de Sterke, C.; Asatryan, A. Photonic band structure calculations using scattering matrices. Phys. Rev. E 2001, 64, 046603. [Google Scholar]
- Poulton, C.G.; Movchan, A.B.; McPhedran, R.C.; Nicorovici, N.A.; Antipovy, A. Eigenvalue problems for doubly periodic elastic structures and phononic band gaps. Proc. R. Soc. A 2000, 456, 2543–2559. [Google Scholar] [CrossRef]
- Collet, M.; Ouisse, M.; Ichchou, M. A floquet-bloch decomposition of the elastodynamical equations: application to bi-dimensional wave’s dispersion computation of damped mechanical system. Int. J. Solids Struct. 2011, 48, 2837–2848. [Google Scholar] [CrossRef]
- García-Pablos, D.; Sigalas, M.; de Espinosa, F.R.M.; Torres, M.; Kafesaki, M.; García, N. Theory and experiments on elastic band gaps. Phys. Rev. Lett. 2000, 84, 4349–4352. [Google Scholar] [CrossRef] [PubMed]
- Montiel, F.; Chung, H.; Karimi, M.; Kessissoglou, N. An analytical and numerical investigation of acoustic attenuation by a finite sonic crystal. Wave Motion 2017, 70, 135–151. [Google Scholar] [CrossRef]
- Romero-García, V.; Krynkin, A.; García-Raffi, L.M.; Umnova, O.; Sánchez-Pérez, J.V. Multi-resonant scatterers in sonic crystals: Locally multi-resonant acoustic metamaterial. J. Sound Vib. 2013, 332, 184–198. [Google Scholar] [CrossRef] [Green Version]
- Yang, S.; Page, J.; Liu, Z.; Cowan, M.; Chan, C.; Sheng, P. Focusing of sound in a 3d phononic crystal. Phys. Rev. Lett. 2004, 93, 024301. [Google Scholar] [CrossRef] [PubMed]
- Sukhovich, A.; Jing, L.; Page, J.H. Negative refraction and focusing of ultrasound in two-dimensional phononic crystals. Phys. Rev. B 2008, 77, 014301. [Google Scholar] [CrossRef]
- Romero-García, V.; Sánchez-Pérez, J.V.; Garcia-Raffi, L.M. Evanescent waves and deaf bands in sonic crystals. AIP Adv. 2011, 1, 416011–416019. [Google Scholar] [CrossRef]
- Oppenheim, A.V. Discrete-Time Signal Processing; Pearson Education India: London, UK, 1999. [Google Scholar]
- Kosevich, A.M. Acoustics of Elastic Superlattices: Phonon Crystals, The Crystal Lattice: Phonons, Solitons, Dislocations, Superlattices, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2006; Chapter 5; pp. 153–162. [Google Scholar]
- Lardeau, A.; Groby, J.-P.; Romero-García, V. Broadband transmission loss using the overlap of resonances in 3D sonic crystals. Crystals 2016, 6, 51. [Google Scholar] [CrossRef]
- Cavalieri, T.; Cebrecos, A.; Groby, J.-P.; Chaufour, C.; Romero-García, V. Three-dimensional multiresonant lossy sonic crystal for broadband acoustic attenuation: Application to train noise reduction. Appl. Acoust. 2019, 146, 1–8. [Google Scholar] [CrossRef]



© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cebrecos, A.; Romero-García, V.; Groby, J.P. Complex Dispersion Relation Recovery from 2D Periodic Resonant Systems of Finite Size. Appl. Sci. 2019, 9, 478. https://doi.org/10.3390/app9030478
Cebrecos A, Romero-García V, Groby JP. Complex Dispersion Relation Recovery from 2D Periodic Resonant Systems of Finite Size. Applied Sciences. 2019; 9(3):478. https://doi.org/10.3390/app9030478
Chicago/Turabian StyleCebrecos, Alejandro, Vicente Romero-García, and Jean Philippe Groby. 2019. "Complex Dispersion Relation Recovery from 2D Periodic Resonant Systems of Finite Size" Applied Sciences 9, no. 3: 478. https://doi.org/10.3390/app9030478





