Multi-Trait Bayesian Models Enhance the Accuracy of Genomic Prediction in Multi-Breed Reference Populations
Abstract
:1. Introduction
2. Materials and Methods
2.1. Dataset
2.1.1. Real Pig Data
2.1.2. Real Beef Cattle Data
2.2. Multi-Breed Joint Prediction Model mbBayesAB
2.3. Other Models for Comparison with mbBayesAB
2.4. Cross-Validation (CV) and Predictive Accuracy
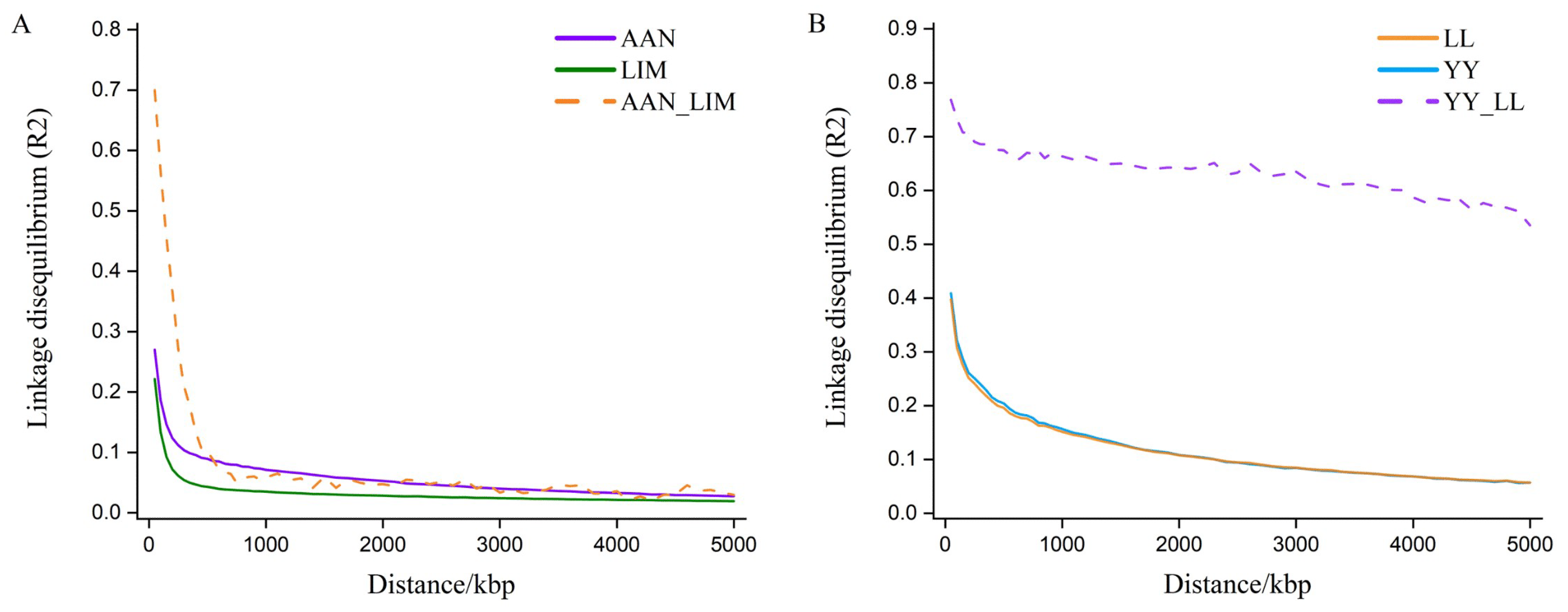
2.5. Genomic Structure Analysis
3. Results
3.1. Population Genomic Structure and Heritability of Traits
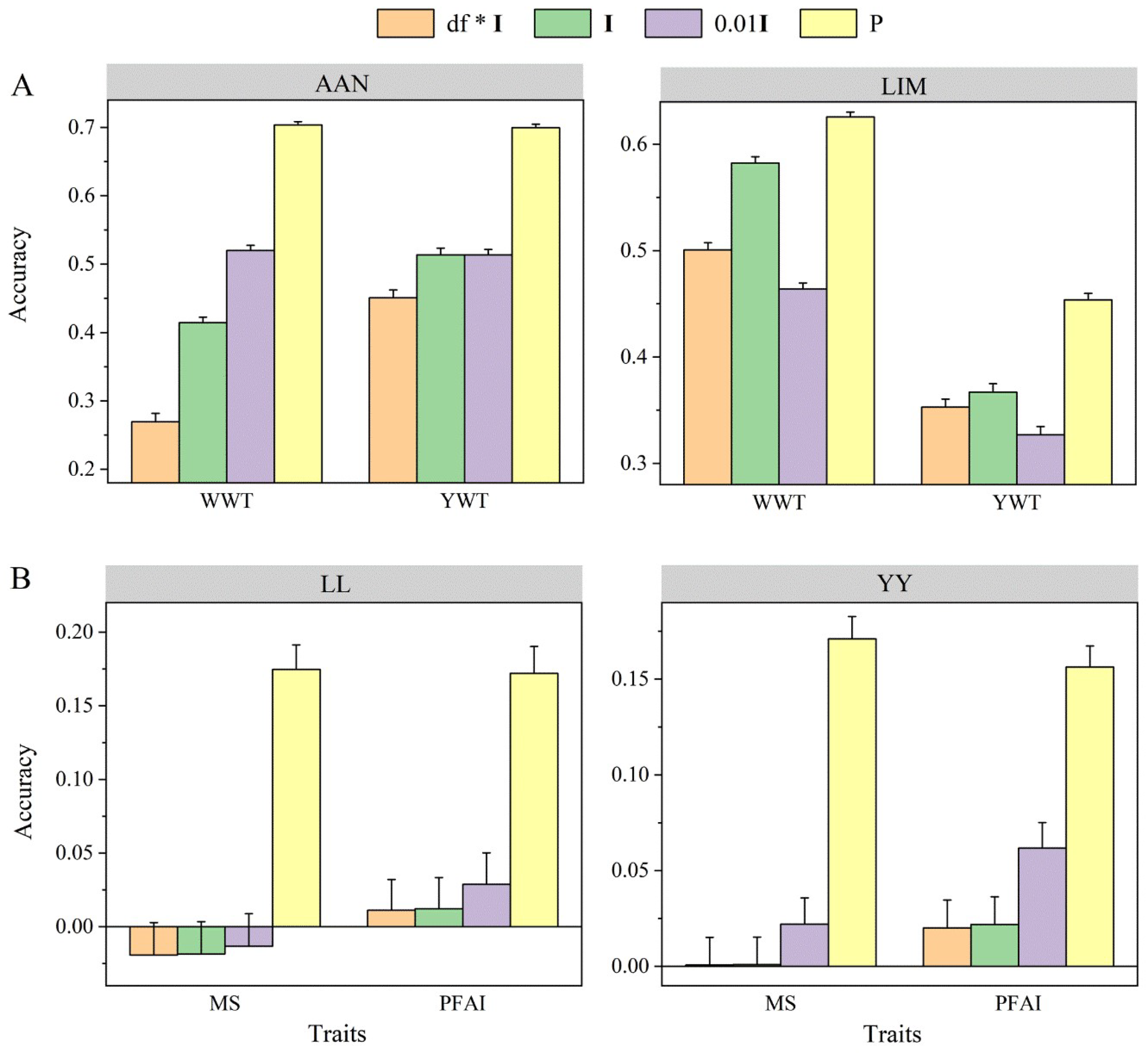
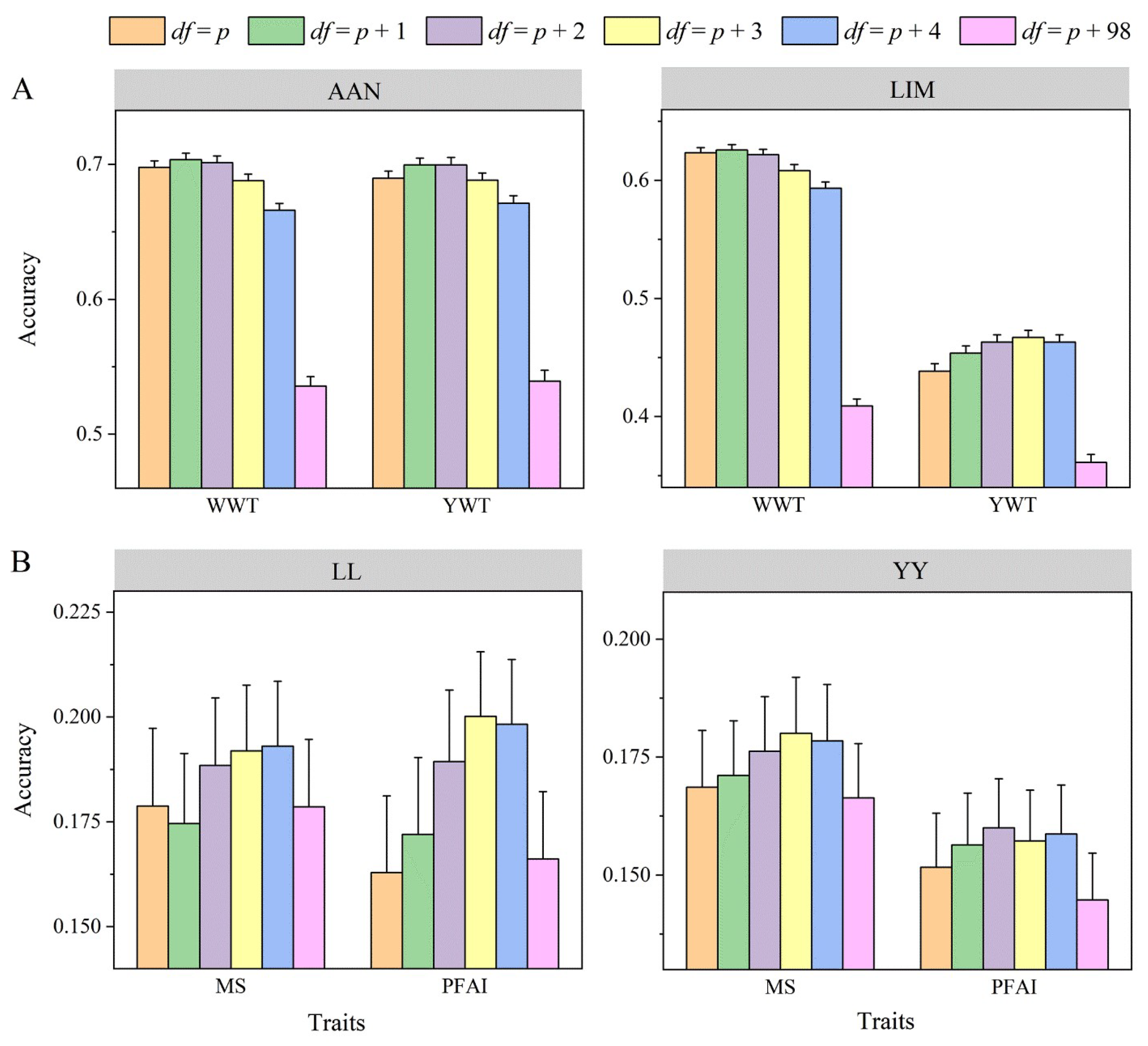
3.2. Degrees of Freedom and Scale Matrix Hyperparameters in IW Prior
3.3. Hierarchical Inverse Wishart Prior
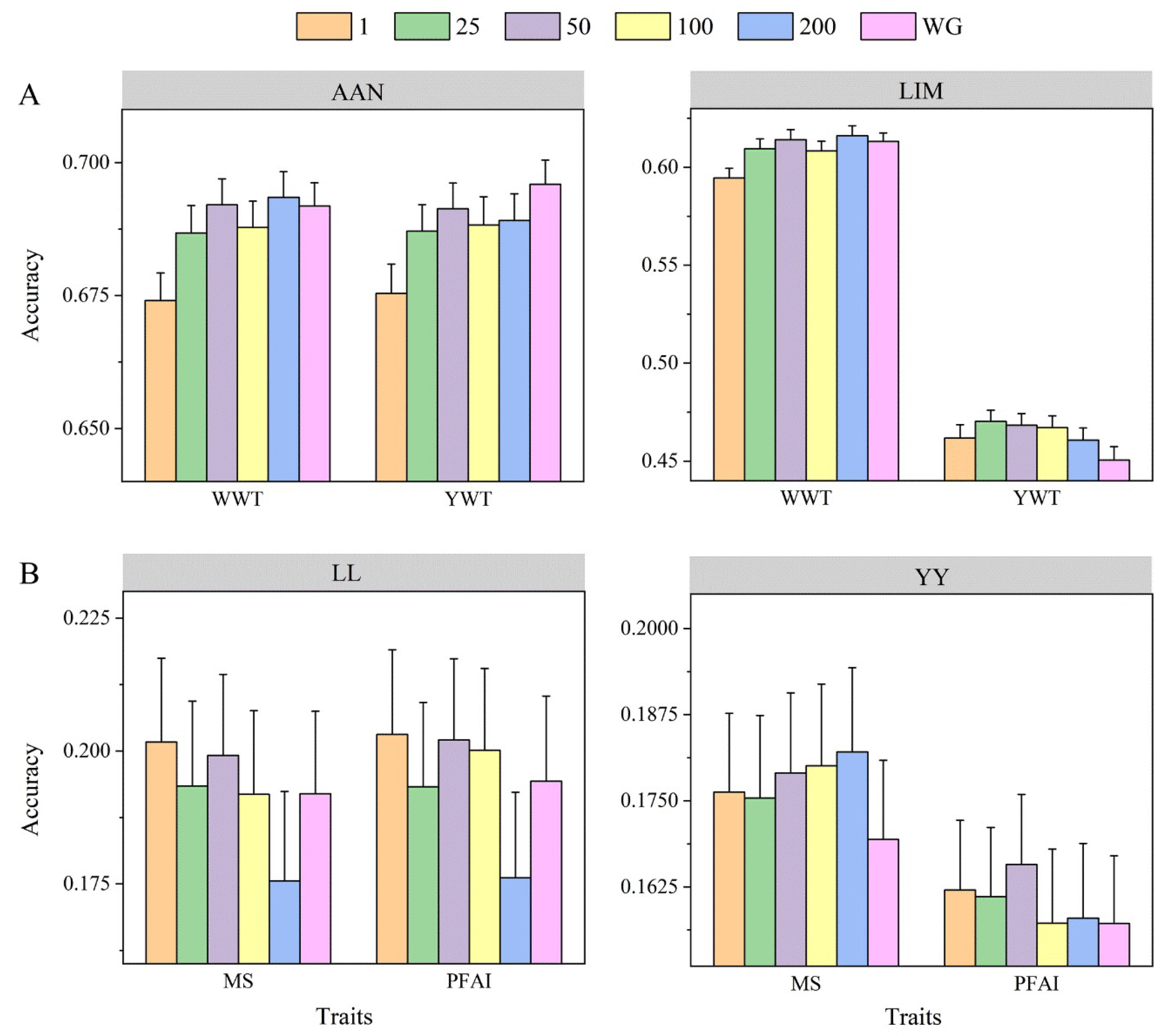
3.4. Number of SNPs in Genome Block Partitioning
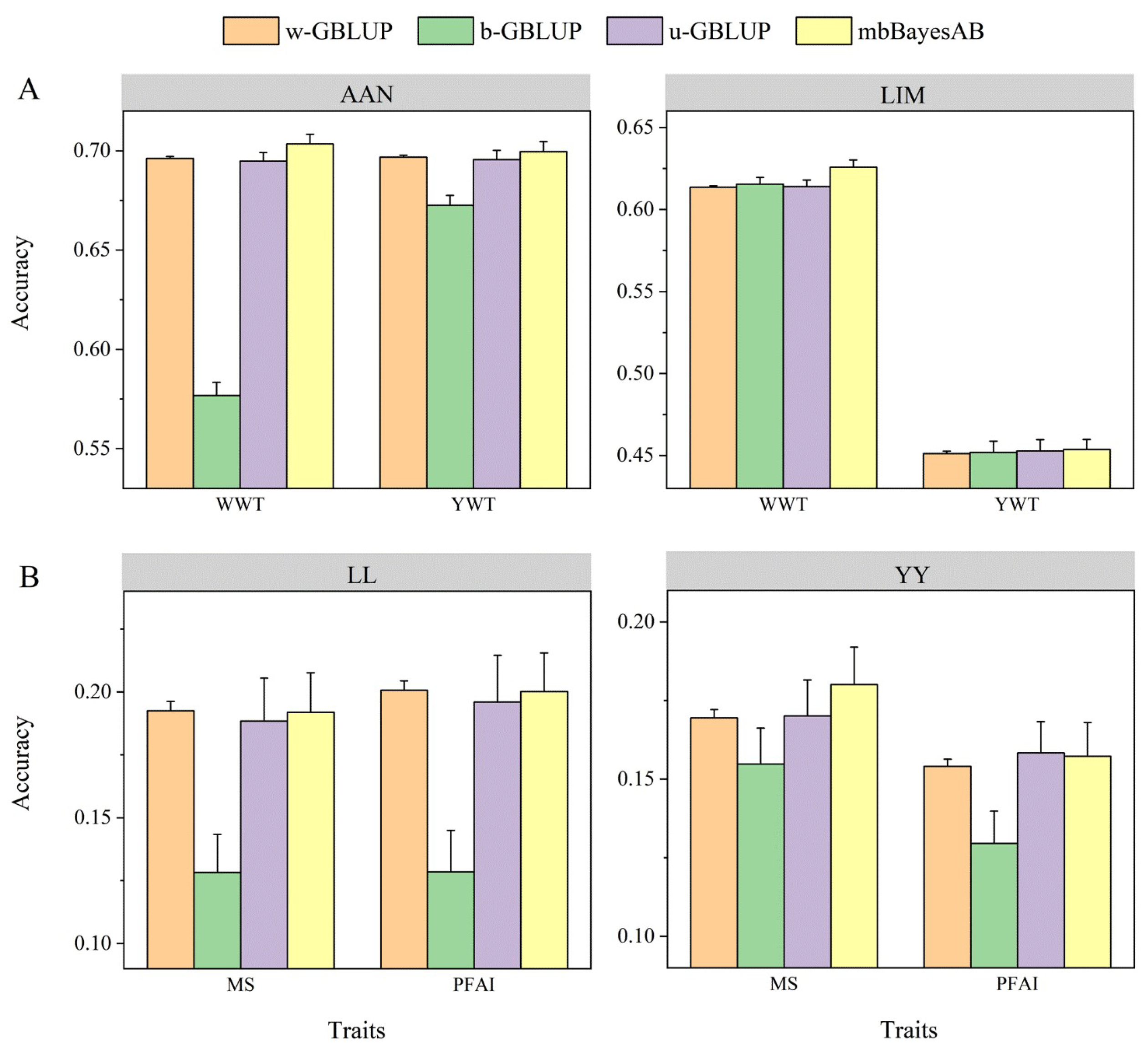
3.5. Prediction Accuracy of mbBayesAB and Commonly Used Joint Prediction Models
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B

References
- Aguilar, I.; Misztal, I.; Johnson, D.L.; Legarra, A.; Tsuruta, S.; Lawlor, T.J. Hot topic: A unified approach to utilize phenotypic, full pedigree, and genomic information for genetic evaluation of Holstein final score. J. Dairy Sci. 2010, 93, 743–752. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Liu, X.; Fu, J.; Wang, H.; Wang, J.; Huang, C.; Prasanna, B.M.; Olsen, M.S.; Wang, G.; Zhang, A. Enhancing Genetic Gain through Genomic Selection: From Livestock to Plants. Plant Commun. 2020, 1, 100005. [Google Scholar] [CrossRef] [PubMed]
- Daetwyler, H.D.; Calus, M.P.; Pong-Wong, R.; de Los, C.G.; Hickey, J.M. Genomic prediction in animals and plants: Simulation of data, validation, reporting, and benchmarking. Genetics 2013, 193, 347–365. [Google Scholar] [CrossRef] [PubMed]
- Jonas, D.; Ducrocq, V.; Fritz, S.; Baur, A.; Sanchez, M.P.; Croiseau, P. Genomic evaluation of regional dairy cattle breeds in single-breed and multibreed contexts. J. Anim. Breed. Genet. 2017, 134, 3–13. [Google Scholar] [CrossRef] [PubMed]
- Van den Berg, I.; Meuwissen, T.H.E.; MacLeod, I.M.; Goddard, M.E. Predicting the effect of reference population on the accuracy of within, across, and multibreed genomic prediction. J. Dairy Sci. 2019, 102, 3155–3174. [Google Scholar] [CrossRef] [PubMed]
- Ma, P.; Huang, J.; Gong, W.; Li, X.; Gao, H.; Zhang, Q.; Ding, X.; Wang, C. The impact of genomic relatedness between populations on the genomic estimated breeding values. J. Anim. Sci. Biotechnol. 2018, 9, 64. [Google Scholar] [CrossRef] [PubMed]
- Faville, M.J.; Ganesh, S.; Cao, M.; Jahufer, M.; Bilton, T.P.; Easton, H.S.; Ryan, D.L.; Trethewey, J.; Rolston, M.P.; Griffiths, A.G.; et al. Predictive ability of genomic selection models in a multi-population perennial ryegrass training set using genotyping-by-sequencing. Theor. Appl. Genet. 2018, 131, 703–720. [Google Scholar] [CrossRef] [PubMed]
- Thomasen, J.R.; Sorensen, A.C.; Lund, M.S.; Guldbrandtsen, B. Adding cows to the reference population makes a small dairy population competitive. J. Dairy Sci. 2014, 97, 5822–5832. [Google Scholar] [CrossRef] [PubMed]
- Ai, H.; Huang, L.; Ren, J. Genetic diversity, linkage disequilibrium and selection signatures in Chinese and Western pigs revealed by genome-wide SNP markers. PLoS ONE 2013, 8, e56001. [Google Scholar] [CrossRef] [PubMed]
- Cardoso, T.F.; Amills, M.; Bertolini, F.; Rothschild, M.; Marras, G.; Boink, G.; Jordana, J.; Capote, J.; Carolan, S.; Hallsson, J.H.; et al. Patterns of homozygosity in insular and continental goat breeds. Genet. Sel. Evol. 2018, 50, 56. [Google Scholar] [CrossRef] [PubMed]
- Lund, M.S.; van den Berg, I.; Ma, P.; Brondum, R.F.; Su, G. Review: How to improve genomic predictions in small dairy cattle populations. Animal 2016, 10, 1042–1049. [Google Scholar] [CrossRef] [PubMed]
- Lund, M.S.; Su, G.; Janss, L.; Guldbrandtsen, B.; Brondurn, R.F. Invited review: Genomic evaluation of cattle in a multi-breed context. Livest. Sci. 2014, 166, 101–110. [Google Scholar] [CrossRef]
- Samorè, A.B.; Fontanesi, L. Genomic selection in pigs: State of the art and perspectives. Ital. J. Anim. Sci. 2016, 15, 211–232. [Google Scholar] [CrossRef]
- VanRaden, P.M. Symposium review: How to implement genomic selection. J. Dairy Sci. 2020, 103, 5291–5301. [Google Scholar] [CrossRef] [PubMed]
- Gebreyesus, G.; Bovenhuis, H.; Lund, M.S.; Poulsen, N.A.; Sun, D.; Buitenhuis, B. Reliability of genomic prediction for milk fatty acid composition by using a multi-population reference and incorporating GWAS results. Genet. Sel. Evol. 2019, 51, 16. [Google Scholar] [CrossRef] [PubMed]
- Ye, S.; Song, H.; Ding, X.; Zhang, Z.; Li, J. Pre-selecting markers based on fixation index scores improved the power of genomic evaluations in a combined Yorkshire pig population. Animal 2020, 14, 1555–1564. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L.; Ding, X.; Zhang, Q.; Wang, Y.; Lund, M.S.; Su, G. Consistency of linkage disequilibrium between Chinese and Nordic Holsteins and genomic prediction for Chinese Holsteins using a joint reference population. Genet. Sel. Evol. 2013, 45, 7. [Google Scholar] [CrossRef] [PubMed]
- Calus, M.P.; Huang, H.; Vereijken, A.; Visscher, J.; Ten, N.J.; Windig, J.J. Genomic prediction based on data from three layer lines: A comparison between linear methods. Genet. Sel. Evol. 2014, 46, 57. [Google Scholar] [CrossRef] [PubMed]
- Fangmann, A.; Bergfelder-Drüing, S.; Tholen, E.; Simianer, H.; Erbe, M. Can multi-subpopulation reference sets improve the genomic predictive ability for pigs? J. Anim. Sci. 2015, 93, 5618–5630. [Google Scholar] [CrossRef] [PubMed]
- Olson, K.M.; VanRaden, P.M.; Tooker, M.E. Multibreed genomic evaluations using purebred Holsteins, Jerseys, and Brown Swiss. J. Dairy Sci. 2012, 95, 5378–5383. [Google Scholar] [CrossRef] [PubMed]
- Calus, M.; Goddard, M.E.; Wientjes, Y.; Bowman, P.J.; Hayes, B.J. Multibreed genomic prediction using multitrait genomic residual maximum likelihood and multitask Bayesian variable selection. J. Dairy Sci. 2018, 101, 4279–4294. [Google Scholar] [CrossRef] [PubMed]
- Lehermeier, C.; Schön, C.; de Los Campos, G. Assessment of Genetic Heterogeneity in Structured Plant Populations Using Multivariate Whole-Genome Regression Models. Genetics 2015, 201, 323–337. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Lund, M.S.; Janss, L.; Wang, C.; Ding, X.; Zhang, Q.; Su, G. The patterns of genomic variances and covariances across genome for milk production traits between Chinese and Nordic Holstein populations. BMC Genet. 2017, 18, 26. [Google Scholar] [CrossRef] [PubMed]
- Wientjes, Y.C.; Bijma, P.; Veerkamp, R.F.; Calus, M.P. An Equation to Predict the Accuracy of Genomic Values by Combining Data from Multiple Traits, Populations, or Environments. Genetics 2016, 202, 799–823. [Google Scholar] [CrossRef] [PubMed]
- Shi, H.; Mancuso, N.; Spendlove, S.; Pasaniuc, B. Local Genetic Correlation Gives Insights into the Shared Genetic Architecture of Complex Traits. Am. J. Hum. Genet. 2017, 101, 737–751. [Google Scholar] [CrossRef] [PubMed]
- Werme, J.; van der Sluis, S.; Posthuma, D.; de Leeuw, C.A. An integrated framework for local genetic correlation analysis. Nat. Genet. 2022, 54, 274–282. [Google Scholar] [CrossRef] [PubMed]
- Lupi, A.S.; Sumpter, N.A.; Leask, M.P.; Sullivan, J.O.; Fadason, T.; de Los Campos, G.; Merriman, T.R.; Reynolds, R.J.; Vazquez, A.I. Local genetic covariance between serum urate and kidney function estimated with Bayesian multitrait models. G3 Genes Genomes Genet. 2022, 12, jkac158. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z. A Note on Wishart and Inverse Wishart Priors for Covariance Matrix. J. Behav. Data Sci. 2021, 1, 119–126. [Google Scholar] [CrossRef]
- Alvarez, I.; Niemi, J.; Simpson, M. Bayesian inference for a covariance matrix. In Proceedings of the 26th Annual Conference on Applied Statistics in Agriculture, Manhattan, KS, USA, 27–29 April 2014. [Google Scholar] [CrossRef]
- Riecke, T.V.; Sedinger, B.S.; Williams, P.J.; Leach, A.G.; Sedinger, J.S. Estimating correlations among demographic parameters in population models. Ecol. Evol. 2019, 9, 13521–13531. [Google Scholar] [CrossRef] [PubMed]
- Sarkar, P.; Khare, K.; Ghosh, M. High-dimensional Posterior Consistency in Multi-response Regression models with Non-informative Priors for Error Covariance Matrix. arXiv 2023, arXiv:2305.13743. [Google Scholar]
- Tokuda, T.; Goodrich, B.; Van Mechelen, I.; Gelman, A.; Tuerlinckx, F. Visualizing Distributions of Covariance Matrices; Technical Report; Columbia University: New York, NY, USA, 2011; p. 18. [Google Scholar]
- Akinc, D.; Vandebroek, M. Bayesian estimation of mixed logit models: Selecting an appropriate prior for the covariance matrix. J. Choice Model. 2018, 29, 133–151. [Google Scholar] [CrossRef]
- Hurtado Rúa, S.M.; Mazumdar, M.; Strawderman, R.L. The choice of prior distribution for a covariance matrix in multivariate meta-analysis: A simulation study. Stat. Med. 2015, 34, 4083–4104. [Google Scholar] [CrossRef] [PubMed]
- Xie, L.; Qin, J.; Rao, L.; Tang, X.; Cui, D.; Chen, L.; Xu, W.; Xiao, S.; Zhang, Z.; Huang, L. Accurate prediction and genome-wide association analysis of digital intramuscular fat content in longissimus muscle of pigs. Anim. Genet. 2021, 52, 633–644. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Kim, J.M.; Garrick, D.J. Increasing the accuracy of genomic prediction in pure-bred Limousin beef cattle by including cross-bred Limousin data and accounting for an F94L variant in MSTN. Anim. Genet. 2019, 50, 621–633. [Google Scholar] [CrossRef] [PubMed]
- Train, K.; Sonnier, G. Mixed Logit with Bounded Distributions of Correlated Partworths. In Applications of Simulation Methods in Environmental and Resource Economics; Scarpa, R., Alberini, A., Eds.; Springer: Dordrecht, The Netherlands, 2005; pp. 117–134. [Google Scholar]
- Elhezzani, N.S. Improved estimation of SNP heritability using Bayesian multiple-phenotype models. Eur. J. Hum. Genet. 2018, 26, 723–734. [Google Scholar] [CrossRef] [PubMed]
- Huang, A.; Wand, M.P. Simple Marginally Noninformative Prior Distributions for Covariance Matrices. Bayesian Anal. 2013, 8, 439–452. [Google Scholar] [CrossRef]
- Mulder, J.; Pericchi, L.R. The Matrix-F Prior for Estimating and Testing Covariance Matrices. Bayesian Anal. 2018, 13, 1193–1214. [Google Scholar] [CrossRef]
- Karaman, E.; Lund, M.S.; Su, G. Multi-trait single-step genomic prediction accounting for heterogeneous (co)variances over the genome. Heredity 2020, 124, 274–287. [Google Scholar] [CrossRef] [PubMed]
- Purcell, S.; Neale, B.; Todd-Brown, K.; Thomas, L.; Ferreira, M.A.R.; Bender, D.; Maller, J.; Sklar, P.; de Bakker, P.I.W.; Daly, M.J.; et al. PLINK: A Tool Set for Whole-Genome Association and Population-Based Linkage Analyses. Am. J. Hum. Genet. 2007, 81, 559–575. [Google Scholar] [CrossRef] [PubMed]
- Badke, Y.M.; Bates, R.O.; Ernst, C.W.; Schwab, C.; Steibel, J.P. Estimation of linkage disequilibrium in four US pig breeds. BMC Genomics 2012, 13, 24. [Google Scholar] [CrossRef] [PubMed]
- Rossi, P.E.; Allenby, G.M.; McCulloch, R. Bayesian Statistics and Marketing; Wiley: New York, NY, USA, 2005; p. 364. [Google Scholar]
- Ren, D.; Cai, X.; Lin, Q.; Ye, H.; Teng, J.; Li, J.; Ding, X.; Zhang, Z. Impact of linkage disequilibrium heterogeneity along the genome on genomic prediction and heritability estimation. Genet. Sel. Evol. 2022, 54, 47. [Google Scholar] [CrossRef] [PubMed]
- Gianola, D.; de Los Campos, G.; Hill, W.G.; Manfredi, E.; Fernando, R. Additive Genetic Variability and the Bayesian Alphabet. Genetics 2009, 183, 347–363. [Google Scholar] [CrossRef] [PubMed]
- Ruoyong, Y.; James, O.B. Estimation of a Covariance Matrix Using the Reference Prior. Ann. Stat. 1994, 22, 1195–1211. [Google Scholar] [CrossRef]
- Kass, R.E.; Steffey, D. Approximate Bayesian inference in conditionally independent hierarchical models (parametric empirical Bayes models). J. Am. Stat. Assoc. 1989, 84, 717–726. [Google Scholar] [CrossRef]
- Zhang, M.; Xiao, O.Y.; Lim, J.; Wang, X. Goodness-of-fit testing for meta-analysis of rare binary events. Sci. Rep. 2023, 13, 17712. [Google Scholar] [CrossRef] [PubMed]
- Leon, L.; Wendt, H.; Tourneret, J.Y.; Abry, P. A Bayesian Framework for Multivariate Multifractal Analysis. IEEE Trans. Signal Process. 2022, 70, 3663–3675. [Google Scholar] [CrossRef]
- O’Malley, A.J.; Zaslavsky, A.M. Domain-Level Covariance Analysis for Multilevel Survey Data With Structured Nonresponse. J. Am. Stat. Assoc. 2008, 103, 1405–1418. [Google Scholar] [CrossRef]
- Gebreyesus, G.; Lund, M.S.; Buitenhuis, B.; Bovenhuis, H.; Poulsen, N.A.; Janss, L.G. Modeling heterogeneous (co)variances from adjacent-SNP groups improves genomic prediction for milk protein composition traits. Genet. Sel. Evol. 2017, 49, 89. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Wang, Z.; Xu, L.; Li, Q.; Gao, H.; Ma, H.; Cai, W.; Chen, Y.; Gao, X.; Zhang, L.; et al. Genomic prediction of carcass traits using different haplotype block partitioning methods in beef cattle. Evol. Appl. 2022, 15, 2028–2042. [Google Scholar] [CrossRef] [PubMed]
- Karaman, E.; Su, G.; Croue, I.; Lund, M.S. Genomic prediction using a reference population of multiple pure breeds and admixed individuals. Genet. Sel. Evol. 2021, 53, 46. [Google Scholar] [CrossRef] [PubMed]
- Van den Berg, I.; MacLeod, I.M.; Reich, C.M.; Breen, E.J.; Pryce, J.E. Optimizing genomic prediction for Australian Red dairy cattle. J. Dairy Sci. 2020, 103, 6276–6298. [Google Scholar] [CrossRef] [PubMed]
- Haile-Mariam, M.; MacLeod, I.M.; Bolormaa, S.; Schrooten, C.; O’Connor, E.; de Jong, G.; Daetwyler, H.D.; Pryce, J.E. Value of sharing cow reference population between countries on reliability of genomic prediction for milk yield traits. J. Dairy Sci. 2020, 103, 1711–1728. [Google Scholar] [CrossRef] [PubMed]
- Raymond, B.; Wientjes, Y.; Bouwman, A.C.; Schrooten, C.; Veerkamp, R.F. A deterministic equation to predict the accuracy of multi-population genomic prediction with multiple genomic relationship matrices. Genet. Sel. Evol. 2020, 52, 21. [Google Scholar] [CrossRef] [PubMed]
- Vargas, J.N.; Notter, D.R.; Taylor, J.B.; Brown, D.J.; Mousel, M.R.; Lewis, R.M. Combined purebred and crossbred genetic evaluation of Columbia, Suffolk, and crossbred lamb birth and weaning weights: Systematic effects and heterogeneous variances. J. Anim. Sci. 2024, 102, skad410. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Lund, M.S.; Zhang, Q.; Costa, C.N.; Ducrocq, V.; Su, G. Short communication: Improving accuracy of predicting breeding values in Brazilian Holstein population by adding data from Nordic and French Holstein populations. J. Dairy Sci. 2016, 99, 4574–4579. [Google Scholar] [CrossRef] [PubMed]
- Song, H.; Zhang, Q.; Ding, X. The superiority of multi-trait models with genotype-by-environment interactions in a limited number of environments for genomic prediction in pigs. J. Anim. Sci. Biotechnol. 2020, 11, 88. [Google Scholar] [CrossRef] [PubMed]
- Kjetså, M.V.; Gjuvsland, A.B.; Grindflek, E.; Meuwissen, T. Effects of reference population size and structure on genomic prediction of maternal traits in two pig lines using whole-genome sequence-, high-density- and combined annotation-dependent depletion genotypes. J. Anim. Breed. Genet. 2024, 1–15. [Google Scholar] [CrossRef] [PubMed]
- VanRaden, P.M. Efficient methods to compute genomic predictions. J. Dairy Sci. 2008, 91, 4414–4423. [Google Scholar] [CrossRef] [PubMed]
| Species | Traits 1 | Breed 2 | Records | Va 3 | Ve 4 | h2 (SE) 5 |
|---|---|---|---|---|---|---|
| Pig | PFAI | YY | 641 | 0.31 | 1.30 | 0.19(0.07) |
| LL | 228 | 0.67 | 1.35 | 0.33(0.16) | ||
| MS | YY | 641 | 0.05 | 0.18 | 0.22(0.07) | |
| LL | 228 | 0.09 | 0.20 | 0.31(0.16) | ||
| Beef cattle | YWT | LIM | 1528 | 1601.40 | 1497.88 | 0.52(0.05) |
| AAN | 796 | 1116.65 | 340.43 | 0.77(0.04) | ||
| WWT | LIM | 1897 | 3133.74 | 994.59 | 0.76(0.03) | |
| AAN | 797 | 347.75 | 94.44 | 0.79(0.04) |
| Species | Breed 1 | Traits 2 | Prior 3 | Genetic Correlation 4 | Accuracy 5 |
|---|---|---|---|---|---|
| Beef cattle | AAN | WWT | IW | 0.065 ± 0.005 | 0.704 ± 0.005 |
| HIW-WI | 0.053 ± 0.006 | 0.699 ± 0.005 | |||
| HIW-IG | 0.050 ± 0.005 | 0.698 ± 0.005 | |||
| YWT | IW | 0.050 ± 0.005 | 0.700 ± 0.005 | ||
| HIW-WI | 0.039 ± 0.006 | 0.698 ± 0.005 | |||
| HIW-IG | 0.051 ± 0.005 | 0.690 ± 0.005 | |||
| LIM | WWT | IW | 0.065 ± 0.005 | 0.626 ± 0.005 | |
| HIW-WI | 0.053 ± 0.006 | 0.624 ± 0.005 | |||
| HIW-IG | 0.050 ± 0.005 | 0.623 ± 0.004 | |||
| YWT | IW | 0.050 ± 0.005 | 0.454 ± 0.006 | ||
| HIW-WI | 0.039 ± 0.006 | 0.452 ± 0.006 | |||
| HIW-IG | 0.051 ± 0.005 | 0.438 ± 0.006 | |||
| Pig | LL | MS | IW | −0.071 ± 0.007 | 0.175 ± 0.017 |
| HIW-WI | −0.035 ± 0.008 | 0.186 ± 0.018 | |||
| HIW-IG | −0.038 ± 0.007 | 0.179 ± 0.019 | |||
| PFAI | IW | −0.081 ± 0.007 | 0.172 ± 0.018 | ||
| HIW-WI | −0.057 ± 0.007 | 0.160 ± 0.019 | |||
| HIW-IG | −0.069 ± 0.006 | 0.163 ± 0.018 | |||
| YY | MS | IW | −0.071 ± 0.007 | 0.171 ± 0.012 | |
| HIW-WI | −0.035 ± 0.008 | 0.172 ± 0.012 | |||
| HIW-IG | −0.038 ± 0.007 | 0.169 ± 0.012 | |||
| PFAI | IW | −0.081 ± 0.007 | 0.156 ± 0.011 | ||
| HIW-WI | −0.057 ± 0.007 | 0.155 ± 0.011 | |||
| HIW-IG | −0.069 ± 0.006 | 0.152 ± 0.011 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W.; Zhang, M.; Du, H.; Wu, J.; Zhou, L.; Liu, J. Multi-Trait Bayesian Models Enhance the Accuracy of Genomic Prediction in Multi-Breed Reference Populations. Agriculture 2024, 14, 626. https://doi.org/10.3390/agriculture14040626
Li W, Zhang M, Du H, Wu J, Zhou L, Liu J. Multi-Trait Bayesian Models Enhance the Accuracy of Genomic Prediction in Multi-Breed Reference Populations. Agriculture. 2024; 14(4):626. https://doi.org/10.3390/agriculture14040626
Chicago/Turabian StyleLi, Weining, Meilin Zhang, Heng Du, Jianliang Wu, Lei Zhou, and Jianfeng Liu. 2024. "Multi-Trait Bayesian Models Enhance the Accuracy of Genomic Prediction in Multi-Breed Reference Populations" Agriculture 14, no. 4: 626. https://doi.org/10.3390/agriculture14040626






