Long Wave Flow Interaction with a Single Square Structure on a Sloping Beach
Abstract
:1. Introduction
1.1. Background
1.2. Objectives
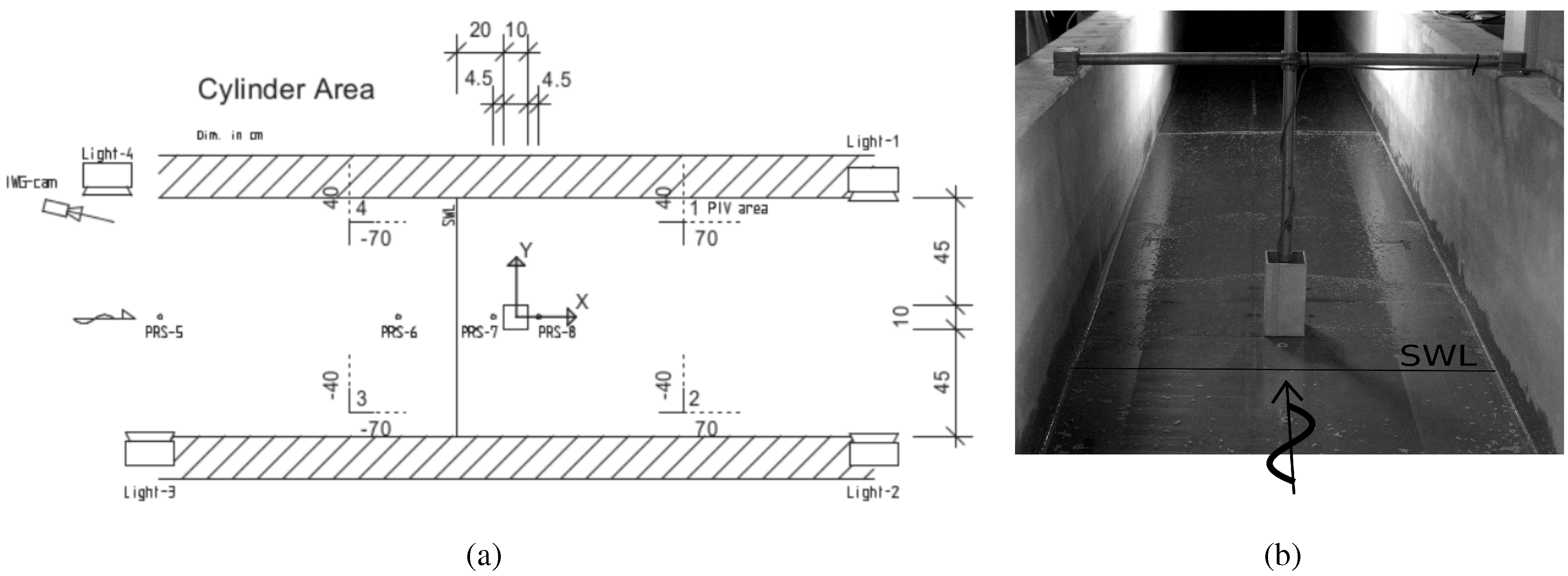
2. Experimental Setup
2.1. Stationary Force Measurement Tests
2.2. Transient Flow Tests

| WC-ID | Wave Condition | Wave Height | Wave Period | Wave Length | Iribarren Number | ||
|---|---|---|---|---|---|---|---|
| [-] | [-] | H [m] | T [s] | L [m] | [-] | [-] | ξ [-] |
| 01 | Base case | 0.08 | 60 | 102.9 | 0.133 | 3.9 × 10−4 | 6.63 |
| 02 | Low amplitude | 0.04 | 60 | 102.9 | 0.067 | 1.9 × 10−4 | 9.37 |
| 03 | Long period | 0.08 | 90 | 154.4 | 0.133 | 2.6 × 10−4 | 9.94 |
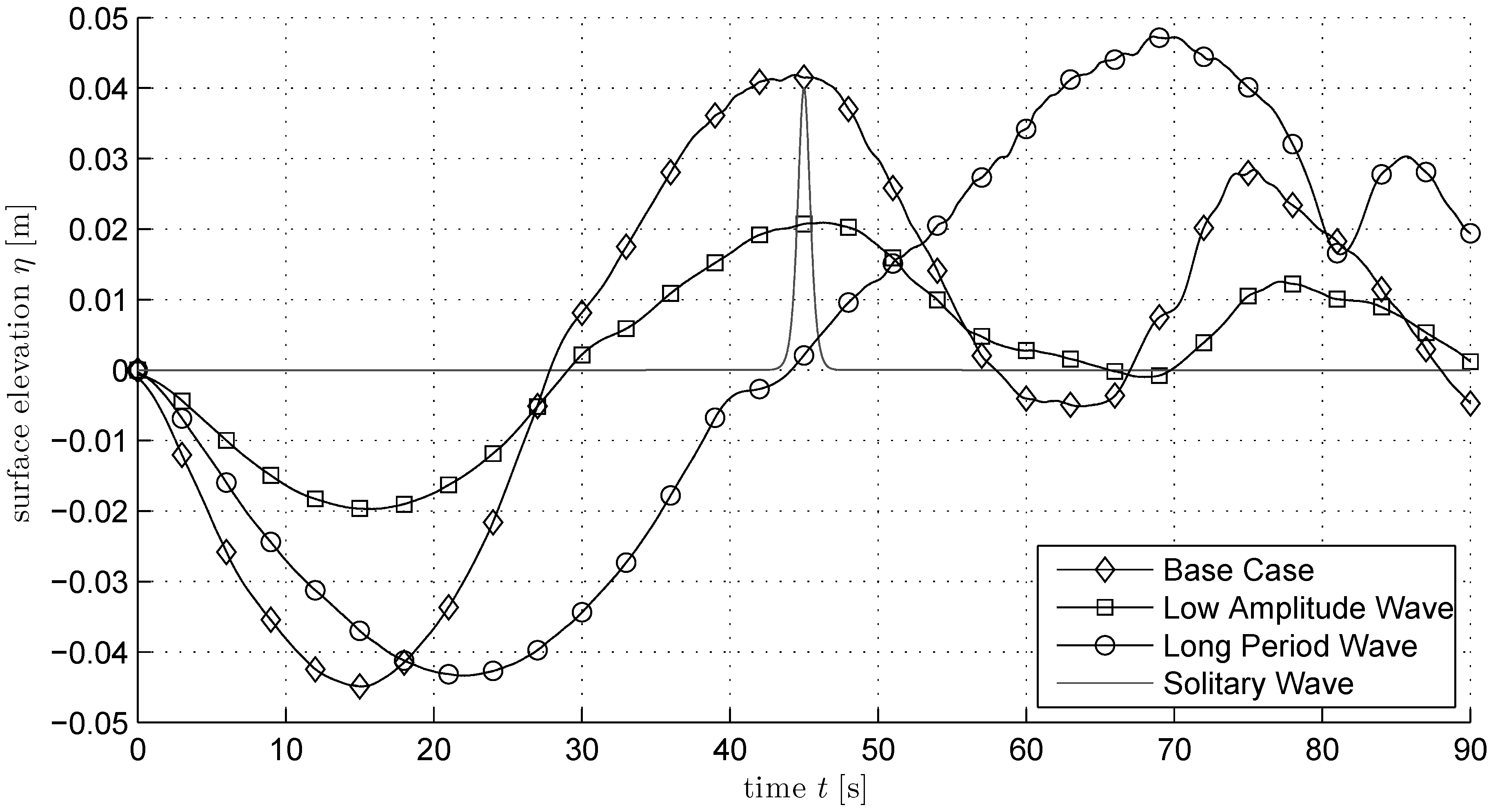
3. Experiments
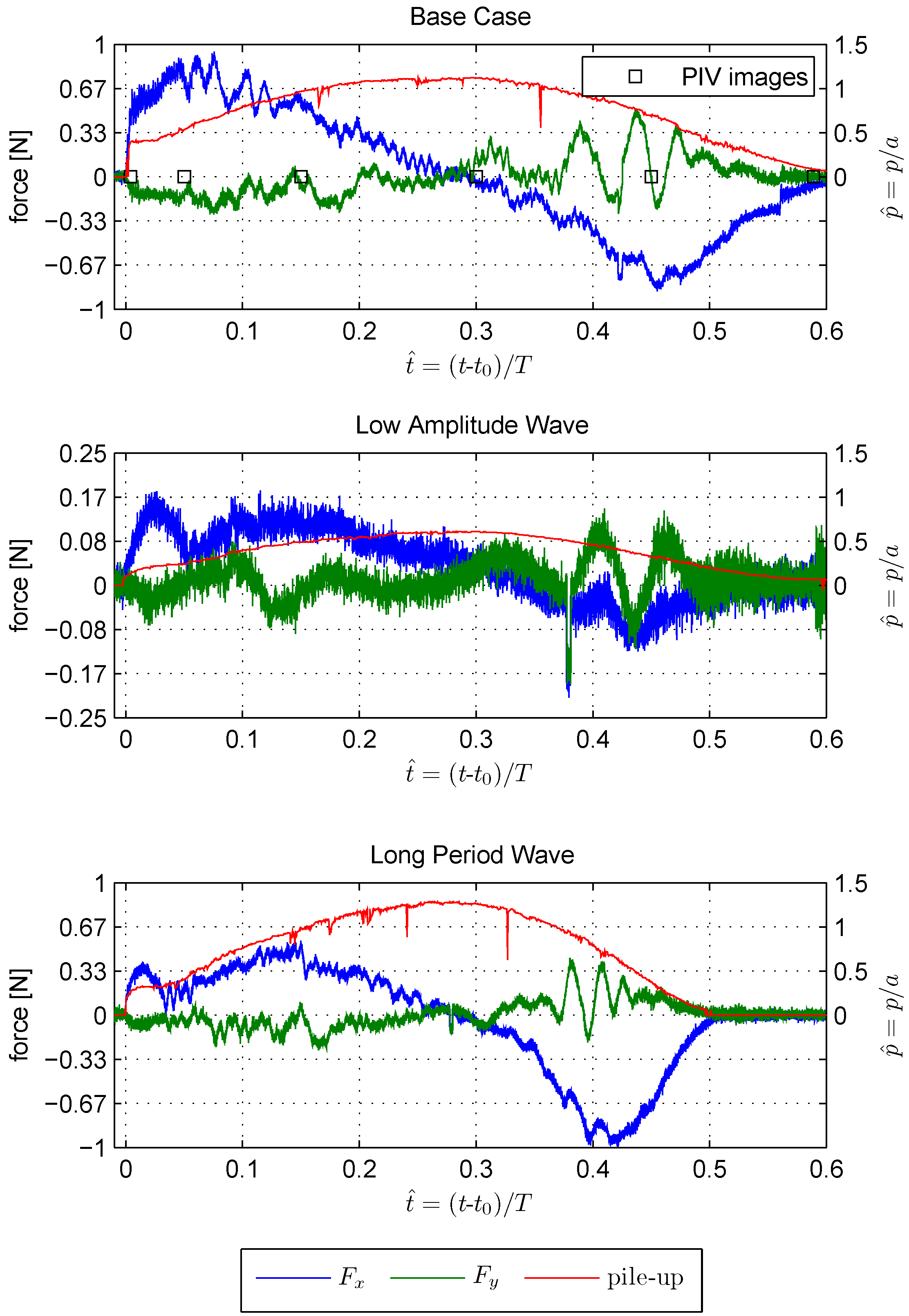
3.1. Time-Variant Transient Flow
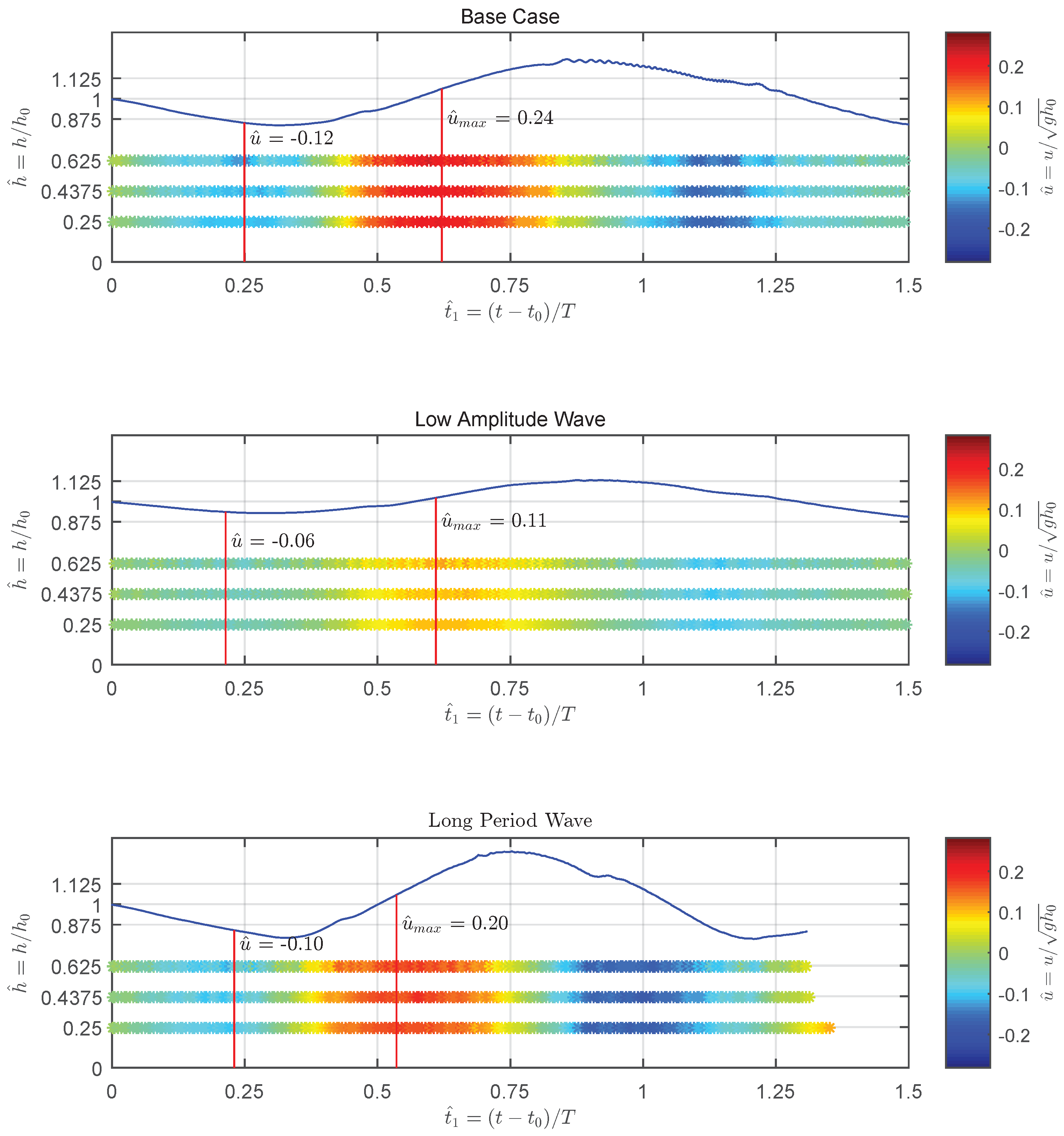
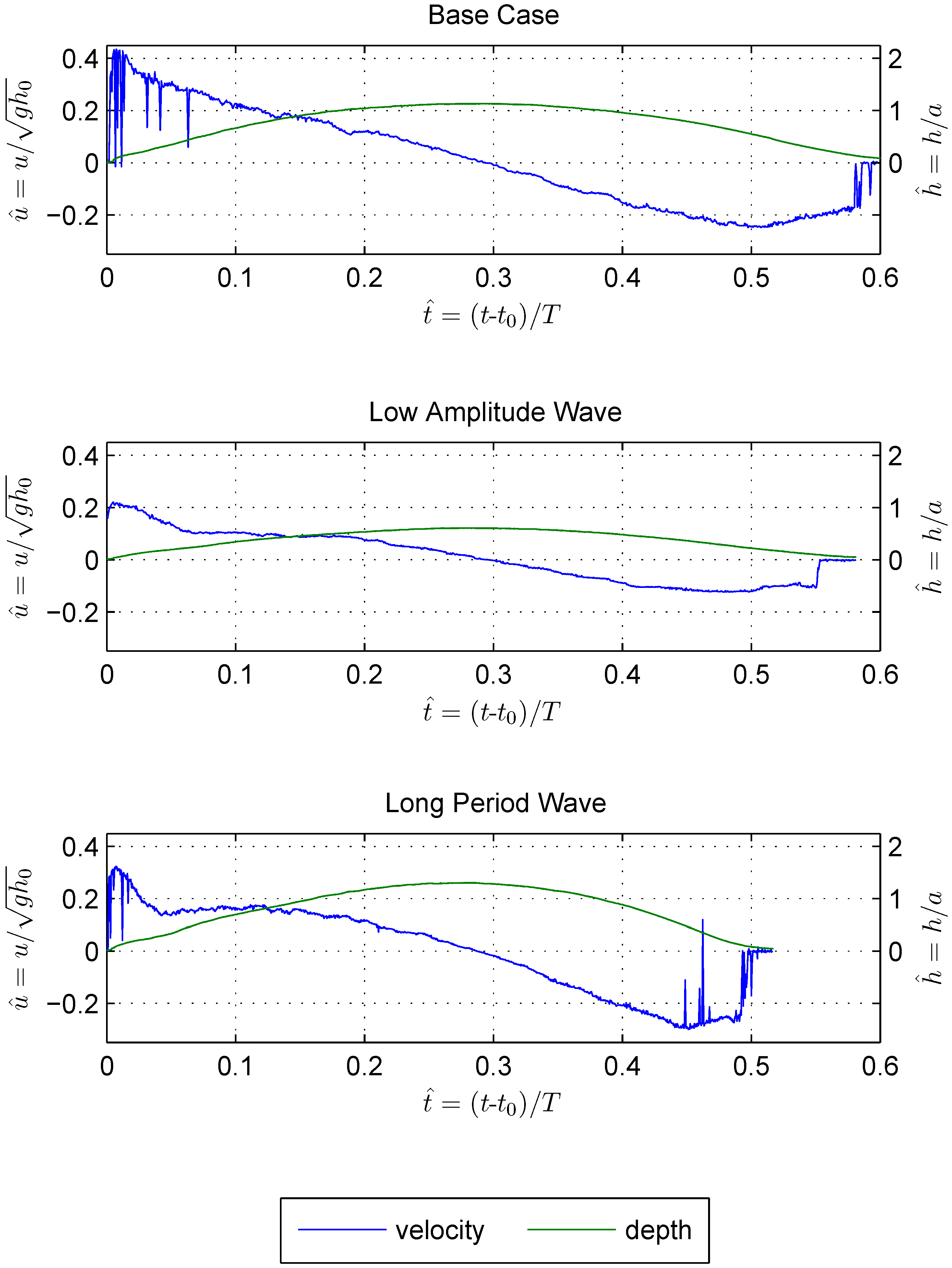
3.2. Flow Pattern
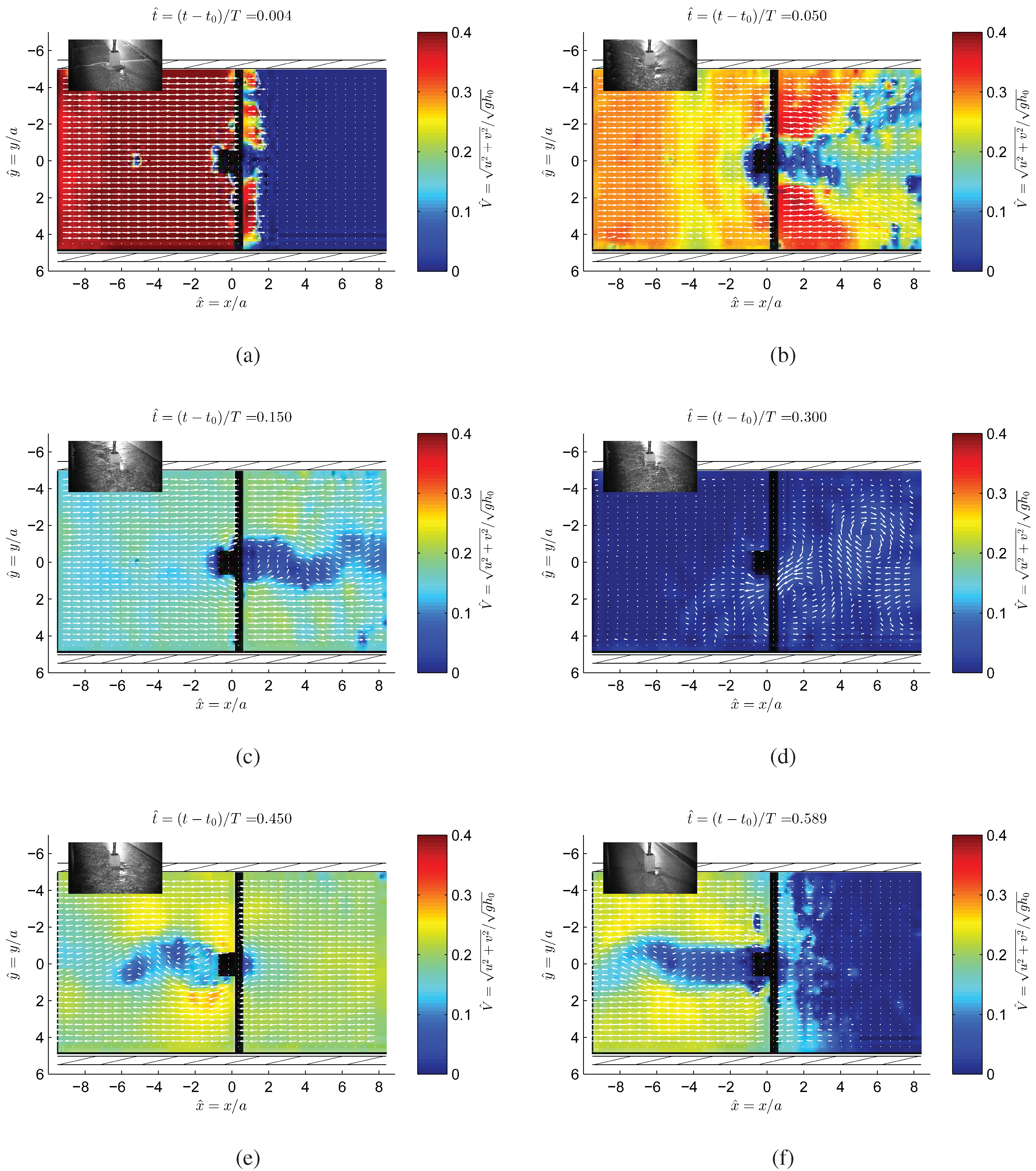
3.3. Horizontal Forces
| WC-ID | [m] | [N] | [-] | [-] | ||
|---|---|---|---|---|---|---|
| up | down | left | right | |||
| 01 | 0.12 | 6.60 | 0.14 | −0.13 | 0.08 | −0.05 |
| 02 | 0.06 | 1.89 | 0.10 | −0.11 | 0.07 | −0.10 |
| 03 | 0.13 | 7.79 | 0.07 | −0.13 | 0.06 | −0.03 |
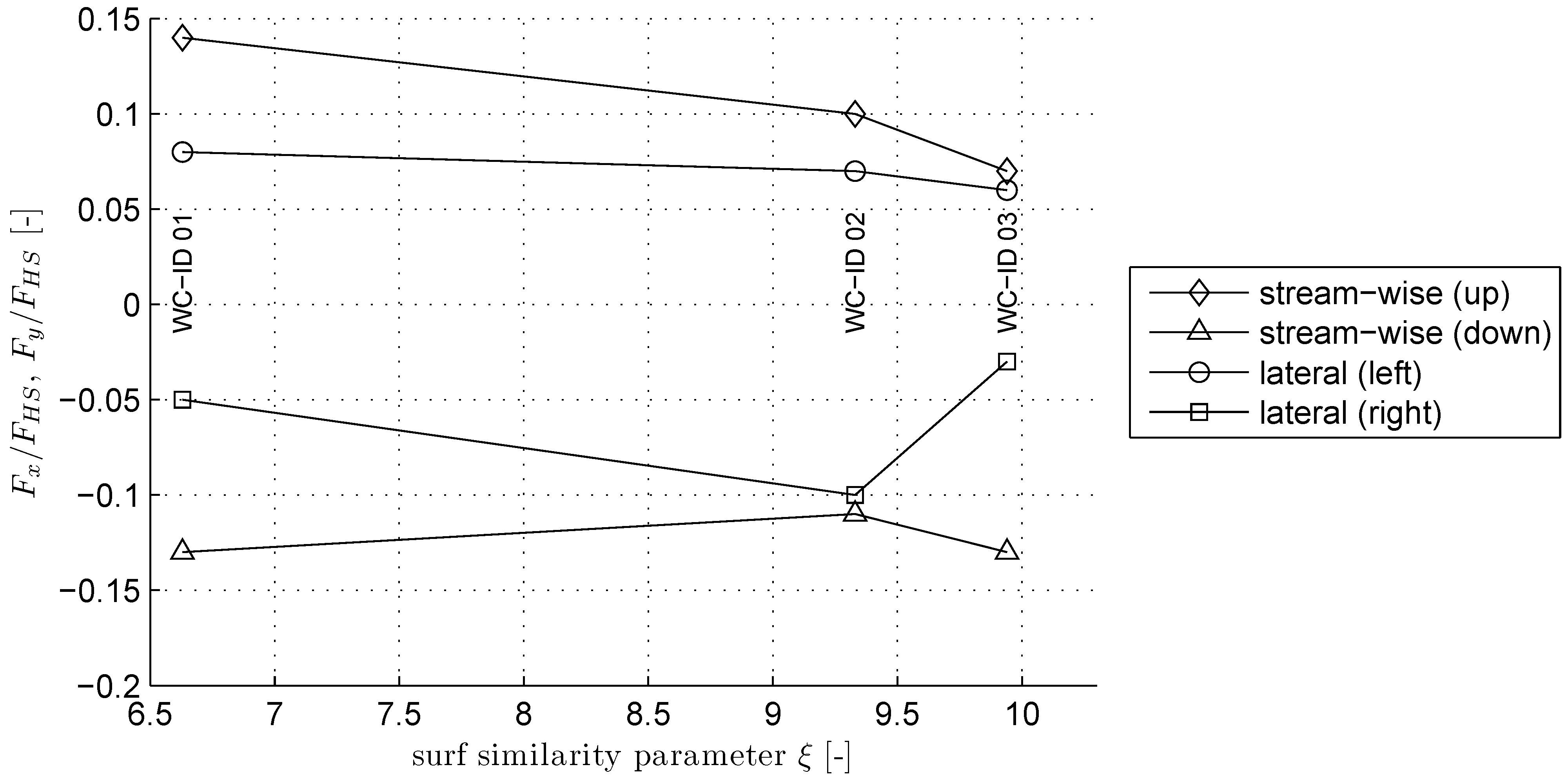
4. Discussion
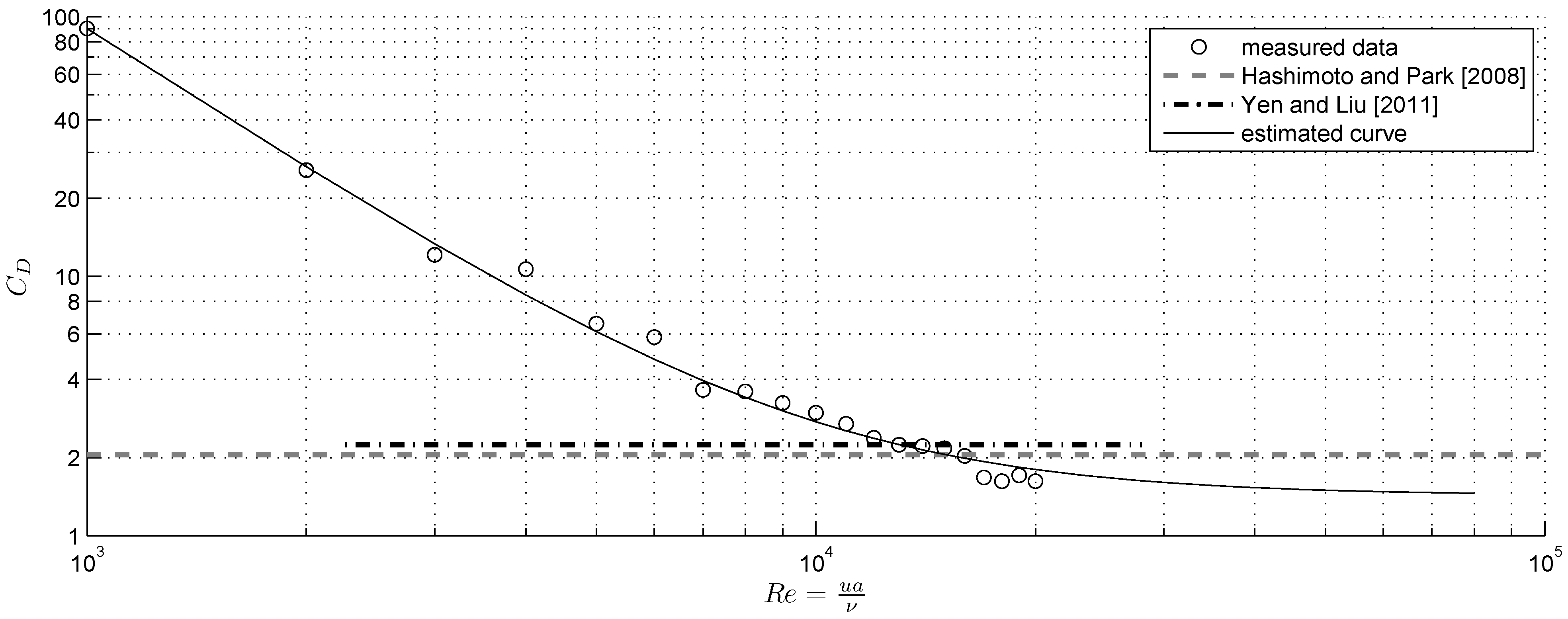
4.1. Drag Force Coefficient, Reynolds, Froude, Keulegan-Carpenter Number
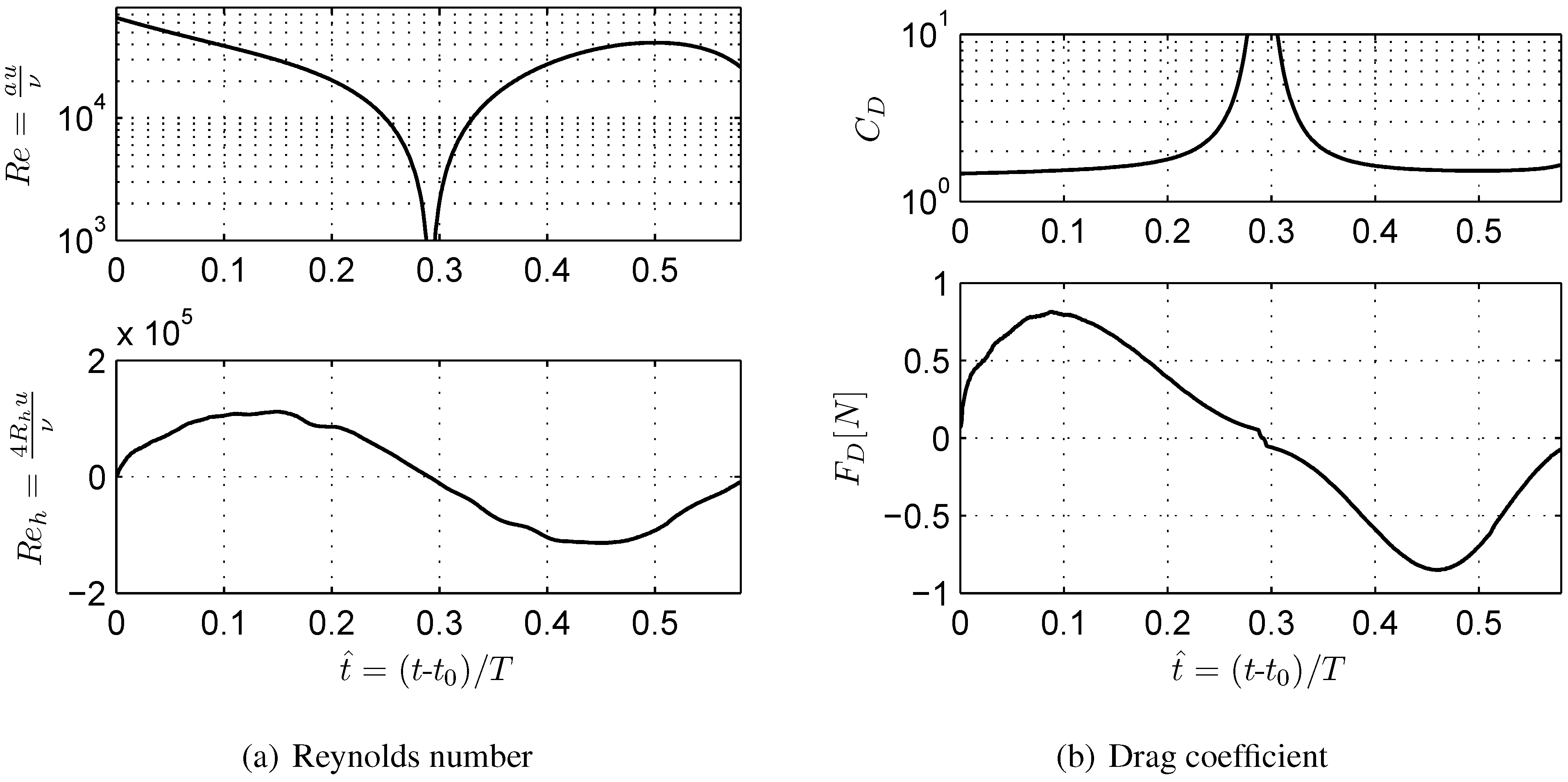
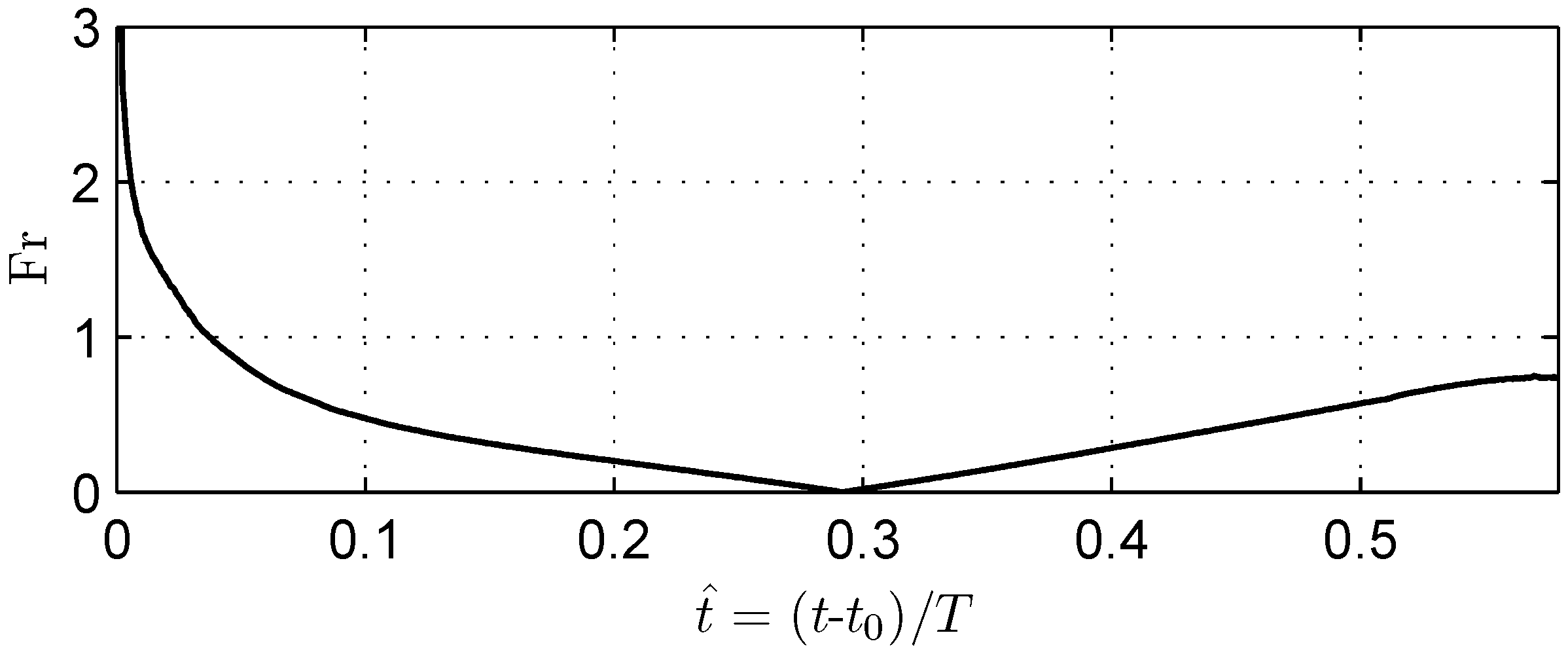
4.2. Comparison with Prototype-Scale Cases
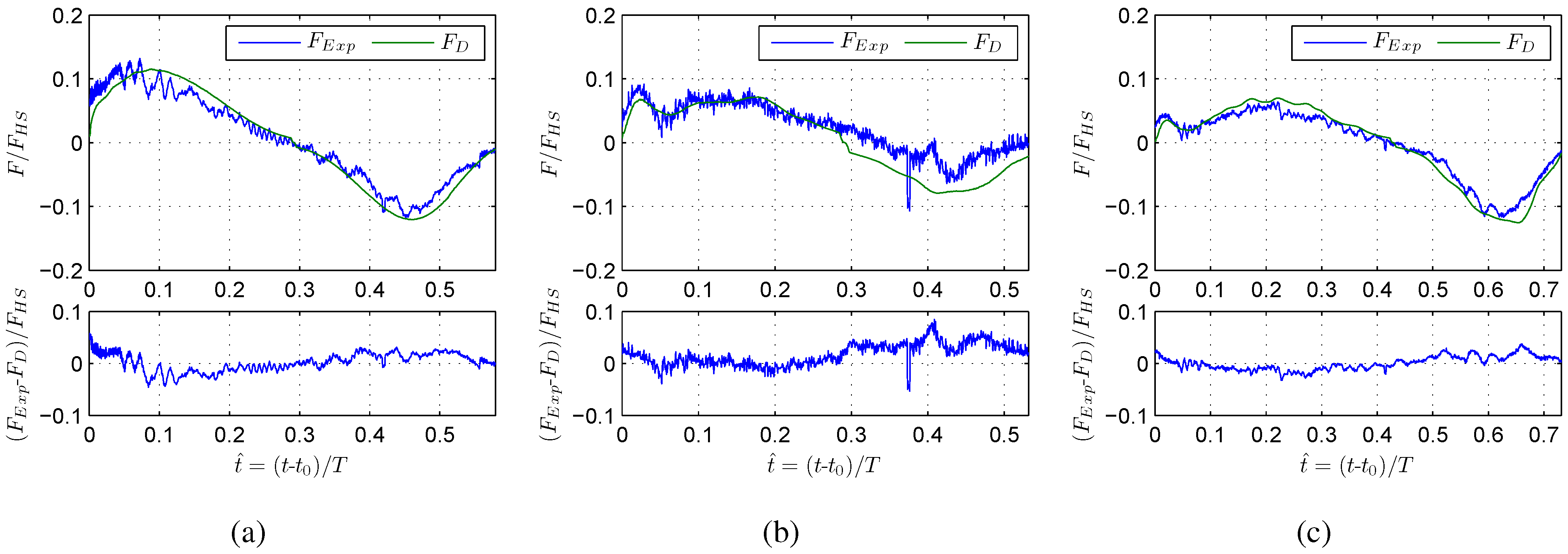
4.3. Comparison of Experimental and Computed Drag Forces
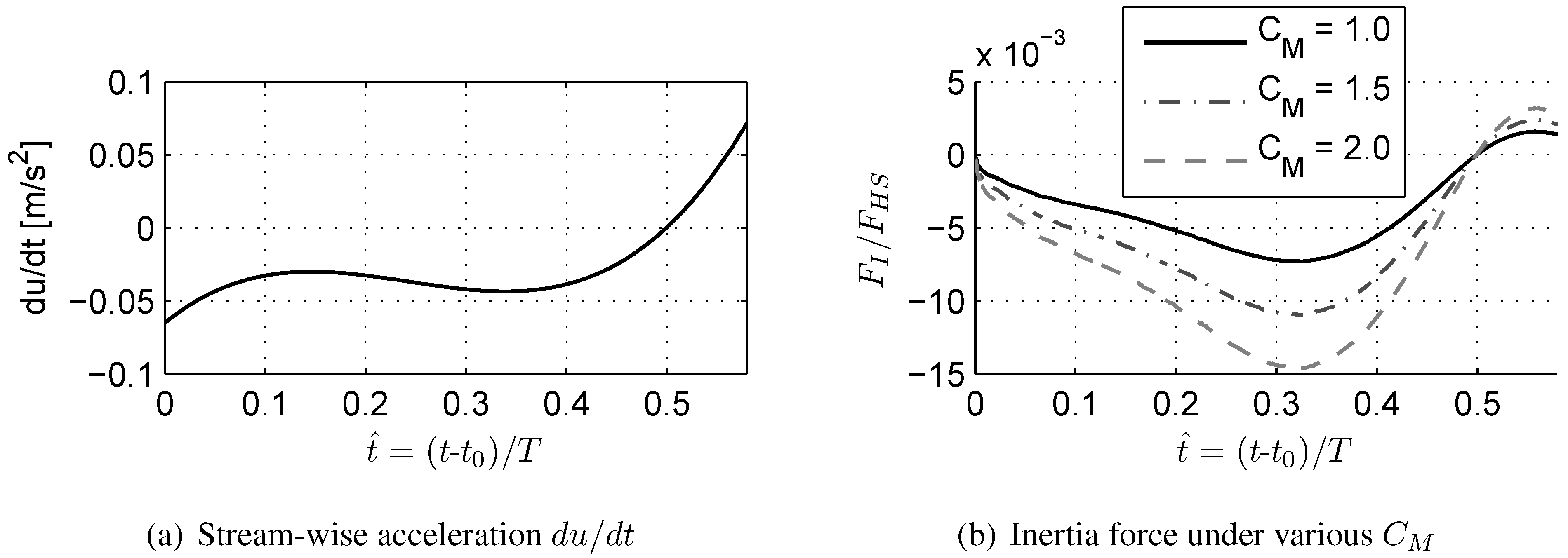
4.4. Analytically-Derived Inertial Forces
5. Conclusions
- Drag force coefficients which are a function of Reynolds numbers vary over the course of the flow-structure interaction. For the analytical computation of drag forces for a structure impacted by a transient flow it is thus important to incorporate the time-history of drag force coefficients rather than constant values. It was found that the calculated drag coefficients are well within the range of reported values found in the literature.
- Flow patterns around the structure consist of a series of complex, but meaningful physical processes and incorporate bow wave propagation upstream, hydraulic jump condition, turbulent wake development behind the structure and vortex shedding during the flow run-up and the draw-down over the beach which led to a considerably contribution towards the lateral total forces in all three cases.
- Using the water depth, the stream-wise velocity and drag force coefficients available at the location of a structure involved in flow-structure interaction it was possible to accurately predict the time-history of the drag forces generated from a given hydraulic configuration. However, using this method, it was not possible to confirm if oscillation-induced force contributions occur as a result of vortex shedding. To investigate this in more detail, experimental tests remain a valuable resource of information.
- As the hydraulic configurations applied are transient in nature, inertial forces might contribute to the total force exerted to the structure under investigation. However, inertia forces which were also found to occur during the flow run-up and draw-down are of an order of magnitude smaller than those drag forces exerted onto the structure. For the range of flow conditions investigated in this experimental program, it was found that one may neglect inertial forces for flows exhibiting the investigated range of flow periods.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Taubenböck, H.; Goseberg, N.; Setiadi, N.; Lämmel, G.; Moder, F.; Oczipka, M.; Klüpfel, H.; Wahl, R.; Schlurmann, T.; Strunz, G.; et al. Last-Mile preparation to a potential disaster—Interdisciplinary approach towards tsunami early warning and an evacuation information system for the coastal city of Padang, Indonesia. Nat. Hazards Earth Syst. Sci. 2009, 9, 1509–1528. [Google Scholar] [CrossRef]
- Taubenböck, H.; Goseberg, N.; Lämmel, G.; Setiadi, N.; Schlurmann, T.; Nagel, K.; Siegert, F.; Birkmann, J.; Traub, K.P.; Dech, S.; et al. Risk reduction at the “Last-Mile”: An attempt to turn science into action by the example of Padang, Indonesia. Nat. Hazards 2013, 65, 915–945. [Google Scholar] [CrossRef]
- Cheung, J.; Melbourne, W. Turbulence effects on some aerodynamic parameters of a circular cylinder at supercritical numbers. J. Wind Eng. Ind. Aerodyn. 1983, 14, 399–410. [Google Scholar] [CrossRef]
- Sumer, B.; Christiansen, N.; Fredsoe, J. The horseshoe vortex and vortex shedding around a vertical wall-mounted cylinder exposed to waves. J. Fluid Mech. 1997, 332, 41–70. [Google Scholar]
- Li, C.W.; Lin, P. A numerical study of three-dimensional wave interaction with a square cylinder. Ocean Eng. 2001, 28, 1545–1555. [Google Scholar] [CrossRef]
- Sundar, V.; Vengatesan, V.; Anandkumar, G.; Schlenkhoff, A. Hydrodynamic coefficients for inclined cylinders. Ocean Eng. 1998, 25, 277–294. [Google Scholar] [CrossRef]
- Cui, X.; Gray, J. Gravity-driven granular free-surface flow around a circular cylinder. J. Fluid Mech. 2013, 720, 314–337. [Google Scholar] [CrossRef]
- Alam, M.; Zhou, Y.; Wang, X. The wake of two side-by-side square cylinders. J. Fluid Mech. 2011, 669, 432–471. [Google Scholar] [CrossRef]
- Ramsden, J. Forces on a vertical wall due to long waves, bores, and dry-bed surges. J. Waterw. Port Coast. Ocean Eng. 1996, 122, 134–141. [Google Scholar] [CrossRef]
- Nouri, Y.; Nistor, I.; Palermo, D.; Cornett, A. Experimental Investigation of Tsunami Impact on Free Standing Structures. Coast Eng. J. 2010, 52, 43–70. [Google Scholar] [CrossRef]
- Goseberg, N. Reduction of maximum tsunami run-up due to the interaction with beachfront development—Application of single sinusoidal waves. Nat. Hazards Earth Syst. Sci. 2013, 13, 2991–3010. [Google Scholar] [CrossRef]
- Strusinska-Correia, A.; Husrin, S.; Oumeraci, H. Tsunami damping by mangrove forest: A laboratory study using parameterized trees. Nat. Hazards Earth Syst. Sci. 2013, 13, 483–503. [Google Scholar] [CrossRef]
- Park, H.; Cox, D.T.; Lynett, P.J.; Wiebe, D.M.; Shin, S. Tsunami inundation modeling in constructed environments: A physical and numerical comparison of free-surface elevation, velocity, and momentum flux. Coast. Eng. 2013, 79, 9–21. [Google Scholar] [CrossRef]
- Goseberg, N.; Schlurmann, T. Non-stationary flow around buildings during run-up of tsunami waves on a plain beach. In Proceedings of the 34th Conference on Coastal Engineering, Seoul, Korea, 15–20 June 2014.
- Kinsman, B. Wind Waves: Their Generation and Propagation on the Ocean Surface; Prentice-Hall: Englewood Cliffs, NY, USA, 1965. [Google Scholar]
- Liu, P.L.F.; Cho, Y.S.; Briggs, M.J.; Kanoglu, U.; Synolakis, C.E. Runup of solitary waves on a circular island. J. Fluid Mech. 1995, 302, 259–285. [Google Scholar] [CrossRef]
- Seiffert, B.; Hayatdavoodi, M.; Ertekin, R.C. Experiments and computations of solitary-wave forces on a coastal-bridge deck. Part I: Flat Plate. Coast. Eng. 2014, 88, 194–209. [Google Scholar]
- Aguiniga, F.; Jaiswal, M.; Sai, J.; Cox, D.; Gupta, R.; Van De Lindt, J. Experimental study of tsunami forces on structures. In Proceedings of the ASCE Engineering Mechanics Conference, Los Angeles, CA, United States, 8–11 August 2010.
- Chanson, H. Tsunami surges on dry coastal plains: Application of dam break wave equations. Coast. Eng. J. 2006, 48, 355–370. [Google Scholar] [CrossRef]
- Goseberg, N.; Wurpts, A.; Schlurmann, T. Laboratory-scale generation of tsunami and long waves. Coast. Eng. 2013, 79, 57–74. [Google Scholar] [CrossRef]
- Morison, J.; Johnson, J.; Schaaf, S. The force exerted by surface waves on piles. J. Pet. Technol. 1950, 2, 149–154. [Google Scholar] [CrossRef]
- Journée, J.; Massie, W. Offshore Hydromechanics, 1st ed.; Delft University of Technology: Delft, The Netherlandsï¼, 2001. [Google Scholar]
- Chakrabarti, S. Handbook of Offshore Engineering; Elsevier: Amsterdam, The Netherlands, 2005; Volume 1. [Google Scholar]
- Zhu, S.; Moule, G. Numerical calculation of forces induced by short-crested waves on a vertical cylinder of arbitrary cross-section. Ocean Eng. 1994, 21, 645–662. [Google Scholar] [CrossRef]
- Cai, S.; Long, X.; Gan, Z. A method to estimate the forces exerted by internal solitons on cylindrical piles. Ocean Eng. 2003, 30, 673–689. [Google Scholar] [CrossRef]
- De Vos, L.; Frigaard, P.; de Rouck, J. Wave run-up on cylindrical and cone shaped foundations for offshore wind turbines. Coast. Eng. 2007, 54, 17–29. [Google Scholar] [CrossRef]
- Hildebrandt, A.; Sparboom, U.; Oumeraci, H. Wave Forces on Groups of Slender Cylinders in Comparison to an Isolated Cylinder due to Non-Breaking Waves; World Scientific: Hamburg, Germany, 2008. [Google Scholar]
- Yeh, H. Maximum Fluid Forces in the Tsunami Runup Zone. J. Waterw. Port Coast. Ocean Eng. 2006, 132, 496–500. [Google Scholar] [CrossRef]
- Yen, S.; Liu, J. Wake flow behind two side-by-side square cylinders. Int. J. Heat Fluid Flow 2011, 32, 41–51. [Google Scholar] [CrossRef]
- Hashimoto, H.; Park, K. Two-dimensional urban flood simulation: Fukuoka flood disaster in 1999. WIT Trans. Ecol. Environ. 2008, 118, 59–67. [Google Scholar]
- Madsen, P.A.; Fuhrman, D.R.; Schäffer, H.A. On the solitary wave paradigm for tsunamis. J. Geophys. Res. 2008, 113, C12012. [Google Scholar] [CrossRef]
- Madsen, P.A.; Schäffer, H.A. Analytical solutions for tsunami runup on a plane beach: single waves, N-waves and transient waves. J. Fluid Mech. 2010, 645, 27–57. [Google Scholar] [CrossRef]
- Nezu, I.; Nakagawa, H. Turbulence in Open-Channel Flows; A.A. Balkema: Rotterdam, The Netherlands, 1993. [Google Scholar]
- Raffel, M.; Willert, C.E.; Kompenhans, J. Particle Image Velocimetry: A Practical Guide; Springer: Berlin, Germany; New York, NY, USA, 1998. [Google Scholar]
- Sveen, J.K. An introduction to MatPIV v. 1.6. 1. In Preprint series. Mechanics and Applied Mathematics; the Free Software Foundation, Inc.: Boston, MA, USA, 2004. [Google Scholar]
- Mo, W.; Jensen, A.; Liu, P.L.F. Plunging solitary wave and its interaction with a slender cylinder on a sloping beach. Ocean Eng. 2014, 74, 48–60. [Google Scholar] [CrossRef]
- Xioa, H.; Huang, W. Numerical modeling of wave runup and forces on an idealized beachfront house. Ocean Eng. 2008, 35, 106–116. [Google Scholar] [CrossRef]
- Schüttrumpf, H. Wellenüberlauf bei Seedeichen—Experimentelle und theoretische Untersuchungen. Ph.D. Thesis, Technical University Carolo-Wilhelmina, Braunschweig, Germany, 2001. [Google Scholar]
- Arnason, H.; Petroff, C.; Yeh, H. Tsunami bore impingement onto a vertical column. J. Disaster Res. 2009, 4, 391–403. [Google Scholar]
- Fritz, H.M.; Phillips, D.A.; Okayasu, A.; Shimozono, T.; Liu, H.; Mohammed, F.; Skanavis, V.; Synolakis, C.E.; Takahashi, T. The 2011 Japan tsunami current velocity measurements from survivor videos at Kesennuma Bay using LiDAR. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Hayashi, S.; Koshimura, S. The 2011 Tohoku tsunami flow velocity estimation by the aerial video analysis and numerical modeling. J. Disaster Res. 2013, 8, 561–572. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bremm, G.C.; Goseberg, N.; Schlurmann, T.; Nistor, I. Long Wave Flow Interaction with a Single Square Structure on a Sloping Beach. J. Mar. Sci. Eng. 2015, 3, 821-844. https://doi.org/10.3390/jmse3030821
Bremm GC, Goseberg N, Schlurmann T, Nistor I. Long Wave Flow Interaction with a Single Square Structure on a Sloping Beach. Journal of Marine Science and Engineering. 2015; 3(3):821-844. https://doi.org/10.3390/jmse3030821
Chicago/Turabian StyleBremm, Gian C., Nils Goseberg, Torsten Schlurmann, and Ioan Nistor. 2015. "Long Wave Flow Interaction with a Single Square Structure on a Sloping Beach" Journal of Marine Science and Engineering 3, no. 3: 821-844. https://doi.org/10.3390/jmse3030821
APA StyleBremm, G. C., Goseberg, N., Schlurmann, T., & Nistor, I. (2015). Long Wave Flow Interaction with a Single Square Structure on a Sloping Beach. Journal of Marine Science and Engineering, 3(3), 821-844. https://doi.org/10.3390/jmse3030821






