Construction of a Static Model for Power Generation of OTEC Plant Using Uehara Cycle Based on Experimental Data
Abstract
:1. Introduction
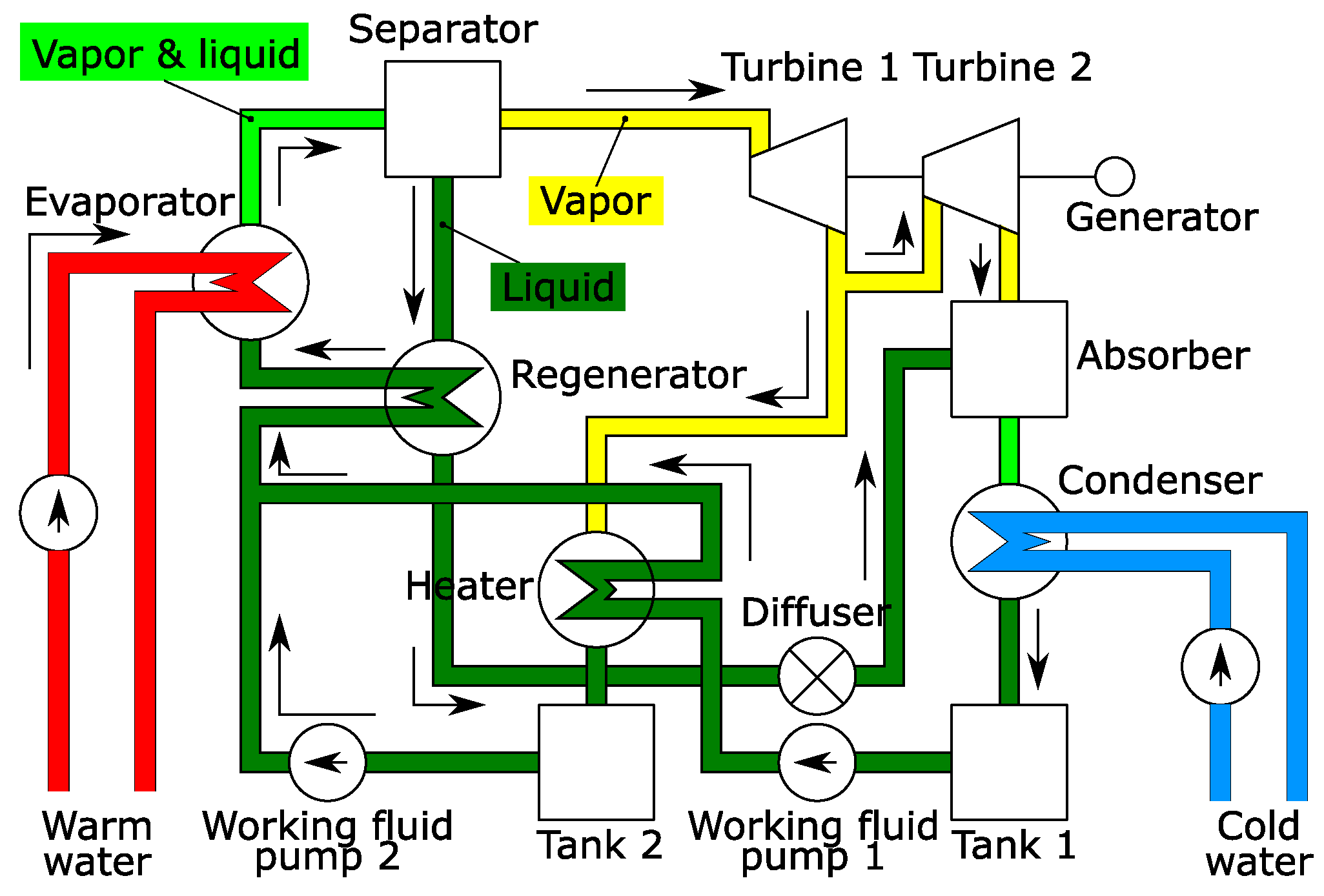
2. OTEC Plant Using Uehara Cycle
3. Construction of Static Model for Power Generation
3.1. Heat Source Side Model
3.2. Cold Source Side Model
4. Evaluation by Numerical Simulation
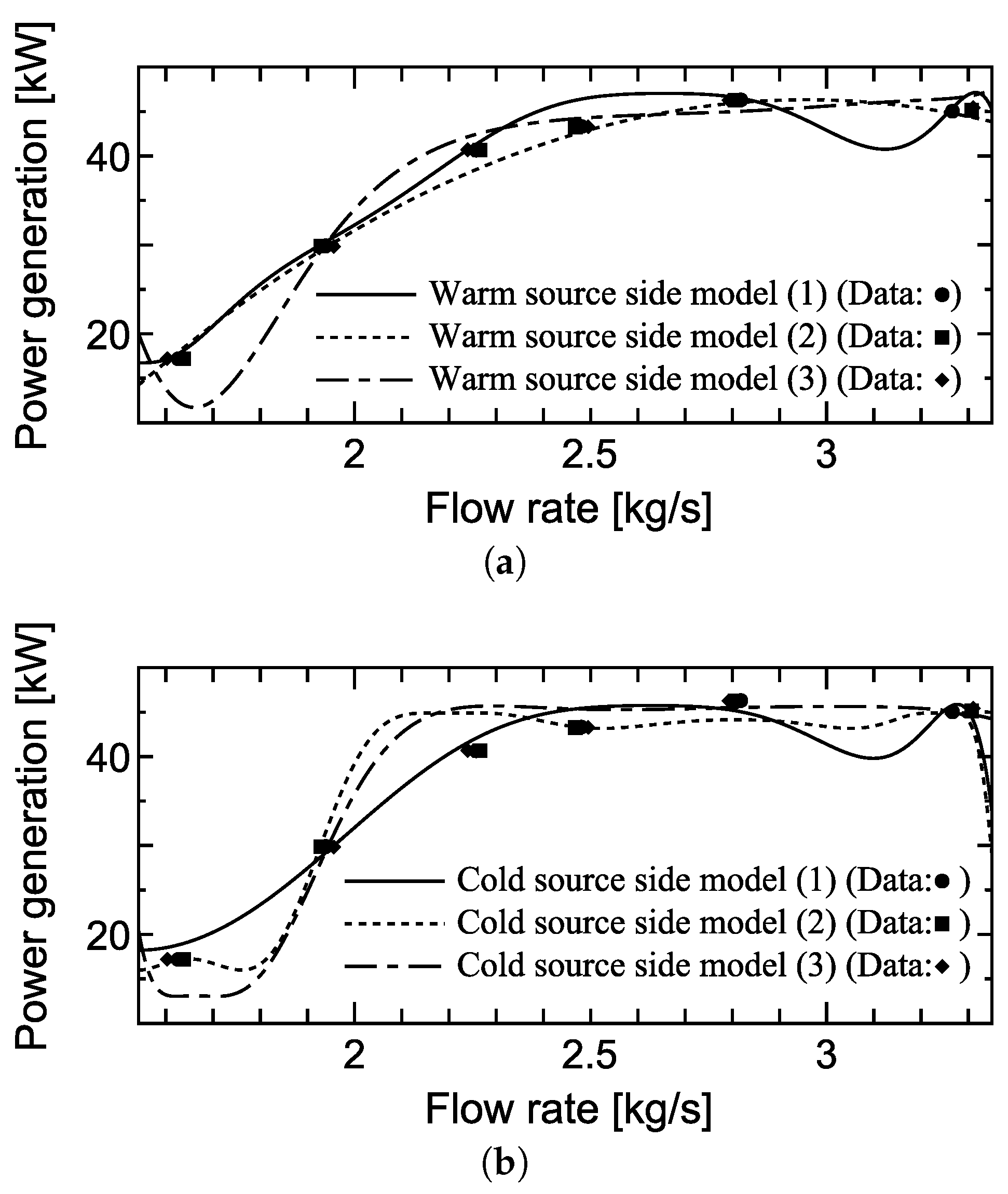
4.1. Derivation of Input-Output Relations
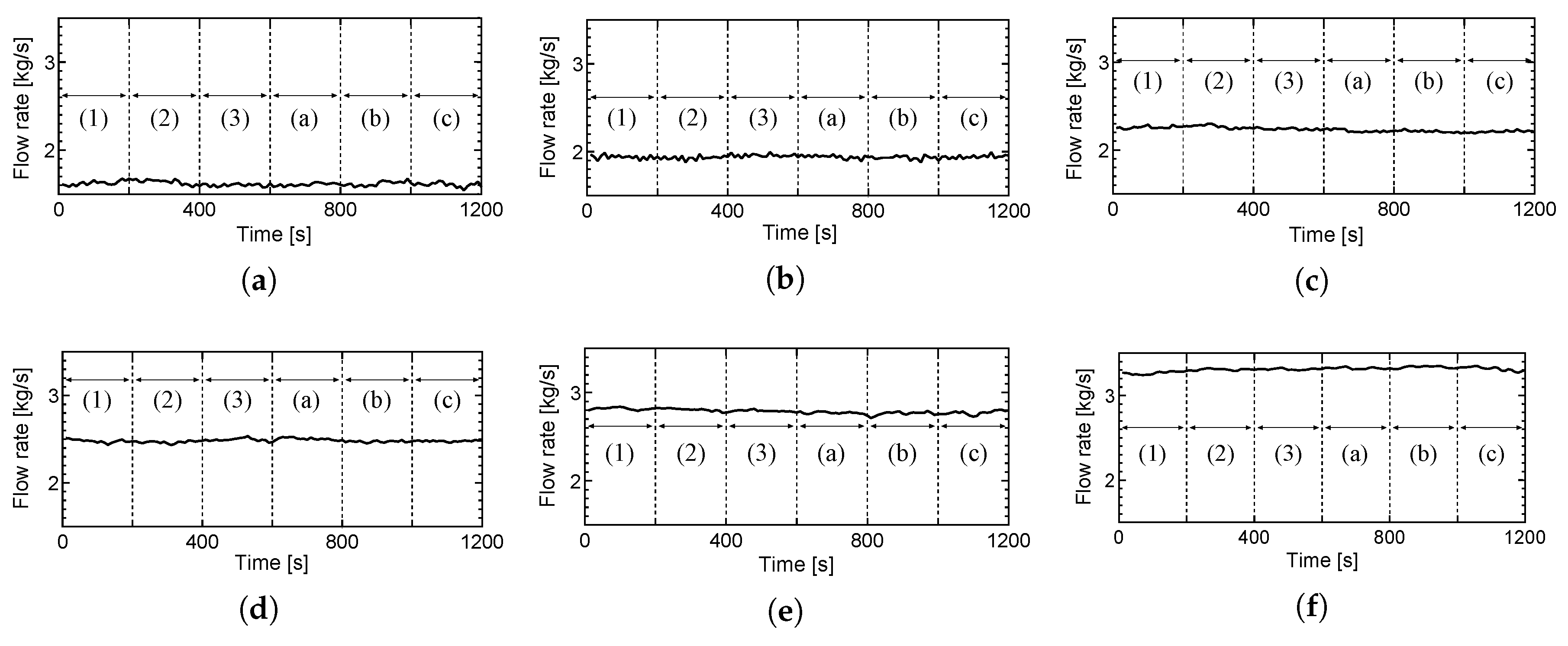
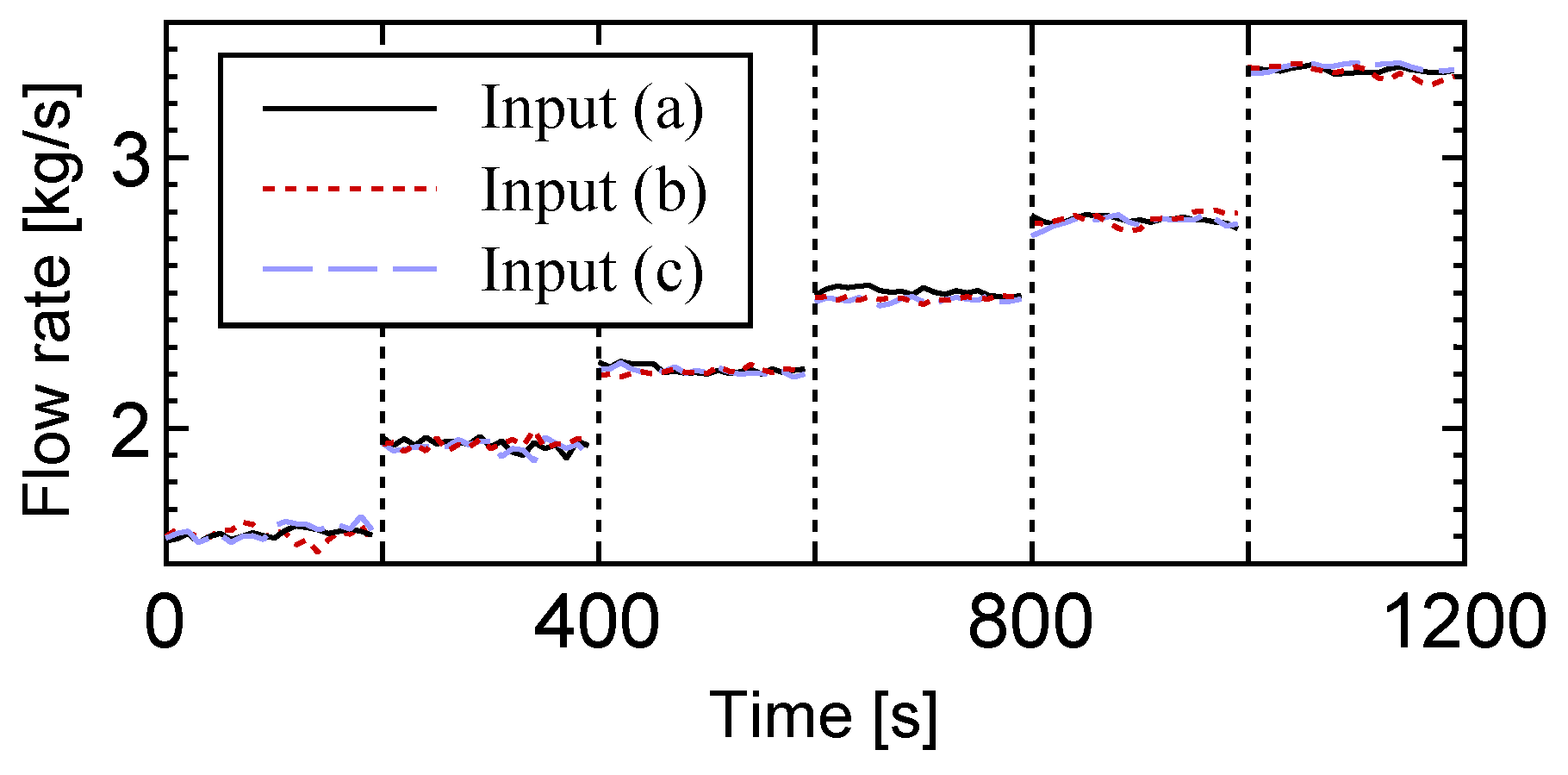
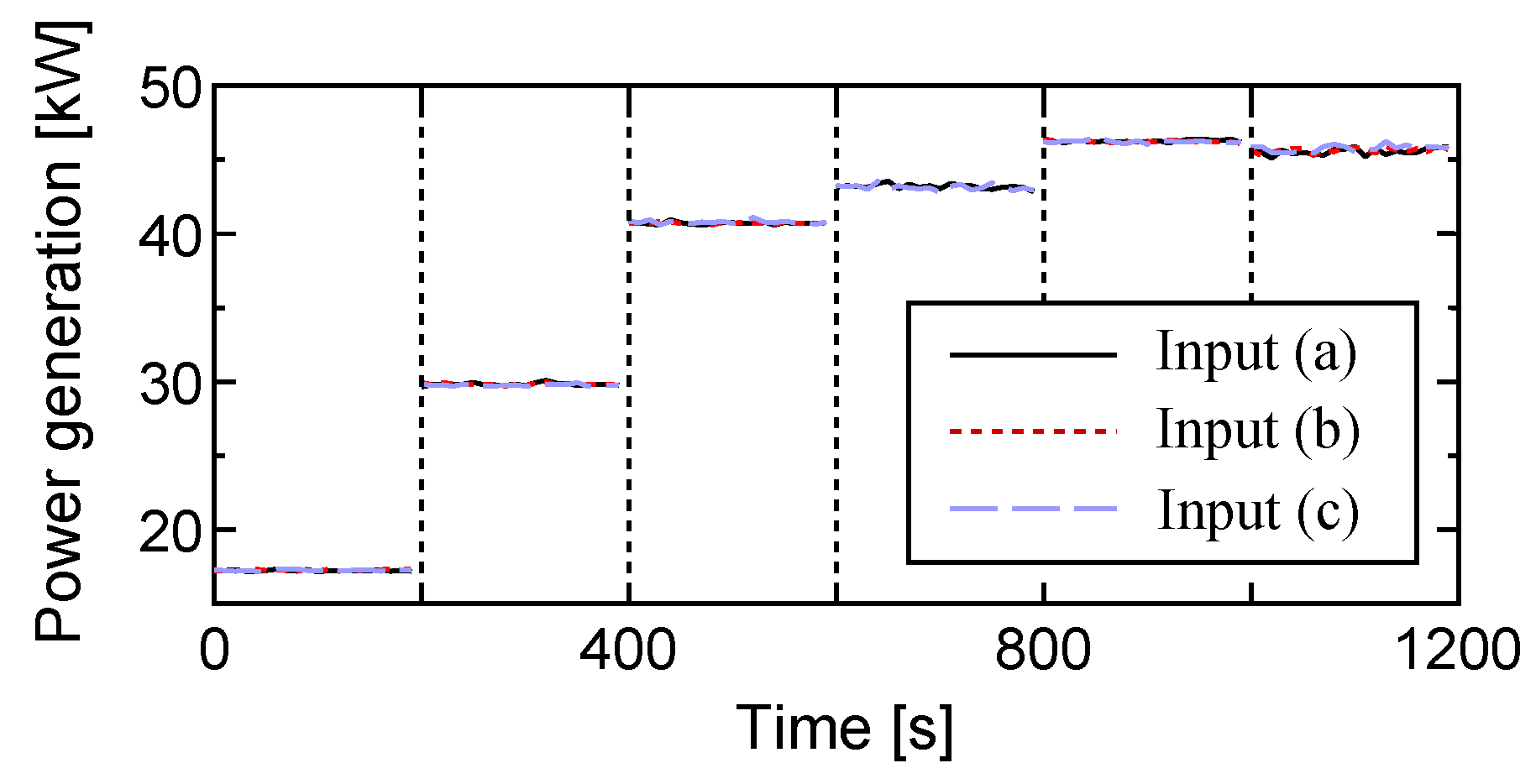
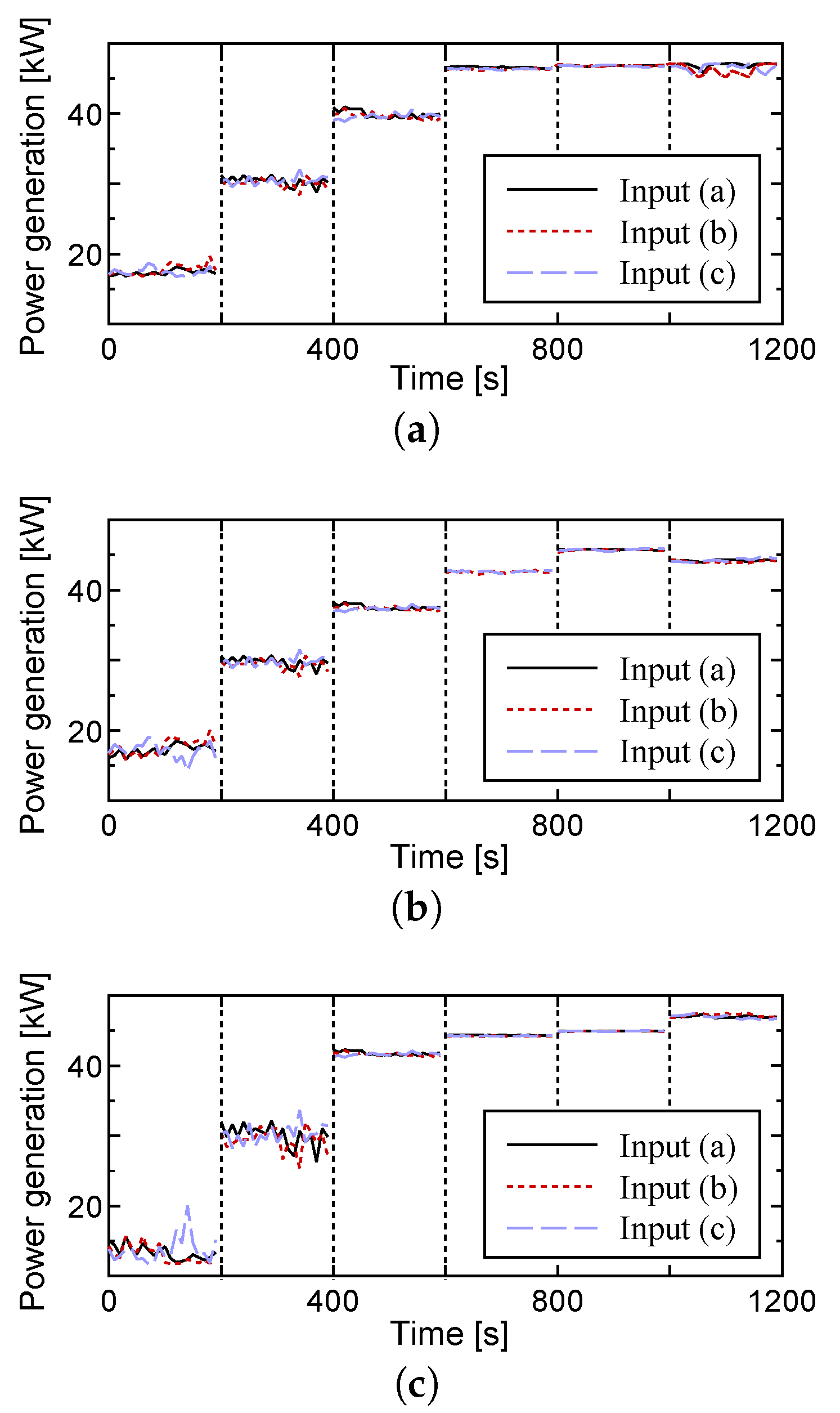
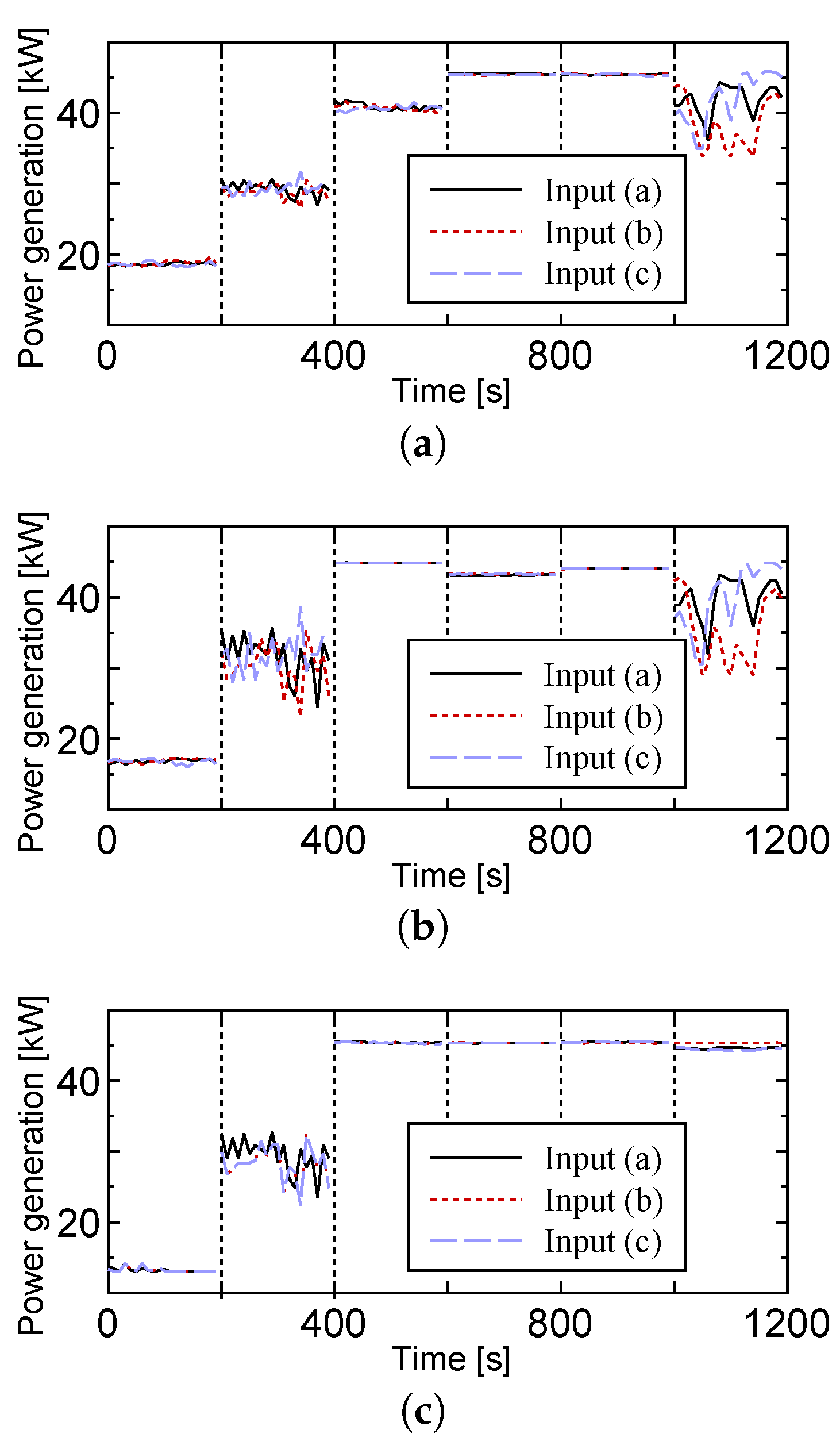
4.2. Numerical Simulations by Using Experimental Data as Input
4.3. Computational Time for Numerical Simulation
5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Khaligh, A.; Onar, O.C. Energy Harvesting, Solar, Wind, and Ocean Energy Conversion Systems; CRC Press: Boca Raton, FL, USA, 2010; pp. 305–341. [Google Scholar]
- Kim, A.S.; Kim, H.J.; Lee, H.S.; Cha, S. Dual-use open cycle ocean thermal energy conversion (OC-OTEC) using multiple condensers for adjustable power generation and seawater desalination. Renew. Energy 2016, 85, 344–358. [Google Scholar] [CrossRef]
- Azhar, M.S.; Rizvi, G.; Dincer, I. Integration of renewable energy based multigeneration system with desalination. Desalination 2017, 404, 72–78. [Google Scholar] [CrossRef]
- Ikegami, Y.; Sasaki, H.; Gouda, T.; Uehara, H. Experimental study on a spray flash desalination (influence of the direction of injection). Desalination 2006, 194, 81–89. [Google Scholar] [CrossRef]
- Uehara, H.; Nakaoka, T.; Tashiro, H.; Koga, T. A Note on the Spray Flash Desalination Apparatus; IOES: Saga, Japan, 1989; pp. 1–11. (In Japanese) [Google Scholar]
- Uehara, H.; Ikegami, Y.; Nakaoka, T.; Hirota, T. Experimental Study of a Spray Flash Desalination. Bull. Soc. Sea Water Sci. Jpn. 1997, 51, 34–42. (In Japanese) [Google Scholar]
- Goto, S.; Yamamoto, Y.; Sugi, T.; Yasunaga, T.; Ikegami, Y.; Nakamura, M. Construction of Simulation Model for Spray Flash Desalination System. Electr. Eng. Jpn. 2010, 170, 9–17. [Google Scholar] [CrossRef]
- VanZwieten, J.H.; Rauchenstein, L.T.; Lee, L. An assessment of Florida’s ocean thermal energy conversion (OTEC). Renew. Sustain. Energy Rev. 2017, 75, 683–691. [Google Scholar] [CrossRef]
- Syamsuddin, M.L.; Attamimi, A.; Nugraha, A.P.; Gibran, S.; Afifah, A.Q.; Oriana, N. OTEC Potential in The Indonesian Seas. Energy Procedia 2015, 65, 215–222. [Google Scholar] [CrossRef]
- Rajagopalan, K.; Nihous, G.C. Estimates of global Ocean Thermal Energy Conversion (OTEC) resources using an ocean general circulation model. Renew. Energy 2013, 50, 532–540. [Google Scholar] [CrossRef]
- Kamogawa, H. OTEC Research in Japan. Energy 1980, 5, 481–492. [Google Scholar] [CrossRef]
- Uehara, H.; Dilao, C.O.; Nakaoka, T. Conceptual Design of Ocean Thermal Energy Conversion (OTEC) Power Plants in the Philippines. Sol. Energy 1988, 41, 431–441. [Google Scholar] [CrossRef]
- Chong, H.Y.; Lam, W.H. Ocean renewable energy in Malaysia: The potential of the Straits of Malacca. Renew. Sustain. Energy Rev. 2013, 23, 169–178. [Google Scholar] [CrossRef]
- Inui, E.; Nagatomo, K.; Nakaoka, T.; Nishida, T.; Uehara, H.; Miyara, A. Investigation of Marine Meteorology Off the Coast of the Oki-No-Erabu Island for Ocean Thermal Energy Conversion; IOES: Saga, Japan, 1990; pp. 1–7. (In Japanese) [Google Scholar]
- Inui, E.; Nagatomo, K.; Nishida, T.; Ikegami, Y.; Nakaoka, T.; Uehara, H. Investigation of Energy Source in World Oceans for Ocean Thermal Energy Conversion (OTEC); IOES: Saga, Japan, 1994; pp. 1–7. (In Japanese) [Google Scholar]
- Nakaoka, T.; Nishida, T.; Ichinose, J.; Tabuchi, K.; Kamano, K.; Ikegami, Y.; Uehara, H. Oceanograohic Observations Off the Coast of the Fiji Island and the Oceanic Characteristic (Observations of 2003); IOES: Saga, Japan, 2004; pp. 1–19. (In Japanese) [Google Scholar]
- Yang, M.H.; Yeh, R.H. Analysis of optimization in an OTEC plant using organic Rankine cycle. Renew. Energy 2014, 68, 25–34. [Google Scholar] [CrossRef]
- Sun, F.; Ikegami, Y.; Jia, B.; Arima, H. Optimization design and exergy analysis of organic rankine cycle in ocean thermal energy conversion. Appl. Ocean Res. 2012, 35, 38–46. [Google Scholar] [CrossRef]
- Kusuda, E.; Morisaki, T.; Ikegami, Y. Performance Test of Double-stage Rankine Cycle experimental plant for OTEC. Procedia Eng. 2015, 105, 713–718. [Google Scholar] [CrossRef]
- Murata, A.; Takazawa, H.; Kajikawa, T. Experimental Study of Transient Modeling of Closed Cycle Otec Power System. IEEJ Trans. Power Energy 1987, 107, 123–130. (In Japanese) [Google Scholar] [CrossRef]
- Nakaoka, T.; Uehara, H. Performance Test of a Shell-and-Plate Type Evaporator for OTEC. Exp. Therm. Fluid Sci. 1988, 1, 283–291. [Google Scholar] [CrossRef]
- Nakaoka, T.; Uehara, H. Performance Test of a Shell-and-Plate-Type Condenser for OTEC. Exp. Therm. Fluid Sci. 1988, 1, 275–281. [Google Scholar] [CrossRef]
- Jitsuhara, S.; Nakamura, M.; Ikegami, Y.; Uehara, H. Controller Design for Vapor Temperatures of OTEC Plant Based on Reduced Order Model. Trans. Soc. Instrum. Control Eng. 1994, 30, 1060–1068. (In Japanese) [Google Scholar] [CrossRef]
- Yasunaga, T.; Ikegami, Y.; Monde, M. Performance Test of OTEC with Ammonia/water as Working Fluid Using Shell and Plate Type Heat Exchangers, Effects of Heat Source Temperature and Flow Rate. Trans. Jpn. Soc. Mech. Eng. Ser. B 2008, 74, 445–452. (In Japanese) [Google Scholar] [CrossRef]
- Takazawa, H.; Amano, M.; Kajikawa, T. At-Sea Experiments of Ocean-Based OTEC Experimental Facility in Toyama Bay. IEEJ Trans. Sens. Micromach. 1992, 112, 277–284. (In Japanese) [Google Scholar] [CrossRef]
- Kalina, A.I. Generation of Energy by Means of a Working Fluid, and Regeneration of a Working Fluid. U.S. Patent 4346561, 24 November 1982. [Google Scholar]
- Uehara, H.; Ikegami, Y.; Nishida, T. Performance Analysis of OTEC System Using a Cycle with Absorption and Extraction Processes. Trans. Jpn. Soc. Mech. Eng. Ser. B 1998, 64, 384–389. (In Japanese) [Google Scholar] [CrossRef]
- Ikegami, Y.; Yasunaga, T.; Harada, H. Performance Experiments on Ocean Thermal Energy Conversion System Using the Uehara Cycle. Bull. Soc. Sea Water Sci. Jpn. 2006, 60, 32–38. (In Japanese) [Google Scholar]
- Goto, S.; Motoshima, Y.; Sugi, T.; Yasunaga, T.; Ikegami, Y.; Nakamura, M. Construction of Simulation Model for OTEC Plant Using Uehara Cycle. Electr. Eng. Jpn. 2011, 176, 1–13. [Google Scholar] [CrossRef]
- PROPATH. Available online: http://www.mech.kyushu-u.ac.jp/~heat/propath/ (accessed on 26 December 2017).
- Institute of Ocean Energy, Saga University, Japan. Available online: http://www.ioes.saga-u.ac.jp/en/ (accessed on 26 December 2017).


| Parameter (Unit) | Value |
|---|---|
| Temperature of Warm Water (C) | 30 |
| Temperature of cold water (C) | 9 |
| Flow rate of warm water (kg/s) | 111.1 |
| Flow rate of cold water (kg/s) | 111.1 |
| Mass fraction of working fluid (kg/kg) | 0.97 |
| Flow rate of working fluid (kg/s) | 1.67, 1.94, 2.22, 2.50, 2.78, 3.33 |
| Sampling time (s) | 10 |
| (a) Warm Source Side Model | |||
| Data | (1) | (2) | (3) |
| Polynomial | 3 | 1 | 1 |
| Polynomial | 4 | 2 | 2 |
| Polynomial | 4 | 1 | 1 |
| Polynomial | 3 | 2 | 3 |
| Polynomial | 3 | 1 | 1 |
| Polynomial | 1 | 1 | 2 |
| Polynomial | 3 | 1 | 3 |
| IAE (kW·s) | 1254.0 | 1207.4 | 2025.2 |
| (b) Cold Source Side Model | |||
| Data | (1) | (2) | (3) |
| Polynomial | 1 | 3 | 4 |
| Polynomial | 2 | 1 | 4 |
| Polynomial | 2 | 3 | 1 |
| Polynomial | 1 | 2 | 3 |
| Polynomial | 4 | 3 | 2 |
| Polynomial | 2 | 2 | 2 |
| IAE (kW·s) | 1600.7 | 2222.8 | 2851.2 |
| (a) IAE by Warm Source Side Model Constructed from Data Interval (1) | |||||||
| Working Fluid Flow Rate (kg/s) | 1.67 | 1.94 | 2.22 | 2.50 | 2.78 | 3.33 | Total |
| Input (a) (kW·s) | 59.9 | 159.7 | 169.1 | 681.5 | 109.8 | 275.1 | 1455.1 |
| Input (b) (kW·s) | 126.8 | 115.9 | 213.7 | 628.9 | 119.3 | 174.9 | 1379.6 |
| Input (c) (kW·s) | 84.8 | 147.5 | 237.2 | 649.7 | 110.6 | 167.0 | 1396.7 |
| (b) IAE by Warm Source Side Model Constructed from Data Interval (2) | |||||||
| Working Fluid Flow Rate (kg/s) | 1.67 | 1.94 | 2.22 | 2.50 | 2.78 | 3.33 | Total |
| Input (a) (kW·s) | 114.7 | 104.6 | 630.3 | 42.6 | 102.5 | 275.9 | 1270.6 |
| Input (b) (kW·s) | 197.1 | 125.9 | 666.3 | 122.8 | 107.0 | 322.9 | 1542.0 |
| Input (c) (kW·s) | 174.4 | 93.8 | 687.9 | 95.8 | 94.2 | 301.8 | 1447.9 |
| (c) IAE by Warm Source Side Model Constructed from Data Interval (3) | |||||||
| Working Fluid Flow Rate (kg/s) | 1.67 | 1.94 | 2.22 | 2.50 | 2.78 | 3.33 | Total |
| Input (a) (kW·s) | 772.9 | 244.0 | 210.9 | 227.7 | 270.1 | 284.4 | 2010.0 |
| Input (b) (kW·s) | 840.7 | 250.0 | 182.4 | 207.8 | 268.4 | 306.4 | 2055.6 |
| Input (c) (kW·s) | 764.2 | 224.0 | 162.3 | 220.7 | 262.7 | 232.8 | 1866.7 |
| (a) IAE by Cold Source Side Model Constructed from Data Interval (1) | |||||||
| Working Fluid Flow Rate (kg/s) | 1.67 | 1.94 | 2.22 | 2.50 | 2.78 | 3.33 | Total |
| Input (a) (kW·s) | 275.6 | 166.6 | 81.4 | 469.4 | 169.6 | 750.4 | 1913.0 |
| Input (b) (kW·s) | 301.2 | 224.5 | 60.8 | 442.8 | 158.8 | 1419.9 | 2607.9 |
| Input (c) (kW·s) | 275.1 | 158.2 | 68.1 | 457.7 | 169.4 | 762.0 | 1890.5 |
| (b) IAE by Cold Source Side Model Constructed from Data Interval (2) | |||||||
| Working Fluid Flow Rate (kg/s) | 1.67 | 1.94 | 2.22 | 2.50 | 2.78 | 3.33 | Total |
| Input (a) (kW·s) | 73.0 | 610.2 | 836.8 | 26.0 | 429.3 | 1125.4 | 3100.7 |
| Input (b) (kW·s) | 66.7 | 479.6 | 835.0 | 35.1 | 427.9 | 2040.3 | 3884.6 |
| Input (c) (kW·s) | 85.2 | 548.1 | 819.9 | 37.1 | 423.8 | 1158.0 | 3072.1 |
| (c) IAE by Cold Source Side Model Constructed from Data Interval (3) | |||||||
| Working Fluid Flow Rate (kg/s) | 1.67 | 1.94 | 2.22 | 2.50 | 2.78 | 3.33 | Total |
| Input (a) (kW·s) | 803.2 | 362.2 | 941.5 | 423.2 | 161.5 | 196.8 | 2888.3 |
| Input (b) (kW·s) | 805.6 | 436.2 | 928.4 | 434.1 | 158.7 | 243.4 | 3006.4 |
| Input (c) (kW·s) | 786.9 | 324.4 | 911.2 | 440.2 | 154.8 | 225.5 | 2843.1 |
| (a) Warm Source Side Model | ||||
| Data | (1) | (2) | (3) | Average (s) |
| Input (a) | 0.02367 | 0.02320 | 0.02361 | 0.02349 |
| Input (b) | 0.02334 | 0.02324 | 0.02313 | 0.02324 |
| Input (c) | 0.02337 | 0.02321 | 0.02299 | 0.02319 |
| Average (s) | 0.02346 | 0.02322 | 0.02324 | 0.02331 |
| (b) Cold Source Side Model | ||||
| Data | (1) | (2) | (3) | Average (s) |
| Input (a) | 0.01944 | 0.01929 | 0.01948 | 0.01940 |
| Input (b) | 0.01936 | 0.01987 | 0.01932 | 0.01951 |
| Input (c) | 0.01926 | 0.01940 | 0.01949 | 0.01938 |
| Average (s) | 0.01935 | 0.01952 | 0.01943 | 0.01943 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Matsuda, Y.; Yoshitake, T.; Sugi, T.; Goto, S.; Morisaki, T.; Yasunaga, T.; Ikegami, Y. Construction of a Static Model for Power Generation of OTEC Plant Using Uehara Cycle Based on Experimental Data. J. Mar. Sci. Eng. 2018, 6, 18. https://doi.org/10.3390/jmse6010018
Matsuda Y, Yoshitake T, Sugi T, Goto S, Morisaki T, Yasunaga T, Ikegami Y. Construction of a Static Model for Power Generation of OTEC Plant Using Uehara Cycle Based on Experimental Data. Journal of Marine Science and Engineering. 2018; 6(1):18. https://doi.org/10.3390/jmse6010018
Chicago/Turabian StyleMatsuda, Yoshitaka, Takuma Yoshitake, Takenao Sugi, Satoru Goto, Takafumi Morisaki, Takeshi Yasunaga, and Yasuyuki Ikegami. 2018. "Construction of a Static Model for Power Generation of OTEC Plant Using Uehara Cycle Based on Experimental Data" Journal of Marine Science and Engineering 6, no. 1: 18. https://doi.org/10.3390/jmse6010018
APA StyleMatsuda, Y., Yoshitake, T., Sugi, T., Goto, S., Morisaki, T., Yasunaga, T., & Ikegami, Y. (2018). Construction of a Static Model for Power Generation of OTEC Plant Using Uehara Cycle Based on Experimental Data. Journal of Marine Science and Engineering, 6(1), 18. https://doi.org/10.3390/jmse6010018





