BEM Modeling for Stress Sensitivity of Nonlocal Thermo-Elasto-Plastic Damage Problems
Abstract
:1. Introduction
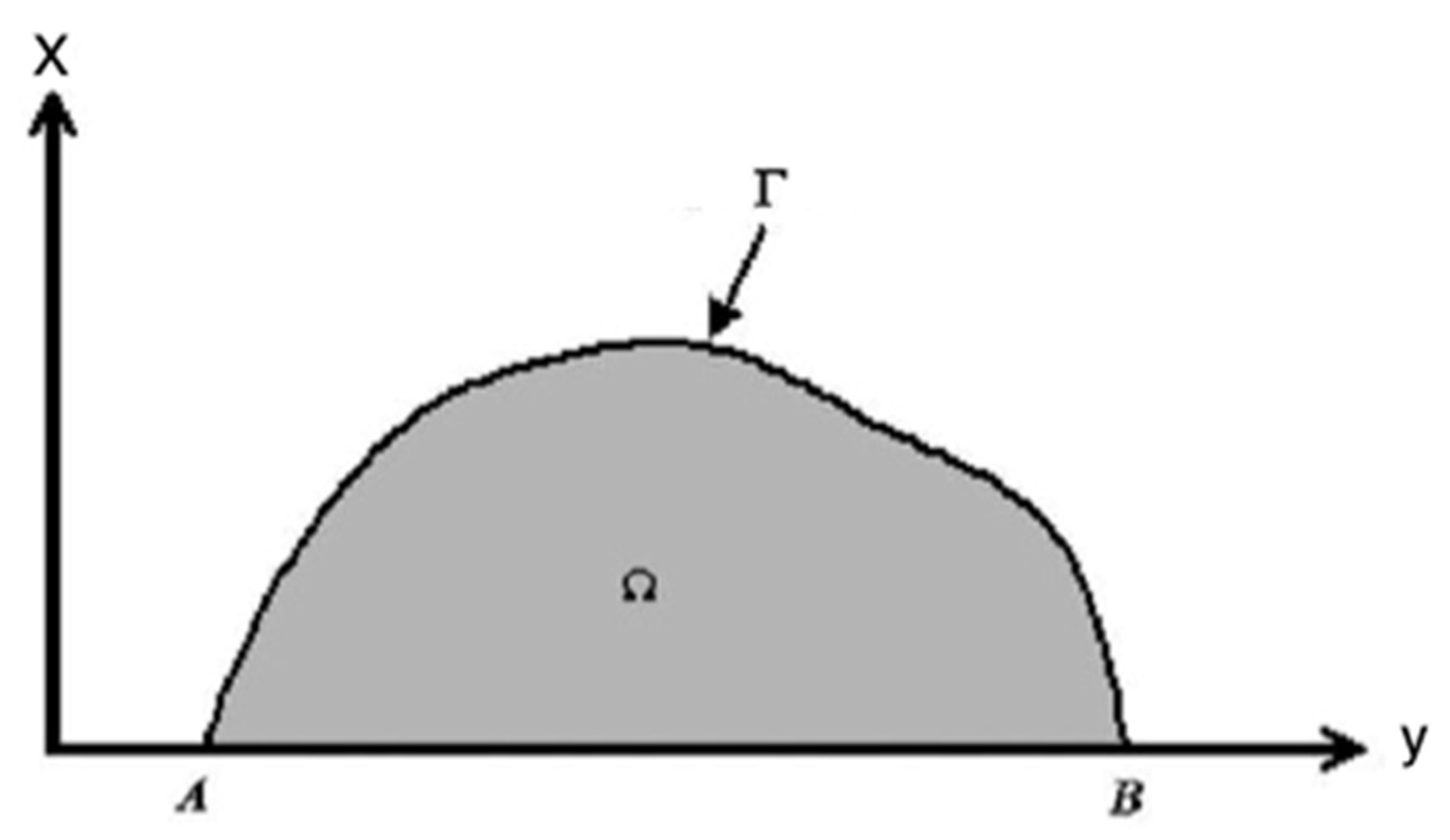
2. Formulation of the Problem
3. BEM Modeling of the Temperature Field
4. BEM Modeling of Thermo-Elasto-Plastic Deformation
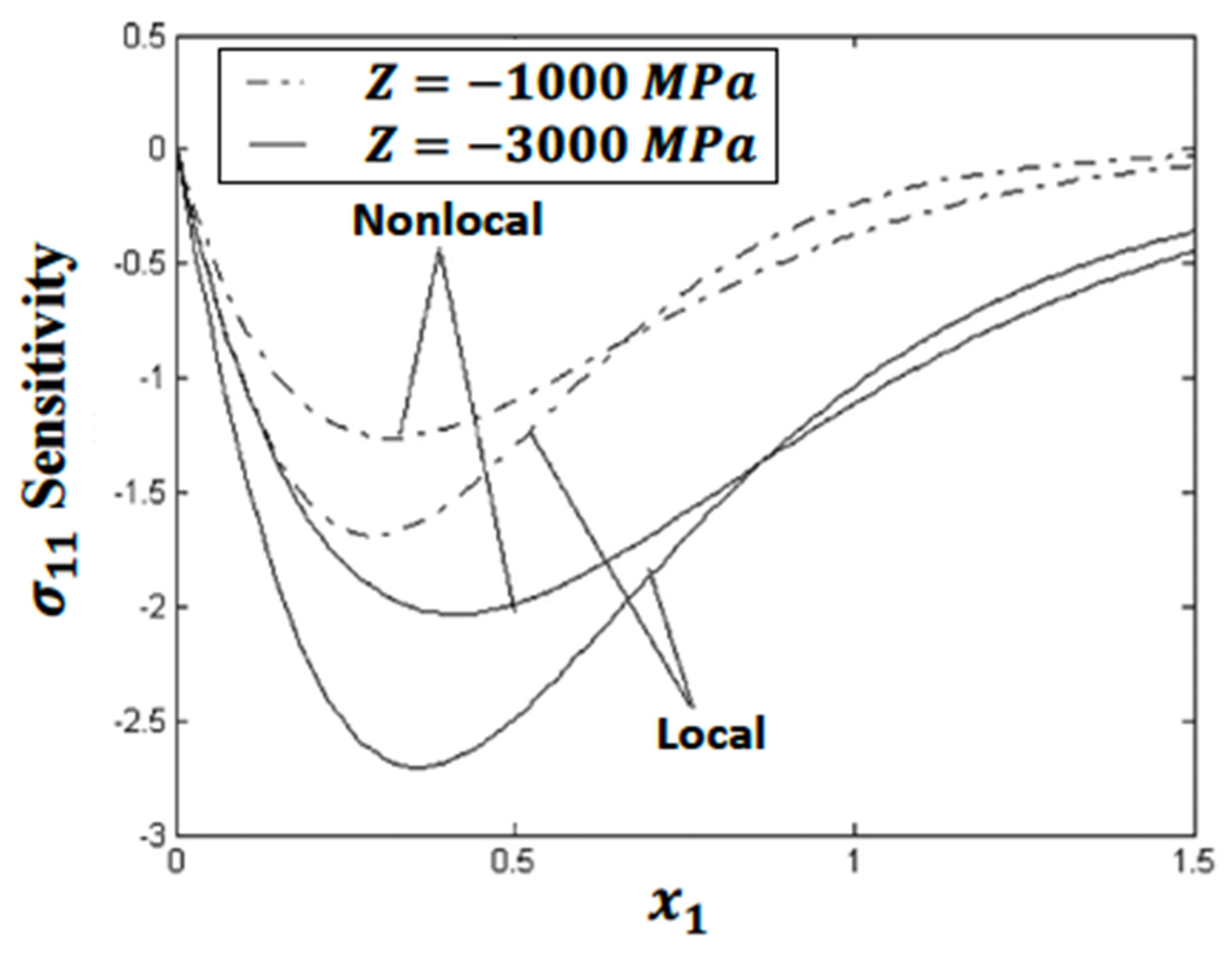
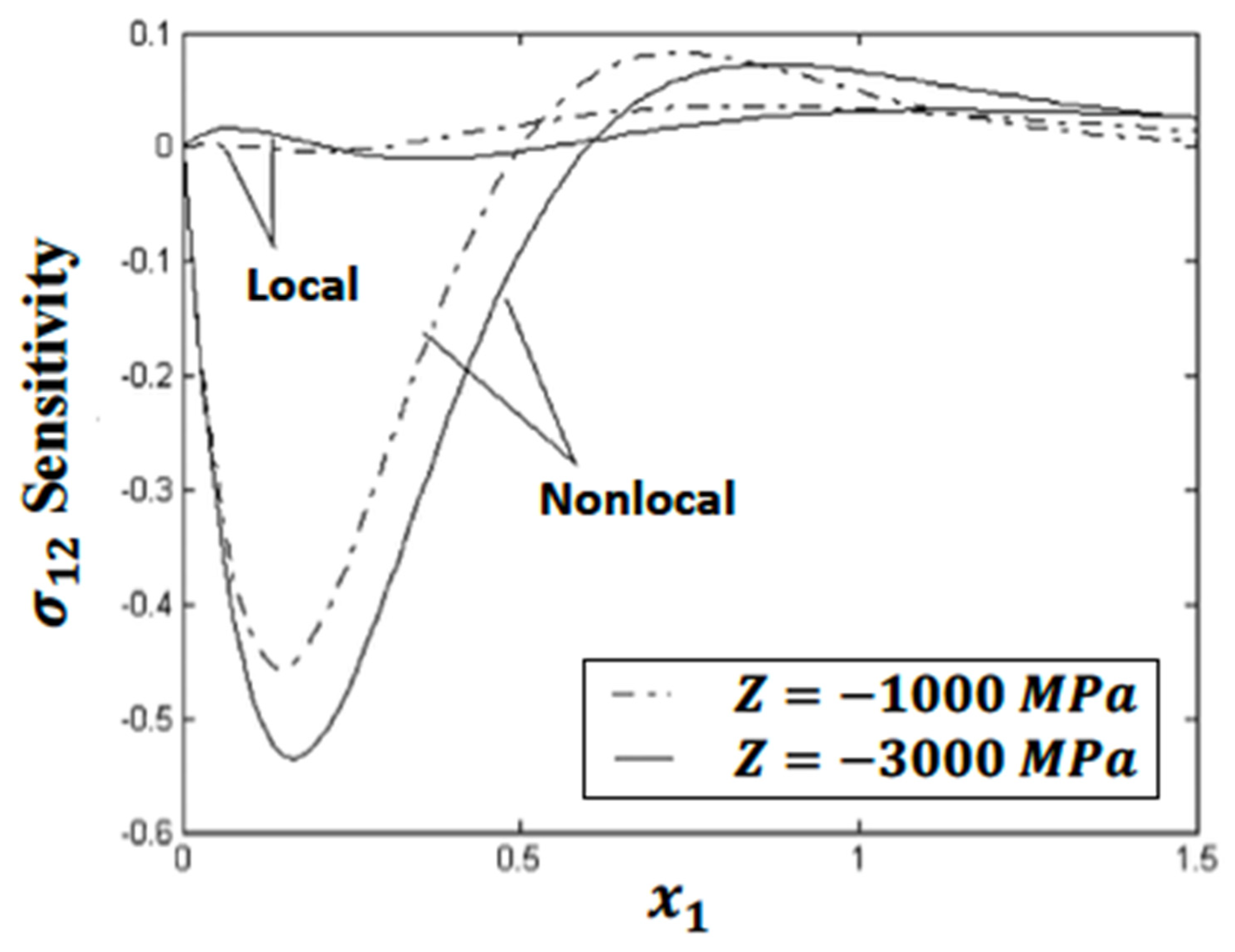
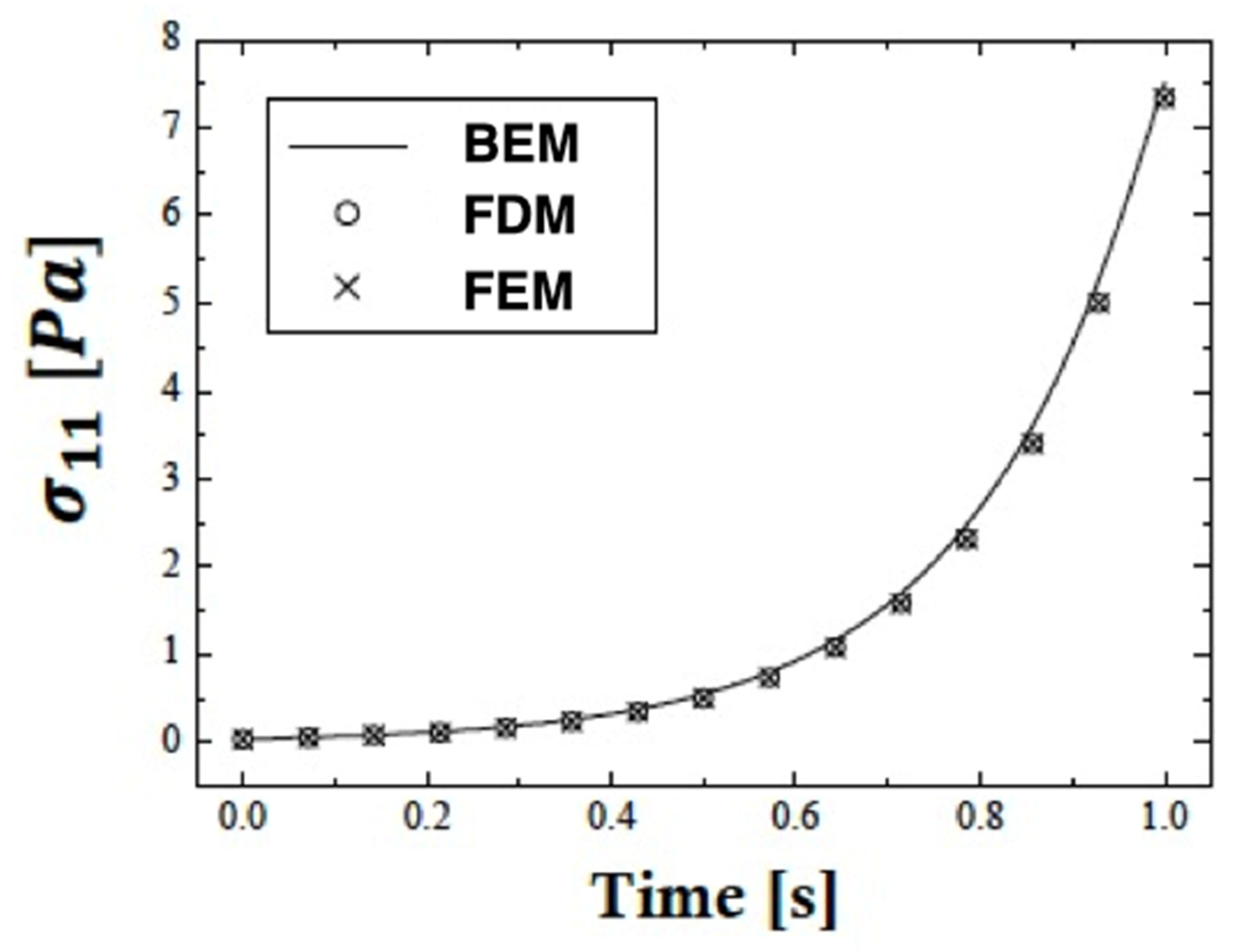
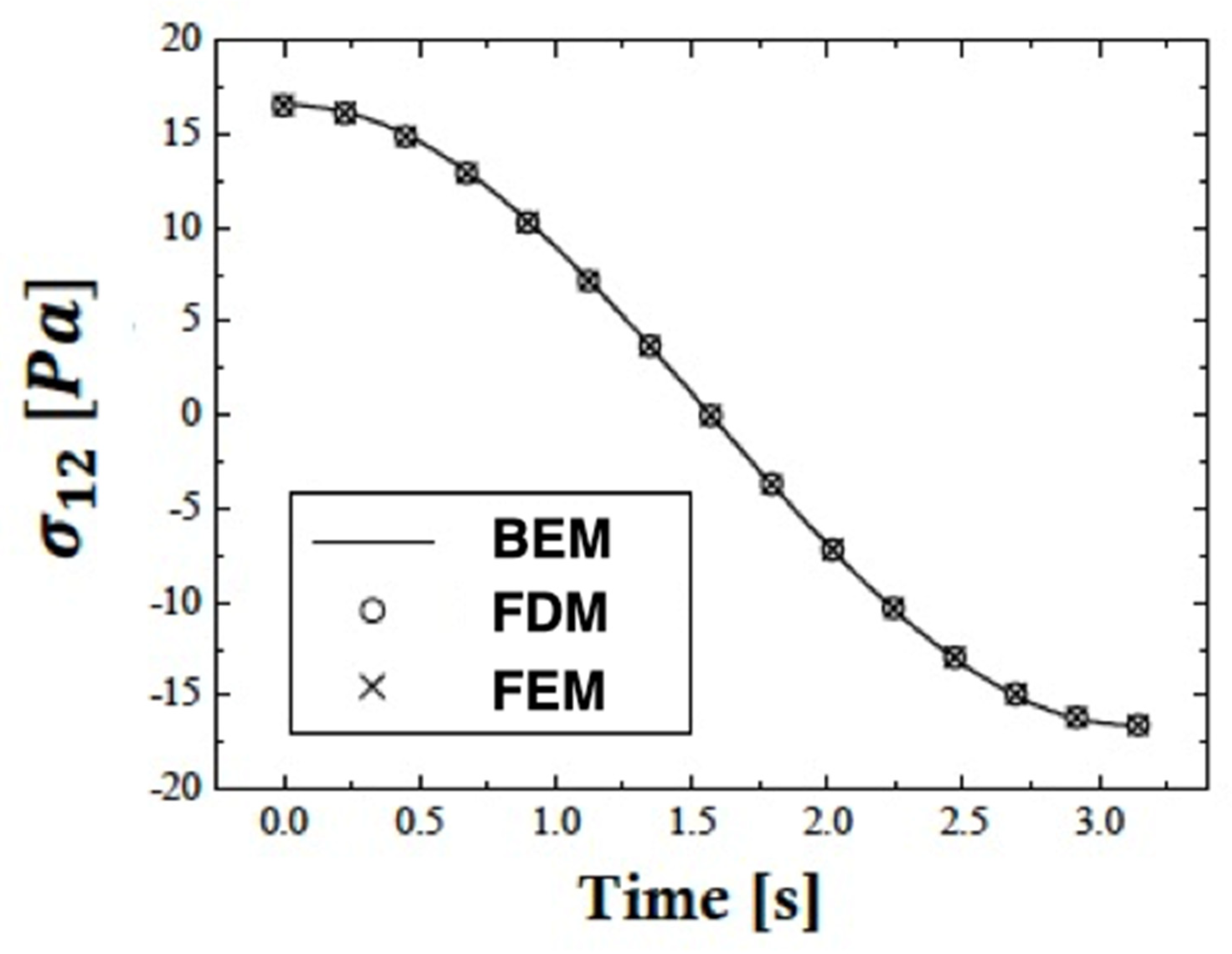
5. Numerical Results and Discussion
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Nonlocal weight function | Domain | ||
| Boundary | Work-hardening function | ||
| Dirac delta function of argument | CPV | Cauchy principal value | |
| Total heat energy | Solid specific heat capacity | ||
| Plastic strain intensity | Tensor depending on the stress tensor | ||
| Plastic strain rate | Area of an infinitesimal portion of | ||
| Plastic strain increment | Length of an infinitesimal part of | ||
| Temperature | Second kind elliptic integral | ||
| Absolute zero temperature | Effective stress | ||
| Outward normal derivative of on | Identity matrix | ||
| Solid thermal conductivity | First kind elliptic integral | ||
| Lamé elastic constants | hardening-softening parameter | ||
| Proportionality coefficient | Material characteristic length | ||
| Spatial non-local average | component unit vector normal to | ||
| Elastic stress intensity | Control function | ||
| Stress rate tensor | Solid Volume | ||
| Plastic stress rate | Cylindrical Coordinates | ||
| Elastic stress rate | S | Solid Surface | |
| Elastic stress increment | Deviator of stresses | ||
| Plastic stress increment | Traction rate | ||
| Unit vector tangent to boundary at | Fundamental displacement | ||
| Displacement rate |
References
- Noye, B.J.; Dehghan, M.; VanderHoek, J. Explicit finite difference methods for two-dimensional diffusion with a non-local boundary condition. Int. J. Eng. Sci. 1994, 32, 1829–1834. [Google Scholar] [CrossRef]
- Gumel, A.B.; Ang, W.T.; Twizell, E.H. Efficient parallel algorithm for the two-dimensional diffusion equation subject to specification of mass. Int. J. Comput. Math. 1997, 64, 153–163. [Google Scholar] [CrossRef]
- Dehghan, M. Numerical solution of a parabolic equation subject to specification of energy. Appl. Math. Comput. 2004, 149, 31–45. [Google Scholar] [CrossRef]
- Ang, W.T.; Ooi, E.H. A dual-reciprocity boundary element approach for solving axisymmetric heat equation subject to specification of energy. Eng. Anal. Bound. Elem. 2008, 32, 210–215. [Google Scholar] [CrossRef]
- Bažant, Z.P. Instability, ductility and size effect in strain softening concrete. J. Eng. Mech. Div. (ASCE) 1976, 12, 331–344. [Google Scholar] [CrossRef]
- Sandler, I.S. Strain-softening for static and dynamic problems. In Proceedings of the Symposium on Constitutive Equations: Micro, Macro and Computational Aspects; Willam, K.J., Ed.; ASME: New York, NY, USA, 1984; pp. 217–231. [Google Scholar]
- Bažant, Z.P.; Lin, F.-B. Non-local yield degradation. Int. J. Numer. Methods Eng. 1988, 26, 1805–1823. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Belytschko, T.B.; Chang, T.P. Continuum theory for strain-softening. J. Eng. Mech. Div. (ASCE) 1984, 110, 1666–1692. [Google Scholar] [CrossRef]
- Bažant, Z.P. Crack band model for fracture of geomaterials. In Proceedings of the 4th International Conference on Numerical Methods in Geomechanics, Edmonton, AB, Canada, 31 May–4 June 1982; Eisenstein, Z., Ed.; pp. 1137–1152. [Google Scholar]
- Bažant, Z.P.; Ožbolt, J. Nonlocal microplane model for fracture, damage and size effect in structures. J. Eng. Mech. (ASCE) 1990, 116, 2485–2505. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Ožbolt, J. Compression failure of quasibrittle material; Nonlocal microplane model. J. Eng. Mech. (ASCE) 1992, 118, 540–556. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Cedolin, L. Stability of Structures; Oxford University Press: Oxford, UK, 1991. [Google Scholar]
- Bažant, Z.P.; Planas, J. Fracture and Size Effect in Concrete and Other Quasibrittle Materials; CRC Press: Boca Raton, FL, USA, 1998. [Google Scholar]
- Kröner, E. Elasticity theory of materials with long-range cohesive forces. Int. J. Solids Struct. 1967, 4, 731–742. [Google Scholar] [CrossRef]
- Eringen, A.C.; Edelen, D.G.B. On nonlocal elasticity. Int. J. Eng. Sci. 1972, 10, 233–248. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Pijaudier-Cabot, G. Modeling of distributed damage by nonlocal continuum with local strain. In Proceedings of the 4th International Conference on Numerical Methods in Fracture Mechanics, San Antonio, TX, USA, 23–27 March 1987; pp. 411–432. [Google Scholar]
- Pijaudier-Cabot, G.; Bažant, Z.P. Nonlocal damage theory. J. Eng. Mech. (ASCE) 1987, 113, 1512–1533. [Google Scholar] [CrossRef]
- Jirásek, M. Nonlocal models for damage and fracture: Comparison of approaches. Int. J. Solids Struct. 1998, 35, 4133–4145. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Jirásek, M. Nonlocal integral formulations of plasticity and damage: Survey of progress. J. Eng. Mech. (ASCE) 2002, 128, 1119–1149. [Google Scholar] [CrossRef]
- Swedlow, J.L.; Cruse, T.A. Formulation of boundary integral equations for three-dimensional flow. Int. J. Solids Struct. 1971, 7, 1673–1683. [Google Scholar] [CrossRef]
- Ricardella, P.C. An Implementation of the Boundary Integral Technique for Planar Problems of Elasticity and Elasto-Plasticity. Ph.D. Thesis, Carnegie-Mellon University, Pittsburgh, RI, USA, 1973. [Google Scholar]
- Chaudonneret, M. Boundary integral equation method for visco-plasticity analysis. J. Mécanique Appliquée 1977, 1, 113–131. [Google Scholar]
- Kumar, V.; Mukherjee, S. A boundary integral equation formulation for time dependent inelastic deformation in metals. Int. J. Mech. Sci. 1975, 19, 713–724. [Google Scholar] [CrossRef]
- Banerjee, P.K.; Cathie, D.N.; Davies, T.G. Two and three-dimensional problems of elastoplasticity. In Developments in Boundary Element Methods; Applied Science Publishers: London, UK, 1979; Volume 1, pp. 63–95. [Google Scholar]
- Banerjee, P.K.; Cathie, D.N. Boundary element methods for axisymmetric plasticity. In Innovative Numerical Methods for the Applied Engineering Science; Shaw, R.P., Pilkey, W., Pilkey, B., Wilson, R., Lakis, A., Chaudouet, A., Marino, C., Eds.; University of Virginia Press: Charlottesville, VA, USA, 1980. [Google Scholar]
- Telles, J.C.F.; Brebbia, C.A. Boundary elements in plasticity. Appl. Math. Model. 1981, 5, 275–281. [Google Scholar] [CrossRef]
- Henry, D.P.; Banerjee, P.K. A new BEM formulation for two and three-dimensional elastoplasticity using particular integrals. Int. J. Numer. Methods Eng. 1988, 26, 2079–2096. [Google Scholar] [CrossRef]
- Leitao, V.; Alabadi, M.H.; Rooke, D.P. The dual boundary element formulation for elastoplastic fracture mechanics. Int. J. Numer. Methods Eng. 1995, 38, 315–333. [Google Scholar] [CrossRef]
- Herding, U.; Kuhn, G. A field boundary element formulation for damage mechanics. Eng. Anal. Bound. Elem. 1996, 18, 137–147. [Google Scholar] [CrossRef]
- Balaš, J.; Sládek, J.; Sládek, V. Stress Analysis by Boundary Element Methods; Elsevier: Amsterdam, The Netherlands, 1989. [Google Scholar]
- Brebbia, C.A.; Telles, J.C.F.; Wrobel, L.C. Boundary Element Techniques, Theory and Applications in Engineering; Springer: Berlin/Heidelberg, Germany, 1984. [Google Scholar]
- Abramowitz, M.; Stegun, I. Handbook of Mathematical Functions; Dover: New York, NY, USA, 1970. [Google Scholar]
- París, F.; Cañas, J. Boundary Element Method: Fundamentals and Applications; Oxford University Press: Oxford, UK, 1997. [Google Scholar]
- Wang, K.; Mattheij, R.M.M.; ter Morsche, H.G. Alternative DRM formulations. Eng. Anal. Bound. Elem. 2003, 27, 175–181. [Google Scholar] [CrossRef]
- Sládek, J.; Sládek, V.; Bažant, Z.P. Non-local boundary integral formulation for softening damage. Int. J. Numer. Methods Eng. 2003, 57, 103–116. [Google Scholar] [CrossRef]
- Sládek, V.; Sládek, J. Non-singular boundary integral representation of stresses. Int. J. Numer. Methods Eng. 1992, 33, 1481–1499. [Google Scholar] [CrossRef]
- Sládek, V.; Sládek, J. Displacement gradients in BEM formulation for small strain plasticity. Eng. Anal. Bound. Elem. 1999, 23, 471–477. [Google Scholar] [CrossRef]
- Tanaka, M.; Sládek, V.; Sládek, J. Regularization techniques applied to boundary element methods. Appl. Mech. Rev. (ASME) 1994, 47, 457–499. [Google Scholar] [CrossRef]
- Xu, Z.; Alonso, J.J.; Darve, E. A numerically stable communication avoiding S-step GMRES algorithm. arXiv 2023, arXiv:2303.08953. [Google Scholar] [CrossRef]
- Shao, X.H.; Kang, C.B. Modified DTS iteration methods for spatial fractional diffusion equations. Mathematics 2023, 11, 931. [Google Scholar] [CrossRef]
- She, Z.H.; Qiu, L.M.; Qu, W. An unconditionally convergent RSCSCS iteration method for Riesz space fractional diffusion equations with variable coefficients. Math. Comput. Simul. 2023, 203, 633–646. [Google Scholar] [CrossRef]
- Fahmy, M.A. Shape design sensitivity and optimization for two-temperature generalized magneto-thermoelastic problems using time-domain DRBEM. J. Therm. Stress. 2018, 41, 119–138. [Google Scholar] [CrossRef]
- Fahmy, M.A. Shape design sensitivity and optimization of anisotropic functionally graded smart structures using bicubic B-splines DRBEM. Eng. Anal. Bound. Elem. 2018, 87, 27–35. [Google Scholar] [CrossRef]
- Fahmy, M.A.; Alsulami, M.O. Boundary Element and Sensitivity Analysis of Anisotropic Thermoelastic Metal and Alloy Discs with Holes. Materials 2022, 15, 1828. [Google Scholar] [CrossRef] [PubMed]
- Fahmy, M.A. Three-Dimensional Boundary Element Strategy for Stress Sensitivity of Fractional-Order Thermo-Elastoplastic Ultrasonic Wave Propagation Problems of Anisotropic Fiber-Reinforced Polymer Composite Material. Polymers 2022, 14, 2883. [Google Scholar] [CrossRef] [PubMed]
- Fahmy, M.A.; Alsulami, M.O.; Abouelregal, A.E. Sensitivity analysis and design optimization of 3T rotating thermoelastic structures using IGBEM. AIMS Math. 2022, 7, 19902–19921. [Google Scholar] [CrossRef]
- Ricci, S.; Brünig, M. Numerical Analysis of Nonlocal Anisotropic Continuum Damage. Int. J. Damage Mech. 2007, 16, 283–299. [Google Scholar] [CrossRef]
- Su, C.; Lu, D.; Zhou, X.; Wang, G.; Zhuang, X.; Du, X. An implicit stress update algorithm for the plastic nonlocal damage model of concrete. Comput. Methods Appl. Mech. Eng. 2023, 414, 116189. [Google Scholar] [CrossRef]


| Method | Iter. | CPU Time | Rr | Err. | |
|---|---|---|---|---|---|
| SCAS-GMRES | 40 | 0.0123 | 1.84e−07 | 1.62e−09 | |
| FMDTS | 70 | 0.0567 | 6.62e−07 | 1.84e−07 | |
| UC-RSCSCS | 80 | 0.0795 | 8.42e−07 | 2.56e−06 | |
| SCAS-GMRES | 50 | 0.0594 | 0.16e−06 | 2.12e−08 | |
| FMDTS | 100 | 0.2278 | 1.68e−05 | 4.25e−06 | |
| UC-RSCSCS | 140 | 0.3784 | 1.09e−04 | 0.48e−05 | |
| SCAS-GMRES | 60 | 0.1768 | 2.45e−05 | 1.74e−07 | |
| FMDTS | 280 | 0.7948 | 1.76e−04 | 3.82e−05 | |
| UC-RSCSCS | 300 | 0.8964 | 1.34e−03 | 4.54e−04 |
| BEM | FDM | FEM | |
|---|---|---|---|
| Number of nodes | 50 | 50,000 | 45,000 |
| Number of elements | 25 | 15,000 | 13,000 |
| CPU time [min.] | 3 | 150 | 130 |
| Memory [Mbyte] | 1 | 130 | 110 |
| Disc space [Mbyte] | 0 | 190 | 170 |
| Accuracy of results [%] | 1.0 | 2.6 | 2.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fahmy, M.A. BEM Modeling for Stress Sensitivity of Nonlocal Thermo-Elasto-Plastic Damage Problems. Computation 2024, 12, 87. https://doi.org/10.3390/computation12050087
Fahmy MA. BEM Modeling for Stress Sensitivity of Nonlocal Thermo-Elasto-Plastic Damage Problems. Computation. 2024; 12(5):87. https://doi.org/10.3390/computation12050087
Chicago/Turabian StyleFahmy, Mohamed Abdelsabour. 2024. "BEM Modeling for Stress Sensitivity of Nonlocal Thermo-Elasto-Plastic Damage Problems" Computation 12, no. 5: 87. https://doi.org/10.3390/computation12050087





