To Bind or Not to Bind? A Comprehensive Characterization of TIR1 and Auxins Using Consensus In Silico Approaches
Abstract
:1. Introduction
2. Materials and Methods
2.1. De Novo Design of Putative Auxins and Molecular Decoys
2.2. Machine Learning
2.3. Molecular Modelling of Auxins
2.3.1. Mixed Solvent Molecular Dynamics
2.3.2. Assessment of Pocket Solvation and Its Role in Auxin Recognition
2.3.3. Molecular Dynamics
2.3.4. Coarse Metadynamics
3. Results and Discussion
3.1. De Novo Design of Putative Auxins and Decoys
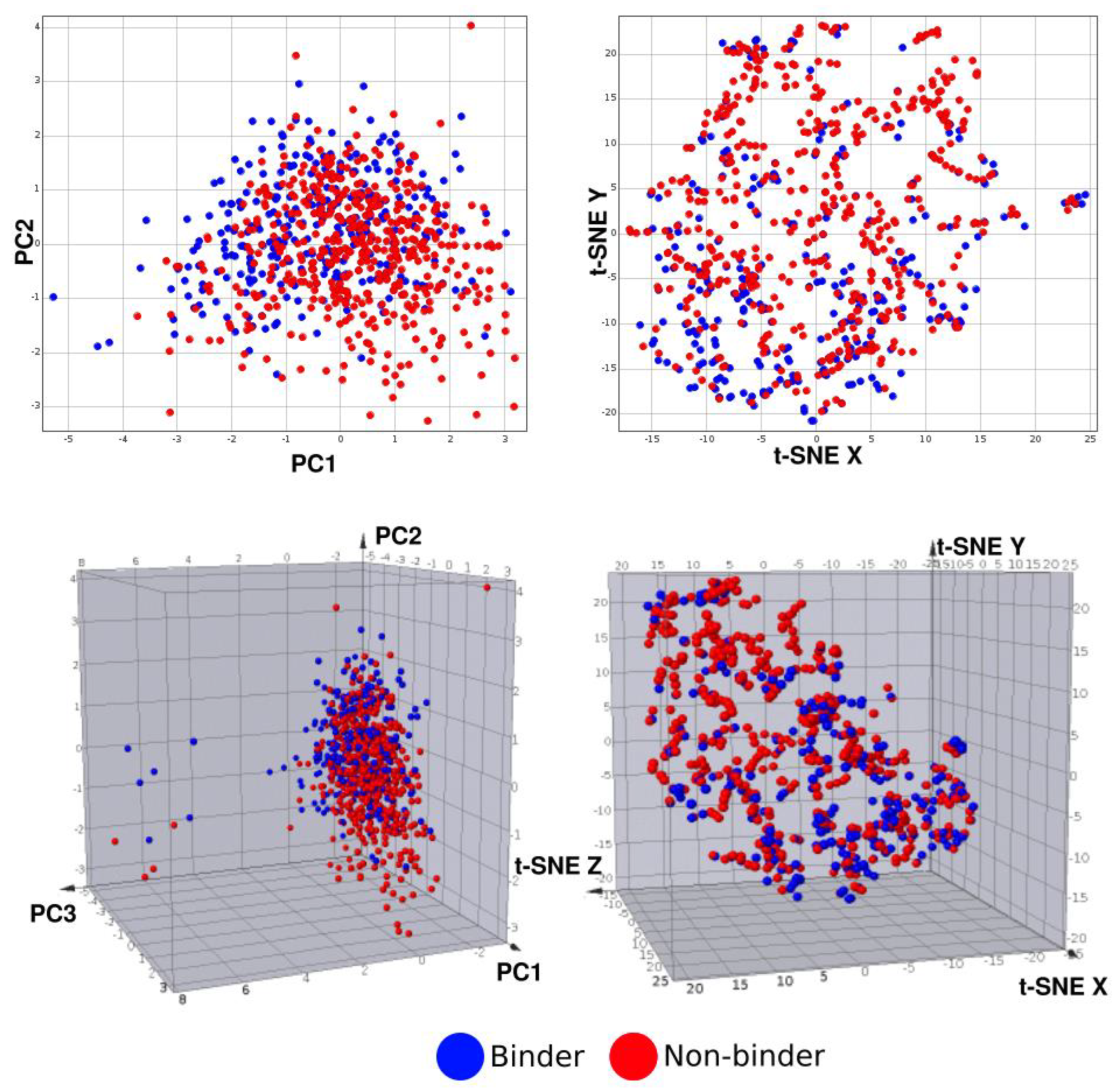
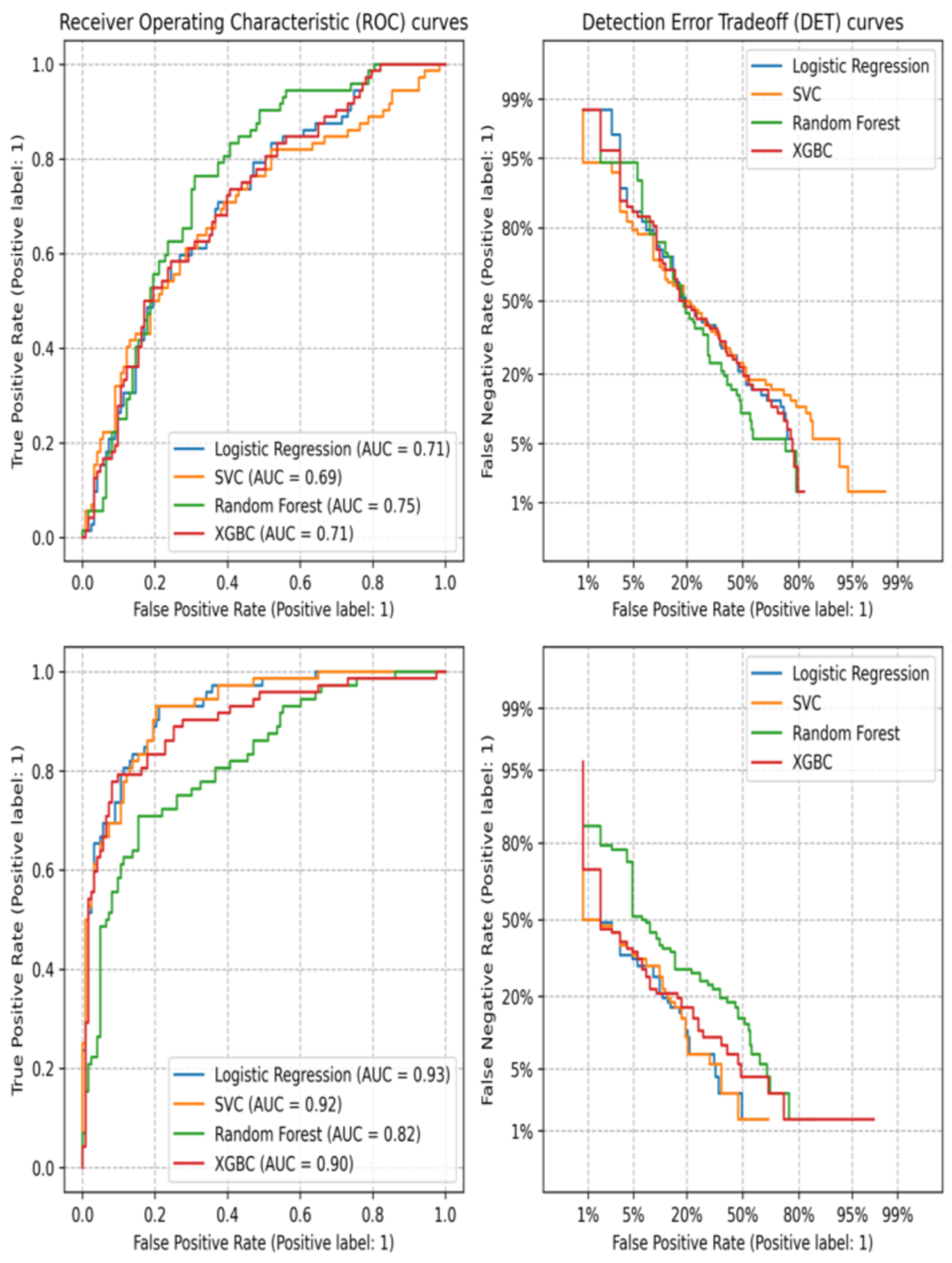
3.2. Machine Learning
- Validations curves: To visualize the trend of variance and suggest the presence of bias; either underfitting or overfitting.
- Learning curves: Convey information on the learning rate as a function of n in data; i.e., if the provided examples are enough for effective classification or if the addition of data may benefit scoring.
- ROC curves and Matthews correlation coefficient (MCC): These provide a general description of the predictive power due to their relation with the confusion matrix. The inclusion of both is complementary. As MCC can take values between −1 and 1, it is possible to assess if a model is indeed providing a significant difference when applied or if its success relies more on chance, even when the area under the curve of the ROC plot would suggest otherwise.
- Detection error trade-off: Similar to the ROC curve, this metric gives information on the success of classification tasks. During classification, there is always a trade-off between the rate of falsely classified values. Therefore, this plot conveys the trend of said trade-off; an ideal classifier would keep a low rate of both false positives and false negatives, resulting in a curve downward and to the left, an inverse of sorts to an expected ROC curve. All these plots can be found in the Supplementary Information (Figures S2–S9). ROC curves and error trade-off for the models’ best models are shown in Figure 2.
3.3. Molecular Modelling of Auxins
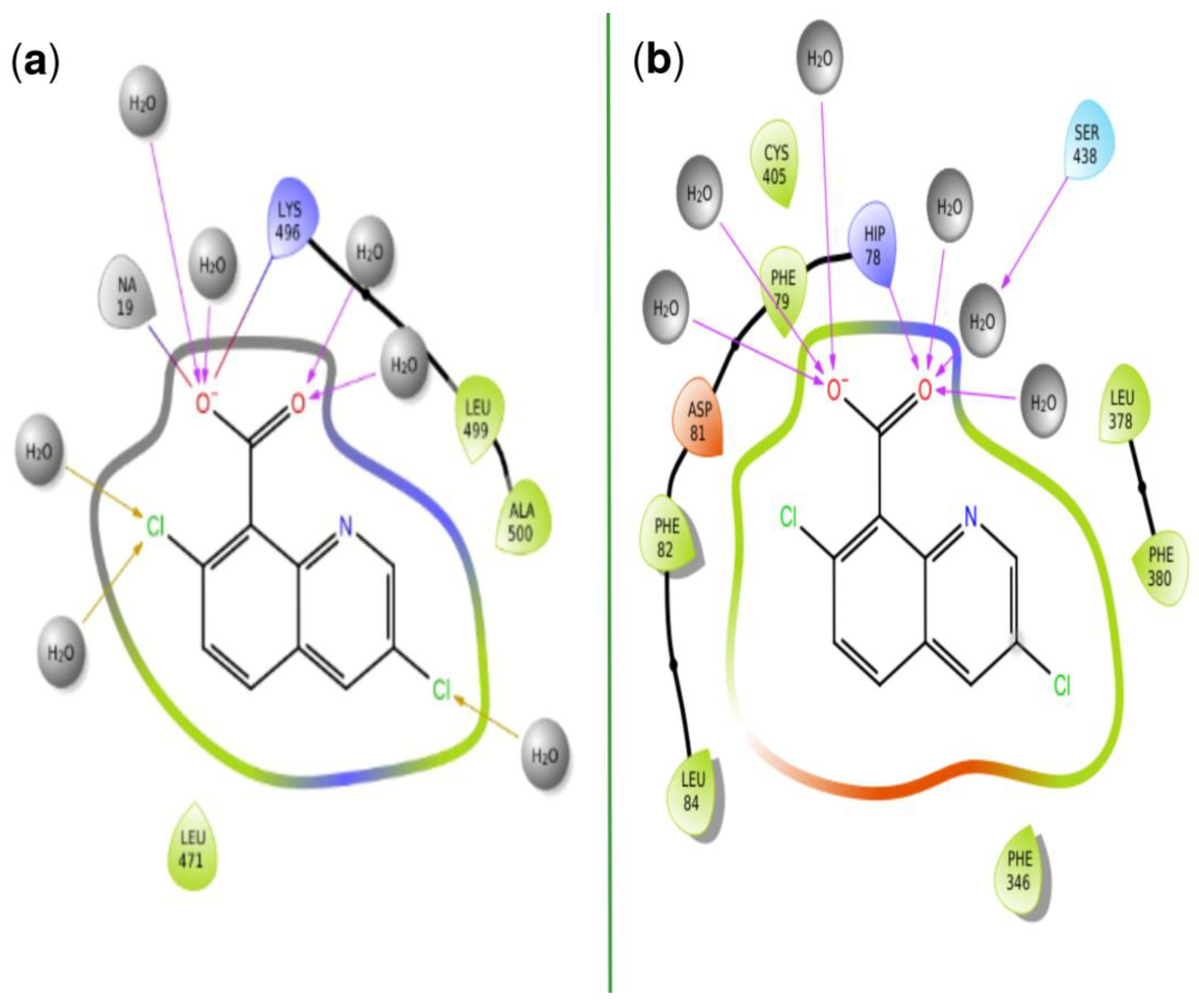
3.3.1. Mixed Solvents Molecular Dynamics
3.3.2. Assessment of Pocket Solvation and Its Role in Auxin Recognition
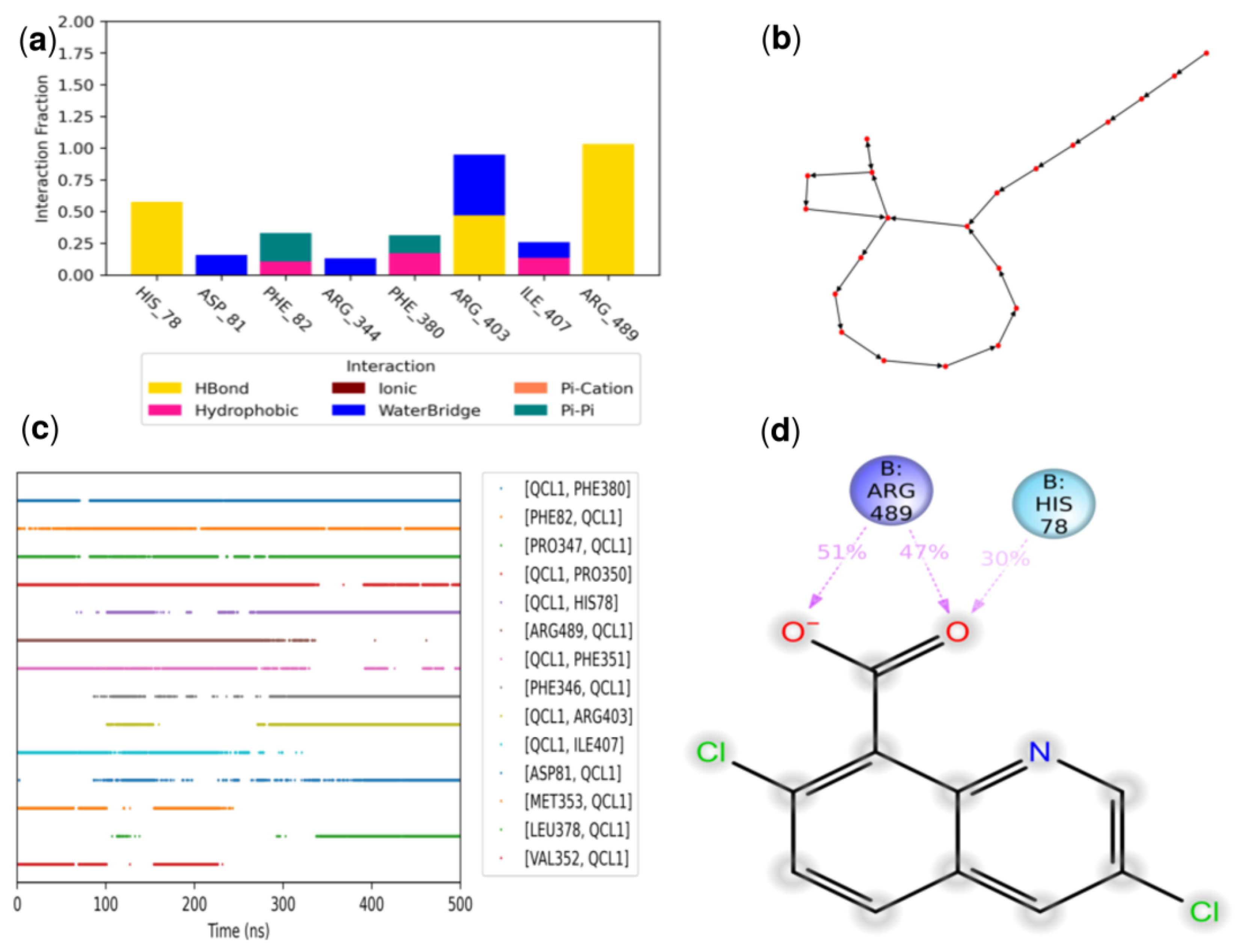
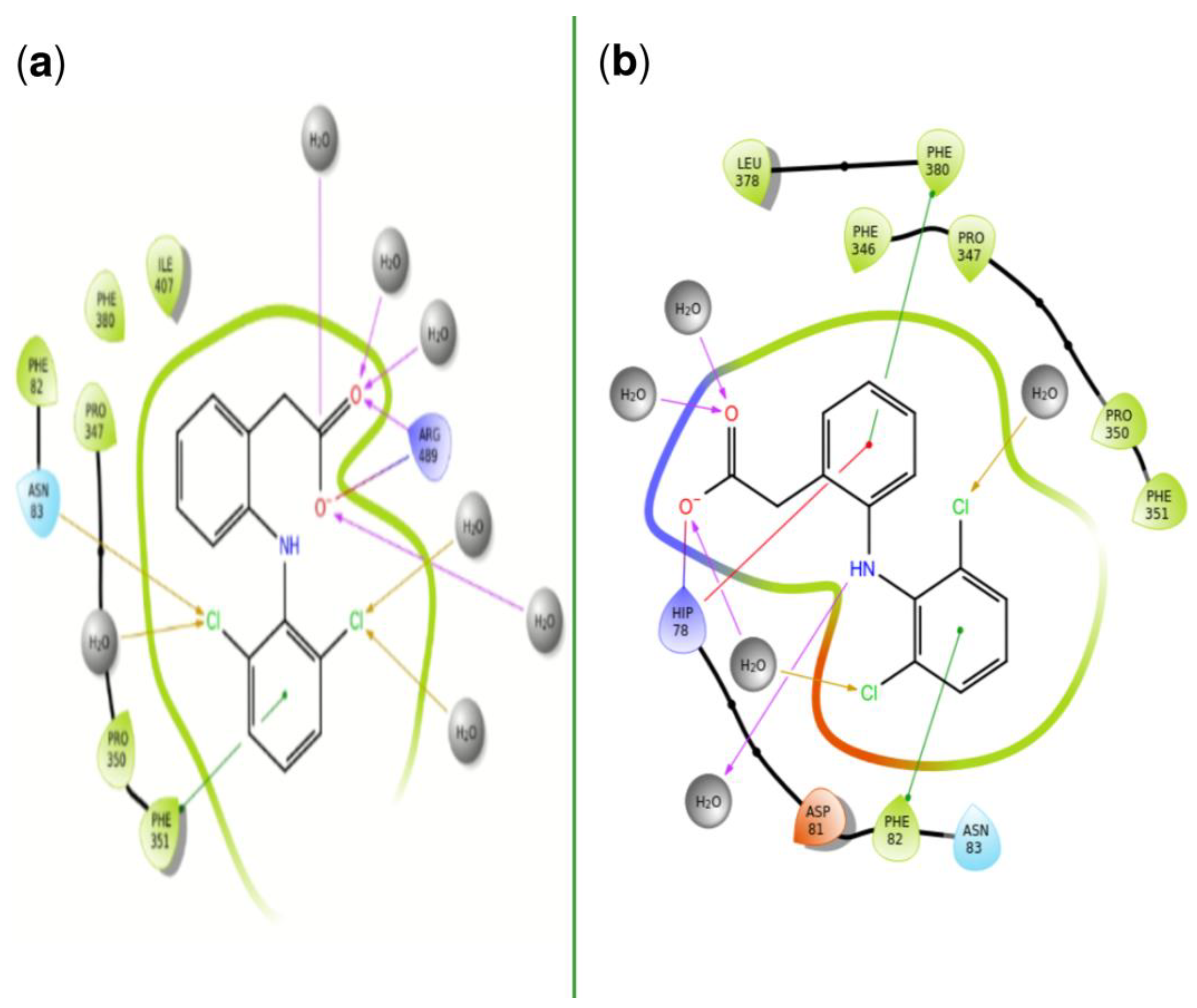
3.3.3. Molecular Dynamics
3.3.4. Coarse Metadynamics
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ritchie, H.; Rosado, P.; Roser, M. Agricultural Production. Our World in Data, January 2023. Available online: https://ourworldindata.org/agricultural-production (accessed on 17 March 2024).
- 2.1 Food Security Indicators—Latest Updates and Progress towards Ending Hunger and Ensuring Food Security. Available online: https://www.fao.org/3/cc0639en/online/sofi-2022/food-security-nutrition-indicators.html (accessed on 17 March 2024).
- Carvalho-Moore, P.; Rangani, G.; Heiser, J.; Findley, D.; Bowe, S.J.; Roma-Burgos, N. PPO2 Mutations in Amaranthus palmeri: Implications on Cross-Resistance. Agriculture 2021, 11, 760. [Google Scholar] [CrossRef]
- Shaner, D.L. Lessons Learned From the History of Herbicide Resistance. Weed Sci. 2014, 62, 427–431. [Google Scholar] [CrossRef]
- Heap, I. The International Survey of Herbicide Resistant Weeds. Available online: http://www.weedscience.com/Home.aspx (accessed on 1 February 2024).
- Gupta, P.K. Chapter 37—Herbicides and Fungicides. In Reproductive and Developmental Toxicology, 2nd ed.; Gupta, R.C., Ed.; Academic Press: Cambridge, MA, USA, 2017; pp. 657–679. ISBN 978-0-12-804239-7. [Google Scholar]
- Panchal, D.; Mistry, J.; Amin, D. Auxin. In Practical Handbook on Agricultural Microbiology; Amaresan, N., Patel, P., Amin, D., Eds.; Springer: New York, NY, USA, 2022; pp. 251–255. ISBN 978-1-07-161724-3. [Google Scholar]
- Teale, W.D.; Paponov, I.A.; Palme, K. Auxin in action: Signalling, transport and the control of plant growth and development. Nat. Rev. Mol. Cell Biol. 2006, 7, 847–859. [Google Scholar] [CrossRef]
- Hayashi, K.; Neve, J.; Hirose, M.; Kuboki, A.; Shimada, Y.; Kepinski, S.; Nozaki, H. Rational Design of an Auxin Antagonist of the SCFTIR1 Auxin Receptor Complex. ACS Chem. Biol. 2012, 7, 590–598. [Google Scholar] [CrossRef] [PubMed]
- Grossmann, K. Mediation of Herbicide Effects by Hormone Interactions. J. Plant Growth Regul. 2003, 22, 109–122. [Google Scholar] [CrossRef]
- Yu, H.; Moss, B.L.; Jang, S.S.; Prigge, M.; Klavins, E.; Nemhauser, J.L.; Estelle, M. Mutations in the TIR1 Auxin Receptor That Increase Affinity for Auxin/Indole-3-Acetic Acid Proteins Result in Auxin Hypersensitivity. Plant Physiol. 2013, 162, 295–303. [Google Scholar] [CrossRef]
- Dharmasiri, N. Auxin signaling and regulated protein degradation. Trends Plant Sci. 2004, 9, 302–308. [Google Scholar] [CrossRef]
- Wang, R.; Estelle, M. Diversity and specificity: Auxin perception and signaling through the TIR1/AFB pathway. Curr. Opin. Plant Biol. 2014, 21, 51–58. [Google Scholar] [CrossRef] [PubMed]
- Todd, O.E.; Figueiredo, M.R.A.; Morran, S.; Soni, N.; Preston, C.; Kubeš, M.F.; Napier, R.; Gaines, T.A. Synthetic auxin herbicides: Finding the lock and key to weed resistance. Plant Sci. 2020, 300, 110631. [Google Scholar] [CrossRef]
- Ma, Q.; Grones, P.; Robert, S. Auxin signaling: A big question to be addressed by small molecules. J. Exp. Bot. 2018, 69, 313–328. [Google Scholar] [CrossRef]
- Chéron, N.; Jasty, N.; Shakhnovich, E.I. OpenGrowth: An Automated and Rational Algorithm for Finding New Protein Ligands. J. Med. Chem. 2016, 59, 4171–4188. [Google Scholar] [CrossRef]
- Imrie, F.; Bradley, A.R.; Deane, C.M. Generating property-matched decoy molecules using deep learning. Bioinformatics 2021, 37, 2134–2141. [Google Scholar] [CrossRef]
- Moriwaki, H.; Tian, Y.-S.; Kawashita, N.; Takagi, T. Mordred: A molecular descriptor calculator. J. Cheminform. 2018, 10, 4. [Google Scholar] [CrossRef]
- Kursa, M.B.; Rudnicki, W.R. Feature selection with the Boruta package. J. Stat. Softw. 2010, 36, 1–13. [Google Scholar] [CrossRef]
- Sander, T.; Freyss, J.; von Korff, M.; Rufener, C. DataWarrior: An Open-Source Program For Chemistry Aware Data Visualization And Analysis. J. Chem. Inf. Model. 2015, 55, 460–473. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; ACM: New York, NY, USA, 2016; pp. 785–794. [Google Scholar]
- Prieto-Martínez, F.D.; Fernández-de Gortari, E.; Medina-Franco, J.L.; Espinoza-Fonseca, L.M. An in silico pipeline for the discovery of multitarget ligands: A case study for epi-polypharmacology based on DNMT1/HDAC2 inhibition. Artif. Intell. Life Sci. 2021, 1, 100008. [Google Scholar] [CrossRef]
- Landrum, G.; Tosco, P.; Kelley, B.; Ric; Cosgrove, D.; Sriniker; Vianello, R.; gedeck; NadineSchneider; Jones, G.; et al. rdkit/rdkit: 2024_03_1 (Q1 2024) Release Beta; Zenodo: Geneva, Switzerland, 2024. [Google Scholar] [CrossRef]
- Feng, H.; Zhang, Y.; Bos, P.H.; Chambers, J.M.; Dupont, M.M.; Stockwell, B.R. K-RasG12D Has a Potential Allosteric Small Molecule Binding Site. Biochemistry 2019, 58, 2542–2554. [Google Scholar] [CrossRef]
- Ghanakota, P.; Carlson, H.A. Driving Structure-Based Drug Discovery through Cosolvent Molecular Dynamics: Miniperspective. J. Med. Chem. 2016, 59, 10383–10399. [Google Scholar] [CrossRef]
- Barrera-Téllez, F.J.; Prieto-Martínez, F.D.; Hernández-Campos, A.; Martínez-Mayorga, K.; Castillo-Bocanegra, R. In Silico Exploration of the Trypanothione Reductase (TryR) of L. mexicana. Int. J. Mol. Sci. 2023, 24, 16046. [Google Scholar] [CrossRef]
- Ladbury, J.E. Just add water! The effect of water on the specificity of protein-ligand binding sites and its potential application to drug design. Chem. Biol. 1996, 3, 973–980. [Google Scholar] [CrossRef] [PubMed]
- Shadrick, W.R.; Slavish, P.J.; Chai, S.C.; Waddell, B.; Connelly, M.; Low, J.A.; Tallant, C.; Young, B.M.; Bharatham, N.; Knapp, S.; et al. Exploiting a water network to achieve enthalpy-driven, bromodomain-selective BET inhibitors. Bioorganic Med. Chem. 2018, 26, 25–36. [Google Scholar] [CrossRef]
- Ge, Y.; Wych, D.C.; Samways, M.L.; Wall, M.E.; Essex, J.W.; Mobley, D.L. Enhancing Sampling of Water Rehydration on Ligand Binding: A Comparison of Techniques. J. Chem. Theory Comput. 2022, 18, 1359–1381. [Google Scholar] [CrossRef] [PubMed]
- Lukauskis, D.; Samways, M.L.; Aureli, S.; Cossins, B.P.; Taylor, R.D.; Gervasio, F.L. Open Binding Pose Metadynamics: An Effective Approach for the Ranking of Protein–Ligand Binding Poses. J. Chem. Inf. Model. 2022, 62, 6209–6216. [Google Scholar] [CrossRef] [PubMed]
- Bowers, K.; Chow, E.; Xu, H.; Dror, R.; Eastwood, M.; Gregersen, B.; Klepeis, J.; Kolossvary, I.; Moraes, M.; Sacerdoti, F.; et al. Scalable Algorithms for Molecular Dynamics Simulations on Commodity Clusters. In Proceedings of the ACM/IEEE SC 2006 Conference (SC’06), Tampa, FL, USA, 11–17 November 2006. [Google Scholar]
- Predescu, C.; Bergdorf, M.; Shaw, D.E. Midtown splines: An optimal charge assignment for electrostatics calculations. J. Chem. Phys. 2020, 153, 224117. [Google Scholar] [CrossRef]
- McGibbon, R.T.; Harrigan, M.; Beauchamp, K.; Klein, C.; Swails, J.; Hernández, C.; Peastman; Scherer, M.K.; Schwantes, C.; Pfrstg; et al. Mdtraj/mdtraj: MDTraj 1.9 2017; Zenodo: Geneva, Switzerland, 2019. [Google Scholar] [CrossRef]
- Aldeghi, M.; Ross, G.A.; Bodkin, M.J.; Essex, J.W.; Knapp, S.; Biggin, P.C. Large-scale analysis of water stability in bromodomain binding pockets with grand canonical Monte Carlo. Commun. Chem. 2018, 1, 19. [Google Scholar] [CrossRef] [PubMed]
- De Ruiter, A.; Oostenbrink, C. Free energy calculations of protein-ligand interactions. Curr. Opin. Chem. Biol. 2011, 15, 547–552. [Google Scholar] [CrossRef]
- Samways, M.L.; Bruce Macdonald, H.E.; Essex, J.W. grand: A Python Module for Grand Canonical Water Sampling in OpenMM. J. Chem. Inf. Model. 2020, 60, 4436–4441. [Google Scholar] [CrossRef] [PubMed]
- Nittinger, E.; Flachsenberg, F.; Bietz, S.; Lange, G.; Klein, R.; Rarey, M. Placement of Water Molecules in Protein Structures: From Large-Scale Evaluations to Single-Case Examples. J. Chem. Inf. Model. 2018, 58, 1625–1637. [Google Scholar] [CrossRef]
- El Khoury, L.; Santos-Martins, D.; Sasmal, S.; Eberhardt, J.; Bianco, G.; Ambrosio, F.A.; Solis-Vasquez, L.; Koch, A.; Forli, S.; Mobley, D.L. Comparison of affinity ranking using AutoDock-GPU and MM-GBSA scores for BACE-1 inhibitors in the D3R Grand Challenge 4. J. Comput.-Aided Mol. Des. 2019, 33, 1011–1020. [Google Scholar] [CrossRef]
- Lee, S.; Sundaram, S.; Armitage, L.; Evans, J.P.; Hawkes, T.; Kepinski, S.; Ferro, N.; Napier, R.M. Defining Binding Efficiency and Specificity of Auxins for SCFTIR1/AFB-Aux/IAA Co-receptor Complex Formation. ACS Chem. Biol. 2014, 9, 673–682. [Google Scholar] [CrossRef] [PubMed]
- Cho, M.; Kim, K. Diclofenac modified the root system architecture of Arabidopsis via interfering with the hormonal activities of auxin. J. Hazard. Mater. 2021, 413, 125402. [Google Scholar] [CrossRef]
- Korb, O.; Bowden, S.; Olsson, T.; Frenkel, D.; Liebeschuetz, J.; Cole, J. Ensemble docking revisited. J. Cheminform. 2010, 2, P25. [Google Scholar] [CrossRef]
- Korb, O.; Stützle, T.; Exner, T.E. Empirical scoring functions for advanced Protein-Ligand docking with PLANTS. J. Chem. Inf. Model. 2009, 49, 84–96. [Google Scholar] [CrossRef] [PubMed]
- Ren, X.; Shi, Y.-S.; Zhang, Y.; Liu, B.; Zhang, L.-H.; Peng, Y.-B.; Zeng, R. Novel Consensus Docking Strategy to Improve Ligand Pose Prediction. J. Chem. Inf. Model. 2018, 58, 1662–1668. [Google Scholar] [CrossRef]
- Kurkinen, S.T.; Lätti, S.; Pentikäinen, O.T.; Postila, P.A. Getting Docking into Shape Using Negative Image-Based Rescoring. J. Chem. Inf. Model. 2019, 59, 3584–3599. [Google Scholar] [CrossRef]
- ten Brink, T.; Exner, T.E. Influence of Protonation, Tautomeric, and Stereoisomeric States on Protein−Ligand Docking Results. J. Chem. Inf. Model. 2009, 49, 1535–1546. [Google Scholar] [CrossRef]
- Swenson, D.W.H.; Roet, S.; Faruk, N. Dwhswenson/contact_map: Contact_map 0.7.0; Zenodo: Geneva, Switzerland, 2020. [Google Scholar] [CrossRef]
- Bussi, G.; Laio, A. Using metadynamics to explore complex free-energy landscapes. Nat. Rev. Phys. 2020, 2, 200–212. [Google Scholar] [CrossRef]
- Masetti, M.; Cavalli, A.; Recanatini, M.; Gervasio, F.L. Exploring Complex Protein−Ligand Recognition Mechanisms with Coarse Metadynamics. J. Phys. Chem. B 2009, 113, 4807–4816. [Google Scholar] [CrossRef]
- Provasi, D. Ligand-Binding Calculations with Metadynamics. In Biomolecular Simulations: Methods and Protocols; Bonomi, M., Camilloni, C., Eds.; Springer: New York, NY, USA, 2019; pp. 233–253. ISBN 978-1-4939-9608-7. [Google Scholar]
- Raniolo, S.; Limongelli, V. Ligand binding free-energy calculations with funnel metadynamics. Nat. Protoc. 2020, 15, 2837–2866. [Google Scholar] [CrossRef]
- Wang, J.; Ishchenko, A.; Zhang, W.; Razavi, A.; Langley, D. A highly accurate metadynamics-based Dissociation Free Energy method to calculate protein–protein and protein–ligand binding potencies. Sci. Rep. 2022, 12, 2024. [Google Scholar] [CrossRef] [PubMed]
- Uzunova, V.V.; Quareshy, M.; del Genio, C.I.; Napier, R.M. Tomographic docking suggests the mechanism of auxin receptor TIR1 selectivity. Open Biol. 2016, 6, 160139. [Google Scholar] [CrossRef] [PubMed]
- Leeson, P.D. Molecular inflation, attrition and the rule of five. Adv. Drug Deliv. Rev. 2015, 101, 22–33. [Google Scholar] [CrossRef] [PubMed]
- Hopkins, A.L.; Keserü, G.M.; Leeson, P.D.; Rees, D.C.; Reynolds, C.H. The role of ligand efficiency metrics in drug discovery. Nat. Rev. Drug Discov. 2014, 13, 105–121. [Google Scholar] [CrossRef]
- Maggiora, G.M. On Outliers and Activity CliffsWhy QSAR Often Disappoints. J. Chem. Inf. Model. 2006, 46, 1535. [Google Scholar] [CrossRef]
- Stumpfe, D.; Hu, H.; Bajorath, J. Evolving Concept of Activity Cliffs. ACS Omega 2019, 4, 14360–14368. [Google Scholar] [CrossRef]
- Stumpfe, D.; Hu, H.; Bajorath, J. Advances in exploring activity cliffs. J. Comput.-Aided Mol. Des. 2020, 34, 929–942. [Google Scholar] [CrossRef]
- Lipinski, C.A.; Lombardo, F.; Dominy, B.W.; Feeney, P.J. Experimental and computational approaches to estimate solubility and permeability in drug discovery and development settings1. Adv. Drug Deliv. Rev. 2001, 46, 3–26. [Google Scholar] [CrossRef]
- Shultz, M.D. Two Decades under the Influence of the Rule of Five and the Changing Properties of Approved Oral Drugs. J. Med. Chem. 2019, 62, 1701–1714. [Google Scholar] [CrossRef]
- Giblin, K.A.; Hughes, S.J.; Boyd, H.; Hansson, P.; Bender, A. Prospectively Validated Proteochemometric Models for the Prediction of Small-Molecule Binding to Bromodomain Proteins. J. Chem. Inf. Model. 2018, 58, 1870–1888. [Google Scholar] [CrossRef]
- Skyner, R.E.; McDonagh, J.L.; Groom, C.R.; van Mourik, T.; Mitchell, J.B.O. A review of methods for the calculation of solution free energies and the modelling of systems in solution. Phys. Chem. Chem. Phys. 2015, 17, 6174–6191. [Google Scholar] [CrossRef]
- Deshpande, M.; Kuramochi, M.; Karypis, G. Data Mining Algorithms for Virtual Screening of Bioactive Compounds. In Data Mining in Biomedicine; Pardalos, P.M., Boginski, V.L., Vazacopoulos, A., Eds.; Springer: Boston, MA, USA, 2007; pp. 59–90. ISBN 978-0-387-69319-4. [Google Scholar]
- Lima, A.N.; Philot, E.A.; Trossini, G.H.G.; Scott, L.P.B.; Maltarollo, V.G.; Honorio, K.M. Use of machine learning approaches for novel drug discovery. Expert Opin. Drug Discov. 2016, 11, 225–239. [Google Scholar] [CrossRef]
- Patlewicz, G.; Wambaugh, J.F.; Felter, S.P.; Simon, T.W.; Becker, R.A. Utilizing Threshold of Toxicological Concern (TTC) with high throughput exposure predictions (HTE) as a risk-based prioritization approach for thousands of chemicals. Comput. Toxicol. 2018, 7, 58–67. [Google Scholar] [CrossRef] [PubMed]
- Vogel, S.M.; Bauer, M.R.; Boeckler, F.M. DEKOIS: Demanding Evaluation Kits for Objective in Silico Screening—A Versatile Tool for Benchmarking Docking Programs and Scoring Functions. J. Chem. Inf. Model. 2011, 51, 2650–2665. [Google Scholar] [CrossRef]
- Stein, R.M.; Yang, Y.; Balius, T.E.; O’Meara, M.J.; Lyu, J.; Young, J.; Tang, K.; Shoichet, B.K.; Irwin, J.J. Property-Unmatched Decoys in Docking Benchmarks. J. Chem. Inf. Model. 2021, 61, 699–714. [Google Scholar] [CrossRef] [PubMed]
- Li, G.-B.; Yang, L.-L.; Wang, W.-J.; Li, L.-L.; Yang, S.-Y. ID-Score: A New Empirical Scoring Function Based on a Comprehensive Set of Descriptors Related to Protein–Ligand Interactions. J. Chem. Inf. Model. 2013, 53, 592–600. [Google Scholar] [CrossRef] [PubMed]
- Lu, J.; Hou, X.; Wang, C.; Zhang, Y. Incorporating Explicit Water Molecules and Ligand Conformation Stability in Machine-Learning Scoring Functions. J. Chem. Inf. Model. 2019, 59, 4540–4549. [Google Scholar] [CrossRef] [PubMed]
- Mobley, D.L.; Dill, K.A. Binding of Small-Molecule Ligands to Proteins: “What You See” Is Not Always “What You Get”. Structure 2009, 17, 489–498. [Google Scholar] [CrossRef]
- Liu, K.; Kokubo, H. Exploring the Stability of Ligand Binding Modes to Proteins by Molecular Dynamics Simulations: A Cross-docking Study. J. Chem. Inf. Model. 2017, 57, 2514–2522. [Google Scholar] [CrossRef]
- Brenke, R.; Kozakov, D.; Chuang, G.-Y.; Beglov, D.; Hall, D.; Landon, M.R.; Mattos, C.; Vajda, S. Fragment-based identification of druggable ‘hot spots’ of proteins using Fourier domain correlation techniques. Bioinformatics 2009, 25, 621–627. [Google Scholar] [CrossRef]
- Ghanakota, P.; Van Vlijmen, H.; Sherman, W.; Beuming, T. Large-Scale Validation of Mixed-Solvent Simulations to Assess Hotspots at Protein–Protein Interaction Interfaces. J. Chem. Inf. Model. 2018, 58, 784–793. [Google Scholar] [CrossRef] [PubMed]
- Hao, G.-F.; Yang, G.-F. The Role of Phe82 and Phe351 in Auxin-Induced Substrate Perception by TIR1 Ubiquitin Ligase: A Novel Insight from Molecular Dynamics Simulations. PLoS ONE 2010, 5, e10742. [Google Scholar] [CrossRef]
- Tan, X.; Calderon-Villalobos, L.I.A.; Sharon, M.; Zheng, C.; Robinson, C.V.; Estelle, M.; Zheng, N. Mechanism of auxin perception by the TIR1 ubiquitin ligase. Nature 2007, 446, 640–645. [Google Scholar] [CrossRef] [PubMed]
- Mockaitis, K.; Estelle, M. Auxin receptors and plant development: A new signaling paradigm. Annu. Rev. Cell Dev. Biol. 2008, 24, 55–80. [Google Scholar] [CrossRef]
- Juárez-Mercado, K.E.; Prieto-Martínez, F.D.; Sánchez-Cruz, N.; Peña-Castillo, A.; Prada-Gracia, D.; Medina-Franco, J.L. Expanding the Structural Diversity of DNA Methyltransferase Inhibitors. Pharmaceuticals 2021, 14, 17. [Google Scholar] [CrossRef]
- Swinburne, T.D.; Wales, D.J. Defining, Calculating, and Converging Observables of a Kinetic Transition Network. J. Chem. Theory Comput. 2020, 16, 2661–2679. [Google Scholar] [CrossRef]
- Ross, G.A.; Morris, G.M.; Biggin, P.C. One Size Does Not Fit All: The Limits of Structure-Based Models in Drug Discovery. J. Chem. Theory Comput. 2013, 9, 4266–4274. [Google Scholar] [CrossRef] [PubMed]
- Anighoro, A.; Bajorath, J. Three-Dimensional Similarity in Molecular Docking: Prioritizing Ligand Poses on the Basis of Experimental Binding Modes. J. Chem. Inf. Model. 2016, 56, 580–587. [Google Scholar] [CrossRef]
- Quareshy, M.; Prusinska, J.; Li, J.; Napier, R. A cheminformatics review of auxins as herbicides. J. Exp. Bot. 2018, 69, 265–275. [Google Scholar] [CrossRef]
- Epp, J.B.; Alexander, A.L.; Balko, T.W.; Buysse, A.M.; Brewster, W.K.; Bryan, K.; Daeuble, J.F.; Fields, S.C.; Gast, R.E.; Green, R.A.; et al. The discovery of ArylexTM active and RinskorTM active: Two novel auxin herbicides. Bioorganic Med. Chem. 2016, 24, 362–371. [Google Scholar] [CrossRef] [PubMed]
- Prusinska, J.; Uzunova, V.; Schmitzer, P.; Weimer, M.; Bell, J.; Napier, R.M. The differential binding and biological efficacy of auxin herbicides. Pest Manag. Sci. 2023, 79, 1305–1315. [Google Scholar] [CrossRef] [PubMed]








| PDBID | 2P1M | 2P1P | 2P1Q | 2P1O | 2P1N |
|---|---|---|---|---|---|
| 2P1M | (RMSD 0.16 Å) H78 − 0.32 F79 − 0.18 D81 − 0.31 F82 − 0.19 C405 − 0.27 S438 − 0.19 L439 − 0.22 S440 − 0.19 S462 − 0.18 | (RMSD 0.22 Å) H78 − 0.3 F79 − 0.3 D81 − 0.58 F82 − 0.45 C405 − 0.27 R435 − 0.23 S438 − 0.23 L439 − 0.3 R489 − 0.22 | (RMSD 0.27 Å) H78 − 0.36 D81 − 0.59 F82 − 0.52 C405 − 0.29 L439 − 0.87 | (RMSD 0.33 Å) H78 − 0.41 F79 − 0.38 D81 − 0.55 F82 − 0.35 C405 − 0.54 L439 − 0.85 V463 − 0.49 A464 − 0.58 R489 − 0.33 | |
| 2P1P | (RMSD 0.16 Å) F79 − 0.18 D81 − 0.28 F82 − 0.52 L439 − 0.2 A464 − 0.2 R484 − 0.22 | (RMSD 0.22 Å) D81 − 0.29 F82 − 0.6 A464 − 0.22 | (RMSD 0.26 Å) F79 − 0.26 D81 − 0.29 F82 − 0.45 C405 − 0.37 R435 − 0.27 L439 − 0.66 V463 − 0.37 A464 − 0.54 | ||
| 2P1Q | (RMSD 0.14 Å) F49 − 0.15 L439 − 0.62 S440 − 0.16 | (RMSD 0.22 Å) H78 − 0.28 C405 − 0.29 R435 − 0.35 L439 − 0.62 V463 − 0.42 A464 − 0.4 | |||
| 2P1O | (RMSD 0.19 Å) H78 − 0.3 F82 − 0.22 C405 − 0.31 R435 − 0.28 V463 − 0.43 A464 − 0.42 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prieto-Martínez, F.D.; Mendoza-Cañas, J.; Martínez-Mayorga, K. To Bind or Not to Bind? A Comprehensive Characterization of TIR1 and Auxins Using Consensus In Silico Approaches. Computation 2024, 12, 94. https://doi.org/10.3390/computation12050094
Prieto-Martínez FD, Mendoza-Cañas J, Martínez-Mayorga K. To Bind or Not to Bind? A Comprehensive Characterization of TIR1 and Auxins Using Consensus In Silico Approaches. Computation. 2024; 12(5):94. https://doi.org/10.3390/computation12050094
Chicago/Turabian StylePrieto-Martínez, Fernando D., Jennifer Mendoza-Cañas, and Karina Martínez-Mayorga. 2024. "To Bind or Not to Bind? A Comprehensive Characterization of TIR1 and Auxins Using Consensus In Silico Approaches" Computation 12, no. 5: 94. https://doi.org/10.3390/computation12050094
APA StylePrieto-Martínez, F. D., Mendoza-Cañas, J., & Martínez-Mayorga, K. (2024). To Bind or Not to Bind? A Comprehensive Characterization of TIR1 and Auxins Using Consensus In Silico Approaches. Computation, 12(5), 94. https://doi.org/10.3390/computation12050094






