Effects of Double Diffusive Convection and Inclined Magnetic Field on the Peristaltic Flow of Fourth Grade Nanofluids in a Non-Uniform Channel
Abstract
:1. Introduction
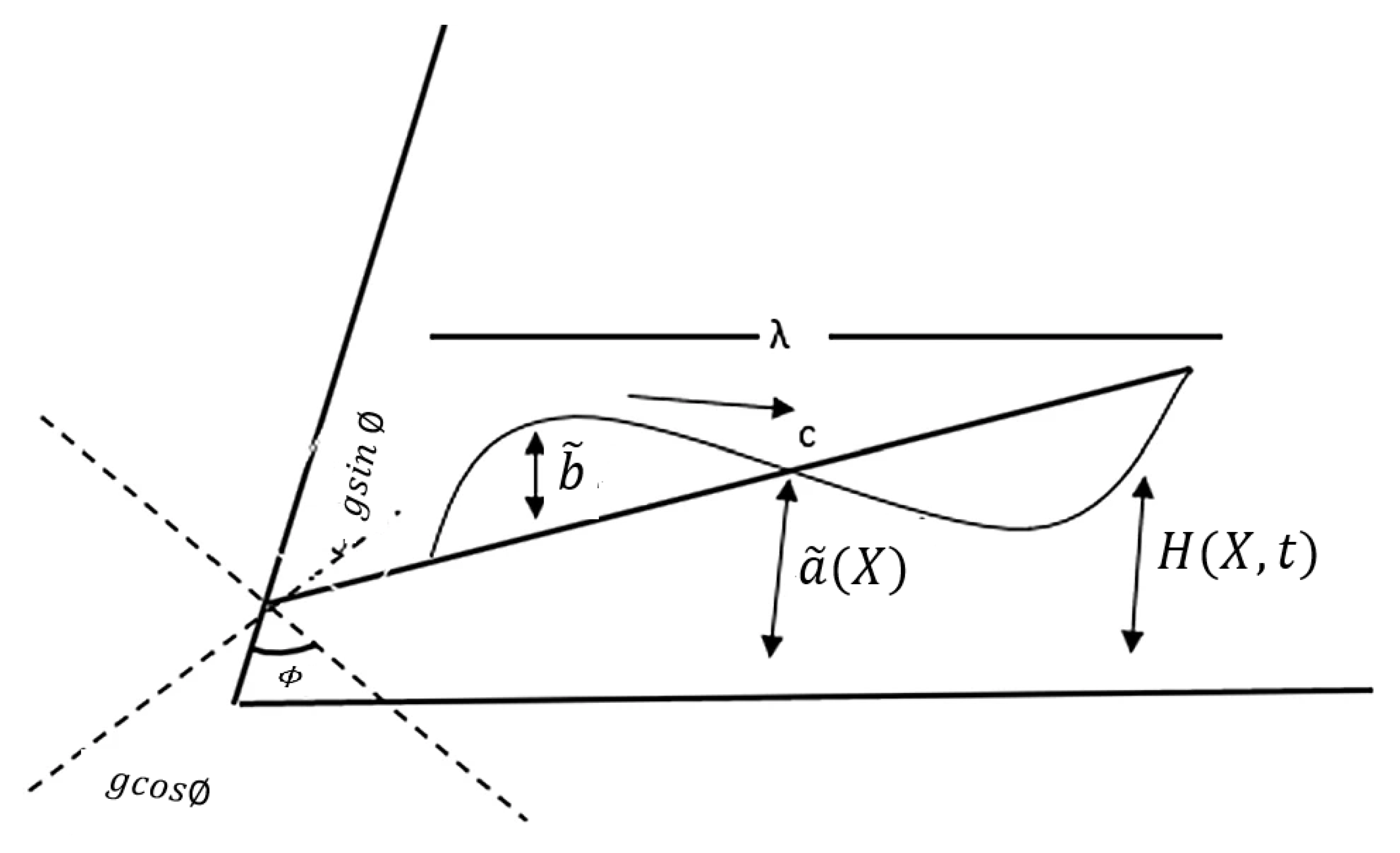
2. Mathematical Formulation
3. Different Wave Forms
- (1)
- Multi-sinusoidal wave:
- (2)
- Trapezoidal wave:
- (3)
- Triangular wave:
- (4)
- Square wave:
4. Solution to the Problem
4.1. Exact Solution
4.2. Numerical Solution
- The results of this study were reduced to the classical results of viscous fluids when . This special case corresponded to a very simplified model in a comparison to the present model since it only related to Newtonian viscous flows in the absence of nanofluid and thermophysical phenomena.
- The results of Bég and Tripathi [37] could be used for our problem in the limited case when .
5. Graphical Outcomes
6. Conclusions
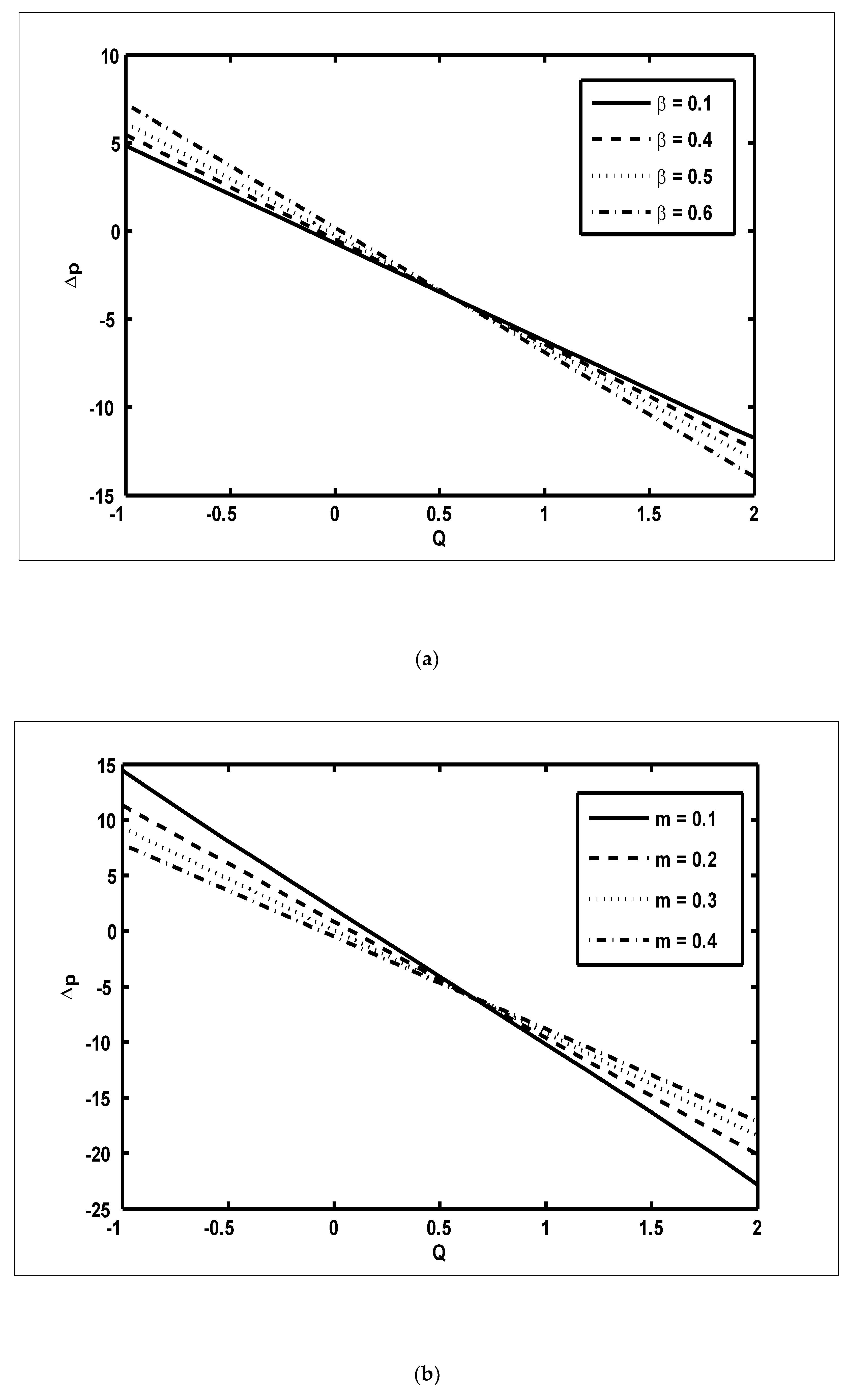
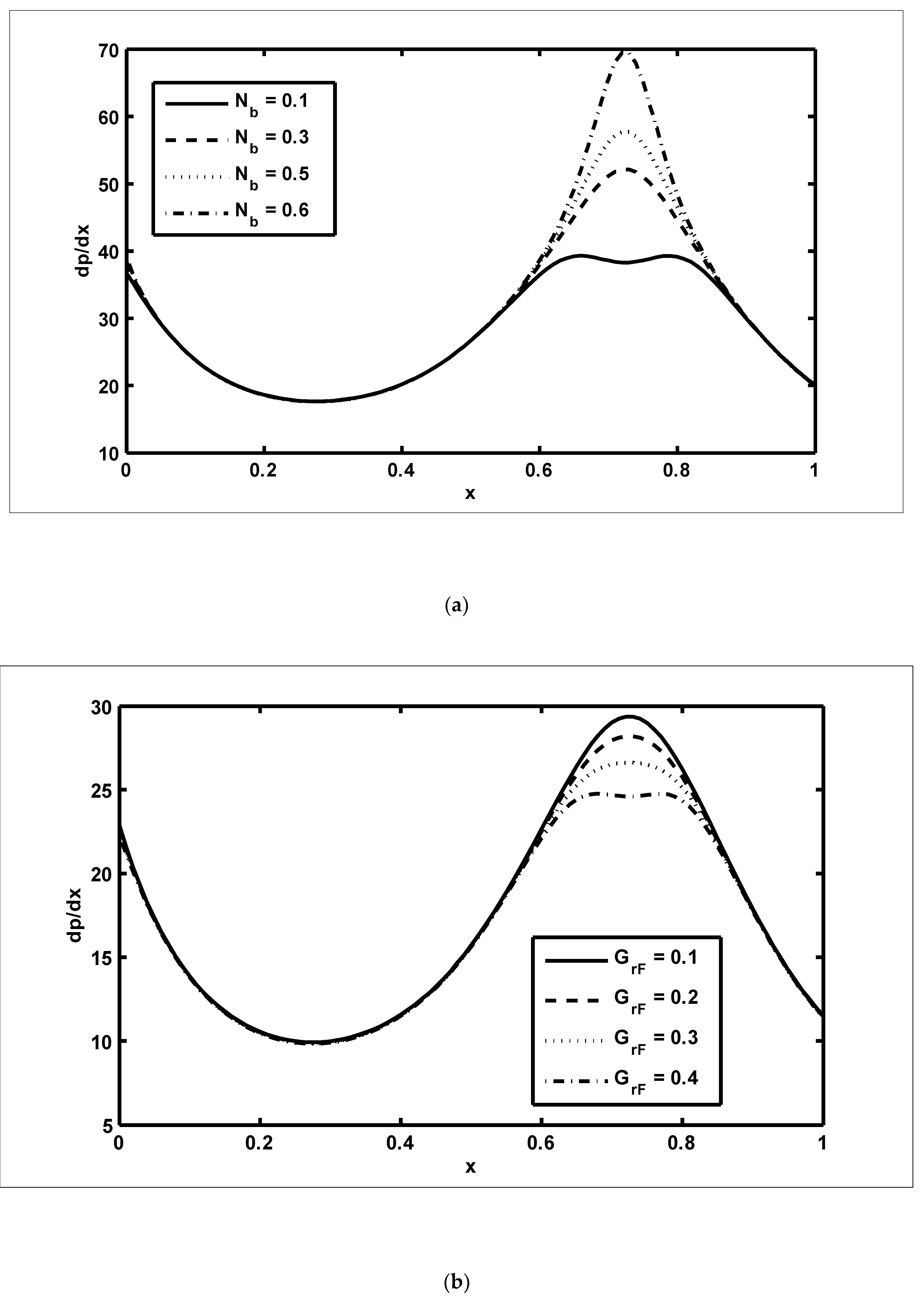
- The pressure gradient increased with increasing values of the Brownian motion parameter, whereas it decreased with increasing values of the nanoparticle Grashof number;
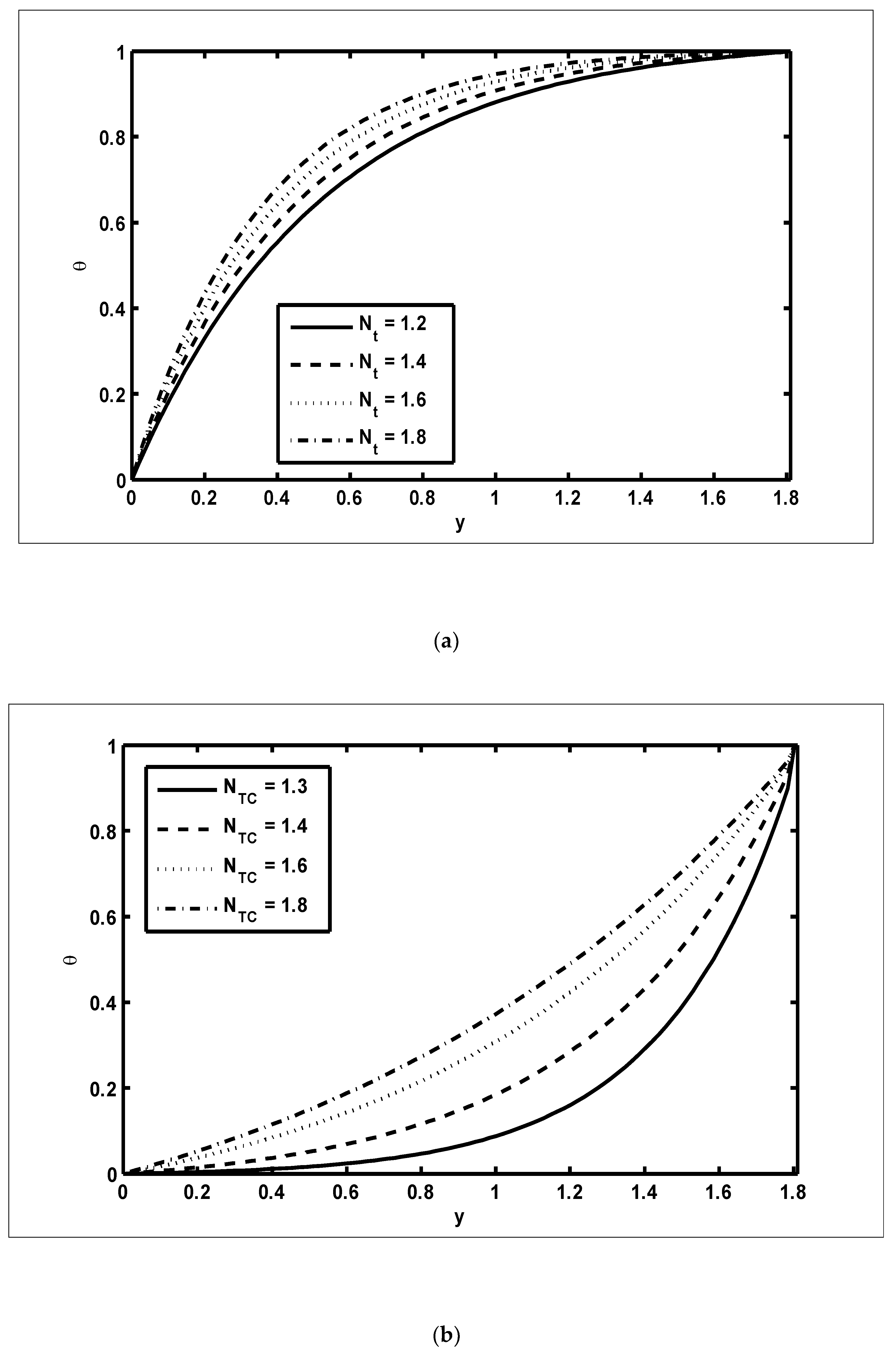
- The temperature profiles increased with increasing values of the thermophoresis parameter and Dufour parameter, while the concentration profiles decreased with increasing values of the Brownian motion parameter and Soret parameter;
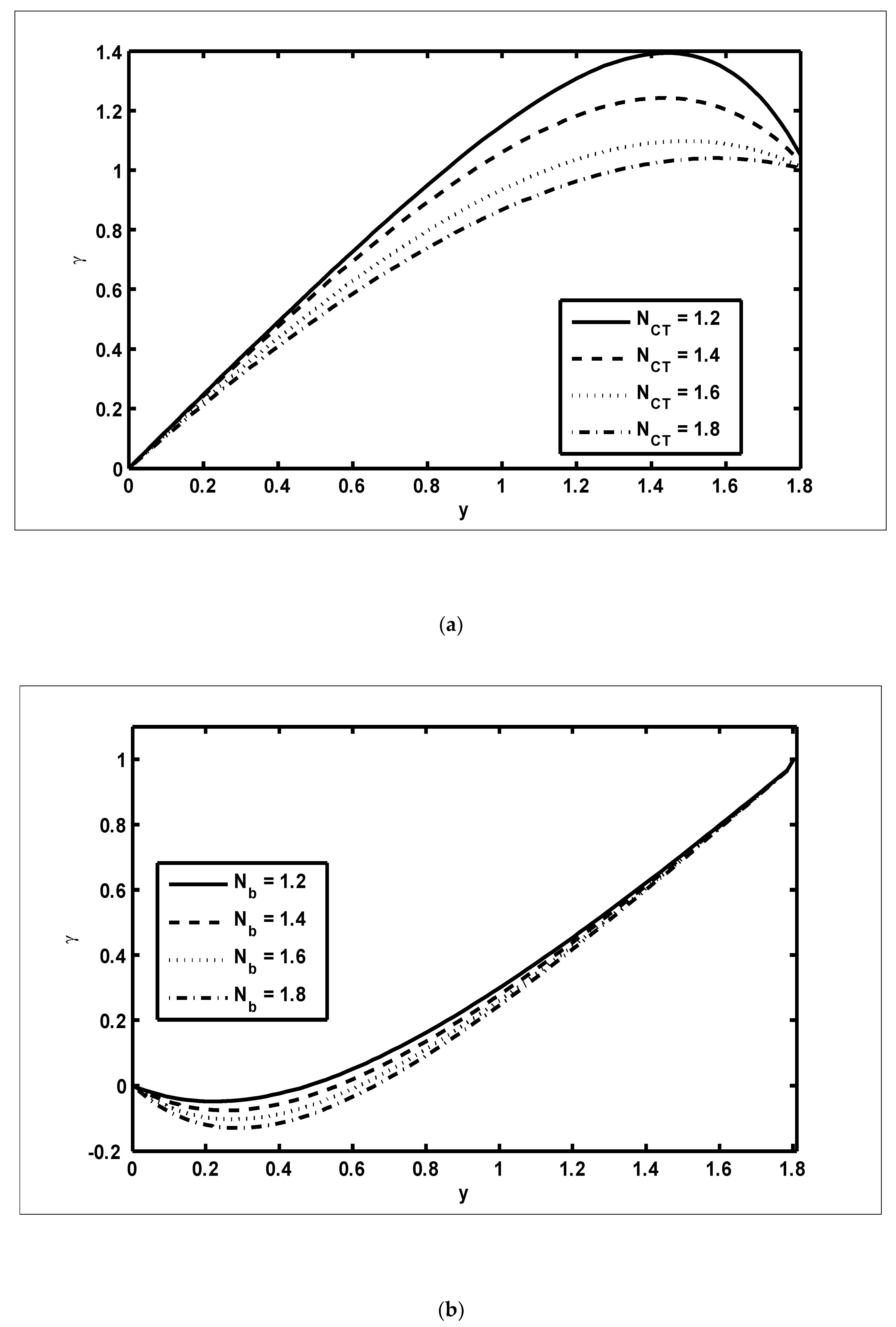
- The nanoparticle fractions decreased with increasing values of the Brownian motion parameter, whereas they increased with increasing values of the thermophoresis parameter;
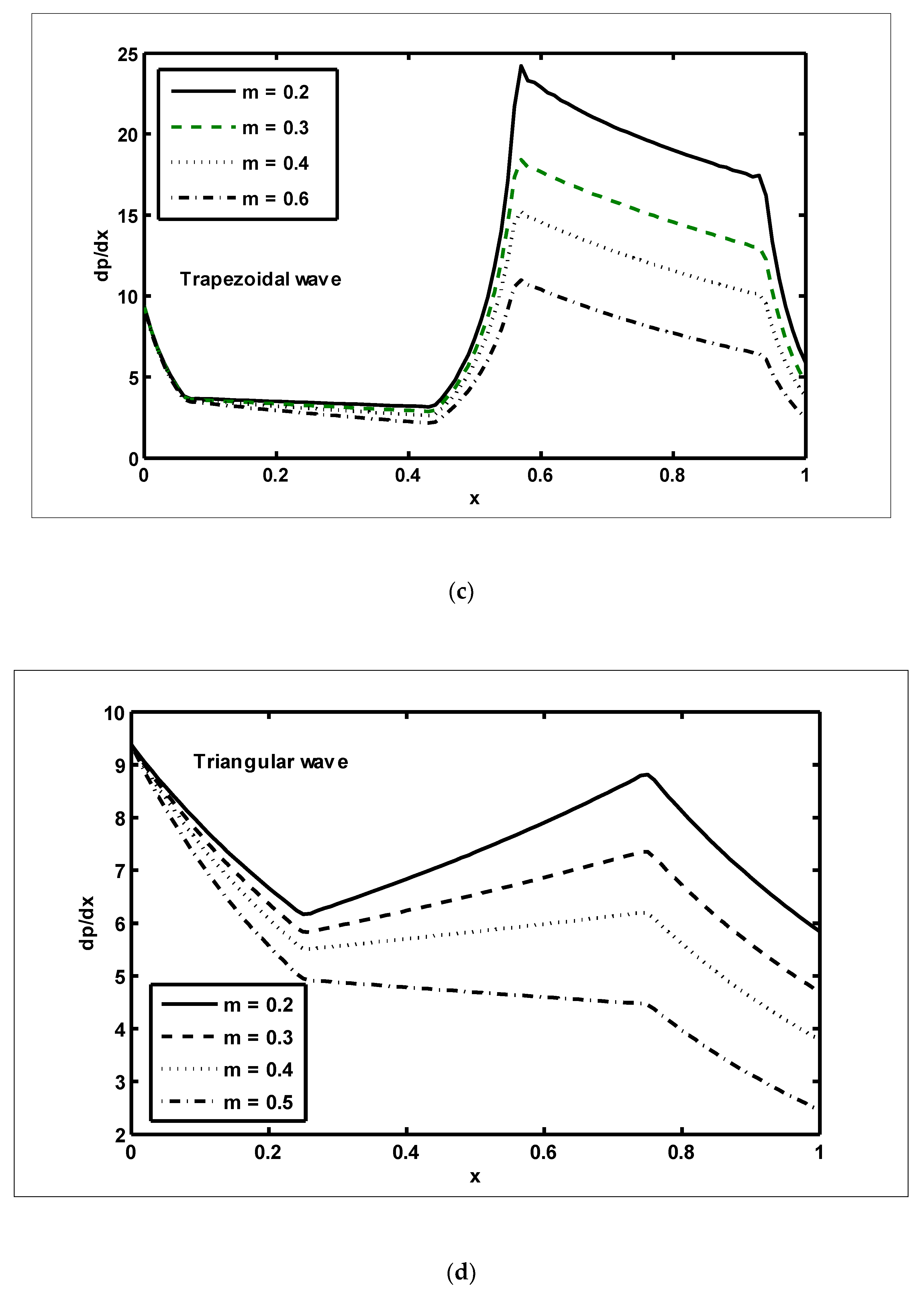
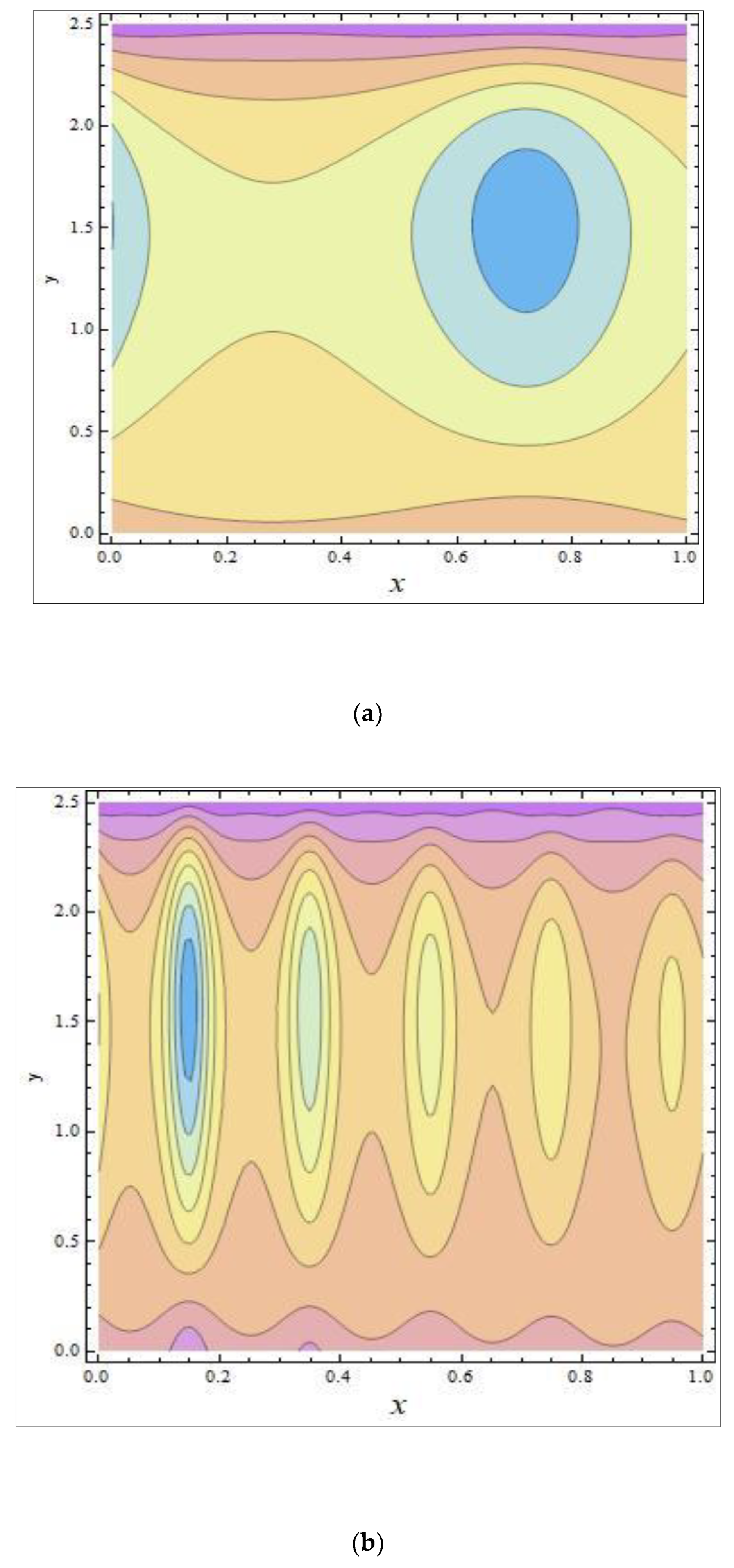
- The number and size of trapped masses increased with increasing values of the Brownian motion parameter, while they decreased with increasing values of the non-uniform parameter.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Latham, T.W. Fluid Motion in a Peristaltic Pump. Master’s Thesis, MIT, Cambridge, UK, 1966. [Google Scholar]
- Shapiro, A.H.; Jaffrin, M.Y.; Weinberg, S.L. Peristaltic pumping with long wavelengths at low reynolds number. J. Fluid Mech. 1969, 37, 799–825. [Google Scholar] [CrossRef]
- Haider, S.; Ijaz, N.; Zeeshan, A.; Li, Y.-Z. Magneto-hydrodynamics of a solid-liquid two-phase fluid in rotating channel due to peristaltic wavy movement. Int. J. Numer. Methods Heat Fluid Flow 2019, 30, 2501–2516. [Google Scholar] [CrossRef]
- Riaz, A.; Ellahi, R.; Bhatti, M.M.; Marin, M. Study of heat and mass transfer in the Eyring-Powell model of fluid propagating peristaltically through a rectangular complaint channel. Heat Transf. Res. 2019, 16, 1539–1560. [Google Scholar] [CrossRef]
- Saleem, N.; Hayat, T.; Alsaedi, A. Effects of induced magnetic field and slip condition on peristaltic transport with heat and mass transfer in a non-uniform channel. Int. J. Phys. Sci. 2012, 72, 191–204. [Google Scholar]
- Bhatti, M.M.; Zeeshan, A.; Tripathi, D.; Ellahi, R. Thermally developed peristaltic propulsion of magnetic solid particles in Biorheological fluids. Indian J. Phys. 2018, 92, 423–430. [Google Scholar] [CrossRef]
- Safia Akram, K.S.; Mekheimer, Y.; Elmaboud, A. Particulate suspension slip flow induced by peristaltic waves in a rectangular duct: Effect of lateral walls. Alex. Eng. J. 2018, 57, 407–414. [Google Scholar] [CrossRef]
- Akram, S.; Nadeem, S. Influence of induced magnetic field and heat transfer on the peristaltic motion of a Jeffrey fluid in an asymmetric channel: Closed form solutions. J. Magn. Magn. Mater. 2013, 328, 11–20. [Google Scholar] [CrossRef]
- Kothandapani, M.; Pushparaj, V.; Prakash, J. Effect of magnetic field on peristaltic flow of a fourth grade fluid in a tapered asymmetric channel. J. King Saud Univ. Eng. Sci. 2018, 30, 86–95. [Google Scholar] [CrossRef]
- Ijaz, N.; Riaz, A.; Zeeshan, A.; Ellahi, R.; Sait, S.M. Buoyancy Driven Flow with Gas-Liquid Coatings of Peristaltic Bubbly Flow in Elastic Walls. Coatings 2020, 10, 115. [Google Scholar] [CrossRef]
- Choi, S.U.S. Enhancing thermal conductivity of fluid with nanoparticles developments and Applications of non-Newtonian Flow. ASME J. Heat Transf. 1995, 66, 99–105. [Google Scholar]
- Masuda, H.; Ebata, A.; Teramae, K.; Hishinuma, N. Alteration of thermal conductivity and viscosity of liquid by dispersing ultra-fine particles. Netsu Bussei 1993, 7, 227–233. [Google Scholar] [CrossRef]
- Buongiorno, J.; Hu, W. Nanofluid coolants for advanced nuclear power plants. In Proceedings of the ICAPP ’05, Seoul, Korea, 15–19 May 2005; pp. 15–19. [Google Scholar]
- Das, S.K.; Choi, S.U.S.; Patel, H.E. Heat transfer in nanofluids—A review. Heat Transf. Eng. 2006, 27, 3–19. [Google Scholar] [CrossRef]
- Das, S.K.; Choi, S.U.; Yu, W.; Pradeep, T. Nanofluid Science and Technology; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2007. [Google Scholar]
- Wang, X.-Q.; Mujumdar, A.S. Heat transfer characteristics of nanofluids: A review. Int. J. Therm. Sci. 2007, 46, 1–19. [Google Scholar] [CrossRef]
- Buongiorno, J. Convective transport in nanofluids. J. Heat Transf. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Akbar, N.S.; Nadeem, S. Endoscopic effects on peristaltic flow of a nanofluid. Commun. Theor. Phys. 2011, 56, 761–768. [Google Scholar] [CrossRef]
- Ellahi, R.; Zeeshan, A.; Hussain, F.; Asadollahi, A. Peristaltic blood flow of couple stress fluid suspended with nanoparticles under the influence of chemical reaction and activation energy. Symmetry 2019, 11, 276. [Google Scholar] [CrossRef]
- Riaz, A.; Khan, S.U.-D.; Zeeshan, A.; Khan, S.U.; Hassan, M.; Muhammad, T. Thermal analysis of peristaltic flow of nanosized particles within a curved channel with second-order partial slip and porous medium. J. Therm. Anal. 2021, 143, 1997–2009. [Google Scholar] [CrossRef]
- Nadeem, S.; Riaz, A.; Ellahi, R.; Akbar, N.S. Mathematical model for the peristaltic flow of Jeffrey fluid with nanoparticles phenomenon through a rectangular duct. Appl. Nanosci. 2013, 4, 613–624. [Google Scholar] [CrossRef]
- Mekheimer, K.; Hasona, W.; Abo-Elkhair, R.; Zaher, A. Peristaltic blood flow with gold nanoparticles as a third grade nanofluid in catheter: Application of cancer therapy. Phys. Lett. A 2018, 382, 85–93. [Google Scholar] [CrossRef]
- Ellahi, R.; Raza, M.; Akbar, N.S. Study of peristaltic flow of nanofluid with entropy generation in a porous medium. J. Porous Media 2017, 20, 461–478. [Google Scholar] [CrossRef]
- Hussain, F.; Ellahi, R.; Zeeshan, A.; Vafai, K. Modelling study on heated couple stress fluid peristaltically conveying gold nanoparticle through coaxial tube: A remedy for gland tumor and arthritis. J. Mol. Liq. 2018, 268, 149–155. [Google Scholar] [CrossRef]
- Ramesh, K.; Prakash, J. Thermal analysis for heat transfer enhancement in electroosmosis-modulated peristaltic transport of Sutterby nanofluids in a microfluidic vessel. J. Therm. Anal. Calorim. 2019, 138, 1311–1326. [Google Scholar] [CrossRef]
- Landeghem, F.; Maier-Hauff, K.; Jordan, A. Post mortem studies in glioblastoma patients treated with thermotherapy using magnetic nanoparticles. Biomaterials 2009, 30, 52–57. [Google Scholar] [CrossRef] [PubMed]
- Foster, K. Thermal and nonthermal mechanisms of interaction of radio-frequency energy with biological systems. IEEE Trans. Plasma Sci. 2000, 28, 15–23. [Google Scholar] [CrossRef]
- Zhu, L.; Xu, L.; Chencinski, N. Quantification of the 3-D electromagnetic power absorption rate in tissue during transurethral prostatic microwave thermotherapy using heat transfer model. IEEE Trans. Biomed. Eng. 1998, 45, 1163–1172. [Google Scholar]
- Akram, S. Nanofluid effects on peristaltic transport of a fourth grade fluid in the occurrence of inclined magnetic field. Sci. Iran. 2016, 23, 1502–1516. [Google Scholar] [CrossRef]
- Kothandapani, M.; Prakash, J. Effects of thermal radiation parameter and magnetic field on the peristaltic motion of Williamson nanofluids in a tapered asymmetric channel. Int. J. Heat Mass Transf. 2015, 81, 234–245. [Google Scholar] [CrossRef]
- Habib, D.; Salamat, N.; Ahsan, M.; Abdal, S.; Siddique, I.; Ali, B. Significance of bioconvection and mass transpiration for MHD micropolar Maxwell nanofluid flow over an extending sheet*. Waves Random Complex Media 2022, 1–15. [Google Scholar] [CrossRef]
- Prakash, J.; Siva, E.P.; Tripathi, D.; Beg, O.A. Thermal slip and radiative heat transfer effects on electroosmotic magneto nanoliquid peristaltic propulsion through a microchannel. Heat Transf. Asian Res. 2019, 48, 2882–2908. [Google Scholar] [CrossRef]
- Awan, A.U.; Ahammad, N.A.; Majeed, S.; Gamaoun, F.; Ali, B. Significance of hybrid nanoparticles, Lorentz and Coriolis forces on the dynamics of water based flow. Int. Commun. Heat Mass Transf. 2022, 135, 106084. [Google Scholar] [CrossRef]
- Wang, F.; Asjad, M.I.; Rehman, S.U.; Ali, B.; Hussain, S.; Gia, T.N.; Muhammad, T.; Williamson, M.H.D. Nanofluid Flow over a Slender Elastic Sheet of Irregular Thickness in the Presence of Bioconvection. Nanomaterials 2021, 11, 2297. [Google Scholar] [CrossRef] [PubMed]
- Khan, S.A.; Eze, C.; Lau, K.T.; Ali, B.; Ahmad, S.; Ni, S.; Zhao, J. Study on the novel suppression of heat transfer deterioration of supercritical water flowing in vertical tube through the suspension of alumina nanoparticles. Int. Commun. Heat Mass Transf. 2022, 132, 105893. [Google Scholar] [CrossRef]
- Singh, O.P.; Srinivasan, J. Effect of Rayleigh numbers on the evolution of double-diffusive salt fingers. Phys. Fluids 2014, 26, 062104. [Google Scholar] [CrossRef]
- Bég, O.A.; Tripathi, D. Mathematica simulation of peristaltic pumping with double-diffusive convection in nanofluids a bio-nanoengineering model, Proceedings of the Institution of Mechanical Engineers, Part N. J. Nanoeng. Nanosyst. 2012, 225, 99–114. [Google Scholar]
- Alolaiyan, H.; Riaz, A.; Razaq, A.; Saleem, N.; Zeeshan, A.; Bhatti, M.M. Effects of double diffusion convection on Third grade nanofluid through a curved compliant peristaltic channel. Coatings 2020, 10, 154. [Google Scholar] [CrossRef]
- Akram, S.; Zafar, M.; Nadeem, S. Peristaltic transport of a Jeffrey fluid with double-diffusive convection in nanofluids in the presence of inclined magnetic field. Int. J. Geom. Methods Mod. Phys. 2018, 15, 1850181. [Google Scholar] [CrossRef]
- Kuznetsov, A.V.; Nield, D.A. Double-diffusive natural convective boundary-layer flow of a nanofluid past a vertical plate. Int. J. Therm. Sci. 2011, 50, 712–717. [Google Scholar] [CrossRef]
- Sharma, A.; Tripathi, D.; Sharma, R.K.; Tiwari, A.K. Analysis of double diffusive convection in electroosmosis regulated peristaltic transport of nanofluids. Physica A 2019, 535, 122148. [Google Scholar] [CrossRef]
- Nield, D.A.; Kuznetsov, A.V. The onset of double diffusive convection in a nanofluid layer. Int. J. Heat Fluid Flow 2011, 32, 771–776. [Google Scholar] [CrossRef]
- Akram, S.; Razia, A.; Afzal, F. Effects of velocity second slip model and induced magnetic field on peristaltic transport of non-Newtonian fluid in the presence of double-diffusivity convection in nanofluids. Arch. Appl. Mech. 2020, 90, 1583–1603. [Google Scholar] [CrossRef]
- Asha, S.K.; Sunitha, G. Thermal radiation and hall effects on peristaltic blood flow with double diffusion in the presence of nanoparticles. Case Stud. Therm. Eng. 2020, 17, 100560. [Google Scholar] [CrossRef]
- Narayana, M.; Sibanda, P. On the solution of double-diffusive convective flow due to a cone by a linearization method. J. Appl. Math. 2012, 2012, 587357. [Google Scholar] [CrossRef] [Green Version]





| Velocity Profile (u) | |||
|---|---|---|---|
| Present Work | Viscous Fluid | Bég and Tripathi [37] | |
| 0 | 2.7954 | 2.89268 | 2.95852 |
| 2.76701 | 2.85902 | 2.92114 | |
| 2.68047 | 2.75708 | 2.80836 | |
| 2.53245 | 2.58482 | 2.61918 | |
| 2.31785 | 2.33935 | 2.35242 | |
| 2.0296 | 2.01684 | 2.00664 | |
| 1.65823 | 1.61226 | 1.58005 | |
| 1.19132 | 1.1191 | 1.07026 | |
| 0.612152 | 0.528699 | 0.473961 | |
| 0.103582 | 0.171164 | 0.213634 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, Y.; Akram, S.; Razia, A.; Hussain, A.; Alsulaimani, H.A. Effects of Double Diffusive Convection and Inclined Magnetic Field on the Peristaltic Flow of Fourth Grade Nanofluids in a Non-Uniform Channel. Nanomaterials 2022, 12, 3037. https://doi.org/10.3390/nano12173037
Khan Y, Akram S, Razia A, Hussain A, Alsulaimani HA. Effects of Double Diffusive Convection and Inclined Magnetic Field on the Peristaltic Flow of Fourth Grade Nanofluids in a Non-Uniform Channel. Nanomaterials. 2022; 12(17):3037. https://doi.org/10.3390/nano12173037
Chicago/Turabian StyleKhan, Yasir, Safia Akram, Alia Razia, Anwar Hussain, and H. A. Alsulaimani. 2022. "Effects of Double Diffusive Convection and Inclined Magnetic Field on the Peristaltic Flow of Fourth Grade Nanofluids in a Non-Uniform Channel" Nanomaterials 12, no. 17: 3037. https://doi.org/10.3390/nano12173037





